1 Раздел № 2 Математические модели реализации задач

1 Раздел № 2 Математические модели реализации задач оптимального выбора Тема № 1 Формализация задачи оптимизации

2 Формализация задачи оптимизации Классификация экономических задач с точки зрения моделирования: Хорошо структурированные – все основные зависимости могут быть выражены количественно. Неструктурированные — все основные зависимости могут быть описаны лишь качественно. Слабоструктурированные – допускают как количественное, так и качественное описание зависимостей.

3 Формализация задачи оптимизации Хорошо структурируемые задачи принято называть программируемыми (program – план, программа). Для решения этих задач используют методы математического программирования Математическое программирование – математическая дисциплина, изучающаяся теорию и методы решения задач о нахождении экстремумов функций на множествах векторного пространства, заданных с помощью линейных и нелинейных ограничений.

4 Формализация задачи оптимизации Математические модели, позволяющие определить из области допустимых решений наилучшее решение по заранее заданному критерию, принято называть оптимизационными моделями, а задачи, решаемые с их помощью, — задачами оптимального выбора.

5 Формализация задачи оптимизации Характеристика задач оптимального выбора: Наличие цели, достижение которой является решением задачи. Наличие критерия для сопоставления качества альтернатив Наличие альтернативных средств достижения цели Наличие способов оценки затрат ресурсов, необходимых для каждой альтернативы Наличие способа отображения связей между целями, альтернативами и затратами

6 Формализация задачи оптимизации Критерий оптимальности — показатель, используемый для сравнительной оценки вариантов допустимых решений (альтернатив). Целевая функция – формализованный критерий оптимальности, записанный в математическом виде.

7 Формализация задачи оптимизации Этапы формализации задач оптимального выбора: 1. Формирование системы неизвестных. Выявление элементов, описывающих структуру моделируемой системы, и описание их в виде переменных. 2. Формирование системы ограничений. Описание в формальном виде условий (ресурсных, организационно-экономических, технологических и т. д. ), которые должны быть соблюдены при реализации задачи. 3. Формулирование критерия оптимальности и запись его в виде целевой функции задачи математического программирования.

8 Формализация задачи оптимизации Общий вид задачи математического программирования: Z = F(X) ═> min/max φ i (X) ≤ 0, I = 1, 2, …, k, h j (X) = 0, j = k+1, k+2, …, m. где: Х=(х 1 , х 2 , …, х n ) – система неизвестных; φi(X), hj(X) – система ограничений; Z – критерий оптимальности; F(X) – целевая функция

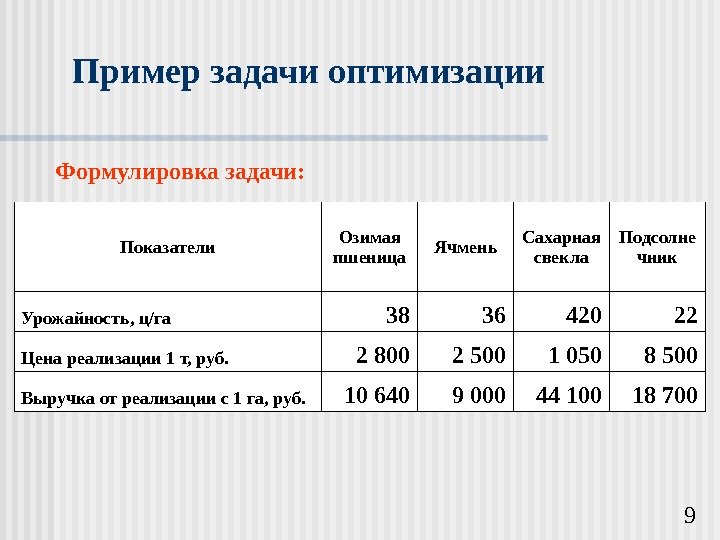
9 Пример задачи оптимизации Показатели Озимая пшеница Ячмень Сахарная свекла Подсолне чник Урожайность, ц/га 38 36 420 22 Цена реализации 1 т, руб. 2 800 2 500 1 050 8 500 Выручка от реализации с 1 га, руб. 10 640 9 000 44 100 18 700 Формулировка задачи:

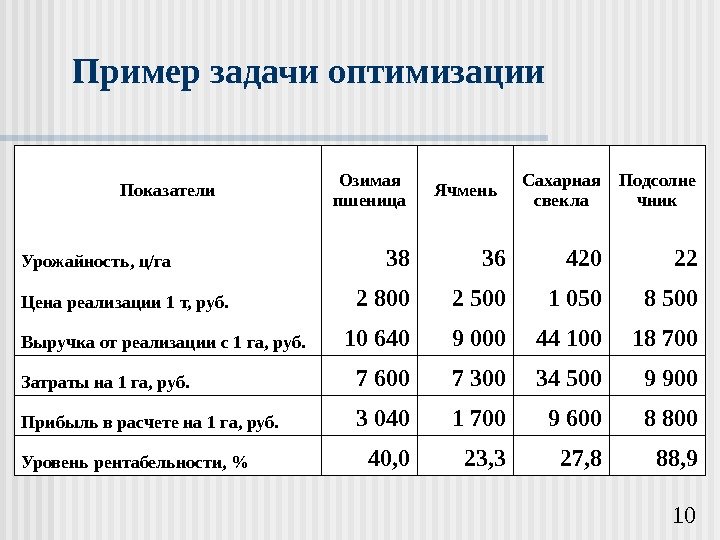
10 Пример задачи оптимизации Показатели Озимая пшеница Ячмень Сахарная свекла Подсолне чник Урожайность, ц/га 38 36 420 22 Цена реализации 1 т, руб. 2 800 2 500 1 050 8 500 Выручка от реализации с 1 га, руб. 10 640 9 000 44 100 18 700 Затраты на 1 га, руб. 7 600 7 300 34 500 9 900 Прибыль в расчете на 1 га, руб. 3 040 1 700 9 600 8 800 Уровень рентабельности, % 40, 0 23, 3 27, 8 88,

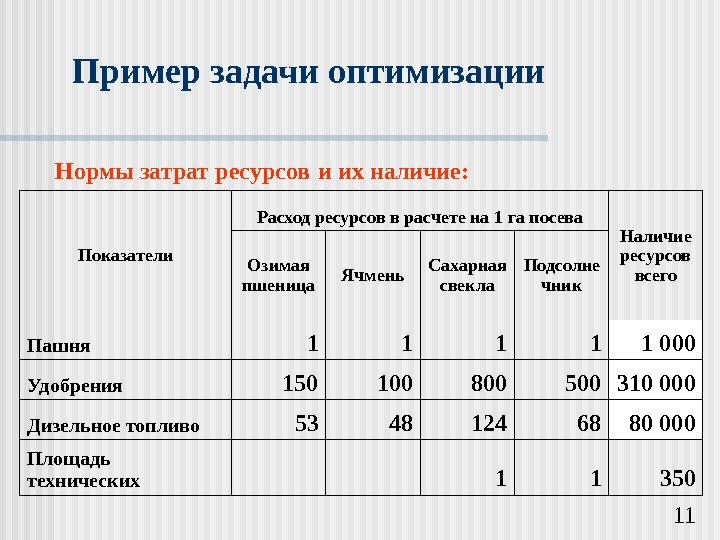
11 Пример задачи оптимизации Нормы затрат ресурсов и их наличие: Показатели Расход ресурсов в расчете на 1 га посева Наличие ресурсов всего. Озимая пшеница Ячмень Сахарная свекла Подсолне чник Пашня 1 1 1 000 Удобрения 150 100 800 500 310 000 Дизельное топливо 53 48 124 68 80 000 Площадь технических

12 Формализация задачи оптимизации Постановка задачи: Исходя из наличия ресурсов и агротехнических требований, найти такое сочетание сельскохозяйственных культур, которое обеспечивало бы получение максимальной суммы прибыли.

13 Формализация задачи оптимизации Система неизвестных: Х 1 – площадь посева озимой пшеницы; Х 2 – площадь посева ячменя; Х 3 – площадь посева сахарной свеклы; Х 4 – площадь посева подсолнечника.

14 Формализация задачи оптимизации Система ограничений: Ограничения по использованию ресурсов: Х j — площадь посева j-той сельскохозяйственной культуры; а ij — затраты ресурсов i-го вида на 1 га посева j-й сельскохоз. культуры; b i — объем имеющихся ресурсов i-го вида. Условия неотрицательности переменных: Х j ≥ 0 Jj ijijbxa

15 Формализация задачи оптимизации Система ограничений: Ограничения по использованию: Пашни: 1 х1 + 1 х2 + 1 х3 + 1 х4 ≤ 1 000 Удобрений: 150 х1 + 100 х2 + 800 х3 + 500 х4 ≤ 310 000 Диз. топлива: 53 х1 + 48 х2 + 124 х3 + 68 х4 ≤ 80 000 Пашни под технические: 1 х3 + 1 х4 ≤

16 Формализация задачи оптимизации Критерий оптимальности: максимизация суммы прибыли Целевая функция: где: с j – выход прибыли с 1 га посева j -ой сельскохоз. культуры Z max = 3040 х1 + 1700 х2 + 9600 х3 + 8800 х4 Jj jj xc. Z max

17 Формализация задачи оптимизации 1 х1 + 1 х2 + 1 х3 + 1 х4 ≤ 1 000 150 х1 + 100 х2 + 800 х3 + 500 х4 ≤ 310 000 53 х1 + 48 х2 + 124 х3 + 68 х4 ≤ 80 000 1 х3 + 1 х4 ≤ 325 3040 х1 + 1700 х2 + 9600 х3 + 8800 х4 → max

18 Формализация задачи оптимизации Результаты решения: Прибыль 5 156 000 руб. Х 1 – площадь посева озимой пшеницы 650 га Х 2 – площадь посева ячменя 0 га Х 3 – площадь посева сахарной свеклы 125 га Х 4 – площадь посева подсолнечника 225 га Недоиспользование дизтоплива 14 750 кг