da0309c927e276294db21d90365a0755.ppt
- Количество слайдов: 51
 1
1
 PROGRAM GALACTICA FOR THE SOLUTION OF THE SPACE DYNAMICS TASKS : Dynamics and evolution of Solar system bodies; Passive motion of spacecrafts; The evolution of the assembly of bodies, including galaxies. J. J. Smulsky Institute of Earth's Cryosphere SB RAS, Tyumen, E-mail: Jsmulsky@mail. ru, webpage: http: //www. smul 1. newmail. ru/. Year of Russia in Spain Exhibition "scientific, technical and innovative achievements of Russia" 12 -15 May 2011 Madrid 2
PROGRAM GALACTICA FOR THE SOLUTION OF THE SPACE DYNAMICS TASKS : Dynamics and evolution of Solar system bodies; Passive motion of spacecrafts; The evolution of the assembly of bodies, including galaxies. J. J. Smulsky Institute of Earth's Cryosphere SB RAS, Tyumen, E-mail: Jsmulsky@mail. ru, webpage: http: //www. smul 1. newmail. ru/. Year of Russia in Spain Exhibition "scientific, technical and innovative achievements of Russia" 12 -15 May 2011 Madrid 2
 CONTENTS 1. Differential equations of the celestial bodies motion and the method of their solution. 2. Illustration of the motion of bodies at the integration of differential equations by Galactica. 3. The evolution of the orbits for 100 million years. 4. Precession of the orbits. 5. Compound model of the Earth’s rotation. 6. Compound model of the Sun’s rotation. 7. The motion of the asteroid Apophis. 8. Optimizing passive orbit using gravimanevr 9. Multilayer circular structures 10. References 11. Acknowledgments 12. Some information 3
CONTENTS 1. Differential equations of the celestial bodies motion and the method of their solution. 2. Illustration of the motion of bodies at the integration of differential equations by Galactica. 3. The evolution of the orbits for 100 million years. 4. Precession of the orbits. 5. Compound model of the Earth’s rotation. 6. Compound model of the Sun’s rotation. 7. The motion of the asteroid Apophis. 8. Optimizing passive orbit using gravimanevr 9. Multilayer circular structures 10. References 11. Acknowledgments 12. Some information 3
 View of planshet at the exhibition 4
View of planshet at the exhibition 4
 1. Differential equations of the celestial bodies motion and the method of their solution At the interaction of bodies under the Newton's law of gravitation their motion are described by differential equations [1] : (1) where - the radius-vector of a body with mass mi relative to the center of mass of bodies; - the radius vector from the body with mass mk to the body with a mass mi; G – the gravitational constant.
1. Differential equations of the celestial bodies motion and the method of their solution At the interaction of bodies under the Newton's law of gravitation their motion are described by differential equations [1] : (1) where - the radius-vector of a body with mass mi relative to the center of mass of bodies; - the radius vector from the body with mass mk to the body with a mass mi; G – the gravitational constant.
 The equations for the Solar system
The equations for the Solar system
 2. Illustration of the motion of bodies at the integration of differential equations by Galactica 7
2. Illustration of the motion of bodies at the integration of differential equations by Galactica 7
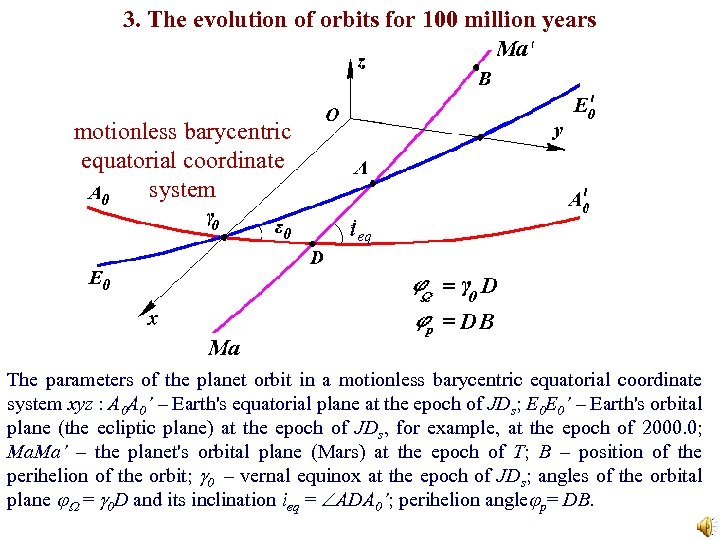 3. The evolution of orbits for 100 million years motionless barycentric equatorial coordinate system ieq The parameters of the planet orbit in a motionless barycentric equatorial coordinate system xyz : A 0 A 0’ – Earth's equatorial plane at the epoch of JDs; E 0 E 0’ – Earth's orbital plane (the ecliptic plane) at the epoch of JDs, for example, at the epoch of 2000. 0; Ma. Ma’ – the planet's orbital plane (Mars) at the epoch of Т; B – position of the perihelion of the orbit; 0 – vernal equinox at the epoch of JDs; angles of the orbital plane = 0 D and its inclination ieq = ADA 0’; perihelion angle р= DB.
3. The evolution of orbits for 100 million years motionless barycentric equatorial coordinate system ieq The parameters of the planet orbit in a motionless barycentric equatorial coordinate system xyz : A 0 A 0’ – Earth's equatorial plane at the epoch of JDs; E 0 E 0’ – Earth's orbital plane (the ecliptic plane) at the epoch of JDs, for example, at the epoch of 2000. 0; Ma. Ma’ – the planet's orbital plane (Mars) at the epoch of Т; B – position of the perihelion of the orbit; 0 – vernal equinox at the epoch of JDs; angles of the orbital plane = 0 D and its inclination ieq = ADA 0’; perihelion angle р= DB.
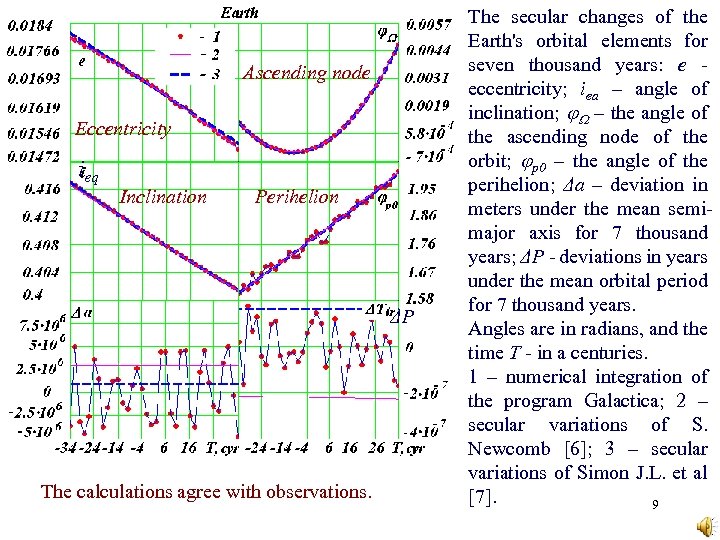 Ascending node Eccentricity ieq Inclination Perihelion ΔP The calculations agree with observations. The secular changes of the Earth's orbital elements for seven thousand years: e - eccentricity; iea – angle of inclination; – the angle of the ascending node of the orbit; р0 – the angle of the perihelion; Δa – deviation in meters under the mean semimajor axis for 7 thousand years; ΔP - deviations in years under the mean orbital period for 7 thousand years. Angles are in radians, and the time T - in a centuries. 1 – numerical integration of the program Galactica; 2 – secular variations of S. Newcomb [6]; 3 – secular variations of Simon J. L. et al [7]. 9
Ascending node Eccentricity ieq Inclination Perihelion ΔP The calculations agree with observations. The secular changes of the Earth's orbital elements for seven thousand years: e - eccentricity; iea – angle of inclination; – the angle of the ascending node of the orbit; р0 – the angle of the perihelion; Δa – deviation in meters under the mean semimajor axis for 7 thousand years; ΔP - deviations in years under the mean orbital period for 7 thousand years. Angles are in radians, and the time T - in a centuries. 1 – numerical integration of the program Galactica; 2 – secular variations of S. Newcomb [6]; 3 – secular variations of Simon J. L. et al [7]. 9
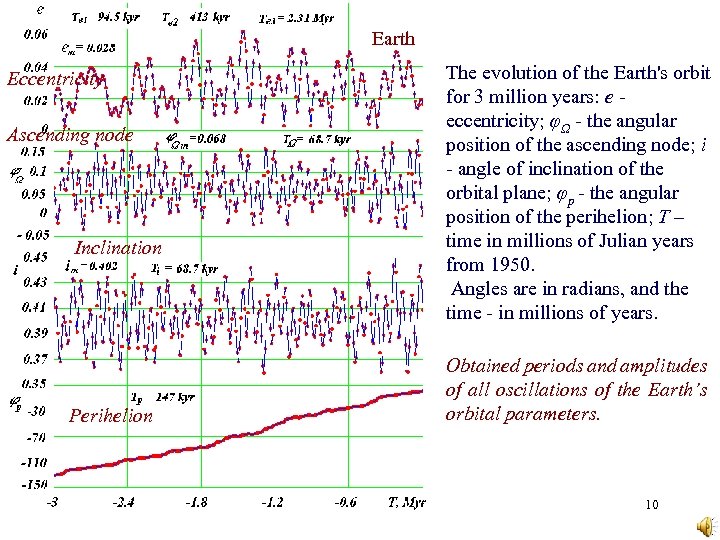 Earth Eccentricity Ascending node Inclination Perihelion The evolution of the Earth's orbit for 3 million years: е - eccentricity; φΩ - the angular position of the ascending node; i - angle of inclination of the orbital plane; φр - the angular position of the perihelion; Т – time in millions of Julian years from 1950. Angles are in radians, and the time - in millions of years. Obtained periods and amplitudes of all oscillations of the Earth’s orbital parameters. 10
Earth Eccentricity Ascending node Inclination Perihelion The evolution of the Earth's orbit for 3 million years: е - eccentricity; φΩ - the angular position of the ascending node; i - angle of inclination of the orbital plane; φр - the angular position of the perihelion; Т – time in millions of Julian years from 1950. Angles are in radians, and the time - in millions of years. Obtained periods and amplitudes of all oscillations of the Earth’s orbital parameters. 10
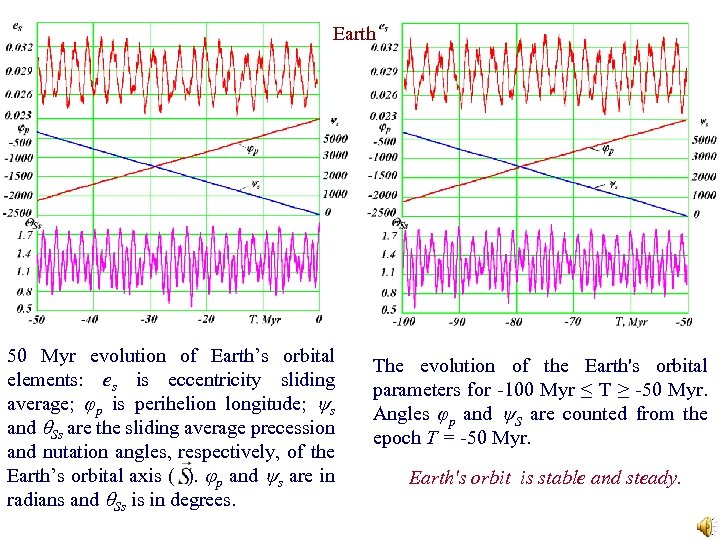 Earth 50 Myr evolution of Earth’s orbital elements: es is eccentricity sliding average; φp is perihelion longitude; ys and Ss are the sliding average precession and nutation angles, respectively, of the Earth’s orbital axis ( ). р and ys are in radians and Ss is in degrees. The evolution of the Earth's orbital parameters for -100 Myr ≤ T ≥ -50 Myr. Angles φр and y. S are counted from the epoch Т = -50 Myr. Earth's orbit is stable and steady.
Earth 50 Myr evolution of Earth’s orbital elements: es is eccentricity sliding average; φp is perihelion longitude; ys and Ss are the sliding average precession and nutation angles, respectively, of the Earth’s orbital axis ( ). р and ys are in radians and Ss is in degrees. The evolution of the Earth's orbital parameters for -100 Myr ≤ T ≥ -50 Myr. Angles φр and y. S are counted from the epoch Т = -50 Myr. Earth's orbit is stable and steady.
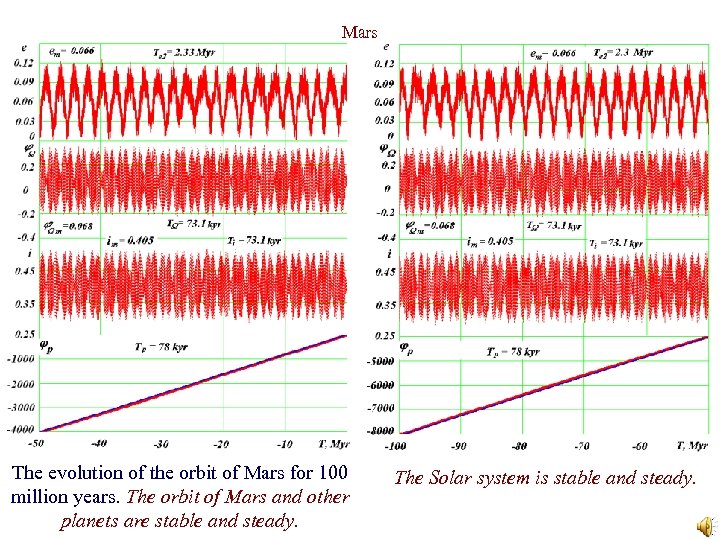 Mars The evolution of the orbit of Mars for 100 million years. The orbit of Mars and other planets are stable and steady. The Solar system is stable and steady.
Mars The evolution of the orbit of Mars for 100 million years. The orbit of Mars and other planets are stable and steady. The Solar system is stable and steady.

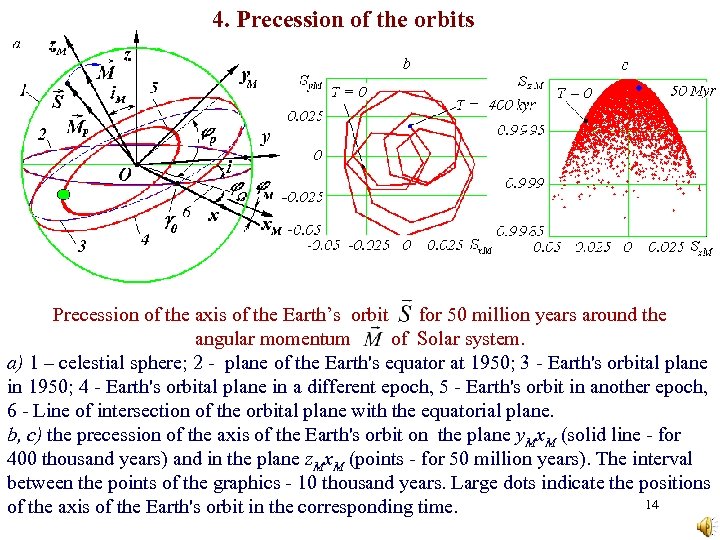 4. Precession of the orbits Precession of the axis of the Earth’s orbit for 50 million years around the angular momentum of Solar system. a) 1 – celestial sphere; 2 - plane of the Earth's equator at 1950; 3 - Earth's orbital plane in 1950; 4 - Earth's orbital plane in a different epoch, 5 - Earth's orbit in another epoch, 6 - Line of intersection of the orbital plane with the equatorial plane. b, c) the precession of the axis of the Earth's orbit on the plane y. Mx. M (solid line - for 400 thousand years) and in the plane z. Mx. M (points - for 50 million years). The interval between the points of the graphics - 10 thousand years. Large dots indicate the positions 14 of the axis of the Earth's orbit in the corresponding time.
4. Precession of the orbits Precession of the axis of the Earth’s orbit for 50 million years around the angular momentum of Solar system. a) 1 – celestial sphere; 2 - plane of the Earth's equator at 1950; 3 - Earth's orbital plane in 1950; 4 - Earth's orbital plane in a different epoch, 5 - Earth's orbit in another epoch, 6 - Line of intersection of the orbital plane with the equatorial plane. b, c) the precession of the axis of the Earth's orbit on the plane y. Mx. M (solid line - for 400 thousand years) and in the plane z. Mx. M (points - for 50 million years). The interval between the points of the graphics - 10 thousand years. Large dots indicate the positions 14 of the axis of the Earth's orbit in the corresponding time.
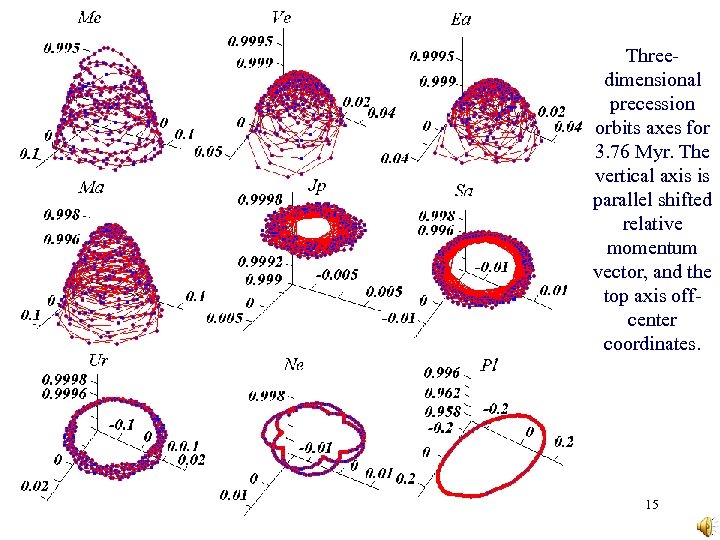 Threedimensional precession orbits axes for 3. 76 Myr. The vertical axis is parallel shifted relative momentum vector, and the top axis offcenter coordinates. 15
Threedimensional precession orbits axes for 3. 76 Myr. The vertical axis is parallel shifted relative momentum vector, and the top axis offcenter coordinates. 15
 1. Evolution of the orbits of the planets and the Moon is the result of four movements: 1) the precession of the orbit, 2) nutation oscillation of the orbit axis, 3) the oscillations of eccentricity of the orbit, 4) rotation of the orbit in its plane (the rotation of the perihelion). 2. The axis of the Moon's orbit precesses relative moving Earth's orbit axes, i. e. as the axis of the Earth’s rotation precesses. These results have allowed to investigate the evolution of Earth's axis by different way, as well as create a compound model of the rotating Earth. 16
1. Evolution of the orbits of the planets and the Moon is the result of four movements: 1) the precession of the orbit, 2) nutation oscillation of the orbit axis, 3) the oscillations of eccentricity of the orbit, 4) rotation of the orbit in its plane (the rotation of the perihelion). 2. The axis of the Moon's orbit precesses relative moving Earth's orbit axes, i. e. as the axis of the Earth’s rotation precesses. These results have allowed to investigate the evolution of Earth's axis by different way, as well as create a compound model of the rotating Earth. 16
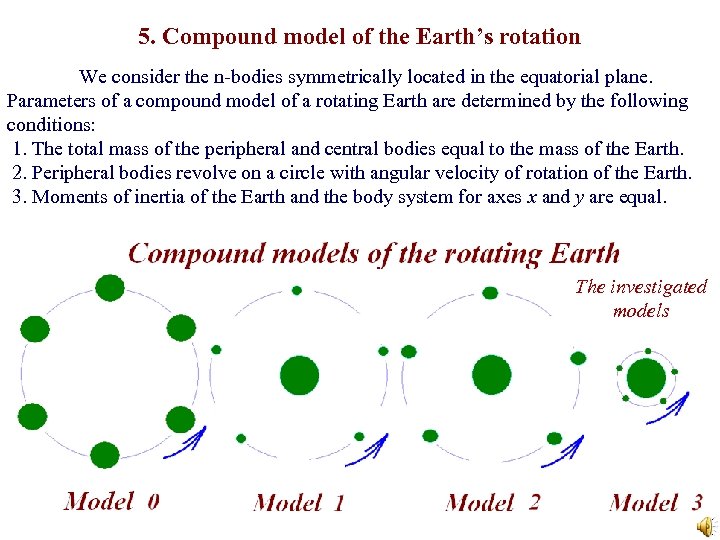 5. Compound model of the Earth’s rotation We consider the n-bodies symmetrically located in the equatorial plane. Parameters of a compound model of a rotating Earth are determined by the following conditions: 1. The total mass of the peripheral and central bodies equal to the mass of the Earth. 2. Peripheral bodies revolve on a circle with angular velocity of rotation of the Earth. 3. Moments of inertia of the Earth and the body system for axes x and y are equal. The investigated models 17
5. Compound model of the Earth’s rotation We consider the n-bodies symmetrically located in the equatorial plane. Parameters of a compound model of a rotating Earth are determined by the following conditions: 1. The total mass of the peripheral and central bodies equal to the mass of the Earth. 2. Peripheral bodies revolve on a circle with angular velocity of rotation of the Earth. 3. Moments of inertia of the Earth and the body system for axes x and y are equal. The investigated models 17
 Illustration of model of the Earth’s rotation and other bodies of Solar system 18
Illustration of model of the Earth’s rotation and other bodies of Solar system 18
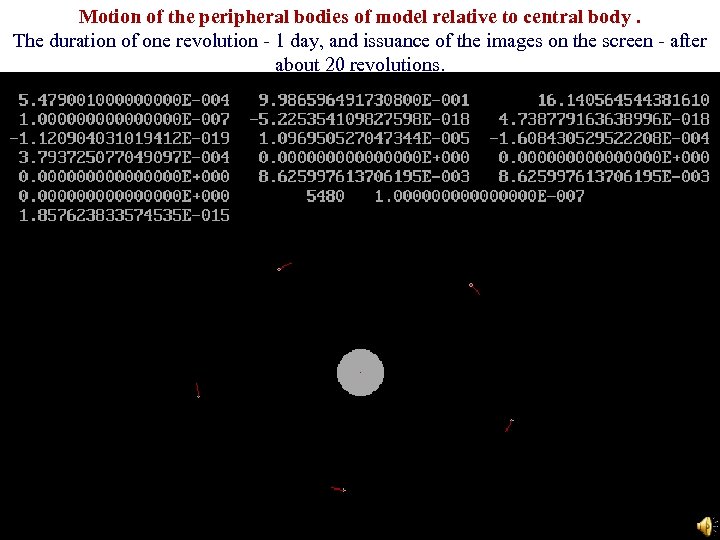 Motion of the peripheral bodies of model relative to central body. The duration of one revolution - 1 day, and issuance of the images on the screen - after about 20 revolutions. 19
Motion of the peripheral bodies of model relative to central body. The duration of one revolution - 1 day, and issuance of the images on the screen - after about 20 revolutions. 19
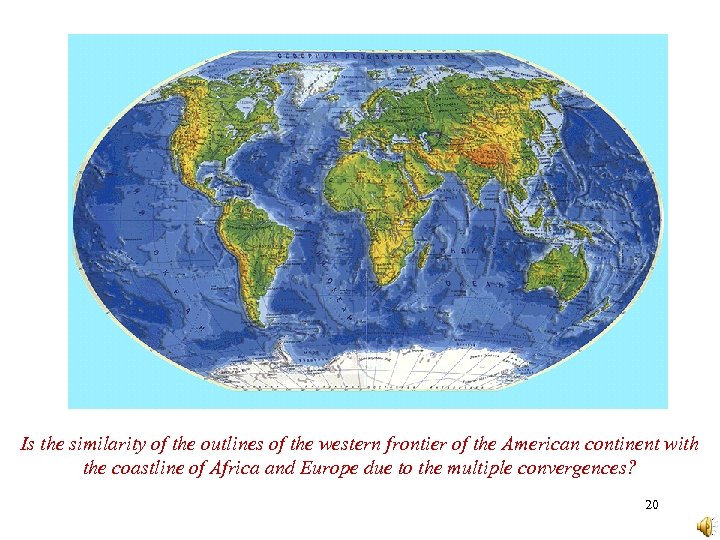 Is the similarity of the outlines of the western frontier of the American continent with the coastline of Africa and Europe due to the multiple convergences? 20
Is the similarity of the outlines of the western frontier of the American continent with the coastline of Africa and Europe due to the multiple convergences? 20
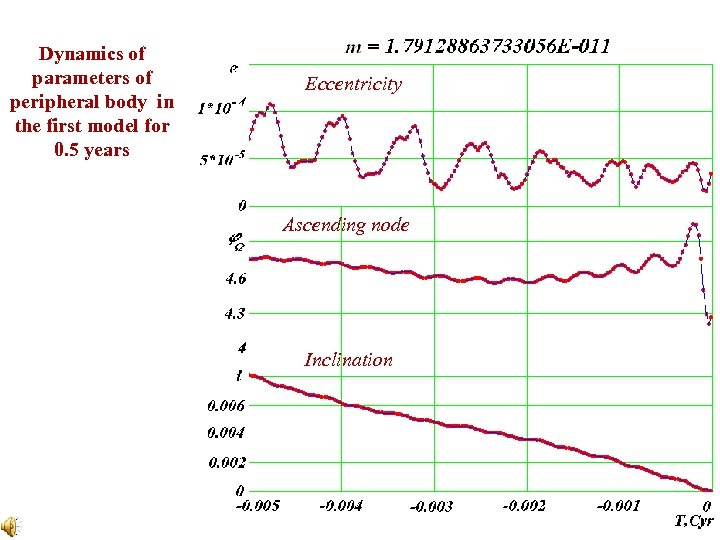 Dynamics of parameters of peripheral body in the first model for 0. 5 years Eccentricity Ascending node Inclination 21
Dynamics of parameters of peripheral body in the first model for 0. 5 years Eccentricity Ascending node Inclination 21
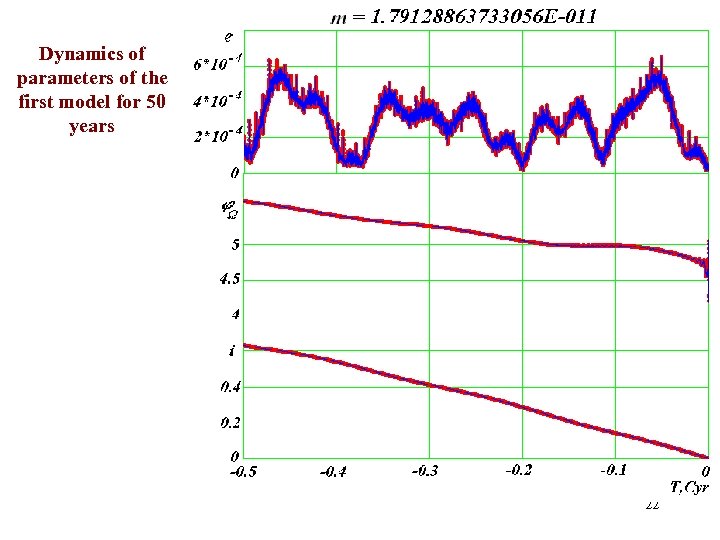 Dynamics of parameters of the first model for 50 years 22
Dynamics of parameters of the first model for 50 years 22
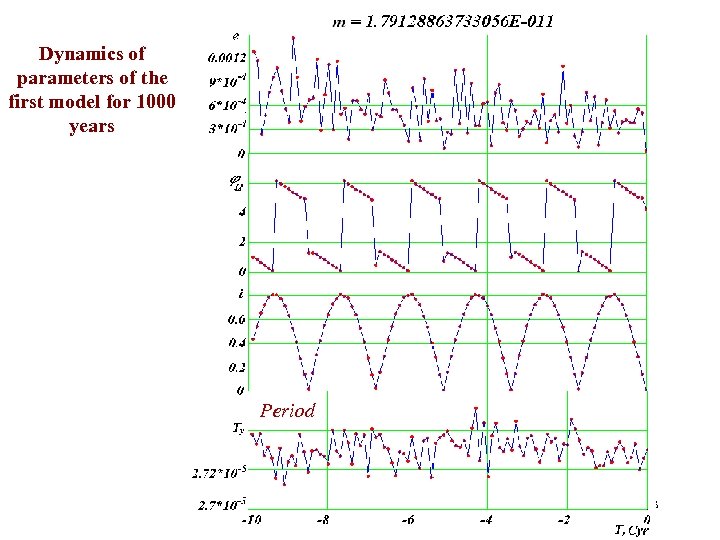 Dynamics of parameters of the first model for 1000 years Period 23
Dynamics of parameters of the first model for 1000 years Period 23
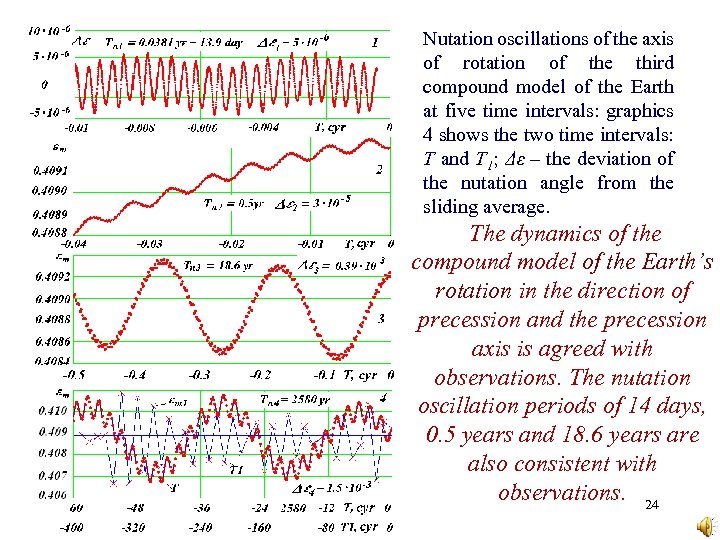 Nutation oscillations of the axis of rotation of the third compound model of the Earth at five time intervals: graphics 4 shows the two time intervals: T and T 1; Δε – the deviation of the nutation angle from the sliding average. The dynamics of the compound model of the Earth’s rotation in the direction of precession and the precession axis is agreed with observations. The nutation oscillation periods of 14 days, 0. 5 years and 18. 6 years are also consistent with observations. 24
Nutation oscillations of the axis of rotation of the third compound model of the Earth at five time intervals: graphics 4 shows the two time intervals: T and T 1; Δε – the deviation of the nutation angle from the sliding average. The dynamics of the compound model of the Earth’s rotation in the direction of precession and the precession axis is agreed with observations. The nutation oscillation periods of 14 days, 0. 5 years and 18. 6 years are also consistent with observations. 24
 6. Compound model of the Sun’s rotation As a result of integrating the equations of motion of the planets, Moon and Sun we received perihelion velocity of Mercury 529. 9" per century relative to the motionless space. We have found that according to observations [11 -12] the perihelion velocity relative to the motionless space is equal to 582. 3“ in a century. Therefore, the difference between them is 52. 4" per century, and not as it was accepted in the early 20 -th century, 41“ per century. If inside the orbit of Mercury is the planet a certain mass, it could make the rotation of the perihelion of Mercury in 52. 4“ per century and at the same time did not exert significant influence on other planets. This planet is not. But the Sun rotates around its axis, and the moving mass of its substances can affect the Mercury as well as the above assumed planet. For this purpose, a compound model of the Sun rotation is developed [11 -12]. 25
6. Compound model of the Sun’s rotation As a result of integrating the equations of motion of the planets, Moon and Sun we received perihelion velocity of Mercury 529. 9" per century relative to the motionless space. We have found that according to observations [11 -12] the perihelion velocity relative to the motionless space is equal to 582. 3“ in a century. Therefore, the difference between them is 52. 4" per century, and not as it was accepted in the early 20 -th century, 41“ per century. If inside the orbit of Mercury is the planet a certain mass, it could make the rotation of the perihelion of Mercury in 52. 4“ per century and at the same time did not exert significant influence on other planets. This planet is not. But the Sun rotates around its axis, and the moving mass of its substances can affect the Mercury as well as the above assumed planet. For this purpose, a compound model of the Sun rotation is developed [11 -12]. 25
 Compound model of the Sun rotation and its parameters for the mass of the Sun MS = 1. 98892 1030 kg and its radius RS = 6. 97113 108 m: 1 – a compound model of the Sun; 2 – the central body; 3 – peripheral body of model No. 5; 4 – Mercury; 5 – Venus; 6 – Earth and Moon; 7 – Mars; other planets are outside the figure. The positions of the bodies are given at 12. 30. 1949, the lines of the bodies represent the vectors their velocities. No Model 2 3 4 5 n 5 5 5 10 m 1 10 -23 kg 604. 8 1. 966 1. 565 0. 782 a 10 -10 m 2. 528358 2. 528449
Compound model of the Sun rotation and its parameters for the mass of the Sun MS = 1. 98892 1030 kg and its radius RS = 6. 97113 108 m: 1 – a compound model of the Sun; 2 – the central body; 3 – peripheral body of model No. 5; 4 – Mercury; 5 – Venus; 6 – Earth and Moon; 7 – Mars; other planets are outside the figure. The positions of the bodies are given at 12. 30. 1949, the lines of the bodies represent the vectors their velocities. No Model 2 3 4 5 n 5 5 5 10 m 1 10 -23 kg 604. 8 1. 966 1. 565 0. 782 a 10 -10 m 2. 528358 2. 528449
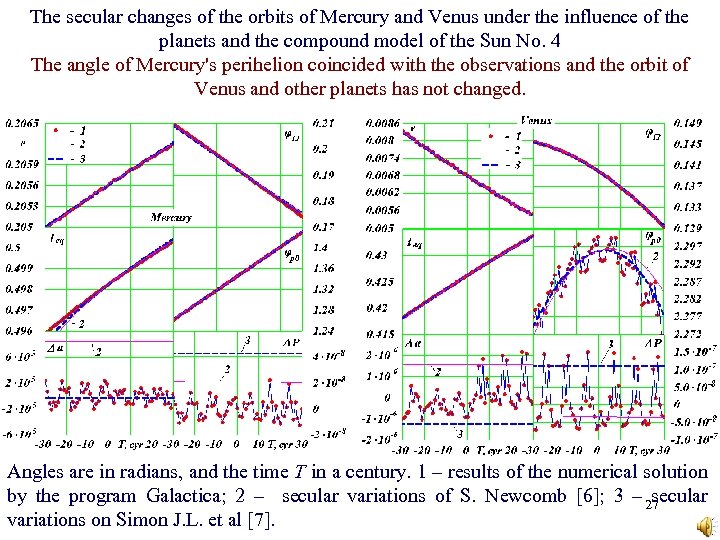 The secular changes of the orbits of Mercury and Venus under the influence of the planets and the compound model of the Sun No. 4 The angle of Mercury's perihelion coincided with the observations and the orbit of Venus and other planets has not changed. Angles are in radians, and the time T in a century. 1 – results of the numerical solution by the program Galactica; 2 – secular variations of S. Newcomb [6]; 3 – 27 secular variations on Simon J. L. et al [7].
The secular changes of the orbits of Mercury and Venus under the influence of the planets and the compound model of the Sun No. 4 The angle of Mercury's perihelion coincided with the observations and the orbit of Venus and other planets has not changed. Angles are in radians, and the time T in a century. 1 – results of the numerical solution by the program Galactica; 2 – secular variations of S. Newcomb [6]; 3 – 27 secular variations on Simon J. L. et al [7].
 7. The motion of the asteroid Apophis The authors of several papers, e. g. [13 -14] and others have shown that the asteroid Apophis at April 13, 2029 will be approach at a distance from the center of the Earth in the range of 5. 62 to 6. 3 of its radius, and because of the chaotic change of orbit the further prediction of motion becomes impossible. These authors believe that there is some probability of collision with Earth in 2036. We analyzed the problem and found that the uncertainty in the trajectory of Apophis due to imperfections in the methods of its determination. We have integrated the differential equations of motion of Apophis, the planets, Moon and Sun for 1000 years by Galactica [15] and studied its evolution of the orbit. At April 13, 2029 Apophis will approach at a distance Rmin = 38 ÷ 39 thousand km from the center of the Earth and its closer passage will not be during 1000 years. 28
7. The motion of the asteroid Apophis The authors of several papers, e. g. [13 -14] and others have shown that the asteroid Apophis at April 13, 2029 will be approach at a distance from the center of the Earth in the range of 5. 62 to 6. 3 of its radius, and because of the chaotic change of orbit the further prediction of motion becomes impossible. These authors believe that there is some probability of collision with Earth in 2036. We analyzed the problem and found that the uncertainty in the trajectory of Apophis due to imperfections in the methods of its determination. We have integrated the differential equations of motion of Apophis, the planets, Moon and Sun for 1000 years by Galactica [15] and studied its evolution of the orbit. At April 13, 2029 Apophis will approach at a distance Rmin = 38 ÷ 39 thousand km from the center of the Earth and its closer passage will not be during 1000 years. 28
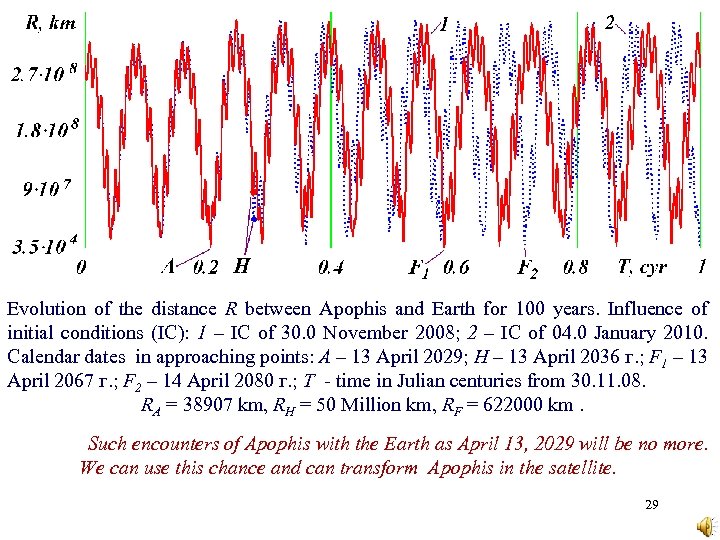 Evolution of the distance R between Apophis and Earth for 100 years. Influence of initial conditions (IC): 1 – IC of 30. 0 November 2008; 2 – IC of 04. 0 January 2010. Calendar dates in approaching points: A – 13 April 2029; H – 13 April 2036 г. ; F 1 – 13 April 2067 г. ; F 2 – 14 April 2080 г. ; T - time in Julian centuries from 30. 11. 08. RA = 38907 km, RH = 50 Million km, RF = 622000 km. Such encounters of Apophis with the Earth as April 13, 2029 will be no more. We can use this chance and can transform Apophis in the satellite. 29
Evolution of the distance R between Apophis and Earth for 100 years. Influence of initial conditions (IC): 1 – IC of 30. 0 November 2008; 2 – IC of 04. 0 January 2010. Calendar dates in approaching points: A – 13 April 2029; H – 13 April 2036 г. ; F 1 – 13 April 2067 г. ; F 2 – 14 April 2080 г. ; T - time in Julian centuries from 30. 11. 08. RA = 38907 km, RH = 50 Million km, RF = 622000 km. Such encounters of Apophis with the Earth as April 13, 2029 will be no more. We can use this chance and can transform Apophis in the satellite. 29
 The motion of the asteroid over 2 years, when it approaches to Earth 13. 04. 2029; the view from the south pole. 30
The motion of the asteroid over 2 years, when it approaches to Earth 13. 04. 2029; the view from the south pole. 30
 Possible use of Apophis-satellite Many of the pioneers of cosmonautics had thought the exploration of space using large manned space stations. However, to deliver from the Earth such a large mass poses a serious technical and environmental problems. Therefore, thanks to a happy occasion, we can create a habitable station, turning the asteroid Apophis in the satellite. There applications other are possible such It satellites. basis of the serve can as for the Space lift. It can be used as a "shuttle" to deliver goods to the Moon. In this case, the satellite must have an elongated orbit with a perigee radius close to the radius of the geostationary orbit, and apogee radius, approaching to radius of lunar orbit. Then the cargo from the geostationary orbit at perigee would be board on Apophis-satellite and then these goods could be delivered at the apogee to the Moon. The last two applications are possible if the satellite motion coincides with direction of the Earth rotation and the direction of the Moon orbiting. 31
Possible use of Apophis-satellite Many of the pioneers of cosmonautics had thought the exploration of space using large manned space stations. However, to deliver from the Earth such a large mass poses a serious technical and environmental problems. Therefore, thanks to a happy occasion, we can create a habitable station, turning the asteroid Apophis in the satellite. There applications other are possible such It satellites. basis of the serve can as for the Space lift. It can be used as a "shuttle" to deliver goods to the Moon. In this case, the satellite must have an elongated orbit with a perigee radius close to the radius of the geostationary orbit, and apogee radius, approaching to radius of lunar orbit. Then the cargo from the geostationary orbit at perigee would be board on Apophis-satellite and then these goods could be delivered at the apogee to the Moon. The last two applications are possible if the satellite motion coincides with direction of the Earth rotation and the direction of the Moon orbiting. 31
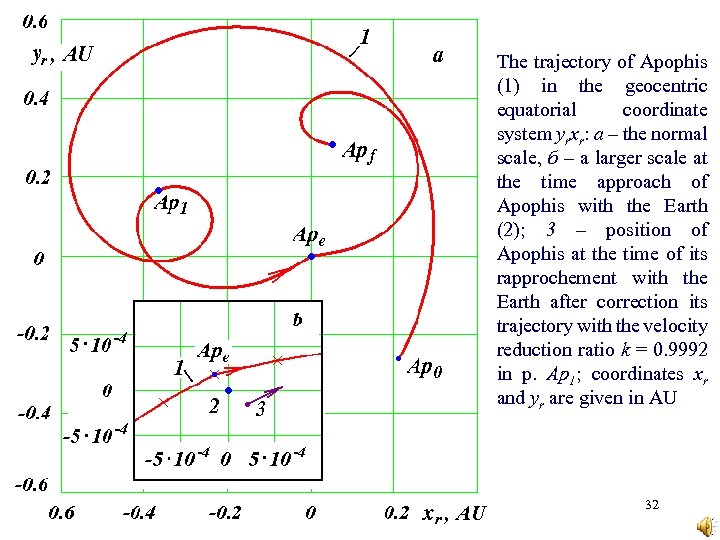 The trajectory of Apophis (1) in the geocentric equatorial coordinate system yrxr: а – the normal scale, б – a larger scale at the time approach of Apophis with the Earth (2); 3 – position of Apophis at the time of its rapprochement with the Earth after correction its trajectory with the velocity reduction ratio k = 0. 9992 in p. Ap 1; coordinates xr and yr are given in AU 32
The trajectory of Apophis (1) in the geocentric equatorial coordinate system yrxr: а – the normal scale, б – a larger scale at the time approach of Apophis with the Earth (2); 3 – position of Apophis at the time of its rapprochement with the Earth after correction its trajectory with the velocity reduction ratio k = 0. 9992 in p. Ap 1; coordinates xr and yr are given in AU 32
 The transformation of Apophis in the satellite with the necessary direction of orbiting For the transformation of Apophis in the satellite with the necessary direction of its motion, it is necessary before 0. 443 years to Apophis approach with the Earth to reduce its velocity on 2. 54 m/c. Approach of Apophis with the Earth after correction its velocity (in the coordinates relative to the Earth). 33
The transformation of Apophis in the satellite with the necessary direction of orbiting For the transformation of Apophis in the satellite with the necessary direction of its motion, it is necessary before 0. 443 years to Apophis approach with the Earth to reduce its velocity on 2. 54 m/c. Approach of Apophis with the Earth after correction its velocity (in the coordinates relative to the Earth). 33
 If the Apophis velocity will be reduced on 3. 5 km/s, then it become a satellite with the same direction of revolution around the Earth as the Moon. Our studies have given that the satellite orbit is stable. Therefore, it can perform its task for a long time. Apophis satellite orbiting around the Earth in the same direction as the Moon. 34
If the Apophis velocity will be reduced on 3. 5 km/s, then it become a satellite with the same direction of revolution around the Earth as the Moon. Our studies have given that the satellite orbit is stable. Therefore, it can perform its task for a long time. Apophis satellite orbiting around the Earth in the same direction as the Moon. 34
 The transformation of an asteroid in the satellite is a very difficult task. However, the solution to this problem greatly increases the opportunity to prevent a serious asteroid hazard. Therefore, if the society undertakes efforts for its actualization, it would indicate the transition from purely theoretical research to practical work in protect the Earth from asteroid hazard. 35
The transformation of an asteroid in the satellite is a very difficult task. However, the solution to this problem greatly increases the opportunity to prevent a serious asteroid hazard. Therefore, if the society undertakes efforts for its actualization, it would indicate the transition from purely theoretical research to practical work in protect the Earth from asteroid hazard. 35
 36
36
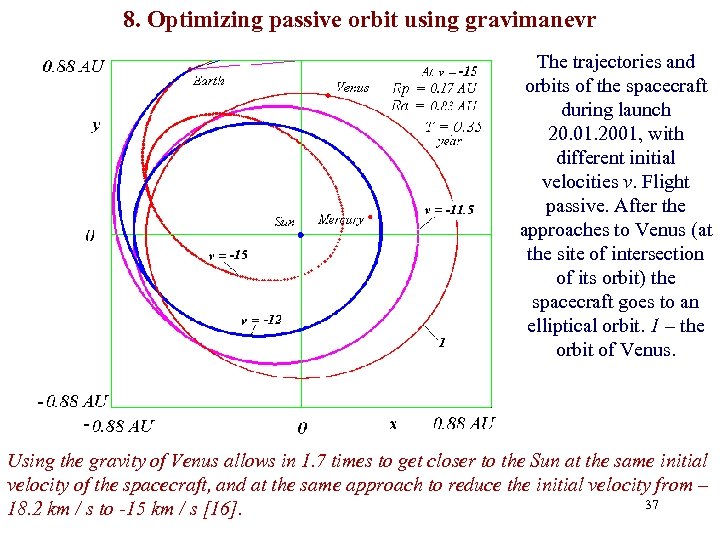 8. Optimizing passive orbit using gravimanevr The trajectories and orbits of the spacecraft during launch 20. 01. 2001, with different initial velocities v. Flight passive. After the approaches to Venus (at the site of intersection of its orbit) the spacecraft goes to an elliptical orbit. 1 – the orbit of Venus. Using the gravity of Venus allows in 1. 7 times to get closer to the Sun at the same initial velocity of the spacecraft, and at the same approach to reduce the initial velocity from – 37 18. 2 km / s to -15 km / s [16].
8. Optimizing passive orbit using gravimanevr The trajectories and orbits of the spacecraft during launch 20. 01. 2001, with different initial velocities v. Flight passive. After the approaches to Venus (at the site of intersection of its orbit) the spacecraft goes to an elliptical orbit. 1 – the orbit of Venus. Using the gravity of Venus allows in 1. 7 times to get closer to the Sun at the same initial velocity of the spacecraft, and at the same approach to reduce the initial velocity from – 37 18. 2 km / s to -15 km / s [16].
 9. Multilayered circular structures Evolution of multi-ring structures are important for understanding the problems of existence and stability of rings of the planets, globular star clusters and galaxies. Creating ring structures based on the following two conditions [17]. 1. For body, located outside of the ring structure, the exerted force equals to the force, which would create a body located in the center of the structure and has a mass equal to the mass of the entire structure. 2. For body, located inside the ring structure, the total force exerted by all its bodies is equal to zero. 38
9. Multilayered circular structures Evolution of multi-ring structures are important for understanding the problems of existence and stability of rings of the planets, globular star clusters and galaxies. Creating ring structures based on the following two conditions [17]. 1. For body, located outside of the ring structure, the exerted force equals to the force, which would create a body located in the center of the structure and has a mass equal to the mass of the entire structure. 2. For body, located inside the ring structure, the total force exerted by all its bodies is equal to zero. 38
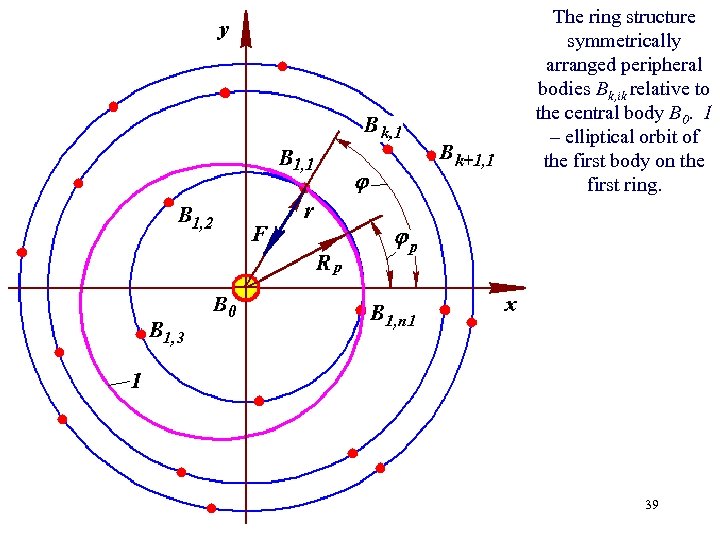 The ring structure symmetrically arranged peripheral bodies Bk, ik relative to the central body B 0. 1 – elliptical orbit of the first body on the first ring. 39
The ring structure symmetrically arranged peripheral bodies Bk, ik relative to the central body B 0. 1 – elliptical orbit of the first body on the first ring. 39
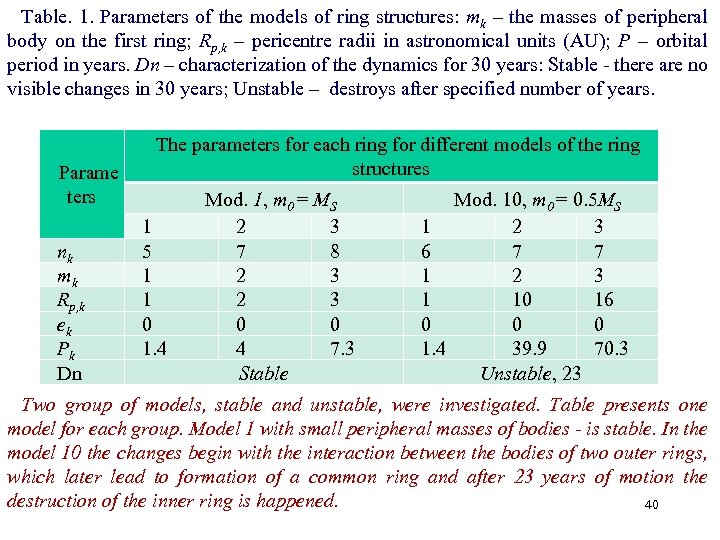 Table. 1. Parameters of the models of ring structures: mk – the masses of peripheral body on the first ring; Rp, k – pericentre radii in astronomical units (AU); P – orbital period in years. Dn – characterization of the dynamics for 30 years: Stable - there are no visible changes in 30 years; Unstable – destroys after specified number of years. Parame ters nk mk Rp, k ek Pk Dn The parameters for each ring for different models of the ring structures 1 5 1 1 0 1. 4 Mod. 1, m 0 = MS 2 3 7 8 2 3 0 0 4 7. 3 Stable Mod. 10, m 0 = 0. 5 MS 1 2 3 6 7 7 1 2 3 1 10 16 0 0 0 1. 4 39. 9 70. 3 Unstable, 23 Two group of models, stable and unstable, were investigated. Table presents one model for each group. Model 1 with small peripheral masses of bodies - is stable. In the model 10 the changes begin with the interaction between the bodies of two outer rings, which later lead to formation of a common ring and after 23 years of motion the destruction of the inner ring is happened. 40
Table. 1. Parameters of the models of ring structures: mk – the masses of peripheral body on the first ring; Rp, k – pericentre radii in astronomical units (AU); P – orbital period in years. Dn – characterization of the dynamics for 30 years: Stable - there are no visible changes in 30 years; Unstable – destroys after specified number of years. Parame ters nk mk Rp, k ek Pk Dn The parameters for each ring for different models of the ring structures 1 5 1 1 0 1. 4 Mod. 1, m 0 = MS 2 3 7 8 2 3 0 0 4 7. 3 Stable Mod. 10, m 0 = 0. 5 MS 1 2 3 6 7 7 1 2 3 1 10 16 0 0 0 1. 4 39. 9 70. 3 Unstable, 23 Two group of models, stable and unstable, were investigated. Table presents one model for each group. Model 1 with small peripheral masses of bodies - is stable. In the model 10 the changes begin with the interaction between the bodies of two outer rings, which later lead to formation of a common ring and after 23 years of motion the destruction of the inner ring is happened. 40
 Dynamics of 10 -th model of the ring structure: m 0 = 0. 5 m. S. 41
Dynamics of 10 -th model of the ring structure: m 0 = 0. 5 m. S. 41
 10. References 1. Smulsky, J. J. Theory of Interaction. - Ekaterinburg, Russia: Publishing house "Cultural Information Bank", 2004. - 304 p. http: //www. ikz. ru/~smulski/TVful. A 5_2. pdf. 2. Duboshin, G. N. (Editor), 1976. Celestial Mechanics and Astrodynamics: A Handbook [in Russian]. Nauka, Moscow. 3. Stendish E. M. JPL Planetary and Lunar Ephemerides, DE 405/LE 405. //Interoffice memorandum: JPL IOM 312. F - 98 -048. August 26. 1998. (ftp: //ssd. jpl. nasa. gov/pub/eph/export/DE 405/). 4. Melnikov, V. P. , Smulsky, J. J. , Krotov O. I. , Smulsky, L. J. Orbits of The Earth And The Sun And Possible Their Influences On of The Earth Cryosphere (Statement of a Problem And The First Results)// Cryosphere of the Earth. - 2000. - Vol. IV, No. 3, Pp. 3 -13. (In Russian). 5. Laskar J. Marginal stability and chaos in the Solar System/ Ferraz Mello S. et al. (eds. ) Dynamics, ephemerides and astrometry of the Solar System. – IAU: Netherlands. – 1996. Pp. 75 – 88. 6. Newcomb S. The elements of the four inner planets and the fundamental constants of astronomy. Washington: Government printing office. 1895. – 202 p. 42
10. References 1. Smulsky, J. J. Theory of Interaction. - Ekaterinburg, Russia: Publishing house "Cultural Information Bank", 2004. - 304 p. http: //www. ikz. ru/~smulski/TVful. A 5_2. pdf. 2. Duboshin, G. N. (Editor), 1976. Celestial Mechanics and Astrodynamics: A Handbook [in Russian]. Nauka, Moscow. 3. Stendish E. M. JPL Planetary and Lunar Ephemerides, DE 405/LE 405. //Interoffice memorandum: JPL IOM 312. F - 98 -048. August 26. 1998. (ftp: //ssd. jpl. nasa. gov/pub/eph/export/DE 405/). 4. Melnikov, V. P. , Smulsky, J. J. , Krotov O. I. , Smulsky, L. J. Orbits of The Earth And The Sun And Possible Their Influences On of The Earth Cryosphere (Statement of a Problem And The First Results)// Cryosphere of the Earth. - 2000. - Vol. IV, No. 3, Pp. 3 -13. (In Russian). 5. Laskar J. Marginal stability and chaos in the Solar System/ Ferraz Mello S. et al. (eds. ) Dynamics, ephemerides and astrometry of the Solar System. – IAU: Netherlands. – 1996. Pp. 75 – 88. 6. Newcomb S. The elements of the four inner planets and the fundamental constants of astronomy. Washington: Government printing office. 1895. – 202 p. 42
 7. Simon J. L. , Bretagnon P. , Chapront J. et. al. Numerical Expression for Precession Formulae and Mean Elements for the Moon and the Planets // Astron. and Astrophys. – 1994, vol. 282, p. 663 -683. 8. Cohen C. J. , Hubbard E. C. ; Oesterwinter C. Planetary Elements for 10, 000 Years//Celestial Mechanics. - 1973. - No. 3. -Pp. 438 -448. 9. Brouwer D. , Van Woerkom A. J. J. The secular variation of the orbital elements of the principal planets// Astr. Pap. - 1950. – 13, 2. 10. Laskar J. , Correia A. C. M. , Gastineau M. , Joutel F. , Levrard B. and Robutel P. Long term evolution and chaotic diffusion of the insolation quantities of Mars//Icarus. 2004. -Vol. 170, Iss. 2. -P. 343 -364. 11. Smulsky J. J. Compound model of rotation of the Sun and displacement of Mercury perihelion / The Fundamental and Applied Problems of the Mechanics: Proceeding of the VI All-Russian scientific Conference, devoted 130 -th anniversary of Tomsk state university and 40 -th anniversary NII of Applied Mathematics and the Mechanics of Tomsk State University. Tomsk, September 30 - October 2, 2008 - Tomsk: University Publishing House. – 2008 - Pp. 433 -434. (In Russian). 12. Smulsky J. J. Gravitation, Field and Rotation of Mercury Perihelion// Proceedings of the Natural Philosophy Alliance. 15 th Annual Conference 7 -11 April 2008 at the University of New Mexiko, Albuquuerque, USA. Vol. 5, No. 2. Published by Space Time Analyses, Ltd. Arlington, MA, USA. - 2009. - Pp. 254 -260. http: //www. ikz. ru/~smulski/Papers/08 Smulsky 2 c. pdf. 43
7. Simon J. L. , Bretagnon P. , Chapront J. et. al. Numerical Expression for Precession Formulae and Mean Elements for the Moon and the Planets // Astron. and Astrophys. – 1994, vol. 282, p. 663 -683. 8. Cohen C. J. , Hubbard E. C. ; Oesterwinter C. Planetary Elements for 10, 000 Years//Celestial Mechanics. - 1973. - No. 3. -Pp. 438 -448. 9. Brouwer D. , Van Woerkom A. J. J. The secular variation of the orbital elements of the principal planets// Astr. Pap. - 1950. – 13, 2. 10. Laskar J. , Correia A. C. M. , Gastineau M. , Joutel F. , Levrard B. and Robutel P. Long term evolution and chaotic diffusion of the insolation quantities of Mars//Icarus. 2004. -Vol. 170, Iss. 2. -P. 343 -364. 11. Smulsky J. J. Compound model of rotation of the Sun and displacement of Mercury perihelion / The Fundamental and Applied Problems of the Mechanics: Proceeding of the VI All-Russian scientific Conference, devoted 130 -th anniversary of Tomsk state university and 40 -th anniversary NII of Applied Mathematics and the Mechanics of Tomsk State University. Tomsk, September 30 - October 2, 2008 - Tomsk: University Publishing House. – 2008 - Pp. 433 -434. (In Russian). 12. Smulsky J. J. Gravitation, Field and Rotation of Mercury Perihelion// Proceedings of the Natural Philosophy Alliance. 15 th Annual Conference 7 -11 April 2008 at the University of New Mexiko, Albuquuerque, USA. Vol. 5, No. 2. Published by Space Time Analyses, Ltd. Arlington, MA, USA. - 2009. - Pp. 254 -260. http: //www. ikz. ru/~smulski/Papers/08 Smulsky 2 c. pdf. 43
 13. Giorgini J. D. , Benner L. A. M. , Ostro S. I. , Nolan H. C. , Busch M. W. Predicting the Earth encounters of (99942) Apophis // Icarus. 2008 v. 193, pp. 1 -19. 14. Ryhlova L. V. , Shustov B. M. , Pol’ V. G. , Suhanov K. G. Scientific Problems of the Aasteroid Hazard / Near-Earth Astronomy 2007 / / Proceedings of International Conference, September 3 -7, 2007, Terskol. International Centre for Astronomical, Medical and Environmental Research of the National Academy of Sciences of Ukraine and the Institute of Astronomy. Nalchik, 2008, pp. 25 -33. 15. Smulsky J. J. , Smulsky Ya. J. Evolution of Movement of Asteroids Apophis and 1950 DA for 1000 Years and their Possible Use / Institute of the Earth Cryosphere SB RAS. - Tyumen, 2011. - 36 p. - Fig. : 10. Refer. : 27. - Russian. - Dep. In VINITI 25. 01. 11. No. 21 -V 2011. (In Russian). 16. Smulsky J. J. Optimization of Passive Orbit with the Use of Gravity Maneuver // Cosmic Research, 2008, Vol. 46, No. 5, pp. 456– 464. Original Russian Text ©, 2008, published in Kosmicheskie Issledovaniya, 2008, Vol. 46, No. 5, pp. 484– 492. 17. Smulsky J. J. Designing of ring structures // The Fundamental and Applied Problems of the Mechanics: Proceeding of the VI All-Russian scientific Conference, devoted 130 th anniversary of Tomsk state university and 40 -th anniversary NII of Applied Mathematics and the Mechanics of Tomsk State University. Tomsk, September 30 - October 2, 2008 - Tomsk: University Publishing House. – 2008 - Pp. 431 -432. (In Russian). 44
13. Giorgini J. D. , Benner L. A. M. , Ostro S. I. , Nolan H. C. , Busch M. W. Predicting the Earth encounters of (99942) Apophis // Icarus. 2008 v. 193, pp. 1 -19. 14. Ryhlova L. V. , Shustov B. M. , Pol’ V. G. , Suhanov K. G. Scientific Problems of the Aasteroid Hazard / Near-Earth Astronomy 2007 / / Proceedings of International Conference, September 3 -7, 2007, Terskol. International Centre for Astronomical, Medical and Environmental Research of the National Academy of Sciences of Ukraine and the Institute of Astronomy. Nalchik, 2008, pp. 25 -33. 15. Smulsky J. J. , Smulsky Ya. J. Evolution of Movement of Asteroids Apophis and 1950 DA for 1000 Years and their Possible Use / Institute of the Earth Cryosphere SB RAS. - Tyumen, 2011. - 36 p. - Fig. : 10. Refer. : 27. - Russian. - Dep. In VINITI 25. 01. 11. No. 21 -V 2011. (In Russian). 16. Smulsky J. J. Optimization of Passive Orbit with the Use of Gravity Maneuver // Cosmic Research, 2008, Vol. 46, No. 5, pp. 456– 464. Original Russian Text ©, 2008, published in Kosmicheskie Issledovaniya, 2008, Vol. 46, No. 5, pp. 484– 492. 17. Smulsky J. J. Designing of ring structures // The Fundamental and Applied Problems of the Mechanics: Proceeding of the VI All-Russian scientific Conference, devoted 130 th anniversary of Tomsk state university and 40 -th anniversary NII of Applied Mathematics and the Mechanics of Tomsk State University. Tomsk, September 30 - October 2, 2008 - Tomsk: University Publishing House. – 2008 - Pp. 431 -432. (In Russian). 44
 11. Acknowledgments This work was supported by grants from the Governor of the Tyumen region 2003 and 2004 and by integration program of the Presidium of RAS № 13 in 2008 – 2011. Calculations were performed on the supercomputers of the Siberian Supercomputing Centre SSCC SB RAS at the ICMMG SB RAS. In work on different stages involved were: L. I. Smulsky, Ya. I. Smulsky, P. A. Apasev, O. I. Krotov, M. E. Chikmareva, M. A. Ponomarev, I. V. Bineev, E. N. Nevidimova, N. J. Apohin, V. S. Botvin, E. A. Kovrizhkina, A. A. Pavlova, I. A. Shabolina, M. L. Panova and E. F. Safina. 45
11. Acknowledgments This work was supported by grants from the Governor of the Tyumen region 2003 and 2004 and by integration program of the Presidium of RAS № 13 in 2008 – 2011. Calculations were performed on the supercomputers of the Siberian Supercomputing Centre SSCC SB RAS at the ICMMG SB RAS. In work on different stages involved were: L. I. Smulsky, Ya. I. Smulsky, P. A. Apasev, O. I. Krotov, M. E. Chikmareva, M. A. Ponomarev, I. V. Bineev, E. N. Nevidimova, N. J. Apohin, V. S. Botvin, E. A. Kovrizhkina, A. A. Pavlova, I. A. Shabolina, M. L. Panova and E. F. Safina. 45
 12. Some information 1. Results of equation (1) solutions and planets orbit evolution for 100 million years are accessible on site: : http: //www. ikz. ru/~smulski/Data/Orbt. Data/. 2. Now there are several our books: 2. 1. Smulsky J. J. Theory of Interaction. - Ekaterinburg, Russia: Publishing house "Cultural Information Bank", 2004. - 304 p. http: //www. ikz. ru/~smulski/TVful. A 5_2. pdf. 2. 2. Grebenikov E. A. , Smulsky J. J. Evolution of the Mars Orbit on Time Span in Hundred Millions Years / Reports on Applied Mathematics. Russian Academy of Sciences: A. A. Dorodnicyn Computing Center. Moscow. - 2007. 63 p. (In Russian). http: //www. ikz. ru/~smulski/Papers/Ev Ma 100 m 4 t 2. pdf.
12. Some information 1. Results of equation (1) solutions and planets orbit evolution for 100 million years are accessible on site: : http: //www. ikz. ru/~smulski/Data/Orbt. Data/. 2. Now there are several our books: 2. 1. Smulsky J. J. Theory of Interaction. - Ekaterinburg, Russia: Publishing house "Cultural Information Bank", 2004. - 304 p. http: //www. ikz. ru/~smulski/TVful. A 5_2. pdf. 2. 2. Grebenikov E. A. , Smulsky J. J. Evolution of the Mars Orbit on Time Span in Hundred Millions Years / Reports on Applied Mathematics. Russian Academy of Sciences: A. A. Dorodnicyn Computing Center. Moscow. - 2007. 63 p. (In Russian). http: //www. ikz. ru/~smulski/Papers/Ev Ma 100 m 4 t 2. pdf.
 2. 3. Melnikov V. P. , Smulsky J. J. Astronomical theory of ice ages: New approximations. Solutions and challenges. – Novosibirsk: Academic Publishing House “GEO”, 2009. – 182 p. http: //www. ikz. ru/~smulski/Papers/As. Th. An. R. pdf.
2. 3. Melnikov V. P. , Smulsky J. J. Astronomical theory of ice ages: New approximations. Solutions and challenges. – Novosibirsk: Academic Publishing House “GEO”, 2009. – 182 p. http: //www. ikz. ru/~smulski/Papers/As. Th. An. R. pdf.
 4. Scientific sate: http: //www. smul 1. newmail. ru/
4. Scientific sate: http: //www. smul 1. newmail. ru/
 5. Popular sate: http: //zhurnal. lib. ru/s/smulxskij_i_i/
5. Popular sate: http: //zhurnal. lib. ru/s/smulxskij_i_i/
 Thank you for your attention! 50
Thank you for your attention! 50
 51
51


