1. Принцип Даламбера 1. 1.

1. Принцип Даламбера 1. 1. Принцип Даламбера для материальной точки Найдем сначала выражение принципа для одной материальной точки. Пусть на материальную точку с массой m действует система активных сил, равнодействующую которых обозначим и реакция связи N (если точка является несвободной). Под действием всех этих сил точка будет двигаться по отношению к инерциальной системе отсчета с некоторым ускорением а.

• Введем в рассмотрение величину имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки. Тогда оказывается, что движение точки обладает следующим свойством: если в любой момент времени к действующим на точку активным силам и реакции связи присоединить силу инерции, то полученная система сил будет уравновешенной (рис. 1. 1), то есть

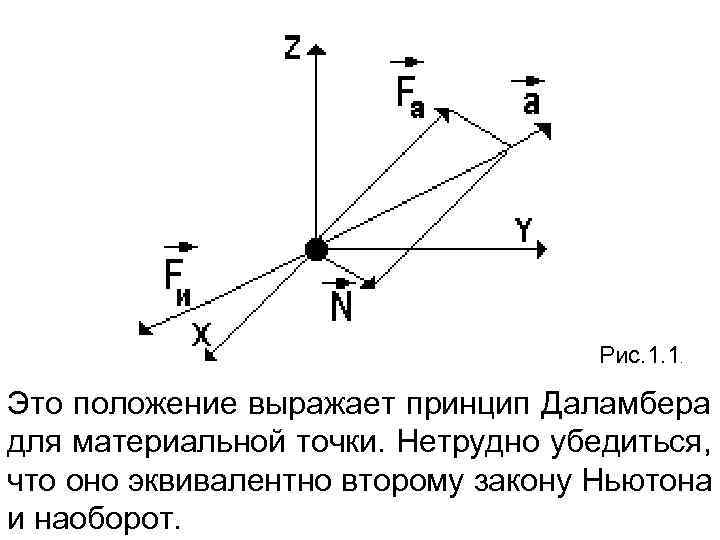
Рис. 1. 1. Это положение выражает принцип Даламбера для материальной точки. Нетрудно убедиться, что оно эквивалентно второму закону Ньютона и наоборот.

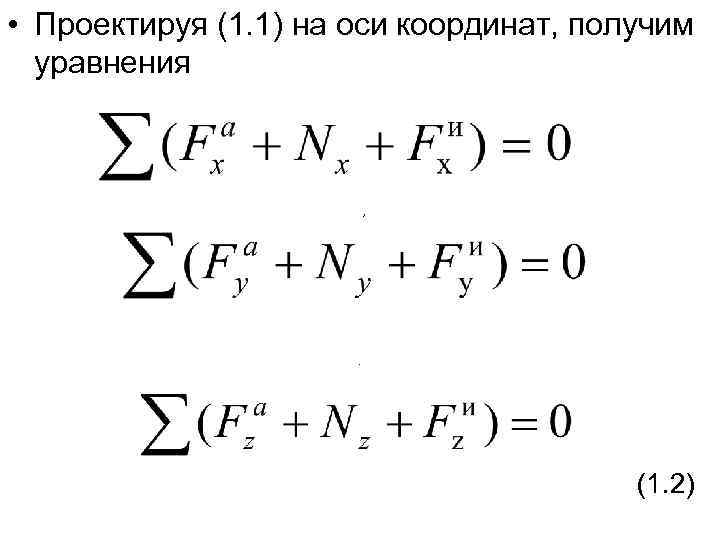
• Проектируя (1. 1) на оси координат, получим уравнения , (1. 2)

• Эти уравнения, по существу динамические, а по виду статические, называются уравнениями кинетостатики. Решение динамических задач путем составления кинетостатических уравнений называется методом кинетостатики. Применения этих уравнений особенно эффективно при определении динамических реакций, то есть составляющих реакций, которые возникают при движении тел.

• Пример. Автомобиль массы 1000 кг движется по выпуклому мосту со скоростью 10 м/с. Радиус кривизны в середине моста 50 м. определить силу давления автомобиля на мост в его середине ( рис. 1. 2).

Решение. Принимаем автомобиль за материальную точку, на которую действует сила тяжести Р и реакция моста N. В соответствии с принципом Даламбера прикладываем к ней силу инерции, Ускорение при движении точки по окружности равно

и направлено к центру кривизны, значит сила инерции в противоположную сторону. Полученная система сил является уравновешенной и, проектируя ее на нормаль, получим Подставляя значения и учитывая, что Р= mg ( g =9, 8 м/с 2 – ускорение свободного падения), получаем

Давление автомобиля на мост численно равно реакции моста и направлено в противоположную сторону. Из выражения для N следует, что реакция зависит от скорости движения. Очевидно, что максимальная скорость прохождения автомобиля через мост найдется из условия N=0. Из условий примера откуда

1. 2. Принцип Даламбера для механической системы Рассмотрим механическую систему, состоящую из n материальных точек (рис. 1. 3). Выделим какую-нибудь из точек системы с массой mk. Под действием приложенных к ней внешних и внутренних сил и (в которые входят и активные силы, и реакции связей) точка будет двигаться по отношению к инерциальной системе отсчета с некоторым ускорением

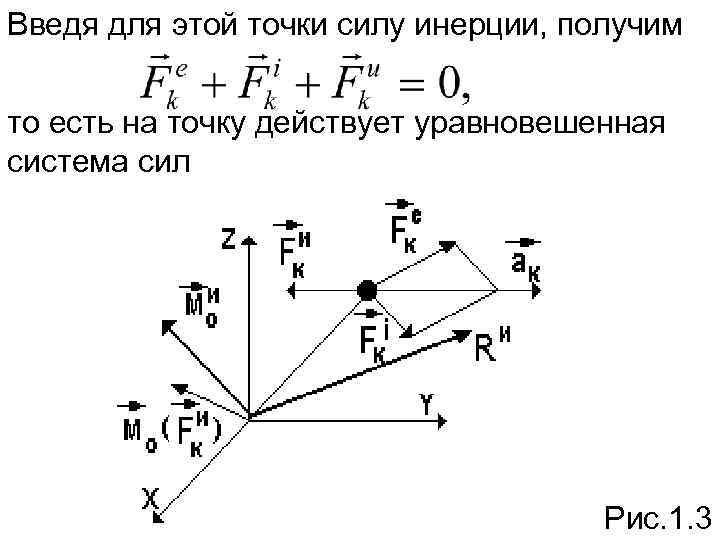
Введя для этой точки силу инерции, получим то есть на точку действует уравновешенная система сил Рис. 1. 3

Повторяя такие рассуждения для каждой из точек системы, придем к следующему результату, выражающему принцип Даламбера для системы: если в любой момент времени к каждой из точек системы кроме действующих на нее внешних и внутренних сил присоединить соответствующие силы инерции, то полученная система сил будет уравновешенной, и к ней можно применять все уравнения статики. Математически принцип Даламбера для системы выражается векторными равенствами вида, которые, очевидно, эквивалентны дифференциальным уравнениям движения системы.

Следовательно, из принципа Даламбера можно получить все общие теоремы динамики. Значение принципа Даламбера состоит в том, что при непосредственном его применении к задачам динамики уравнения движения системы составляются в форме хорошо известных уравнений равновесия; это делает единообразным подход к решению задач и часто упрощает соответствующие расчеты, а именно в этом состоит суть метода кинетостатики. Кроме того, в соединении с принципом возможных перемещений, который будет рассмотрен в следующей главе, принцип Даламбера позволяет получить новый общий метод решения задач динамики.

Из статики известно, что геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра О равны нулю, причем это справедливо для сил, действующих не только на твердое тело, но и на любую изменяемую механическую систему. Тогда на основании принципа Даламбера должно быть (1. 3) (1. 4)

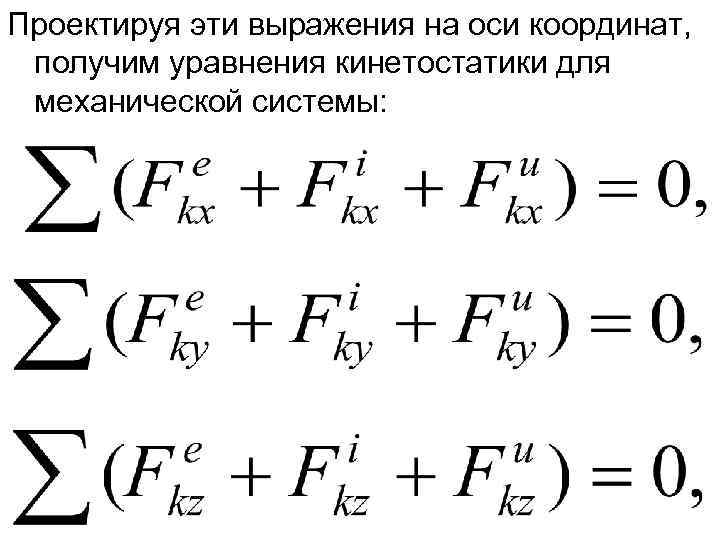
Проектируя эти выражения на оси координат, получим уравнения кинетостатики для механической системы:

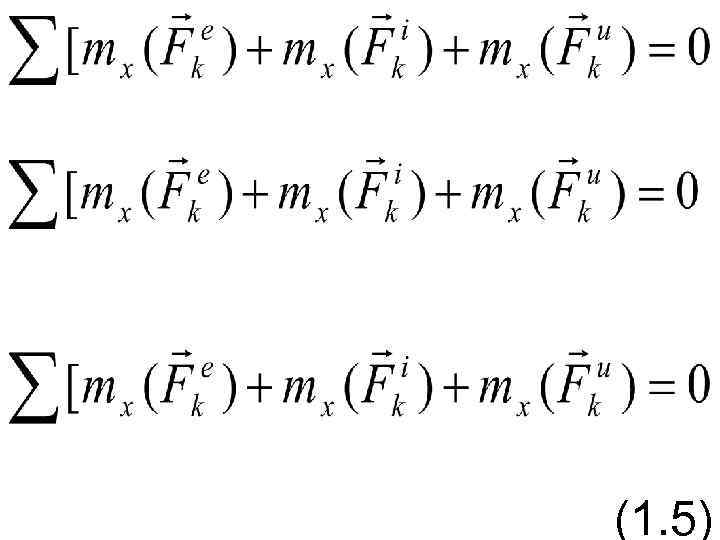
(1. 5)

• Введем обозначения Величины и представляют собою главный вектор и главный момент относительно центра О системы сил инерции. В результате, учитывая, что геометрическая сумма внутренних сил и сумма их моментов равны нулю, из уравнений (1. 3) – (1. 4) получим (1. 6)

Применение этих, вытекающих из принципа Даламбера, уравнений, упрощает процесс решения задач, так как они не содержат внутренних сил. Чтобы пользоваться ими при решении задач, надо знать выражения главного вектора и главного момента сил инерции. В заключение следует подчеркнуть, что при изучении движения по отношению к инерциальной системе отсчета, которое здесь и рассматривается, силы инерции вводятся только тогда, когда для решения задач применяется принцип Даламбера.

1. 3. Главный вектор и главный момент сил инерции Из уравнений (1. 6) следует, что Сравнивая первое из равенств с уравнением теоремы о движении центра масс, получим ( 1. 7)

то есть главный вектор сил инерции механической системы (в частности, твердого тела) равен произведению массы системы (тела) на ускорение центра масс и направлен противоположно этому ускорению. Сравнив теперь второе из равенств (1. 6) с уравнением,

выражающим теорему об изменении кинетического момента, и учтя, что аналогичным будет соотношение для моментов относительно оси, получим то есть главный момент сил инерции механической системы (твердого тела) относительно некоторого центра О или оси z равен взятой со знаком минус производной по времена от кинетического момента системы (тела) относительно того же центра или той же оси.

1. 4. Приведение сил инерции твердого тела Систему сил инерции твердого тела можно заменить одной силой, равной и приложенной в произвольно выбранном центре О, и парой с моментом, равным Рассмотрим несколько частных случаев. 1. Поступательное движение. В этом случае ускорения всех точек тела одинаковы и равны ускорению центра масс тела, тогда все силы инерции образуют систему параллельных сил, аналогичных силам тяжести, и поэтому, как и силы тяжести, имеют равнодействующую, проходящую через точку С.

Следовательно, при поступательном движении силы инерции твердого тела приводятся к равнодействующей, равной и проходящей через центр масс тела. 2. Вращение вокруг оси, проходящей через центр масс тела. Если тело вращается вокруг оси Cz, проходящей через центр масс С тела, то так как . Следовательно, в этом случае система сил инерции тела приводится к одной только паре с моментом лежащей в плоскости симметрии тела.

Так кинетический момент относительно оси вращающегося тела равен то есть Следовательно, величина момента будет равна произведению осевого момента инерции на угловое ускорение тела, а направлен он будет противоположно угловому ускорению.

3. Плоскопараллельное движение. Если тело имеет плоскость симметрии и движется параллельно этой плоскости то очевидно система сил инерции тела приведется к лежащим в плоскости симметрии силе, равной и приложенной в центре масс тела, и паре сил моментом Пример. На однородный диск массой m 2 намотана нить, к которой привязан груз массой m 1. Определить ускорение груза, реакцию опоры и силу натяжения нити (рис. 1. 4). Решение. Применим принцип Даламбера для системы, состоящей из груза и диска. Прикладываем внешние силы Р 1, Р 2, No, к грузу – силу инерции

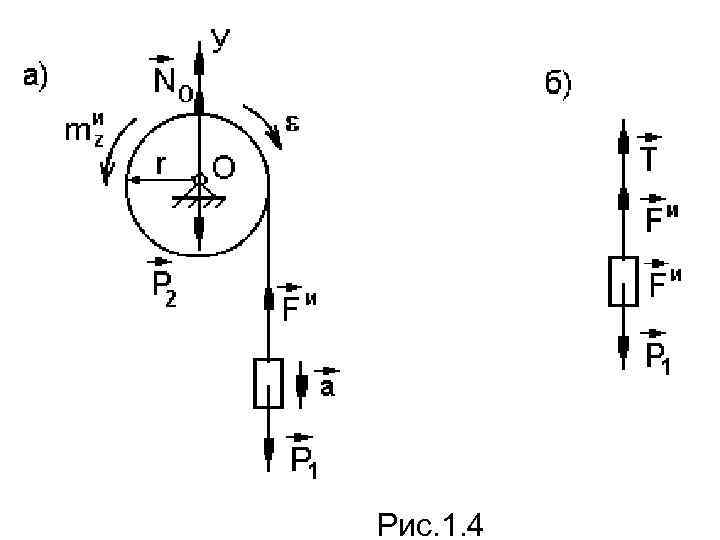
Рис. 1. 4

Силы инерции в диске приводятся к паре с моментом Составляем уравнения равновесия: Подставляя значения в уравнение (а), получим

Из уравнения (б) находим Для нахождения силы натяжения нити применим принцип Даламбера отдельно для груза (рис. 1. 4, б). Составляем уравнение равновесия груза Рассмотрим применение принципа Даламбера к исследованию динамического равновесия конического маятника.

Пример. Конический маятник состоит из тонкого однородного прямолинейного стержня АВ длиной L. Стержень шарнирно прикреплен к вертикальному валу, который вращается равномерно с угловой скоростью (рис. 1. 5). Определить угол отклонения конуса a.

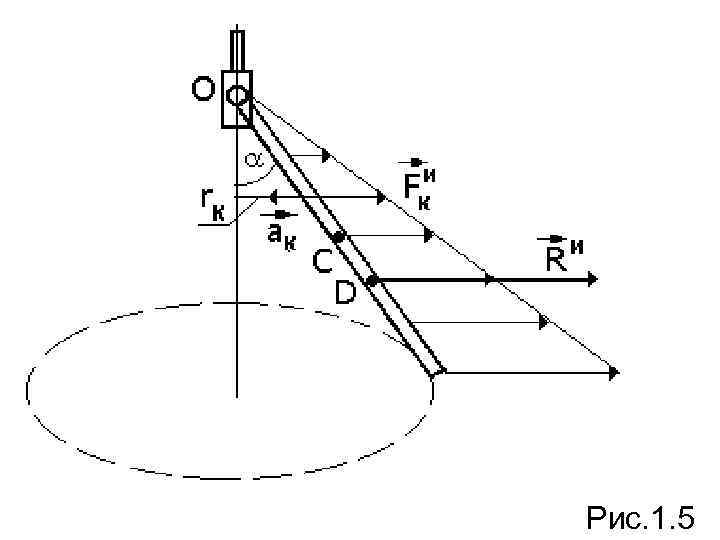
Рис. 1. 5

Решение. Механическая система представляет собой однородный стержень, на который действует активная сила тяжести Р=Мg. К каждому элементу стержня массой mk приложим силу инерции где rk – расстояние от элемента до оси вращении стержня. Силы инерции направлены противоположно ускорениям и пропорциональны расстояниям rk, то есть образуют систему параллельных сил, распределенных по линейному закону. Центр этих сил находится на расстоянии

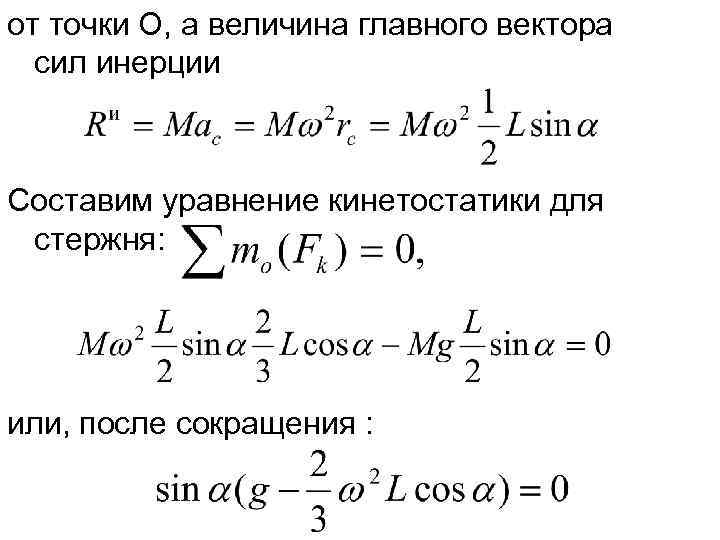
от точки О, а величина главного вектора сил инерции Составим уравнение кинетостатики для стержня: или, после сокращения :

Уравнение имеет два решения а) б) Эти выражения определяют угол a для всех возможных значений Подставив в последнее решение найдем критическую величину угловой скорости

• Если , то надо использовать решение (а), то есть стержень будет вертикальным. Если , то стержень будет описывать коническую поверхность с углом a, определяемым по формуле (б), из которой следует, что каждому значению соответствует вполне определенное значение угла a. • Хотя сила инерции была введены довольно формально, как взятое с обратным знаком произведение массы точки на ее ускорение, можно определить действие сил инерции в реальных инженерных сооружениях.

Пример. Однородный диск радиуса R и массой М вращается с постоянной угловой скоростью вокруг своего вертикального диаметра (рис. 1. 6). Определить силу, разрывающую его по диаметру.

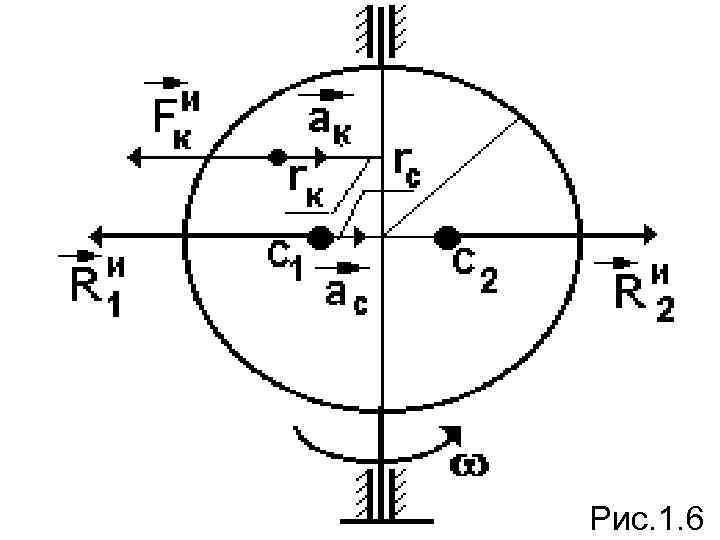
Рис. 1. 6

Решение. Каждая точка диска движется по окружности с постоянной скоростью, следовательно, имеет ускорение, равное нормальному, то есть направленное к оси вращения. Значит силы инерции всех точек, расположенных слева от оси вращения направлены влево и приводятся главному вектору сил инерции полудиска:

Как видно из ответа, разрывное усилие отлично от нуля и сильно зависит от угловой скорости вращения, то есть силы инерции при больших скоростях могут привести к разрыву маховиков, наждачных кругов и других быстровращающихся деталей.

1. 5. Давление на опоры вращающихся тел Отдельную группу представляют задачи по определению давления на опоры вращающихся тел, поскольку подобные конструкции широко используются в технике. Пример. Конструкция, состоит из вертикальной оси, к которой под прямым углом невесомый стержень, на конце которого прикреплен точечный груз массой m (рис. 1. 7). Ось вращается равномерно с угловой скоростью Определить давление на опоры А и В.

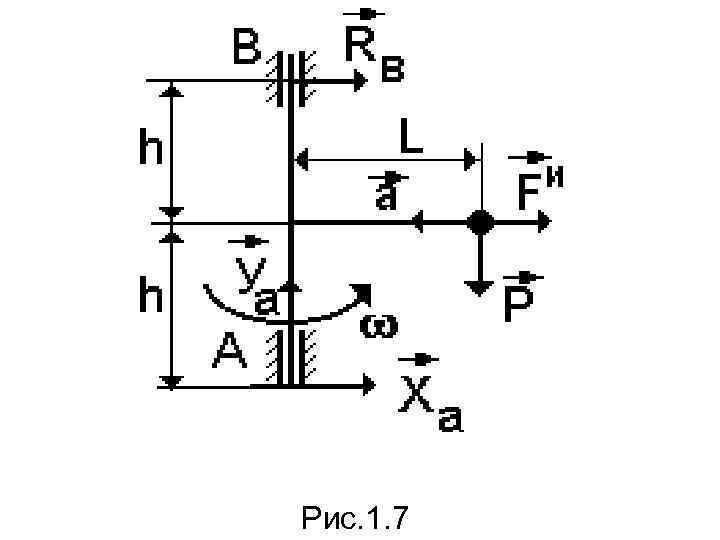
Рис. 1. 7

Решение. В соответствии с принципом Даламбера прикладываем к системе активную силу – вес точки P=mg, силу инерции и реакции опор Rв, Ха, Уа ( реакцию опоры А разлагаем на две составляющие). Следовательно, на систему будет действовать уравновешенная плоская система сил, для которой можно составить три уравнения равновесия:

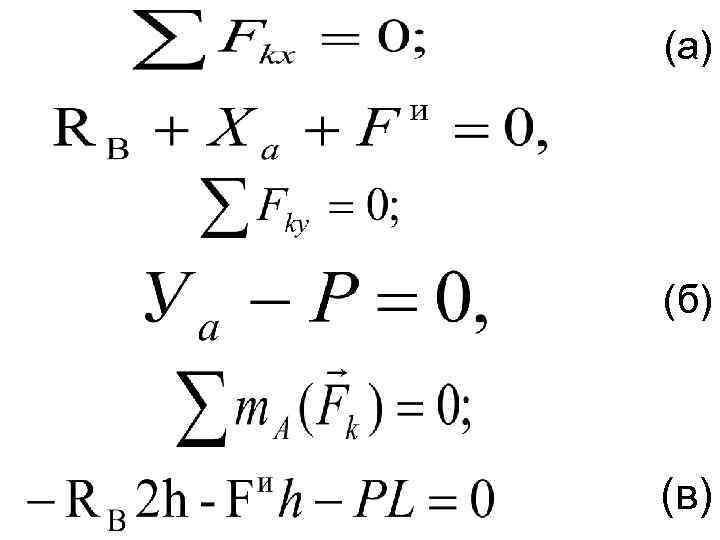
(а) (б) (в)

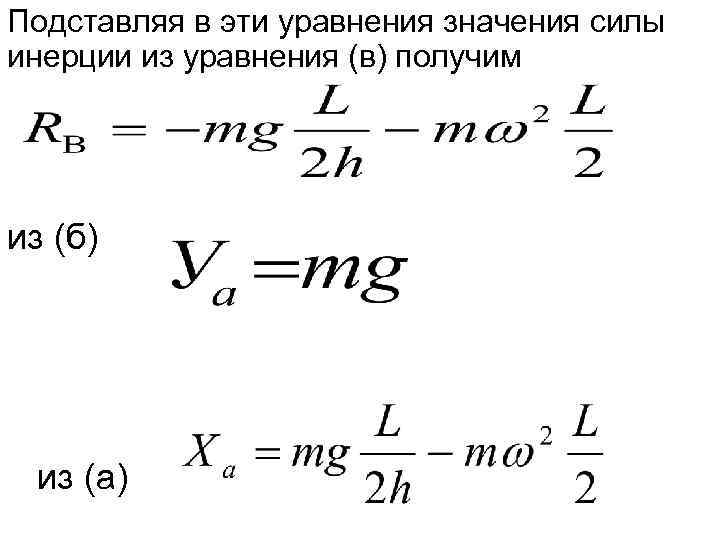
Подставляя в эти уравнения значения силы инерции из уравнения (в) получим из (б) из (а)

• Отсюда видно, что реакции RВ и Ха будут состоять из двух составляющих, одна из которых не зависит от скорости вращения, а другая зависит. Обозначим - статическая реакция опоры В, - динамическая реакция опоры В.

Зададимся значениями величин, входящих в эти формулы, например, h=L=1 м, m=1 кг, =100 рад/с, тогда

Таким образом, величина динамических реакций может во много раз превосходить величину статических реакций. Следует отметить, что при разгоне и торможении вращающегося тела кроме нормальных появляются и касательные ускорения и касательные силы инерции, вызывающие дополнительные давления на опоры, поэтому в данные периоды они максимальны. Поскольку давления на опоры по направлению противоположны реакциям, а по величине равны, то при больших угловых скоростях переменные по направлению нагрузки на опоры со временем неизбежно приводят к повреждению и выходу опор из строя. Поэтому при проектировании конструкций машин, в которые входят быстровращающиеся детали, возникает задача уменьшения динамических реакций.

1. 6. Причины возникновения динамических реакций и способы их устранения Как видно из предыдущего материала причиной возникновения динамических реакций вращающихся тел являются силы инерции, возникающие при движении точек тел по окружности. Рассмотрим конструкции, изображенные на рис. 1. 8.

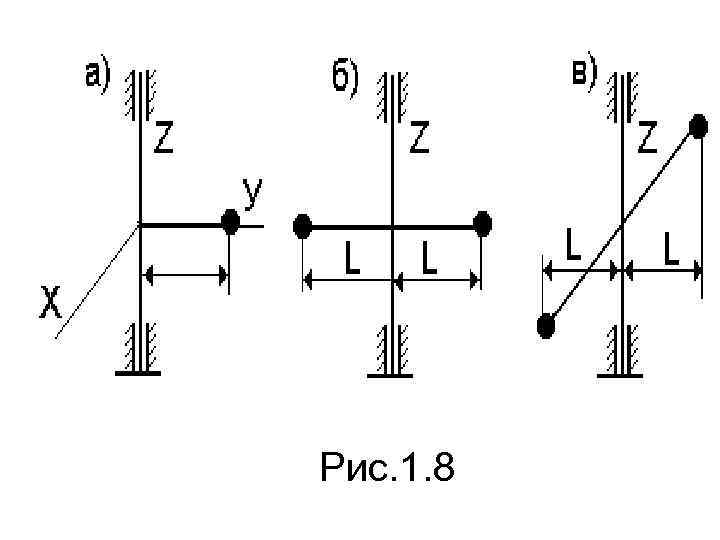
Рис. 1. 8

Конструкция на рис. 1. 8, б является симметричной относительно оси вращения, центр масс ее находится на оси. В этом случае силы инерции грузов образуют уравновешенную систему сил и динамические реакции будут равны нулю. У конструкции на рис. 1. 8, в центр масс также находится на оси вращения, однако она несимметрична относительно оси Z, при этом динамические реакции будут наблюдаться. Для того, чтобы характеризовать симметрию или асимметрию тел или всей конструкции в целом, вводятся понятия центробежных моментов инерции.

Центробежными моментами инерции тела называются величины, определяемые равенствами: (1. 8) где mk- массы отдельных точек, xk , yk и zk – координаты этих точек.

В зависимости от формы тела и расположения осей центробежные моменты инерции могут быть положительными, отрицательными или равными нулю. Для тел, имеющих ось симметрии, центробежные моменты инерции, содержащие в индексах эту ось равны нулю. Такие оси называются главными осями инерции, а осевые моменты инерции относительно этих осей – главными моментами инерции. В каждой точке тела можно построить три главные оси инерции. Главные оси инерции, построенные в центре масс, называются главными центральными осями инерции. Нетрудно убедиться, что для конструкции на рис. 1. 8, б ось Z является главной, а на рис. 1. 8, в – нет.

Особый интерес представляет вопрос о том, как должна быть распределена масса тела по его объему, чтобы динамические давления на опоры при вращении тела вокруг неподвижной оси отсутствовали. Другими словами: какова должна быть геометрия масс тела, чтобы его ось вращения не «била» по подшипникам? Рассмотрим тело, равномерно вращающееся вокруг оси АВ, закрепленной в подшипниках (рис. 1. 9).

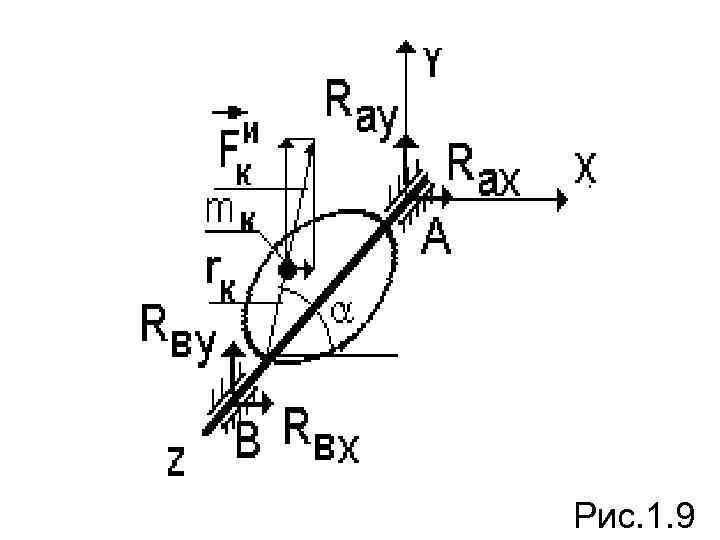
Рис. 1. 9

Свяжем с телом произвольную систему координат, как это показано на рисунке, и рассмотрим произвольную точку mk , расстояние до оси вращения которой равно rk, а координаты ее - xk, yk, zk. Так как тело вращается равномерно, то все точки его будут иметь только нормальное ускорение, а силы инерции – центробежными

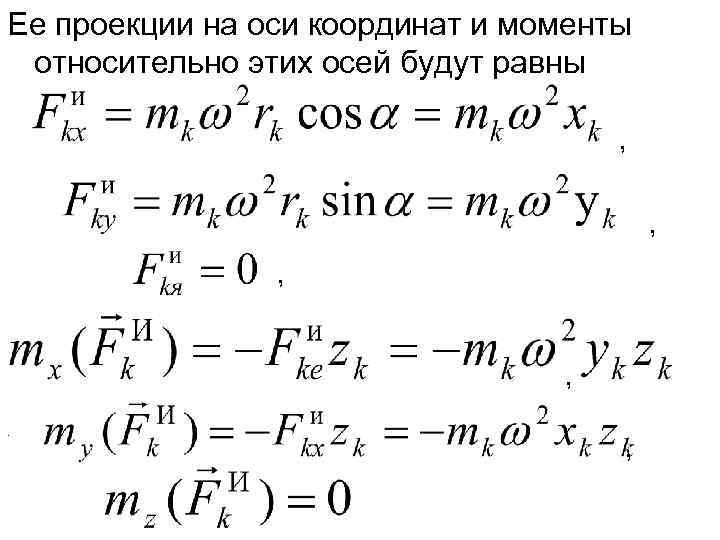
Ее проекции на оси координат и моменты относительно этих осей будут равны , , ,

Составим кинетостатические уравнения равновесия для пространственной системы сил, действующей на тело, при этом реакции подшипников А и В разложим на две составляющие –Rax, Ray, Rвx, Rвy (а) (б) (в) (г)

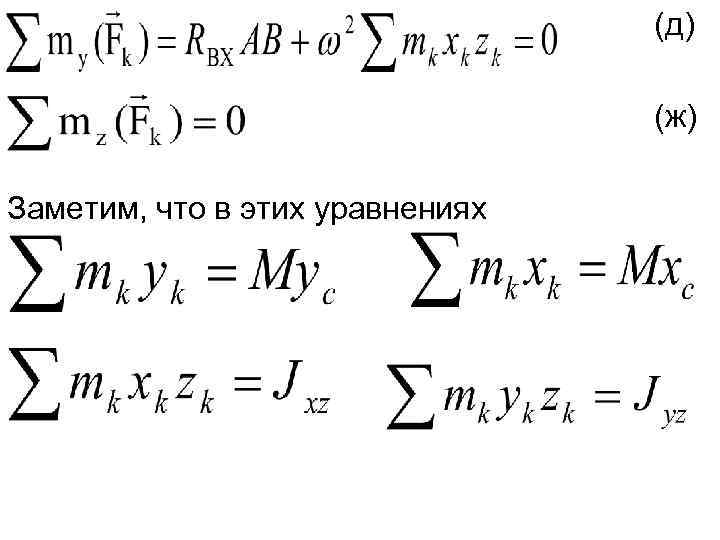
(д) (ж) Заметим, что в этих уравнениях

Подставляя эти значения в выражения (а)-(ж) получим

Из этого следует, что для уничтожения динамических реакций необходимо выполнение двух условий: 1) Хс=Ус=0 , то есть центр масс должен находиться на оси вращения, 2) Jxz=Jyz=0, то есть ось вращения должна быть главной осью инерции. Другими словами: при вращении тела динамические давления на опоры будут отсутствовать, если ось вращения будет главной центральной осью инерции, например, при вращении осесимметричного тела вокруг оси симметрии ( рис. 1. 8, б).

Однако даже если спроектированная деталь будет теоретически симметричной, при изготовлении достичь этих условий невозможно из-за поля допусков размеров, неоднородности материала и других причин. Кроме того, в процессе эксплуатации детали могут деформироваться, что приводит к отклонению от первоначальной формы. Поэтому для уменьшения динамических реакций быстровращающиеся тела подвергают уравновешиванию или балансировке. Различают статическую и динамическую балансировку.

Цель статической балансировки – достижение первого условия, то есть Хс=Ус=0. Данной операции подвергаются детали имеющие небольшие осевые размеры, например, диски колес автомобилей, маховики и т. п. (в этом случае значения Jxz и Jyz незначительны). Процесс выполняется на станках для статической балансировки путем присоединения или удаления к детали точечной массы. Схема статической балансировки показана на рис 1. 10.

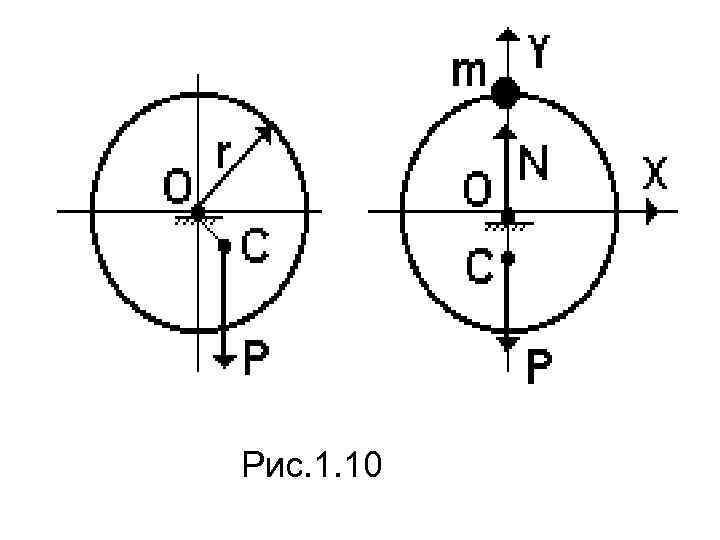
Рис. 1. 10

Пусть центр масс детали смещен на расстояние ОС от оси вращения. Тогда, если установить тело на опору, после нескольких качаний тело установится в положении равновесия, таким образом можно установить место расположения точечного груза. Массу этого груза можно найти из условия откуда m=M. OC/r,

(М – масса детали, r –расстояние от точечной массы до оси вращения). Расстояние ОС определяется путем измерение динамического давления на опору. Так как то

Аналогичный результат можно получить, если удалить данную массу с противоположной стороны детали. Динамической балансировке подвергаются детали, имеющие большие осевые размеры – коленчатые и распределительные валы и т. п. Цель ее – сделать ось вращения главной центральной осью инерции. Процесс выполняется на специальных станках для динамической балансировки, а цель может быть достигнута путем присоединения двух точечных масс.