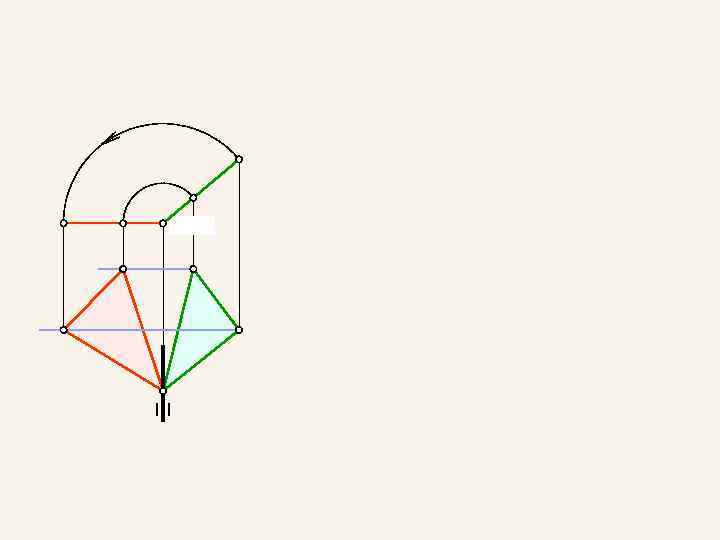1. Предмет и метод начертательной геометрии 1.

1. Предмет и метод начертательной геометрии

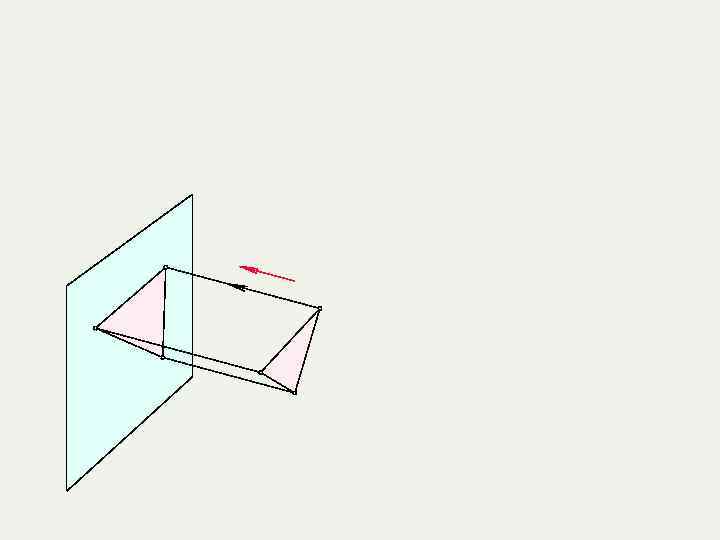
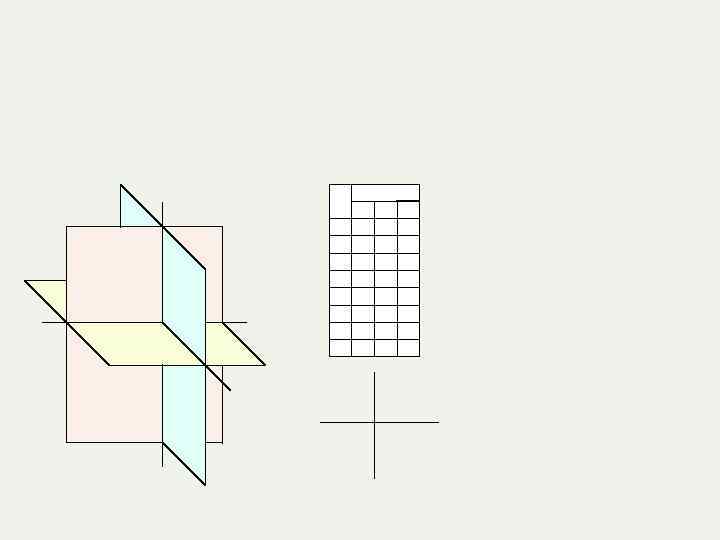
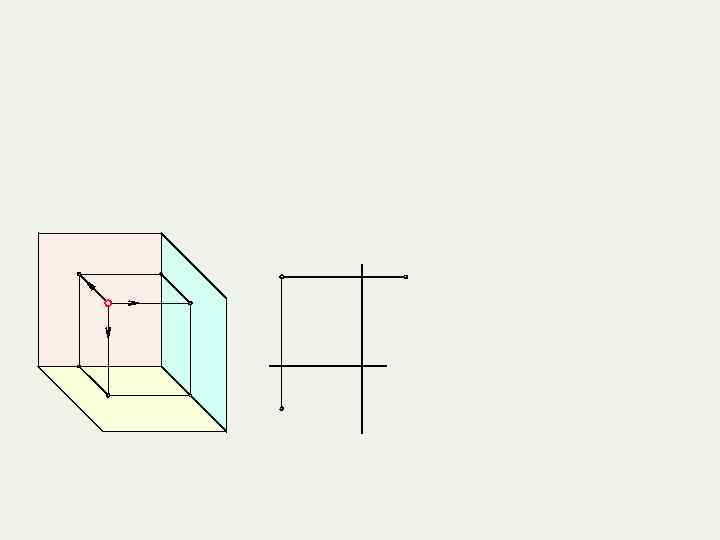
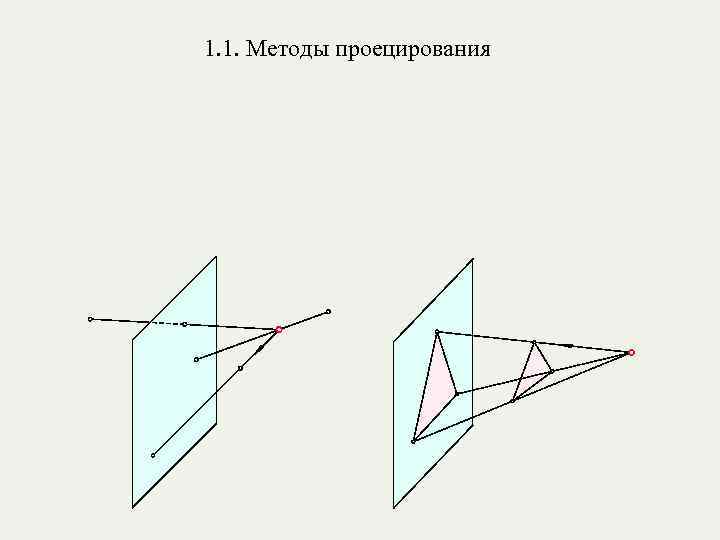1. 1. Методы проецирования

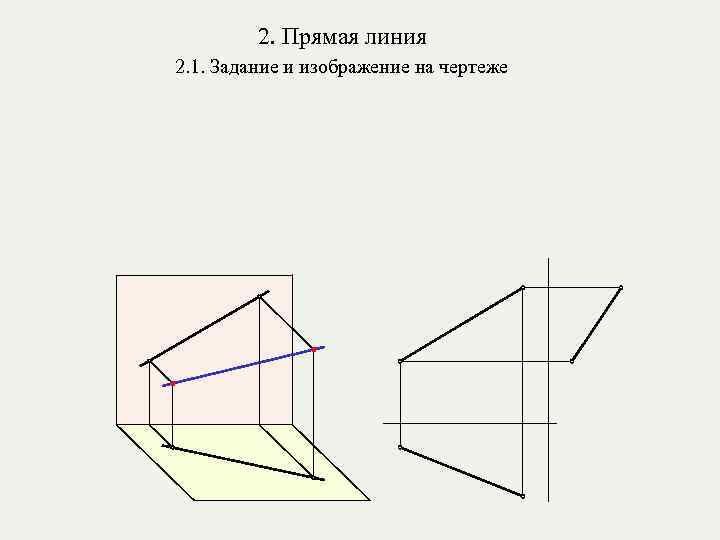2. Прямая линия 2. 1. Задание и изображение на чертеже

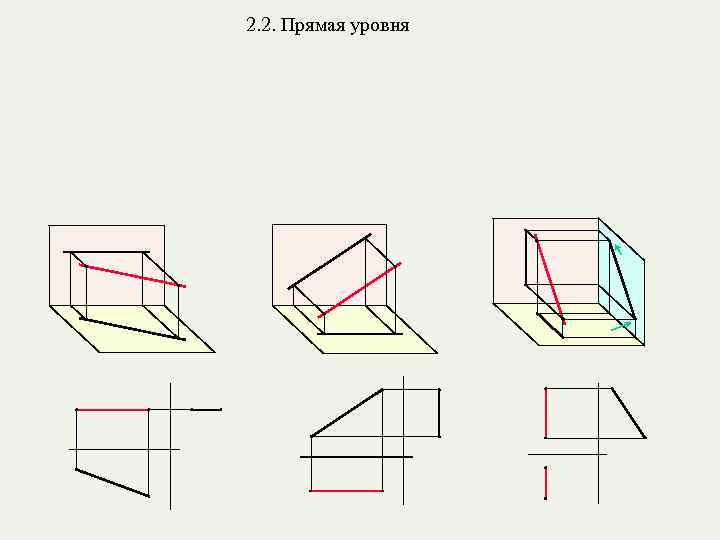2. 2. Прямая уровня

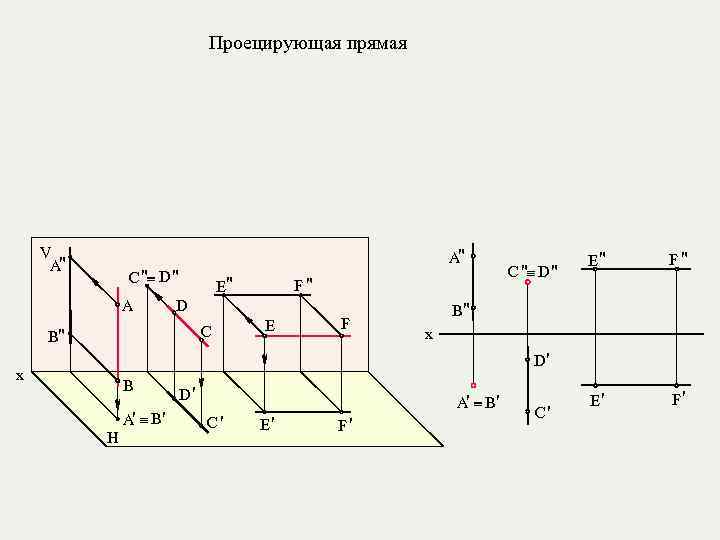Проецирующая прямая V A" A" _ C "_ D " A E" F" D C B" E F C "_ D " E" F" E' F' B" x D' x B _ A' _ B' H D' _ A' _ B ' C' E' F' C'

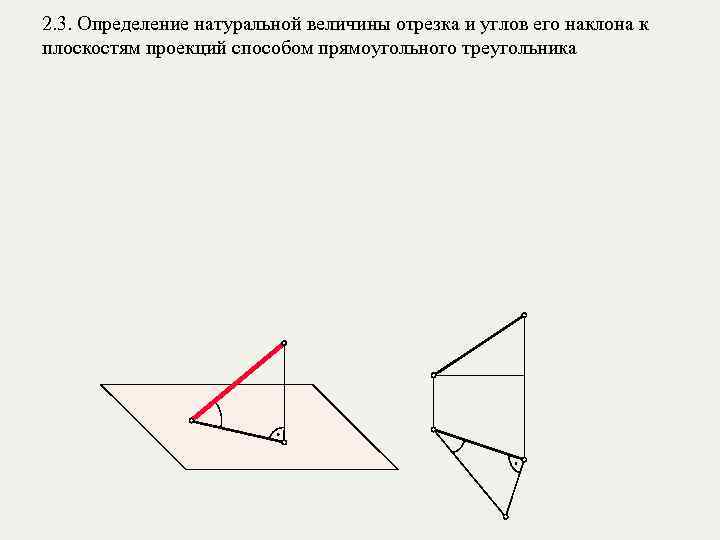2. 3. Определение натуральной величины отрезка и углов его наклона к плоскостям проекций способом прямоугольного треугольника

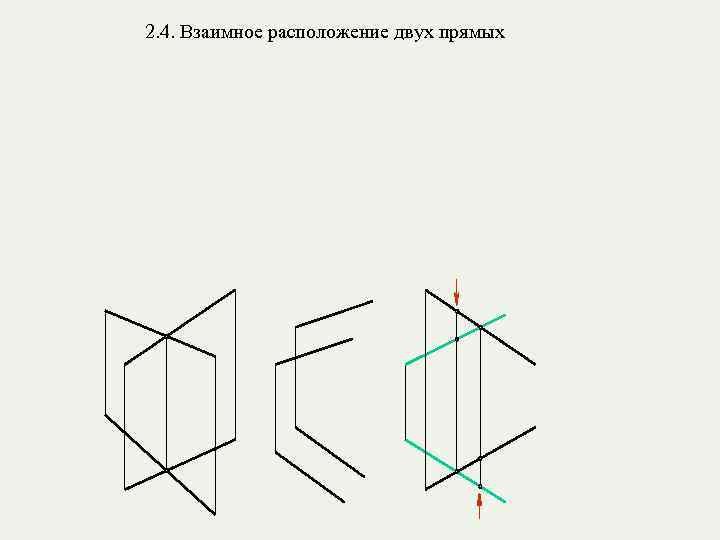2. 4. Взаимное расположение двух прямых

2. 5. Взаимное расположение точки и прямой Из свойств параллельного проецирования (свойство принадлежности) известно, что если точка лежит на прямой, то ее проекции должны лежать на одноименных проекциях этой прямой. Поэтому, из четырех точек A, B, C и D, приведенных на чертеже, лишь одна точка А лежит на прямой. Точка В находится над прямой, так как она расположена выше, чем горизонтально конкурирующая с ней точка прямой a (фронтальная проекция этой точки прямой a отмечена кстиком). Аналогично, точка С находится перед прямой a, точка D расположена ниже и дальше точки прямой a. Определение взаимного положения точки и профильной прямой выполняется с помощью построения профильной проекции. На чертеже точка С расположена над и перед прямой AB.

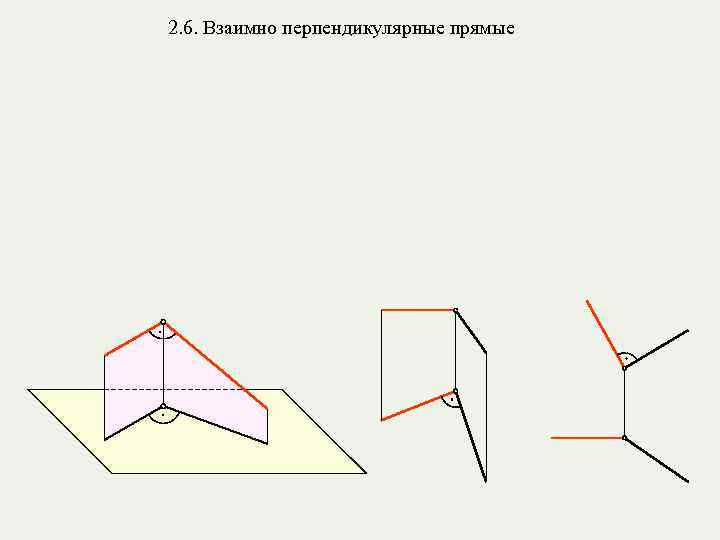2. 6. Взаимно перпендикулярные прямые

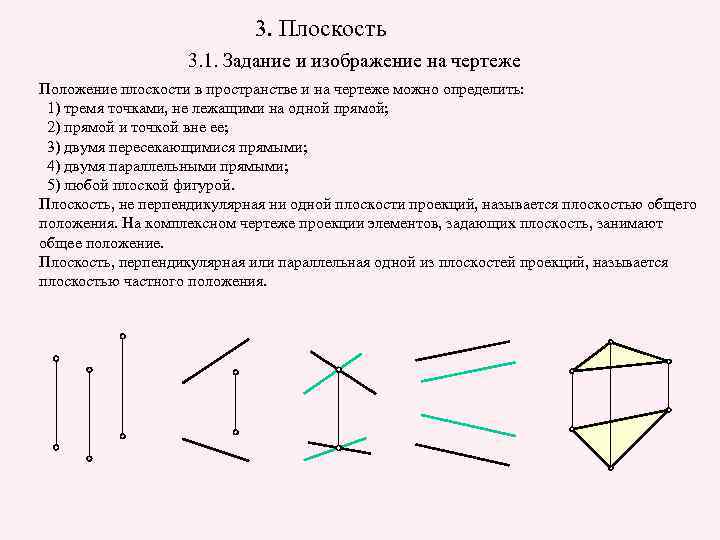3. Плоскость 3. 1. Задание и изображение на чертеже Положение плоскости в пространстве и на чертеже можно определить: 1) тремя точками, не лежащими на одной прямой; 2) прямой и точкой вне ее; 3) двумя пересекающимися прямыми; 4) двумя параллельными прямыми; 5) любой плоской фигурой. Плоскость, не перпендикулярная ни одной плоскости проекций, называется плоскостью общего положения. На комплексном чертеже проекции элементов, задающих плоскость, занимают общее положение. Плоскость, перпендикулярная или параллельная одной из плоскостей проекций, называется плоскостью частного положения.

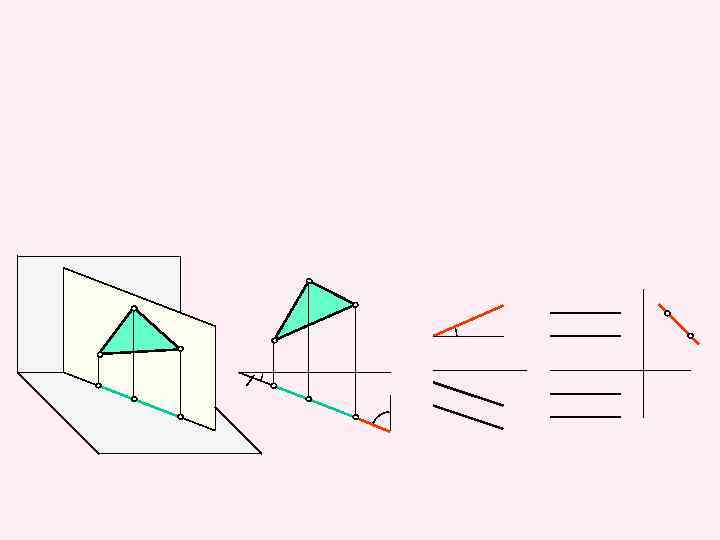
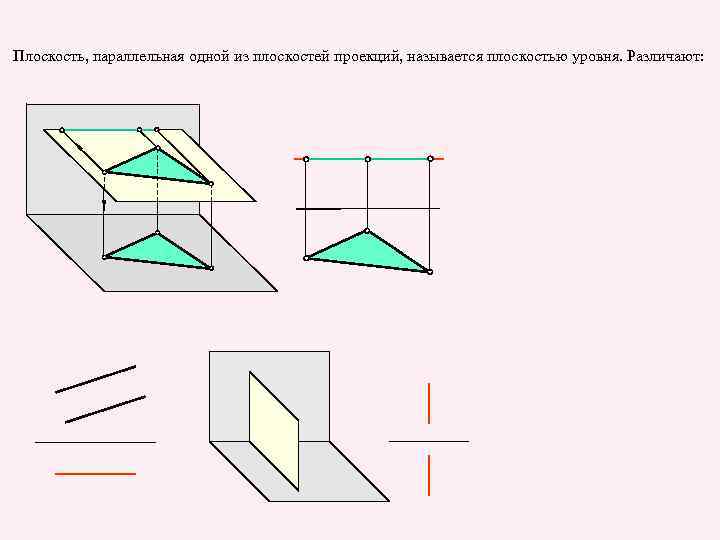Плоскость, параллельная одной из плоскостей проекций, называется плоскостью уровня. Различают:

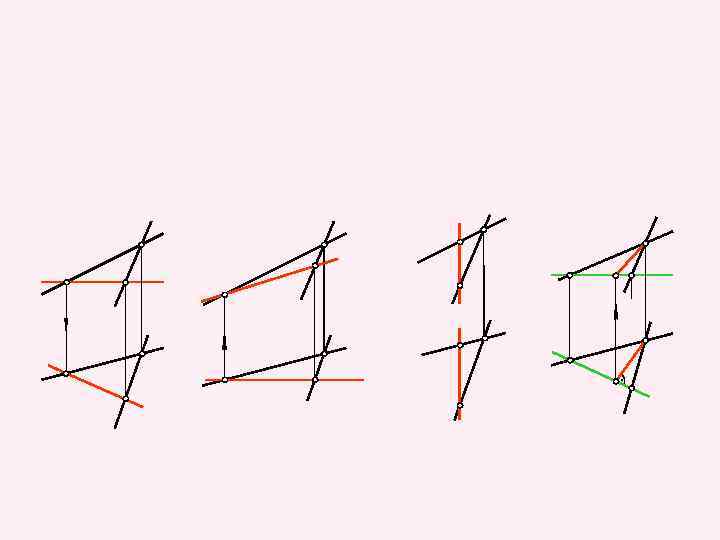
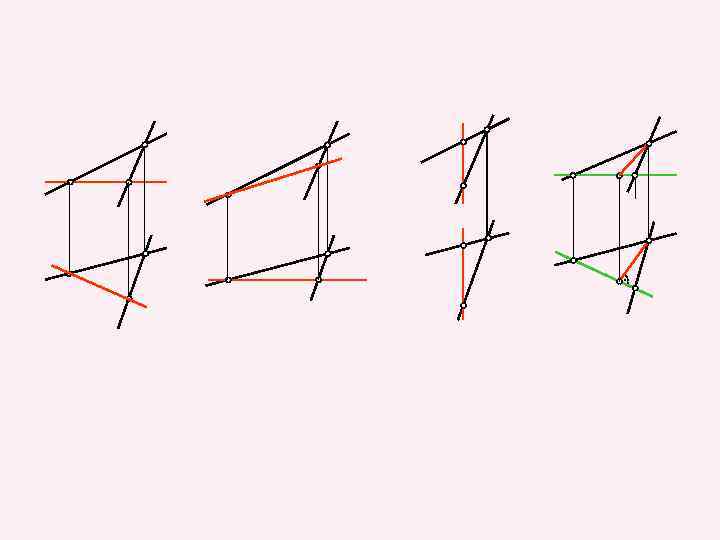
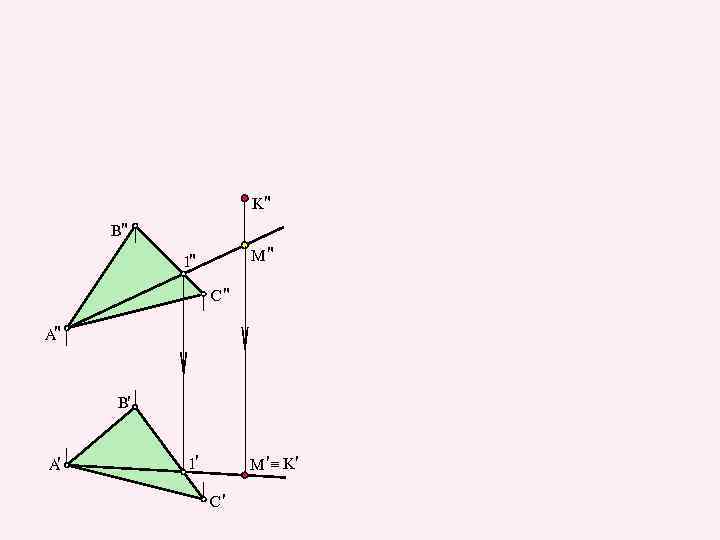K" B" M" 1" C" A" B' A' _ M '_ K' 1' C'

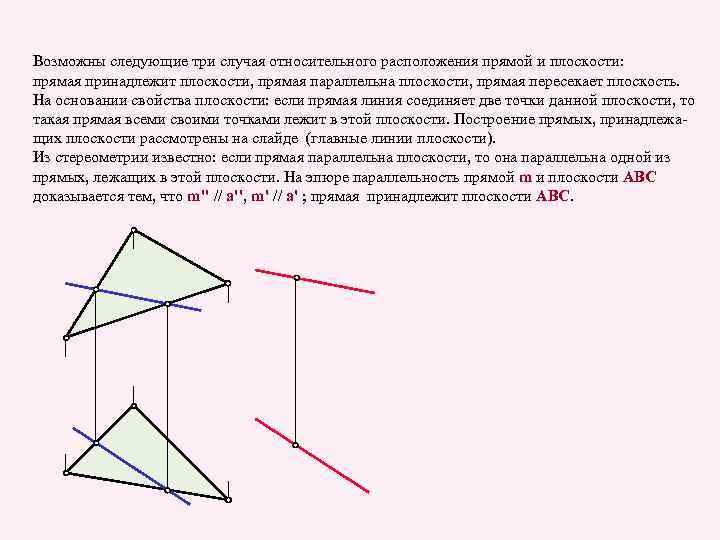Возможны следующие три случая относительного расположения прямой и плоскости: прямая принадлежит плоскости, прямая параллельна плоскости, прямая пересекает плоскость. На основании свойства плоскости: если прямая линия соединяет две точки данной плоскости, то такая прямая всеми своими точками лежит в этой плоскости. Построение прямых, принадлежащих плоскости рассмотрены на слайде (главные линии плоскости). Из стереометрии известно: если прямая параллельна плоскости, то она параллельна одной из прямых, лежащих в этой плоскости. На эпюре параллельность прямой m и плоскости ABC доказывается тем, что m'' // a'', m' // a' ; прямая принадлежит плоскости ABC.

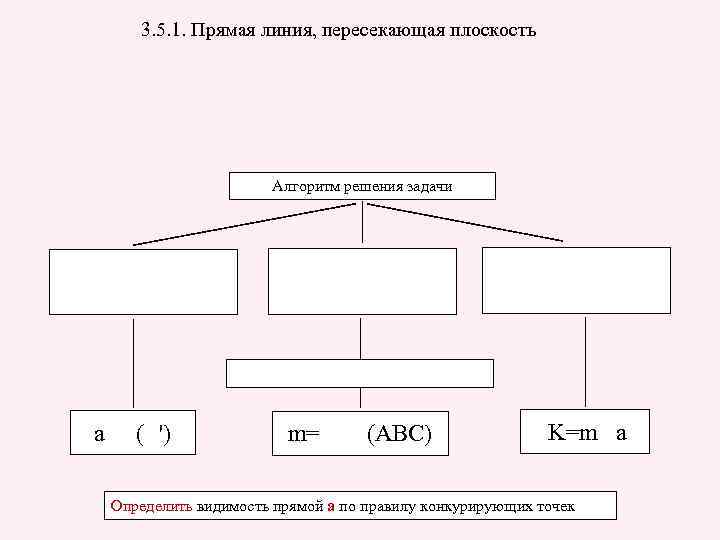3. 5. 1. Прямая линия, пересекающая плоскость Алгоритм решения задачи a ( ') m= (ABC) K=m a Определить видимость прямой a по правилу конкурирующих точек

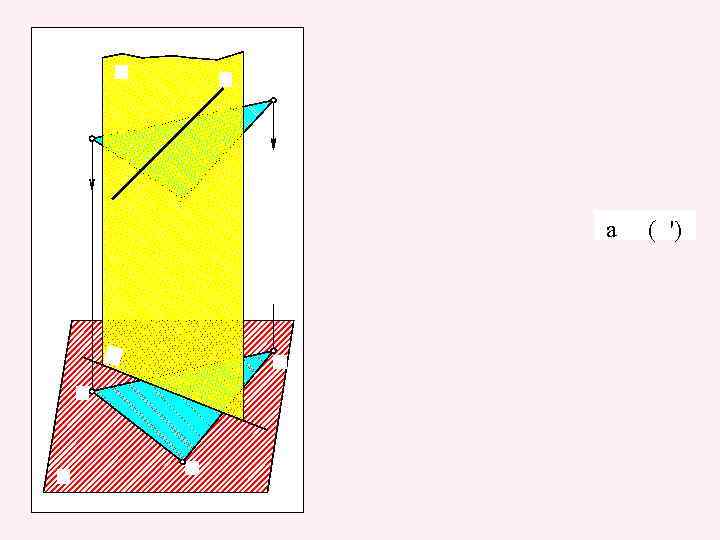a ( ')

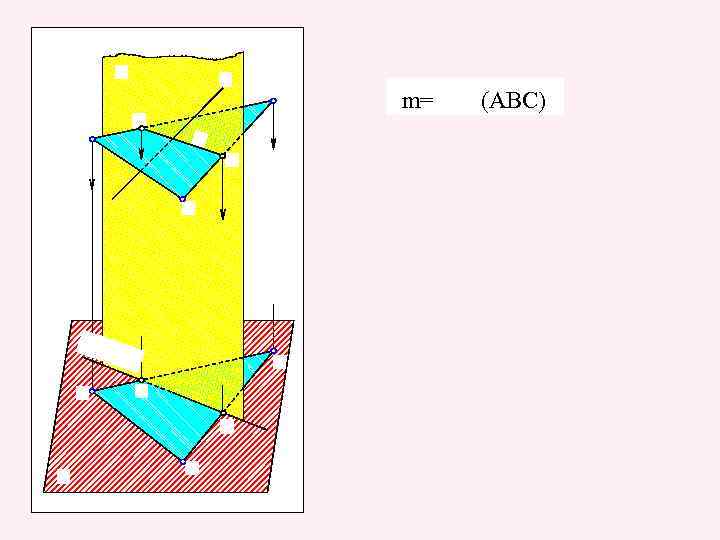m= (ABC)

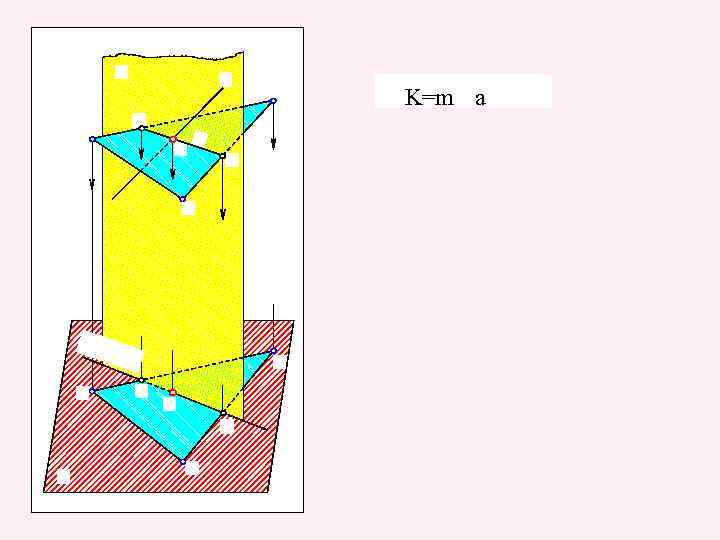K=m a

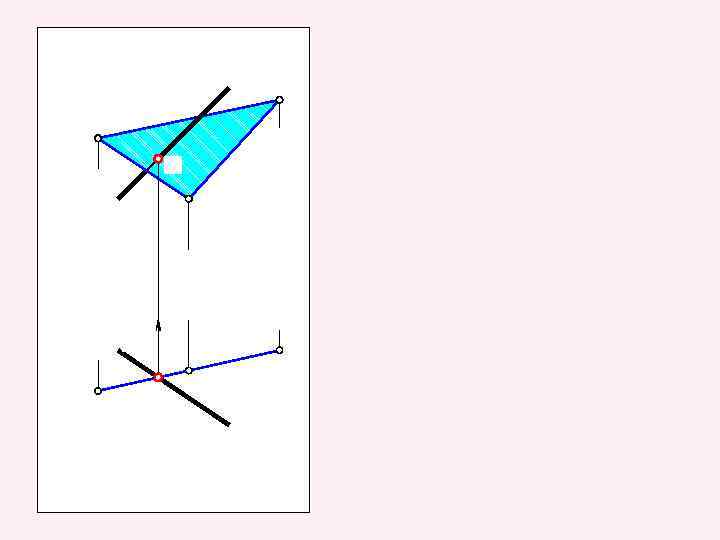
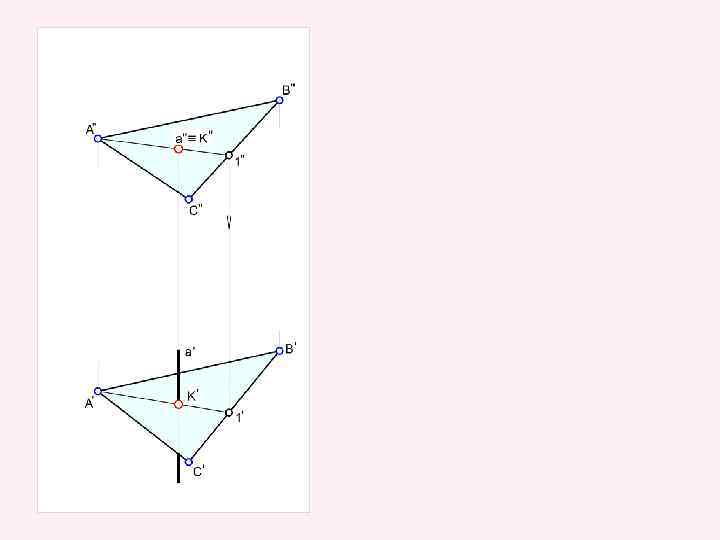
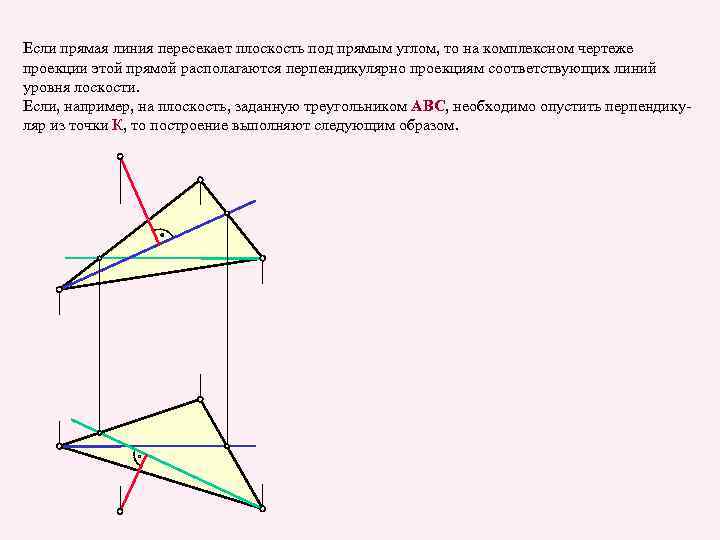Если прямая линия пересекает плоскость под прямым углом, то на комплексном чертеже проекции этой прямой располагаются перпендикулярно проекциям соответствующих линий уровня лоскости. Если, например, на плоскость, заданную треугольником ABC, необходимо опустить перпендикуляр из точки К, то построение выполняют следующим образом.

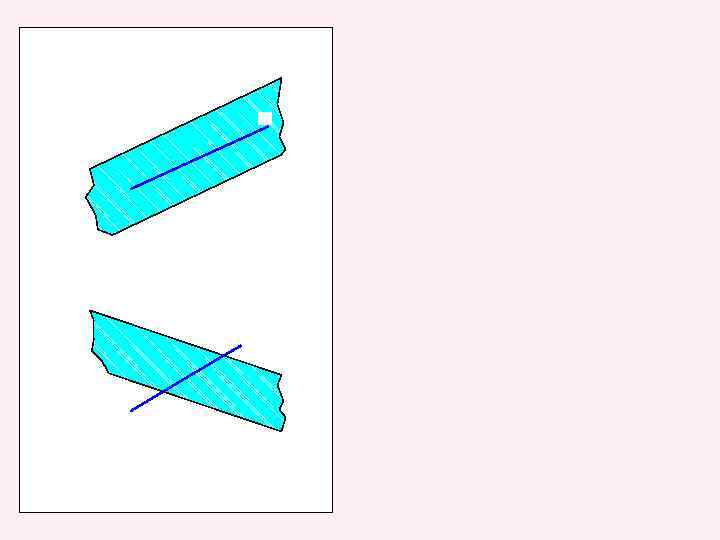
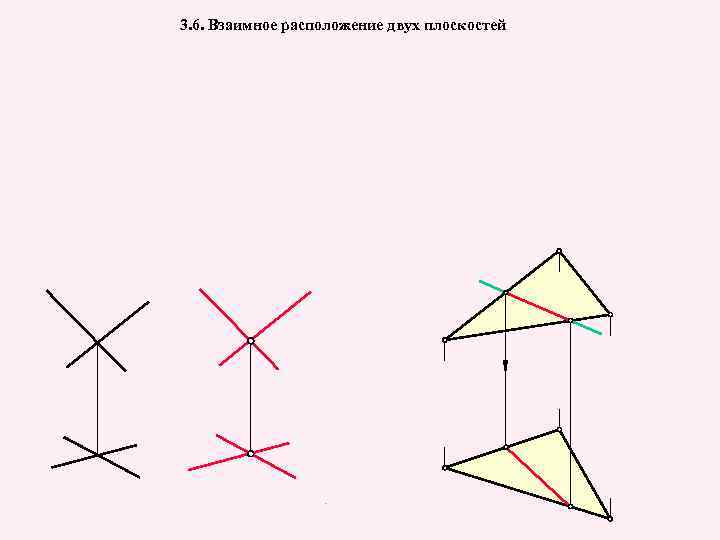3. 6. Взаимное расположение двух плоскостей

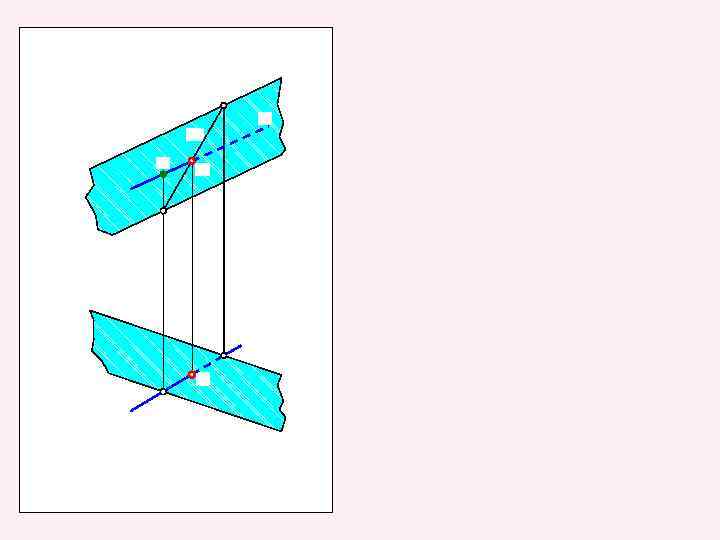
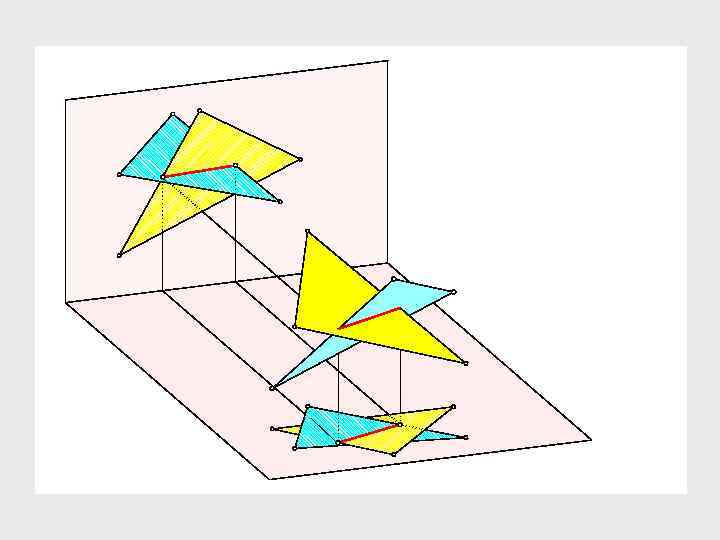
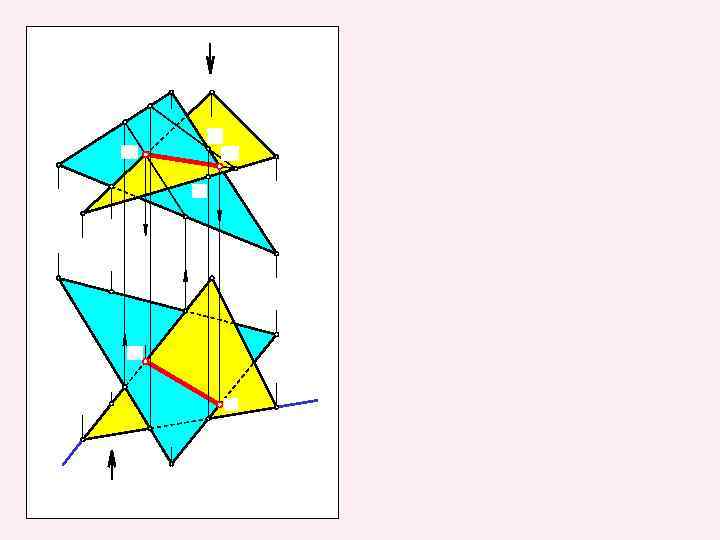
Определение линии пересечения двух плоскостей общего положения

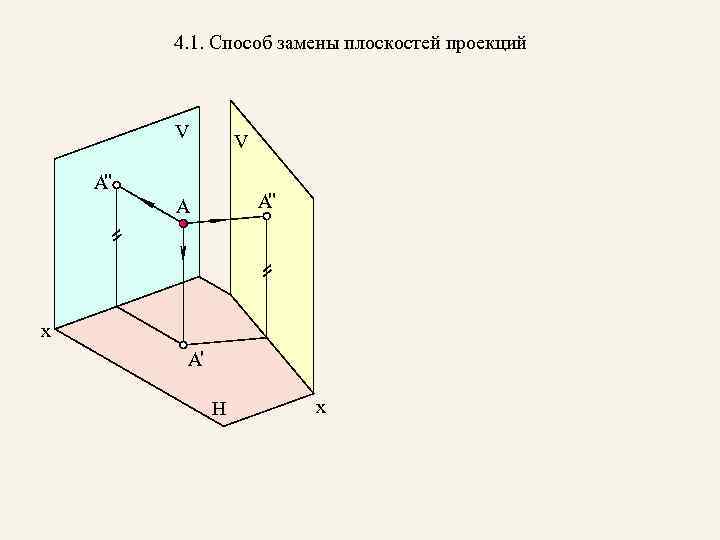4. 1. Способ замены плоскостей проекций V V " A A x A' H x

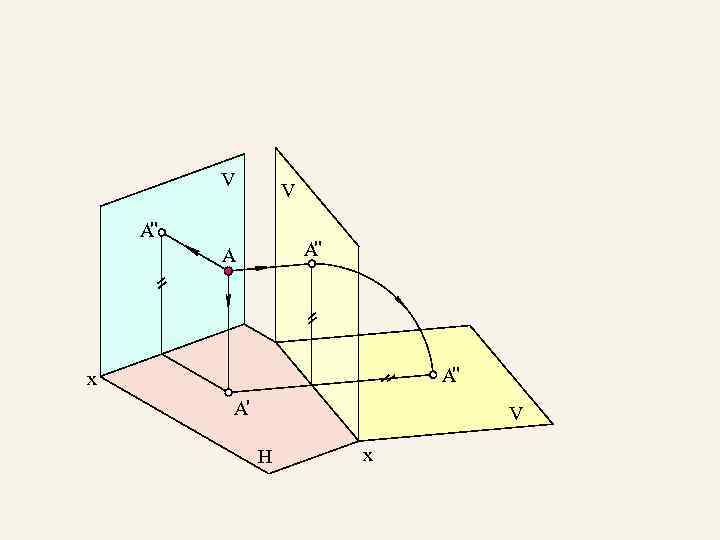V V " A A " A x A' V H x

Решение четырех основных задач способом замены плоскостей проекций V A" A A" V a" a" B" x a A' a' H B" B B' x

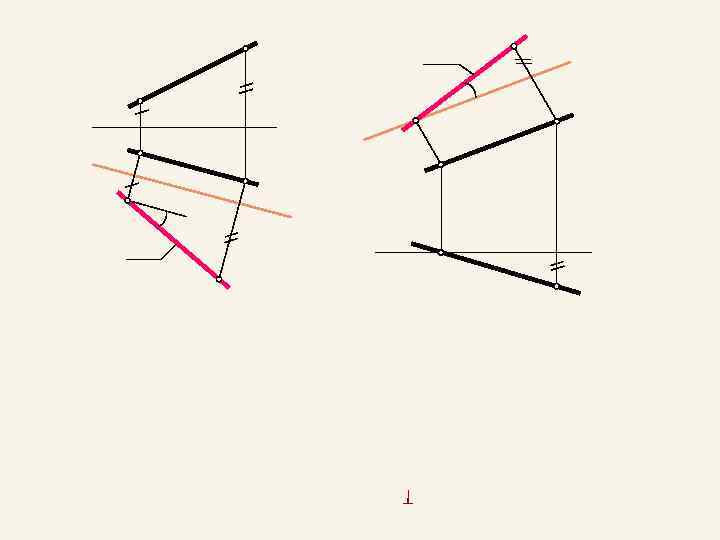
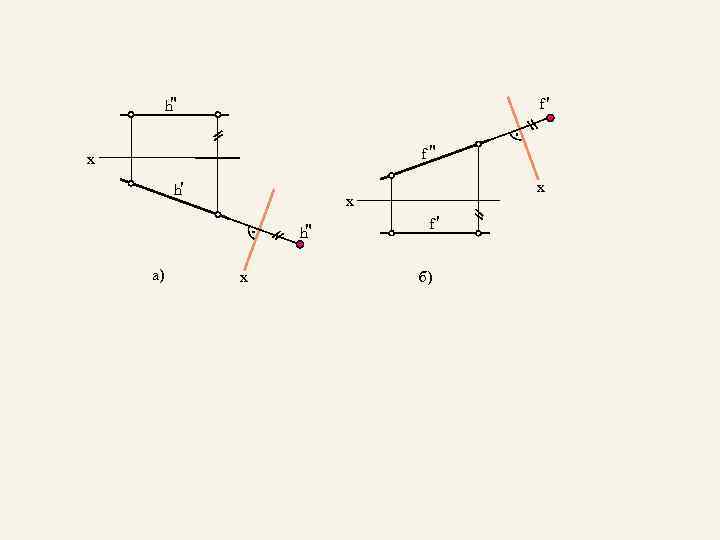f' h" f" x h' x h" а) x x f' б)

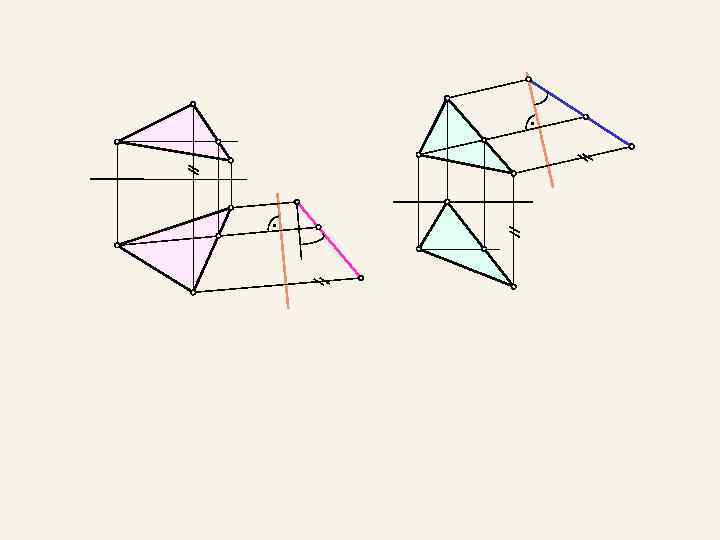
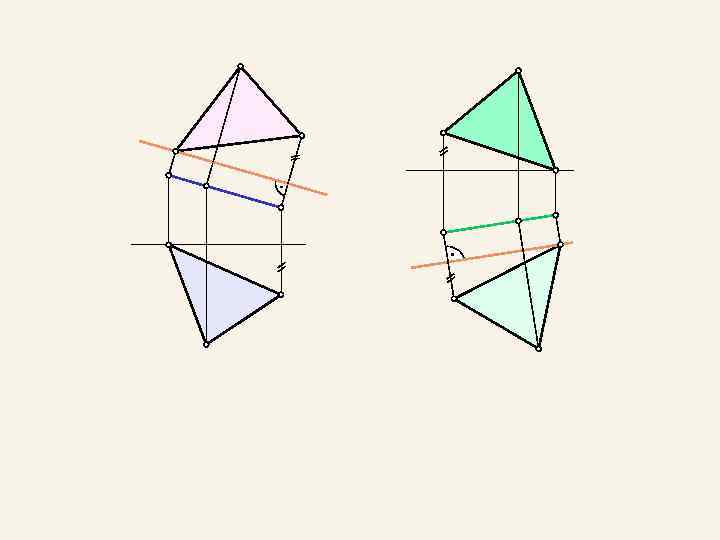
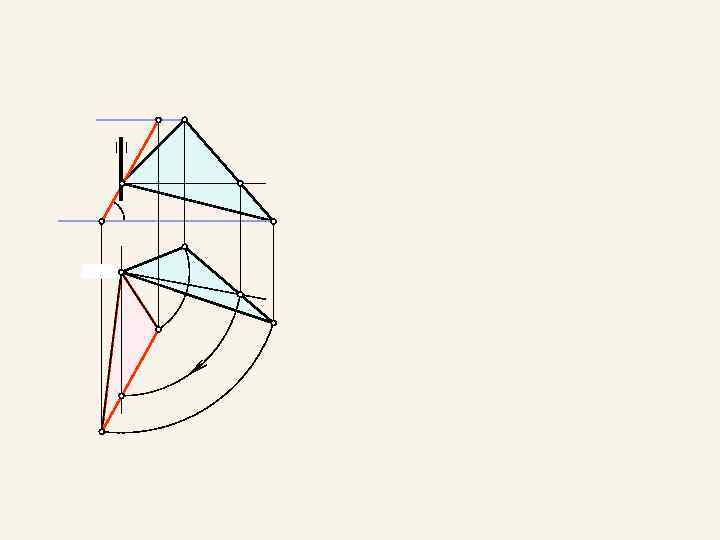
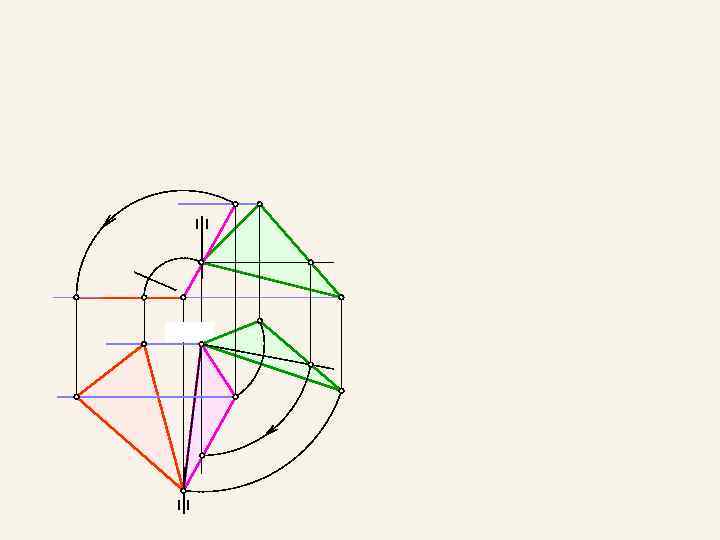
4. 2. Способ врашения вокруг проецирующей оси

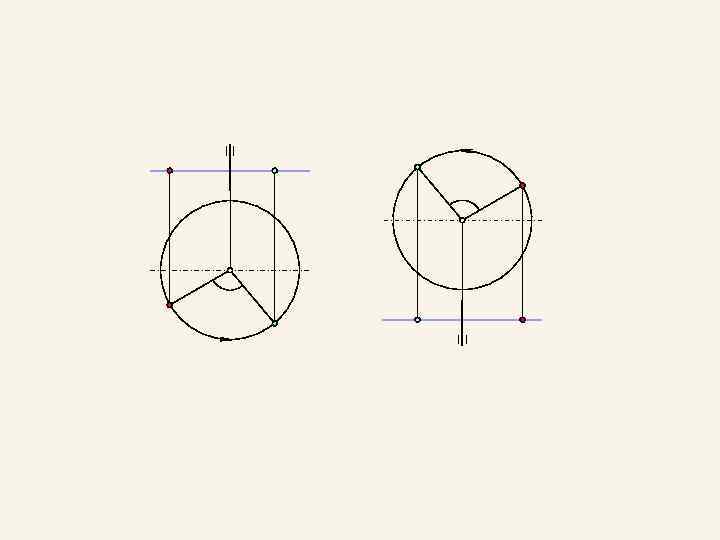
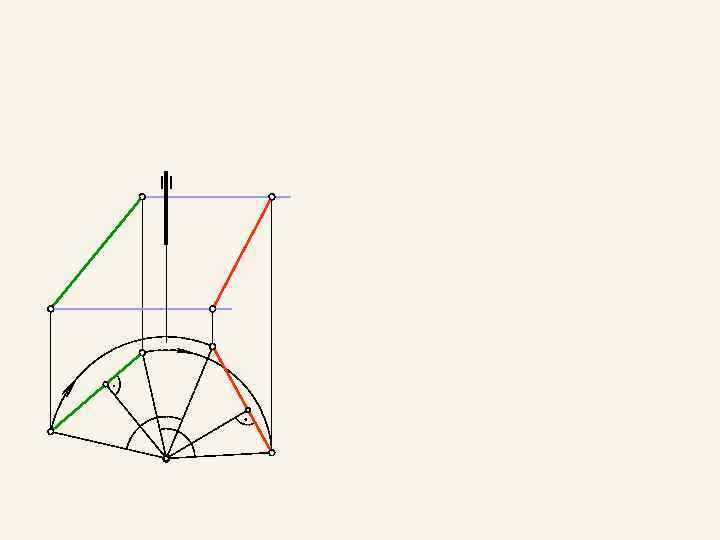
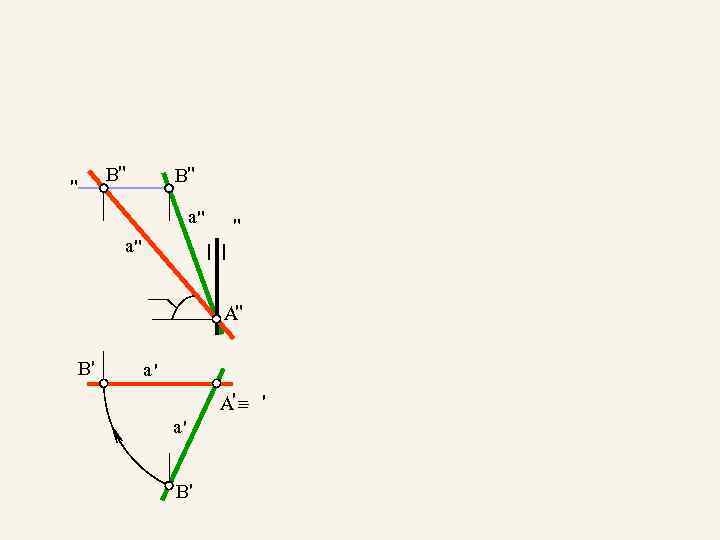" B" B" a" a" " A" B' a' _ A' _ ' a' B'

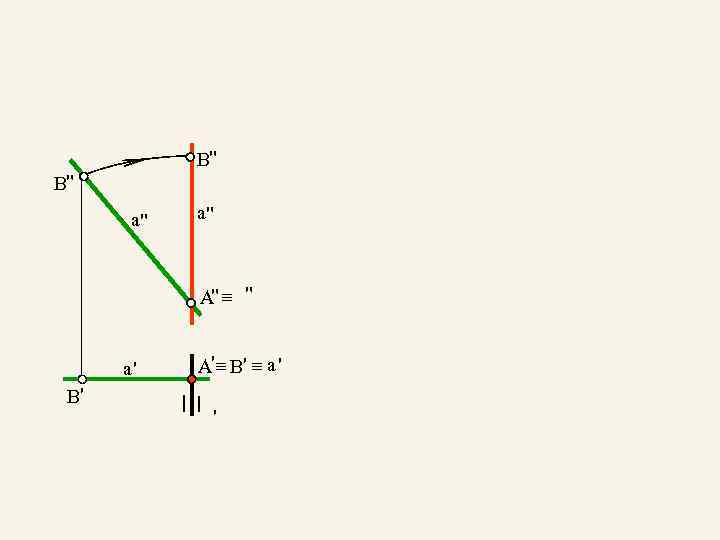B" B" a" a" _ A" _ " a' B' _ _ A' _ B' _ a ' '