1 Практическое занятие 1 Интерференция света СОДЕРЖАНИЕ ТЕОРИИ

1 Практическое занятие 1. Интерференция света СОДЕРЖАНИЕ ТЕОРИИ 1. Интерференция света. Условие максимума и минимума интерференции. Опыт Юнга 2. Интерференция в тонких пленках. Полосы равного наклона и полосы равной толщины. Литература: 1. Сборник вопросов упражнений и задач по курсу общей физики. Ч. III. № 2616(3). - Таганрог, 1999. 2. Методическое пособие к решению задач по курсу общей физики. Ч. III. № 3126 -3. - Таганрог, 2001.

ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ 1. Условие наблюдения максимума интенсивности света при интерференции от двух точечных когерентных источников или узких щелей: Условие наблюдения минимума: 2. Координата максимумов и минимумов интенсивности света на экране при интерференции от двух параллельных щелей: Ширина интерференционной полосы (расстояние между двумя соседними максимумами или минимумами): 3. Оптическая разность хода 2 -х световых волн при интерференции в тонких плёнках: а) в отражённом свете : б) в проходящем свете : 4. Радиус колец Ньютона: светлые кольца в отражённом свете и тёмные кольца в проходящем свете (k = 1, 2, 3, … - номер кольца): Тёмные кольца в отражённом и светлые в проходящем свете: Справочный материал: Показатель преломления: - воды (мыльной воды): n = 1, 33 - стекла: n = 1, 5

1 A. (16. 5) В опыте Юнга отверстия освещаются монохроматическим светом ( = 600 нм). Расстояние между отверстиями d = 1 мм, расстояние от отверстий до экрана L = 3 м. Найти положение трёх первых светлых полос. = 600 нм d =1 мм L = 3 м Y 1, 2, 3 - ? Максимум интенсивности при интерференции световых волн от двух источников S 1 и S 2 в точке наблюдения Р будет, если разность хода лучей r равна целому числу длин волн: Величину r найдем, определив r 1 и r 2 : Приравняем правые части:

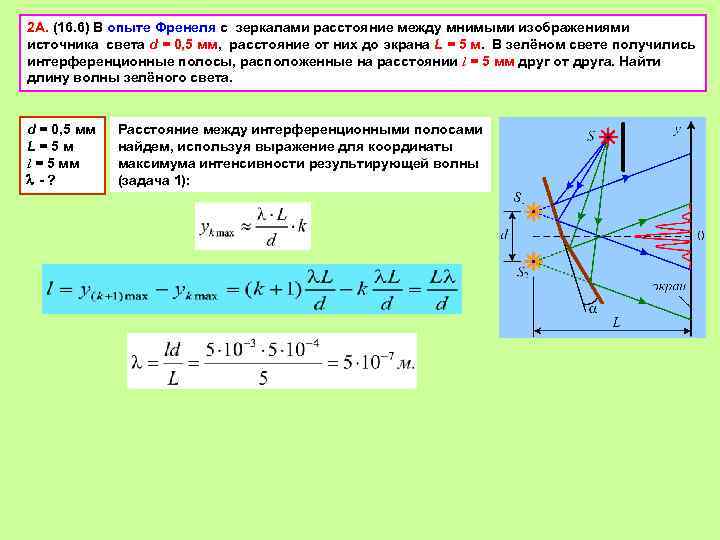2 A. (16. 6) В опыте Френеля с зеркалами расстояние между мнимыми изображениями источника света d = 0, 5 мм, расстояние от них до экрана L = 5 м. В зелёном свете получились интерференционные полосы, расположенные на расстоянии l = 5 мм друг от друга. Найти длину волны зелёного света. d = 0, 5 мм L = 5 м l = 5 мм - ? Расстояние между интерференционными полосами найдем, используя выражение для координаты максимума интенсивности результирующей волны (задача 1):

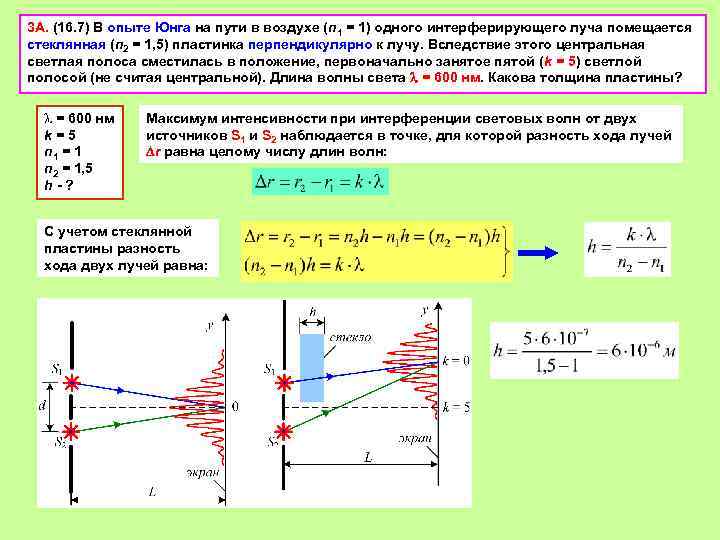3 А. (16. 7) В опыте Юнга на пути в воздухе (n 1 = 1) одного интерферирующего луча помещается стеклянная (n 2 = 1, 5) пластинка перпендикулярно к лучу. Вследствие этого центральная светлая полоса сместилась в положение, первоначально занятое пятой (k = 5) светлой полосой (не считая центральной). Длина волны света = 600 нм. Какова толщина пластины? l = 600 нм k = 5 n 1 = 1 n 2 = 1, 5 h - ? Максимум интенсивности при интерференции световых волн от двух источников S 1 и S 2 наблюдается в точке, для которой разность хода лучей r равна целому числу длин волн: С учетом стеклянной пластины разность хода двух лучей равна:

4 A. (16. 9) На мыльную плёнку падает белый свет под углом = 45 к поверхности плёнки. При какой наименьшей толщине плёнки d отражённые лучи будут окрашены в жёлтый цвет ( = 600 нм)? a = 45 l = 600 нм n = 1, 33 d - ? Максимум интенсивности результирующей волны при интерференции 2 -х лучей, отразившихся от тонкой пленки, при условии, что водяная пленка оптически более плотная среда, чем воздух, описывается уравнением: (1) Оптическая разность хода лучей, которая обеспечивает интерференцию отражённых лучей в плёнке, имеющей наименьшую толщину d, соответствует одной длине волны, т. е. k = 1. С учетом этого получаем: PS: Ответ не совпал с приведенным в решебнике, где формула (1) записана для пленки из оптически менее плотной среды, чем воздух, в следующем виде:

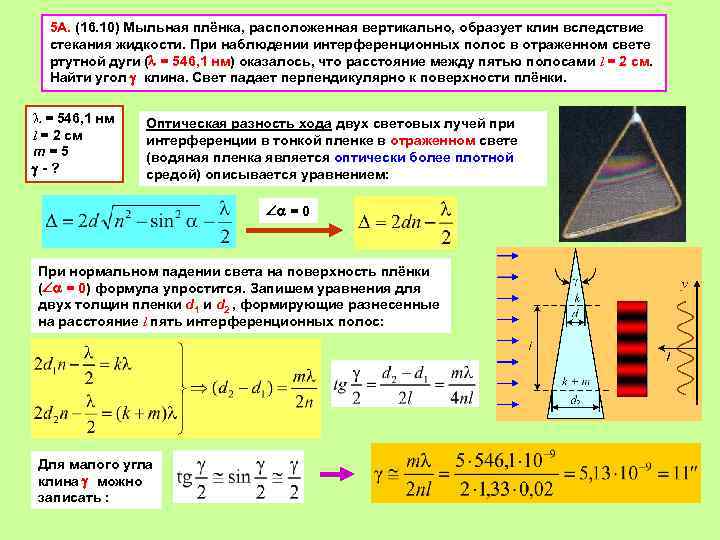5 A. (16. 10) Мыльная плёнка, расположенная вертикально, образует клин вследствие стекания жидкости. При наблюдении интерференционных полос в отраженном свете ртутной дуги ( = 546, 1 нм) оказалось, что расстояние между пятью полосами l = 2 см. Найти угол клина. Свет падает перпендикулярно к поверхности плёнки. l = 546, 1 нм l = 2 см m = 5 - ? Оптическая разность хода двух световых лучей при интерференции в тонкой пленке в отраженном свете (водяная пленка является оптически более плотной средой) описывается уравнением: = 0 При нормальном падении света на поверхность плёнки ( = 0) формула упростится. Запишем уравнения для двух толщин пленки d 1 и d 2 , формирующие разнесенные на расстояние l пять интерференционных полос: Для малого угла клина можно записать :

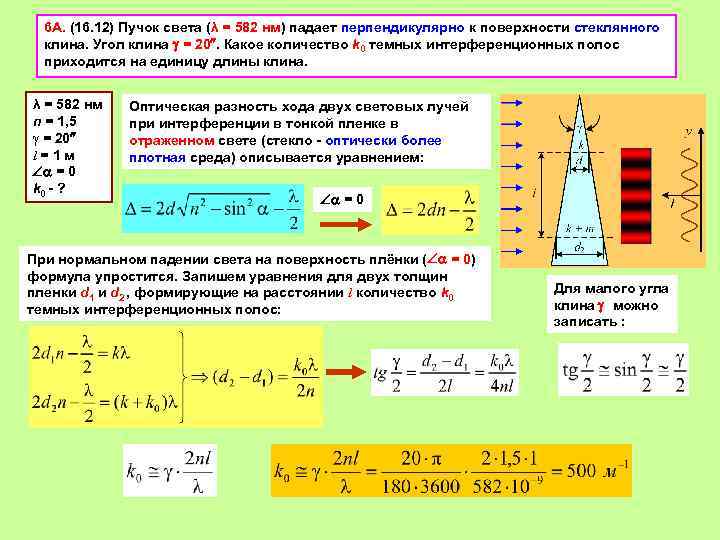6 А. (16. 12) Пучок света (λ = 582 нм) падает перпендикулярно к поверхности стеклянного клина. Угол клина = 20. Какое количество k 0 темных интерференционных полос приходится на единицу длины клина. λ = 582 нм n = 1, 5 g = 20 l = 1 м = 0 k 0 - ? Оптическая разность хода двух световых лучей при интерференции в тонкой пленке в отраженном свете (стекло - оптически более плотная среда) описывается уравнением: = 0 При нормальном падении света на поверхность плёнки ( = 0) формула упростится. Запишем уравнения для двух толщин пленки d 1 и d 2 , формирующие на расстоянии l количество k 0 темных интерференционных полос: Для малого угла клина можно записать :

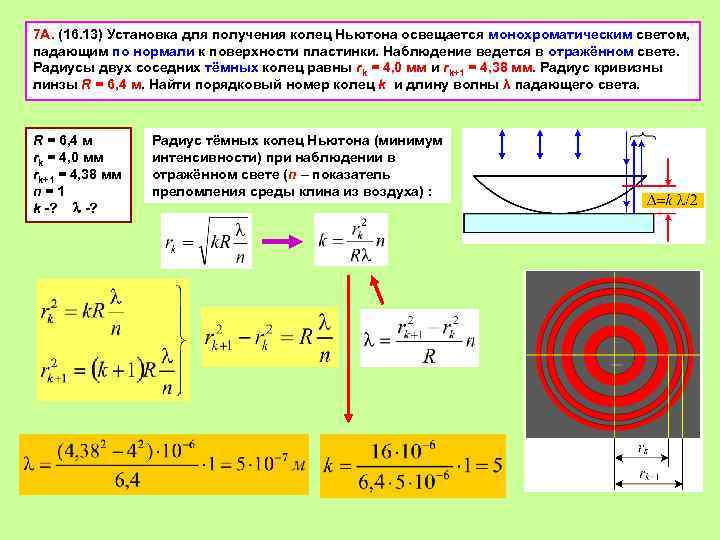7 А. (16. 13) Установка для получения колец Ньютона освещается монохроматическим светом, падающим по нормали к поверхности пластинки. Наблюдение ведется в отражённом свете. Радиусы двух соседних тёмных колец равны rk = 4, 0 мм и rk+1 = 4, 38 мм. Радиус кривизны линзы R = 6, 4 м. Найти порядковый номер колец k и длину волны λ падающего света. R = 6, 4 м rk = 4, 0 мм rk+1 = 4, 38 мм n = 1 k -? Радиус тёмных колец Ньютона (минимум интенсивности) при наблюдении в отражённом свете (n – показатель преломления среды клина из воздуха) :

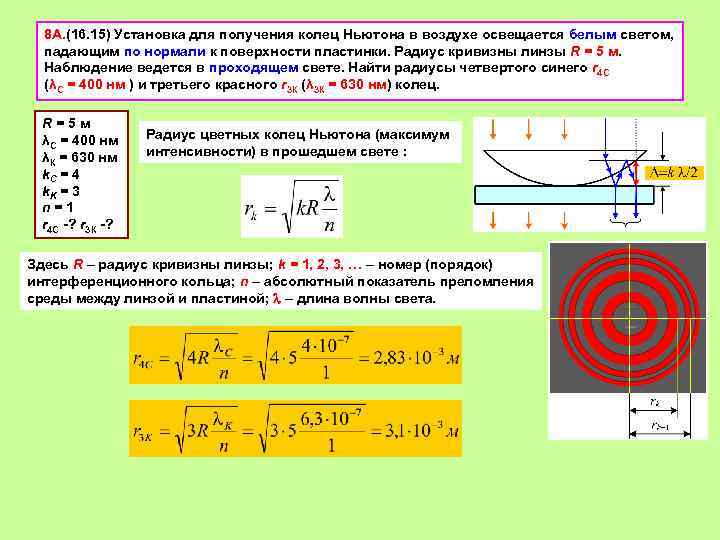8 А. (16. 15) Установка для получения колец Ньютона в воздухе освещается белым светом, падающим по нормали к поверхности пластинки. Радиус кривизны линзы R = 5 м. Наблюдение ведется в проходящем свете. Найти радиусы четвертого синего r 4 С (λС = 400 нм ) и третьего красного r 3 К (λ 3 К = 630 нм) колец. R = 5 м λС = 400 нм λК = 630 нм k. C = 4 k. K = 3 n = 1 r 4 С -? r 3 К -? Радиус цветных колец Ньютона (максимум интенсивности) в прошедшем свете : Здесь R – радиус кривизны линзы; k = 1, 2, 3, … – номер (порядок) интерференционного кольца; n – абсолютный показатель преломления среды между линзой и пластиной; – длина волны света.

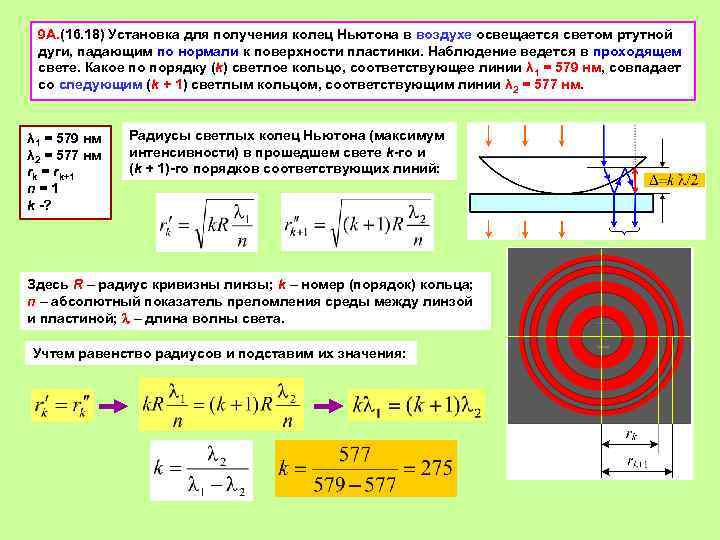9 А. (16. 18) Установка для получения колец Ньютона в воздухе освещается светом ртутной дуги, падающим по нормали к поверхности пластинки. Наблюдение ведется в проходящем свете. Какое по порядку (k) светлое кольцо, соответствующее линии λ 1 = 579 нм, совпадает со следующим (k + 1) светлым кольцом, соответствующим линии λ 2 = 577 нм. λ 1 = 579 нм λ 2 = 577 нм rk = rk+1 n = 1 k -? Радиусы светлых колец Ньютона (максимум интенсивности) в прошедшем свете k-го и (k + 1)-го порядков соответствующих линий: Здесь R – радиус кривизны линзы; k – номер (порядок) кольца; n – абсолютный показатель преломления среды между линзой и пластиной; – длина волны света. Учтем равенство радиусов и подставим их значения:

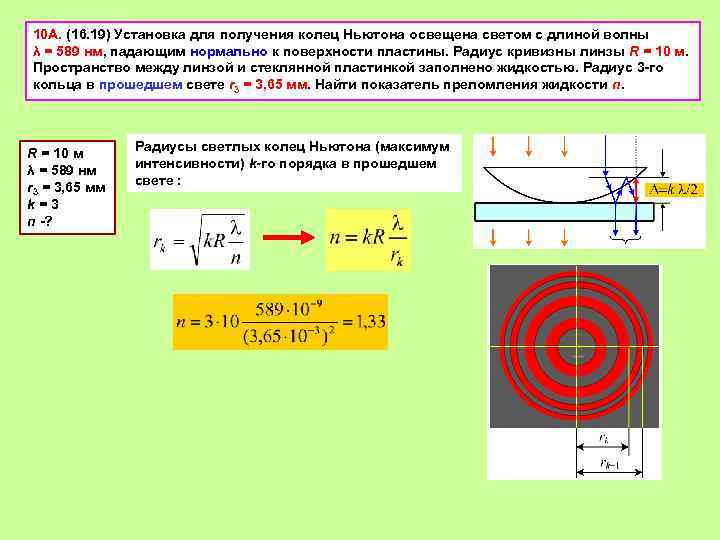10 А. (16. 19) Установка для получения колец Ньютона освещена светом с длиной волны λ = 589 нм, падающим нормально к поверхности пластины. Радиус кривизны линзы R = 10 м. Пространство между линзой и стеклянной пластинкой заполнено жидкостью. Радиус 3 -го кольца в прошедшем свете r 3 = 3, 65 мм. Найти показатель преломления жидкости n. R = 10 м λ = 589 нм r 3 = 3, 65 мм k = 3 n -? Радиусы светлых колец Ньютона (максимум интенсивности) k-го порядка в прошедшем свете :

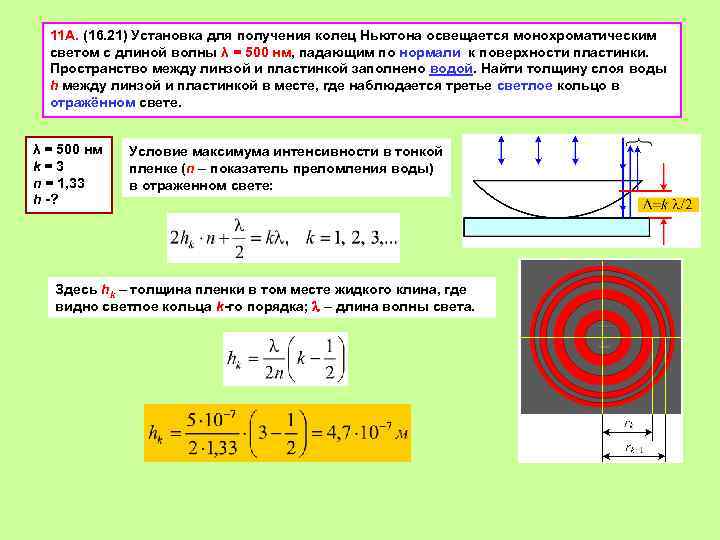11 А. (16. 21) Установка для получения колец Ньютона освещается монохроматическим светом с длиной волны λ = 500 нм, падающим по нормали к поверхности пластинки. Пространство между линзой и пластинкой заполнено водой. Найти толщину слоя воды h между линзой и пластинкой в месте, где наблюдается третье светлое кольцо в отражённом свете. λ = 500 нм k = 3 n = 1, 33 h -? Условие максимума интенсивности в тонкой пленке (n – показатель преломления воды) в отраженном свете: Здесь hk – толщина пленки в том месте жидкого клина, где видно светлое кольца k-го порядка; – длина волны света.

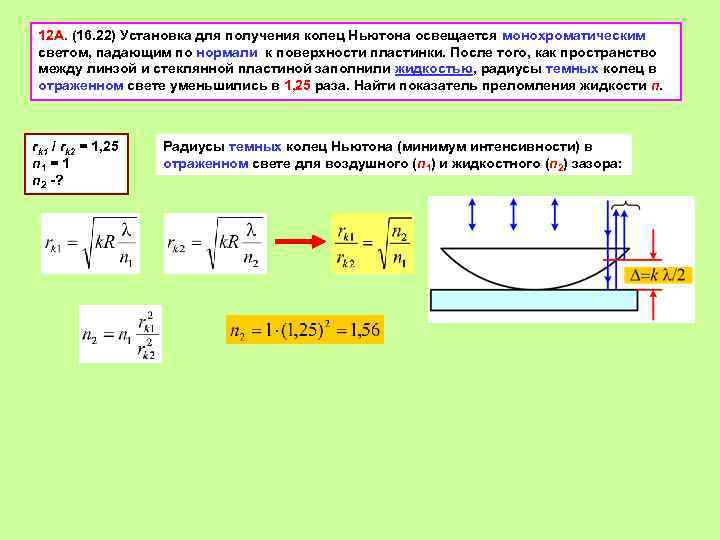12 А. (16. 22) Установка для получения колец Ньютона освещается монохроматическим светом, падающим по нормали к поверхности пластинки. После того, как пространство между линзой и стеклянной пластиной заполнили жидкостью, радиусы темных колец в отраженном свете уменьшились в 1, 25 раза. Найти показатель преломления жидкости n. rk 1 / rk 2 = 1, 25 n 1 = 1 n 2 -? Радиусы темных колец Ньютона (минимум интенсивности) в отраженном свете для воздушного (n 1) и жидкостного (n 2) зазора:

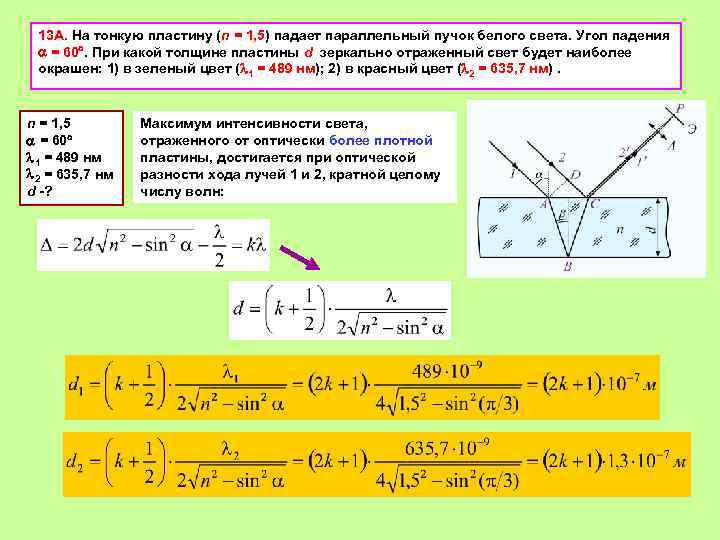13 А. На тонкую пластину (n = 1, 5) падает параллельный пучок белого света. Угол падения = 60. При какой толщине пластины d зеркально отраженный свет будет наиболее окрашен: 1) в зеленый цвет ( 1 = 489 нм); 2) в красный цвет ( 2 = 635, 7 нм). n = 1, 5 = 60 1 = 489 нм 2 = 635, 7 нм d -? Максимум интенсивности света, отраженного от оптически более плотной пластины, достигается при оптической разности хода лучей 1 и 2, кратной целому числу волн:

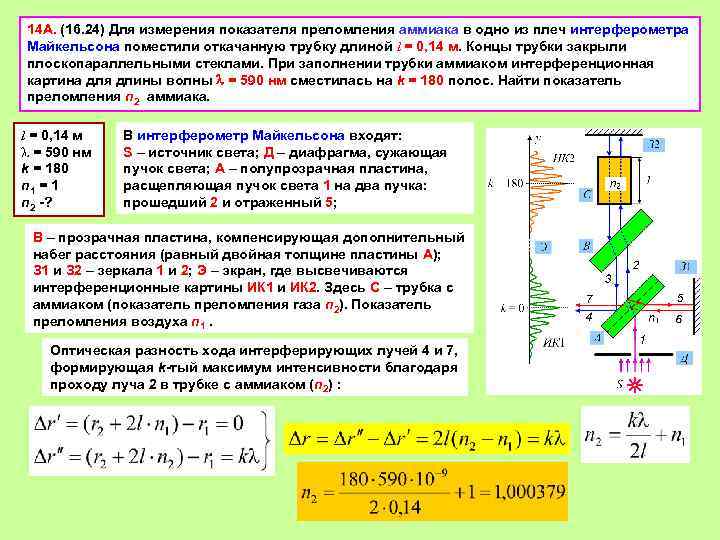14 А. (16. 24) Для измерения показателя преломления аммиака в одно из плеч интерферометра Майкельсона поместили откачанную трубку длиной l = 0, 14 м. Концы трубки закрыли плоскопараллельными стеклами. При заполнении трубки аммиаком интерференционная картина для длины волны = 590 нм сместилась на k = 180 полос. Найти показатель преломления n 2 аммиака. l = 0, 14 м l = 590 нм k = 180 n 1 = 1 n 2 -? В интерферометр Майкельсона входят: S – источник света; Д – диафрагма, сужающая пучок света; А – полупрозрачная пластина, расщепляющая пучок света 1 на два пучка: прошедший 2 и отраженный 5; В – прозрачная пластина, компенсирующая дополнительный набег расстояния (равный двойная толщине пластины А); З 1 и З 2 – зеркала 1 и 2; Э – экран, где высвечиваются интерференционные картины ИК 1 и ИК 2. Здесь С – трубка с аммиаком (показатель преломления газа n 2). Показатель преломления воздуха n 1. Оптическая разность хода интерферирующих лучей 4 и 7, формирующая k-тый максимум интенсивности благодаря проходу луча 2 в трубке с аммиаком (n 2) :

15 А. (16. 27) На поверхность стеклянного объектива нанесена тонкая плёнка, показатель преломления которой n = 1, 2. При какой наименьшей толщине d этой плёнки произойдёт максимальное ослабление отражённого света в средней части видимого спектра? = 550 нм = 0 n = 1, 2 dmin - ? Отражение от верхней и нижней поверхностей пленки происходит в равных условиях, т. е. от среды с большим показателем преломления. Волны 2 и 3 получают при отражении дополнительный набег в полдлины волны ( /2). Поэтому для максимального ослабления отраженной волны (минимум отраженного света) оптическая разность хода лучей 1 и 2 должна быть равна целому числу полуволн : (1) При нормальном падении волны на поверхность пленки ( = 0) выражение (1) упрощается : Наименьшая толщина плёнки d будет в случае, когда оптическая разность хода лучей 2 и 3 составит одну полуволну : Тогда для толщины плёнки получаем : Это возможно при условии k = 0, тогда: