№ 1 позиционные системы счисления В школе, во

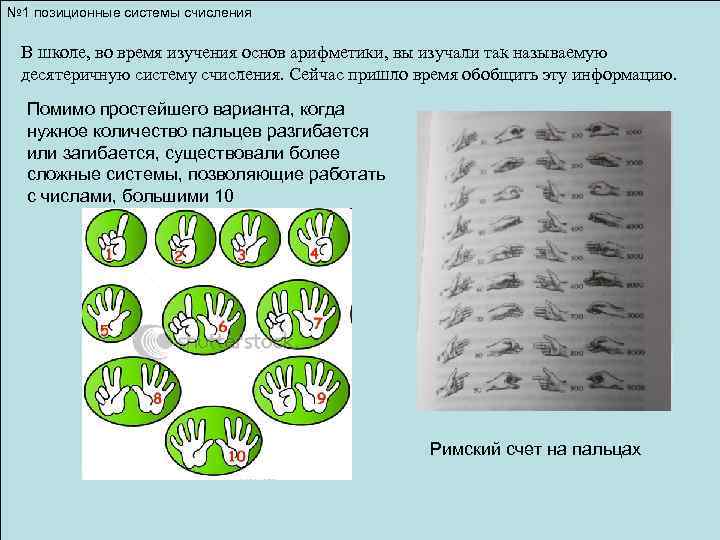№ 1 позиционные системы счисления В школе, во время изучения основ арифметики, вы изучали так называемую десятеричную систему счисления. Сейчас пришло время обобщить эту информацию. Помимо простейшего варианта, когда нужное количество пальцев разгибается или загибается, существовали более сложные системы, позволяющие работать с числами, большими 10 Римский счет на пальцах 1

№ 2 позиционные системы счисления При письме для обозначения разных чисел использовались определенные значки 2

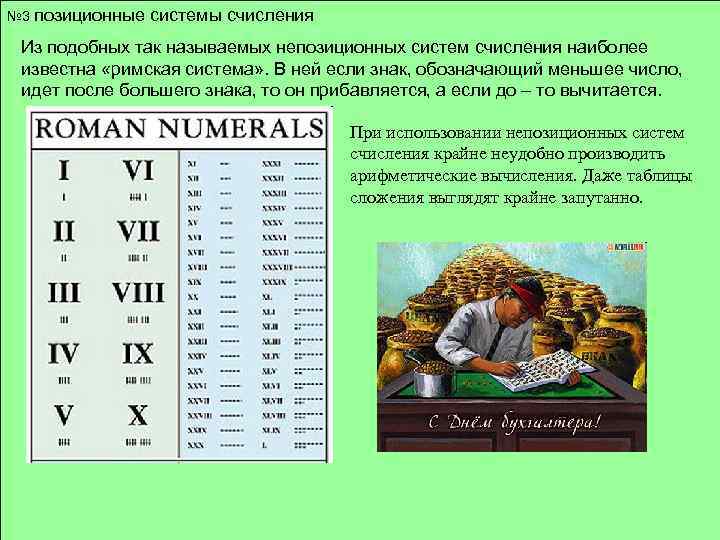№ 3 позиционные системы счисления Из подобных так называемых непозиционных систем счисления наиболее известна «римская система» . В ней если знак, обозначающий меньшее число, идет после большего знака, то он прибавляется, а если до – то вычитается. При использовании непозиционных систем счисления крайне неудобно производить арифметические вычисления. Даже таблицы сложения выглядят крайне запутанно. 3

№ 4 позиционные системы счисления Поэтому человечество перешло на более удобные позиционные системы счисления. В них имеется некоторое количество цифр, а величина числа зависит от того места, на котором стоит цифра. Сейчас наиболее употребительная десятичная система с арабскими цифрами Скрытая «тонкость» позиционных систем – в том, что для их использования нужно было додуматься, что ноль – это тоже число. Ноль в качестве числа ввели арабские средневековые математики. 4

№ 5 позиционные системы счисления Однако кроме десятичной могли использоваться (и используются до сих пор) и другие системы счисления. Подобные неметрические системы счисления имеются в измерении времени (день=24 часам, час – 60 минутам) и некоторых денежных единицах, единицах длины, веса и объема. Почему-то особенно к 5 подобным отклонениям привержены англичане.

№ 6 позиционные системы счисления Удобство позиционных систем счисления, их логичность позволяет легко работать не только с целыми числами, но и с «десятичными дробями» . Для этого в конце числа ставится запятая, после чего числа, если они есть, не умножаются, а делятся на степени десятки: Вариант записи с использованием в качестве разделителя запятой называется «европейским форматом» . В «американском формате» используется точка Для компактной записи очень больших или маленьких чисел используется также так называемый «экспоненциальный формат записи» 6

№ 7 позиционные системы счисления В течение долгого времени недесятичными системами счисления занимались только математики (точнее – они ими тоже не занимались ввиду тривиальности вопроса), но после появления вычислительной техники выяснилось, что ей удобнее работать в недесятичных системах счисления. Точнее – ей удобнее работать в двоичной системе или системах, основанием которой является двойка, но студентов «до кучи» стали учить и позиционным системам с другими основаниями. Сейчас при записи чисел в других позиционных системах тоже используют арабские числа. Если система имеет меньшее основание, то большие числа не используют. Например, в 8 -значной системе используется 8 цифр, то есть от 0 до 7. Если система содержит больше 10 цифр, то вместо недостающих используют заглавные латинские цифры. Например, A=10, B=11, C=12, D=13, E=14, F=15. Контрольный вопрос. Если можно произвольно менять систему счисления, то в каких системах может быть записано число 214? Какое его минимальное значение при выборе произвольной системы счисления? 7

№ 8 позиционные системы счисления Например, в 7 -ричной системе счисления число 214 равно При одновременном использовании нескольких систем счисления разрядность пишется как индекс. Аналогичным образом с дробями. Например: Соответственно в системах с 0 1 2 меньшими основаниями для записи чисел нужно больше 0 0 знаков, но таблицы сложения и умножения значительно проще. 1 0 1 2 Например, это – таблица 2 0 2 11 умножения в троичной системе: 8

№ 9 позиционные системы счисления Практически все электронно-вычислительные машины работают в самой короткой, двоичной системе счисления. Это дает возможность максимально упростить используемые электронные схемы. Таблица сложения в двоичной системе счисления 0 1 0 0 1 10 Таблица умножения в двоичной системе счисления 0 1 0 0 0 1 0 1 9

№ 10 позиционные системы счисления Число в позиционной системе счисления с основанием q может быть представлено в виде полинома по степеням q. Например, в десятичной системе мы имеем число 123, 45 = 1· 102 + 2· 101 + З ·I 00 + 4 · 10 -1 + 5 · 10 -2, а в общем виде это правило запишется так: Х(q)=хn-1 qn-1 + xn-2 qn-2 + …+ x 1 q 1 + x 0 q 0 + x-1 q-1 + x-2 q-2 + … + x-mq-m Здесь: Х(q) — запись числа в системе счисления с основанием q; xi — натуральные числа меньше q. т. е. цифры; n — число разрядов целой части; m — число разрядов дробной части. Записывая слева направо цифры числа, мы получим закодированную запись числа в q-ичной системе счисления: Х(q) = Хn-1 Хn-2…Х 1 Х 0, Х -1 Х -2… Х –m

№ 11 позиционные системы счисления При переводе чисел из одной системы счисления в другую проще всего переводить числа в привычную нам десятичную систему, а потом – в другую. Однако в том случае, если основание одной системы является степенью другой, то переводить можно проще и быстрее. Например, восемь – третья степень двойки. Поэтому при переводе из восьмеричной системы в двоичную можно не «уродоваться» а каждую цифру перевести в трехзначное двоичное число. Например, возьмем 105418. Разложим все цифры: 18=0012 08=0002 58=1012 48=1002 18=0012 В результате имеем: 105418=001011000012=10001011000012 11

№ 12 позиционные системы счисления Аналогичным образом, например, при переводе из двоичной в шестнадцатеричную нужно разбить все цифры (идя от запятой) на четверки, а потом каждую четверку перевести в одну шестнадцатеричную цифру. Пусть у нас, к примеру, есть 11101001011111, 0111012 Разбиваем по четверкам: 11101001011111, 0111012 и переводим в десятичную, а потом в шестнадцатеричную систему. При этом, если надо, то первую четверку дополняем нулями слева, а последнюю - справа: 00112=0 8+0 4+1 2+1 1=0+0+2+1=310=316 10102=1 8+0 4+1 2+0 1=8+0+2+0=1010=A 16 01012=0 8+1 4+0 2+1 1=0+4+0+1=510=516 11012=1 8+1 4+0 2+1 1=8+4+0+1=1310= C 16 00112=0 8+0 4+1 2+1 1=0+0+2+1=310=316 11112=1 8+1 4+1 2+1 1=8+4+2+1=1510= F 16 01112=0 8+1 4+1 2+1 1=0+4+2+1=710=716 01002=0 8+1 4+0 2+0 1=0+4+0+0=416 В результате 11101001011111, 0111012 =3 A 5 C 3 F, 74 12