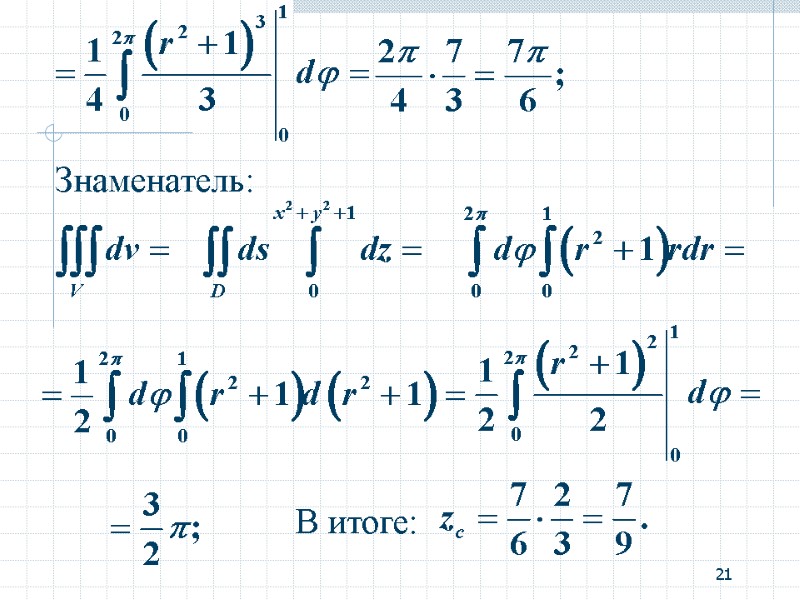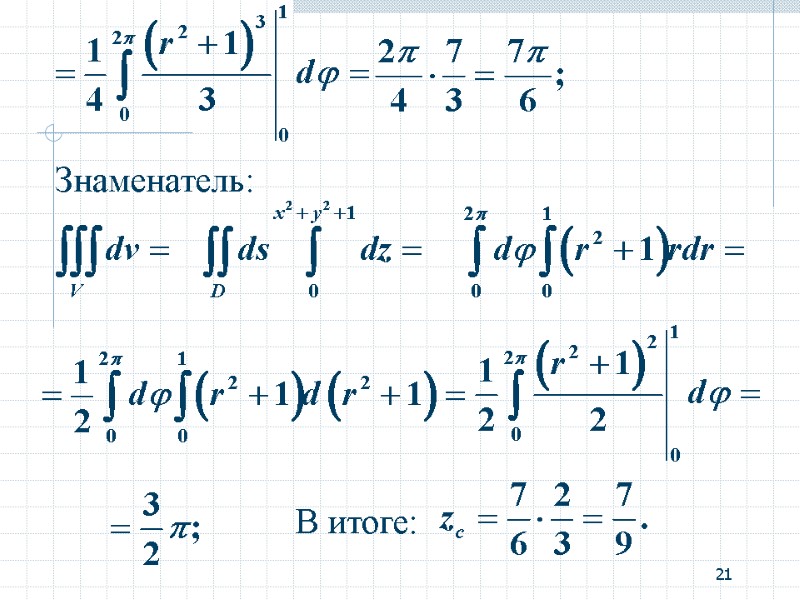1 — поверхностный интеграл первого рода (поверхностный интеграл

1 - поверхностный интеграл первого рода (поверхностный интеграл первого рода – обобщение двойных интегралов по плоской области)

2 то Лемма Если

3 В частном случае прямоугольной области: Доказательство

4

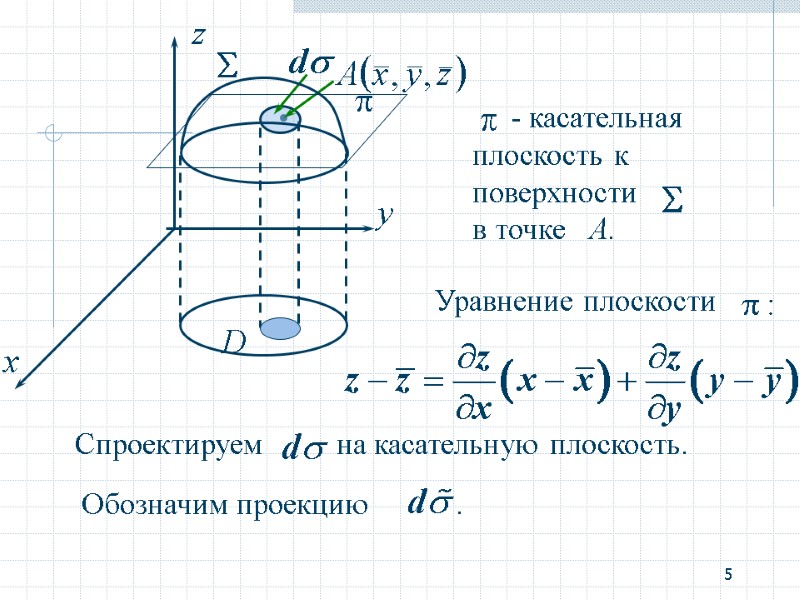5

6 Нормальный вектор к Oxy:

7

8 Поверхностный интеграл первого рода сводится к двойному. то

9 то

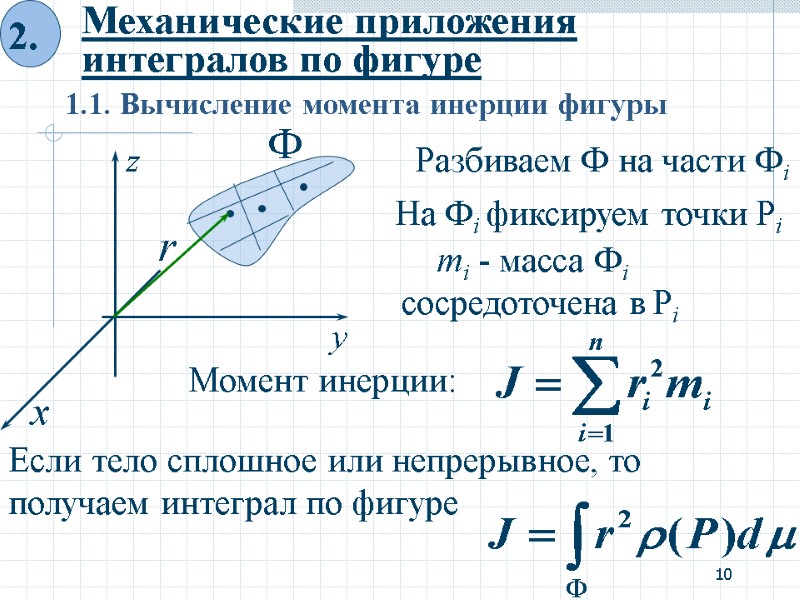10 Механические приложения интегралов по фигуре 1.1. Вычисление момента инерции фигуры Разбиваем Ф на части Фi На Фi фиксируем точки Pi mi - масса Фi сосредоточена в Pi Момент инерции: Если тело сплошное или непрерывное, то получаем интеграл по фигуре

11 1.2. Осевые моменты (моменты инерции фигуры относительно осей координат) Рассмотрим пространственную фигуру

12 1.3. Моменты инерции относительно координатных плоскостей

13 1.3. Полярный момент (момент инерции относительно начала координат O(0,0,0)) О – полюс.

14 Пример Найти момент инерции относительно плоскости Oxy однородной боковой поверхности цилиндра, задаваемой уравнением Решение

15

16 1.4. Статические моменты. Координаты центра тяжести фигуры. Разобьем фигуру на элементарные области – ni материальных точек массой mi. Координаты центра тяжести системы точек:

17 где называются статическими моментами системы относительно плоскостей Oyz, Oxz, Oxy.

18 Если фигура имеет центр симметрии, ось симметрии, плоскость симметрии, то статические моменты относительно центра, оси, плоскости равны 0. Если фигура непрерывна, то при предельном переходе получаем интегралы

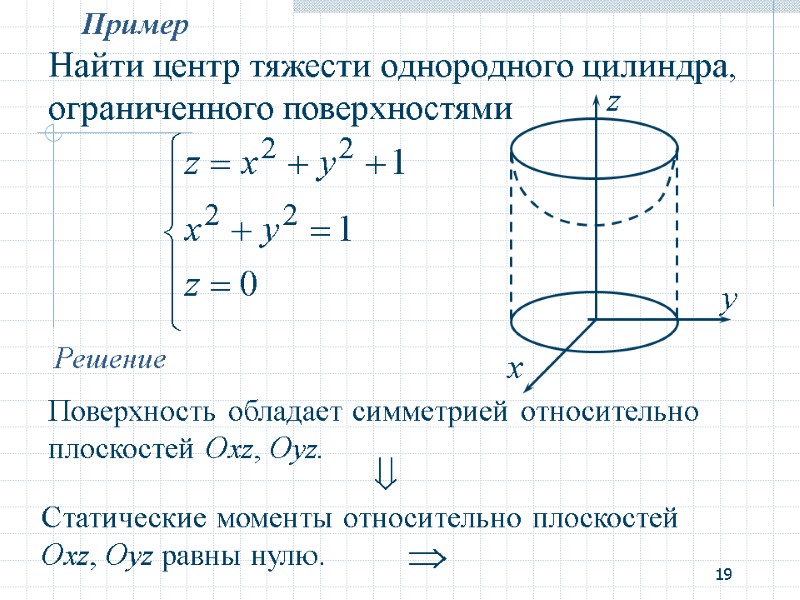19 Пример Найти центр тяжести однородного цилиндра, ограниченного поверхностями Решение Поверхность обладает симметрией относительно плоскостей Oxz, Oyz. Статические моменты относительно плоскостей Oxz, Oyz равны нулю.

20 Цилиндр однородный Числитель:

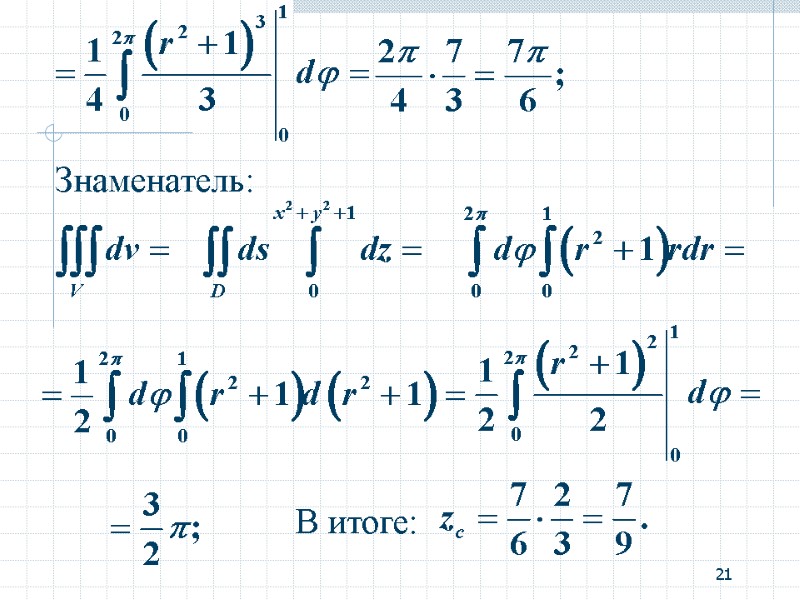21 Знаменатель: В итоге: