1 По данным на рисунке найдите площадь треугольника

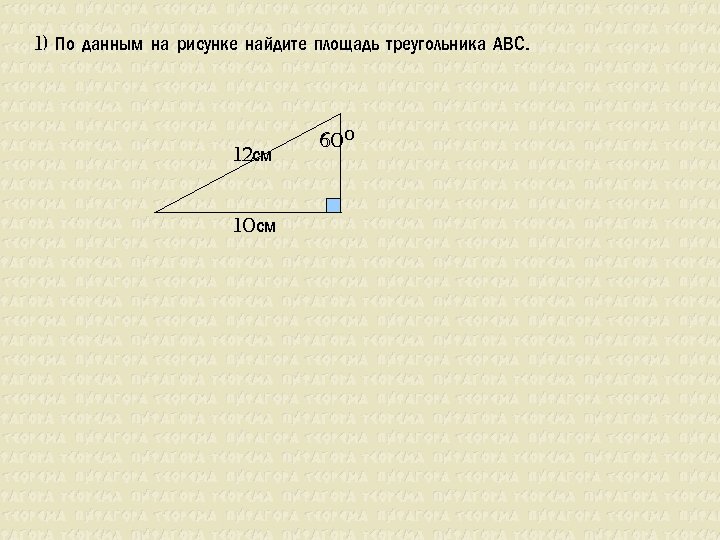1) По данным на рисунке найдите площадь треугольника АВС. 12 см 10 см 600

2) По данным рисунка докажите, что четырехугольник k. Mnp — квадрат. b 6 k M 5 c 7 8 4 3 a 1 p 2 n d 3) Найдите острые углы прямоугольного треугольника, если гипотенуза составляет 18 см, а катет 9 см.

«Геометрия владеет двумя сокровищами: одно из них — это теорема Пифагора. . . » Иоганн Кеплер.

Пифагор Самосский (ок. 580 – ок. 500 г. до н. э. )

О Пифагоре • Пифагор Самосский родился на острове Самосс в Самосский Ионическом море. • Пифагор – едва ли не самый популярный учёный за всю историю человечества. • Пифагор был не только учёным, но и основателем первой научной школы. Он был и воспитателем душ, проповедником собственной «пифагорейской» этики, философом. • Он принимал в свою школу только тех юношей, которые промолчали в течение пяти лет. Значит, при занятиях математикой нужна абсолютная тишина для того, чтобы можно было сосредоточить все внимание на решении того или другого утверждения.

• Сегодня известно около 500 различных доказательств теоремы Пифагора геометрических, алгебраических, механических и прочих. Трудно найти человека, который не знал бы её шуточную формулировку: «Пифагоровы штаны во все стороны равны» . Рассмотрим один из примеров доказательства теоремы Пифагора.

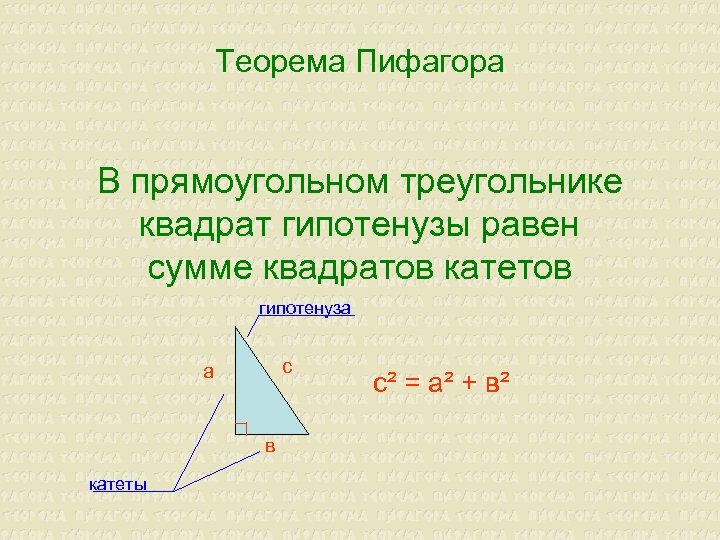Теорема Пифагора В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов гипотенуза с а в катеты с² = а² + в²

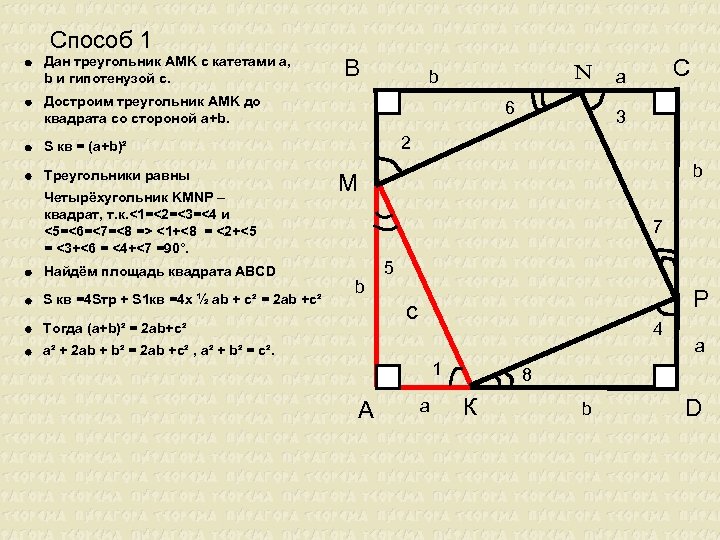Способ 1 Дан треугольник AMK с катетами a, b и гипотенузой c. В n b Достроим треугольник AMK до квадрата со стороной a+b. 6 Четырёхугольник KMNP – квадрат, т. к. <1=<2=<3=<4 и <5=<6=<7=<8 => <1+<8 = <2+<5 = <3+<6 = <4+<7 =90°. Найдём площадь квадрата ABCD S кв =4 Sтр + S 1 кв =4 x ½ ab + c² = 2 ab +c² 3 2 S кв = (a+b)² Треугольники равны C a b М 7 b 5 P c Тогда (a+b)² = 2 ab+c² 4 a² + 2 ab + b² = 2 ab +c² , a² + b² = c². 1 А a a 8 К b D

A Способ 2 4 M 3 a b C 1 b 2 B a D Дан треугольник ABC c катетами a и b. Продолжим отрезок СВ за точку В и построим треугольник ВМD: BD=a,

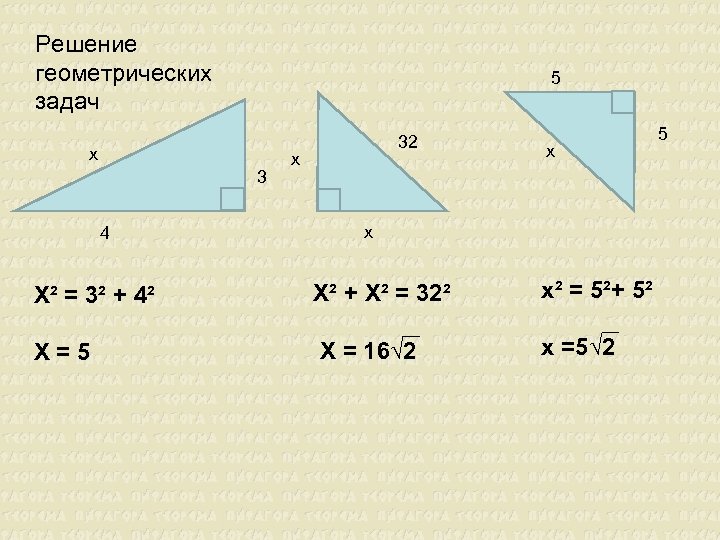Решение геометрических задач 5 x 3 4 32 x x x Х² = 3² + 4² Х² + Х² = 32² х² = 5²+ 5² Х=5 Х = 16√ 2 х =5√ 2 5

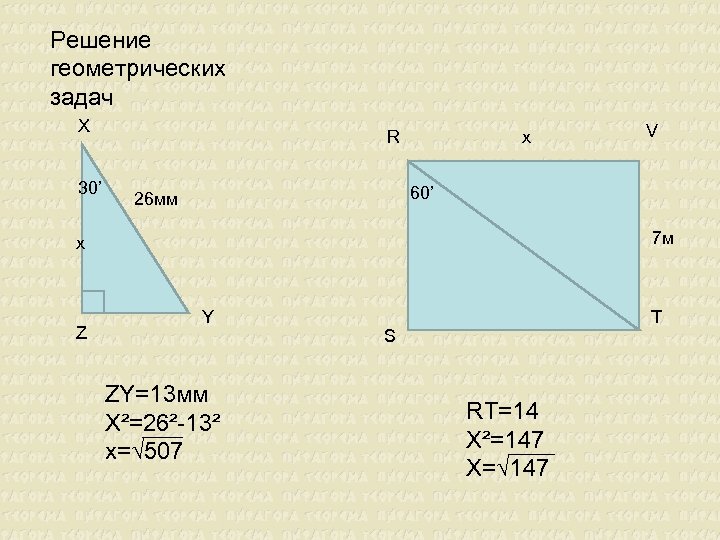Решение геометрических задач X 30’ R x 60’ 26 мм 7 м x Z V Y ZY=13 мм X²=26²-13² x=√ 507 T S RT=14 X²=147 X=√ 147

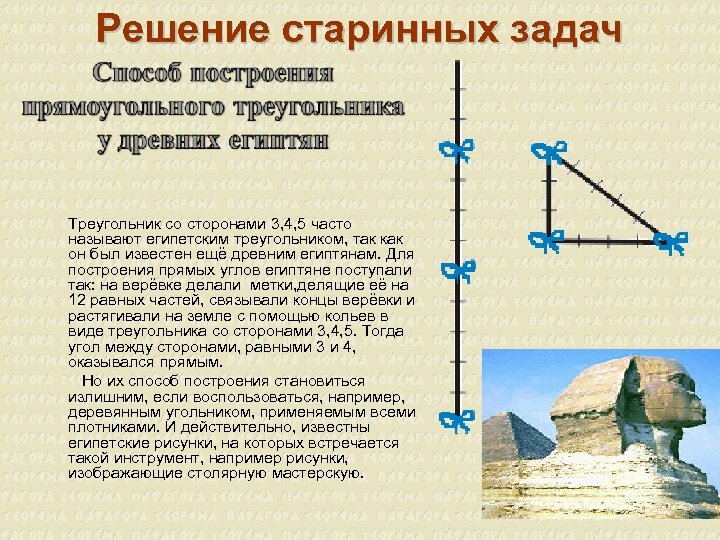Решение старинных задач Треугольник со сторонами 3, 4, 5 часто называют египетским треугольником, так как он был известен ещё древним египтянам. Для построения прямых углов египтяне поступали так: на верёвке делали метки, делящие её на 12 равных частей, связывали концы верёвки и растягивали на земле с помощью кольев в виде треугольника со сторонами 3, 4, 5. Тогда угол между сторонами, равными 3 и 4, оказывался прямым. Но их способ построения становиться излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, например рисунки, изображающие столярную мастерскую.

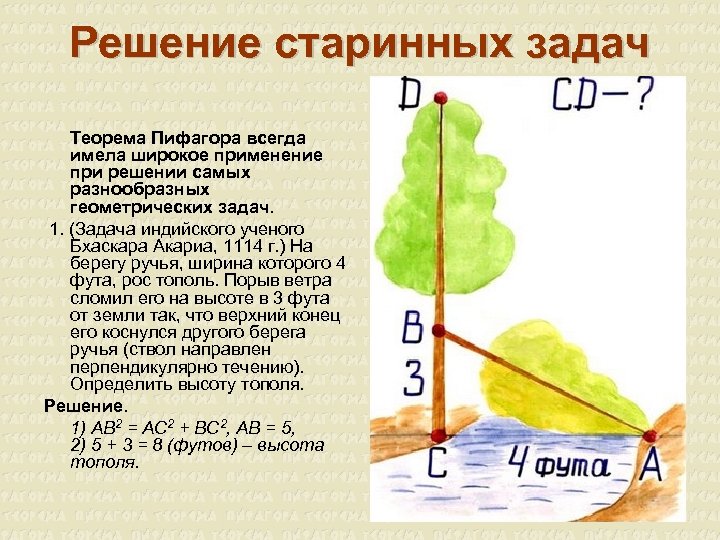Решение старинных задач Теорема Пифагора всегда имела широкое применение при решении самых разнообразных геометрических задач. 1. (Задача индийского ученого Бхаскара Акариа, 1114 г. ) На берегу ручья, ширина которого 4 фута, рос тополь. Порыв ветра сломил его на высоте в 3 фута от земли так, что верхний конец его коснулся другого берега ручья (ствол направлен перпендикулярно течению). Определить высоту тополя. Решение. 1) AB 2 = AC 2 + BC 2, AB = 5, 2) 5 + 3 = 8 (футов) – высота тополя.

Задача из учебника «Арифметика» Леонтия Магницкого «Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать» .

ОБЛАСТИ ПРИМЕНЕНИЯ • Архитектура и строительство • Мобильная связь • Астрономия

• • Архитектура В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг половине ширины, (b/2) для внутренних дуг Остается еще полная окружность, касающаяся четырех дуг. Т. к. она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра.

Архитектура • В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2 и r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой b/2 -p. По теореме Пифагора имеем: • (b/4+p)=( b/4)+( b/4 -p) • или • b/16+ bp/2+p=b/16+b/4 -bp+p, • откуда • bp/2=b/4 -bp. • Разделив на b и приводя подобные члены, получим: • (3/2)p=b/4, p=b/6.

Строительство • Крыши • Молниеотводы

Строительство "Чтобы найти поверхность крыши, все скаты которой имеют равный уклон, нужно умножить перекрываемую площадь на длину какого-нибудь стропила и разделить полученное произведение на проекцию этого стропила на перекрываемую площадь. "

Строительство При строительстве любого сооружения, рассчитывают расстояния, центры тяжести, размещение опор, балок и т. д.

Строительство крыши При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки. Например: в доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки AC=8 м. , и AB=BF. Решение: Треугольник ADC - равнобедренный AB=BC=4 м. , BF=4 м. Если предположить, что FD=1, 5 м. , тогда: А) Из треугольника DBC: DB=2, 5 м. , Б) Из треугольника ABF:

Молниеотвод • Известно, что молниеотвод защищает от молнии все предметы, расстояние которых от его основания не превышает его удвоенной высоты. Необходимо определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту. • Решение: • По теореме Пифагора h 2≥ a 2+b 2, значит h≥(a 2+b 2)1/2.

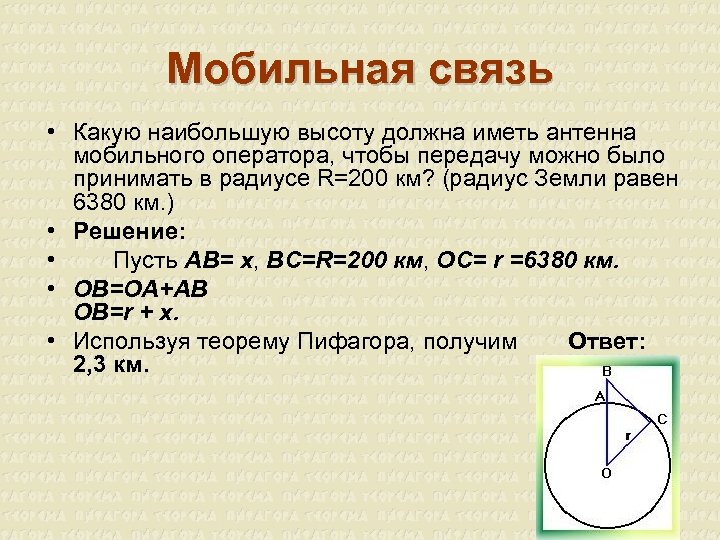Мобильная связь • Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км. ) • Решение: • Пусть AB= x, BC=R=200 км, OC= r =6380 км. • OB=OA+AB OB=r + x. • Используя теорему Пифагора, получим Ответ: 2, 3 км.

Астрономия • На этом рисунке показаны точки A и B и путь светового луча от A к B и обратно. Путь луча показан изогнутой стрелкой для наглядности, на самом деле, световой луч - прямой. • Какой путь проходит луч? Поскольку свет идет туда и обратно одинаковый путь, спросим сразу: чему равно расстояние между точками?

Астрономия • В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку. В шутку, хотя и не совсем безосновательно , было решено передать обитателям Марса сигнал в виде теоремы Пифагора. Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.

Пифагорэто не только великий математик, но и великий мыслитель своего времени.

1. Мысль — превыше всего между людьми на земле. 2. Не садись на хлебную меру (т. е. не живи праздно). 3. Уходя, не оглядывайся (т. е. перед смертью не цепляйся за жизнь). 4. По торной дороге не ходи (т. е. следуй не мнениям толпы, а мнениям немногих понимающих). 5. Ласточек в доме не держи (т. е. не принимай гостей болтливых и не сдержанных на язык). 6. Будь с тем, кто ношу взваливает, не будь с тем, кто ношу сваливает (т. е. поощряй людей не к праздности, а к добродетели, к труду). 7. В перстне изображений не носи (т. е. не выставляй напоказ перед людьми, как ты судишь и думаешь о богах).

Значение теоремы Пифагора • Значение теоремы Пифагора состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии и решить множество задач. Из-за этого многие ученые называют эту теорему самой главной в геометрии.

Значение теоремы Пифагора • Кроме этого, практическое значение теоремы Пифагора и обратной ему теоремы заключается в том, что с их помощью можно найти длины отрезков, не измеряя самих отрезков.

Значение теоремы В целом, значение теоремы, кроме вышесказанного, заключается в том, что она применяется практически во всех современных технологиях, а также открывает простор для создания и придумывания новых. Пребудет вечной истина, как скоро Ее познает слабый человек! И ныне теорема Пифагора Верна, как и в его далекий век.