1 Переходные процессы и законы коммутации 2 Переходные




















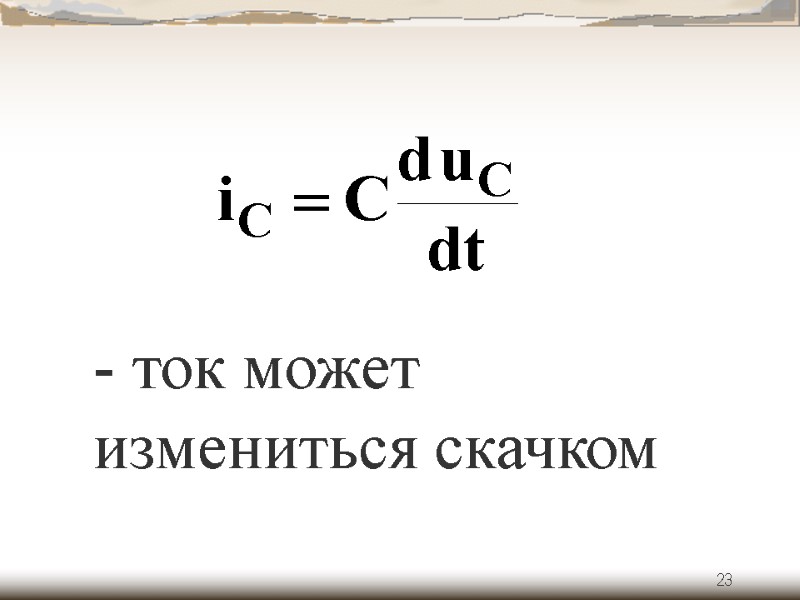




























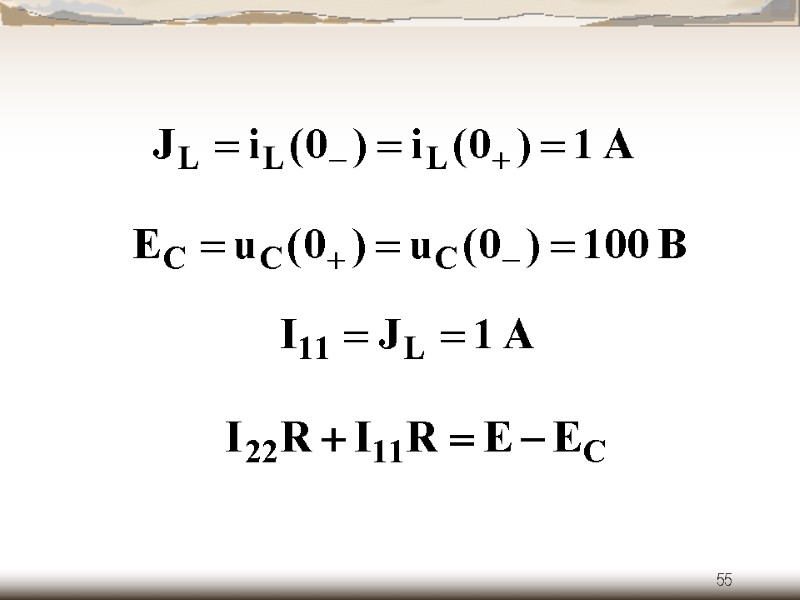
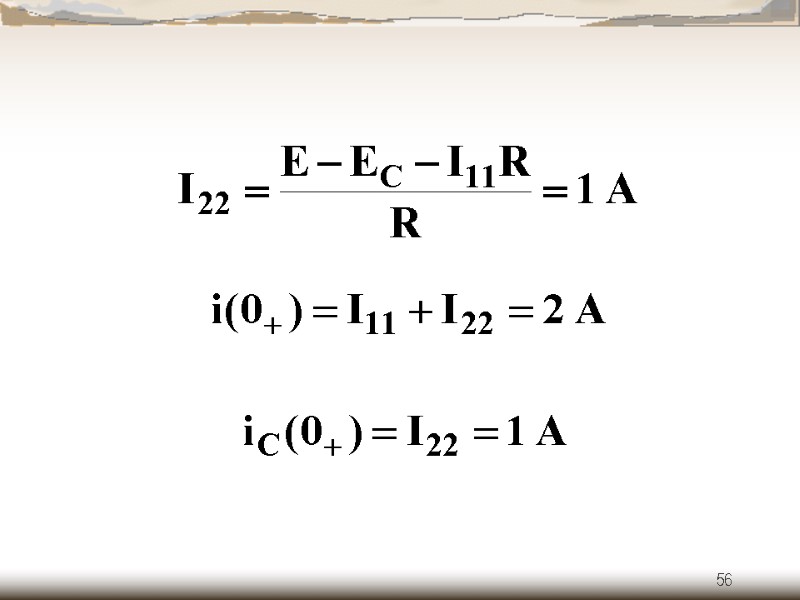
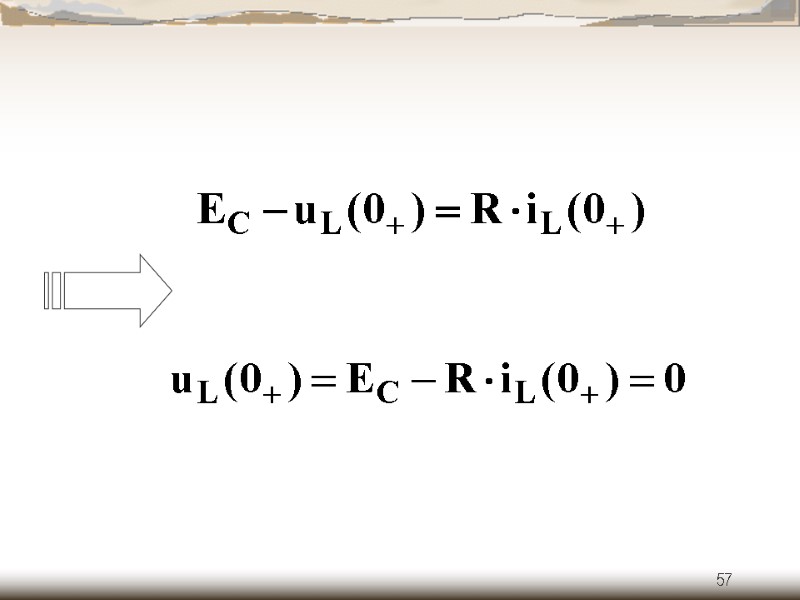


10446-el_tech_lc_12.ppt
- Количество слайдов: 59
 1 Переходные процессы и законы коммутации
1 Переходные процессы и законы коммутации
 2 Переходные процессы возникают при включении или отключении источников, элементов цепи, при коротких замыканиях и обрывах проводов, а также при различных импульсных воздействиях на цепь, например, при грозовых разрядах
2 Переходные процессы возникают при включении или отключении источников, элементов цепи, при коротких замыканиях и обрывах проводов, а также при различных импульсных воздействиях на цепь, например, при грозовых разрядах
 3 Переходный процесс или переходный режим цепи – это изменение во времени напряжений и токов от одних установившихся значений к другим установившимся значениям
3 Переходный процесс или переходный режим цепи – это изменение во времени напряжений и токов от одних установившихся значений к другим установившимся значениям
 4 Установившиеся значения напряжений и токов характеризуют установившийся режим цепи и могут оставаться неизменными бесконечно долго, причем эти значения задаются источниками электрической энергии
4 Установившиеся значения напряжений и токов характеризуют установившийся режим цепи и могут оставаться неизменными бесконечно долго, причем эти значения задаются источниками электрической энергии
 5 При анализе и расчете переходных процессов будем считать, что переходные процессы возникают при включении или отключении элементов цепи посредством ключей, причем эта коммутация происходит мгновенно быстро в момент времени t=0
5 При анализе и расчете переходных процессов будем считать, что переходные процессы возникают при включении или отключении элементов цепи посредством ключей, причем эта коммутация происходит мгновенно быстро в момент времени t=0
 6 Ключ замыкается:
6 Ключ замыкается:
 7 Ключ замыкается:
7 Ключ замыкается:
 8 Ключ замыкается:
8 Ключ замыкается:
 9 Ключ размыкается:
9 Ключ размыкается:
 10 Ключ размыкается:
10 Ключ размыкается:
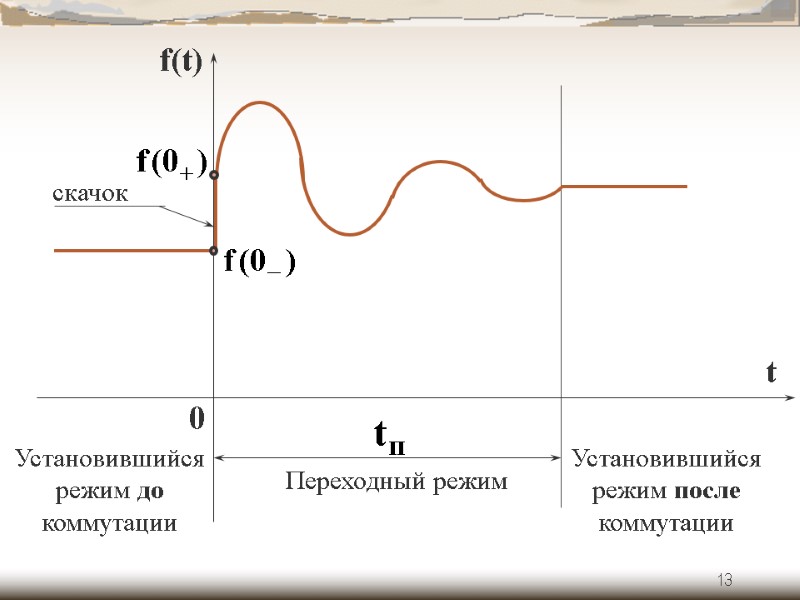
 11 при времени t= переходный процесс теоретически заканчивается и наступает новый установившийся режим время t<0 характеризует режим цепи до коммутации момент времени t=0- соответствует последнему моменту перед коммутацией
11 при времени t= переходный процесс теоретически заканчивается и наступает новый установившийся режим время t<0 характеризует режим цепи до коммутации момент времени t=0- соответствует последнему моменту перед коммутацией
 12 момент времени t=0+ соответствует первому моменту времени после коммутации скачок – это мгновенное изменение напряжения или тока при t=0+
12 момент времени t=0+ соответствует первому моменту времени после коммутации скачок – это мгновенное изменение напряжения или тока при t=0+
 13 f(t) t Установившийся режим до коммутации Переходный режим Установившийся режим после коммутации 0
13 f(t) t Установившийся режим до коммутации Переходный режим Установившийся режим после коммутации 0
 14 Законы коммутации
14 Законы коммутации
 15 + 1. Первый закон коммутации
15 + 1. Первый закон коммутации
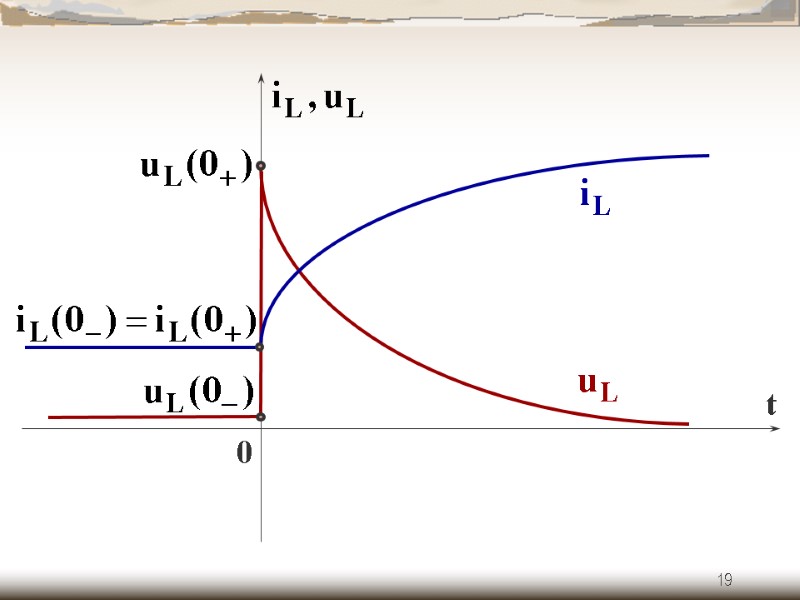
 16 Ток в индуктивности не может измениться скачком
16 Ток в индуктивности не может измениться скачком
 17 Это объясняется тем, что энергия магнитного поля индуктивного элемента WL=LiL2/2 , Дж не может измениться мгновенно, для чего потребовалась бы бесконечно большая мощность PL=dWL/dt= , Вт и бесконечно большое напряжение uL=d(LiL)/dt= , В а это не реально
17 Это объясняется тем, что энергия магнитного поля индуктивного элемента WL=LiL2/2 , Дж не может измениться мгновенно, для чего потребовалась бы бесконечно большая мощность PL=dWL/dt= , Вт и бесконечно большое напряжение uL=d(LiL)/dt= , В а это не реально
 18 - напряжение может измениться скачком
18 - напряжение может измениться скачком
 19 t 0
19 t 0
 20 + 2. Второй закон коммутации
20 + 2. Второй закон коммутации
 21 Напряжение на емкости не может измениться скачком
21 Напряжение на емкости не может измениться скачком
 22 Это объясняется тем, что энергия электрического поля емкостного элемента WC=CuC2/2 , Дж не может измениться мгновенно, для чего потребовалась бы бесконечно большая мощность PC=dWC/dt= , Вт и бесконечно большой ток iC=d(CuC)/dt= , А а это не реально
22 Это объясняется тем, что энергия электрического поля емкостного элемента WC=CuC2/2 , Дж не может измениться мгновенно, для чего потребовалась бы бесконечно большая мощность PC=dWC/dt= , Вт и бесконечно большой ток iC=d(CuC)/dt= , А а это не реально
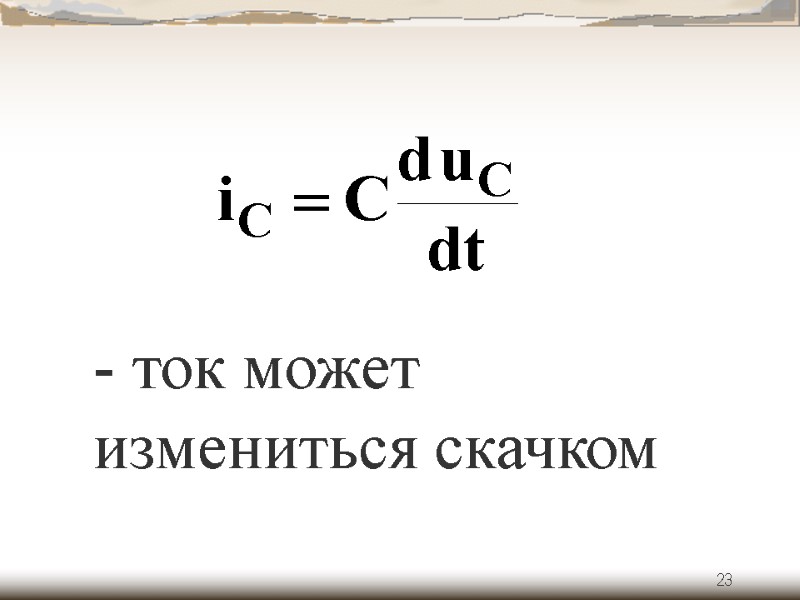 23 - ток может измениться скачком
23 - ток может измениться скачком
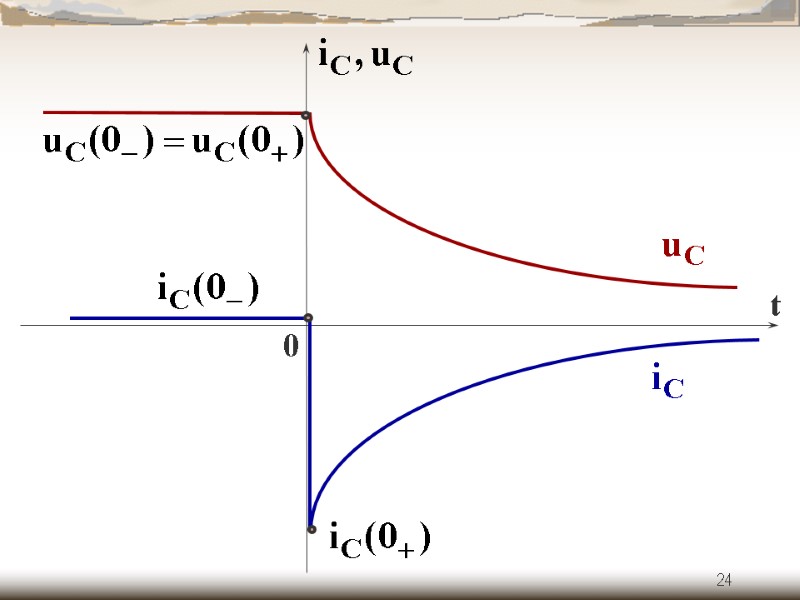
 24 t 0
24 t 0
 25 Переходный процесс обусловлен наличием в цепи L и C
25 Переходный процесс обусловлен наличием в цепи L и C
 26 К л а с с и ч е с к и й метод расчета переходных процессов
26 К л а с с и ч е с к и й метод расчета переходных процессов
 27 Используется для линейных цепей, которые характеризуются линейными дифференциальными уравнениями, составляемыми при помощи законов Кирхгофа для цепи после коммутации
27 Используется для линейных цепей, которые характеризуются линейными дифференциальными уравнениями, составляемыми при помощи законов Кирхгофа для цепи после коммутации
 28 - уравнение 1
28 - уравнение 1
 29 это линейное неоднородное дифференциальное уравнение n- порядка для тока или напряжения f(t) переходного процесса при t>0 (схема после коммутации)
29 это линейное неоднородное дифференциальное уравнение n- порядка для тока или напряжения f(t) переходного процесса при t>0 (схема после коммутации)
 30 Где: постоянные коэффициенты, определяемые параметрами (R, L, C) и структурой цепи после коммутации
30 Где: постоянные коэффициенты, определяемые параметрами (R, L, C) и структурой цепи после коммутации
 31 Где: функция, определяемая (независимыми) источниками цепи после коммутации
31 Где: функция, определяемая (независимыми) источниками цепи после коммутации
 32 Решение уравнения 1:
32 Решение уравнения 1:
 33 Где: принужденная составляющая – это частное решение уравнения 1, зависящее от F(t)
33 Где: принужденная составляющая – это частное решение уравнения 1, зависящее от F(t)
 34 Где: свободная составляющая – это общее решение однородного уравнения 1 при F(t) = 0
34 Где: свободная составляющая – это общее решение однородного уравнения 1 при F(t) = 0
 35 При постоянных и гармонических источниках это установившееся значение после коммутации
35 При постоянных и гармонических источниках это установившееся значение после коммутации
 36 зависит от корней характеристического уравнения и начальных условий
36 зависит от корней характеристического уравнения и начальных условий
 37 Характеристическое уравнение 3:
37 Характеристическое уравнение 3:
 38 а) если корни уравнения 3 вещественные, отрицательные и разные
38 а) если корни уравнения 3 вещественные, отрицательные и разные
 39 То тогда
39 То тогда
 40 б) если корни уравнения 3 вещественные, отрицательные и одинаковые, т.е.
40 б) если корни уравнения 3 вещественные, отрицательные и одинаковые, т.е.
 41 То тогда
41 То тогда
 42 в) если корни уравнения 3 комплексные и попарно сопряженные, т.е.
42 в) если корни уравнения 3 комплексные и попарно сопряженные, т.е.
 43 То тогда
43 То тогда
 44 Где: постоянные интегрирования, определяемые начальными условиями
44 Где: постоянные интегрирования, определяемые начальными условиями
 45 Где: коэффициенты затухания свободных колебаний
45 Где: коэффициенты затухания свободных колебаний
 46 Где: угловые частоты свободных колебаний
46 Где: угловые частоты свободных колебаний
 47 Различают: а) независимые начальные условия и
47 Различают: а) независимые начальные условия и
 48 б) зависимые начальные условия и другие величины
48 б) зависимые начальные условия и другие величины
 49 в) принужденные значения, определяемые из расчета установившегося режима после коммутации
49 в) принужденные значения, определяемые из расчета установившегося режима после коммутации
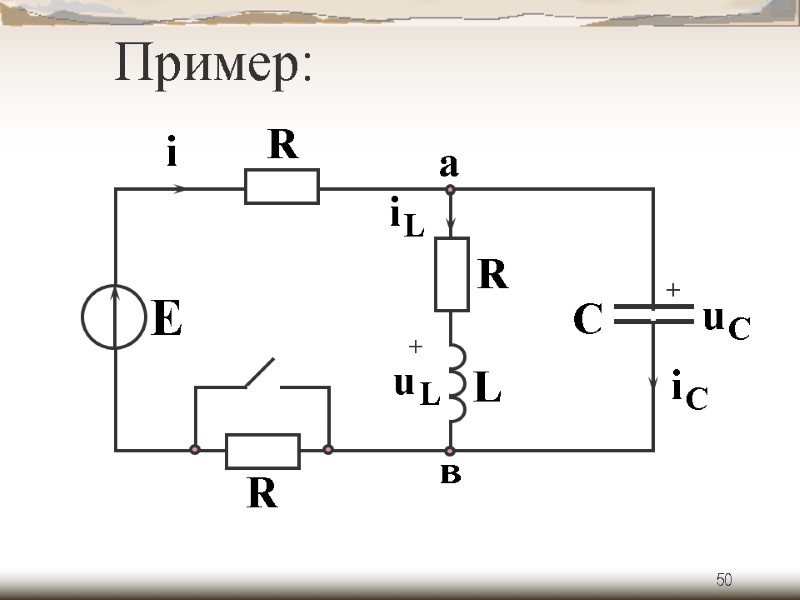
 50 + + Пример:
50 + + Пример:
 51 Дано: Определить: начальные условия и принужденные составляющие
51 Дано: Определить: начальные условия и принужденные составляющие
 52 а) независимые начальные условия (схема до коммутации)
52 а) независимые начальные условия (схема до коммутации)
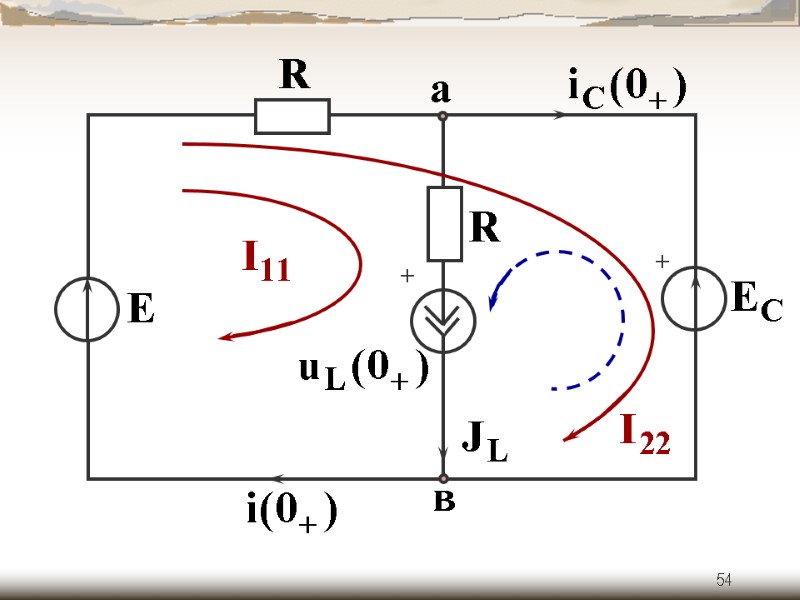
 53 б) зависимые начальные условия (схема после коммутации при )
53 б) зависимые начальные условия (схема после коммутации при )
 54 + +
54 + +
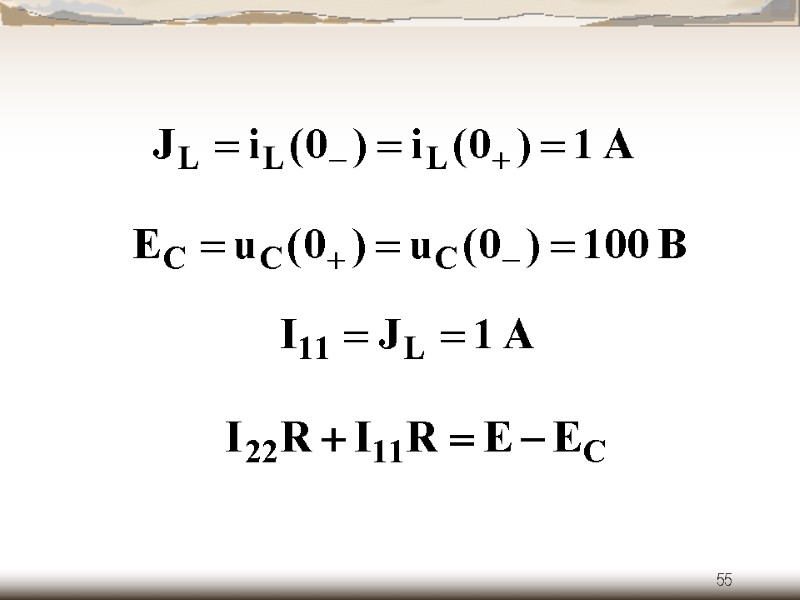 55
55
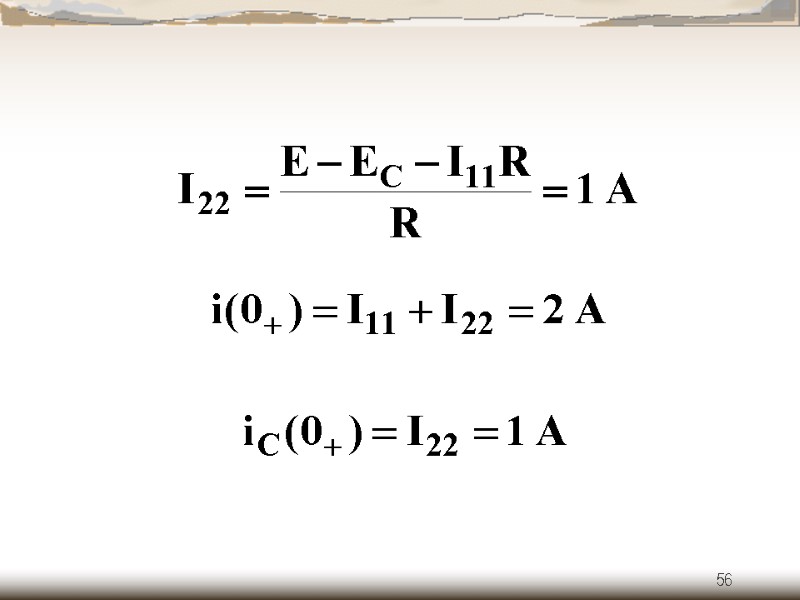 56
56
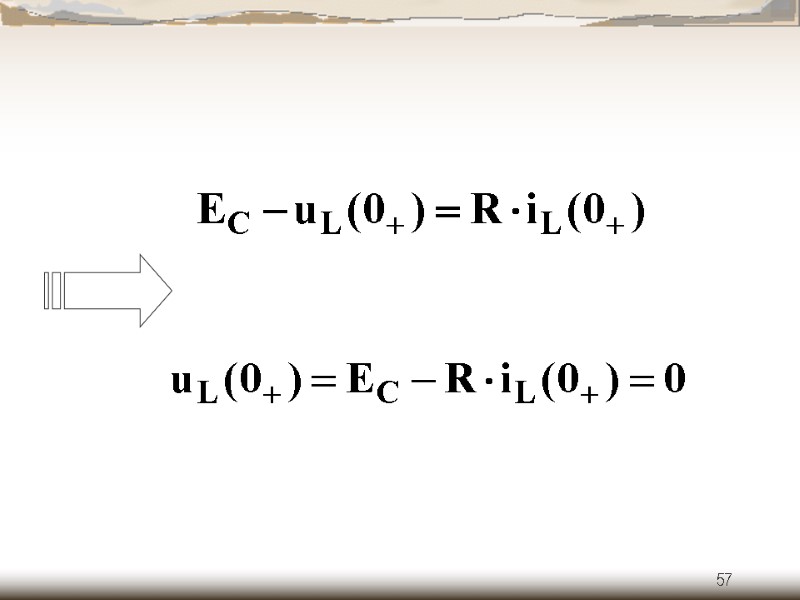 57
57
 58 в) принужденные составляющие (схема после коммутации при t = ) При постоянных источниках: L – закоротка, С – разрыв.
58 в) принужденные составляющие (схема после коммутации при t = ) При постоянных источниках: L – закоротка, С – разрыв.
 59
59

