 1. Окружность
1. Окружность
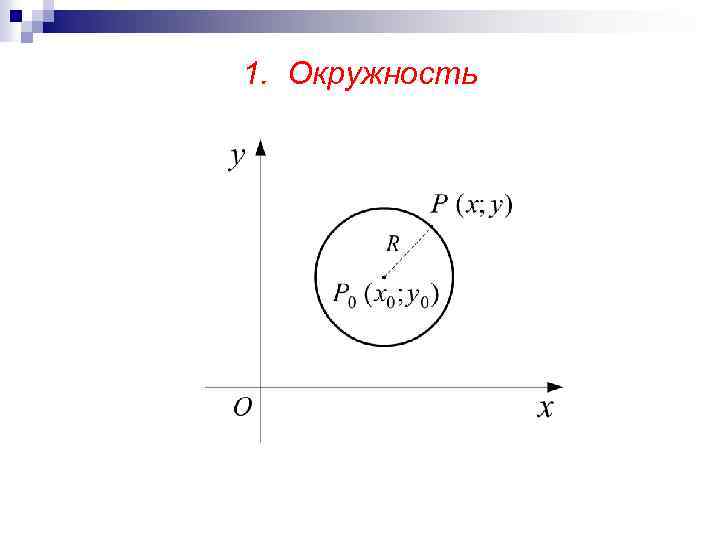
 1. Окружность n Каноническое уравнение окружности с центром в точке Р 0(х0; у0) и радиуса R имеет вид: Если центр окружности расположен в начале координат, то ее уравнение имеет вид:
1. Окружность n Каноническое уравнение окружности с центром в точке Р 0(х0; у0) и радиуса R имеет вид: Если центр окружности расположен в начале координат, то ее уравнение имеет вид:
 2. Эллипс
2. Эллипс
 2. Эллипс n Выведем каноническое уравнение эллипса с центром в начале координат. 3) Обозначим 4) Учитывая, что
2. Эллипс n Выведем каноническое уравнение эллипса с центром в начале координат. 3) Обозначим 4) Учитывая, что
 2. Эллипс n Получим каноническое уравнение эллипса с центром в начале координат:
2. Эллипс n Получим каноническое уравнение эллипса с центром в начале координат:
 2. Эллипс n Эксцентриситет эллипса – отношение фокального расстояния 2 с к длине большой оси 2 а:
2. Эллипс n Эксцентриситет эллипса – отношение фокального расстояния 2 с к длине большой оси 2 а:
 2. Эллипс n В общем случае уравнение эллипса имеет вид: где а - координаты центра эллипса, - его полуоси.
2. Эллипс n В общем случае уравнение эллипса имеет вид: где а - координаты центра эллипса, - его полуоси.
 3. Гипербола
3. Гипербола
 3. Гипербола n Выведем каноническое уравнение гиперболы. 3) Обозначим 4) Учитывая, что
3. Гипербола n Выведем каноническое уравнение гиперболы. 3) Обозначим 4) Учитывая, что
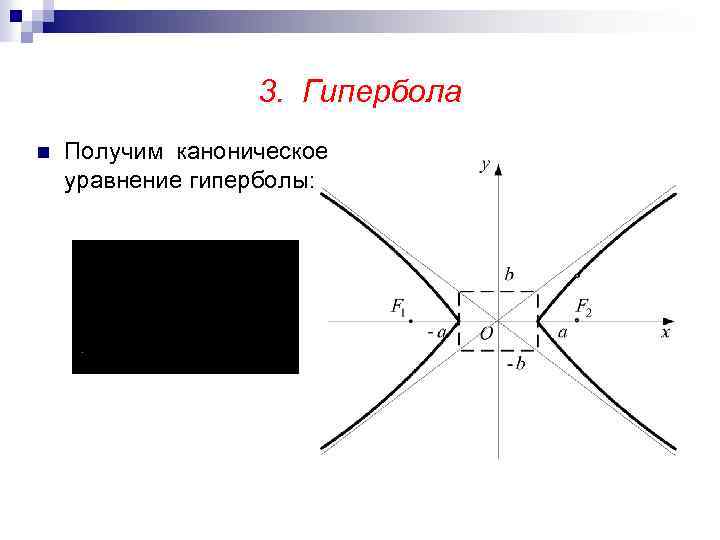 3. Гипербола n Получим каноническое уравнение гиперболы:
3. Гипербола n Получим каноническое уравнение гиперболы:
 3. Гипербола n Эксцентриситет гиперболы – отношение фокального расстояния 2 с к длине действительной оси 2 а:
3. Гипербола n Эксцентриситет гиперболы – отношение фокального расстояния 2 с к длине действительной оси 2 а:
 4. Парабола
4. Парабола
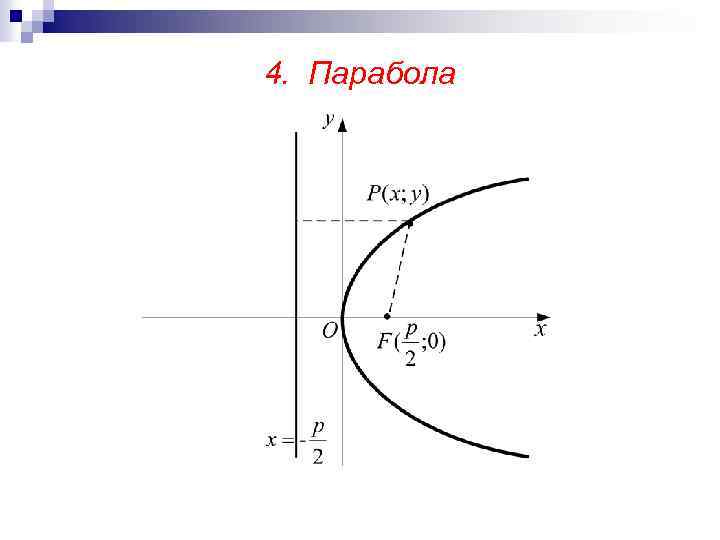
 4. Парабола n Выведем каноническое уравнение параболы. После преобразований получим каноническое уравнение параболы: n
4. Парабола n Выведем каноническое уравнение параболы. После преобразований получим каноническое уравнение параболы: n
 4. Парабола n Другие виды уравнения параболы с вершиной в точке (х0; у0):
4. Парабола n Другие виды уравнения параболы с вершиной в точке (х0; у0):