1 НОУ ВПО Московский институт права Статистика

1

НОУ ВПО «Московский институт права» Статистика Преподаватель: КТН, доцент Манкевич Александр Валерьевич 2

Литература 1. Теория статистики: учебник /под ред. Р. А. Шмойловой. М. : Финансы и статистика, 2007 г. 2. Практикум по теории статистики: учебное пособие/ под ред. Р. А. Шмойловой. М. : Финансы и статистика, 2007 г. 3. Теория статистики: Учебник /под ред. проф. Г. Л. Громыко. 2 е изд. перераб. и доп. М. : ИНФРА М, 2005 г. – 476 с. – (Классический университетский учебник). 3

Т-1. Статистика как наука 1. Понятие статистики. Развитие статистики как науки. 2. Предмет и метод статистики. Задачи теории статистики. 3. Организация статистики. 1. Понятие статистики. Развитие статистики как науки Термин «статистика» произошел от латинских слов stato (государство) и status (положение вещей, политическое состояние). 4

«Статистика есть наука о том, как, не умея мыслить и понимать, заставить делать это цифры» В. Ключевский «Есть три разновидности лжи: ложь, гнусная ложь и официальная статистика» Б. Дизраели Статистика, строгая муза, Ты реешь над каждой судьбой. Ничто для тебя не обуза, Никто не обижен тобой. ……………………. Умру - и меня понемногу Забудут друзья и родня. Статистика – муза итогов, Лишь ты не забудешь меня. Статистика Вадим Шернер 5

В настоящее время под статистикой понимают: 1. Статистика - совокупность сведений (фактов) о разных явлениях в той или иной стране или ее регионах. 7 «я» : семейная статистика 30% детей в России рождаются в неполной семье, а точнее у матерей-одиночек. Статистика других стран немногим отличается от нашей: в США – 33% матерей всех новорожденных – незамужние женщины, в Исландии – 64% (это самый высокий показатель в Европе), в Швеции – 54%, в Великобритании – 38%, в Финляндии – 37%. Результаты Интернет-опроса, который провела компания ACNielsen. 6

2. Статистика - практическая деятельность людей, направленная на сбор, обработку и анализ массовых данных, относящихся к тем или иным сферам общественной жизни. 3. Статистика - некий параметр ряда случайных величин, получаемый по определенному алгоритму из результатов индивидуальных наблюдений. 4. Статистика - наука, изучающая с количественной стороны массовые явления и их закономерности. 7

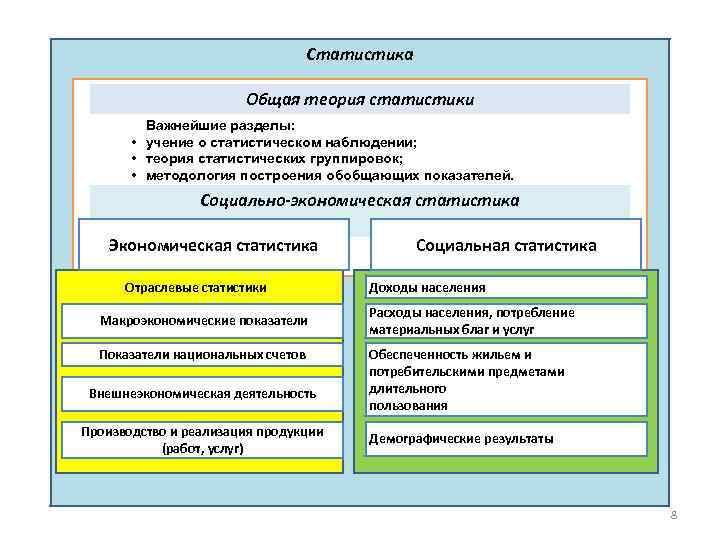Статистика Общая теория статистики Важнейшие разделы: • учение о статистическом наблюдении; • теория статистических группировок; • методология построения обобщающих показателей. Социально-экономическая статистика Экономическая статистика Отраслевые статистики Макроэкономические показатели Показатели национальных счетов Внешнеэкономическая деятельность Производство и реализация продукции (работ, услуг) Социальная статистика Доходы населения Расходы населения, потребление материальных благ и услуг Обеспеченность жильем и потребительскими предметами длительного пользования Демографические результаты 8

История направлений развития статистической науки 1. Описательная школа ОПИСАНИЕ ДОСТОПРИМЕЧАТЕЛЬНОСТЕЙ ГОСУДАРСТВА: ТЕРРИТОРИИ, НАСЕЛЕНИЯ, КЛИМАТА, ПОЛИТИЧЕСКОГО Герман Конринг (1606 -1681). УСТРОЙСТВА, ВЕРОИСПОВЕДАНИЯ, ВЕДЕНИЯ ХОЗЯЙСТВА, ТОРГОВЛИ, БЛАГОСОСТОЯНИЯ ГОСУДАРСТВА И ГРАЖДАН Готфрид Ахенваль (1719— 1772) Но! ввел термин «статистика» . БЕЗ АНАЛИЗА ЗАКОНОМЕРНОСТЕЙ И ВЗАИМОСВЯЗЕЙ МЕЖДУ ЯВЛЕНИЯМИ 2. «Политическая арифметика» Уильям Петти (1623— 1687) ВЫЯВЛЕНИЕ НА ОСНОВЕ БОЛЬШОГО ЧИСЛА НАБЛЮДЕНИЙ "изобретатель статистики» . РАЗЛИЧНЫХ ЗАКОНОМЕРНОСТЕЙ И ВЗАИМОСВЯЗЕЙ 3. Математико-статистический • Фрэнсис Гальтон (1822— 1911) • Карл Пирсон (1857 -1936) • Вильям Госсет (1876 -1937) • Рональд Фишер (1890— 1968) • Морис Дж. Кендэл (р. 1907) Раздел математики • дисперсионный анализ, • анализ временных рядов, • проверка гипотез

История развития статистики в России В правильной научной постановке статистического дела в России большая заслуга принадлежит Русскому географическому обществу, основанному в 1845 г. и имевшему в своем составе отделение статистики. Особое место в истории русской статистики занимает выдающийся русский географ, известный и как статистик, Петрович Семенов - Тян-Шанский. Он является своего рода отцом русской государственной статистики. ВТОРАЯ ПОЛОВИНА XIX — НАЧАЛО XX В. БЫЛИ ДЛЯ РОССИИ ПЕРИОДОМ БУРНОГО РАЗВИТИЯ СТАТИСТИЧЕСКОЙ НАУКИ И ПРАКТИКИ. БОЛЬШАЯ ЗАСЛУГА В ЭТОМ ПРИНАДЛЕЖИТ ПРЕДСТАВИТЕЛЯМ АКАДЕМИЧЕСКОЙ СТАТИСТИКИ: ПАФНУТИЙ ЛЬВОВИЧ ЧЕБЫШЁВ (1821— 1894), СФОРМУЛИРОВАВШИЙ ЗАКОН БОЛЬШИХ ЧИСЕЛ; АНДРЕЙ АНДРЕЕВИЧ МАРКОВ (1856— 1922) — СОЗДАТЕЛЬ МАТЕМАТИЧЕСКОЙ ТЕОРИИ, СПОСОБНОЙ ОПИСАТЬ СЛОЖНЫЕ ЯВЛЕНИЯ ( «цепи МАРКОВА» ) АЛЕКСАНДР МИХАЙЛОВИЧ ЛЯПУНОВ (1857— 1918), заложивший в практику основы ВЫБОРОЧНОГО НАБЛЮДЕНИЯ В СТАТИСТИКЕ. 10

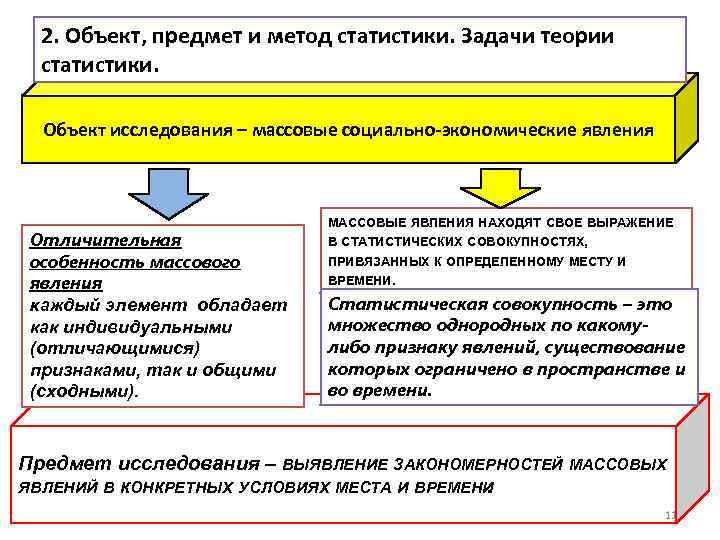2. Объект, предмет и метод статистики. Задачи теории статистики. Объект исследования – массовые социально-экономические явления Отличительная особенность массового явления каждый элемент обладает как индивидуальными (отличающимися) признаками, так и общими (сходными). МАССОВЫЕ ЯВЛЕНИЯ НАХОДЯТ СВОЕ ВЫРАЖЕНИЕ В СТАТИСТИЧЕСКИХ СОВОКУПНОСТЯХ, ПРИВЯЗАННЫХ К ОПРЕДЕЛЕННОМУ МЕСТУ И ВРЕМЕНИ. Статистическая совокупность – это множество однородных по какомулибо признаку явлений, существование которых ограничено в пространстве и во времени. Предмет исследования – ВЫЯВЛЕНИЕ ЗАКОНОМЕРНОСТЕЙ МАССОВЫХ ЯВЛЕНИЙ В КОНКРЕТНЫХ УСЛОВИЯХ МЕСТА И ВРЕМЕНИ. 11

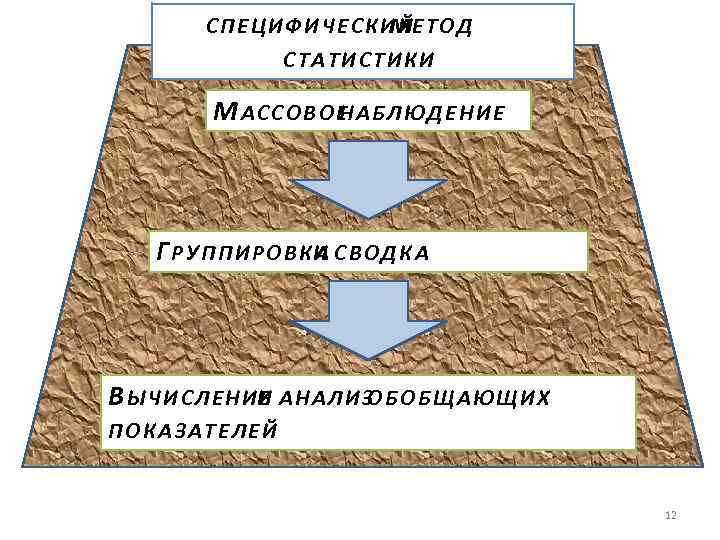С П Е Ц И Ф И Ч Е С К И ЙЕ Т О Д М СТАТИСТИКИ МАССОВОЕ АБЛЮДЕНИЕ Н Г Р У П П И Р О В КИ С В О Д К А А В Ы Ч И С Л Е Н ИИ А Н А Л И З Б О Б Щ А Ю Щ И Х Е О ПОКАЗАТЕЛЕЙ 12

Основные задачи изучения статистических совокупностей • Получение итоговых данных • Определение структуры и соотношения отдельных частей совокупностей; • Изучение особенности распределения единиц совокупности по отдельным признакам; • Выявление взаимосвязи между отдельными показателями; • Изучение динамики отдельных показателей; • Оценка выборочных данных и пр. 13

Статистика оперирует числовыми данными, которые обусловлены влиянием множества различных факторов, причин, одни из которых являются главными, существенными, а другие — случайными. Абстрагироваться от случайного и выявить типичное, закономерное — основная задача статистики, и эту задачу можно решить только на основе массовых данных. СТАТИСТИЧЕСКИЕ ЗАКОНОМЕРНОСТИ ОБНАРУЖИВАЮТСЯ ПРИ МАССОВОМ НАБЛЮДЕНИИ БЛАГОДАРЯ ДЕЙСТВИЮ ЗАКОНА БОЛЬШИХ ЧИСЕЛ. СУЩНОСТЬ ЗАКОНА БОЛЬШИХ ЧИСЕЛ - ПО МЕРЕ УВЕЛИЧЕНИЯ ЧИСЛА НАБЛЮДЕНИЙ ВЛИЯНИЕ СЛУЧАЙНЫХ ФАКТОРОВ В СВОДНЫХ ХАРАКТЕРИСТИКАХ СОВОКУПНОСТИ ВЗАИМОПОГАШАЮТСЯ И НА ПОВЕРХНОСТЬ ВЫСТУПАЕТ ДЕЙСТВИЕ ОСНОВНЫХ ФАКТОРОВ, КОТОРЫЕ И ОПРЕДЕЛЯЮТ ЗАКОНОМЕРНОСТЬ. 14

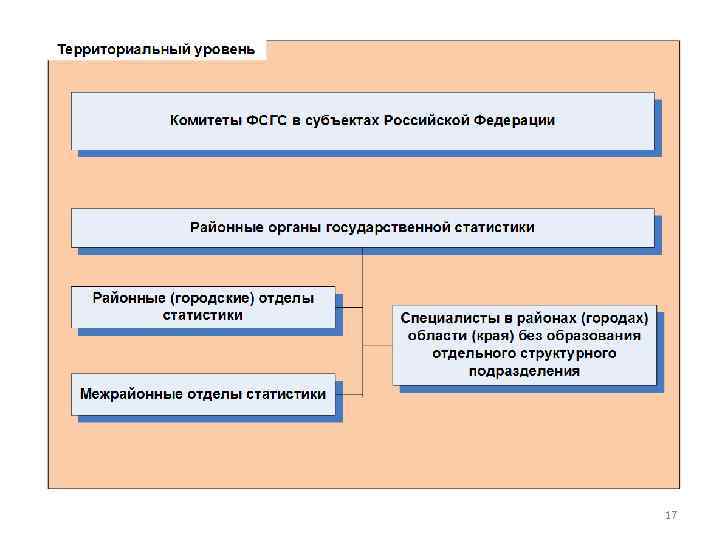
3. Организация статистики 15

16

17

18

Т 2. Сбор статистической информации. 1. Понятие статистического наблюдения. 2. Организационные формы, виды и способы статистического наблюдения. 3. Точность статистического наблюдения. Литература: [1], стр. 56 -80 [2], стр. 16 -28

1. Понятие статистического наблюдения Статистическое наблюдение - массовое, планомерное, научно организованное наблюдение за явлениями социальной и экономической жизни, которое заключается в регистрации отобранных признаков у каждой единицы совокупности Организационные формы статистического наблюдения • статистическая отчетность; • специально организованные статистические обследования (наблюдения); • регистры. Статистическая отчетность — это особая форма организации сбора данных государственной статистикой о деятельности хозяйствующих субъектов через специально заполняемые последними документы-бланки, именуемые формами статистической отчетности.

В настоящее время разработана унифицированная отчетность, включающая следующие формы: • П-1 «Сведения о производстве и отгрузке товаров и услуг» ; • П-2 «Сведения об инвестициях» ; • П-3 «Сведения о финансовом состоянии предприятия» ; • П-4 «Сведения о численности, заработной плате и движении работников» ; • Малые предприятия с 1999 г. отчитываются ежеквартально лишь по форме ПМ «Сведения об основных показателях деятельности малого предприятия» .

В случаях, когда необходимо получить сведения, по которым отсутствует отчетность, когда требуется уточнить или дополнить данные той или иной отчетности проводятся специально организованные статистические наблюдения в виде переписей или специальных обследований (выборочных или сплошных). По данным переписей населения, на июнь 2007 года численность населения Земли составила около 6, 4 млрд. человек. Страны-лидеры по количеству жителей распределяются следующим образом: 1 -е место: Китай – 1 321 851 888 чел. 2 -е место: Индия – 1 100 866 154 чел. 3 -е место: США – 300 139 947 чел. 4 -е место: Индонезия – 234 693 997 чел. 5 -е место: Бразилия – 186 010 647 чел. 6 -е место: Пакистан – 164 741 924 чел. 7 -е место: Бангладеш – 150 448 339 чел. 8 -е место: Россия – 142 000 752 чел. 9 -е место: Нигерия – 133 031 164 чел. 10 -е место: Япония – 127 433 494 чел.

Регистр — это поименованный и постоянно уточняемый перечень тех или иных единиц наблюдения, созданный для непрерывного длительного статистического наблюдения за определенной совокупностью. В России действует Единый государственный регистр предприятий и организаций (ЕГРПО) всех форм собственности. В нем содержатся такие сведения о каждом предприятии, как: среднесписочная численность работников, остаточная стоимость основных средств, уставный фонд, балансовая прибыль и др.

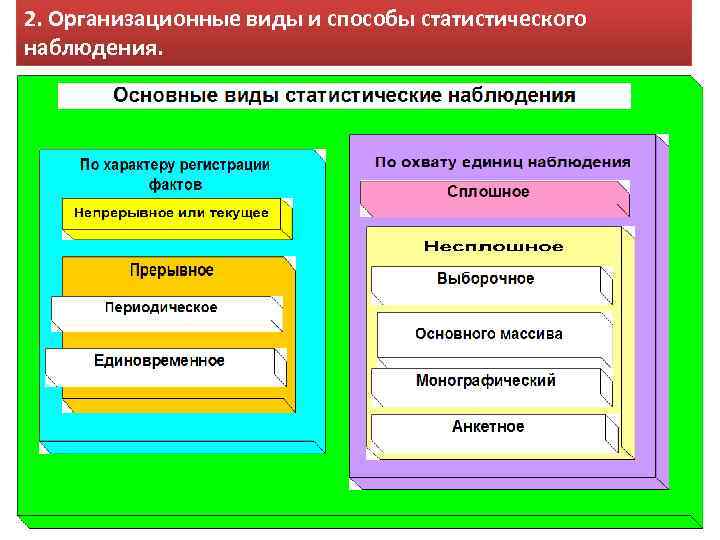2. Организационные виды и способы статистического наблюдения.

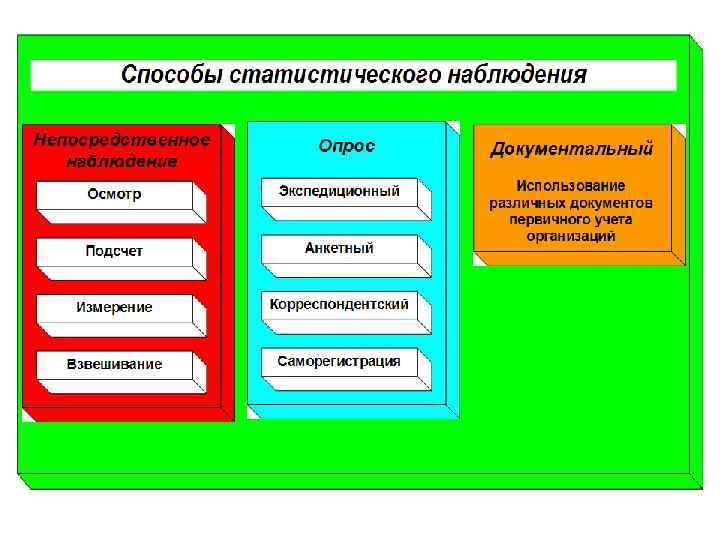
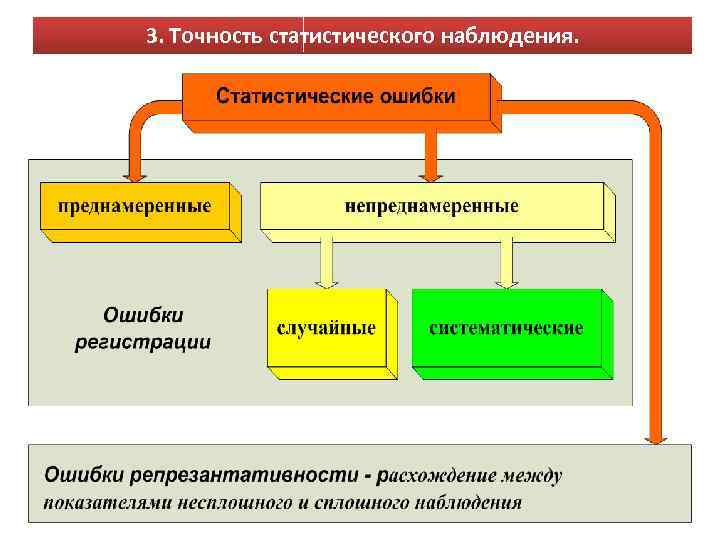3. Точность статистического наблюдения.

Т 3. Изображение статистических данных 1. Статистические таблицы. 2. Статистические графики. Литература [1], стр. 128 -182 [2], стр. 53 -99

1. Статистические таблицы. Статистическая таблица — это форма наиболее краткого и рационального изложения цифровых данных об изучаемой статистической совокупности. Незаполненная цифрами статистическая таблица называется макетом. Макет таблицы — это сетка, состоящая из горизонтальных строк и вертикальных колонок (граф), каждая из которых имеет название. Клетки, образуемые на пересечении строк и колонок, заполняют статистическими данными. Подлежащим таблицы называется объект, отдельные единицы или его части (группы), которые характеризуются соответствующими показателями. Сказуемым называются показатели, которые характеризуют подлежащее. Подлежащее таблицы обычно составляет название ее строк, сказуемое — название колонок.

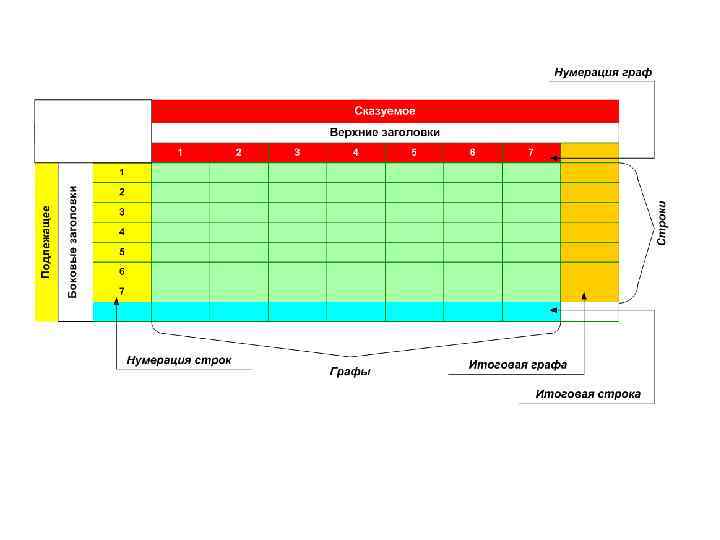
Подлежащее статистической таблицы может быть простым и сложным. По характеру подлежащего различают простые, групповые и комбинационные таблицы. В простой таблице подлежащее представляет перечень отдельных единиц изучаемого объекта. Например, перечень предприятий и организаций или перечень отдельных дат (годы, кварталы и т. д. ). В групповых таблицах статистическая совокупность разбивается на отдельные группы по какому-то одному признаку. При этом каждую группу можно охарактеризовать одним или несколькими показателями. В комбинационных таблицах объект исследования, т. е. подлежащее, разбивается на группы не по одному, а по нескольким признакам.

Число браков и разводов в России Год Число браков, тысяч 1960 1970 1980 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 1499, 6 1319, 2 1464, 6 1319, 9 1277, 2 1053, 7 1106, 7 1080, 6 1075, 2 866, 7 928, 4 848, 7 911, 2 897, 3 1001, 6 1019, 8 Число разводов, тысяч 184, 4 396, 6 580, 7 559, 9 597, 9 639, 2 663, 3 680, 5 665, 9 562, 4 555, 2 501, 7 532, 5 627, 7 763, 5 853, 6 На 1000 человек населения браков разводов 12, 5 10, 1 3 10, 6 4, 2 8, 9 3, 8 8, 6 4 7, 1 4, 3 7, 5 4, 5 7, 4 4, 6 7, 3 4, 5 5, 9 3, 8 6, 3 3, 8 5, 8 3, 4 6, 3 3, 7 6, 2 4, 3 6, 9 5, 3 7, 1 6 Источник: Инвестиции в России. 2003: Стат. сб. — М. : Госкомстат России, 2003. — С. 98.

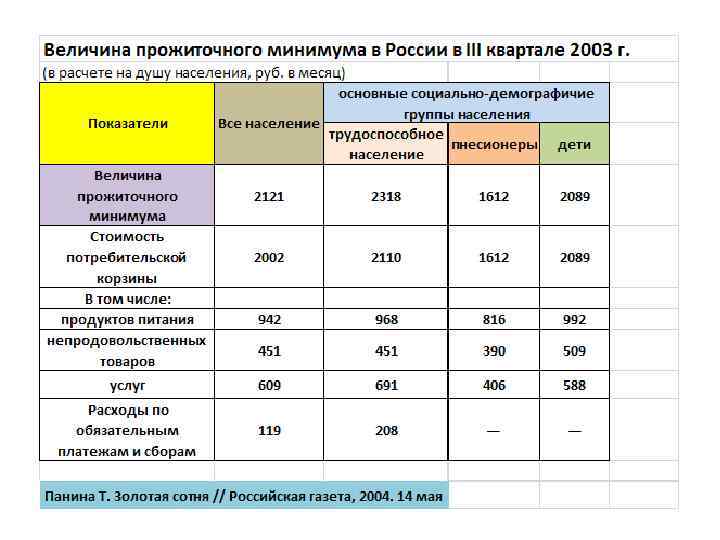
При построении статистических таблиц следует соблюдать ряд условий. 1. Каждая таблица должна иметь краткий заголовок, который в то же время должен достаточно полно и четко отражать содержание анализируемого объекта. 2. Все строки и графы таблицы должны иметь названия, при этом повторяющиеся термины следует выносить в общие заголовки. 3. В строках и графах таблицы должны быть указаны единицы измерения. Единая единица измерения для всех строк и столбцов должна быть вынесена за пределы таблицы и размещена с правой стороны над таблицей. 4. Необходимо указывать источники данных, приведенных в таблице (название обследования с указанием организации, которая его проводила, название публикации или указание на условность данных).

При заполнении таблиц используют следующие условные обозначения: • «. . . » (многоточие) - явление существует, но сведений о нем нет; • «О» (ноль) - явление существует, но значение его показателя меньше половины единицы, принятой при округлении; • «—» (тире) — явление отсутствует; • «х» (крестик) - клетка не подлежит заполнению.

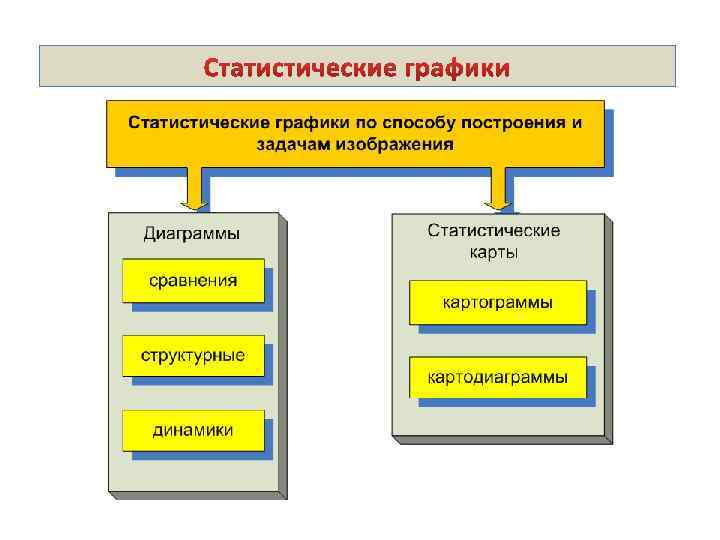
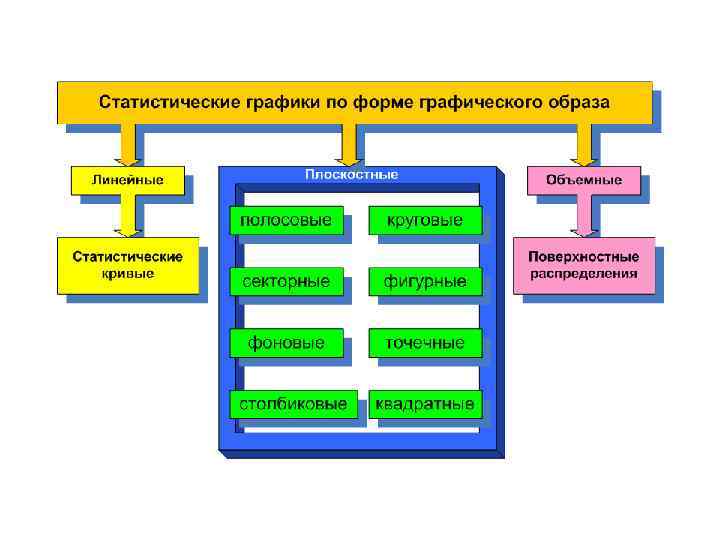
СТОЛБИКОВАЯ ДИАГРАММА 500 470 450 400 Китай 350 Иран 317 300 Саудовская Аравия 250 Пакистан 200 США 150 143 135 100 50 42 0 Приведенные в исполнение смертные приговоры в 2007 г. Newsweek № 17 2008 г.

Способы оплаты мобильной связи, в % Другое 1 Платит работодатель 5 Через интернет 5 По карточке предоплаты 8 13 Через банкомат В кассах магазинов 3 В автоматах моментальной оплаты 33 В офисе оператора 3 29 В салоне сотовой связи 0 10 20 Источник: www. computerbild. ru 09. 2007 30 40

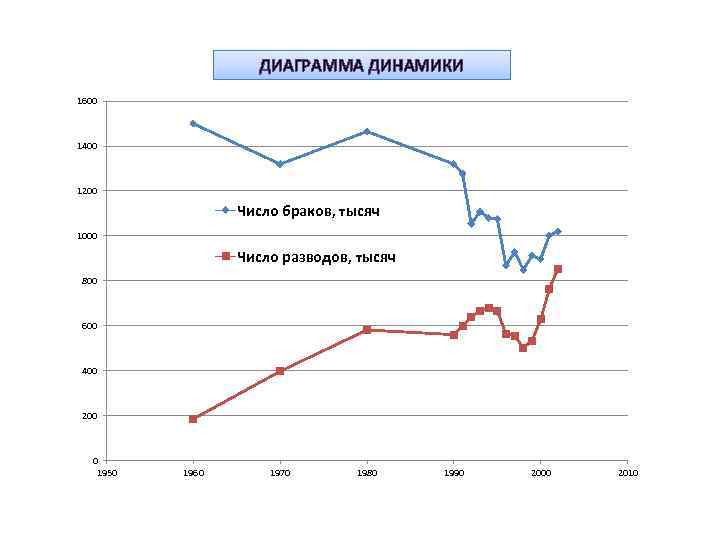ДИАГРАММА ДИНАМИКИ 1600 1400 1200 Число браков, тысяч 1000 Число разводов, тысяч 800 600 400 200 0 1950 1960 1970 1980 1990 2000 2010

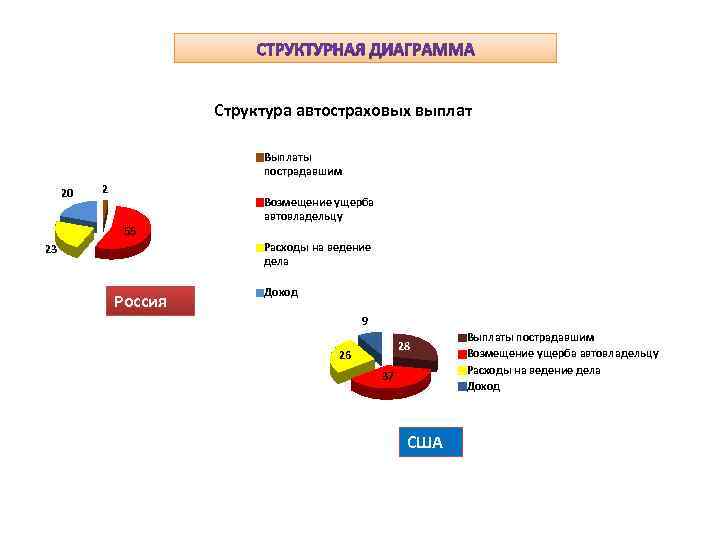Структура автостраховых выплат Выплаты пострадавшим 20 2 Возмещение ущерба автовладельцу 55 Расходы на ведение дела 23 Россия Доход 9 28 26 37 США Выплаты пострадавшим Возмещение ущерба автовладельцу Расходы на ведение дела Доход

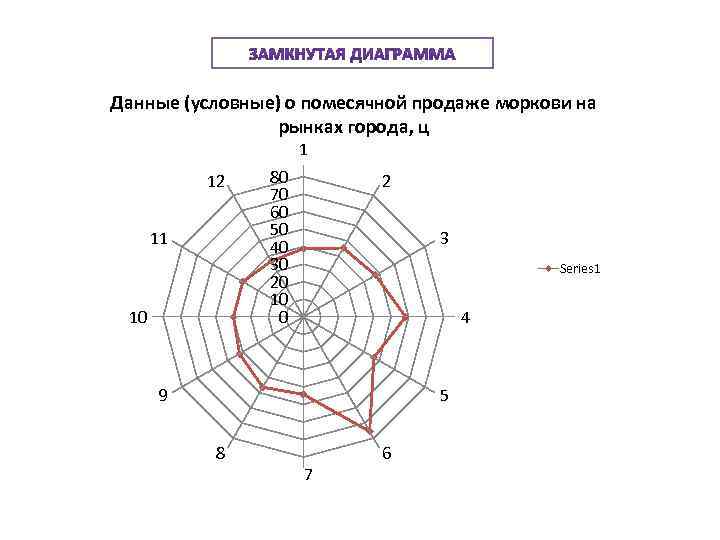Данные (условные) о помесячной продаже моркови на рынках города, ц 1 12 11 10 80 70 60 50 40 30 20 10 0 2 3 Series 1 4 9 5 8 7 6

44

Т 4. СТАТИСТИЧЕСКАЯ СВОДКА И ГРУППИРОВКА 1. Задачи и содержание сводки. 2. Виды группировок. 3. Ряды распределения и группировки. Литература: [1], стр. 81 -127 [2], стр. 29 -53

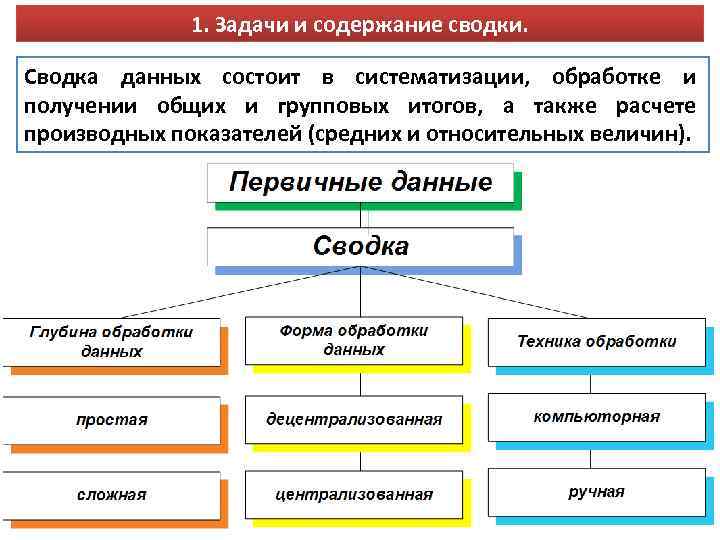1. Задачи и содержание сводки. Сводка данных состоит в систематизации, обработке и получении общих и групповых итогов, а также расчете производных показателей (средних и относительных величин). 03. 02. 2018 Теория статистика Лк-3 46

2. Виды группировок. Группировкой называется расчленение единиц статистической совокупности на группы, однородные по какому-либо одному или нескольким признакам. С помощью метода группировок решаются следующие задачи: • выделение типов социально – экономических явлений; • изучение структуры явления; • выявление связи и зависимости между явлениями. Формирование группировки • выбор группировочного признака; • определение числа групп; • фиксация вариантов; • подсчет частот.

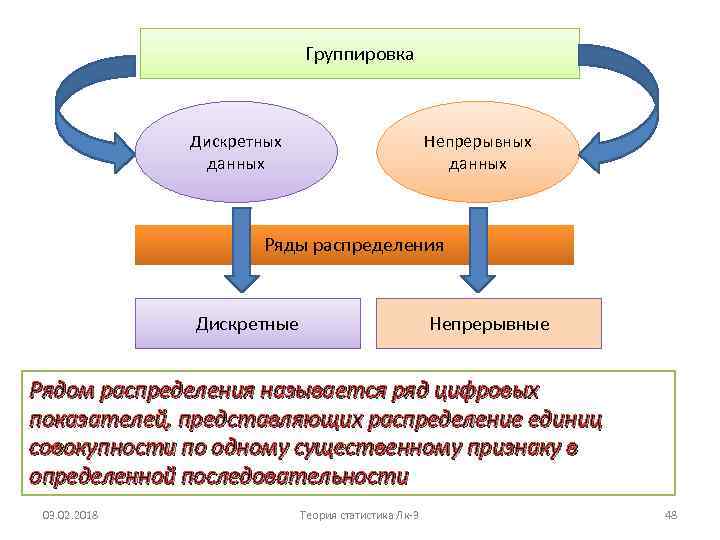Группировка Дискретных данных Непрерывных данных Ряды распределения Дискретные Непрерывные Рядом распределения называется ряд цифровых показателей, представляющих распределение единиц совокупности по одному существенному признаку в определенной последовательности 03. 02. 2018 Теория статистика Лк-3 48

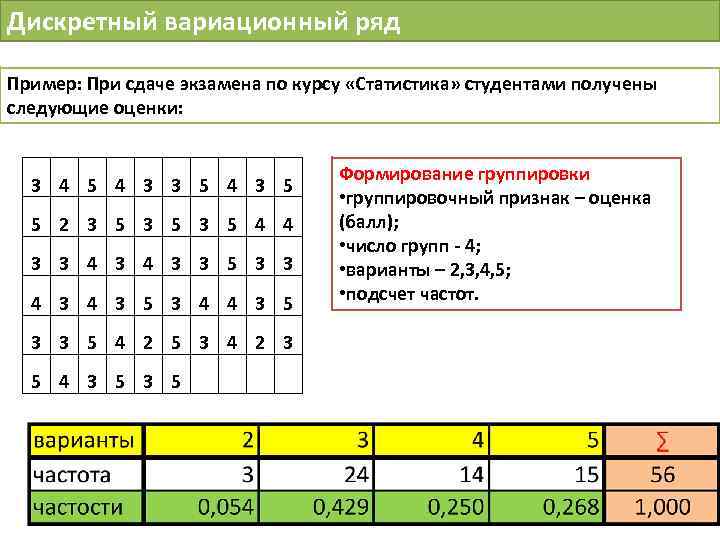Дискретный вариационный ряд Пример: При сдаче экзамена по курсу «Статистика» студентами получены следующие оценки: 3 4 5 4 3 3 5 4 3 5 5 2 3 5 3 5 4 4 3 3 5 3 3 4 3 5 3 4 4 3 5 Формирование группировки • группировочный признак – оценка (балл); • число групп - 4; • варианты – 2, 3, 4, 5; • подсчет частот. 3 3 5 4 2 5 3 4 2 3 5 4 3 5 49

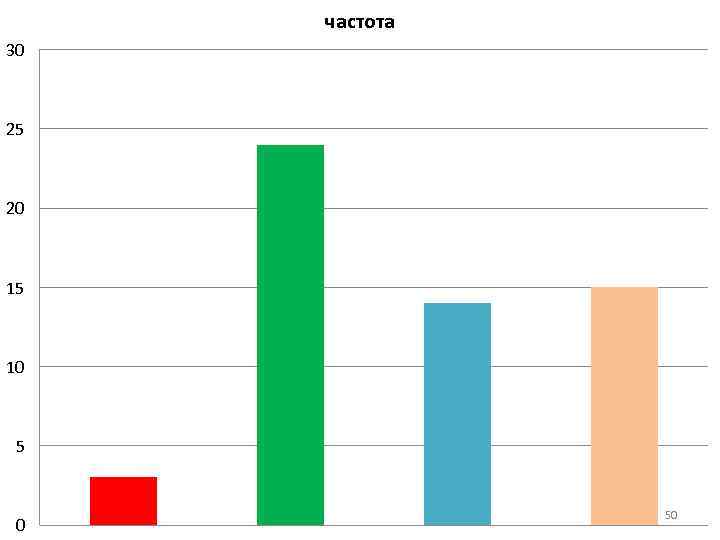частота 30 25 20 15 10 5 0 50

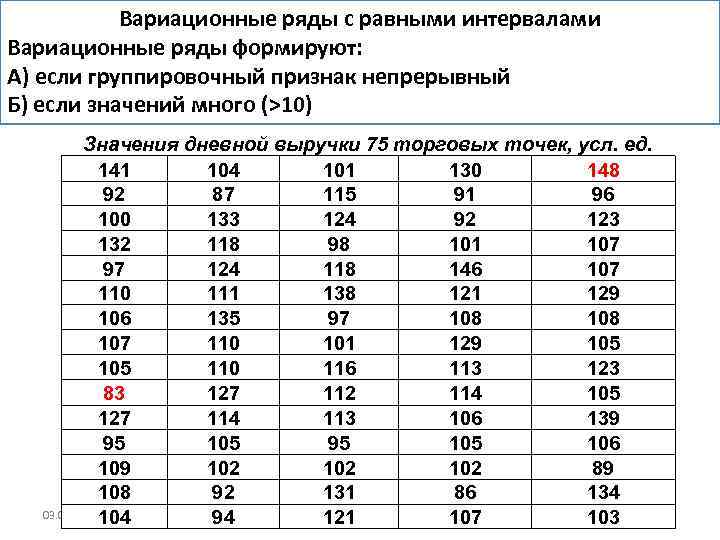Вариационные ряды с равными интервалами Вариационные ряды формируют: А) если группировочный признак непрерывный Б) если значений много (>10) Значения дневной выручки 75 торговых точек, усл. ед. 141 104 101 130 148 92 87 115 91 96 100 133 124 92 123 132 118 98 101 107 97 124 118 146 107 110 111 138 121 129 106 135 97 108 107 110 101 129 105 110 116 113 123 83 127 112 114 105 127 114 113 106 139 95 105 106 109 102 102 89 108 92 131 86 134 03. 02. 2018104 Теория статистика Лк-3 94 121 107 103 51

1. Определение числа групп Формула Старджесса 2. Определение интервалов группировки Размах данных Шаг интервала 52

3. Формирование интервалов вариационного ряда Истинные значения Min= 83 Max= 148 R= 65 m= 7 Границы интервального ряда h = 9, 3 Рекомендация Как можно меньше значащих цифр лев граница прав граница 80 90 90 100 110 120 130 140 150 Выбранные значения Min= 80 Max= 150 R= 70 m= 7 h = 10 интервал 1 й интервал 2 й интервал 3 й интервал 4 й интервал 5 й интервал 6 й интервал 7 й интервал 53

4. Подсчет частот (Определяется число значений попадающих в каждый из интервалов) Схема «конвертов» При попадании значения в интервал ставят точку либо черточку Каждый полный «конверт» содержит 10 объектов 54

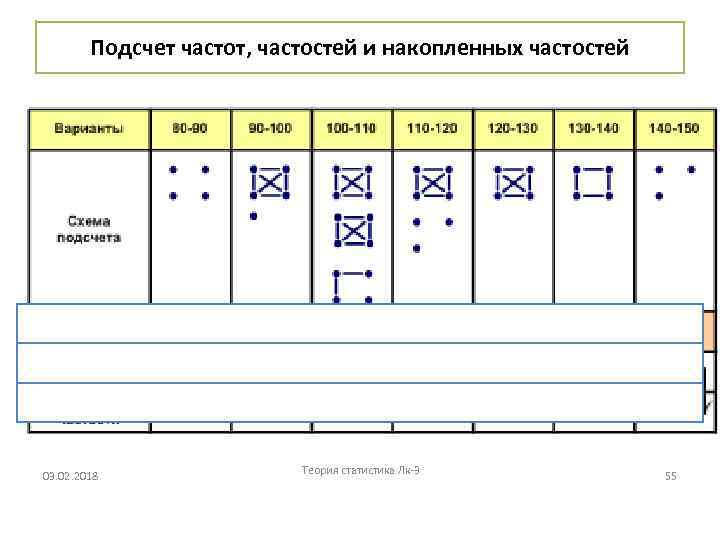Подсчет частот, частостей и накопленных частостей 03. 02. 2018 Теория статистика Лк-3 55

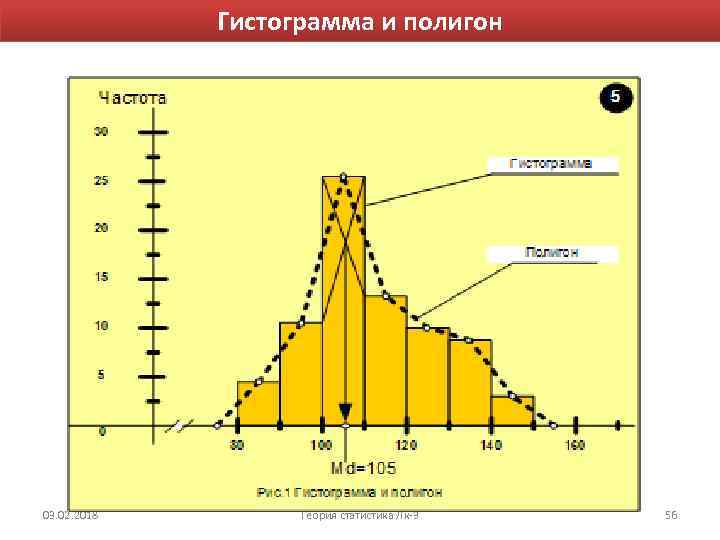Гистограмма и полигон 03. 02. 2018 Теория статистика Лк-3 56

Выборочная функция распределения и кумулята 03. 02. 2018 Теория статистика Лк-3 57

58

Т 5. ОБОБЩАЮЩИЕ СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ 1. Абсолютные и относительные величины 2. Средние показатели 3. Показатели вариации Л[1], стр 186 -238

1. Абсолютные и относительные величины Под статистическим показателем понимается обобщающая количественная характеристика изучаемого объекта или его свойства. Требования к статистическому показателю В нем должны быть указаны: • статистическая структура показателя (т. е. , что это такое - среднее значение, сумма, процент к итогу и т. д. ); • его содержание (население, инвестиции, объем добычи и т. д. ); • позиция в классификации, совокупность объектов (обрабатывающая промышленность России, предприятия торговли); • единица измерения (человек, тонна, километр и др. ); • время (на начало года, за 1990 -2002 гг. и т. п. ); • специальные уточнения.

В зависимости от методов расчета обобщающие показатели могут быть: • абсолютными, • относительными, • средними величинами. Абсолютные обобщающие показатели — это число единиц по совокупности в целом или по ее отдельным группам, которое получают в результате суммирования зарегистрированных значений признаков первичного статистического материала. Любая абсолютная величина всегда имеет свою единицу измерения, присущую тем или иным явлениям.

Широкое применение находят натуральные единицы измерения, как простые (тонна, штука, квадратный и кубический метр, километр и т. д. ), так и сложные, представляющие собой комбинацию двух величин (тоннокилометр, киловатт-час и др. ). В качестве абсолютных обобщающих показателей используют стоимостные показатели, они позволяют соизмерить величины, которые нельзя соизмерить в натуральной форме (например, расходы населения). Кроме того, в качестве абсолютных обобщающих показателей используют и показатели, измеренные в человеко-днях или человеко-часах.

Разновидностью натуральных показателей являются условно-натуральные показатели. Их применяют для получения абсолютных обобщающих показателей, когда отдельные группы слагаемых, входящие в совокупность, не поддаются непосредственному суммированию. С помощью специальных коэффициентов пересчета слагаемые выражают в единой стандартной единице измерения, что позволяет получить обобщающий показатель. Например, различные виды топлива соизмеряют по условному топливу с теплотворной способностью 7000 ккал/кг.

Относительная величина представляет собой результат деления (сравнения) двух величин. В числителе дроби стоит величина, которую сравнивают, в знаменателе — величина, с которой сравнивают. Последняя называется базой (или основанием) сравнения. Если основание принимается за 100, относительная величина выражается в процентах (%), если за 1000 — в промилле (‰), если за 10000 — в продецимилле Если сравниваемая величина больше базы сравнения в 2 раза и более, то обычно выбирают форму коэффициента. Если относительная величина близка к единице, как правило, ее выражают в процентах.

• • • Различают относительные величины динамики, структуры сравнения, интенсивности координации. Относительные показатели сравнения (ОПСр) получают в результате сопоставления одноименных абсолютных показателей, относящихся к разным совокупностям. Пример: Золотой запас на конец 2000 г. органов денежнокредитного регулирования России – 12, 36 млн тройских унций, США – 261, 61 млн тройских унций. ОПСр=12, 36/261, 61=0, 047 (4, 7%).

2. Средние показатели Средняя величина - это обобщающая характеристика множества индивидуальных значений некоторого количественного признака. Средняя, являясь функцией множества индивидуальных значений, представляет одним значением всю совокупность и отражает то общее, что присуще всем ее единицам. Наиболее часто применяются следующие средние величины: • средняя арифметическая; • средняя гармоническая; • средняя геометрическая; • средняя квадратическая.

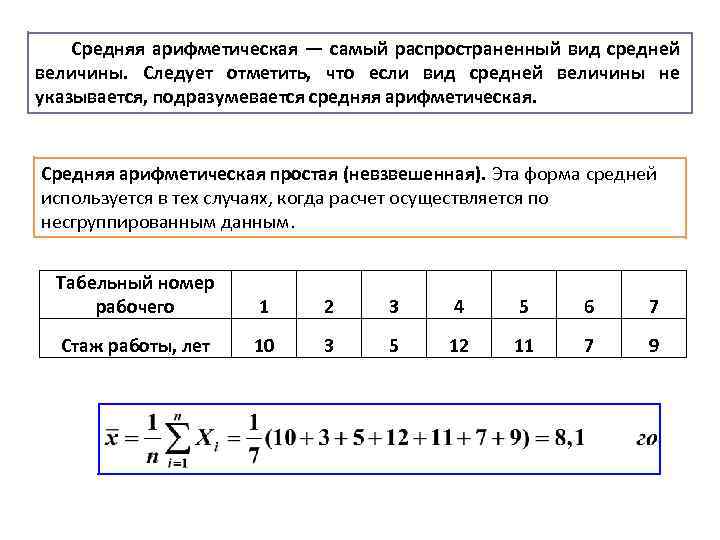Средняя арифметическая — самый распространенный вид средней величины. Следует отметить, что если вид средней величины не указывается, подразумевается средняя арифметическая. Средняя арифметическая простая (невзвешенная). Эта форма средней используется в тех случаях, когда расчет осуществляется по несгруппированным данным. Табельный номер рабочего 1 2 3 4 5 6 7 Стаж работы, лет 10 3 5 12 11 7 9

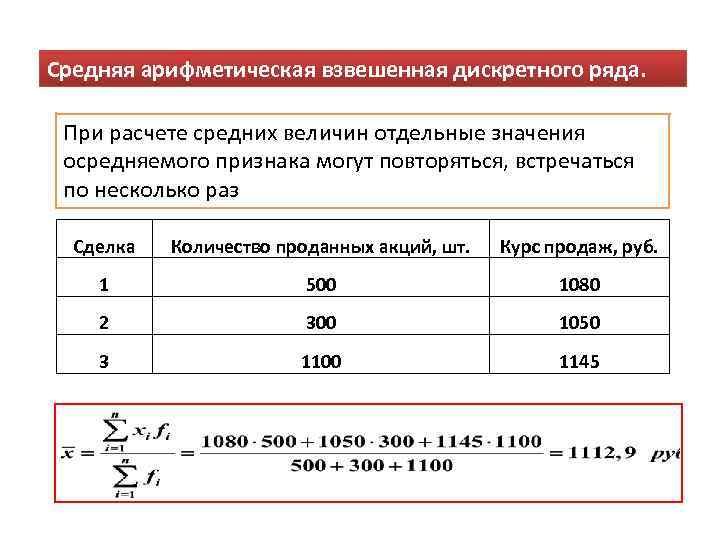Средняя арифметическая взвешенная дискретного ряда. При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз Сделка Количество проданных акций, шт. Курс продаж, руб. 1 500 1080 2 300 1050 3 1100 1145

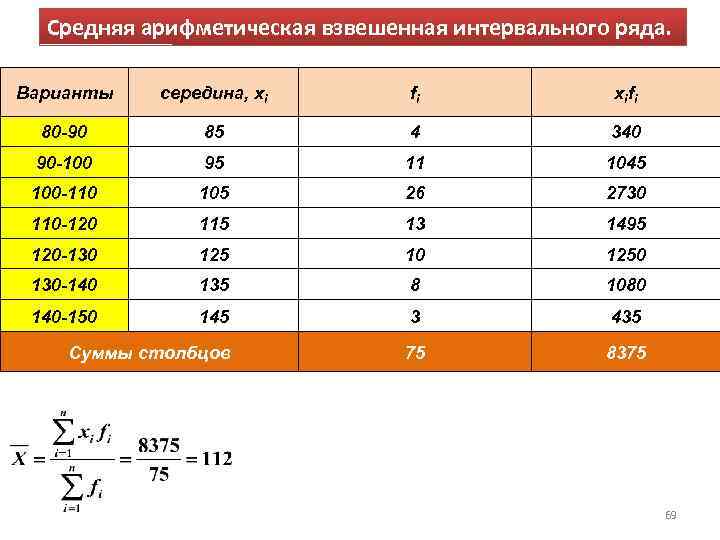Средняя арифметическая взвешенная интервального ряда. Варианты середина, хi fi xifi 80 -90 85 4 340 90 -100 95 11 1045 100 -110 105 26 2730 110 -120 115 13 1495 120 -130 125 10 1250 130 -140 135 8 1080 140 -150 145 3 435 Суммы столбцов 75 8375 69

Структурные средние. Мода (Mo) – это значение признака, которое чаще всего встречается в вариационном ряду. Свойства • вокруг нее концентрируется большая часть вариантов (характеристика ходового товара); • устойчива к «выбросам» на хвостах; • приближенно оценивается по гистограмме.

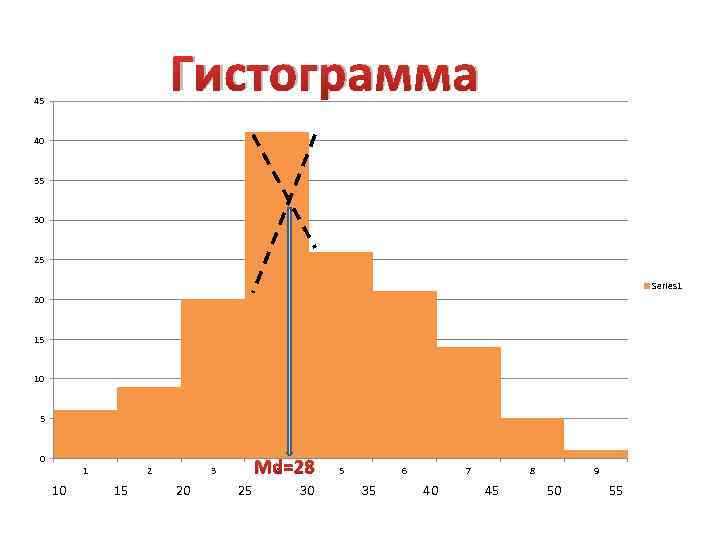Гистограмма 45 40 35 30 25 Series 1 20 15 10 5 0 1 10 2 15 Md=28 4 3 20 25 30 5 6 35 7 40 8 45 9 50 55

Нижняя граница модального интервала Ширина модального интервала Частота интервала предшествующая модальному Частота интервала следующего за модальным 72

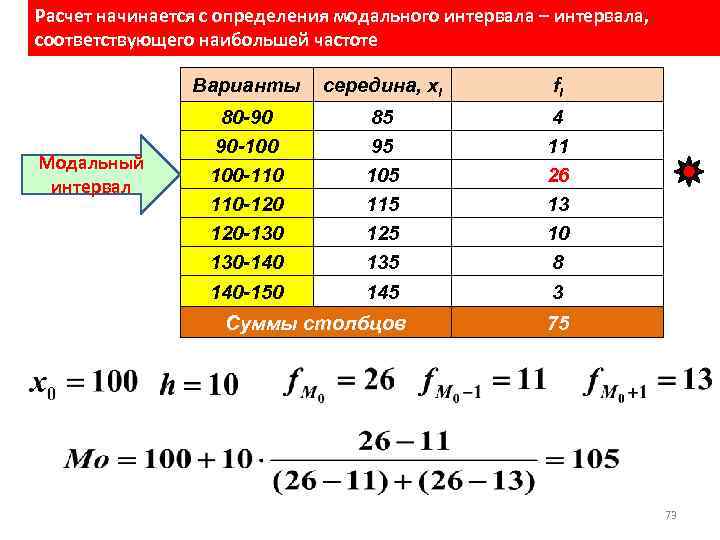Расчет начинается с определения модального интервала – интервала, соответствующего наибольшей частоте Варианты Модальный интервал середина, хi fi 80 -90 90 -100 100 -110 110 -120 120 -130 130 -140 140 -150 85 95 105 115 125 135 145 4 11 26 13 10 8 3 Суммы столбцов 75 73

Медиана (Me) – это значение признака, которое приходится на середину ранжированного ряда. Свойства • устойчива к выбросам на «хвостах» ; • сумма абсолютных отклонений значений признака от Me меньше, чем от другой величины • приближенно оценивается по кумуляте.

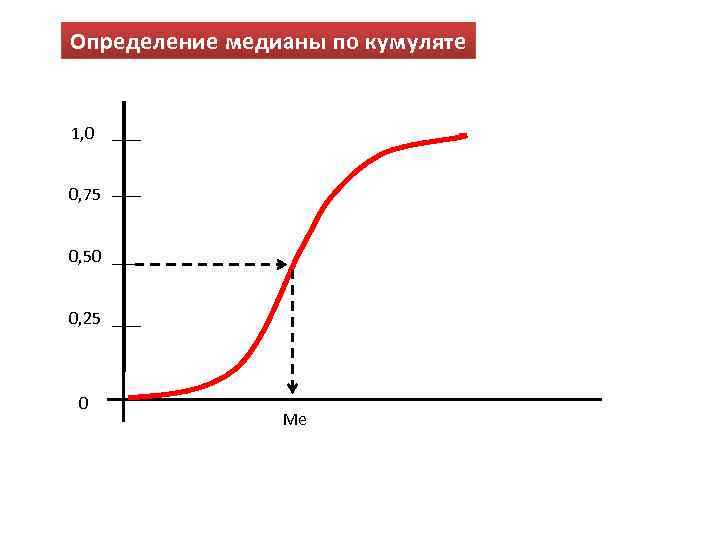Определение медианы по кумуляте 1, 0 0, 75 0, 50 0, 25 0 Ме

Нижняя граница медианного интервала Ширина медианного интервала Сумма частот Накопленная частота интервалов до медианного Частота медианного интервала 76

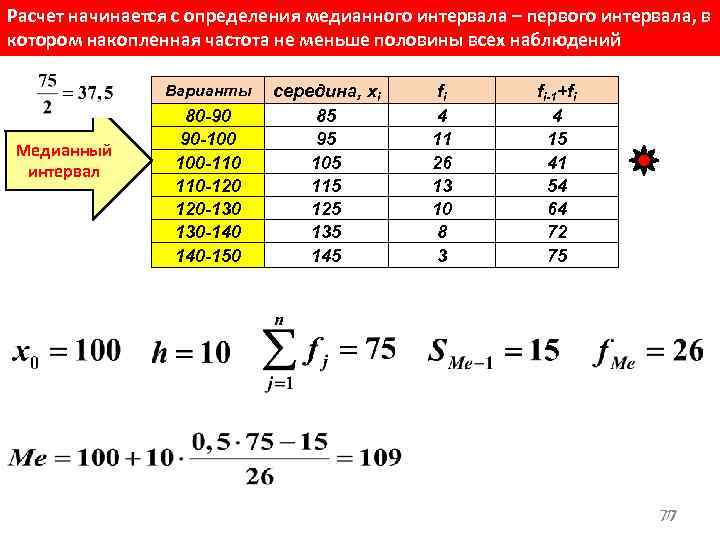Расчет начинается с определения медианного интервала – первого интервала, в котором накопленная частота не меньше половины всех наблюдений Варианты Медианный интервал 80 -90 90 -100 100 -110 110 -120 120 -130 130 -140 140 -150 середина, хi 85 95 105 115 125 135 145 fi 4 11 26 13 10 8 3 fi-1+fi 4 15 41 54 64 72 75 77 77

Обобщение понятие медианы Нижний квартиль – значение, меньше которого расположено 25% признака Верхний квартиль – значение, меньше которого расположено 75% признака Нижняя граница интервала Ширина квартильного интервала Накопленная частота до Частота квартильного интервала

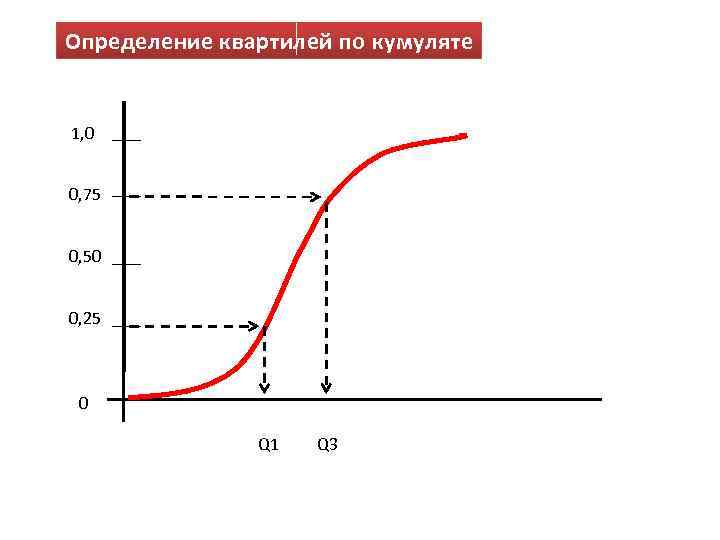Определение квартилей по кумуляте 1, 0 0, 75 0, 50 0, 25 0 Q 1 Q 3

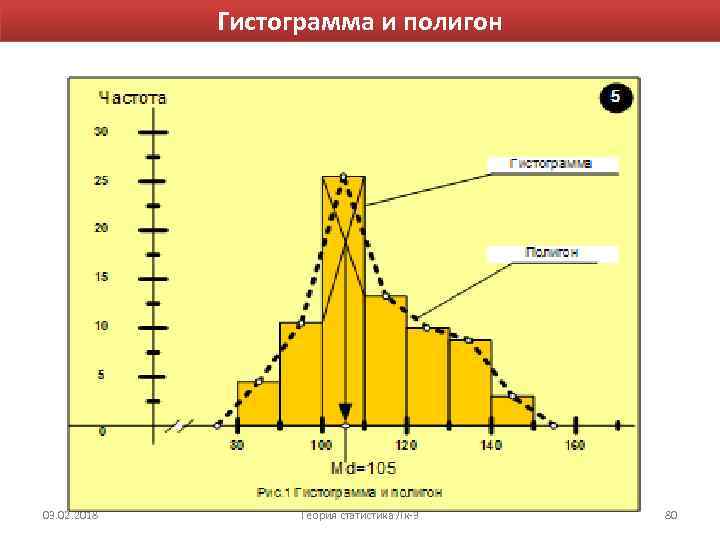Гистограмма и полигон 03. 02. 2018 Теория статистика Лк-3 80

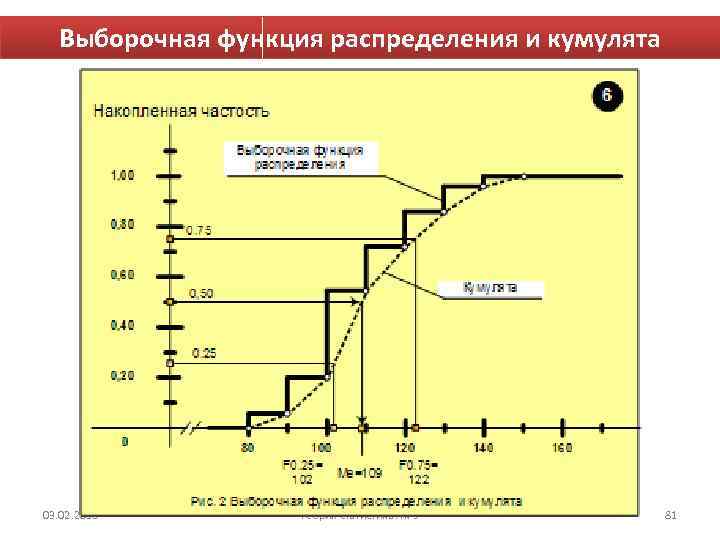Выборочная функция распределения и кумулята 03. 02. 2018 Теория статистика Лк-3 81

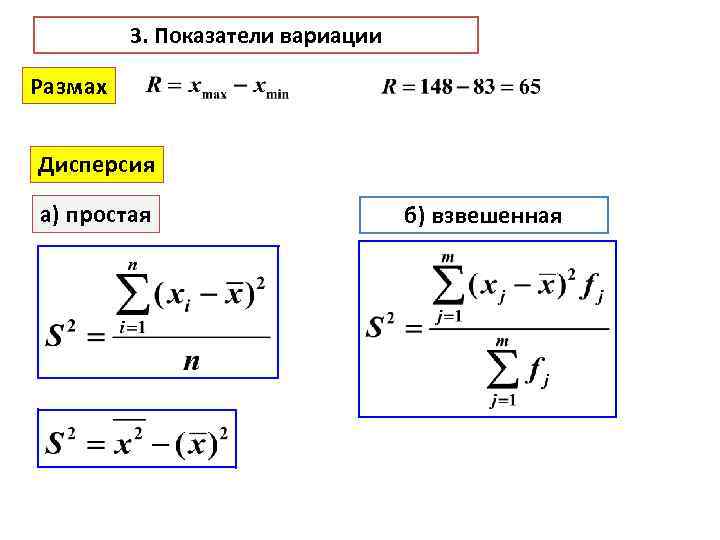3. Показатели вариации Размах Дисперсия а) простая б) взвешенная

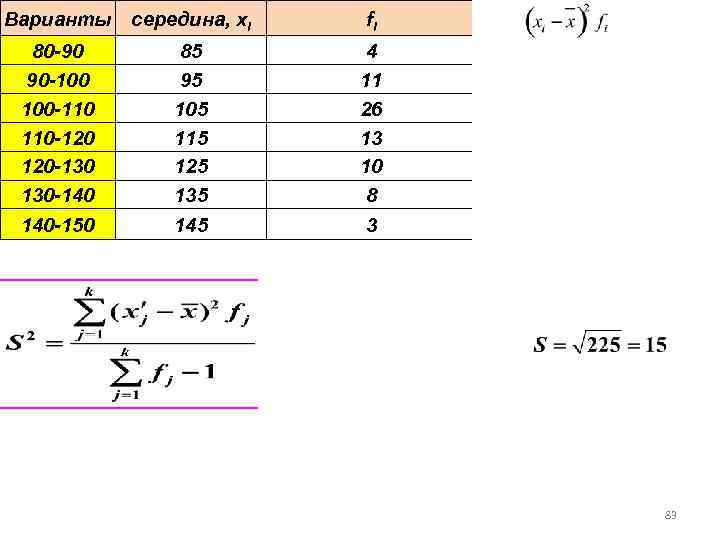Варианты середина, хi 80 -90 90 -100 100 -110 110 -120 120 -130 130 -140 140 -150 85 95 105 115 125 135 145 fi 4 11 26 13 10 8 3 2916 3179 1274 117 1690 4232 3267 16675 83

Коэффициент осцилляции Коэффициент вариации Полумежквартильный размах В распределениях приблизительно симметричных

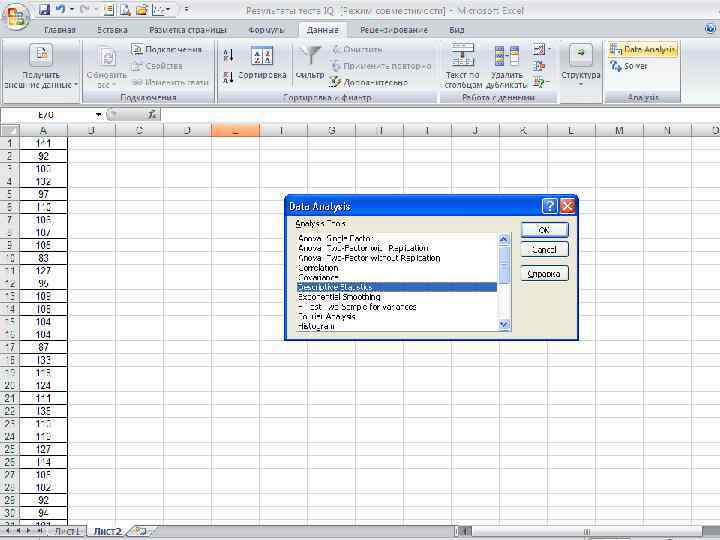
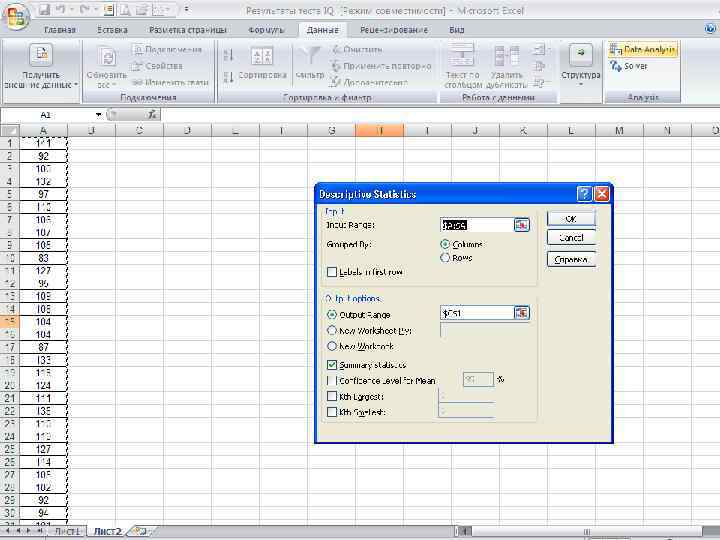
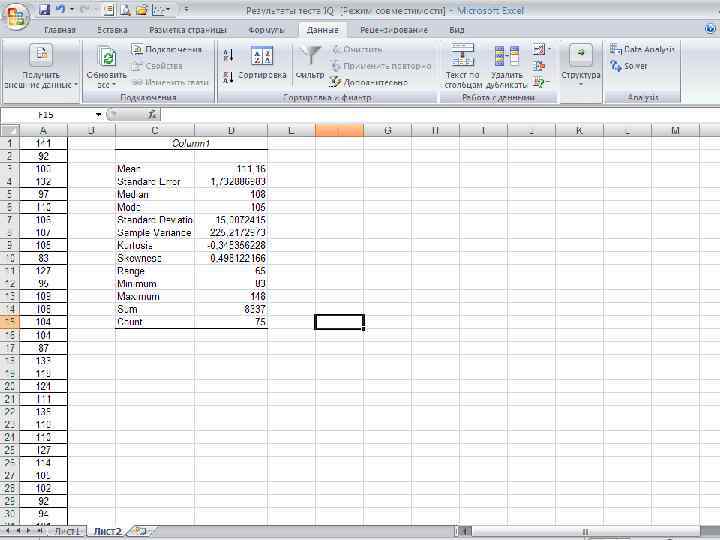
Среднее значение =112 Мода =105 Медиана =109 Гипотеза: дневная выручка подчиняется нормальному распределению Нижний квартиль =101 Верхний квартиль =122 Межквартильный размах=21 Размах =65 Дисперсия =225 СКО =15 Коэффициент вариации, %=13, 4 Расчеты значительно упрощаются в ППП Excel Данные Анализ данных Описательная статистика 85

86

87

88

89

Т 6. Парная регрессия • 1. Регрессиный анализ • 2. Корреляционный анализ

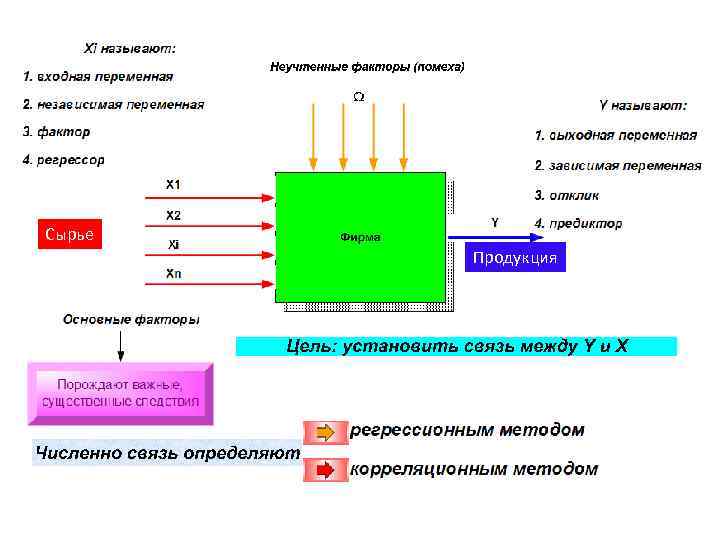Сырье Продукция

Первый шаг регрессионного анализа – выбор вида функциональной зависимости f(x) - случайная величина

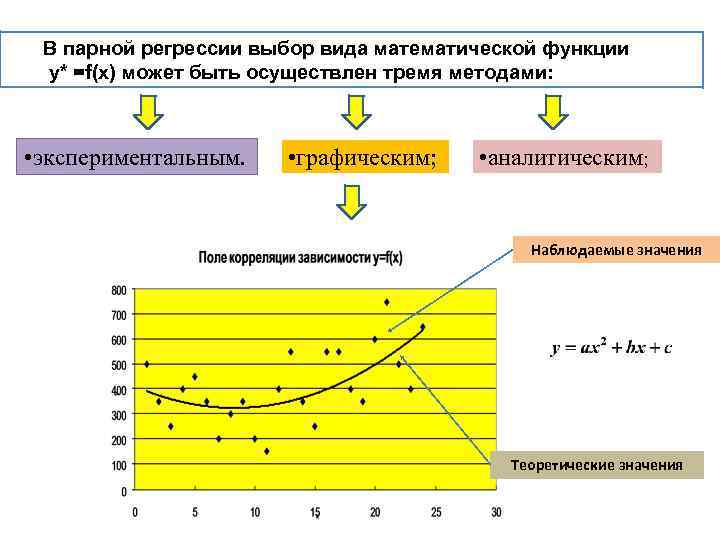В парной регрессии выбор вида математической функции y* =f(x) может быть осуществлен тремя методами: • экспериментальным. • графическим; • аналитическим; Наблюдаемые значения Теоретические значения

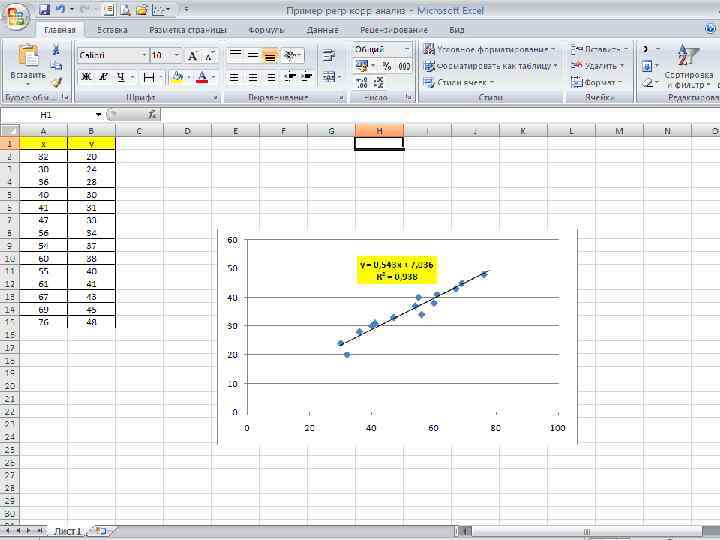
Второй шаг регрессионного анализа – определение параметров выбранной функции f(x) Основной аналитический метод определения параметров - метод наименьших квадратов Пусть выбрана линейная функция y=f(x)=a+bx. Необходимо определить параметры а и b. Метод наименьших квадратов позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений результативного признака у от расчетных (теоретических) у * минимальна:

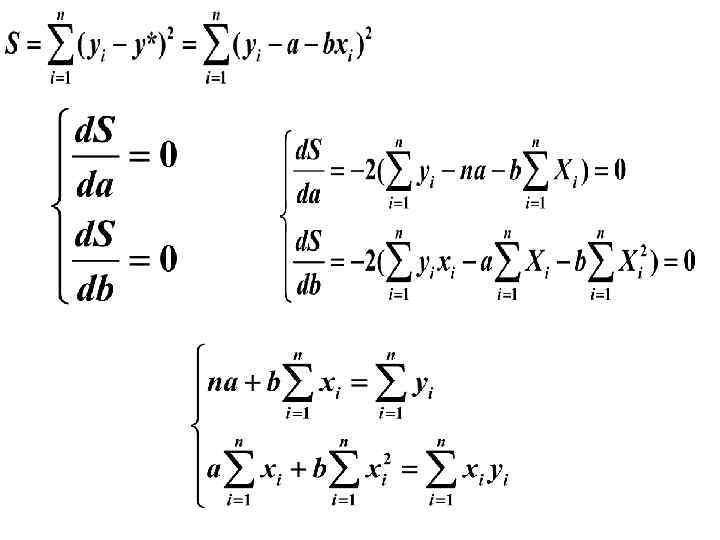
Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Знак при коэффициенте регрессии показывает направление связи — связь прямая — связь обратная. Пример: если функция издержек (у, тыс. руб. ) выражается как , где х количество единиц продукции, то, дополнительный прирост продукции на одну единицу требует увеличения затрат в среднем на 2 тыс. руб.

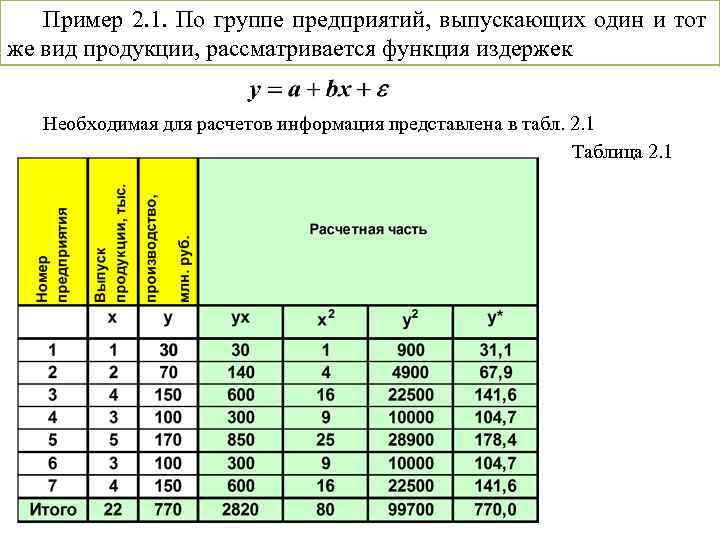Пример 2. 1. По группе предприятий, выпускающих один и тот же вид продукции, рассматривается функция издержек Необходимая для расчетов информация представлена в табл. 2. 1 Таблица 2. 1

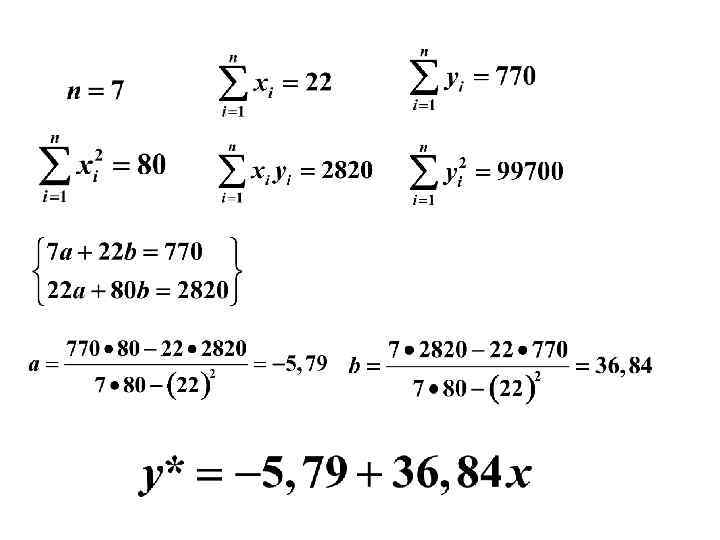
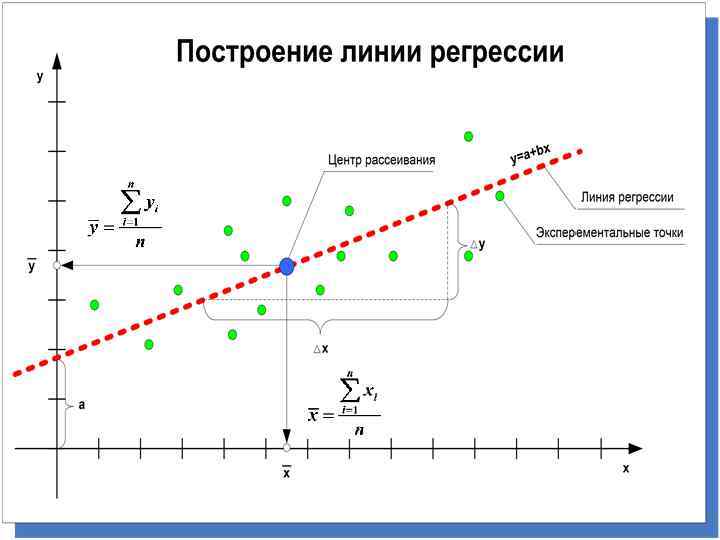
ТОЧЕЧНЫЙ ПРОГНОЗ НА ОСНОВЕ ЛИНЕЙНОГО УРАВНЕНИЯ РЕГРЕССИИ В прогнозных расчетах по уравнению регрессии определяется предсказываемое значение как точечный прогноз путем подстановки в линейное уравнение регрессии соответствующего значения х Пример: Определить средний уровень производства, если выпуск продукции достигнет 6 млн. шт. Решение: х=6 Ответ: Средний уровень производства должен составлять 215, 3 млн. руб. Однако точечный прогноз явно нереален, поэтому он дополняется расчетом стандартной ошибки. 102

ИНТЕРВАЛЬНЫЙ ПРОГНОЗ НА ОСНОВЕ ЛИНЕЙНОГО УРАВНЕНИЯ РЕГРЕССИИ А) интервальный прогноз среднего значения -интервальный прогноз среднего значения отклика при заданном х=хk - параметр нормального распределения уровня α -стандартная ошибка предсказанного среднего значения у при заданном хk Формула стандартной ошибки предсказываемого среднего значения у при заданном значении xk характеризует ошибку положения линии регрессии с вероятностью α.

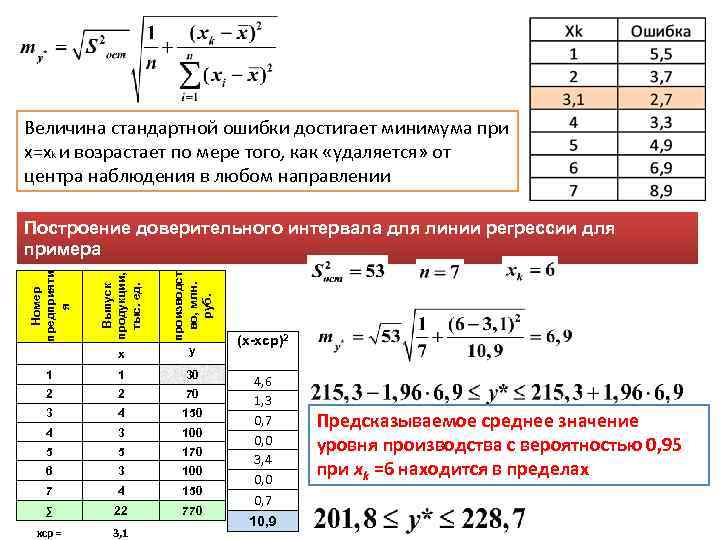Величина стандартной ошибки достигает минимума при х=хk и возрастает по мере того, как «удаляется» от центра наблюдения в любом направлении производст во, млн. руб. x y 1 1 30 2 2 70 3 4 150 4 3 100 5 5 170 6 3 100 7 4 150 ∑ 22 770 хср = 3, 1 Номер предприяти я Выпуск продукции, тыс. ед. Построение доверительного интервала для линии регрессии для примера (х-хср)2 4, 6 1, 3 0, 7 0, 0 3, 4 0, 0 0, 7 10, 9 Предсказываемое среднее значение уровня производства с вероятностью 0, 95 при xk =6 находится в пределах

300. 0 две гиперболы по обе стороны от линии регрессии определяют 95 %-ные доверительные интервалы для среднего значения у при заданном значении х. 250. 0 269. 6 228. 7 201. 8 188. 1 200. 0 168. 8 148. 1 150. 0 234. 6 135. 0 113. 8 103. 0 100. 0 75. 2 60. 6 41. 7 50. 0 20. 4 0. 0 0 1 2 3 4 5 6 7 8

Б) интервальный прогноз индивидуального значения у Однако фактические значения у варьируют около среднего значения у*. Индивидуальные значения у могут отклоняться от у* на величину случайной ошибки ε, дисперсия которой оценивается как остаточная дисперсия на одну степень свободы S 2. Поэтому ошибка предсказываемого индивидуального значения у должна включать не только стандартную ошибку , но и случайную ошибку S Средняя ошибка прогнозируемого индивидуального значения у составит: Предсказываемое индивидуальное значение уровня производства с вероятностью 0, 95 при xk =6 находится в пределах Интервал достаточно широк прежде всего за счет малого объема наблюдений

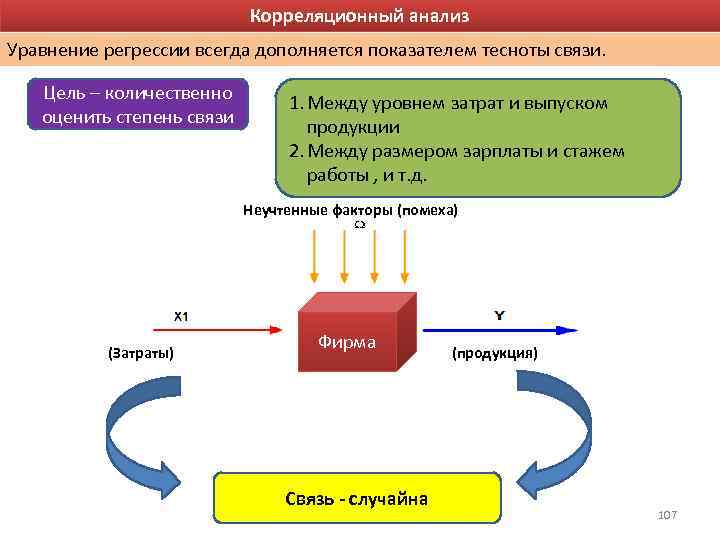Корреляционный анализ Уравнение регрессии всегда дополняется показателем тесноты связи. Цель – количественно оценить степень связи 1. Между уровнем затрат и выпуском продукции 2. Между размером зарплаты и стажем работы , и т. д. Неучтенные факторы (помеха) (Затраты) Фирма Связь - случайна (продукция) 107

Теснота связи численно оценивается с помощью коэффициентов корреляции При положительной корреляции при увеличении числовых значений одного ряда соответственно увеличиваются числовые значения другого ряда. При отрицательной корреляции увеличению числовых значений одного ряда соответствует уменьшение числовых значений другого ряда. Общая классификация корреляционных связей № п/п Тип связи Сила связи 1 Сильная (тесная) связь более 0, 7 2 Средняя связь от 0, 50 до 0, 69 3 Умеренная связь от 0, 30 до 0, 50 4 Слабая связь от 0, 20 до 0, 29 5 Очень слабая связь менее 0, 2 108

Коэффициент корреляции Пирсона Условия применимости: 1. Распределение признаков приблизительно нормально 2. Одинаковое число наблюдений 3. Измерения количественные или в порядковой шкале 109

Связь между коэффициентом корреляции и коэффициентом регрессии 110

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака.

Т 7. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ 1. 2. 3. 4. Понятие о временных рядах динамики. Исчисление средних показателей Смыкание временных рядов. Модели временных рядов Цели анализа временных рядов: 1. определение природы ряда 2. прогнозирование (предсказание будущих значений временного ряда по настоящим и прошлым значениям). Временной ряд представляет собой числовые значения определенного статистического показателя в последовательные моменты или периоды времени (т. е. расположенные в хронологическом порядке). Временные ряды представляют в виде таблицы или графически. При графическом изображении ряда динамики на оси абсцисс строится шкала времени t, а на оси ординат — шкала уровней ряда у.

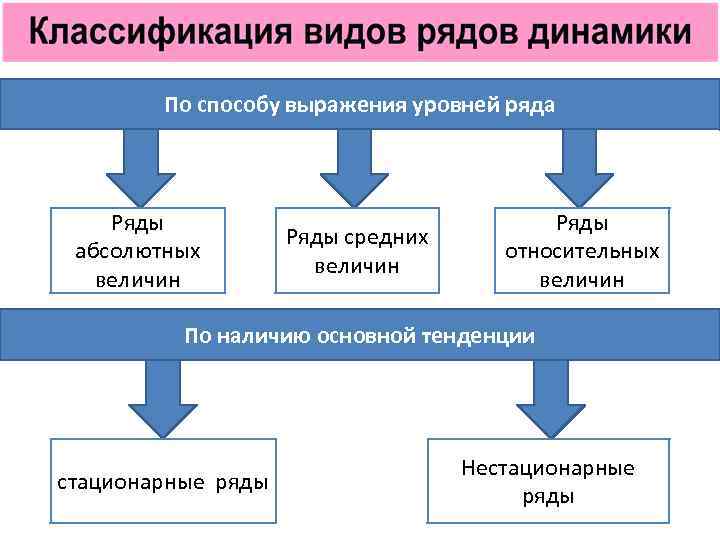По способу выражения уровней ряда Ряды абсолютных величин Ряды средних величин Ряды относительных величин По наличию основной тенденции стационарные ряды Нестационарные ряды

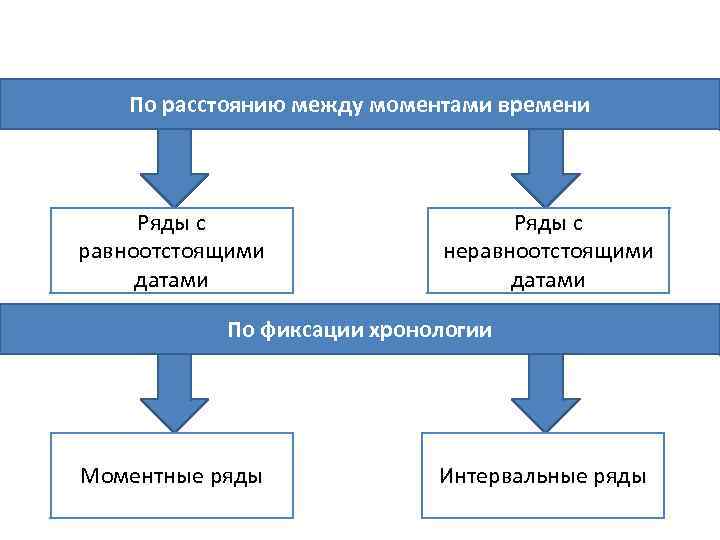По расстоянию между моментами времени Ряды с равноотстоящими датами Ряды с неравноотстоящими датами По фиксации хронологии Моментные ряды Интервальные ряды

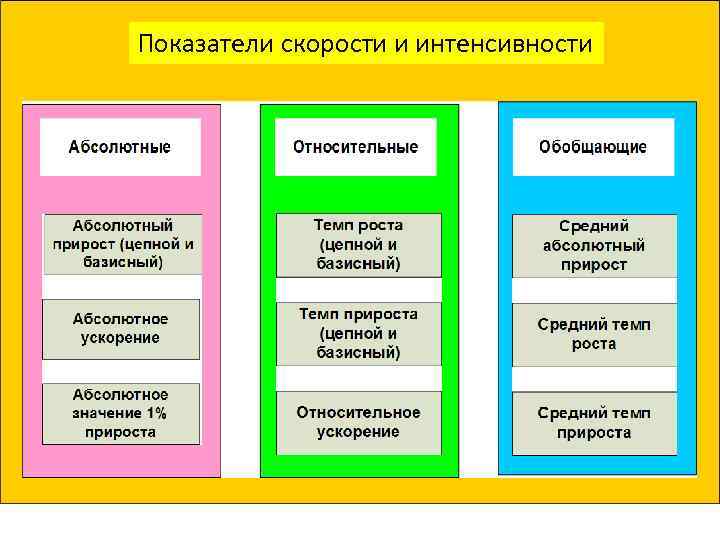Показатели скорости и интенсивности

122

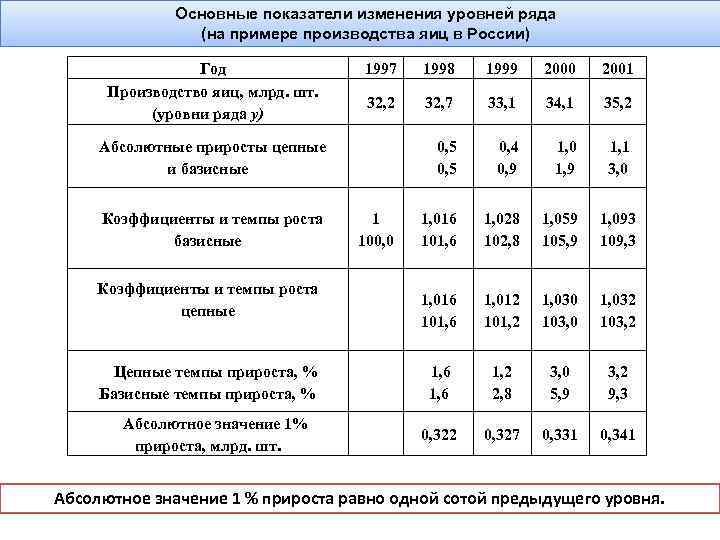Основные показатели изменения уровней ряда (на примере производства яиц в России) Год Производство яиц, млрд. шт. (уровни ряда у) 1997 1998 1999 2000 2001 32, 2 32, 7 33, 1 34, 1 35, 2 Абсолютные приросты цепные и базисные 0, 5 0, 4 0, 9 1, 0 1, 9 1 100, 0 1, 016 101, 6 1, 028 102, 8 1, 059 105, 9 1, 093 109, 3 Коэффициенты и темпы роста цепные 1, 016 101, 6 1, 012 101, 2 1, 030 103, 0 1, 032 103, 2 Цепные темпы прироста, % Базисные темпы прироста, % Абсолютное значение 1% прироста, млрд. шт. Коэффициенты и темпы роста базисные 1, 1 3, 0 1, 6 1, 2 3, 0 3, 2 1, 6 2, 8 5, 9 9, 3 0, 322 0, 327 0, 331 0, 341 Абсолютное значение 1 % прироста равно одной сотой предыдущего уровня.

Исчисление средних показателей в рядах динамики Обобщенной характеристикой динамического ряда может служить прежде всего средний уровень ряда у. Поскольку средняя величина в данном случае рассчитывается из меняющихся во времени показателей, то она называется средней хронологической. Для разных видов рядов динамики средний уровень рассчитывается неодинаково. Так, в интервальном ряду абсолютных величин с равными периодами (интервалами) средний уровень рассчитывается как средняя арифметическая простая из уровней ряда: В моментном ряду с равноотстоящими датами

Средний коэффициент роста n n или Средний темп роста Средний темп прироста

Анализ временных рядов, отражающих развитие экономических процессов, начинается с оценки данных. Уровни исследуемого показателя обязательно должны быть сопоставимы, однородны и устойчивы. Количество наблюдений в них должно быть достаточно велико. Сопоставимость предполагает формирование всех уровней по одной и той же методике, использование одинаковой единицы измерения и шага наблюдений. Требование однородности данных предполагает отсутствие сильных изломов тенденций, а также нетипичных, аномальных наблюдений. Устойчивость характеризуется преобладанием закономерности над случайностью в изменении уровней ряда. Требование полноты данных обусловливается тем, что закономерность может обнаружиться лишь при наличии минимально допустимого объема наблюдений. Если целью исследования является построение модели динамики, то число уровней ряда наблюдений должно быть не меньше 7— 10. 126

Следующим этапом анализа экономических процессов является выявление тенденций в развитии исследуемого показателя. Наличие тенденций среднего уровня на графике становится более ясным, когда на нем отражены сглаженные значения исходных данных. Наиболее распространенными методами сглаживания являются методы: • простой скользящей средней, • взвешенной скользящей средней, • экспоненциального сглаживания. В значительной части экономических процессов имеют место сезонные колебания. Влияние сезонности на экономику вполне однозначно — это аритмия производственных процессов. Для того, чтобы можно было целенаправленно влиять на сезонность, необходимо уметь ее измерять и анализировать, уметь предвидеть развитие процессов, 127

2. Сопоставимость уровней и смыкание рядов динамики Одно из требований, которые предъявляются к анализируемым рядам динамики, — сопоставимость уровней ряда. Несопоставимость уровней может возникнуть по разным причинам: • изменение границ территории, к которой отнесены те или иные показатели; • изменение методологии учета или расчета показателей. Например, если в одни годы средняя урожайность какой либо сельскохозяйственной культуры рассчитывалась с засеянной площади, а в другие — с убранной, то уровни несопоставимы. • изменение даты учета. (Например, учет скота в течение ряда лет проводился по состоянию на 1 октября, а затем — на 1 января); • изменение единиц измерения или счета. (Например, если меняется масштаб цен); • различная продолжительность периодов, к которым относятся уровни. (Например, нельзя строить ряд, где одни уровни являются месячными показателями, а другие квартальными или годовыми).

Следовательно, прежде чем анализировать уровни ряда динамики, надо, исходя из цели исследования, убедиться в их сопоставимости. Если данные несопоставимы, необходимо добиться их сопоставимости, прибегнув к дополнительным расчетам. Смыкание рядов динамики Под смыканием рядов динамики понимают объединение в один ряд (более длинный) двух или нескольких рядов, уровни которых исчислены по разным методологиям или в разных границах. При этом для осуществления такого смыкания необходимо, чтобы имелись данные для одного из периодов (переходного), исчисленные по двум методологиям.

Прогнозирование экономических процессов Экономическое прогнозирование (ЭП) — это процесс разработки экономических прогнозов, основанных на научных методах познания экономических явлений и использования всей совокупности методов, средств и способов экономической прогностики. Основное содержание ЭП — качественный и количественный анализ реальных экономических процессов, выявление объективных условий, факторов и тенденций развития. Адекватность означает максимальное приближение теоретичес кой модели к устойчивым, существенным закономерностям. На практике это означает, что построенные модели должны быть сначала проверены с точки зрения их способности имитировать уже сложившиеся тенденции. Модель прогнозирования представляет собой модель исследуемого объекта, записанную в математической форме. Она должна позволить получить информацию о возможных состояниях объекта в будущем и (или) путях и сроках их осуществления. 130

В большинстве методов, используемых в настоящее время в практической деятельности, заложены следующие основные предложения: • основные наблюдавшиеся в прошлом факторы, тенденции и зависимости сохранятся; • развитие экономических процессов может быть представлено в виде плавной траектории, т. е. оно должно обладать некоторой инерционностью; • экономические процессы имеют вероятностный характер, а развитие исследуемого объекта определяется суммарным влиянием закономерности и случайности. Последнее предположение обусловливает целесообразность использования статистических методов прогнозирования, 131

Процесс прогнозирования, опирающийся на статистические методы, распадается на следующие этапы: • Обоснование теоретических предположений, являющихся исходными для составления прогноза, и выбор системы показателей, адекватно отображающих развитие объекта. • Сбор и предварительный анализ данных. • Количественная оценка взаимосвязей показателей и параметров моделей. • Определение прогнозных значений на основе построенной модели. • Экстраполяция выявленных тенденций (продление на будущее) позволяет получить точечный прогноз. Однако вероятность точного попадания в эту точку практически равна нулю. Отсюда следует необходимость вычисления перспективных оценок в виде "вилки" через 132 доверительные интервалы.

Основной формой представления информации о динамике экономических показателей являются временные ряды (ВР) наблюдений Статистические методы исследования исходят из предположения о возможности представления уровней ряда в виде суммы компонент, отражающих закономерность и случайность развития: , где Т— тренд (долговременная тенденция) развития; E(i) — остаточная компонента. Основная цель статистического анализа временных рядов — изучение соотношения закономерности и случайности в формировании значений уровней ряда с оценкой количественной меры их влияния. 133

Формирование уровней ряда определяется закономерностями трех основных типов: v тенденцией среднего; v тенденцией взаимосвязи между уровня ряда; v тенденцией взаимосвязи между параметрами «входа и выхода» . Первая из них решается с помощью моделей кривых роста, вторая — с помощью адаптивных методов и моделей, третья — на основе эконометрического моделирования. Для отражения тенденций изменения исследуемого показателя в моделях кривых роста используются разнообразные математические функции, в которых задействован только один фактор — время (t). Из большого числа кривых роста воспользуемся простейшей линейной моделью вида: 134

Пример. По одной из областей России имеются данные о численности безработных, определенные за 1993 -1995 гг. на 1 октября, а за 1995 -1997 гг. - на конец марта (табл. 8. 7). Год на 1 октября, тыс. чел на конец марта, тыс. чел Сомкнутый ряд II, % 1993 1994 1995 1996 1997 20 22, 5 25 27 29 32, 5 21, 6 24, 3 80 90 27 29 32, 5 100 107, 4 120, 4

Модели временного ряда. Аддитивной модель: Мультипликативная модель: , где Т тренд, S – сезонная компонента, Е – случайная компонента. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.

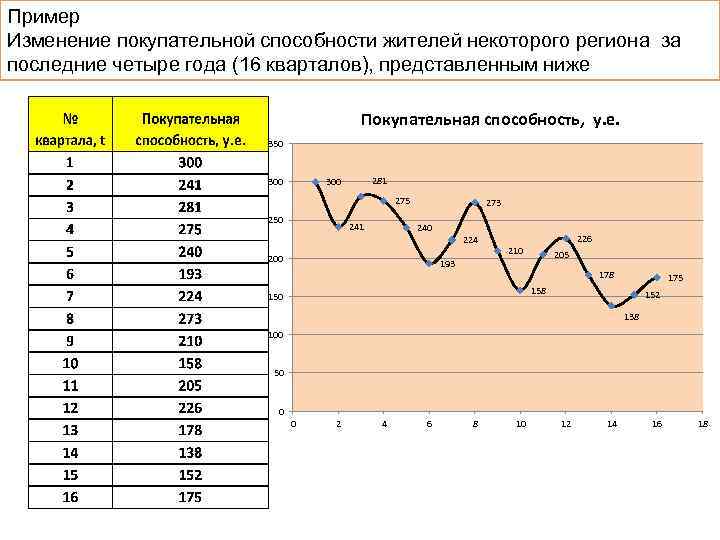Пример Изменение покупательной способности жителей некоторого региона за последние четыре года (16 кварталов), представленным ниже Покупательная способность, у. е. 350 300 281 300 275 250 241 273 240 224 200 226 210 205 193 178 175 158 150 152 138 100 50 0 0 2 4 6 8 10 12 14 16 18

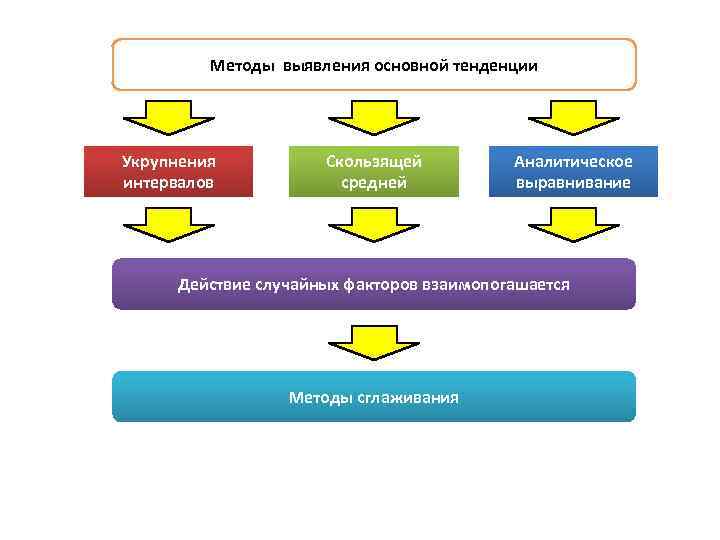Методы выявления основной тенденции Укрупнения интервалов Скользящей средней Аналитическое выравнивание Действие случайных факторов взаимопогашается Методы сглаживания

Метод скользящей средней Фактические уровни заменяются средними уровнями, рассчитанными для последовательно подвижных (скользящих) укрупненных интервалов, охватывающих m уровней ряда Если m нечетно, то среднее «попадает» на среднюю дату. Если m четно, то среднее «попадает» между датами. В последнем случае применяется центрирование. Недостаток метода – сглаженный ряд укорачивается на (m-1)/2 c каждого конца, если m – нечетна, и на m/2 – если m – четно. Сезонная компонента остается

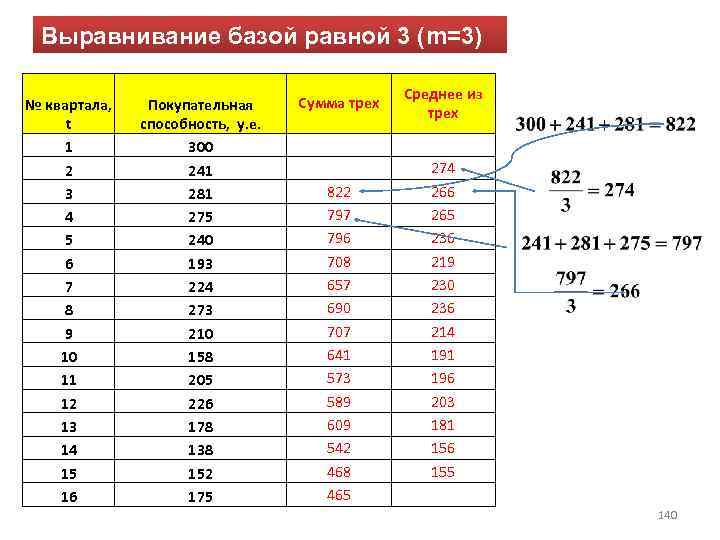Выравнивание базой равной 3 (m=3) № квартала, t 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Покупательная способность, у. е. 300 241 281 275 240 193 224 273 210 158 205 226 178 138 152 175 Среднее из трех Сумма трех 822 797 796 708 657 690 707 641 573 589 609 542 468 465 274 266 265 236 219 230 236 214 191 196 203 181 156 155 140

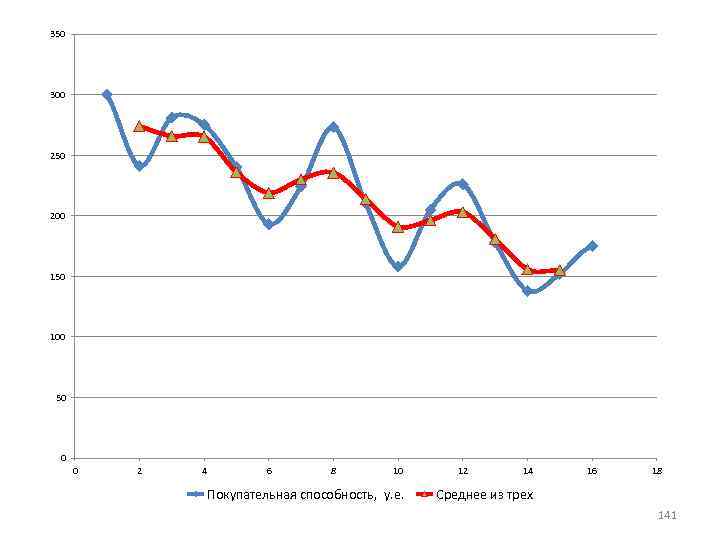350 300 250 200 150 100 50 0 0 2 4 6 8 10 Покупательная способность, у. е. 12 14 16 18 Среднее из трех 141

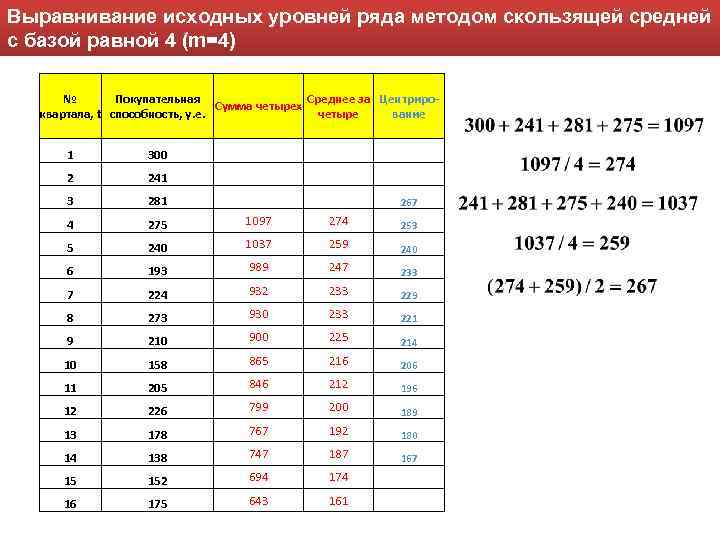Выравнивание исходных уровней ряда методом скользящей средней с базой равной 4 (m=4) № Покупательная Среднее за Центриро. Сумма четырех квартала, t способность, у. е. четыре вание 1 300 2 241 3 281 4 275 1097 274 253 5 240 1037 259 240 6 193 989 247 233 7 224 932 233 229 8 273 930 233 221 9 210 900 225 214 10 158 865 216 206 11 205 846 212 196 12 226 799 200 189 13 178 767 192 180 14 138 747 187 167 15 152 694 174 16 175 643 161 267

350 300 250 200 150 100 50 0 0 2 4 6 8 10 12 14 16 18 143

Аналитическое выравнивание ряда с помощью линейного тренда. Переход к условным датам

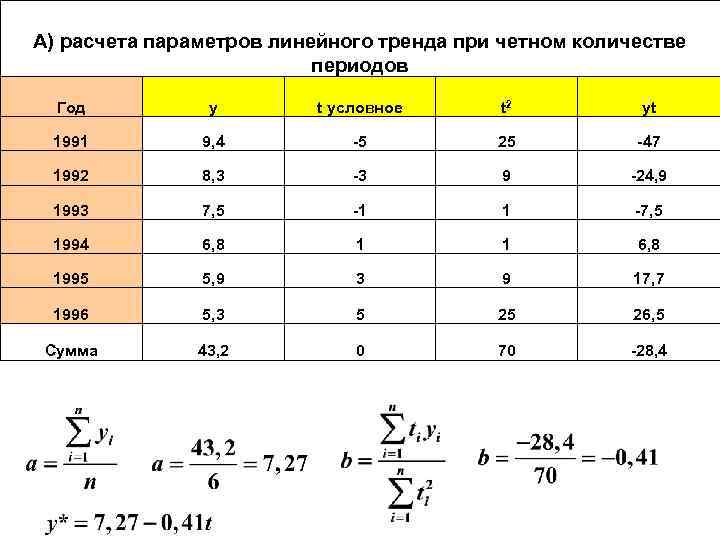А) расчета параметров линейного тренда при четном количестве периодов Год y t условное t 2 yt 1991 9, 4 -5 25 -47 1992 8, 3 -3 9 -24, 9 1993 7, 5 -1 1 -7, 5 1994 6, 8 1 1 6, 8 1995 5, 9 3 9 17, 7 1996 5, 3 5 25 26, 5 Сумма 43, 2 0 70 -28, 4

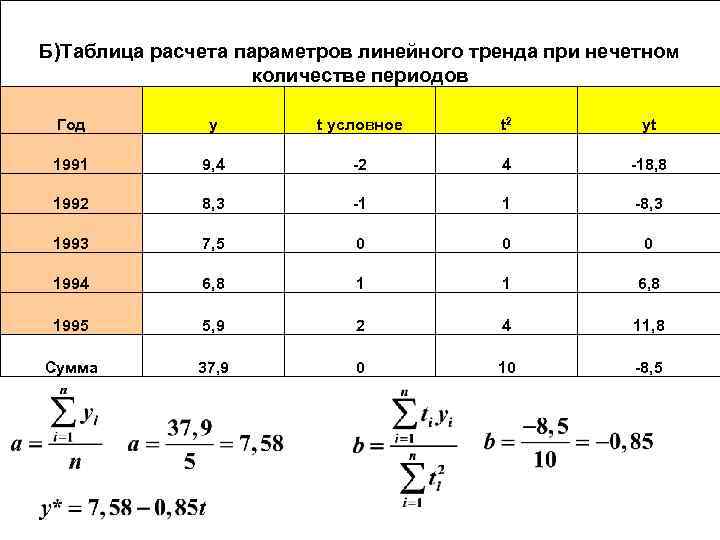Б)Таблица расчета параметров линейного тренда при нечетном количестве периодов Год y t условное t 2 yt 1991 9, 4 -2 4 -18, 8 1992 8, 3 -1 1 -8, 3 1993 7, 5 0 0 0 1994 6, 8 1 1 6, 8 1995 5, 9 2 4 11, 8 Сумма 37, 9 0 10 -8, 5

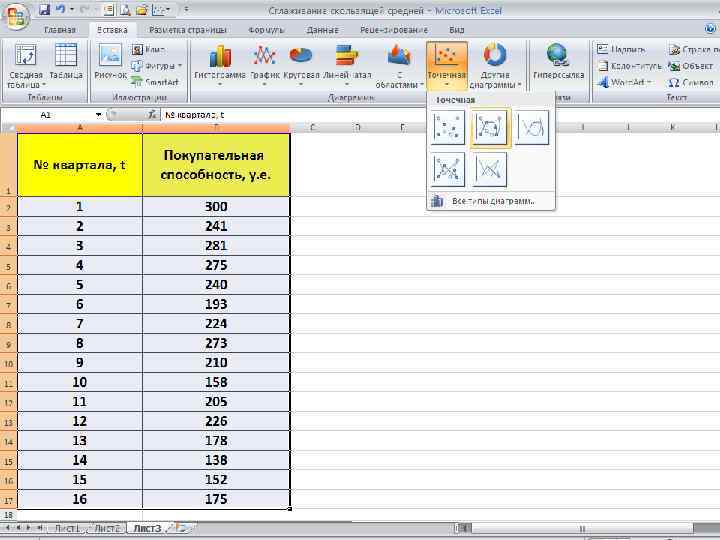147

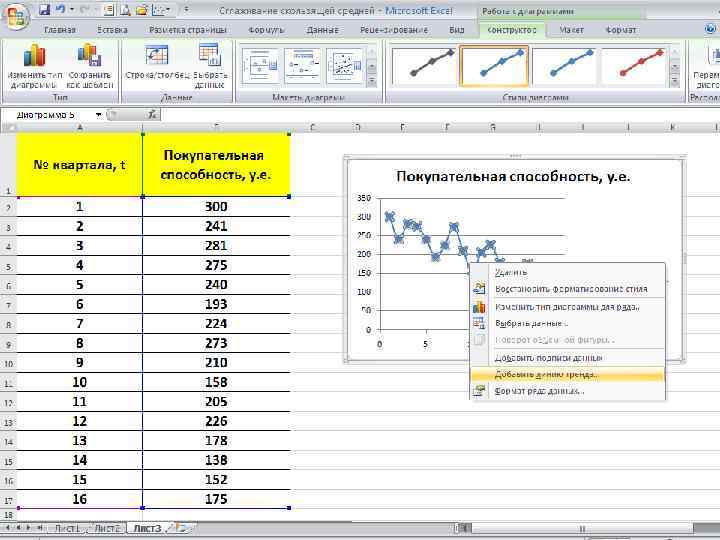148

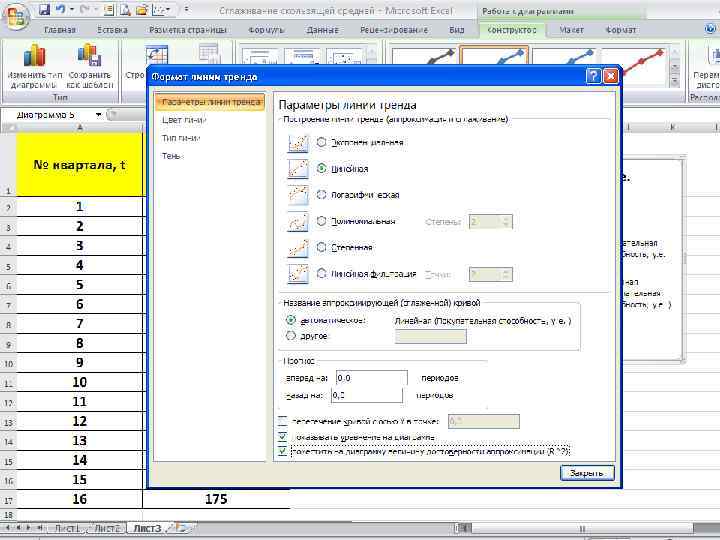149

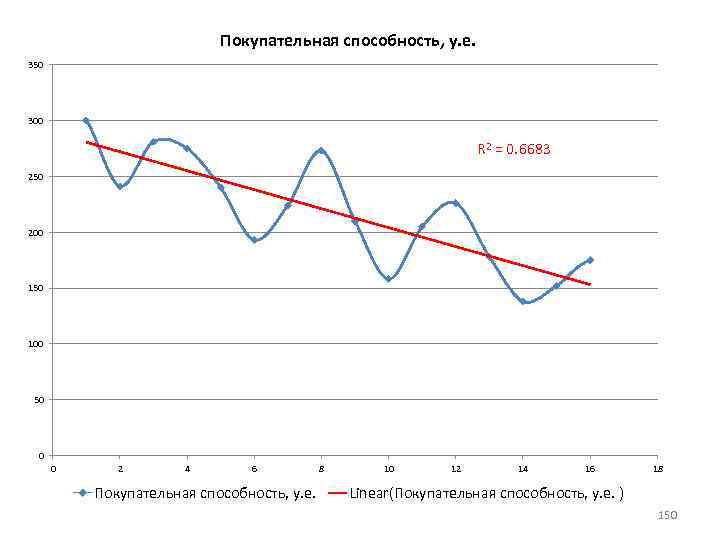Покупательная способность, у. е. 350 300 R 2 = 0. 6683 250 200 150 100 50 0 0 2 4 6 8 Покупательная способность, у. е. 10 12 14 16 18 Linear(Покупательная способность, у. е. ) 150

Отражает ли модель закономерность изменения исследуемого показателя, можно ли полученные значения Y(t) рассматривать как тенденцию? Для этого модель должна обладать определенными статистическими свойствами. Модель считается хорошей со статистической точки зрения, если она адекватна и достаточно точна. Модель является адекватной, если: §математическое ожидание значений остаточного ряда близко к нулю, §значения остаточного ряда случайны, независимы и подчинены нормальному закону распределения. Проверка равенства математическое ожидание нулю осуществляется по критерию Стьюдента: Если , то гипотеза о равенстве нулю отклоняется. 151

Проверку случайности уровней ряда остатков проводят на основе критерия поворотных точек. В соответствии с ним каждый уровень ряда сравнивается с двумя рядом стоящими. Если он больше или меньше их, то эта точка считается поворотной. Далее подсчитывается сумма поворотных точек “pvr". В случайном ряду чисел должно выполняться строгое неравенство: Двойные скобки здесь означают, что от результата вычислений берется целая часть числа (не путать с процедурой округления!). Для первого и последнего наблюдения проставим прочерк. Ноль — если точка неповоротная, и единицу, если она поворотная. 152

При проверке независимости (отсутствия автокорреляции) определяется отсутствие в ряду остатков систематической составляющей. Это проверяется с помощью DW-критерия Дарбина-Уотсона: Основная проблема автокорреляции остатков связана с положительной серийной корреляцией. Дарбином и Уотсоном были разработаны специальные таблицы, в которых приводятся нижние (d. L) и верхние (d. U) границы значений DW, указывающие на положительную автокорреляцию. При этом проверяются гипотезы: H 0: автокорреляции не существует; Н 1: существует положительная автокорреляция. Если DW < d. L , то принимается гипотеза Н 1. Если DW> d. U, то принимается гипотеза Н 0. Существует неопределенность в принятии или непринятии гипотез, если d. L

Соответствие ряда остатков нормальному закону распределения определим при помощи /^ критерия где £тах — максимальный уровень ряда остатков; £min — минимальный уровень ряда остатков; SE — среднее квадратическое отклонение. Если значение этого критерия попадает между табулированными границами с заданным уровнем вероятности, то гипотеза о нормаль ном распределении ряда остатков принимается. Для N = 10 и 5% ного уровня значимости этот интервал равен (2, 7— 3, 7). Следовательно, свойст во нормальности распределения выполняется, что позволяет строить доверительный интервал прогноза. Для характеристики точности воспользуемся средней относитель ной ошибкой: Величина менее 5 % свидетельствует о хорошем уровне точности модели (ошибка до 15 % считается приемлемой). 154

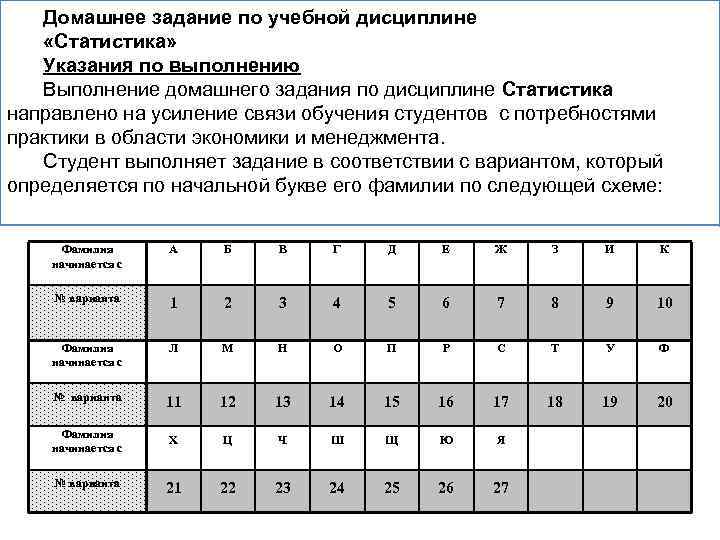Домашнее задание по учебной дисциплине «Статистика» Указания по выполнению Выполнение домашнего задания по дисциплине Статистика направлено на усиление связи обучения студентов с потребностями практики в области экономики и менеджмента. Студент выполняет задание в соответствии с вариантом, который определяется по начальной букве его фамилии по следующей схеме: Фамилия начинается с А Б В Г Д Е Ж З И К № варианта 1 2 3 4 5 6 7 8 9 10 Фамилия начинается с Л М Н О П Р С Т У Ф № варианта 11 12 13 14 15 16 17 18 19 20 Фамилия начинается с Х Ц Ч Ш Щ Ю Я № варианта 21 22 23 24 25 26 27

Требования к оформлению. Домашняя работа содержит: • титульный лист, • оглавление, • текст задания, соответствующего выполняемому варианту, • расчетную часть, в которой помещают решение задач, • список использованной литературы. Домашняя работа выполняется на компьютере: описательная часть в текстовом редакторе WORD, шрифт 12, Times New Roman, на одной стороне листа стандартного формата; расчетная часть и таблицы с использованием ППП Excel. Титульный лист оформляется по общим правилам, принятым в институте, с обязательным указанием № варианта. Графики исполняются с помощью мастера диаграмм ППП Excel. Как исключение, допускается очень аккуратное рукописное исполнение работы. Листы домашнего задания должны иметь сквозную нумерацию и быть сшитыми (скрепленными). Работы, выполненные с нарушениями правил оформления возвращаются без проверки. Домашняя работа представляется в учебную часть не позднее 2 -х недель до начала экзамена (зачета). Студенты, не выполнившие домашнюю работу или не получившие 156 допуск по работе, к экзамену (зачету) не допускаются.

Решить задачи Задача 1. Обследовано 50 торговых точек по объему ежедневного дохода. Данные обследования приведены в приложении 1. Провести группировку торговых точек по объему ежедневного дохода. Построить гистограмму, полигон, кумуляту. Вычислить выборочные характеристики: среднее, дисперсию, среднее квадратическое отклонение, моду, медиану, нижний и верхний квартили, коэффициент вариации. Выдвинуть гипотезу о законе распределения дохода. Задача 2. Имеются (приложение 2) ежемесячные уровни (тыс. у. е. ) дохода фирмы в 2008 г. Графически отобразить динамику производства. Рассчитать цепные и базисные: • абсолютные приросты (изменения) уровней; • темпы роста; • темпы прироста (снижения) уровней, а также средние значения ряда, темпа роста и прироста. Провести сглаживание методом скользящей средней с базой равной четырем. Осуществить аналитическое выравнивание сглаженной зависимости по линейному тренду. Оценить ожидаемый уровень производства в январе 2009 г. 157

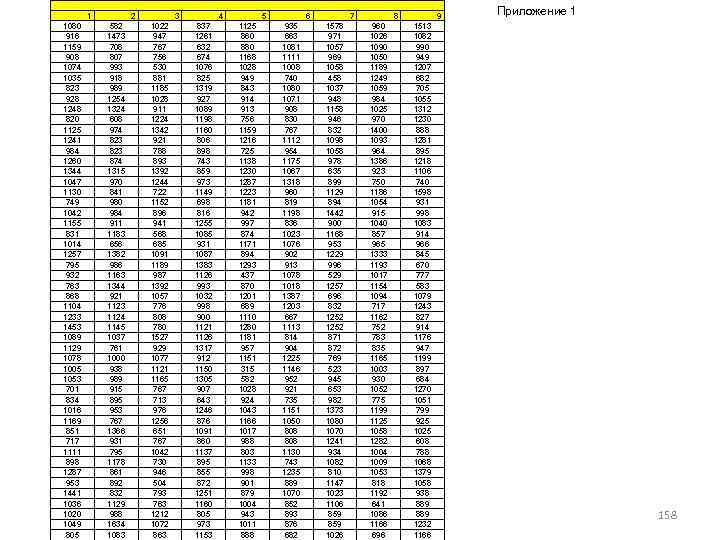1 1080 916 1159 908 1074 1035 823 928 1248 820 1125 1241 984 1260 1344 1047 1130 749 1042 1155 831 1014 1257 795 932 763 868 1104 1233 1453 1089 1129 1078 1005 1053 701 834 1016 1169 851 717 1111 898 1287 953 1441 1036 1020 1049 805 2 582 1473 708 807 993 918 989 1254 1324 608 974 823 874 1315 970 841 980 984 911 1183 656 1382 986 1163 1344 921 1123 1124 1145 1037 761 1000 938 989 915 895 953 767 1366 931 795 1178 861 892 832 1129 988 1634 1083 3 1022 947 767 756 530 881 1185 1028 911 1224 1342 921 788 893 1392 1244 722 1152 896 941 568 685 1091 1189 987 1392 1057 776 808 780 1527 929 1077 1121 1165 767 713 976 1256 651 767 1042 730 946 504 793 763 1212 1072 863 4 837 1261 632 674 1076 825 1319 927 1089 1198 1160 806 898 743 859 973 1149 698 816 1255 1085 931 1087 1383 1126 993 1032 998 900 1121 1126 1317 912 1150 1305 907 643 1246 876 1091 860 1137 895 855 872 1251 1160 805 973 1153 5 1125 860 880 1168 1028 949 843 914 913 756 1159 1216 725 1138 1230 1287 1223 1181 942 997 874 1171 894 1293 437 870 1201 689 1110 1280 1181 957 1151 315 582 1028 924 1043 1166 1017 988 803 1133 998 901 879 1004 943 1011 888 6 935 663 1081 1111 1008 740 1080 1071 908 830 767 1112 954 1175 1067 1318 960 819 1198 836 1023 1076 902 913 1078 1018 1387 1203 667 1113 814 904 1225 1146 952 921 735 1151 1050 808 1130 743 1235 889 1070 852 893 876 682 7 1578 971 1057 969 1058 458 1037 948 1158 946 832 1098 1058 978 635 899 1129 894 1442 900 1168 953 1229 996 529 1257 696 832 1252 871 872 769 523 945 653 982 1373 1080 1070 1241 934 1082 810 1147 1023 1106 859 1026 8 960 1026 1090 1050 1189 1249 1059 984 1025 970 1400 1093 964 1386 923 750 1186 1054 915 1040 857 965 1333 1193 1017 1154 1094 717 1162 752 783 835 1165 1003 930 1052 775 1199 1125 1058 1282 1004 1009 1053 818 1192 641 1086 1166 696 9 1513 1082 990 949 1207 682 705 1055 1312 1230 888 1281 895 1218 1106 740 1598 931 998 1083 914 966 845 670 777 583 1079 1243 827 914 1176 947 1199 897 684 1270 1051 799 925 1025 608 788 1068 1379 1058 938 889 1232 1166 Приложение 1 158

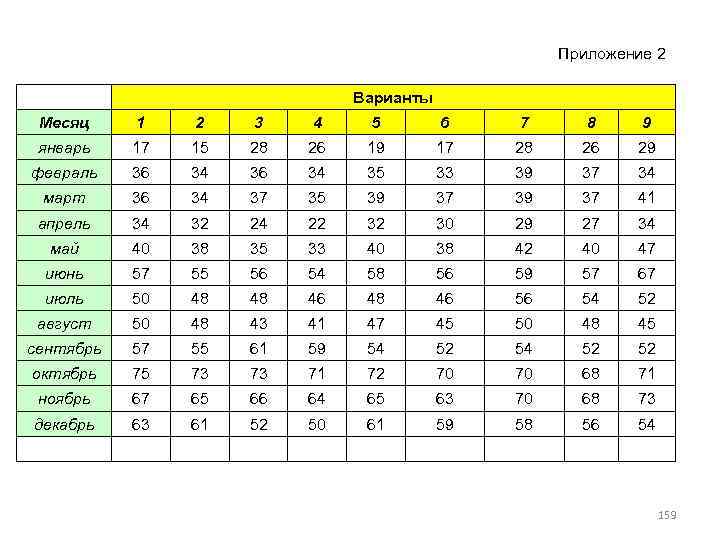Приложение 2 Варианты Месяц 1 2 3 4 5 6 7 8 9 январь 17 15 28 26 19 17 28 26 29 февраль 36 34 35 33 39 37 34 март 36 34 37 35 39 37 41 апрель 34 32 24 22 32 30 29 27 34 май 40 38 35 33 40 38 42 40 47 июнь 57 55 56 54 58 56 59 57 67 июль 50 48 48 46 56 54 52 август 50 48 43 41 47 45 50 48 45 сентябрь 57 55 61 59 54 52 52 октябрь 75 73 73 71 72 70 70 68 71 ноябрь 67 65 66 64 65 63 70 68 73 декабрь 63 61 52 50 61 59 58 56 54 159