1 НЕТРАДИЦІЙНІ СЕМАНТИКИ ЛОГІК КВАЗІАРНИХ ПРЕДИКАТІВ
























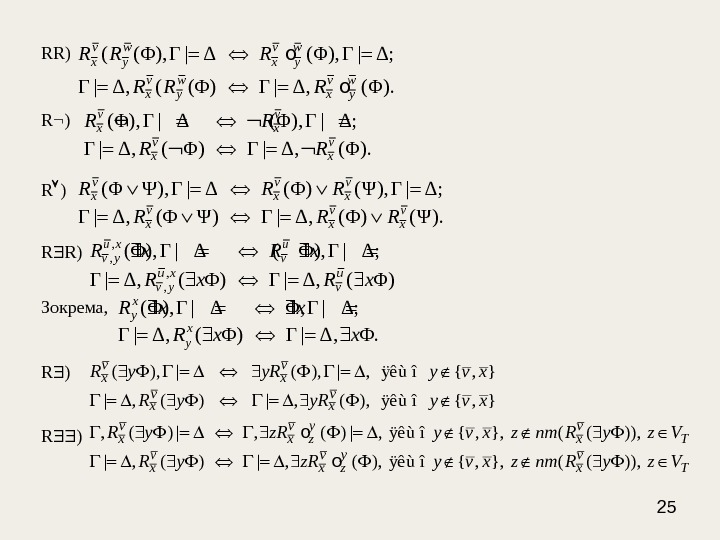





- Размер: 471.5 Кб
- Количество слайдов: 30
Описание презентации 1 НЕТРАДИЦІЙНІ СЕМАНТИКИ ЛОГІК КВАЗІАРНИХ ПРЕДИКАТІВ по слайдам
 1 НЕТРАДИЦІЙНІ СЕМАНТИКИ ЛОГІК КВАЗІАРНИХ ПРЕДИКАТІВ Характерним для програмування й моделювання є використання часткових необов язково однозначних відображень над складними даними. Тому постає проблема дослідження КНЛ із нетрадиційними семантиками. Класична логіка – це логіка тотальних однозначних предикатів Логіки часткових однозначних предикатів – із неокласичною семантикою. Логіки тотальних неоднозначних предикатів – із пересиченою семантикою. Логіки часткових неоднозначних предикатів – із загальною семантикою. Центральним поняттям логіки є поняття логічного слідування. Воно може бути формалізованим за допомогою відношень логічного наслідку. Дослідимо відношення логічного наслідку для КНЛ – часткових однозначних – тотальних неоднозначних – часткових неоднозначних квазіарних предикатів. Відношення логічного наслідку індукують відповідні відношення еквівалентності, вони поширюються на множини формул. В різних семантиках такі відношення мають різні властивості, а в класичній логіці усі вони збігаються.
1 НЕТРАДИЦІЙНІ СЕМАНТИКИ ЛОГІК КВАЗІАРНИХ ПРЕДИКАТІВ Характерним для програмування й моделювання є використання часткових необов язково однозначних відображень над складними даними. Тому постає проблема дослідження КНЛ із нетрадиційними семантиками. Класична логіка – це логіка тотальних однозначних предикатів Логіки часткових однозначних предикатів – із неокласичною семантикою. Логіки тотальних неоднозначних предикатів – із пересиченою семантикою. Логіки часткових неоднозначних предикатів – із загальною семантикою. Центральним поняттям логіки є поняття логічного слідування. Воно може бути формалізованим за допомогою відношень логічного наслідку. Дослідимо відношення логічного наслідку для КНЛ – часткових однозначних – тотальних неоднозначних – часткових неоднозначних квазіарних предикатів. Відношення логічного наслідку індукують відповідні відношення еквівалентності, вони поширюються на множини формул. В різних семантиках такі відношення мають різні властивості, а в класичній логіці усі вони збігаються.
 2 Різновиди квазіарних предикатів V -квазіарни й предикат на A – це ф ункці я вигляду Р : V A { T , F } Область істинності та область хибності предиката Р : T ( P ) = P – 1 ( T ) = { d V A | T P ( d )}; F ( P ) = P – 1 ( F ) = { d V A | F P ( d )}. Якщо Р однозначний, то T ( P ) F ( P ) = . Якщо Р тотальний, то T ( P ) F ( P ) = V A. Предикат P : V A { T , F } назвемо: – тотально істинним, якщо T ( P ) = V A ; – тотально хибним, якщо F ( P ) = V A ; – тотожно істинним , якщо T ( P ) = V A і F ( P ) = ; – тотожно хибним, якщо T ( P ) = і F ( P ) = V A ; – тотально насиченим, якщо T ( P ) = F ( P ) = V A ; – неспростовним , або частково істинним, якщо F ( P ) = ; – виконуваним, якщо T ( P ) .
2 Різновиди квазіарних предикатів V -квазіарни й предикат на A – це ф ункці я вигляду Р : V A { T , F } Область істинності та область хибності предиката Р : T ( P ) = P – 1 ( T ) = { d V A | T P ( d )}; F ( P ) = P – 1 ( F ) = { d V A | F P ( d )}. Якщо Р однозначний, то T ( P ) F ( P ) = . Якщо Р тотальний, то T ( P ) F ( P ) = V A. Предикат P : V A { T , F } назвемо: – тотально істинним, якщо T ( P ) = V A ; – тотально хибним, якщо F ( P ) = V A ; – тотожно істинним , якщо T ( P ) = V A і F ( P ) = ; – тотожно хибним, якщо T ( P ) = і F ( P ) = V A ; – тотально насиченим, якщо T ( P ) = F ( P ) = V A ; – неспростовним , або частково істинним, якщо F ( P ) = ; – виконуваним, якщо T ( P ) .
 3 Предикат P : D { T , F } монотонний , якщо d d’ P ( d ) P ( d’ ). Окремим випадком монотонності є еквітонність – збереження прийнятого значення при розширенні даних. Предикат P : D { T , F } еквітонний , якщо із P ( d ) та d d випливає P ( d ) = P ( d ). Для однозначних предикатів монотонність стає еквітонністю. Традиційне визначення еквітонного предиката: Однозначний предикат P : D { T , F } еквітонний, якщо із P ( d ) та d d випливає P ( d ) = P ( d ). Монотонність предиката означає, що прийняте ним значення зберігається при розширенні даних. Для однозначних часткових предикатів це може трактуватися як збереження «інформативності» предиката при збільшенні «інформативності» вхідних даних.
3 Предикат P : D { T , F } монотонний , якщо d d’ P ( d ) P ( d’ ). Окремим випадком монотонності є еквітонність – збереження прийнятого значення при розширенні даних. Предикат P : D { T , F } еквітонний , якщо із P ( d ) та d d випливає P ( d ) = P ( d ). Для однозначних предикатів монотонність стає еквітонністю. Традиційне визначення еквітонного предиката: Однозначний предикат P : D { T , F } еквітонний, якщо із P ( d ) та d d випливає P ( d ) = P ( d ). Монотонність предиката означає, що прийняте ним значення зберігається при розширенні даних. Для однозначних часткових предикатів це може трактуватися як збереження «інформативності» предиката при збільшенні «інформативності» вхідних даних.
 4 Для тотальних монотонних предикатів ситуація протилежна: при розширенні вхідних даних «інформативність» може тільки зменшуватися. Тому поняття монотонності малозмістовне для тотальних неоднозначних предикатів. Для них адекватним є дуальне поняття антитонності. Предикат P : D { T , F } антитонний , якщо d d’ P ( d ) P ( d’ ). Якщо P антитонний, то P ( ) складається з усіх значень, які предикат може приймати на D , тобто P ( ) = E P . Для тотальних неоднозначних предикатів антитонність означає: “інформативність” предиката не зменшується при збільшенні “інформативності” вхідних даних. В класі однозначних предикатів антитонними можуть бути лише майже константні предикати: P ( d ) T для всіх d D або P ( d ) F для всіх d D. В класі однозначних предикатів поняття антитонності малозмістовне. Теорема 1. Композиції зберігають властивості еквітонності та антитонності. , , &, , R , , v x x xØ Ú $ «
4 Для тотальних монотонних предикатів ситуація протилежна: при розширенні вхідних даних «інформативність» може тільки зменшуватися. Тому поняття монотонності малозмістовне для тотальних неоднозначних предикатів. Для них адекватним є дуальне поняття антитонності. Предикат P : D { T , F } антитонний , якщо d d’ P ( d ) P ( d’ ). Якщо P антитонний, то P ( ) складається з усіх значень, які предикат може приймати на D , тобто P ( ) = E P . Для тотальних неоднозначних предикатів антитонність означає: “інформативність” предиката не зменшується при збільшенні “інформативності” вхідних даних. В класі однозначних предикатів антитонними можуть бути лише майже константні предикати: P ( d ) T для всіх d D або P ( d ) F для всіх d D. В класі однозначних предикатів поняття антитонності малозмістовне. Теорема 1. Композиції зберігають властивості еквітонності та антитонності. , , &, , R , , v x x xØ Ú $ «
 5 Приклад. Розглянемо наступні предикати. Р 1 та Р 2 тотальні однозначні немонотонні (нееквітонні) й неантитонні, Р 3 та Р 5 монотонні (еквітонні) однозначні, Р 4 та Р 6 монотонні тотальні неоднозначні, Р 7 та Р 9 антитонні часткові однозначні, Р 8 та Р 10 антитонні тотальні неоднозначні. 1 { }, якщо ( ), ( ) { }, якщо ( ). F x asn d P d T x asn d 2 { }, якщо ( ), ( ) { }, якщо ( ). T x asn d P d F x asn d 3 { }, якщо ( ), ( ) , якщо ( ). F x asn d P d x asn d 4 { , }, якщо ( ), ( ) { }, якщо ( ). T F x asn d P d T x asn d 5 { }, якщо ( ), ( ) , якщо ( ). T x asn d P d x asn d 6 { , }, якщо ( ), ( ) { }, якщо ( ). T F x asn d P d F x asn d 7 , якщо ( ), ( ) , якщо ( ). F x asn d P d x asn d 9 { }, якщо ( ), ( ) , якщо ( ). T x asn d P d x asn d 8 { , }, якщо ( ), ( ) { }, якщо ( ). T F x asn d P d T x asn d 10 { , }, якщо ( ), ( ) { }, якщо ( ). T F x asn d P d F x asn d
5 Приклад. Розглянемо наступні предикати. Р 1 та Р 2 тотальні однозначні немонотонні (нееквітонні) й неантитонні, Р 3 та Р 5 монотонні (еквітонні) однозначні, Р 4 та Р 6 монотонні тотальні неоднозначні, Р 7 та Р 9 антитонні часткові однозначні, Р 8 та Р 10 антитонні тотальні неоднозначні. 1 { }, якщо ( ), ( ) { }, якщо ( ). F x asn d P d T x asn d 2 { }, якщо ( ), ( ) { }, якщо ( ). T x asn d P d F x asn d 3 { }, якщо ( ), ( ) , якщо ( ). F x asn d P d x asn d 4 { , }, якщо ( ), ( ) { }, якщо ( ). T F x asn d P d T x asn d 5 { }, якщо ( ), ( ) , якщо ( ). T x asn d P d x asn d 6 { , }, якщо ( ), ( ) { }, якщо ( ). T F x asn d P d F x asn d 7 , якщо ( ), ( ) , якщо ( ). F x asn d P d x asn d 9 { }, якщо ( ), ( ) , якщо ( ). T x asn d P d x asn d 8 { , }, якщо ( ), ( ) { }, якщо ( ). T F x asn d P d T x asn d 10 { , }, якщо ( ), ( ) { }, якщо ( ). T F x asn d P d F x asn d
 6 неспростовна при інтерпретації на моделі мови A (позн. A |= ), якщо A – неспростовний (частково істинний) предикат. усюди (частково) істинна, або неспростовна ( позн. |= ), якщо A |= для кожної моделі мови A. тотально істинна при інтерпретації на A ( позн. A | ), якщо A – тотально істинний предикат. тотально iстинна ( позн. | ), якщо A | » моделі мови A. Аналогічно даємо визначення тотожно істинної формули та виконуваної формули Ім’я x V строго неістотне для формули : x строго неістотне для A » моделі мови A Для кожного р Ps множину синтетично строго неістотних предметних імен задамо за допомогою тотальної функції : Ps 2 V , Така функція продовжується до : Fr 2 V . Для семантичних моделей ЧКНЛ постулюється нескінченність множини тотально строго неістотних імен. ν( ) IT p Ps V p
6 неспростовна при інтерпретації на моделі мови A (позн. A |= ), якщо A – неспростовний (частково істинний) предикат. усюди (частково) істинна, або неспростовна ( позн. |= ), якщо A |= для кожної моделі мови A. тотально істинна при інтерпретації на A ( позн. A | ), якщо A – тотально істинний предикат. тотально iстинна ( позн. | ), якщо A | » моделі мови A. Аналогічно даємо визначення тотожно істинної формули та виконуваної формули Ім’я x V строго неістотне для формули : x строго неістотне для A » моделі мови A Для кожного р Ps множину синтетично строго неістотних предметних імен задамо за допомогою тотальної функції : Ps 2 V , Така функція продовжується до : Fr 2 V . Для семантичних моделей ЧКНЛ постулюється нескінченність множини тотально строго неістотних імен. ν( ) IT p Ps V p
 7 Модель мови АС B = ( A , I B ) дуальна до АС A = ( A , I A ): » Ps Тоді A = ( A , I A ) дуальна до B = ( A , I B ). A = ( A , I A ) – АС з частковими однозначними предикатами дуальна B = ( A , I B ) – і з тотальними неоднозначними предикатами, та навпаки. Теорема. Нехай B = ( A , I B ) дуальна до A = ( A , I A ). Тоді » Fr : 1) 2) A еквітонний B антитонний; A антитонний B еквітонний. Наслідок. A неспростовний на АС A із частковими однозначними предикатами (неокласична семантика) B тотально істинний на дуальній АС B із тотальними неоднозначними предикатами (пересичена семантика). Таким чином, неокласична семантика та пересичена семантика дуальні. (Φ ) та (Φ )B A B AT F F T
7 Модель мови АС B = ( A , I B ) дуальна до АС A = ( A , I A ): » Ps Тоді A = ( A , I A ) дуальна до B = ( A , I B ). A = ( A , I A ) – АС з частковими однозначними предикатами дуальна B = ( A , I B ) – і з тотальними неоднозначними предикатами, та навпаки. Теорема. Нехай B = ( A , I B ) дуальна до A = ( A , I A ). Тоді » Fr : 1) 2) A еквітонний B антитонний; A антитонний B еквітонний. Наслідок. A неспростовний на АС A із частковими однозначними предикатами (неокласична семантика) B тотально істинний на дуальній АС B із тотальними неоднозначними предикатами (пересичена семантика). Таким чином, неокласична семантика та пересичена семантика дуальні. (Φ ) та (Φ )B A B AT F F T
 8 Теорема. 1. Для неокласичної семантики множина тотально істинних формул порожня. 2. Для пересиченої семантики множина неспростовних формул порожня. 3. Для загальної семантики множини тотально істинних і неспростовних формул порожні. Неокласична семантика. Беремо модель мови A таку: кожний ПС інтерпретуємо як всюди невизначений предикат, на такій A кожна формула теж проінтерпретується як всюди невизначений предикат. Пересичена семантика. Беремо модель мови В таку: кожний ПС інтерпретуємо як тотально насичений предикат, на такій В кожна формула теж проінтерпретується як тотально насичений предикат. Загальна семантика. Беремо модель мови A і дуальну модель мови В.
8 Теорема. 1. Для неокласичної семантики множина тотально істинних формул порожня. 2. Для пересиченої семантики множина неспростовних формул порожня. 3. Для загальної семантики множини тотально істинних і неспростовних формул порожні. Неокласична семантика. Беремо модель мови A таку: кожний ПС інтерпретуємо як всюди невизначений предикат, на такій A кожна формула теж проінтерпретується як всюди невизначений предикат. Пересичена семантика. Беремо модель мови В таку: кожний ПС інтерпретуємо як тотально насичений предикат, на такій В кожна формула теж проінтерпретується як тотально насичений предикат. Загальна семантика. Беремо модель мови A і дуальну модель мови В.
 9 Відношення логічного наслідку Введемо 5 «природних» відношень логічного наслідку. В різних семантиках вони мають різні властивості. Задамо відношення наслідку для двох формул при інтерпретації на фіксованій моделі мови АС A. 1) » Істиннісний » наслідок A |= T : A |= T T ( A ). 2) «Хибнісний» наслідок A |= F : A |= F F ( A ). 3) » C ильний» наслідок A |= TF : A |= TF T ( A ) та F ( A ). 4) «Неспростовнісний» наслідок A |= Cl : A |= Cl T ( A ) F ( A ) = . 5 ) » Насичений » наслідок A |= Cm : A |= Cm F ( A ) T ( A ) = V A. Відповідні відношення логічного наслідку: |= T , |= F , |= TF , |= Cl , |= Cm . Їх визначаємо за такою схемою: |= A |= для кожної моделі мови A.
9 Відношення логічного наслідку Введемо 5 «природних» відношень логічного наслідку. В різних семантиках вони мають різні властивості. Задамо відношення наслідку для двох формул при інтерпретації на фіксованій моделі мови АС A. 1) » Істиннісний » наслідок A |= T : A |= T T ( A ). 2) «Хибнісний» наслідок A |= F : A |= F F ( A ). 3) » C ильний» наслідок A |= TF : A |= TF T ( A ) та F ( A ). 4) «Неспростовнісний» наслідок A |= Cl : A |= Cl T ( A ) F ( A ) = . 5 ) » Насичений » наслідок A |= Cm : A |= Cm F ( A ) T ( A ) = V A. Відповідні відношення логічного наслідку: |= T , |= F , |= TF , |= Cl , |= Cm . Їх визначаємо за такою схемою: |= A |= для кожної моделі мови A.
 10 Відношення слабких наслідків – слабкий логічний наслідок (позн. ||= ) , якщо » моделі мови A маємо A |= . – слабкий тотальний наслідок (позн. || ) , якщо » моделі мови A маємо A | . Відношення |= T , |= F , |= TF , |= Cl , |= Cm , ||=, || рефлексивні й транзитивні. Відношення логічного наслідку індукують відповідні відношення логічної еквівалентності. Такі відношення рефлексивні, транзитивні й си метричні. Відношення еквівалентності в АС A : A T , A F , A TF , A Cl , A Cm Відношення логічної еквівалентності: T , F , TF , Cl , Cm Визначаємо їх за такою схемою: A , якщо A |= та A |= ; , якщо |= та |= . TF означає, що та завжди інтерпретуються як один і той же предикат. Справді, для кожної моделі мови A A TF T ( A ) = T ( A ) та F ( A ) = F ( A )
10 Відношення слабких наслідків – слабкий логічний наслідок (позн. ||= ) , якщо » моделі мови A маємо A |= . – слабкий тотальний наслідок (позн. || ) , якщо » моделі мови A маємо A | . Відношення |= T , |= F , |= TF , |= Cl , |= Cm , ||=, || рефлексивні й транзитивні. Відношення логічного наслідку індукують відповідні відношення логічної еквівалентності. Такі відношення рефлексивні, транзитивні й си метричні. Відношення еквівалентності в АС A : A T , A F , A TF , A Cl , A Cm Відношення логічної еквівалентності: T , F , TF , Cl , Cm Визначаємо їх за такою схемою: A , якщо A |= та A |= ; , якщо |= та |= . TF означає, що та завжди інтерпретуються як один і той же предикат. Справді, для кожної моделі мови A A TF T ( A ) = T ( A ) та F ( A ) = F ( A )
 11 Теорема. Нехай АС B = ( A , I B ) дуальна до АС A = ( A , I A ). Тоді: 1) A |= T B |= F та A |= F B |= T ; 2) A |= Cl B |= Cm та A |= Cm B |= Cl . Наслідок. У випадку загальної семантики |= T |= F |= TF . В загальній семантиці кожна АС B є дуальною до деякої АС A. Теорема. Для кожної моделі мови A маємо: 1) A |= T Ø A |= F Ø та A |= F Ø A |= T Ø ; 2) A T Ø A F Ø та A F Ø A T Ø.
11 Теорема. Нехай АС B = ( A , I B ) дуальна до АС A = ( A , I A ). Тоді: 1) A |= T B |= F та A |= F B |= T ; 2) A |= Cl B |= Cm та A |= Cm B |= Cl . Наслідок. У випадку загальної семантики |= T |= F |= TF . В загальній семантиці кожна АС B є дуальною до деякої АС A. Теорема. Для кожної моделі мови A маємо: 1) A |= T Ø A |= F Ø та A |= F Ø A |= T Ø ; 2) A T Ø A F Ø та A F Ø A T Ø.
 12 У випадку неокласичної семантики немає жодної пари формул, які перебувають у відношенні |= Cm . Розглядаємо таку модель мови A , на якій усі ПС інтерпретуються як усюди невизначені предикати, тоді й усі формули на A інтерпретуються як усюди невизначені предикати. У випадку пересиченої семантики немає жодної пари, які перебувають у відношенні |= Cl . Розглядаємо таку модель мови В , на якій усі ПС інтерпретуються як тотально насичені предикати, тоді й усі формули на В інтерпретуються як тотально насичені предикати. У випадку загальної семантики немає жодної пари формул, які перебувають у відношенні |= Cl чи у відношенні |= Cm . Загальна семантика. Маємо єдине природне змістовне відношення |= TF . Неокласична семантика. Можна розглядати відношення |= T , |= F , |= TF , |= Cl. Пересичена семантика. Можна розглядати відношення |= T , |= F , |= TF , |= Cm.
12 У випадку неокласичної семантики немає жодної пари формул, які перебувають у відношенні |= Cm . Розглядаємо таку модель мови A , на якій усі ПС інтерпретуються як усюди невизначені предикати, тоді й усі формули на A інтерпретуються як усюди невизначені предикати. У випадку пересиченої семантики немає жодної пари, які перебувають у відношенні |= Cl . Розглядаємо таку модель мови В , на якій усі ПС інтерпретуються як тотально насичені предикати, тоді й усі формули на В інтерпретуються як тотально насичені предикати. У випадку загальної семантики немає жодної пари формул, які перебувають у відношенні |= Cl чи у відношенні |= Cm . Загальна семантика. Маємо єдине природне змістовне відношення |= TF . Неокласична семантика. Можна розглядати відношення |= T , |= F , |= TF , |= Cl. Пересичена семантика. Можна розглядати відношення |= T , |= F , |= TF , |= Cm.
 13 Поведінка введених відношень логічного наслідку вельми специфічна. Теорема. У випадку неокласичної семантики маємо: 1) & ( ) || ; ||= Ú Ø , невірно & ( ) ||= , невірно || Ú Ø ; 1) & ( ) |= Cl , |= Cl Ú Ø ; 2) & ( ) |= T , & ( ) | F ; 3) | T Ú Ø ; |= F Ú Ø ; 4) Ú & Ø T та невірно Ú & Ø F ; 5) &( Ú Ø ) F та невірно &( Ú Ø ) T . 6) & Ø |= TF ÚØ ; & ( ) |= TF Ú Ø. Теорема. У випадку пересиченої семантики маємо: 1) & ( ) ||= , || Ú Ø ; невірно & ( ) || ; невірно ||= Ú Ø ; 2) & ( ) |= Cm , |= Cm Ú Ø ; 3) & ( ) | T , & ( ) |= F ; 4) |= T Ú Ø ; | F Ú Ø ; 5) Ú & Ø F та невірно Ú & Ø T ; 6) &( Ú Ø ) T та невірно &( Ú Ø ) F . 7) & Ø |= TF ÚØ ; & ( ) |= TF Ú Ø.
13 Поведінка введених відношень логічного наслідку вельми специфічна. Теорема. У випадку неокласичної семантики маємо: 1) & ( ) || ; ||= Ú Ø , невірно & ( ) ||= , невірно || Ú Ø ; 1) & ( ) |= Cl , |= Cl Ú Ø ; 2) & ( ) |= T , & ( ) | F ; 3) | T Ú Ø ; |= F Ú Ø ; 4) Ú & Ø T та невірно Ú & Ø F ; 5) &( Ú Ø ) F та невірно &( Ú Ø ) T . 6) & Ø |= TF ÚØ ; & ( ) |= TF Ú Ø. Теорема. У випадку пересиченої семантики маємо: 1) & ( ) ||= , || Ú Ø ; невірно & ( ) || ; невірно ||= Ú Ø ; 2) & ( ) |= Cm , |= Cm Ú Ø ; 3) & ( ) | T , & ( ) |= F ; 4) |= T Ú Ø ; | F Ú Ø ; 5) Ú & Ø F та невірно Ú & Ø T ; 6) &( Ú Ø ) T та невірно &( Ú Ø ) F . 7) & Ø |= TF ÚØ ; & ( ) |= TF Ú Ø.
 14 Теорема. У випадку загальної семантики: 1) ||= || ; 2 ) & Ø | TF Ú Ø ; & ( ) | TF Ú Ø. Невірними будуть такі співвідношення: A |= T Ø A |= T Ø , Ø A |= T Ø A |= T , A |= F Ø A |= F Ø , Ø A |= F Ø A |= F . A T Ø A T Ø , Ø A T Ø A T , A F Ø A F Ø , Ø A F Ø A F . Таким чином: – для |= T та |= F закон контрапозиції невірний, – для T та F не можна знімати заперечення в обох частинах еквівалентності.
14 Теорема. У випадку загальної семантики: 1) ||= || ; 2 ) & Ø | TF Ú Ø ; & ( ) | TF Ú Ø. Невірними будуть такі співвідношення: A |= T Ø A |= T Ø , Ø A |= T Ø A |= T , A |= F Ø A |= F Ø , Ø A |= F Ø A |= F . A T Ø A T Ø , Ø A T Ø A T , A F Ø A F Ø , Ø A F Ø A F . Таким чином: – для |= T та |= F закон контрапозиції невірний, – для T та F не можна знімати заперечення в обох частинах еквівалентності.
 15 Семантичні властивості логіки квазіарних предикатів Використовуючи TF , можна описати властивості пропозиційних композицій та властивості, пов ‘ язані з композицією реномінації й пропозиційними композиціями. Наведемо для прикладу закони де Моргана: Ø ( P Ú Q ) TF Ø P & Ø Q ; Ø ( P & Q ) TF Ø P ÚØ Q. Приклад. Існують АС A та формула : A |= TF » x та $ x A | Cl , $ x A | Cm . Нехай – це формула » x p p для ПС p. Інтерпретуємо p на АС A так: Маємо T ( p A ) V A , F ( p A ) V A , T ( » x p A ) = V A , F ( » x p A ) = , T ( $ x ( » x p p ) A ) = V A , F ( $ x ( » x p p ) A ) = , T ( » x p p ) A ) = V A , F ( » x p p ) A ) = , T (( » x p p ) A ) V A , F (( » x p p ) A ) V A. Звідси A |= TF » x , $ x A | Cl , $ x A | Cm . { }, якщо ( ), ( ) { }, якщо ( ). A T x asn dp d F x asn d
15 Семантичні властивості логіки квазіарних предикатів Використовуючи TF , можна описати властивості пропозиційних композицій та властивості, пов ‘ язані з композицією реномінації й пропозиційними композиціями. Наведемо для прикладу закони де Моргана: Ø ( P Ú Q ) TF Ø P & Ø Q ; Ø ( P & Q ) TF Ø P ÚØ Q. Приклад. Існують АС A та формула : A |= TF » x та $ x A | Cl , $ x A | Cm . Нехай – це формула » x p p для ПС p. Інтерпретуємо p на АС A так: Маємо T ( p A ) V A , F ( p A ) V A , T ( » x p A ) = V A , F ( » x p A ) = , T ( $ x ( » x p p ) A ) = V A , F ( $ x ( » x p p ) A ) = , T ( » x p p ) A ) = V A , F ( » x p p ) A ) = , T (( » x p p ) A ) V A , F (( » x p p ) A ) V A. Звідси A |= TF » x , $ x A | Cl , $ x A | Cm . { }, якщо ( ), ( ) { }, якщо ( ). A T x asn dp d F x asn d
 16 Основні властивості, пов ‘ язані з композиціями квантифікації. Q 1) $ x $ y TF $ y $ x та » x » y TF » y » x . Q 2) Ø» x TF $ x Ø та Ø$ x TF » x Ø. Q 3) $ x TF » x $ x , $ x TF $ x ; » x TF » x , » x TF $ x » x . Q 4) $ x Ú$ x TF $ x ( Ú ) та » x & » x TF » x ( & ). Q 5) $ x ( & )|= TF $ x & $ x та » x Ú» x |= TF » x ( Ú ). Q 6) $ y » x |= TF » x $ y ; водночас » x $ y | $ y » x . Q 7) » x |= $ x ; водночас » x | , | » x , | $ x . Тут – одне з Cl , Cm , T , F , TF. Q 8) ||= $ x , ||= » x , » x ||= $ x та || $ x , || » x , » x || $ x .
16 Основні властивості, пов ‘ язані з композиціями квантифікації. Q 1) $ x $ y TF $ y $ x та » x » y TF » y » x . Q 2) Ø» x TF $ x Ø та Ø$ x TF » x Ø. Q 3) $ x TF » x $ x , $ x TF $ x ; » x TF » x , » x TF $ x » x . Q 4) $ x Ú$ x TF $ x ( Ú ) та » x & » x TF » x ( & ). Q 5) $ x ( & )|= TF $ x & $ x та » x Ú» x |= TF » x ( Ú ). Q 6) $ y » x |= TF » x $ y ; водночас » x $ y | $ y » x . Q 7) » x |= $ x ; водночас » x | , | » x , | $ x . Тут – одне з Cl , Cm , T , F , TF. Q 8) ||= $ x , ||= » x , » x ||= $ x та || $ x , || » x , » x || $ x .
 17 Для логік часткових однозначних предикатів додаємо властивості: Q 9 P ) |= » x ( » x ) та |= $ x ( » x ); |= » x ( $ x ) та |= $ x ( $ x ); Q 10 P ) не завжди вірні |= $ x , |= » x , » x ||= ; Q 11 P ) для деяких формул можливо: |= » x та невірно |= $ x . Для логік тотальних неоднозначних предикатів додаємо властивості: Q 9) | » x ( » x ) та | $ x ( » x ); | » x ( $ x ) та | $ x ( $ x ); Q 10 Т) не завжди вірні | $ x , | » x , » x || ; Q 11 Т) для деяких формул можливо: | » x та невірно | $ x .
17 Для логік часткових однозначних предикатів додаємо властивості: Q 9 P ) |= » x ( » x ) та |= $ x ( » x ); |= » x ( $ x ) та |= $ x ( $ x ); Q 10 P ) не завжди вірні |= $ x , |= » x , » x ||= ; Q 11 P ) для деяких формул можливо: |= » x та невірно |= $ x . Для логік тотальних неоднозначних предикатів додаємо властивості: Q 9) | » x ( » x ) та | $ x ( » x ); | » x ( $ x ) та | $ x ( $ x ); Q 10 Т) не завжди вірні | $ x , | » x , » x || ; Q 11 Т) для деяких формул можливо: | » x та невірно | $ x .
 18 Теорема. 1) Для логік еквітонних предикатів A |= Cl $ x та » x A |= Cl ; 2) д ля логік антитонних предикатів A |= Cm $ x та » x A |= Cm ; 3) для логік еквітонних предикатів A |= T $ x , » x A |= F та » x ||= , але вони не завжди вірні для логік антитонних предикатів; 4) для логік антитонних предикатів A |= F $ x , » x A |= T та » x || , але вони не завжди вірні для логік еквітонних предикатів; 5) A |= TF $ x та » x A |= TF не завжди вірні для логік еквітонних, так і для логік антитонних предикатів. (Φ)x z. R(Φ)x z. R
18 Теорема. 1) Для логік еквітонних предикатів A |= Cl $ x та » x A |= Cl ; 2) д ля логік антитонних предикатів A |= Cm $ x та » x A |= Cm ; 3) для логік еквітонних предикатів A |= T $ x , » x A |= F та » x ||= , але вони не завжди вірні для логік антитонних предикатів; 4) для логік антитонних предикатів A |= F $ x , » x A |= T та » x || , але вони не завжди вірні для логік еквітонних предикатів; 5) A |= TF $ x та » x A |= TF не завжди вірні для логік еквітонних, так і для логік антитонних предикатів. (Φ)x z. R(Φ)x z. R
 19 Для відношень Cl , Cm , TF справджується теорем а семантичної еквiвалентност і (тут – одне з Cl , Cm , TF ). Теорема. Нехай формула ‘ отримана з заміною деяких входжень формул 1 , . . . , n на 1 , . . . , n вiдповiдно. Якщо 1 1 , . . . , n n , то ‘. Для відношень T та F теорема невірна. Справді, можливі ситуації: – вірно T та невірно Ø T Ø , адже Ø T Ø F ; – вірно F та невірно Ø F Ø.
19 Для відношень Cl , Cm , TF справджується теорем а семантичної еквiвалентност і (тут – одне з Cl , Cm , TF ). Теорема. Нехай формула ‘ отримана з заміною деяких входжень формул 1 , . . . , n на 1 , . . . , n вiдповiдно. Якщо 1 1 , . . . , n n , то ‘. Для відношень T та F теорема невірна. Справді, можливі ситуації: – вірно T та невірно Ø T Ø , адже Ø T Ø F ; – вірно F та невірно Ø F Ø.
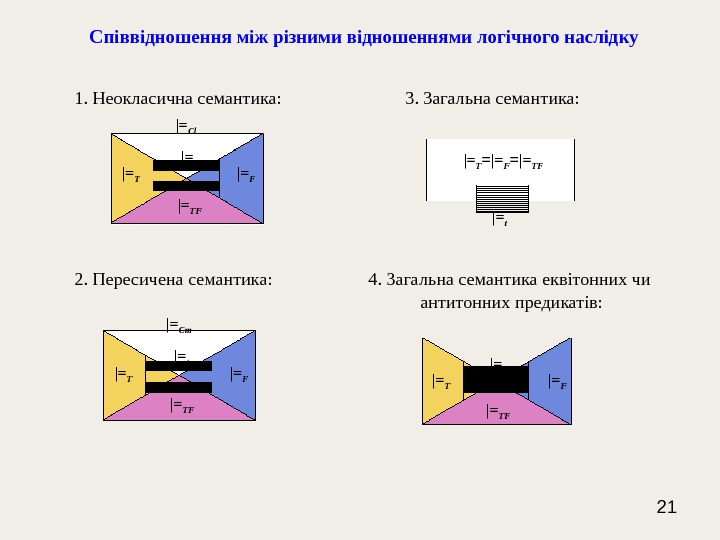
 20 Сп іввідношення між різними відношеннями логічного наслідку у відповідних семантиках 1. Неокласична семантика: |= TF |= T , |= TF |= F , |= T |= Cl , |= F |= Cl ; |= t |= Cl , |= F || =, |= T || ; |= Cm = ; |= t |= T , |= t |= F , |= TF |= t ; |= T ||= , |= F || , ||= |= Cl , || |= Cl . 2. Пересичена семантика: |= TF |= T , |= TF |= F , |= T |= Cm , |= F |= Cm ; |= t |= Cm , |= F || =, |= T || ; |= Cl = ; |= t |= T , |= t |= F , |= TF |= t ; |= T ||= , |= F || , ||= |= Cm , || |= Cm . 3. Загальна семантика: |= TF = |= T = |= F ; |= t |= TF , |= TF |= t ; |= TF || = ||= ; |= Cl = , |= Cm = . 4. Загальна семантика еквітонних чи загальна семантика антитонних: |= TF |= T , |= TF |= F ; |= t |= TF , |= TF |= t ; |= T || , |= F ||= ; |= Cl = , |= Cm = .
20 Сп іввідношення між різними відношеннями логічного наслідку у відповідних семантиках 1. Неокласична семантика: |= TF |= T , |= TF |= F , |= T |= Cl , |= F |= Cl ; |= t |= Cl , |= F || =, |= T || ; |= Cm = ; |= t |= T , |= t |= F , |= TF |= t ; |= T ||= , |= F || , ||= |= Cl , || |= Cl . 2. Пересичена семантика: |= TF |= T , |= TF |= F , |= T |= Cm , |= F |= Cm ; |= t |= Cm , |= F || =, |= T || ; |= Cl = ; |= t |= T , |= t |= F , |= TF |= t ; |= T ||= , |= F || , ||= |= Cm , || |= Cm . 3. Загальна семантика: |= TF = |= T = |= F ; |= t |= TF , |= TF |= t ; |= TF || = ||= ; |= Cl = , |= Cm = . 4. Загальна семантика еквітонних чи загальна семантика антитонних: |= TF |= T , |= TF |= F ; |= t |= TF , |= TF |= t ; |= T || , |= F ||= ; |= Cl = , |= Cm = .
 21 Сп іввідношення між різними відношеннями логічного наслідку 1. Неокласична семантика: 3. Загальна семантика: 2. Пересичена семантика: 4. Загальна семантика еквітонних чи антитонних предикатів: |= T |= F |= TF|= t|= Cl |= Cm |= T |= F |= TF|= t|= T = |= F = |= TF |= t
21 Сп іввідношення між різними відношеннями логічного наслідку 1. Неокласична семантика: 3. Загальна семантика: 2. Пересичена семантика: 4. Загальна семантика еквітонних чи антитонних предикатів: |= T |= F |= TF|= t|= Cl |= Cm |= T |= F |= TF|= t|= T = |= F = |= TF |= t
 22 Відношення логічного наслідку для множин формул Спочатку задамо відношення наслідку для множин формул при інтерпретації на фіксованій моделі мови АС A. Нехай Fr та Fr. A |= Cl , якщо A |= Cm , якщо A |= T , якщо A |= F , якщо A |= TF , якщо Відношення логічного наслідку для множин формул |= T , |= F , |= TF , |= Cl , |= Cm визначаємо за такою схемою: |= , якщо A |= для кожної моделі мови A. Відношення |= T , |= F , |= TF , |= Cl , |= Cm рефлексивні, але не транзитивні. Φ Γ Ψ Δ (Φ ) (Ψ )A AT F I I Φ Γ Ψ Δ (Φ ) (Ψ )V A AF T A U U Φ Γ Ψ Δ (Φ ) (Ψ )A AT T I U Ψ Δ Φ Γ (Ψ ) (Φ )A AF F I U Φ Γ Ψ Δ Φ Γ (Φ ) (Ψ ) та (Ψ ) (Φ )A A A AT T F F I U
22 Відношення логічного наслідку для множин формул Спочатку задамо відношення наслідку для множин формул при інтерпретації на фіксованій моделі мови АС A. Нехай Fr та Fr. A |= Cl , якщо A |= Cm , якщо A |= T , якщо A |= F , якщо A |= TF , якщо Відношення логічного наслідку для множин формул |= T , |= F , |= TF , |= Cl , |= Cm визначаємо за такою схемою: |= , якщо A |= для кожної моделі мови A. Відношення |= T , |= F , |= TF , |= Cl , |= Cm рефлексивні, але не транзитивні. Φ Γ Ψ Δ (Φ ) (Ψ )A AT F I I Φ Γ Ψ Δ (Φ ) (Ψ )V A AF T A U U Φ Γ Ψ Δ (Φ ) (Ψ )A AT T I U Ψ Δ Φ Γ (Ψ ) (Φ )A AF F I U Φ Γ Ψ Δ Φ Γ (Φ ) (Ψ ) та (Ψ ) (Φ )A A A AT T F F I U
 23 Теорема. Нехай АС B = ( A , I B ) дуальна до АС A = ( A , I A ). Тоді 1) A |= T B |= F та A |= F B |= T ; 2) A |= Cl B |= Cm та A |= Cm B |= Cl . Наслідок. У випадку загальної семантики A |= T A |= F A |= TF . У випадку загальної семантики природно розглядати лише |= TF . Для неокласичної семантики можна розглядати |= T , |= F , |= TF , |= Cl ; Для пересиченої семантики можна розглядати |= T , |= F , |= TF , |= Cm . Теорема (заміни еквівалентних). Нехай TF . Тоді: , |= та |= , Замість TF тут можна брати Cl чи Cm . Тоді |= буде відповідно лише відношенням |= Cl чи |= Cm . Отримуємо ще дві різновидності теореми заміни еквівалентних – для логіки часткових однозначних предикатів(із |= Cl ); – для логіки тотальних неоднозначних предикатів (із |= Cm ).
23 Теорема. Нехай АС B = ( A , I B ) дуальна до АС A = ( A , I A ). Тоді 1) A |= T B |= F та A |= F B |= T ; 2) A |= Cl B |= Cm та A |= Cm B |= Cl . Наслідок. У випадку загальної семантики A |= T A |= F A |= TF . У випадку загальної семантики природно розглядати лише |= TF . Для неокласичної семантики можна розглядати |= T , |= F , |= TF , |= Cl ; Для пересиченої семантики можна розглядати |= T , |= F , |= TF , |= Cm . Теорема (заміни еквівалентних). Нехай TF . Тоді: , |= та |= , Замість TF тут можна брати Cl чи Cm . Тоді |= буде відповідно лише відношенням |= Cl чи |= Cm . Отримуємо ще дві різновидності теореми заміни еквівалентних – для логіки часткових однозначних предикатів(із |= Cl ); – для логіки тотальних неоднозначних предикатів (із |= Cm ).
 24 Основні властивості відношення |= C ) Якщо , то |= . U ) Нехай та , тоді |= . Ø Ø ) ØØ , |= ; |= , ØØ |= , . Ú ) Ú , |= та , |= ; |= , Ú |= , , . Ø Ú ) Ø ( Ú ), |= Ø , |= ; |= , Ø ( Ú ) |= , Ø та |= , Ø. Для |= Cl (неокласична семантика) та |= Cm (пересичена семантика): Ø ) Ø , |= , ; |= , Ø , |= . RT ) U ) , , (Φ), Γ | Δ; z v v z x x. R R , , Γ | Δ, (Φ). z v v z x x. R R , , (Φ), Γ | Δ, ÿêù î ν(Φ); y v v z x x. R R y , , Γ | Δ, (Φ), ÿêù î ν(Φ). y v v z x x. R R y
24 Основні властивості відношення |= C ) Якщо , то |= . U ) Нехай та , тоді |= . Ø Ø ) ØØ , |= ; |= , ØØ |= , . Ú ) Ú , |= та , |= ; |= , Ú |= , , . Ø Ú ) Ø ( Ú ), |= Ø , |= ; |= , Ø ( Ú ) |= , Ø та |= , Ø. Для |= Cl (неокласична семантика) та |= Cm (пересичена семантика): Ø ) Ø , |= , ; |= , Ø , |= . RT ) U ) , , (Φ), Γ | Δ; z v v z x x. R R , , Γ | Δ, (Φ). z v v z x x. R R , , (Φ), Γ | Δ, ÿêù î ν(Φ); y v v z x x. R R y , , Γ | Δ, (Φ), ÿêù î ν(Φ). y v v z x x. R R y
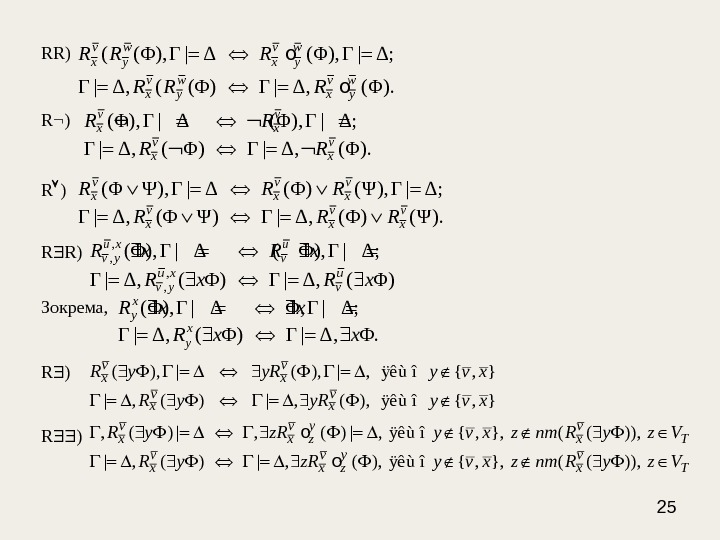 25 RR ) R Ø ) R Ú ) R $ R) Зокрема, R $ ) R $$ )( (Φ), Γ | Δ; ov w x y x y. R R R Γ | Δ, ( (Φ) Γ | Δ, (Φ). ov w x y x y. R R R (Φ), Γ | Δ; v v x x. R R Γ | Δ, ( Φ) Γ | Δ, (Φ). v v x x. R R (Φ Ψ), Γ | Δ (Φ) (Ψ), Γ | Δ; v v v x x x. R R R Γ | Δ, (Φ Ψ) Γ | Δ, (Φ) (Ψ). v v v x x x. R R R , , (Φ), Γ | Δ ( Φ), Γ | Δ; u x u v y v. R x , , Γ | Δ, ( Φ) u x u v y v. R x (Φ), Γ | Δ Φ, Γ | Δ; x y. R x x Γ | Δ, ( Φ) Γ | Δ, Φ. x y. R x x ( ), | , ÿêù î { , }v v x x. R y y. R y v x | , ( ), ÿêù î { , }v v x x. R y y. R y v x , ( ) | , ÿêù î { , }, ( ( )), v v y v x x z x TR y z. R y v x z nm R y z V o | , ( ), ÿêù î { , }, ( ( )), v v y v x x z x TR y z. R y v x z nm R y z V o
25 RR ) R Ø ) R Ú ) R $ R) Зокрема, R $ ) R $$ )( (Φ), Γ | Δ; ov w x y x y. R R R Γ | Δ, ( (Φ) Γ | Δ, (Φ). ov w x y x y. R R R (Φ), Γ | Δ; v v x x. R R Γ | Δ, ( Φ) Γ | Δ, (Φ). v v x x. R R (Φ Ψ), Γ | Δ (Φ) (Ψ), Γ | Δ; v v v x x x. R R R Γ | Δ, (Φ Ψ) Γ | Δ, (Φ) (Ψ). v v v x x x. R R R , , (Φ), Γ | Δ ( Φ), Γ | Δ; u x u v y v. R x , , Γ | Δ, ( Φ) u x u v y v. R x (Φ), Γ | Δ Φ, Γ | Δ; x y. R x x Γ | Δ, ( Φ) Γ | Δ, Φ. x y. R x x ( ), | , ÿêù î { , }v v x x. R y y. R y v x | , ( ), ÿêù î { , }v v x x. R y y. R y v x , ( ) | , ÿêù î { , }, ( ( )), v v y v x x z x TR y z. R y v x z nm R y z V o | , ( ), ÿêù î { , }, ( ( )), v v y v x x z x TR y z. R y v x z nm R y z V o
 26 На відміну від |= Cl та |= Cm , для |= T , |= F та |= TF не можна знімати заперечення, переносячи формулу з лівої частини у праву і навпаки, тому наведені властивості реномінації формулюємо і для зовнішнього заперечення: Ø R T ) Ø U ) Ø RR) Ø R Ø ) Ø R Ú )(Φ), Γ | Δ; v v x x. R R Γ | Δ, ( Φ) Γ | Δ, (Φ); v v x x. R R Γ | Δ, (Φ Ψ) Γ | Δ, (Ψ) òà Γ | Δ, (Φ); v v v x x x. R R R (Φ Ψ), Γ | Δ (Φ), (Ψ), Γ | Δ; v v v x x x. R R R , , (Φ), Γ | Δ; z v v z x x. R R , , Γ | Δ, (Φ); z v v z x x. R R , , (Φ), Γ | Δ, ÿêù î ν(Φ); y v v z x x. R R y , , Γ | Δ, (Φ), ÿêù î ν(Φ); y v v z x x. R R y ( (Φ)), Γ | Δ (Φ), Γ | Δ; v w x y. R R R o Γ | Δ, ( (Φ)) Γ | Δ, (Φ); v w x y. R R R o
26 На відміну від |= Cl та |= Cm , для |= T , |= F та |= TF не можна знімати заперечення, переносячи формулу з лівої частини у праву і навпаки, тому наведені властивості реномінації формулюємо і для зовнішнього заперечення: Ø R T ) Ø U ) Ø RR) Ø R Ø ) Ø R Ú )(Φ), Γ | Δ; v v x x. R R Γ | Δ, ( Φ) Γ | Δ, (Φ); v v x x. R R Γ | Δ, (Φ Ψ) Γ | Δ, (Ψ) òà Γ | Δ, (Φ); v v v x x x. R R R (Φ Ψ), Γ | Δ (Φ), (Ψ), Γ | Δ; v v v x x x. R R R , , (Φ), Γ | Δ; z v v z x x. R R , , Γ | Δ, (Φ); z v v z x x. R R , , (Φ), Γ | Δ, ÿêù î ν(Φ); y v v z x x. R R y , , Γ | Δ, (Φ), ÿêù î ν(Φ); y v v z x x. R R y ( (Φ)), Γ | Δ (Φ), Γ | Δ; v w x y. R R R o Γ | Δ, ( (Φ)) Γ | Δ, (Φ); v w x y. R R R o
 27Ø R $ R) Зокрема, Ø R $ ) Ø R $$ ), , (Φ), Γ | Δ ( Φ), Γ | Δ; u x u v y v. R x , , Γ | Δ, ( Φ)u x u v y v. R x (Φ), Γ | Δ Φ, Γ | Δ; x y. R x x Γ | Δ, ( Φ) Γ | Δ, Φ. x y. R x x ( ), | , ÿêù î { , }v v x x. R y y. R y v x | , ( ), ÿêù î { , }v v x x. R y y. R y v x , ( ) | , ÿêù î { , }, ( ( )), v v y v x x z x TR y z. R y v x z nm R y z V o | , ( ), ÿêù î { , }, ( ( )), v v y v x x z x TR y z. R y v x z nm R y z V o
27Ø R $ R) Зокрема, Ø R $ ) Ø R $$ ), , (Φ), Γ | Δ ( Φ), Γ | Δ; u x u v y v. R x , , Γ | Δ, ( Φ)u x u v y v. R x (Φ), Γ | Δ Φ, Γ | Δ; x y. R x x Γ | Δ, ( Φ) Γ | Δ, Φ. x y. R x x ( ), | , ÿêù î { , }v v x x. R y y. R y v x | , ( ), ÿêù î { , }v v x x. R y y. R y v x , ( ) | , ÿêù î { , }, ( ( )), v v y v x x z x TR y z. R y v x z nm R y z V o | , ( ), ÿêù î { , }, ( ( )), v v y v x x z x TR y z. R y v x z nm R y z V o
 28 Розширення мови індикаторами наявності значення для змінних Предикати z – індикатори наявності в даному d V A значення для предметного імені z V – визначаємо так: Теорема. Справджуються наступні співвідношення: Як окремі випадки отримуємо: Водночас невірними є такі співвідношення: , , ( ( )) (ε ) ( ( )); u x u v y v. R P y R x. PT F T , , ( ( )) (ε ) ( ( )). u u x v v y. R x. P y R P F F F ( ( )) (ε ) ( ); x y. R P y x. PT F T ( ) (ε ) ( ( )); x yx. P y R P F F F , якщо ( ) , ε ( ) , якщо ( ). T d z z d F d z ( ( )) ( ); ( ( )) ( )x x y y. R P x. P T T F F ( ( )) (ε ) ( ); x y. R P y x. P F F F ( ) (ε ) ( ( )). x yx. P y R P T F T ( ) ( ( )); ( ) ( ( ))x x y yx. P R P F F T T
28 Розширення мови індикаторами наявності значення для змінних Предикати z – індикатори наявності в даному d V A значення для предметного імені z V – визначаємо так: Теорема. Справджуються наступні співвідношення: Як окремі випадки отримуємо: Водночас невірними є такі співвідношення: , , ( ( )) (ε ) ( ( )); u x u v y v. R P y R x. PT F T , , ( ( )) (ε ) ( ( )). u u x v v y. R x. P y R P F F F ( ( )) (ε ) ( ); x y. R P y x. PT F T ( ) (ε ) ( ( )); x yx. P y R P F F F , якщо ( ) , ε ( ) , якщо ( ). T d z z d F d z ( ( )) ( ); ( ( )) ( )x x y y. R P x. P T T F F ( ( )) (ε ) ( ); x y. R P y x. P F F F ( ) (ε ) ( ( )). x yx. P y R P T F T ( ) ( ( )); ( ) ( ( ))x x y yx. P R P F F T T
 29 Властивості, пов ‘ язані з елімінацією кванторів (використовують x ): $ R |– ) $ |– ) за умови z V T та z nm ( , , $ х ). $ R v –| ) Допоміжні властивості -розподілу: d ) |= y , |= та |= , y. v ) |= , z за умови z V T та z nm ( ). , , (Φ), Γ | Δ, ε u u x v v z. R x R z за умови { }, , (Σ, ( Φ)). u T vx u z V z nm R x Φ, Γ | Δ (Φ), Γ | Δ, ε x zx R z , , Γ | Δ, ( Φ), ε Γ | Δ, ( Φ), (Φ), ε (при { }). u u u x v v v y. R x y R x R y x u Γ | Δ, Φ, ε Γ | Δ, Φ, (Φ), ε. x yx y x R y
29 Властивості, пов ‘ язані з елімінацією кванторів (використовують x ): $ R |– ) $ |– ) за умови z V T та z nm ( , , $ х ). $ R v –| ) Допоміжні властивості -розподілу: d ) |= y , |= та |= , y. v ) |= , z за умови z V T та z nm ( ). , , (Φ), Γ | Δ, ε u u x v v z. R x R z за умови { }, , (Σ, ( Φ)). u T vx u z V z nm R x Φ, Γ | Δ (Φ), Γ | Δ, ε x zx R z , , Γ | Δ, ( Φ), ε Γ | Δ, ( Φ), (Φ), ε (при { }). u u u x v v v y. R x y R x R y x u Γ | Δ, Φ, ε Γ | Δ, Φ, (Φ), ε. x yx y x R y
 30 Для |= T , |= F , |= TF властивості елімінації дублюються для зовнішнього Ø : Ø$ R |– ) Ø$ |– ) за умови z V T та z nm ( , , $ х ). Ø$ R v –| ) Ø$ v –| ) Наведені вище властивості відношень |= Cl , |= Cm , |= T , |= F , |= TF , пов ’ язані з квантором $ х , можна переформулювати для квантора » х. , , Γ | Δ, ( Φ) Γ | Δ, (Φ), εu u x v v z. R x R z за умови { }, , (Σ, ( Φ)). u T vx u z V z nm R x Γ | Δ, Φ Γ | Δ, (Φ), εx zx R z , , (Φ), Γ | Δ, ε (Φ), ( Φ), Γ | Δ, ε ( { }). u u x u v v y v. R x y R R x y x u Φ, Γ | Δ, ε (Φ), Φ, Γ | Δ, ε. x yx y R x y
30 Для |= T , |= F , |= TF властивості елімінації дублюються для зовнішнього Ø : Ø$ R |– ) Ø$ |– ) за умови z V T та z nm ( , , $ х ). Ø$ R v –| ) Ø$ v –| ) Наведені вище властивості відношень |= Cl , |= Cm , |= T , |= F , |= TF , пов ’ язані з квантором $ х , можна переформулювати для квантора » х. , , Γ | Δ, ( Φ) Γ | Δ, (Φ), εu u x v v z. R x R z за умови { }, , (Σ, ( Φ)). u T vx u z V z nm R x Γ | Δ, Φ Γ | Δ, (Φ), εx zx R z , , (Φ), Γ | Δ, ε (Φ), ( Φ), Γ | Δ, ε ( { }). u u x u v v y v. R x y R R x y x u Φ, Γ | Δ, ε (Φ), Φ, Γ | Δ, ε. x yx y R x y

