Решение_заданий_с_параметрами_математика_15_октября_2015.ppt
- Количество слайдов: 17
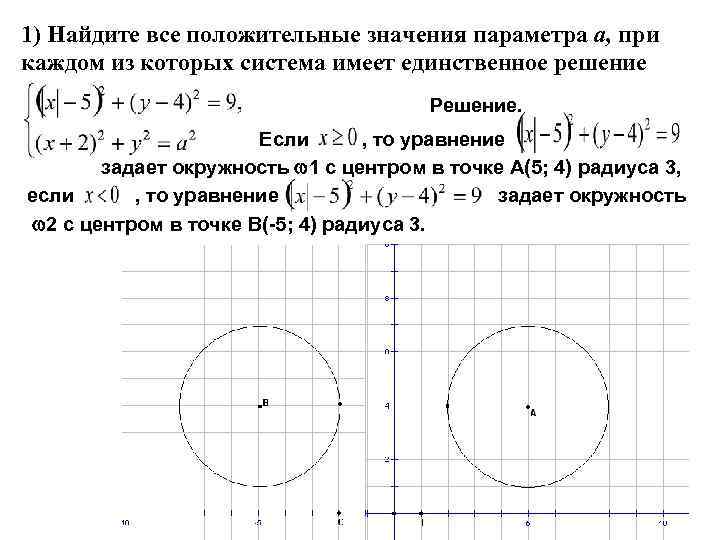 1) Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение Решение. Если , то уравнение задает окружность 1 с центром в точке А(5; 4) радиуса 3, если , то уравнение задает окружность 2 с центром в точке В(-5; 4) радиуса 3.
1) Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение Решение. Если , то уравнение задает окружность 1 с центром в точке А(5; 4) радиуса 3, если , то уравнение задает окружность 2 с центром в точке В(-5; 4) радиуса 3.
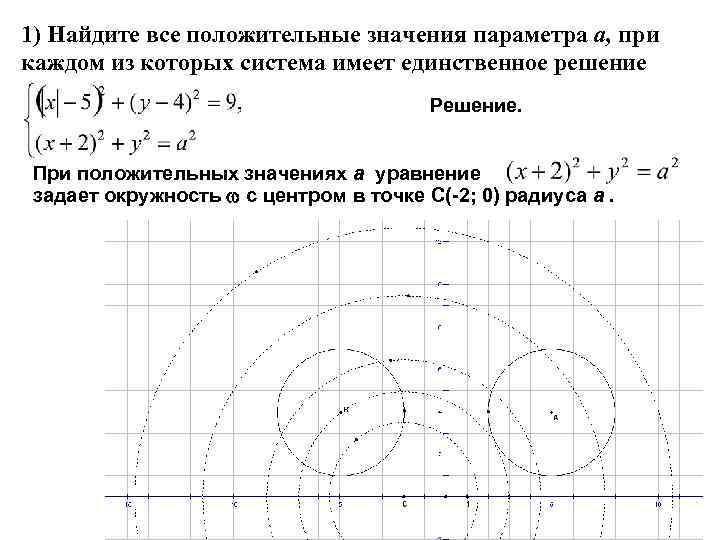 1) Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение Решение. При положительных значениях а уравнение задает окружность с центром в точке С(-2; 0) радиуса а.
1) Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение Решение. При положительных значениях а уравнение задает окружность с центром в точке С(-2; 0) радиуса а.
 1) Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение Решение. Поэтому задача состоит в том, чтобы найти все значения, при каждом из которых окружность имеет единственную общую точку с окружностью 1 или окружностью 2.
1) Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение Решение. Поэтому задача состоит в том, чтобы найти все значения, при каждом из которых окружность имеет единственную общую точку с окружностью 1 или окружностью 2.
 1) Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение Решение. Из точки С проведем луч СА, который пересекает окружность 1 в точках А 1 и А 2, где А 1 лежит между С и А. Также из точки С проведем луч СВ, который пересекает окружность 2 в точках В 1 и В 2, где В 1 лежит между С и В.
1) Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение Решение. Из точки С проведем луч СА, который пересекает окружность 1 в точках А 1 и А 2, где А 1 лежит между С и А. Также из точки С проведем луч СВ, который пересекает окружность 2 в точках В 1 и В 2, где В 1 лежит между С и В.
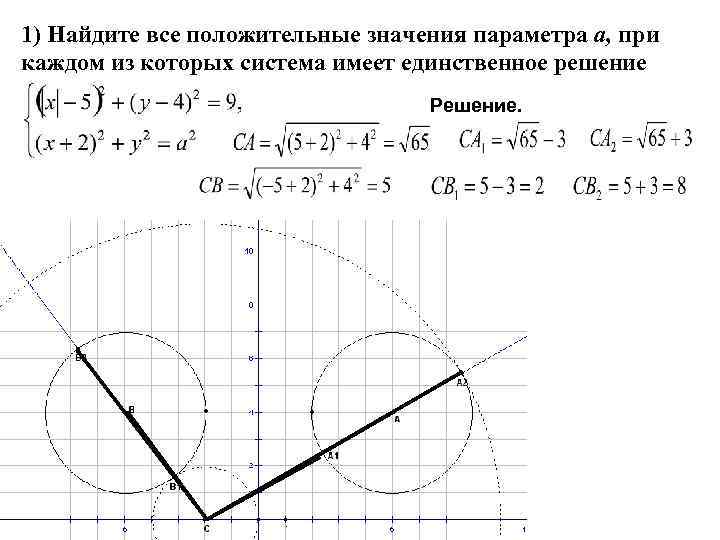 1) Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение Решение.
1) Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение Решение.
 1) Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение Решение. При При или окружности и 1 не пересекаются. окружности и 1 пересекаются в двух точках. окружности и 1 касаются.
1) Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение Решение. При При или окружности и 1 не пересекаются. окружности и 1 пересекаются в двух точках. окружности и 1 касаются.
 1) Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение Решение. При При или окружности и 2 не пересекаются. окружности и 2 пересекаются в двух точках. окружности и 2 касаются.
1) Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение Решение. При При или окружности и 2 не пересекаются. окружности и 2 пересекаются в двух точках. окружности и 2 касаются.
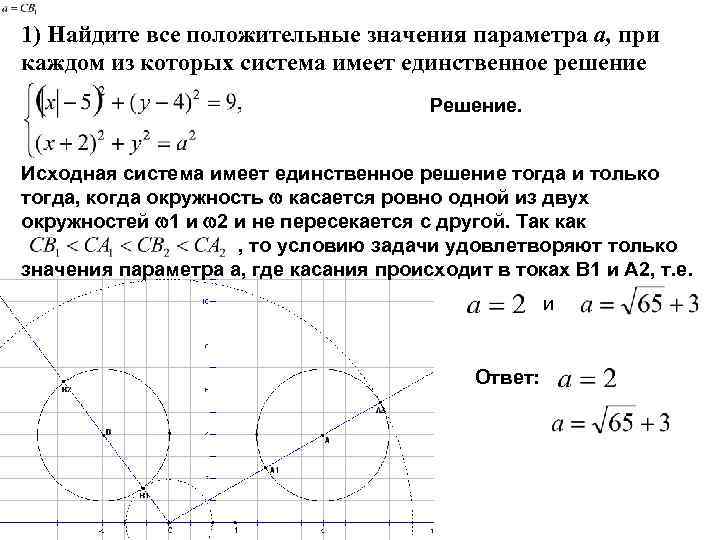 1) Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение Решение. Исходная система имеет единственное решение тогда и только тогда, когда окружность касается ровно одной из двух окружностей 1 и 2 и не пересекается с другой. Так как , то условию задачи удовлетворяют только значения параметра а, где касания происходит в токах В 1 и А 2, т. е. и Ответ:
1) Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение Решение. Исходная система имеет единственное решение тогда и только тогда, когда окружность касается ровно одной из двух окружностей 1 и 2 и не пересекается с другой. Так как , то условию задачи удовлетворяют только значения параметра а, где касания происходит в токах В 1 и А 2, т. е. и Ответ:
 2) При каких значениях параметра а уравнение имеет два различных решения? Решение. Уравнение квадратное относительно. Пусть. Тогда. Так как уравнение имеет решение только при , то решение исходной задачи можно свести к решению следующей задачи: «При каких значениях параметра а уравнение имеет два различных положительных корня? » (1 способ) , , . ,
2) При каких значениях параметра а уравнение имеет два различных решения? Решение. Уравнение квадратное относительно. Пусть. Тогда. Так как уравнение имеет решение только при , то решение исходной задачи можно свести к решению следующей задачи: «При каких значениях параметра а уравнение имеет два различных положительных корня? » (1 способ) , , . ,
 2) При каких значениях параметра а уравнение имеет два различных решения? Решение. «При каких значениях параметра а уравнение имеет два различных положительных корня? » , (1 способ) , . Уравнение различных положительных корня, если: , имеет два
2) При каких значениях параметра а уравнение имеет два различных решения? Решение. «При каких значениях параметра а уравнение имеет два различных положительных корня? » , (1 способ) , . Уравнение различных положительных корня, если: , имеет два
 2) При каких значениях параметра а уравнение имеет два различных решения? Решение. «При каких значениях параметра а уравнение имеет два различных положительных корня? » , (2 способ) , . Уравнение различных положительных корня, если: Ответ: , . имеет два
2) При каких значениях параметра а уравнение имеет два различных решения? Решение. «При каких значениях параметра а уравнение имеет два различных положительных корня? » , (2 способ) , . Уравнение различных положительных корня, если: Ответ: , . имеет два
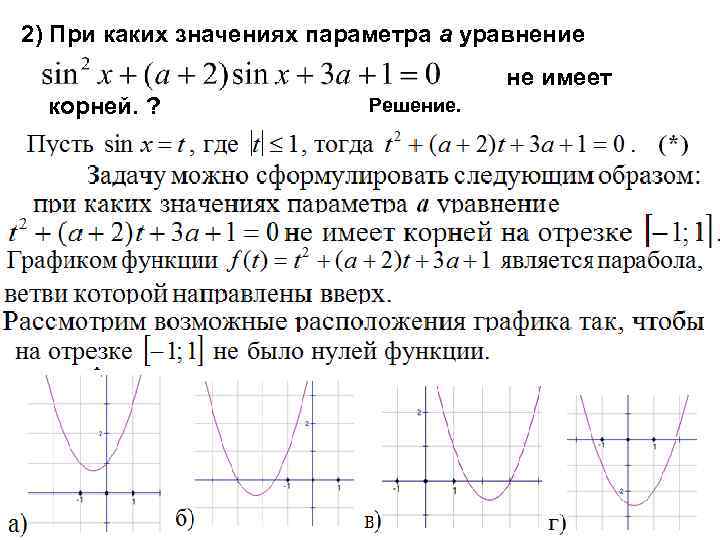 2) При каких значениях параметра а уравнение не имеет корней. ? Решение.
2) При каких значениях параметра а уравнение не имеет корней. ? Решение.
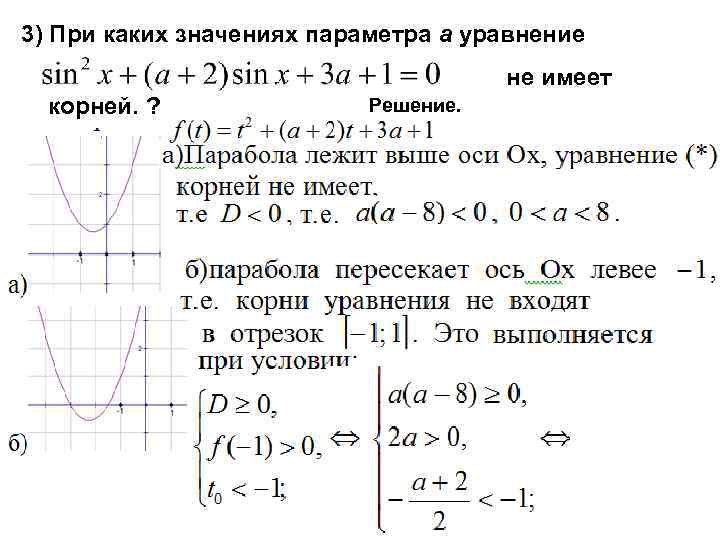 3) При каких значениях параметра а уравнение не имеет корней. ? Решение.
3) При каких значениях параметра а уравнение не имеет корней. ? Решение.
 3) При каких значениях параметра а уравнение не имеет корней. ? Решение.
3) При каких значениях параметра а уравнение не имеет корней. ? Решение.
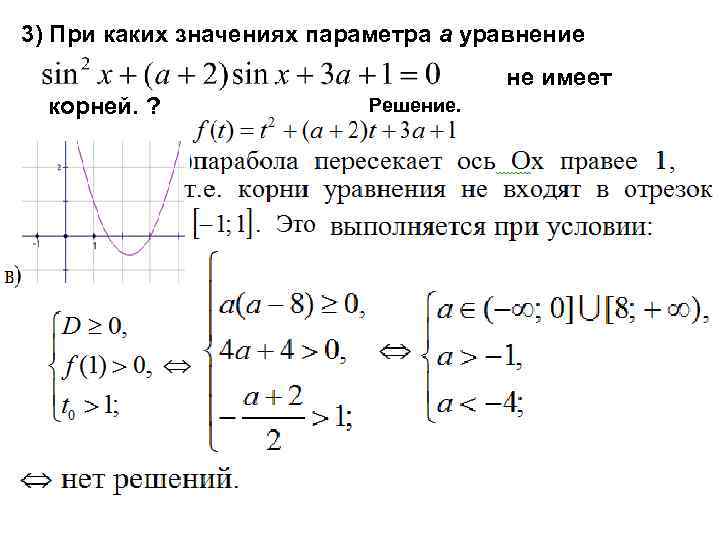 3) При каких значениях параметра а уравнение не имеет корней. ? Решение.
3) При каких значениях параметра а уравнение не имеет корней. ? Решение.
 3) При каких значениях параметра а уравнение не имеет корней. ? Решение.
3) При каких значениях параметра а уравнение не имеет корней. ? Решение.
 4)Найти все значения параметра а, при которых уравнение имеет ровно один корень. Решение. Левую и правую части уравнения можно рассмотреть как функции , которая является возрастающей на R. Поэтому исходное , которое (по теореме: уравнение можно записать так монотонна на промежутке , то уравнение Если функция ) равносильно на промежутке уравнению равносильно уравнению или. Согласно условию исходное уравнение должен иметь ровно один корень, то и уравнение тоже должен иметь один корень, т. е. Ответ:
4)Найти все значения параметра а, при которых уравнение имеет ровно один корень. Решение. Левую и правую части уравнения можно рассмотреть как функции , которая является возрастающей на R. Поэтому исходное , которое (по теореме: уравнение можно записать так монотонна на промежутке , то уравнение Если функция ) равносильно на промежутке уравнению равносильно уравнению или. Согласно условию исходное уравнение должен иметь ровно один корень, то и уравнение тоже должен иметь один корень, т. е. Ответ:


