1 МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ. МЕТОД НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ ДЛЯ

1 МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ. МЕТОД НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ ДЛЯ БАЗИСА И-ИЛИ-НЕ ЛЕКЦИЯ 15 В.И. ХАХАНОВ Факультет компьютерной инженерии и управления, кафедра АПВТ, ХНУРЭ ДИСКРЕТНАЯ МАТЕМАТИКА БУЛЕВА АЛГЕБРА

2 Цель лекции – изучить метод неопределенных коэффициентов для минимизации булевых функций в базисе И-ИЛИ-НЕ, описывающих комбинационные подсхемы цифровых проектов Содержание: Основные предположения Алгоритм нахождения неопределенных коэффициентов Пример реализации алгоритма Тема: Минимизация булевых функций. Метод неопределенных коэффициентов для базиса И-ИЛИ-НЕ

3 Литература Савельев А.Я. Прикладная теория цифровых автоматов. М.: Высш. шк., 1987. С. 194. Хаханов В.І., Хаханова І.В., Кулак Е.М., Чумаченко С.В. Методичні вказівки до практичних занять з курсу “Дискретна математика”. Харків, ХНУРЕ. 2001. С.35-43.

4 Базовые понятия: Булева переменная Булева функция Двоичная система счисления ДНФ Минимальная форма функции Термины Ключевые слова: Минимизация Минимальная ДНФ Неопределенные коэффициенты

5 Основные предположения. 1 Известно, что любую булеву функцию можно представить в дизъюнктивной нормальной форме Для функции от трех переменных общий вид ДНФ можно записать так: (1)

6 Основные предположения. 2 Неопределенные коэффициенты принимают значения 0, 1 и подбираются таким образом, чтобы получающаяся после этого ДНФ была минимальной, т.е. запись ДНФ имела минимальное количество букв При определении ДНФ учитывают свойство: дизъюнкция некоторого числа переменных равна нулю, если все входящие в нее переменные равны нулю; равна единице, если хотя бы одна переменная равна единице (2)

7 Основные предположения. 3 Преобразовывая правую часть формулы (1) на каждом наборе переменных, получаем систему уравнений: (3)

8 Основные предположения. 4 Если функция принимает нулевые значения на соответствующем наборе переменных fi=0, то все коэффициенты, входящие в данное уравнение, равны нулю. Тогда в остальных уравнениях системы (3), где fi=1, следует также положить равными нулю эти коэффициенты.

9 Алгоритм нахождения неопределенных коэффициентов 1. Выбрать строку системы (3), в которой fi=0. Приравнять нулю все коэффициенты этой строки. 2. Если все нулевые строки просмотрены, то перейти к п.3, иначе – п.1. 3. Из всех строк, где fi=1, вычеркнуть равные нулю коэффициенты, определенные в п.1. 4. Переписать модифицированную систему (3) с учетом выполненных преобразований. 5. В модифицированной системе выбрать и положить равными единице минимальное количество коэффициентов с минимальным количеством индексов, чтобы удовлетворить данную систему. 6. Составить минимальную ДНФ по выбранным коэффициентам

10 Time-Out

11 Пример минимизации по методу неопределенных коэффициентов 1 1. Постановка задачи Найти минимальную форму для функции методом неопределенных коэффициентов (4)

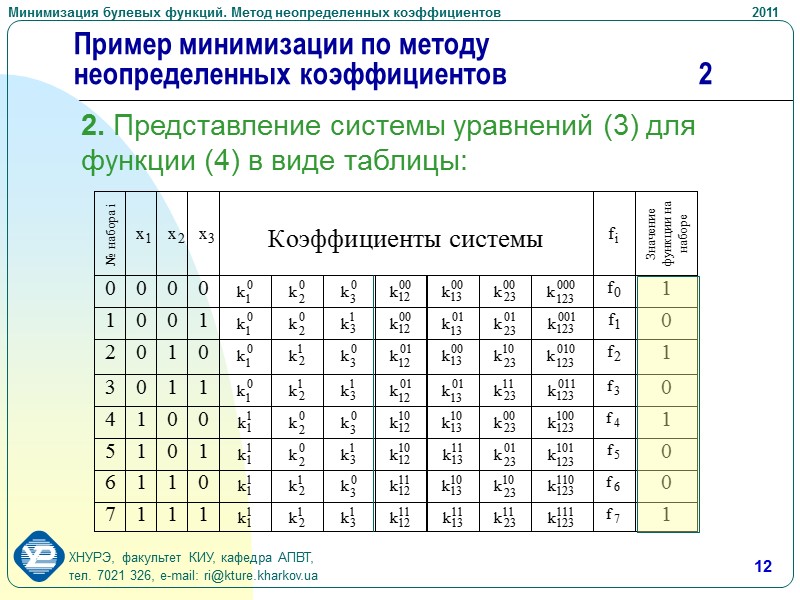
12 Пример минимизации по методу неопределенных коэффициентов 2 2. Представление системы уравнений (3) для функции (4) в виде таблицы:

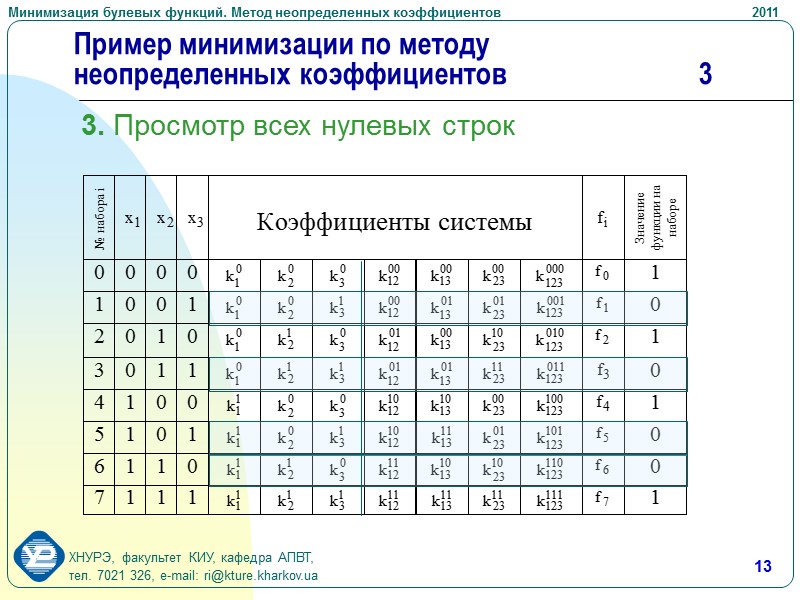
13 Пример минимизации по методу неопределенных коэффициентов 3 3. Просмотр всех нулевых строк

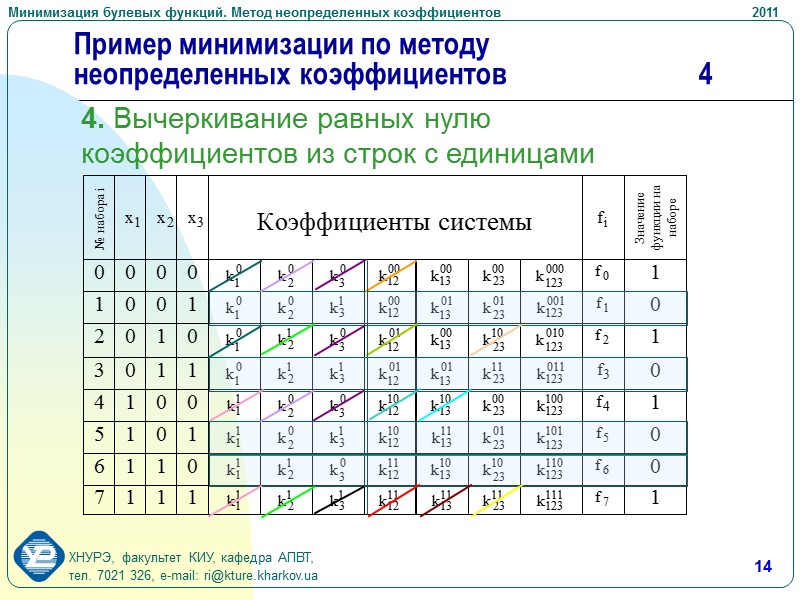
14 Пример минимизации по методу неопределенных коэффициентов 4 4. Вычеркивание равных нулю коэффициентов из строк с единицами

15 Пример минимизации по методу неопределенных коэффициентов 5 5. Модифицированная система уравнений с учетом выполненных преобразований имеет вид:

16 Пример минимизации по методу неопределенных коэффициентов 6 6. Выбор минимального покрытия Для обращения уравнений (0), (2), (4) в тождества достаточно, чтобы хотя бы один из коэффициентов был равен единице.

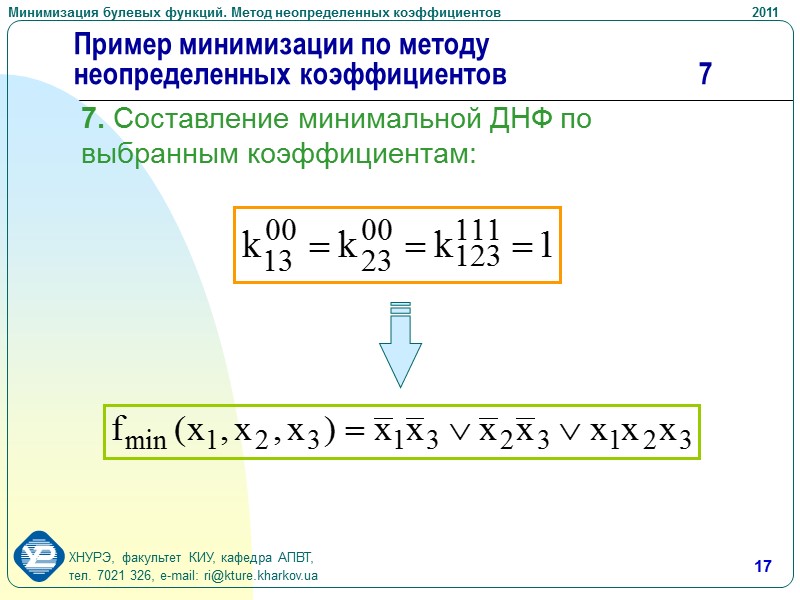
17 Пример минимизации по методу неопределенных коэффициентов 7 7. Составление минимальной ДНФ по выбранным коэффициентам:

18 Пример минимизации по методу неопределенных коэффициентов 8 Можно убедиться путем эквивалентных преобразований, чему равна минимальная форма функции:

19 Выводы Методы минимизации булевых функций используются во всех программных приложениях, связанных с синтезом вычислительных устройств Они позволяют в среднем на 20-30% получить более экономичный проект с позиции аппаратурных затрат Метод неопределенных коэффициентов в базисе И-ИЛИ-НЕ получать минимальные ДНФ для функций от небольшого количества переменных Недостатком метода является неприемлемая размерность таблицы для минимизации функции от более, чем 10 переменных

20 Тест-вопросы 1. На каких двоичных наборах функция f(x,y,z)=(xy)z равна 1 а) 000, д) 100, б) 001, е) 101, в) 010, ж) 110, г) 011, з) 111. 2. Конъюнкция некоторого числа переменных равна единице, когда: а) все переменные равны единице; б) все переменные равны нулю; в) хотя бы одна переменная равна единице; г) хотя бы одна переменная равна нулю. 3. Дизъюнкция некоторого числа переменных равна единице, когда: а) все переменные равны единице; б) все переменные равны нулю; в) хотя бы одна переменная равна единице; г) хотя бы одна переменная равна нулю.