1 Линейные электрические цепи с последовательным соединением элементов

1 Линейные электрические цепи с последовательным соединением элементов

2 Отношение комплексных амплитуд напряжения и тока на входе двухполюсника называется его комплексным входным сопротивлением Учитывая, что и получаем Отношение – полное входное сопротивление (модуль); ψU – ψi – сдвиг фаз между напряжением и током. Как всякое комплексное число, комплексное сопротивление и комплексная проводимость могут быть представлены в показательной, алгебраической и тригонометрической формах.

3 Гармонический ток в элементах электрической цепи Гармонический ток в сопротивлении Если пассивный двухполюсник представляет собой активное сопротивление R, то на основании закона Ома На векторной диаграмме напряжение и ток совпадают по фазе Если к сопротивлению подведено напряжение то через него потечет ток Мгновенная мощность, поступающая в сопротивление Среднее значение мощности за период

4 Гармонический ток в индуктивности Если пассивный двухполюсник представляет собой индуктивность, то Используя метод комплексных амплитуд, получим Амплитуда напряжения Угол сдвига фаз между напряжением и током Очевидно, что входное сопротивление индуктивности - чисто мнимая величина

5 Пусть через индуктивность протекает ток Тогда напряжение на индуктивности Мгновенная мощность, поступающая в индуктивность Энергия магнитного поля индуктивности

6 Гармонический ток в емкости При подключении к источнику гармонического напряжения емкости в цепи потечет ток Используя метод комплексных амплитуд, получаем Сдвиг фаз между напряжением и током Входное сопротивление емкости является чисто мнимой отрицательной величиной Мгновенная мощность, поступающая в емкость Энергия электрического поля емкости

7 Избирательные (резонансные) цепи В общем случае в любой приемной антенне возбуждается одновременно множество э. д. с. различных частот, излучаемых передающими станциями, а также источниками промышленных и атмосферных помех. Радиоприемное устройство должно на фоне всех сигналов выделить один нужный сигнал Реализовать цепи, имеющие частотную характеристику прямоугольной формы, практически не представляется возможным, удается лишь в известной степени приблизиться к подобному виду характеристики, используя для этого избирательные (резонансные) цепи

8 Последовательный колебательный контур. Резонанс напряжений При воздействии гармонической э. д. с. ток в контуре , где а б в

9 а) , X > 0, реактивная составляющая имеет индуктивный характер, ток в контуре отстает от входного напряжения б) , X < 0, реактивная составляющая имеет емкостный характер, ток в контуре опережает входное напряжение в) , X = 0, напряжение и ток в контуре совпадают по фазе, этот режим цепи называется резонансом напряжений. При заданных L и С резонанс наступает на частоте Входное сопротивление контура в этом случае Ток в цепи Напряжения на реактивных элементах где r- характеристическое или волновое сопротивление контура. Поскольку , то , отсюда и происходит название резонанс напряжений. Величина - добротность контура

10 Энергетические соотношения в колебательном контуре Пусть колебательный контур работает на резонансной частоте , тогда . Если в контуре протекает ток , то напряжение на конденсаторе отстает от тока на и равно. Мгновенное значение энергии магнитного и электрического полей, связанных с индуктивностью и емкостью контура:

11 Частотные характеристики последовательного колебательного контура При неизменных E, L, C, R зависимость тока от частоты Безразмерное отношение где называется предельной нормированной частотной характеристикой контура. - фазочастотная характеристика контура.

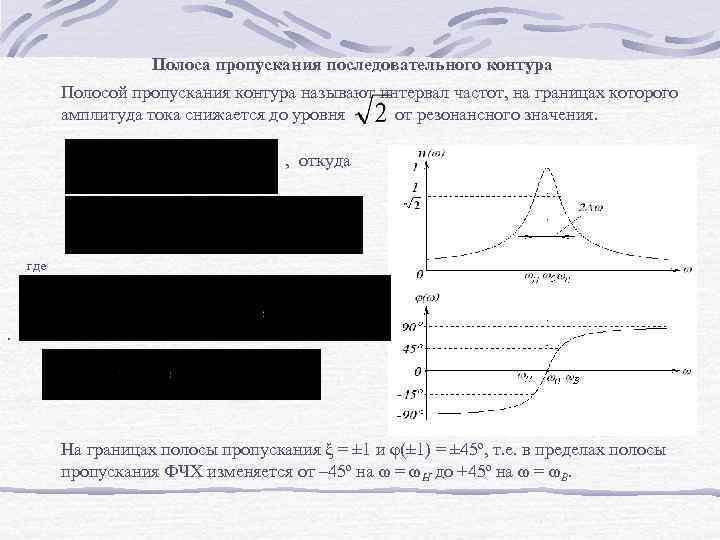Полоса пропускания последовательного контура Полосой пропускания контура называют интервал частот, на границах которого амплитуда тока снижается до уровня от резонансного значения. , откуда где . , На границах полосы пропускания ξ = ± 1 и φ(± 1) = ± 45º, т. е. в пределах полосы пропускания ФЧХ изменяется от – 45º на ω = ωH до +45º на ω = ωB.

Параллельный колебательный контур 12 Если на входных зажимах действует источник с , то и согласно первому закону Кирхгофа На практике контуры составлены из индуктивностей и конденсаторов, имеющих большие добротности, т. е. При ток в индуктивной ветви Этот ток отстает от напряжения на контуре на угол Ток в емкостной ветви Ток опережает напряжение на контуре на угол

13 Очевидно, что ток . Ток в неразветвленной части цепи опережает напряжение на контуре на угол , т. е. реактивная составляющая входного сопротивления имеет емкостный характер. При , . Ток в неразветвленной части цепи отстает от напряжения на контуре на угол , т. е. реактивная составляющая входного сопротивления имеет индуктивный характер. При , . Ток в неразветвленной части цепи совпадает по фазе с напряжением на контуре, т. е. реактивная составляющая входного сопротивления равна нулю. Режим цепи, при котором реактивная составляющая входной проводимости равна нулю, называется резонансом токов.

14 Резонансная частота с учетом и находится из условия равенства нулю реактивной составляющей входной проводимости при определяемой из условия При равенстве активных сопротивлений ветвей или при , что выполняется практически во всем интересующем нас диапазоне частот, , т. е. условия резонанса токов совпадают с условиями резонанса напряжений в последовательном контуре, составленном из тех же элементов L и C.

15 Входные частотные характеристики параллельного колебательного контура Комплексное входное сопротивление контура При , -входное сопротивление последовательного контура, составленного из тех же элементов. На резонансной частоте при Q =100 -200 и r =100 -1000 Ом, к. Ом.

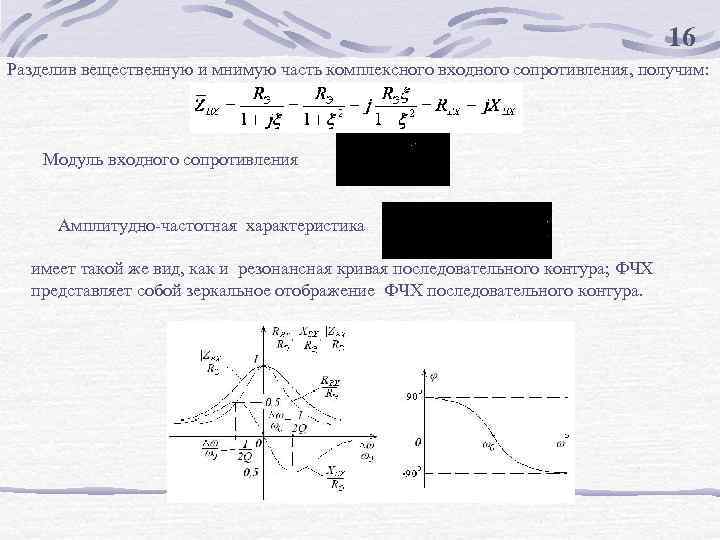16 Разделив вещественную и мнимую часть комплексного входного сопротивления, получим: Модуль входного сопротивления Амплитудно-частотная характеристика имеет такой же вид, как и резонансная кривая последовательного контура; ФЧХ представляет собой зеркальное отображение ФЧХ последовательного контура.

17 Передаточные функции параллельного колебательного контура Комплексные передаточные функции контура по току АЧХ , что аналогично АЧХ последовательного контура при выходном напряжении на емкости. АЧХ , что совпадает с выражением для передаточной функции по напряжению последовательного контура, когда напряжение снимается с индуктивности. При , т. е. ток в контуре в Q раз больше тока в неразветвленной части цепи, поэтому явление резонанса называется резонансом токов.