1 Лекция 5 Дискретные и непрерывные случайные величины

1 Лекция 5 Дискретные и непрерывные случайные величины. Локальная и интегральная теоремы Лапласа. Формула Пуассона. Отклонение частоты от вероятности. Случайные величины. Закон распределения. Математическое ожидание. Дисперсия. Функция распределения. Плотность распределения. Мода и медиана. Квантили. Моменты случайных величин. Асимметрия и эксцесс.

1. Асимптотические формулы для подсчета вероятностей по схеме Бернулли. Такие формулы, называемые асимптотическими, существуют. Среди них наиболее известны локальная и интегральная теоремы Лапласа, теорема Пуассона. 2

3 Приближенную формулу (1) называют локальной формулой Лапласа. Пример 1. Вероятность найти белый гриб среди прочих равна 1/4. Какова вероятность того, что среди 300 грибов белых будет 75?

Использование пакета Maxima Пример 1. Вероятность найти белый гриб среди прочих равна 1/4. Какова вероятность того, что среди 300 грибов белых будет 75? Задаем функцию для решения задачи по локальной теореме Лапласа Вычисляем искомую вероятность. 4

Пример 1. Вероятность найти белый гриб среди прочих равна 1/4. Какова вероятность того, что среди 300 грибов белых будет 75? Используя пакет Maxima эту задачу можно решить по формуле Бернулли Используя пакет Maxima, эту задачу можно решить по формуле Бернулли или локальной теоремы Лапласа. 5

Пусть в условиях примера 1 необходимо найти вероятность того, что белых грибов будет, например, от 70 до 150. В этом случае по теореме сложения вероятность искомого события Вычислить каждое слагаемое можно по локальной формуле Лапласа (1), но большое количество слагаемых делает расчет весьма громоздким. В таких случаях используется следующая теорема. Приближенную формулу (2) называют интегральной формулой Лапласа. Чем больше п, тем точнее эта формула. 6

7

8 Пример 2. В партии из 768 арбузов каждый арбуз оказывается неспелым с вероятностью 1/4. Найти вероятность того, что количество спелых арбузов будет в пределах от 564 до 600. Maxima-программа

9 Пример 3. На факультете насчитывается 1825 студентов. Какова вероятность того, что 1 сентября является днем рождения одновременно четырех студентов факультета? По формуле Бернулли получаем

11 2. Отклонение частоты от вероятности. Пусть проводятся испытания Бернулли с постоянной вероятностью появления события А в каждом из них. Заменяя неравенство равносильным, и применяя интегральную теорему Лапласа, получим: В последнем равенстве воспользовались нечетностью функции Лапласа. Итак, имеем

10

3. Случайные величины. Определение 1. Случайной величиной называется переменная величина, которая в результате испытания принимает одно из своих значений, причем заранее неизвестно, какое именно. Примеры случайных величин: • число очков, выпавших при броске игральной кости; • число появлений герба при 10 бросках монеты; • число выстрелов до первого попадания в цель; • расстояние от центра мишени до пробоины при попадании. Определение 3. Случайная величина называется непрерывной (НСВ), если множество ее возможных значений целиком заполняет некоторый конечный или бесконечный интервал на числовой оси. Наиболее полным, исчерпывающим описанием случайной величины является ее закон распределения. 12

13 Для задания дискретной случайной величины нужно знать все ее возможные значения и вероятности, с которыми принимаются эти значения, т. е. задать ее закон распределения, который может иметь вид таблицы, формулы или графика. Определение 5. Таблица, в которой перечислены все ее возможные значения дискретной случайной величины и соответствующие им вероятности, называется рядом распределения. Для удобства возможные значения дискретной случайной величины располагают в таблицу в порядке их возрастания: (5)

14 Ряд распределения дискретной случайной величины можно изобразить графически в виде полигона или многоугольника распределения вероятностей. Для этого по горизонтальной оси в выбранном масштабе нужно отложить значения случайной величины, а по вертикальной - вероятности этих значений. Соединив эти точки отрезками прямой, получим многоугольник распределения вероятностей.

15 Решение. На оси ОХ откладываем значения 1, 2, 5 и 10, а по оси OY вероятности этих значений. Точки (1; 0, 1), (2; 0, 4), (5; 0, 3), (10; 0, 2) изображают полигон распределения, а ломаная, соединяющая эти точки, - многоугольник распределения вероятностей.

16 4. Математическое ожидание. Ряд распределения полностью определяет дискретную случайную величину. Однако иногда удобнее характеризовать ее с помощью нескольких числовых характеристик, каждая из которых определяет одно из свойств этой случайной величины. Одной из таких числовых характеристик является математическое ожидание. Определение 6. Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие вероятности: Математическое ожидание случайной величины не является случайной величиной, это вполне определенное число. Вероятностный смысл математического ожидания: математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.

17 Свойства математического ожидания: 1) Математическое ожидание константы равно константе: М(С) = С (8) Доказательство: Если рассматривать С как дискретную случайную величину, принимающую только одно значение С с вероятностью р = 1, то М(С) = С·1 = С. 2) Постоянный множитель можно выносить за знак математического ожидания:

18 3) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: Определение 7. Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие значения приняла другая величина. В противном случае случайные величины зависимы. 4) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

19

20 Для вычисления дисперсии существует также формула:

21

22

23

24

25

26

27

28

29

30

31

32

33

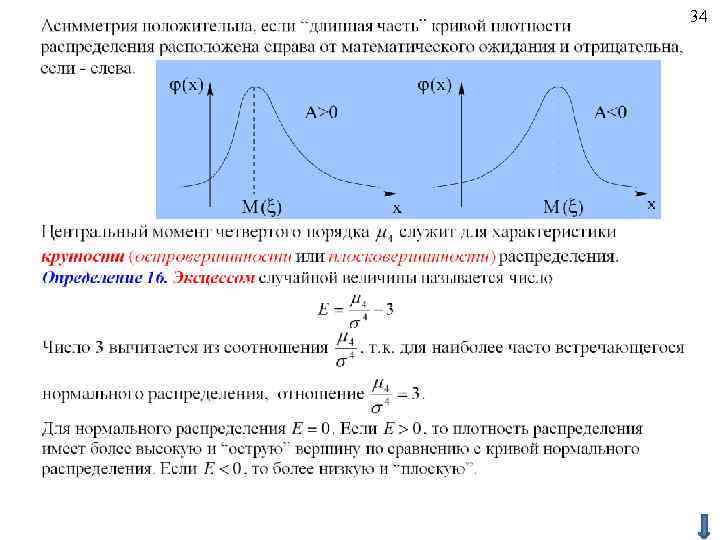34

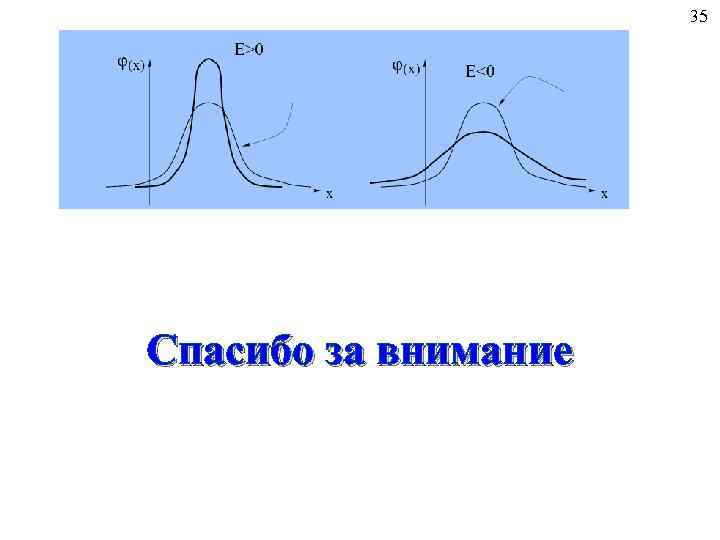35 Спасибо за внимание