Лекция 2.Реш. алг.ур..ppt
- Количество слайдов: 15

1 Лекция 2. ПРИБЛИЖЁННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ В практике инженера наиболее часто возникает потребность в решении алгебраических уравнений. Если порядок уравнения больше 4, то точных решений нет. Здесь следует использовать приближённые методы решения, позволяющие найти корни уравнения с наперёд заданной точностью. Рассмотрим порядок приближённого решения алгебраических уравнений с одним неизвестным. Всякое уравнение с одним неизвестным может быть записано в виде (1) где некоторая функция аргумента. Задача сводится к нахождению значений аргумента , при котором удовлетворяется уравнение (1). Эти значения называются корнями уравнения (1). Решение уравнения распадается на два этапа: 1) Отделение корня уравнения; 2) Уточнение корня уравнения.

2 ОТДЕЛЕНИЕ КОРНЯ УРАВНЕНИЯ Это выделения отрезка, принадлежащего области определения функции , на котором расположен один и только один корень уравнения (1). Границы этого отрезка можно рассматривать как первое приближение искомого значения корня (левая граница – с недостатком, правая – с избытком). Для отделения корня уравнения (1) надо иметь критерий, позволяющий убедиться в том , что, во-первых, на рассматриваемом отрезке имеется корень уравнения (1). А , во-вторых, что этот корень будет единственным на указанном отрезке. Если функция Непрерывна на отрезке значения имеют разные знаки найдётся по крайней мере одна точка т. е. на отрезке , а на концах отрезка её то на этом отрезке , такая, что , найдётся по крайней мере один корень уравнения (1). Геометрически это означает, что если концы графика непрерывной функции находятся по разные стороны оси , то график пересекает ось по крайней мере в одной точке

3 Сформулированные условия не обеспечивают однако единственности корня на рассматриваемом участке. Поэтому для возможности отделения корня уравнения (1) Необходимо наложить на функцию дополнительные условия. Рис. 1 Достаточным дополнительным условием, обеспечивающим единственность корня уравнения (1) на отрезке является требование монотонности функции на этом отрезке. Таким образом, для отделения корня уравнения (1) имеем следующий критерий: если на отрезке функция непрерывна и монотонна, а её значения на концах отрезка имеют разные знаки, то на рассматриваемом отрезке существует один и только один корень уравнения (1).
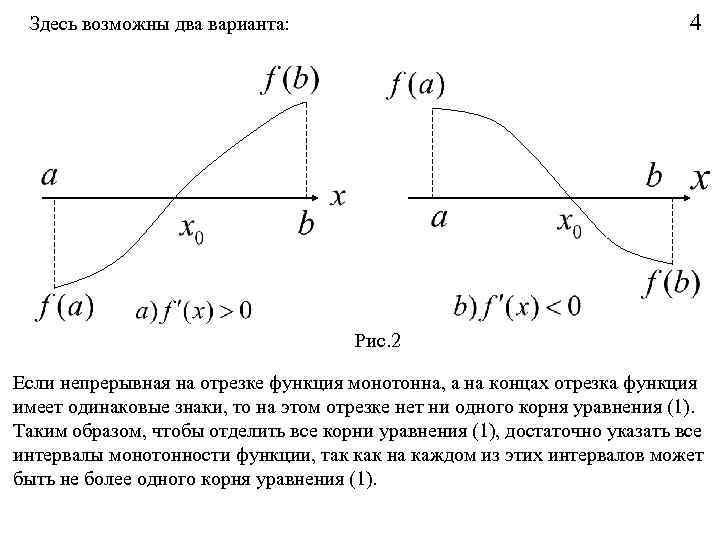
4 Здесь возможны два варианта: Рис. 2 Если непрерывная на отрезке функция монотонна, а на концах отрезка функция имеет одинаковые знаки, то на этом отрезке нет ни одного корня уравнения (1). Таким образом, чтобы отделить все корни уравнения (1), достаточно указать все интервалы монотонности функции, так как на каждом из этих интервалов может быть не более одного корня уравнения (1).
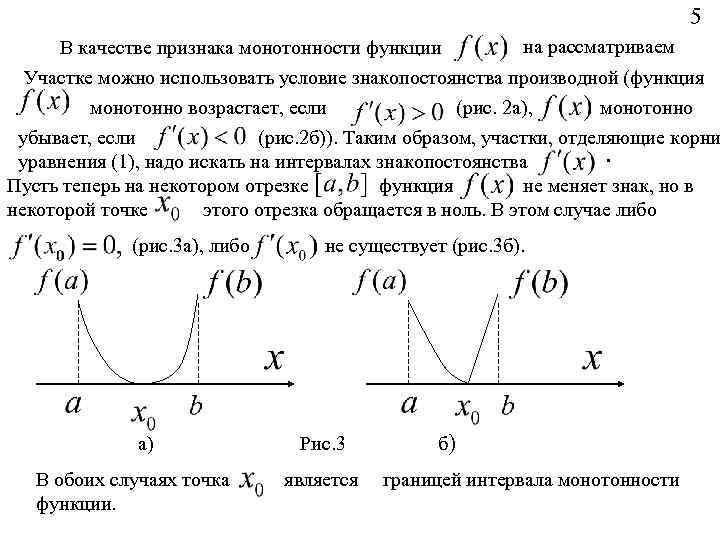
5 на рассматриваем В качестве признака монотонности функции Участке можно использовать условие знакопостоянства производной (функция монотонно возрастает, если (рис. 2 а), монотонно убывает, если (рис. 2 б)). Таким образом, участки, отделяющие корни. уравнения (1), надо искать на интервалах знакопостоянства Пусть теперь на некотором отрезке функция не меняет знак, но в некоторой точке этого отрезка обращается в ноль. В этом случае либо (рис. 3 а), либо а) В обоих случаях точка функции. не существует (рис. 3 б). Рис. 3 является б) границей интервала монотонности

6 Таким образом, задача отделения корней уравнения (1) сводится к задаче отыскания всех нулей функции, точек разрыва производной от функции и перечисления всех её интервалов монотонности. Пример. Отделить корни уравнения Функция и её производная непрерывны на всей числовой оси. Определим интервалы монотонности функции. Для этой цели решим уравнение Его корни Следовательно функция имеет следующие интервалы монотонности Причём, Следовательно интервалы монотонности не содержат корней уравнения, так как функция не меняет знак на этих интервалах. Единственный корень расположен на интервале

7 Будем считать отделение корня завершённым, если указан конечный интервал, содержащий единственный корень уравнения. В данном случае достаточно проверить знак функции в целочисленных точках интервала Имеем . Выберем точки Следовательно, единственный действительный корень данного уравнения лежит на отрезке. Поставленная задача отделения решена. Дальнейшее сужение границ найденного промежутка это уже новая задача – задача об уточнении значения корня. Часто бывает удобным заменить уравнение эквивалентным ему уравнением вида где -некоторые функции переменной , которые мы будем Считать непрерывными и дифференцируемыми практически во всех точках из области их определения. Геометрически найти корень уравнения (1) это значит найти точку пересечения Графика функции с осью . Найти корень уравнения (2) - это
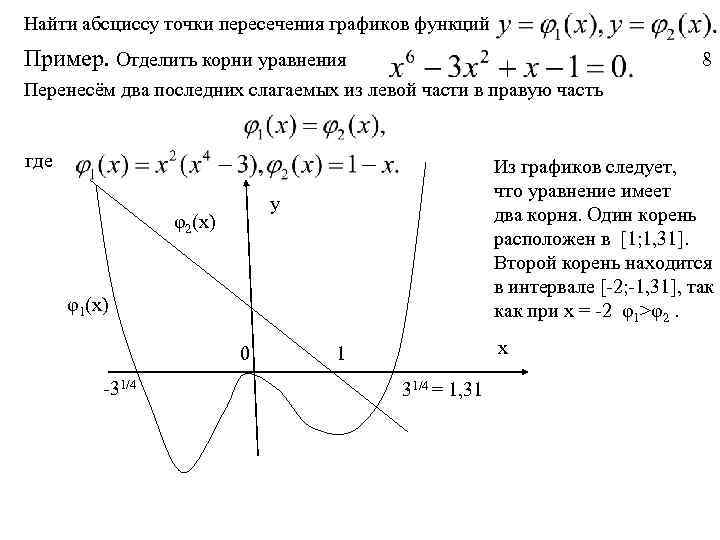
Найти абсциссу точки пересечения графиков функций Пример. Отделить корни уравнения 8 Перенесём два последних слагаемых из левой части в правую часть где Из графиков следует, что уравнение имеет два корня. Один корень расположен в [1; 1, 31]. Второй корень находится в интервале [-2; -1, 31], так как при x = -2 φ1>φ2. y φ2(x) φ1(x) 0 -31/4 x 1 31/4 = 1, 31

Абсолютная и относительная погрешность корня Пусть -точное значение корня, а 9 - его приближённое значение. Истинной погрешностью приближённого значения корня будем называть разность. В большинстве случаев точное значение корня Неизвестно, а потому и неизвестна истинная погрешность его приближённого Значения. Однако, как правило, можно указать число, оценивающее сверху абсолютную величину истинной погрешности приближённого значения. Будем называть это число абсолютной погрешностью приближённого значения корня Относительной погрешностью приближённого значения корня в этом случае называется отношение Пусть нам удалось отделить корни уравнения и на отрезке отделён корень В качестве приближённого значения корня может быть принято любое значение из отрезка. Вопрос в том, какова будет допущена при этом ошибка.

Так как точное значение корня неизвестно, то и неизвестно можем ввести абсолютную погрешность приближённого значения При этом, если в качестве значения взято или соответственно (с недостатком) или . Но мы , взяв 10 , то мы имеем (с избытком). Уточнение значения корня уравнения Из последней формулы следует, что чем меньше отрезок, внутри которого находится точное значение корня , тем меньше абсолютная погрешность его приближённого значения. Поэтому, для уточнения значения корня надо уменьшить отрезок, внутри которого содержится точное значение корня. Процесс последовательного уменьшение отрезков, содержащих искомый корень, называется уточнением корня. Для того чтобы уменьшить отрезок, содержащий корень уравнения, достаточно выбрать некоторую точку внутри отрезка , так чтобы искомое значение корня содержалось либо в отрезке , либо в отрезке. Существую несколько способов уточнения корня, отличающихся способом выбора точки внутри отрезка.

11 Метод хорд Для выбора точки графика функции А) на отрезке заменим на этом отрезке дугу стягивающей её хордой (см. рис. 3) Б) В) Г) Рис. 3 Уравнение прямой, проходящей через точки на всех вариантах рис. 3 имеет вид при , Так как на прямой то из уравнения прямой получим выражение для координаты (2)

Координата есть граница нового более короткого интервала, содержащего 12 искомое точное значение корня. Однако координата может быть как левой, так и правой границей нового интервала. Из рис. 3 следует, что если произведение (рис. 3 а, б) координата есть правая граница нового интервала, содержащего. Если произведение (рис. 3 в, г) , то координата есть левая граница нового интервала, содержащего. Пример. Методом хорд уточнить корень уравнения на отрезке Здесь отделённый . Так как на отрезке то точка границей нового отрезка , содержащего а значение вычисляем по формуле (2) Выбираем значение с недостатком перескочить через точное значение корня отрезка выбираем отрезок. будет левой , причём , чтобы во всяком случае не. Таким образом, в качестве нового

13 Метод касательных (метод Ньютона) Обозначим через один из концов отрезка проходящих, через точку имеет вид Если . Уравнение пучка прямых, , то это уравнение есть уравнение касательной к функции в точке. Так как при то из этого уравнения получаем формулу для расчёта точки пересечения касательной с осью (3) Из концов отрезка или в качестве котором останется внутри отрезка будет выполняться, если а) б) надо выбрать тот конец, при. Можно показать, что это условие (4) в) Рис. 4 г)

Пример. 14 Методом касательных уточнить корень уравнения отделённый на отрезке . Здесь Так как на отрезке то касательную надо проводить на на правом конце отрезка, т. е. получим Подставляя это значение в (3), Ситуация в этом случае соответствует рис. 4 б. Поэтому значение надо взять с избытком чтобы не перейти через точное значение корня. Таким образом, для нового уточнённого отрезка Итерационные методы Отделив корень уравнения, а затем применяя методы уточнения корня, можно получить приближённое значение корня с любой наперёд заданной точностью. Действительно, обозначив исходный отрезок , применив один из методов уточнения корня, получим более узкий отрезок. Применив затем указанный процесс к отрезку , получим ешё более узкий отрезок и т. д. , пока не будет получен отрезок , длина которого не будет соответствовать заданной точности.

15 Описанный процесс называется итерационным. Построение итерационного процесса по методу хорд и касательных осуществляется по уже полученным формулам с учётом итераций. Если на исходном отрезке то, применяя метод касательных, будем последовательно уточнять левую границу отрезка по формуле или применяя метод хорд будем последовательно уточнять правую границу отрезка по формуле Если на исходном отрезке то, применяя метод хорд, будем последовательно уточнять левую границу отрезка по формуле или применяя метод касательных будем последовательно уточнять правую границу по формуле При каждом из двух условий можно чередовать уточнение левой и правой границы отрезка, чередуя применение метода хорд и метода касательных. Процесс надо продолжать до тех пор, пока длина отрезка не станет меньше заданной абсолютной погрешности приближённого значения корня
Лекция 2.Реш. алг.ур..ppt