1 Концепции устойчивого развития нашей цивилизации 1 1

1. Концепции устойчивого развития нашей цивилизации 1. 1. Глобальные проблемы цивилизации Глобальными называются проблемы, возникающие в результате объективного развития общества, создающие угрозу всему человечеству и требующие для своего решения объединенных усилий всего мирового сообщества. К главнейшим глобальным проблемам относятся: 1. Демографическая проблема, связанная с очень быстрым ростом численности человечества. В 1830 г. на Земле проживал 1 млрд. человек; в 1930 г. – 2; в 1960 г. – 3; в 1975 г. – 4; в 1987 г. – 5; в 2000 г. – 6 млрд. человек. Авторы одной из глобальных моделей развития М. Месарович и Э. Пестель в 1974 г. писали: «Мир болен раком, и этот рак - человек» . 2. Продовольственная проблема, связанная с недоеданием, неполноценным питанием и голодом людей. По данным Продовольственной и сельскохозяйственной организации ООН (ФАО) на Земле систематически голодают около 800 млн. человек и около 1, 5 млрд. испытывают недостаток в пище. 3. Энергетическая проблема, связанная с недостатком ископаемого углеводородного топлива на планете. При современных объемах энергопотребления запасов топлива хватит примерно на 150 лет, в том числе нефти – на 35 лет, газа – на 50 лет, каменного угля – на 425 лет (точка отсчета – 1990 г. ). 4. Сырьевая проблема связана в первую очередь с ограниченностью запасов минерального сырья. Весьма ограниченной является технически доступная и экономически эффективная часть многих важных видов полезных ископаемых (нефть как сырье для нефтехимии, руды, сырье для производства удобрений).

5. Проблема обеспечения экономического роста государств, главным образом, слаборазвитых стран третьего мира. Основой экономического роста является расширенное промышленное воспроизводство, а его показатели – объем промышленной продукции на душу населения. 6. Проблема замены природных экосистем на агроценозы, представляющие собой деградированные экосистемы, неспособные к самовоспроизведению и саморегуляции. Площади, занятые агроценозами между 600 с. ш. и 600 ю. ш. , т. е. в зоне устойчивого земледелия, составляют в настоящее время свыше 23% всей площади суши. 7. Проблема деградации и потери пахотных земель. Деградация почв – это падение их плодородия за счет усиленной эксплуатации и недостаточного внесения удобрений. В настоящее время в мире в умеренной стадии деградации находятся 46% почв сельхозугодий, а в сильной и крайней степени – 16%. Потери пахотных земель связаны с эрозией, вторичным засолением и отчуждением сельхозугодий для несельскохозяйственного использования. 8. Проблема урбанизации. Рассматривают три основные характеристики процесса урбанизации: рост площади городов, увеличение доли городского населения и приобретение сельской местностью черт, присущих городам. К 2020 г. ожидается, что площадь городов займет свыше 20% всей жизнепригодной территории суши. 9. Проблема эмиссионного и фоново-параметрического загрязнения атмосферы, гидросферы, педосферы и почво-грунтов. По оценке ООН в 1990 г. на каждого из живущих на планете людей приходилось до 3 т. выбросов загрязняющих веществ. Для Земли эта величина достигает 2 ∙ 1010 т / год.

10. Проблема улучшения качества жизни и увеличение ожидаемой продолжительности жизни населения. Качеством жизни называется совокупность условий, обеспечивающих или не обеспечивающих комплекс здоровья человека – личного и общественного, т. е. соответствие среды жизни человека его потребностям. Качество жизни зависит от уровня питания, медицинского обслуживания, загрязнения среды обитания и других факторов. Интегральным показателем качества жизни является ожидаемая продолжительность жизни населения. 11. Предотвращение войн, ликвидация терроризма и преступности. Для достижения этих целей необходимо выделение значительных средств из государственных бюджетов и отвлечение средств от социальных и природных программ. Нерешенные глобальные проблемы ставят под угрозу существование нашей цивилизации. Для предотвращения глобальной катастрофы требуется разработка специальной стратегии поведения человеческого общества. Такая стратегия получила название концепции развития цивилизации. Концепцией вообще называется система взглядов на те или иные явления и процессы. В настоящее время существуют две концепции развития: биосферная и ресурсная.

1. 2. Биосферная концепция развития цивилизации была предложена в 90 -х годы ХХ века В. Г. Горшковым и К. Я. Кондратьевым [Кондратьев, 1996]. Эта концепция входит в предметную область геоэкологии. В. И. Вернадский указывал, что антропогенные воздействия на биосферу соизмеримы с геологическими силами, сформировавшими облик Земли. Устойчивое развитие, согласно биосферной концепции, определяется как «улучшение жизни людей в условиях устойчивой биосферы, т. е. в условиях, когда хозяйственная деятельность не порождает превышение допустимого порога возмущения биосферы, или когда сохраняется такой объем естественной среды, который способен обеспечить устойчивость биосферы с включенной в неё хозяйственной деятельностью человека» . В основе биосферной концепции лежит теория естественной биологической регуляции. Сущность этой теории состоит в том, что биосфера и составляющие её экосистемы обладают мощным механизмом стабилизации природной среды. Такой механизм называется гомеостазом биосферы и экосистем. Гомеостаз обеспечивает близкие к оптимальным условия существования организмов. Трофические и конкурентные взаимодействия организмов обеспечивают высокую степень замкнутости круговоротов углерода, азота, фосфора и других элементов. Это позволяет поддерживать стабильность среды обитания организмов. Циркулирующие в круговоротах массы веществ обычно намного порядков превосходят уровни внешних возмущений. Это способствует компенсации неблагоприятных изменений среды обитания организмов. При этом возвращение природной среды к прежнему состоянию происходит в масштабах времени порядка 103 - 104 лет. Очевидно, что существует пороговая величина возмущения среды обитания, при превышении которой нарушается устойчивость биосферы. Поэтому главным в теории естественной биологической регуляции является установление порога устойчивости биосферы.

Авторы биосферной концепции считают, что биосфера обладает свойством устойчивости, т. е. способностью компенсировать любые возмущения, вызываемые хозяйственной деятельностью человека, до тех пор, пока потребление человеком продукции биоты не достигает 1%. Остальные 99% продукции биота затрачивает на стабилизацию среды обитания. Таким образом, в соответствии с биосферной концепцией устойчивого развития, критическим является только один вид деятельности человека – потребление продукции биоты. Существующие оценки показывают, что порог допустимого возмущения природной среды был превышен еще в начале ХХ века. Об этом говорят, в частности, оценки замкнутости глобального круговорота углерода и уровни потребления продукции биоты в начале века. В наши дни биота уже не в состоянии обеспечивать глобальную устойчивость биосферы. Хотя сохранившиеся естественные участки биосферы воздействуют в направлении возврата к состоянию устойчивости, их мощность недостаточна. Потребление 1% первичной продукции биосферы связано с затратами энергии порядка 1012 Вт (1 Тера Вт). Чем выше потребление первичной продукции, и, следовательно, чем больше энергетическая мощность страны, тем больший вклад она вносит в разрушение биосферы. Поэтому в качестве интегрального показателя антропогенной дестабилизации окружающей среды авторы концепции предлагают использовать энергетическую мощность народного хозяйства конкретной страны. Вводится понятие коэффициента антропогенного давления Кс, определяемого выражением К C = Э C / Э Z , (1. 1) где ЭC ─ энергетическая мощность хозяйства страны (района, региона), приходящаяся на единицу площади; ЭZ ─ среднеглобальная мощность на единицу площади.

Из формулы (1. 1) следует, что величина коэффициента антропогенного давления по миру в целом равна единице. Современные данные международного экономического и экологического мониторингов [Глоб. экологич. перспектива] позволяют рассчитать коэффициент антропогенного давления для 211 государств мира на два срока: 1980 и 1995 гг. и таким образом не только определить степень антропогенного давления каждого государства на биосферу на конкретные даты, но и выявить тенденции развития этого процесса. Эта работа в качестве дипломного проекта была выполнена студенткой кафедры геоэкологии и природопользования СПб. ГУ Л. А. Мищенко. Данные о величинах KC стран показывают, что экстремальные значения удельной антропогенной нагрузки на биосферу характерны для развитых в экономическом отношении стран мира, таких как: Германия (KC = 66, 8), Франция (39, 2), Бельгия (37, 0), Нидерланды (36, 8), Люксембург (31, 2), Япония (27, 3), Великобритания (19, 3), Израиль (11, 6), Италия (11, 0) и др. Однако, не меньшую роль, особенно в последнее десятилетие XX столетия играют некоторые страны «третьего мира» , которые называют «маленькими драконами» : Виргинские острова (США) (KC = 240, 2), Бахрейн (197, 7), Гуам (58, 8), Тринидад и Табаго (29, 1), Барбадос (19, 4), Пуэрто-Рико (17, 7), Катар (15, 3) и ряд других. Эти государства могут быть отнесены к разряду «экологически неблагоприятных» стран. Однако это не свидетельствует однозначно об их «экологическом неблагополучии» . Обращает на себя внимание то обстоятельство, что значения коэффициента антропогенной нагрузки таких стран, как Соединенные Штаты Америки, Россия, Канада, Китай, Индия, Австралия, сравнительно не велики (4, 7; 0, 5; 1, 8; 1, 5; 0, 3 соответственно). Связано это с тем, что коэффициент антропогенной нагрузки характеризует не абсолютную, а удельную энергетическую мощность страны.

В последние десятилетия для мирового экономического разделения труда характерен перенос экономически развитыми странами экологически опасных, энерго-, ресурсо- и трудоемких производств на территории развивающихся стран. Это ведет к значительному увеличению антропогенной нагрузки в развивающихся странах и ее относительному снижению в экономически развитых. Согласно принятого социально-экологического районирования [Глоб. экологич. перспектива], государства мира объединены в 22 района, которые, в свою очередь, интегрированы в 6 регионов. Степень антропогенного давления на биосферу экономики каждого из районов и регионов иллюстрируют таблицы 1 и 2.

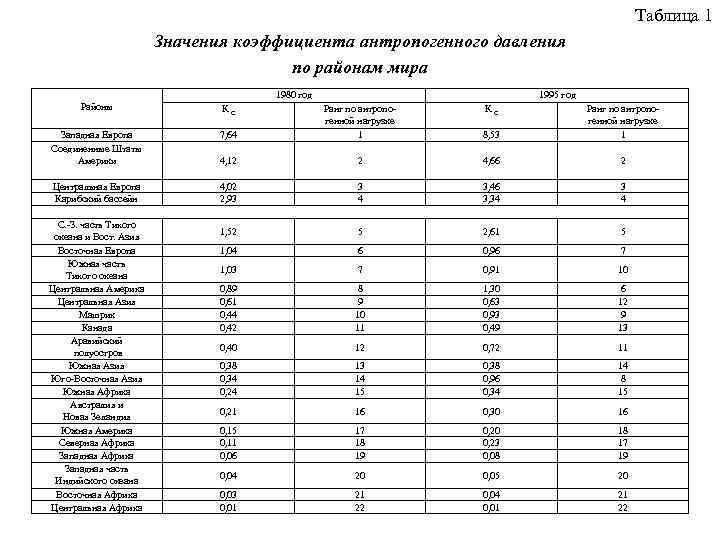Таблица 1 Значения коэффициента антропогенного давления по районам мира Районы 1980 год К C 1995 год Западная Европа Соединенные Штаты Америки 7, 64 Ранг по антропогенной нагрузке 1 К C 8, 53 Ранг по антропогенной нагрузке 1 4, 12 2 4, 66 2 Центральная Европа Карибский бассейн 4, 02 2, 93 3 4 3, 46 3, 34 3 4 1, 52 5 2, 61 5 1, 04 6 0, 96 7 1, 03 7 0, 91 10 0, 89 0, 61 0, 44 0, 42 8 9 10 11 1, 30 0, 63 0, 93 0, 49 6 12 9 13 0, 40 12 0, 72 11 0, 38 0, 34 0, 24 13 14 15 0, 38 0, 96 0, 34 14 8 15 0, 21 16 0, 30 16 0, 15 0, 11 0, 06 17 18 19 0, 20 0, 23 0, 08 18 17 19 0, 04 20 0, 05 20 0, 03 0, 01 21 22 0, 04 0, 01 21 22 С. -З. часть Тихого океана и Вост. Азия Восточная Европа Южная часть Тихого океана Центральная Америка Центральная Азия Машрик Канада Аравийский полуостров Южная Азия Юго-Восточная Азия Южная Африка Австралия и Новая Зеландия Южная Америка Северная Африка Западная часть Индийского океана Восточная Африка Центральная Африка

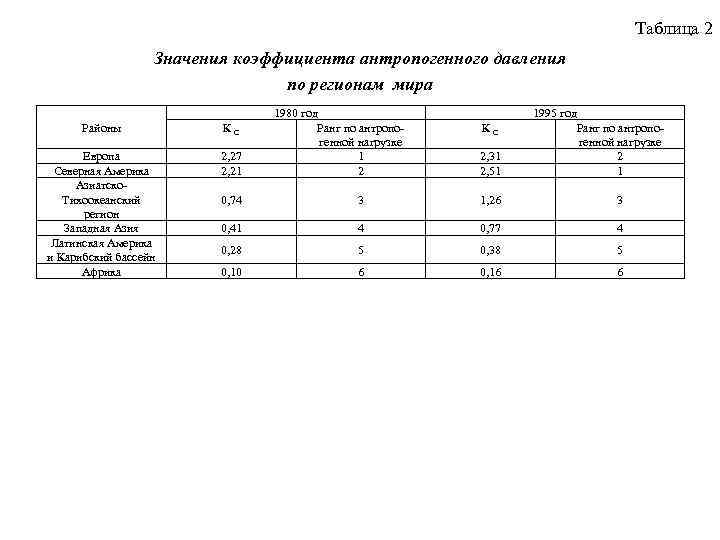Таблица 2 Значения коэффициента антропогенного давления по регионам мира Районы Европа Северная Америка Азиатско. Тихоокеанский регион Западная Азия Латинская Америка и Карибский бассейн Африка К C 2, 27 2, 21 1980 год Ранг по антропогенной нагрузке 1 2 К C 2, 31 2, 51 1995 год Ранг по антропогенной нагрузке 2 1 0, 74 3 1, 26 3 0, 41 4 0, 77 4 0, 28 5 0, 38 5 0, 10 6 0, 16 6

Таблицы иллюстрируют существенные различия в энергетической мощности районов и регионов мира и, как следствие этого, - различия в значениях интегрального показателя антропогенной дестабилизации окружающей среды К C. Из таблиц следует, что регионами, наиболее дестабилизирующими состояние биосферы, являются Европа и Северная Америка, которым принадлежат первые два ранга в классификации территорий по степени антропогенной нагрузки. При этом наибольший вклад в дестабилизацию на Европейском континенте вносит Западная Европа, а в Северной Америке – Соединенные Штаты. Третье место в рейтинге стабильно занимает Азиатско-Тихо-океанский регион. Ведущую роль в нем играют районы: Северо-За-падная часть Тихого океана и Восточная Азия, Юго-Восточная Азия. Причем, если первый из них в течение 15 лет стабильно занимает 5 место, то второй поднял свой рейтинг с 14 до 8 места. Наименьшей энерговооруженностью характеризуются регионы: Латинская Америка и Карибский бассейн, Африка. Если африканскому континенту стабильно принадлежит последний рейтинг как в региональной, так и в районной классификации, то с регионом Латинская Америка и Карибский бассейн не все так просто. Карибский район на протяжении исследуемых 15 лет стабильно занимает 4 место, которое свидетельствует о весьма высоком уровне энерговооруженности этого района и большом вкладе его в дестабилизацию состояния биосферы. Входящий в этот регион район Центральная Америка тоже занимает не самые низкие позиции (8 и 6). А вот район Южная Америка, занимаюший 17 и 18 позиции в рейтинге, также как и регион, в который он входит, по праву относится к наименее энерговооруженным.

«Экологически неблагоприятные» страны прежде всего разрушили свои природные экосистемы. Показателем степени такого разрушения является доля естественных природных ландшафтов от общей площади страны. Так, например, в Нидерландах, Германии, Японии, Корейской республике естественные ландшафты полностью отсутствуют. Оставшиеся нетронутыми участки биосферы суши и Мировой океан принимают на себя нагрузку по стабилизации природной среды. В северном полушарии нетронутые участки биосферы суши располагаются, главным образом, на территории России, Канады, Китая и Алжира. Коэффициент антропогенного давления для России равен 0, 75, для Канады – 0, 49, для Китая – 0, 92 (1, 77), а для Алжира – 0, 11 (0, 22). В России и Канаде сохранились высокопродуктивные лесные сообщества (800 и 642 млн. га соответственно). В Китае и Алжире ненарушенными остаются малопродуктивные высокогорные территории и пустыни. Остальные страны северного полушария имеют на порядок меньшую площадь ненарушенных антропогенным влиянием территорий. В южном полушарии два государства вносят наибольший вклад в стабилизацию природной среды за счет сохранившихся в естественном состоянии экосистем суши. Это Бразилия, для которой коэффициент антропогенного давления Кс = 0, 2, а площадь нетронутых земель S = 273 млн. га, и Австралия, для которой Кс = 0, 27, S = 251 млн. га. При этом в Австралии неосвоенными являются малопродуктивные пустыни, а в Бразилии – высокопродуктивные влажные тропические леса. В целом на суше, за вычетом площади Антарктиды, в естественном состоянии сохранилось только 39% территории.

Помимо констатации величины интегрального показателя антропогенной дестабилизации окружающей среды в различных странах, районах и регионах мира существенный интерес представляет анализ временной изменчивости коэффициента антропогенного давления KC. моменты времени t 1 и t 2 соответственно. Введем понятие показателя прироста коэффициента антропогенного давления, определяемого выражением E = ∆KC / KC , 1 ∆t , (1. 2) где ∆KC = KC , 2 - KC , 1 – приращение коэффициента за интервал времени ∆t; KC , 1 и KC , 2 – значения коэффициента антропогенного давления в моменты времени t 1 и t 2 соответственно. Переходя к пределу при ∆t → 0, выражение (1. 2) запишем в виде lim E = lim ∆KC / KC , 1 ∆t. (1. 3) ∆t → 0 При этом показатель прироста E → ε , где ε – норма, присущая приросту коэффициенту антропогенного давления, а выражение (1. 3) примет вид d KC /dt = ε KC . (1. 4) Это уравнение хорошо известно в экологии. Таким уравнением описывается экспоненциальный рост численности популяции в неограниченной среде (закон Мальтуса), процесс распада радионуклидов, процессы минерализации растворенных органических соединений и т. д. В этом проявляется свойство изоморфизма уравнений, позволяющее применять их для описания различных по своей природе явлений.

Разделяя переменные в уравнении (1. 4) d KC / KC = ε dt (1. 5) и интегрируя его, получаем ln KC = ε t + B. (1. 6) Обозначая через KC , 0 начальное значение коэффициента антропогенного давления (при t = 0), можно определить постоянную интегрирования B = ln KC , 0. Отсюда ln (KC / KC , 0) = ε t (1. 7) или KC = KC , 0 еεt . (1. 8) Это выражение является аналитическим решением уравнения (1. 4). В предположении, что норма прироста коэффициента антропогенного давления ε = const, т. е. при отсутствии факторов, ограничивающих рост энерговооруженности района, из (1. 8) следует, что коэффициент антропогенного давления является экспоненциальной функцией времени. График такой функции можно назвать кривой энергетического потенциала района. Она характеризует максимальную антропогенную нагрузку, которая возможна лишь при отсутствии ограничений на энергетические ресурсы. В таблице 3 приводятся динамические характеристики интегрального показателя антропогенной дестабилизации биосферы.

Из таблицы видно, что наибольший прирост коэффициента антропогенного давления имеет район Северо-Западной части Тихого океана и Восточной Азии. Второй и третий рейтинги принадлежат Западной Европе и Юго-Восточной Азии соответственно. Соединенные Штаты Америки занимают по этому показателю лишь четвертое место. Последние 21 и 22 места в рейтинге занимают районы Южной части Тихого океана и Центральной Европы соответственно. Используя формулу (1. 8) и приведенные в таблице 3 значения показателя прироста коэффициента антропогенного давления E, можно оценить значение коэффициента KC на ту или иную дату при условии, что E = const. Будем полагать, что последнее условие соблюдается до 2010 г. Предвычисленные на эту дату значения интегрального показателя антропогенной дестабилизации биосферы представлены в таблице 4.

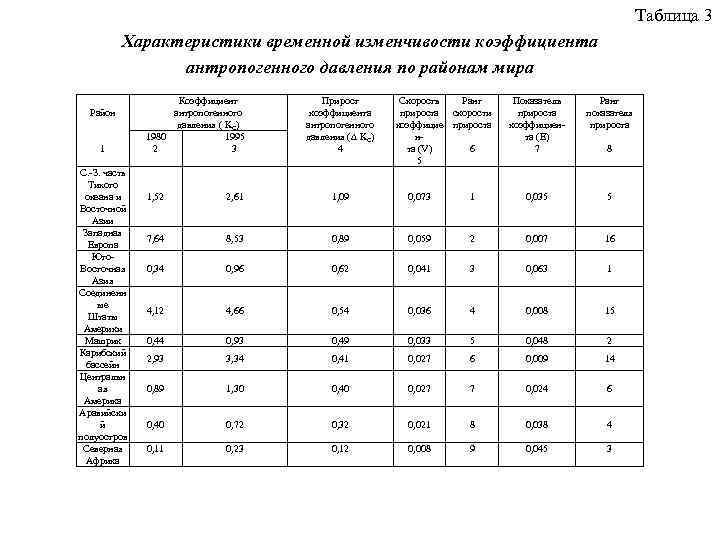Таблица 3 Характеристики временной изменчивости коэффициента антропогенного давления по районам мира Район 1 С. -З. часть Тихого океана и Восточной Азии Западная Европа Юго. Восточная Азия Соединенн ые Штаты Америки Машрик Карибский бассейн Центральн ая Америка Аравийски й полуостров Северная Африка Коэффициент антропогенного давления ( KC) 1980 1995 2 3 Прирост коэффициента антропогенного давления (∆ KC) 4 Скорость Ранг прироста скорости коэффицие прироста н та (V) 6 5 Показатель прироста коэффициента (E) 7 Ранг показателя прироста 8 1, 52 2, 61 1, 09 0, 073 1 0, 035 5 7, 64 8, 53 0, 89 0, 059 2 0, 007 16 0, 34 0, 96 0, 62 0, 041 3 0, 063 1 4, 12 4, 66 0, 54 0, 036 4 0, 008 15 0, 44 0, 93 0, 49 0, 033 5 0, 048 2 2, 93 3, 34 0, 41 0, 027 6 0, 009 14 0, 89 1, 30 0, 40 0, 027 7 0, 024 6 0, 40 0, 72 0, 32 0, 021 8 0, 038 4 0, 11 0, 23 0, 12 0, 008 9 0, 045 3

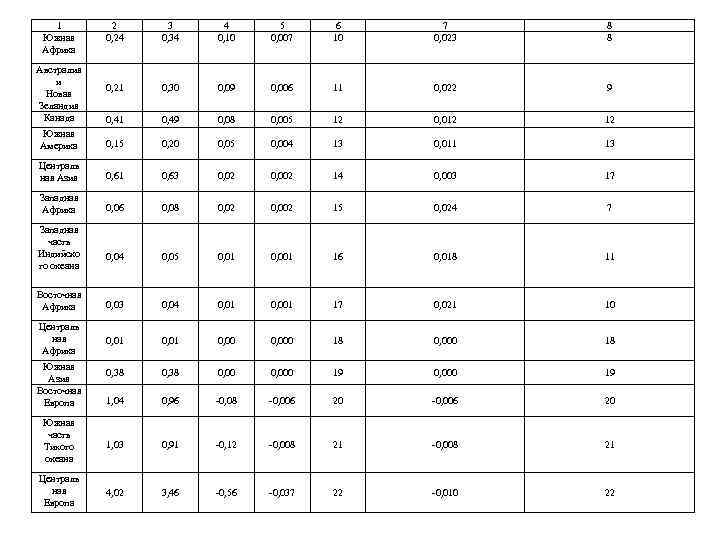1 Южная Африка 2 0, 24 3 0, 34 4 0, 10 5 0, 007 6 10 7 0, 023 8 8 0, 21 0, 30 0, 09 0, 006 11 0, 022 9 0, 41 0, 49 0, 08 0, 005 12 0, 012 12 Южная Америка 0, 15 0, 20 0, 05 0, 004 13 0, 011 13 Централь ная Азия 0, 61 0, 63 0, 02 0, 002 14 0, 003 17 Западная Африка 0, 06 0, 08 0, 02 0, 002 15 0, 024 7 0, 04 0, 05 0, 01 0, 001 16 0, 018 11 Восточная Африка 0, 03 0, 04 0, 01 0, 001 17 0, 021 10 Централь ная Африка 0, 01 0, 000 18 0, 38 0, 000 19 1, 04 0, 96 -0, 08 -0, 006 20 Южная часть Тихого океана 1, 03 0, 91 -0, 12 -0, 008 21 Централь ная Европа 4, 02 3, 46 -0, 56 -0, 037 22 -0, 010 22 Австралия и Новая Зеландия Канада Западная часть Индийско го океана Южная Азия Восточная Европа

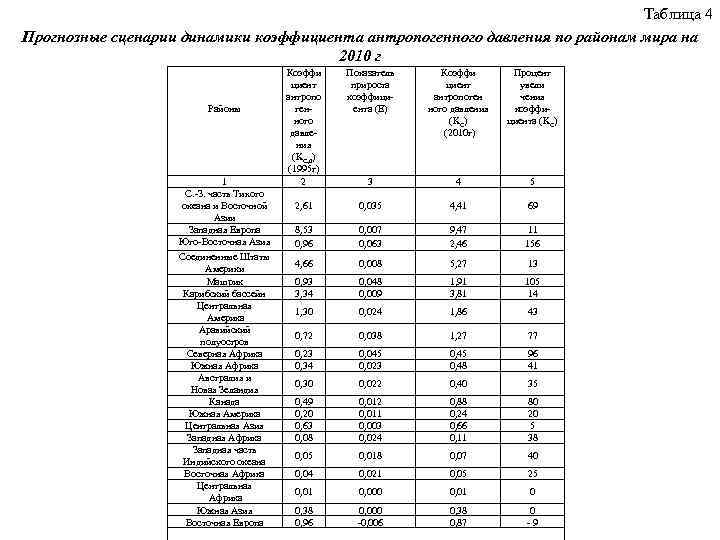Таблица 4 Прогнозные сценарии динамики коэффициента антропогенного давления по районам мира на 2010 г Районы 1 С. -З. часть Тихого океана и Восточной Азии Западная Европа Юго-Восточная Азия Соединенные Штаты Америки Машрик Карибский бассейн Центральная Америка Аравийский полуостров Северная Африка Южная Африка Австралия и Новая Зеландия Канада Южная Америка Центральная Азия Западная Африка Западная часть Индийского океана Восточная Африка Центральная Африка Южная Азия Восточная Европа Коэффи циент антропо генного давления (KC, 0) (1995 г) 2 Показатель прироста коэффициента (Е) Коэффи циент антропоген ного давления (KC) (2010 г) Процент увели чения коэффициента (KC) 3 4 5 2, 61 0, 035 4, 41 69 8, 53 0, 96 0, 007 0, 063 9, 47 2, 46 11 156 4, 66 0, 008 5, 27 13 0, 93 3, 34 0, 048 0, 009 1, 91 3, 81 105 14 1, 30 0, 024 1, 86 43 0, 72 0, 038 1, 27 77 0, 23 0, 34 0, 045 0, 023 0, 45 0, 48 96 41 0, 30 0, 022 0, 40 35 0, 49 0, 20 0, 63 0, 08 0, 012 0, 011 0, 003 0, 024 0, 88 0, 24 0, 66 0, 11 80 20 5 38 0, 05 0, 018 0, 07 40 0, 04 0, 021 0, 05 25 0, 01 0, 000 0, 01 0 0, 38 0, 96 0, 000 -0, 006 0, 38 0, 87 0 - 9

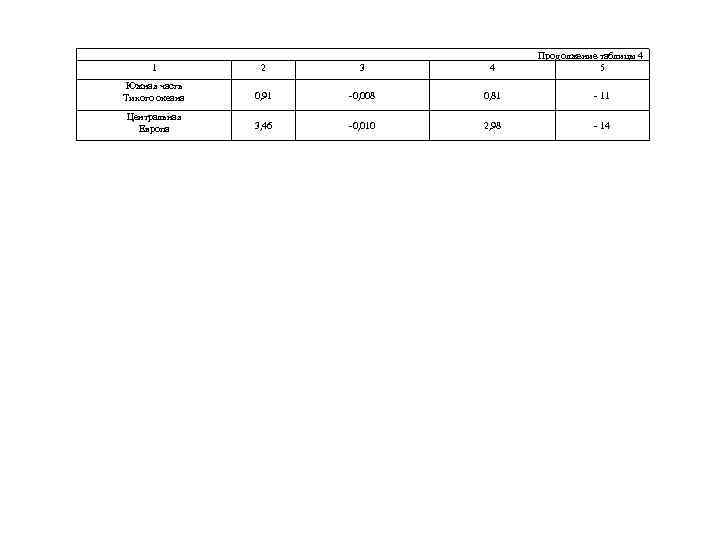Продолжение таблицы 4 5 1 2 3 4 Южная часть Тихого океана 0, 91 -0, 008 0, 81 - 11 Центральная Европа 3, 46 -0, 010 2, 98 - 14

В последнее десятилетие человечество непосредственно использовало 6 – 8% первичной продукции, генерированной биосферой. Таким образом, допустимый предел потребления ресурсов биосферы превышен почти на порядок величины. При этом в мире насчитывается около 1, 5 млрд. недоедающих людей и примерно 800 млн жителей Земли голодает. Кроме того, 30 – 32% годовой продукции «девственной» биоты человечество потребляет косвенным путем: за счет замены естественных биоценозов агроценозами, урбанизации и опустынивания территорий и т. д. , используя для этого мощность в 10 ТВт, получаемую за счет ископаемого топлива. Наша цивилизация использует очень большие мощности для своего экономического развития. На каждого жителя Земли ежегодно в среднем расходуется около 20 тонн сырья. На его переработку расходуется около 800 тонн воды. Первичная продукция биоты, изымаемая цивилизацией из пищевого рациона консументов и деструкторов, не участвует в регуляции и обеспечении устойчивости природных экосистем и биосферы. Таким образом, пишет К. Я. Кондратьев [1996], существующая цивилизация, не обеспечивая хотя бы сносного существования всего населения планеты, оставляет лишь 60% фотосинтетической продукции для питания многих миллионов видов организмов суши, которые, находясь в высокоскоррелированных естественных сообществах, обеспечивали устойчивость окружающей среды на протяжении миллиардов лет. При существующих в настоящее время темпах развития цивилизации и роста населения Земли уже через 30 – 40 лет человечество будет непосредственно потреблять 12 – 16% продукции, генерируемой биосферой. Кроме того, 60 – 64% годовой продукции биоты оно будет потреблять косвенным путем, используя ископаемое топливо.

Таким образом, прямо или косвенно человечество будет использовать около 80% годовой первичной продукции биосферы. Это означает, что с начала ХХ века мир находится в состоянии экологического кризиса, постепенно перерастающего в экологическую катастрофу. Последние десятилетия ХХ века показали, что требуется выработка долгосрочной стратегии и срочных практических мер по обеспечению устойчивого развития цивилизации. Если бы человечество вернулось в пределы хозяйственной ёмкости биосферы, т. е потребляло бы 1% годовой первичной продукции биоты, то экологические проблемы исчезли бы автоматически. В этом случае прекратились бы антропогенные изменения природной среды. Для обеспечения устойчивого развития цивилизации авторы биосферной концепции предлагают принять ряд мер. Главнейшая из них – стабилизация, а затем сокращение численности населения планеты. Но Мир сегодня не готов к этому. В 1994 г. в Каире состоялась конференция ООН по народонаселению и развитию. Она показала, что групповые, национальные и конфессиональные интересы пока преобладают над общечеловеческими. Они даже подавляют чувство страха перед экологической катастрофой. В связи с тем, что по разным причинам пока невозможно перейти к глобальной стратегии сокращения численности населения, авторы биосферной концепции указывают другое решение проблемы. Оно состоит в том, что сохранившиеся ненарушенные экосистемы должны стать центрами восстановления того объема естественных территорий, который необходим для обеспечения устойчивости биосферы. Как уже отмечалось, в настоящее время на суше осталось только 39% ненарушенных хозяйственной деятельностью территорий. Они должны быть сохранены и расширены. Восстановление естественных экосистем занимает сотни лет. Однако их регулирующие способности восстанавливаются значительно быстрее.

В качестве условия успешной реализации стратегии сохранения и расширения естественных экосистем авторы указывают на необходимость единства действий всех государств в этом направлении. Кроме того, они считают также необходимым введение налога за использование биосферы. Налог должен быть пропорционален коэффициенту антропогенного давления на биосферу, и учитывать естественную продуктивность используемой для хозяйственной деятельности территории по отношению к среднеглобальной продуктивности. Полученные средства должны перераспределяться в пользу тех стран, где сохранились значительные массивы высокопродуктивных естественных экосистем и, где наращивание восстановленных экосистем будет наиболее эффективным. Именно такой политике следует Киотский протокол, направленный на регулирование выбросов в атмосферу двуокиси углерода. Расчеты показывают, что при сохранении современной мощности хозяйственной деятельности для стабилизации глобальных изменений биосферы необходимо сокращение площади нарушенных человеком земель с 61% до 38%. Таким образом, человечество должно сократить хозяйственно освоенную площадь суши на 32 млн. км 2. Это при условии, что на выводимой из-под активной хозяйственной деятельности территории первичная продукция будет близка к среднеглобальной, например, в зоне умеренных широт. При восстановлении естественных экосистем в зоне тропических лесов, характеризующихся высокой первичной продуктивностью, площади выводимой из-под активной хозяйственной деятельности территории, могут быть уменьшены. Заметим, однако, что предлагаемый авторами биосферной концепции выход из тупиковой ситуации возможен только при одновременном и пропорциональном сокращении численности населения планеты.

В противном случае вывод из активной хозяйственной деятельности территорий, занятых агроценозами и урбанизированных территорий приведет к безработице, к еще большему увеличению числа недоедающих и голодающих в мире, и, как следствие этого, ─ к социальным взрывам в разных частях планеты.

1. 3. Ресурсная концепция устойчивого развития цивилизации Эта концепция возникла в первой половине 70 -х годов ХХ века в результате анализа серии модельных сценариев развития нашей цивилизации, полученных с помощью глобальных моделей развития Дж. Форрестером, Д. Медоузом, М. Месаровичем и Э. Пестелем и другими исследователями. Ресурсная концепция входит в предметную область социальной экологии как науки, изучающей взаимодействие человеческого общества с окружающей средой, включающей в себя не только природную, но и созданные самим человеком экономическую, социальную, политическую и культурную среды. Устойчивое развитие, согласно ресурсной концепции, это развитие, удовлетворяющее потребности настоящего времени, но не ставящее под угрозу способность будущих поколений удовлетворять свои собст венные потребности. Вторая конференция ООН по окружающей среде и развитию в Рио-де-Жанейро в 1992 г. и Международная конференция по народонаселению в Каире в 1994 г. еще раз подтвердили неразрывную связь социально-экономического развития, демографии и состояния природной среды. Положенные в основу ресурсной концепции глобальные и региональные модели развития представляют собой имитационные модели глобальной или региональных социально-экологических систем, ориентированные на прогноз развития (деградации) биосферы и цивилизации на Земле в целом или в отдельных крупных регионах. Конечной целью моделирования является разработка стратегии предотвращения глобальной социально-экономической и экологической катастрофы.

Моделью называется мысленно представляемая или материально реализованная система, способная отображать и воспроизводить объект исследования и замещать его так, что изучение модели дает новое представление об объекте исследования. Среди различных типов моделей особое место занимают имитационные модели. Имитационная модель, по определению академика Н. Н. Моисеева, это реализованная на ЭВМ математическая модель сложной системы, построенная на грани современных коллективных представлений науки об изучаемом объекте. Идея создания глобальных моделей развития принадлежит профессору Массачусетского технологического института Джею Форрестеру. Ему же принадлежит и приоритет в реализации этой идеи, воплощенной в первых моделях глобального развития «Мир-1» и «Мир-2» Идея глобального моделирования возникла не «вдруг» . Она была подготовлена предшествующим ходом развития математической экономики, демографии, экологии и системного анализа. Заслуга Дж. Форрестера состоит, прежде всего, в том, что он синтезировал достижения этих наук, и обратил их на создание принципиально нового направления системных исследований – глобалистики. Созданию моделей «Мир-1» и «Мир-2» предшествовали работы Дж. Форрестера по имитационному моделированию деятельности корпораций и промышленных предприятий и динамики развития городов. Эти модели, так же как и модели глобального развития, построены на принципах системной динамики – метода изучения поведения сложных систем с нелинейными обратными связями. Этот метод был разработан под руководством Дж. Форрестера в Массачусетском технологическом институте.

Свою концепцию глобального моделирования Дж. Форрестер изложил на заседании комиссии палаты представителей конгресса США следующим образом: «Мой основной тезис состоит в том, что человеческий мозг не способен постигнуть, как функционируют социальные системы. Наши социальные системы принадлежат к классу, который мы называем сложными нелинейными системами со многими цепями обратной связи. На протяжении долгой истории эволюции для человека не было никакой необходимости познавать такие системы до самого недавнего времени. Эволюционный прогресс не наделил нас мыслительной способностью, нужной для правильной интерпретации динамического поведения таких систем, элементом которых мы стали сами. Наши социальные системы несравненно более сложны и трудны для понимания, чем наши технические системы. Почему же мы в таком случае не моделируем социальные системы прежде, чем пытаемся внедрять новые законы и правительственные программы? Я настаиваю на том, что мы обладаем достаточными знаниями для создания полезных моделей социальных систем. И, напротив, не обладаем достаточными знаниями для того, чтобы проектировать наиболее эффективные социальные системы непосредственно, не прибегая предварительно к экспериментальному конструированию этих моделей. И я убежден, опираясь на накапливающиеся данные, что правильное использование социального моделирования может привести к значительно лучшим системам, законам и программам» [Дадаян, 1989]. По своей структуре модель «Мир-2» достаточно проста. Это точечная (пространственно-однородная) модель, представляющая собой систему обыкновенных дифференциальных уравнений пятого порядка, дополненную рядом алгебраических соотношений и графически заданных функций, устанавливающих связь между компонентами модели. Моделировалось поведение пяти компонентов: численности населения Земли; капитала (основных фондов); доли сельскохозяйственного капитала (сельскохозяйственных фондов); невозобновляемых природных ресурсов; загрязнения планеты.

Задача решалась на временном интервале: 1900 – 2100 гг. При этом имеющаяся информация о динамики изучаемых компонентов в период: 1900 – 1970 гг. – использовалась для идентификации параметров модели. Расчеты показали, что при современных темпах развития производства загрязнение окружающей среды к 2050 г. в 7 -8 раз превысит уровень 1970 года. Начиная с 20 -х – 30 -х годов XXI века рост численности населения Земли прекратится, а в течение последующих 75 лет население Земли сократится в 1, 5 – 2 раза. Невозобновляемые природные ресурсы к 2100 г. будут в значительной степени исчерпаны, их останется менее 1/3 от современного уровня запасов. Уменьшение запасов природных и трудовых ресурсов приведет в середине XXI века к существенному сокращению мирового выпуска промышленной продукции. Общее снижение уровня развития цивилизации уменьшит антропогенную нагрузку на окружающую среду. Ее загрязнение к 2100 г. существенно снизится. Но это не приведет к повторному витку расцвета цивилизации (рис. 1. 1). Работы по системной динамике, проводимые в Массачусетском технологическом институте, привлекли внимание Римского клуба – влиятельной общественной филантропической организации, провозгласившей своей целью стимулирование анализа и прогнозирования процессов развития Мира. Римский клуб не только поддержал исследования Дж. Форрестера, но и финансировал ряд выполненных затем исследований по глобальному моделированию, в частности, программы «Пределы роста» Д. Медоуза и «Стратегия выживания» Месаровича - Пестеля. Глобальная модель «Мир-3» была сформулирована и реализована интернациональной группой во главе с учеником Форрестера – Д. Медоуза. Эта модель, так же как и «Мир-2» , относится к классу точечных моделей, но ее внутренняя структура значительно сложнее. Моделируемыми компонентами являются:

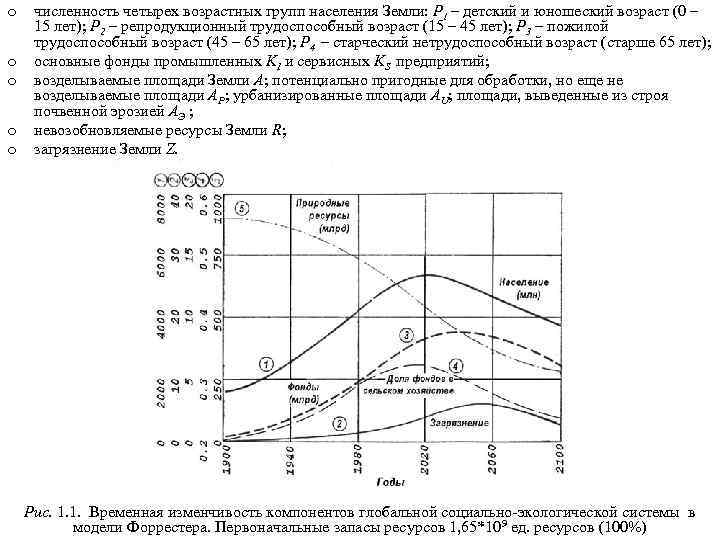o o o численность четырех возрастных групп населения Земли: P 1 – детский и юношеский возраст (0 – 15 лет); P 2 – репродукционный трудоспособный возраст (15 – 45 лет); P 3 – пожилой трудоспособный возраст (45 – 65 лет); P 4 – старческий нетрудоспособный возраст (старше 65 лет); основные фонды промышленных KI и сервисных KS предприятий; возделываемые площади Земли А; потенциально пригодные для обработки, но еще не возделываемые площади АР; урбанизированные площади АU; площади, выведенные из строя почвенной эрозией АЭ ; невозобновляемые ресурсы Земли R; загрязнение Земли Z. Рис. 1. 1. Временная изменчивость компонентов глобальной социально-экологической системы в модели Форрестера. Первоначальные запасы ресурсов 1, 65*109 ед. ресурсов (100%)

В модель входят 12 основных и 16 вспомогательных дифференциальных уравнений, а также ряд алгебраических соотношений и эмпирических функций, характеризующих интенсивности взаимодействий между основными компонентами. Также как и в модели «Мир-2» задача решалась на временном интервале: 1900 – 2100 гг. Результаты моделирования оказались очень близкими к выводам, сделанным Дж. Форрестером. Они показали, что при сохранении современных тенденций развития вслед за бурным ростом цивилизации в конце XX – начале XXI века должна последовать катастрофа, связанная с ростом загрязнения Земли и истощением природных ресурсов, и выражающаяся в существенном спаде промышленного и сельскохозяйственного производства и значительном снижении численности населения Земли (рис. 1. 2. а ).

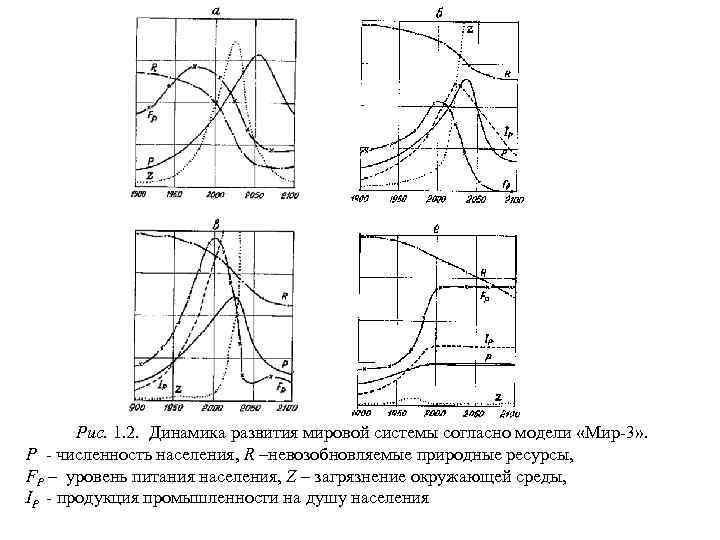Рис. 1. 2. Динамика развития мировой системы согласно модели «Мир-3» . P - численность населения, R –невозобновляемые природные ресурсы, FP – уровень питания населения, Z – загрязнение окружающей среды, IP - продукция промышленности на душу населения

С целью поиска возможных путей выхода из этой катастрофы Д. Медоуз реализовал ряд модельных сценариев. Был рассмотрен вариант с практически неограниченными запасами природных ресурсов. Катастрофа не предотвращается, а лишь несколько сдвигается во времени и наступает в связи с чрезмерным загрязнением окружающей среды (рис. 1. 2. б). В варианте с совершенным контролем над загрязнением катастрофы также не удалось избежать, она наступила из-за недостатка продуктов питания. В варианте с неограниченными природными ресурсами и удвоенной продуктивностью сельскохозяйственного производства катастрофа наступает из-за слишком высоких уровней численности населения и загрязнения окружающей среды (рис. 1. 2. в). В варианте с абсолютным контролем над рождаемостью, определяющим демографическую модель простого воспроизводства населения, катастрофа наступает в связи с чрезмерным расширением производства и истощением природных ресурсов (рис. 1. 2. г). Анализ модельных сценариев привел Д. Медоуза к выводу о том, что ни одна из предохранительных мер, взятая в отдельности, не сможет предотвратить катастрофы. Поэтому были реализованы сценарии, в которых предохранительные меры принимаются в комплексе. Расчеты показали, что избежать упадка нашей цивилизации во второй половине XXI в. можно только путем незамедлительного введения следующего комплекса мер: 1) рождаемость должна обеспечивать лишь простое воспроизводство населения, а его численность должна быть стабилизирована на уровне 1945 г. ; 2) индустриальное развитие должно быть стабилизировано на уровне 1980 г. ; 3) потребление ресурсов на душу населения Земли не должно превышать 1/8 от уровня 1970 г. 4) время жизни основных производственных фондов должно быть увеличено в 1, 5 раза; 5) удельная генерация загрязнения должна быть уменьшена до ¼ уровня 1970 г.

Состояние социально-экологической системы, в которой реализуются все перечисленные меры, Д. Медоуз назвал состоянием глобального равновесия. Актуальность тематики, нетривиальность и дискуссионность выводов Дж. Форрестера и Д. Медоуза послужили стимулами к дальнейшему развитию глобального моделирования. В последующие несколько лет в различных национальных центрах и научных организациях была начата разработка серии проектов глобального моделирования: «Стратегия выживания» , Латиноамериканская модель глобального развития, «Новый взгляд на развитие» и др. В них авторы пытались учесть основное замечание, высказанное в адрес Дж. Форрестера и Д. Медоуза, - чрезмерную, по мнению критиков, схематизацию системы-оригинала, выразившуюся в моделировании «Мира в целом» . Поэтому разработчики новых моделей отказались от использования точечных моделей и перешли к реализации резервуарных (блочных) моделей. Модель М. Месаровича и Э. Пестеля, заказанная Римским клубом, охватывает 10 регионов, выделенных с учетом уровня их экономического развития (Северная Америка, Западная Европа, Япония, Австралия и Южная Америка; СССР и страны Восточной Европы; Латинская Америка; Ближний Восток и Северная Африка; Тропическая Африка; Юго-Восточная Азия; Китай). Население каждого из регионов дифференцировано на 85 одногодичных возрастных групп. В модели выделены 19 категорий промышленного капитала, две разновидности сельскохозяйственного капитала, пять категорий капитала, занятого в энергетике. Отдельно рассматривается капитал, занятый в рыболовстве, в горнодобывающей промышленности. При моделировании уровня питания населения учитывается валовое производство 26 различных пищевых продуктов, в число которых входят не только различные виды зерновых, овощей и мяса, но и мед, яйца и т. д. В нормальных условиях каждый из 10 региональных блоков развивается почти независимо от других. Однако, когда наступает кризис, между блоками возникают очень сильные взаимодействия и характер их поведения изменяется до неузнаваемости. Моделирование развития цивилизации осуществляется на 50 -тилетнем временном интервале. При этом рассматриваются четыре альтернативных сценария.

В базовом сценарии современные отношения между развитыми и развивающимися регионами сохраняются и в будущем. Принимается гипотеза о том, что к концу XX в. в результате осуществления контроля над рождаемостью будет достигнуто демографическое равновесие, и рост численности населения Земли прекратится. Результаты расчетов по этому сценарию показали, что к 2025 г. экономический разрыв между развитыми и развивающими странами существенно возрастет. Например, соотношение по среднедушевому доходу для стран Латинской Америки составит 8 : 1, а для стран Юго. Восточной Азии – 20 : 1. Авторы модели утверждают, что катастрофа не произойдет, если к 2025 г. это соотношение для стран Латинской Америки составит 3 : 1, а для стран Юго. Восточной Азии – 5 : 1. Это может быть достигнуто в результате добровольного перераспределения экономических ресурсов между регионами Земли. При равномерной, начиная с 1975 г. , помощи развивающимся странам – второй модельный сценарий – ее объем к 2025 г. должен составить 7 500 млрд. $. Если же развитые страны начнут осуществлять такую помощь с 2000 г. , то ее объем должен составить 10 700 млрд. $. Таким образом, собственная медлительность будет стоить развитым странам 3 200 млрд. $. Возвращаясь к методическим вопросам глобального моделирования, отметим, что оценка модели М. Месаровича и Э. Пестеля неоднозначна. Многие считают, что она излишне детализирована и усложнена. Авторы «Глобального доклада президенту США о перспективах на 2000 год» дают следующую оценку этой модели: «Вероятно, найдется немного людей, которые разобрались в модели настолько, чтобы на основе того, что она подает на выход, вынести суждение о причинно-следственной связи между поведением мира, отображаемого моделью, и ее структурой… Ее структура чрезвычайно сложна. Настолько, что требуются недели, если не месяцы, чтобы либо понять ее, либо принять на веру… Сделать выводы из анализа модели Месаровича-Пестеля затруднительно… Очень трудно сказать, какие выводы были заранее вмонтированы в модель, а какие получены в результате ее реализации» (Цитируется по монографии С. В. Дадаяна [1989]). Дальнейшее развитие методов глобального моделирования пошло по двум направлениям. За рубежом акцент делается на разработку экономических глобальных моделей, а в СССР развивается геоэкологическое направление глобалистики.

Особое место среди работ экономического направления занимает проект «Будущее мировой экономики» , разработанный по заданию ООН группой специалистов во главе с Василием Леонтьевым. В этом проекте мировая экономическая система агрегирована в 15 регионов, объединяющих 171 государство. Модель построена на основе разработанного В. Леонтьевым метода межотраслевого анализа – метода анализа затрат выпуска продукции, и относится к классу резервуарных моделей. Для каждого из 15 регионов моделируется 45 секторов экономики. Отдельно рассматриваются 22 отрасли обрабатывающей промышленности, строительства, 4 сектора сельскохозяйственного производства, сферы торговли и услуг, транспорта и связи. Моделируется загрязнение окружающей среды восьмью видами загрязнителей, и рассматриваются пять способов ее очистки. Межрегиональные связи моделируются в виде потока капитала и экспортноимпортного обмена сорока видами товаров и услуг. В литературе отмечается, что разработчики модели «Будущее мировой экономики» преднамеренно переопределили ее. Число переменных в модели существенно превышает число уравнений, которые используются для их определения. Это, по мнению разработчиков, обеспечивает значительное число степеней свободы и существенно сказывается на характере получаемых результатов. Моделирование проводилось на период до 2000 г. по восьми альтернативным сценариям развития мировой экономики с различными гипотезами о будущем изменении валового продукта, занятости населения, инвестиций, платежного баланса, внешней торговли, затрат на борьбу с загрязнениями окружающей среды и т. д. Не будем рассматривать здесь результаты моделирования по этим восьми сценариям, отсылая интересующегося читателя к работе В. Леонтьева.

Завершая обзор проектов глобальной экономической динамики, необходимо сказать о системе ЛИНК, разработанной под руководством лауреата Нобелевской премии Л. Клейна в США. Это система разрабатываемых независимо друг от друга различных по структуре и размерам эконометрических моделей стран и регионов мира, которые объединяются в единую Мировую модель посредством субмодели международной торговли. В систему ЛИНК входят модели экономики США (207 уравнений), Канады (183 уравнения), Франции (32 уравнения), Великобритании (226 уравнений), Италии (104 уравнения), Швеции (113 уравнений), Финляндии (114 уравнений) и т. д. Всего свыше 20 региональных моделей. Система ЛИНК предназначена для экономических прогнозов с заблаговременностью до трех лет.

2. Алгоритм модели глобального развития «Мир – 2» 2. 1. Системно-динамический метод Дж. Форрестера В основе системно-динамического метода, разработанного в Массачусетском технологическом институте, лежит балансовый подход. Предполагается, что сложная система может быть структурно представлена в виде совокупности резервуаров, через каждый из которых протекает свой вид жидкости. Количество жидкости ci, содержащейся в i-м резервуаре, является фазовой переменной и в каждый момент времени t определяется разностью υ+i – υ-i скоростей (темпов) ее прихода (υ+i) и расхода (υ-i): dci / dt = υ+i – υ-i, i =1, 2, …, n. (2. 1) Уравнения (2. 1) формально не объединены в единую систему, так как не задан пока конкретный вид функций, определяющих скорости υ+i и υ-i. Эти скорости зависят от переменных системы ci. Таким образом, уравнения (2. 1. ) объединяются в единую систему вида: d ci / d t = f(c 1, c 2, …, cn ; t) (i = 1, 2, …, n) , (2. 2) ci | t=0 = (ci)0 , (2. 3) где ci - компонент (фазовая переменная) социально-экологической системы, являющийся функцией других компонентов и времени t; (ci)0 – значение компонента ci в начальный момент времени t 0. Если система (2. 2) не замкнута, то переменные ci зависят от внешних воздействий. Зависимости между переменными обычно не линейны и могут быть заданы не только аналитически, но и таблично. Система дифференциальных уравнений решается численным методом на ЭВМ для заранее определенных диапазонов изменения времени, начальных данных и других параметров, определяющих поведение системы.

Моделирование выполняется в несколько этапов. На первом этапе осуществляется формулировка вербальной модели системы. Она включает в себя определение цели моделирования, основных переменных модели, временного интервала моделирования. На этом же этапе определяется перечень параметров модели, диапазоны их изменения, начальные условия и другие исходные данные. Заканчивается первый этап построением так называемой причинной диаграммы, которая указывает, какие переменные и их сочетания влияют на каждую переменную системы и в какую сторону (увеличения или уменьшения). При этом обнаруживаются петли обратных связей, имеющиеся в системе. Вторым этапом является математическое описание модели системы. Для его получения сначала строится так называемая потоковая диаграмма, соответствующая причинной диаграмме, построенной на первом этапе. Потоковая диаграмма представляет собой связанную стрелками совокупность обозначений резервуаров, скоростей входных и выходных потоков через каждый из резервуаров, априорных аналитических соотношений и графических (табличных) зависимостей. На этом же этапе записываются дифференциальные уравнения модели в окончательной форме. На третьем этапе моделирования производится численное решение на ЭВМ задачи Коши для системы дифференциальных уравнений модели, сравнение результатов с известными данными, характеризующими поведение моделируемой системы (идентификация модели), выявление параметров, к изменению которых модель наиболее чувствительна. В результате оценивается пригодность модели для прогностических целей. В случае не адекватного описания исследуемой системы имитационной моделью процедура ее создания повторяется с учетом выявленных недостатков.

Для пояснения сказанного рассмотрим простой пример – моделирование роста популяции кроликов без учета возрастной структуры популяции, ограниченности занимаемой ею площади и изменчивости пищевого рациона. Считается, что численность кроликов Р, которая является фазовой переменной, увеличивается с ростом их рождаемости В и убывает с увеличением смертности D. Рождаемость зависит от численности кроликов и от пищевого рациона кролика FP = F/P, где F – количество пищи (например, морковок), съедаемых кроликами за интервал времени Δt. Смертность зависит от численности популяции кроликов и от среднего времени их жизни τ = const. Начальную численность популяции обозначим через Р 0. Причинная диаграмма изменчивости численности популяции кроликов представлена на рис. 2. 1. На ней стрелками указаны взаимосвязи между переменной Р и параметрами модели. Видно, что имеются три петли обратной связи (В – Р, Р – D, P – FP и В). Таков результат первого этапа. Рис. 2. 1 Причинная диаграмма простейшей модели роста популяции кроликов

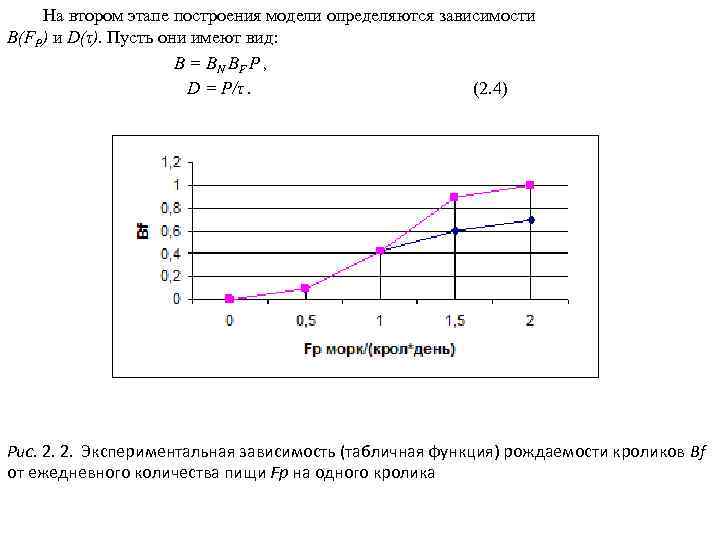На втором этапе построения модели определяются зависимости В(FP) и D(τ). Пусть они имеют вид: B = BN BF P , D = P/τ. (2. 4) Рис. 2. 2. Экспериментальная зависимость (табличная функция) рождаемости кроликов Bf от ежедневного количества пищи Fp на одного кролика

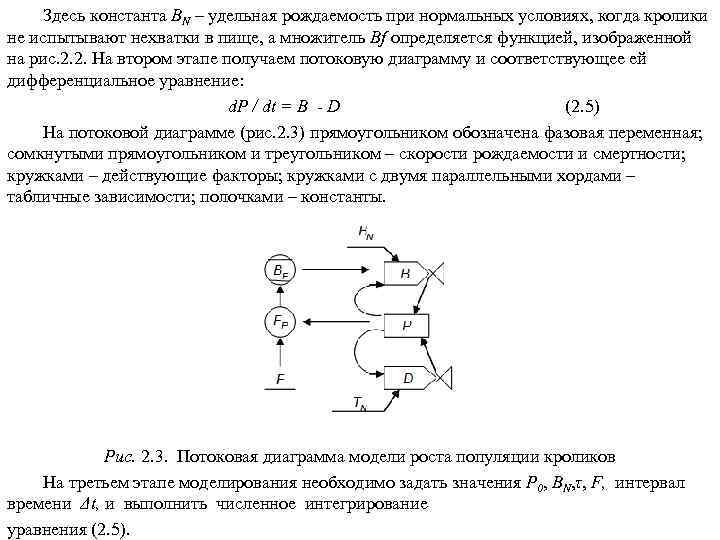Здесь константа BN – удельная рождаемость при нормальных условиях, когда кролики не испытывают нехватки в пище, а множитель Bf определяется функцией, изображенной на рис. 2. 2. На втором этапе получаем потоковую диаграмму и соответствующее ей дифференциальное уравнение: d. P / dt = B - D (2. 5) На потоковой диаграмме (рис. 2. 3) прямоугольником обозначена фазовая переменная; сомкнутыми прямоугольником и треугольником – скорости рождаемости и смертности; кружками – действующие факторы; кружками с двумя параллельными хордами – табличные зависимости; полочками – константы. Рис. 2. 3. Потоковая диаграмма модели роста популяции кроликов На третьем этапе моделирования необходимо задать значения Р 0, BN, τ, F, интервал времени Δt, и выполнить численное интегрирование уравнения (2. 5).

2. 2 Структура и уравнения глобальной модели Дж. Форрестера Компонентами системы являются: Р – население (численность людей, населяющих Землю); К – капитал (основные фонды предприятий); Х – доля сельскохозяйственного капитала (доля основных фондов сельского хозяйства от общего количества основных фондов К); R – ресурсы (невозобновляемые природные ресурсы Земли); Z – загрязнение Земли. Единицей капитала К считается условная величина – капитал, приходящийся на душу населения в начальный момент времени t 0. Доля сельскохозяйственного капитала Х – безразмерная величина. Она определяется как отношение сельскохозяйственного капитала к общему капиталу. За единицу ресурсов R принимается годовое потребление ресурсов на душу населения в момент времени t 0. За единицу загрязнения Z принята условная величина – загрязнение, приходящаяся на душу населения в момент времени t 0.

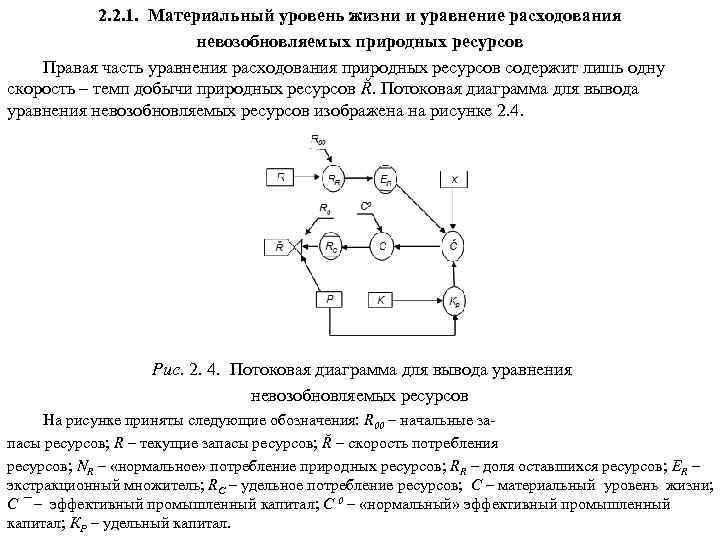2. 2. 1. Материальный уровень жизни и уравнение расходования невозобновляемых природных ресурсов Правая часть уравнения расходования природных ресурсов содержит лишь одну скорость – темп добычи природных ресурсов Ř. Потоковая диаграмма для вывода уравнения невозобновляемых ресурсов изображена на рисунке 2. 4. Рис. 2. 4. Потоковая диаграмма для вывода уравнения невозобновляемых ресурсов На рисунке приняты следующие обозначения: R 00 – начальные запасы ресурсов; R – текущие запасы ресурсов; Ř – скорость потребления ресурсов; NR – «нормальное» потребление природных ресурсов; RR – доля оставшихся ресурсов; ER – экстракционный множитель; RC – удельное потребление ресурсов; С – материальный уровень жизни; С ¯ – эффективный промышленный капитал; С 0 – «нормальный» эффективный промышленный капитал; КР – удельный капитал.

Начальные запасы невозобновляемых природных ресурсов R 00. Это относительная величина. За единицу запасов природных ресурсов принята их добыча в 1970 г. в расчете на душу населения Земли. Считается, что запасов ресурсов при скорости их добычи, которая была в 1970 г. , хватит на 250 лет. Очевидно, что это очень приблизительная оценка. Численность населения Земли в 1970 г. составляла 3, 6 млрд. человек. Произведем простой расчет: (1 ед. ресурсов) ∙ (3, 6 млрд. человек) ∙ (250 лет) = 9000 млрд. ед. ресурсов. Таким образом R 00 = 900 ∙ 109 единиц природных ресурсов. (2. 6) Текущие запасы ресурсов R. Это один из компонентов социально-экологической системы, характеризующих ее состояние. Запасы природных ресурсов связаны только с одним потоком – уменьшающей их скоростью потребления Ř. Текущие запасы определяются путем численного интегрирования системы дифференциальных уравнений глобальной модели развития. Размерность запасов ресурсов R – единицы ресурсов. Скорость потребления ресурсов Ř. определяется произведением трех сомножителей: численности населения Р, «нормального» потребления природных ресурсов NR и удельного потребления ресурсов RC: Ř = Р ∙ RO ∙ RC (С) [ед. рес. / год]. (2. 7) «Нормальное» потребление природных ресурсов RO. Эта постоянная величина определяется как одна единица ресурсов, используемых на душу населения Земли за год. В качестве эталонного принят 1970 г. Таким образом, RO является среднемировой скоростью потребления ресурсов в 1970 г. и вводится в выражение (2. 7) для предания его правой части размерности скорости RO = 1 [ед. рес / чел. ∙ год]. (2. 8)

Удельное потребление ресурсов RС = RС (С) является безразмерной величиной и задается графической (табличной) функцией от аргумента С – материального уровня жизни населения. Рис. 2. 5. Зависимость удельного потребления ресурсов RC от материального уровня жизни С Выход кривой на плато аргументируется тем, что с ростом материального уровня жизни удельное потребление ресурсов уменьшается, поскольку часть капиталовложений направляется на образование и научные исследования в области разработки и внедрения ресурсосберегающих технологий в народное хозяйство. Рисунок 2. 5 иллюстрирует зависимость, в которой удельное потребление ресурсов вначале увеличивается вместе с ростом материального уровня жизни, а затем постепенно достигает насыщения и более не увеличивается. Материальный уровень жизни С – это безразмерная величина. Она характеризует степень изменения эффективности использования промышленного удельного капитала (относительной величины основных фондов на душу населения) С ¯ по сравнению с «нормальной» эффективностью «промышленного» удельного капитала С О. Материальный уровень жизни определяется отношением: С = С ¯/ С О . (2. 9)

Заметим, что термин «промышленный капитал» здесь и далее не несет традиционной смысловой нагрузки, а используется лишь для краткости изложения. На самом деле промышленный капитал в модели означает весь капитал народного хозяйства за вычетом сельскохозяйственного капитала. К нему, таким образом, относятся не только основные фонды промышленности, но и фонды транспорта, строительства, связи и других несельскохозяйственных отраслей экономики. Эффективный промышленный капитал С ¯ непосредственно влияет на уровень жизни населения. Число эффективных единиц капитала на душу населения определяется общим объемом капитала с учетом дефицита природных ресурсов на планете. Дефицит ресурсов означает, что необходимо увеличивать капитал для добычи глубоко залегающего сырья, обогащения бедных руд, использование менее эффективных источников энергии, т. е. что существующее оборудование становится неэффективным. Эффективный промышленный капитал определяется как произведение трех сомножителей: общего капитала на душу населения КР; доли промышленного капитала (1 - Х), где Х – доля сельскохозяйственного капитала; ЕR – экстракционный множитель, связанный со стоимостью добычи ресурсов. С¯= ЕR (1 -Х) КР / (1 -X 0). (2. 10) Экстракционный множитель ЕR = ЕR (RR). С помощью этого безразмерного множителя учитывается возрастание трудности добычи ресурсов по мере их исчерпания. Экстракционный множитель – это безразмерная величина, задаваемая графической (табличной) функцией от аргумента RR – доли оставшихся невозобновляемых ресурсов на момент времени t. Изображенную на рисунке зависимость называют унитарной в том смысле, что при RR = 1 и ЕR = 1.

Рис. 2. 6. Зависимость экстракционного коэффициента ЕR от доли оставшихся ресурсов RR В начальный момент времени t 00, когда ресурсы еще не добывались, RR = 1 и ЕR = 1. В другом предельном случае, когда ресурсы полностью исчерпаны, RR = 0 и ЕR = 0. В этом случае фонды промышленности будут неэффективными. В верхнем правом углу графика кривая ЕR близка к горизонтали, т. к. начальный этап истощения ресурсов не приведет к снижению эффективности основных фондов. В средней части графика кривая ЕR падает круче, а в левой – снова приближается к горизонтали. Это отражает трудности добычи оставшихся ресурсов, когда их запасы становятся более рассеянными и труднодоступными. Оставшаяся доля природных ресурсов RR. Эта безразмерная величина определяется как отношение реально существующих запасов ресурсов R к их первоначальным запасам R 00: RR = R / R 00. (2. 11) «Нормальная» эффективность промышленного удельного капитала С 0. Эта постоянная величина вводится в качестве единицы измерения промышленного капитала и определяется как стоимость основных фондов на душу населения в «эталонном» 1970 г. :

С 0 =1 [ед. фондов / чел ∙ год]. (2. 12) Единичное значение С 0 не изменяет величины материального уровня жизни С, но делает эту характеристику безразмерной. Формально величина С 0 определяется по следующему алгоритму: R 0 = R (t 0). (2. 13) RR 0 = R 0 / R 00 . (2. 14) ER 0 = ER (RR 0). (2. 15) C 0 = ER 0 (1 -X 0) , (2. 16) где Х 0 – доля сельскохозяйственного капитала в общем капитале в эталонном 1970 г. Х 0 = 0. 3. (2. 17) В соответствии с потоковой диаграммой, изображенной на рисунке 2. 4, и введенными обозначениями уравнение расходования невозобновляемых ресурсов запишем в виде: d. R / dt = - PRC (C). (2. 18)

2. 2. 2. Уравнение для капитала Правая часть уравнения для капитала содержит две скорости – темп вложения капитала К 2 и темп убыли капитала за счет износа основных фондов К 1. Потоковая диаграмма для вывода уравнения капитала изображена на рисунке 2. 7. Начальное значение капитала (основных фондов) К 00 – это относительная величина. За единицу капитала принято его количество на душу населения в «эталонном» 1970 г. Считается, что капитал на душу населения в 1900 г. составлял 0. 25 единицы капитала. Численность населения планеты в 1900 г. составляла 1. 6 млрд. человек. Путем простого расчета находим начальное значение капитала в 1900 г. : (0. 25 ед. капитала) ∙ (1. 6 млрд. человек) = 0. 4 млрд. ед. капитала. Таким образом К 00 = 0. 4 ∙ 10 9 [единиц капитала]. (2. 19) Текущая величина капитала К. – это один из компонентов социальноэкологической системы, характеризующий ее состояние. Величина капитала связана с двумя потоками: генерацией капитала К 2 и его убылью К 1. Рис. 2. 7. Потоковая диаграмма для вывода уравнения капитала

Текущая величина капитала определяется путем численного интегрирования системы дифференциальных уравнений глобальной модели развития. Размерность К – ед. фондов. Скорость генерации капитала К 2. Она определяется произведением трех сомножителей: численностью населения Р, «нормальной» скоростью генерации капитала на душу населения СК и инвестиционного коэффициента КС. К 2 = Р ∙СК ∙КС [ед. фондов / год]. (2. 20) «Нормальная» скорость генерации капитала на душу населения СК – это постоянная величина, имеющая значение 0. 05 единиц капитала на человека в год, описывает темп накопления капитала, имевший место в «эталонном» 1970 г. СК = 0. 05 [ед. фондов / чел ∙ год]. (2. 21) Такое значение СК означает, что в условиях 1970 г. ежегодные капиталовложения составляют 0. 05 от существующего капитала. Инвестиционный коэффициент КС = КС (С) является безразмерной величиной и задается графической (табличной) функцией от аргумента С – материального уровня жизни населения. Рисунок 2. 8 иллюстрирует эту зависимость. Коэффициент КС, также как и С в 1970 г. имеет значение 1.

Рис. 2. 8. Зависимость величины инвестиционного коэффициента КС от материального уровня жизни населения С Коэффициент КС выражает возможности населения вкладывать средства в расширение производства при возрастании материального уровня жизни. При нулевом капитале (основных фондах), которому соответствует нулевой материальный уровень жизни, способность к накоплению капитала принимается равной 10% от средней интенсивности накопления капитала в 1970 г. (КС = 0. 1). Форма кривой свидетельствует о том, что капитал неравномерно распределен среди населения. Предполагается, что на начальном этапе накопления капитала его концентрация в руках немногих собственников способствует быстрому его росту. Отклонение возрастания кривой КР от линейного закона роста в сторону насыщения объясняется естественным ослаблением желания населения увеличивать свою обеспеченность с ростом самой обеспеченности. Но даже невозрастающий темп фондообразования стимулирует процесс накопления капитала до высоких значений, прежде чем темп фондообразования не окажется равным темпу износа основных фондов.

Скорость убыли капитала К 1. Убыль капитала связана с износом и устареванием основных фондов и определяется как частное от деления капитала К на долю износа фондов KT. К 1 = К / KT [ед. фондов / год]. (2. 22) Процесс выхода основных фондов из строя носил бы экспоненциальный характер, если бы не было генерации фондов. Доля износа капитала KT - это постоянная величина, принятая равной 0. 025 в год. КТ = 0. 025 [ед. фондов / год]. (2. 23) Такая скорость износа соответствует времени «жизни» фондов в 40 лет. В соответствии с потоковой диаграммой, изображенной на рис. 2. 8, и введенными обозначениями уравнение для капитала запишем в виде: d. K / dt = P CK KC – K ∙ KT . (2. 24)

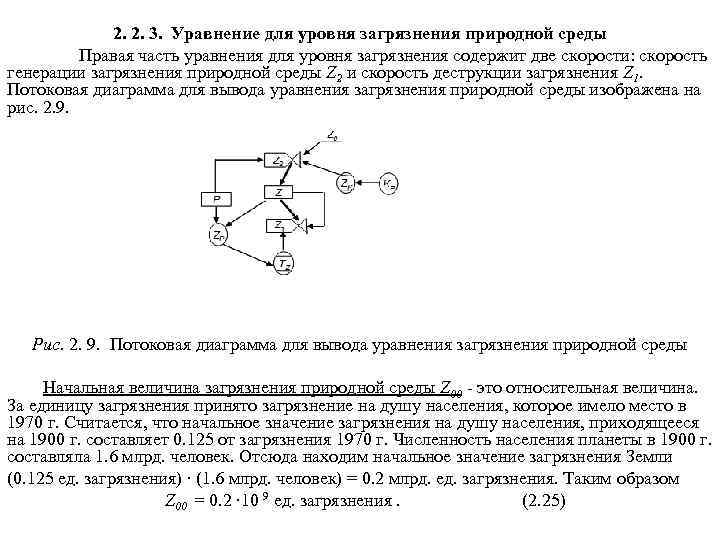2. 2. 3. Уравнение для уровня загрязнения природной среды Правая часть уравнения для уровня загрязнения содержит две скорости: скорость генерации загрязнения природной среды Z 2 и скорость деструкции загрязнения Z 1. Потоковая диаграмма для вывода уравнения загрязнения природной среды изображена на рис. 2. 9. Рис. 2. 9. Потоковая диаграмма для вывода уравнения загрязнения природной среды Начальная величина загрязнения природной среды Z 00 - это относительная величина. За единицу загрязнения принято загрязнение на душу населения, которое имело место в 1970 г. Считается, что начальное значение загрязнения на душу населения, приходящееся на 1900 г. составляет 0. 125 от загрязнения 1970 г. Численность населения планеты в 1900 г. составляла 1. 6 млрд. человек. Отсюда находим начальное значение загрязнения Земли (0. 125 ед. загрязнения) ∙ (1. 6 млрд. человек) = 0. 2 млрд. ед. загрязнения. Таким образом Z 00 = 0. 2 ∙ 10 9 ед. загрязнения. (2. 25)

Текущая величина загрязнения Z. Загрязнение является одним из компонентов социально-экологической системы, характеризующей её состояние. Текущая величина загрязнения определяется двумя потоками: генерацией загрязнения Z 2 и его деструкцией Z 1. Величина загрязнения определяется путем численного интегрирования системы дифференциальных уравнений. Скорость генерации загрязнения Z 2 определяется произведением следующих трех сомножителей: численности населения Р, «нормальной» скорости генерации загрязнений Z 0 и множителя ZK, отражающего зависимость между величиной загрязнения и капиталом (основными фондами) на душу населения Z 2 = P Z 0 ZK [ед. загрязнения / год] (2. 26) «Нормальная» скорость генерации загрязнения Z 0. Это постоянная величина, равная единице загрязнения на душу населения в 1970 г. : Z 0 = 1 [ед. загрязнения / чел. год] (2. 27) Нормальная скорость загрязнения вводится в выражение (2. 26) и уравнение (2. 32) для придания их правым частям размерности скорости. Множитель, отражающий зависимость между величиной загрязнения и величиной основных фондов производства ZK = ZK (KP). Общество, не вооруженное современными средствами производства, генерирует небольшое количество загрязняющих веществ. Сильное загрязнение образуется мощными источниками энергии, в процессе переработки сырья различными отраслями промышленности, и в результате интенсивного ведения сельского хозяйства. Поэтому загрязнение в расчете на душу населения в значительной мере зависит от объема основных фондов на душу населения. Множитель ZK является безразмерной величиной.

Рис. 2. 10. Множитель зависимости величины загрязнения ZK от объема основных фондов КР Изображенная на рис. 2. 10 кривая связывает возрастающую фондовооруженность КР с увеличением скорости образования загрязнений на душу населения ZP. Эта зависимость является унитарной. Действительно, используя 1970 г. , когда КР = 1, в качестве точки отсчета, получаем, что ZK = 1. Верхняя часть кривой постепенно стремится к выходу на плато. Стремление к выходу на плато отражает то обстоятельство, что при возрастании объема капиталовложений структура основных фондов будет изменяться. Большие объемы фондов будут включать в себя капитал, предназначенный для контроля и регулирования величины загрязнения. Если бы структура фондов не изменялась, кривая ZК росла бы вверх с прежним наклоном.

Величина капитала на душу населения КР является аргументом при определении множителя ZK и находится по формуле: КР = К / Р [ед. капитала / чел. ]. (2. 28) Скорость деструкции загрязнения Z 1 зависит от величины загрязнения и от природных процессов самоочищения среды обитания. Поэтому скорость деструкции определяется как частное от деления загрязнения Z на время его разложения TZ: Z 1 = Z / TZ [ед. загрязнения / год]. (2. 29) Время разложения загрязнения TZ (ZP) вводится по аналогии с применяемым в атомной физике понятием полураспада радионуклидов. Формула для скорости деструкции загрязнения (2. 29), как и формула для скорости убыли капитала (2. 22), предполагает экспоненциальный характер процесса деструкции в том случае, когда не поступает новое загрязнение. В модели предполагается зависимость времени деструкции загрязнения TZ от уровня удельного загрязнения ZP (рис. 2. 11). Эта зависимость является унитарной, что соответствует предположению, что загрязнение Z (t 0) было бы абсорбировано за единицу времени (за 1 год в условиях 1970 г. ) на 63%, если бы не генерировалось новое загрязнение и скорость деструкции не уменьшались бы пропорционально Z.

Рис. 2. 11. Зависимость характерного времени деструкции загрязнения TZ от удельного загрязнения ZP Рисунок отображает гипотетическую ситуацию, когда время деструкции 63 % существующего загрязнения возрастает следующим образом: до 5 лет при увеличении уровня загрязнения в 20 раз по сравнению с уровнем 1970 г. ; до 10 лет при росте загрязнения в 40 раз и до 20 лет при 60 -кратном увеличении загрязнения. Таким образом, считается, что небольшие количества загрязнения разлагаются достаточно быстро, а большие приводят к кумулятивному эффекту, тормозящему естественные процессы разложения. Размерность TZ - год. Удельное загрязнение ZP – это безразмерная величина, определяемая как частное от деления реального загрязнения Z на значение уровня загрязнения в 1970 г. , которое задается, так называемым, «стандартным загрязнением» ZC: ZР = Z / ZС . (2. 30) «Стандартное» загрязнение» ZC определяется как загрязнение планеты в 1970 г. Величина ZC рассчитывается как единица загрязнения на душу населения в 1970 г. - Z 0 , умноженная на численность населения в этом году (3. 6 млрд. человек). Таким образом: ZC = 3. 6 ∙ 10 9 [ед. загрязнения]. (2. 31) В соответствии с потоковой диаграммой, изображенной на рис. 2. 10, и введенными обозначениями уравнение для загрязнения природной среды запишем в виде: d. Z / dt = P Z 0 ZK - Z / TZ . (2. 32)

2. 2. 4. Уровень питания населения и уравнение сельскохозяйственного сектора экономики Правая часть уравнения сельскохозяйственного сектора экономики содержит две скорости: скорость прироста доли сельскохозяйственного капитала (основных фондов сельского хозяйства) и Х 2 – скорости износа доли сельскохозяйственных фондов. потоковая диаграмма для вывода уравнения сельскохозяйственного сектора изображена на рис. 2. 12. Определяемое этой диаграммой понятие уровня питания имеет существенное значение в развитии всей социально-экологической системы. Х 2 – прирост доли сельскохозяйственных фондов; Т 2 – задержка внедрения фондов; XQ – индикаторное отношение качества жизни; Q – отношение компонент качества жизни; QC – функция влияния материального уровня на качество жизни; С – материальный уровень жизни; FX – пищевой потенциал основных фондов сельского хозяйства; WP - удельная продуктивность сельского хозяйства; WO – нормальная продуктивность сельского хозяйства; XF - функция влияния уровня питания на индикаторное отношение сельскохозяйственных фондов ко всем фондам народного хозяйства; QF - функция влияния уровня питания на качество жизни; FP – уровень питания населения; XP – удельные капиталовложения в сельское хозяйство; VZ – множитель влияния загрязнения природной среды на продуктивность сельского хозяйства; VP – множитель влияния плотности населения на продуктивность сельского хозяйства; KP – удельный капитал; ZP – удельное загрязнение; PP – плотность населения; X 1 – износ доли сельскохозяйственных фондов; TX – постоянная нормального износа сельскохозяйственных фондов; X 0 – нормальная доля сельскохозяйственных фондов.

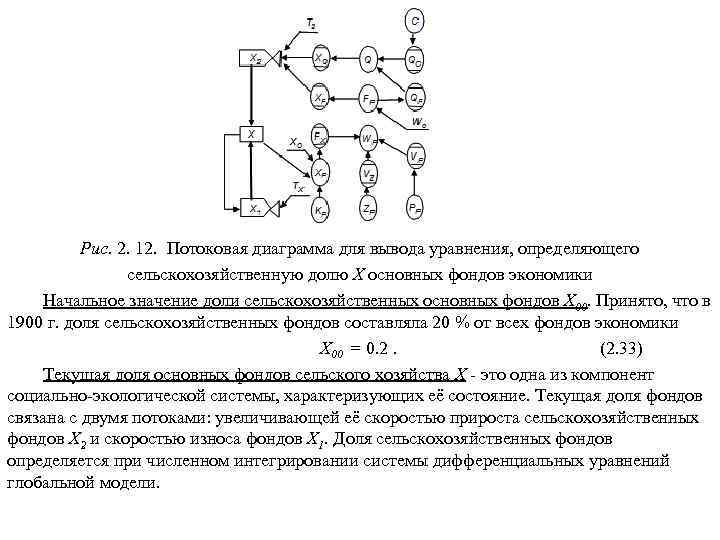Рис. 2. 12. Потоковая диаграмма для вывода уравнения, определяющего сельскохозяйственную долю Х основных фондов экономики Начальное значение доли сельскохозяйственных основных фондов Х 00. Принято, что в 1900 г. доля сельскохозяйственных фондов составляла 20 % от всех фондов экономики Х 00 = 0. 2. (2. 33) Текущая доля основных фондов сельского хозяйства X - это одна из компонент социально-экологической системы, характеризующих её состояние. Текущая доля фондов связана с двумя потоками: увеличивающей её скоростью прироста сельскохозяйственных фондов Х 2 и скоростью износа фондов Х 1. Доля сельскохозяйственных фондов определяется при численном интегрировании системы дифференциальных уравнений глобальной модели.

Удельные капиталовложения в сельское хозяйство ХР. Количество пищи на душу населения зависит от количества основных сельскохозяйственных фондов. Они определяются как фондовооруженность всей экономики на душу населения КР, умноженная на «нормальную» часть фондов сельского хозяйства Х 0. ХР = КР ∙ X / Х 0 [ед. фондов / чел]. (2. 34) В результате вычисляется величина сельскохозяйственных фондов на душу населения, которая затем используется для определения относительного уровня питания. Нормальная часть сельскохозяйственных фондов Х 0 - это постоянная величина, принятая равной 0. 3 от основных фондов всей экономики: Х 0 = 0. 3. (2. 35) Такое значение Х 0 приводит к тому, что «нормальные» удельные капиталовложения в сельское хозяйство ХР в «эталонном» 1970 г. равны единице. Пищевой потенциал основных сельскохозяйственных фондов FX = FX (XP). Капиталовложения в сельское хозяйство на душу населения в значительной мере определяют продуктивность сельского хозяйства. Рис. 2. 13. Зависимость продуктивности сельскохозяйственного производства FX от удельных капиталовложений в сельское хозяйство XP

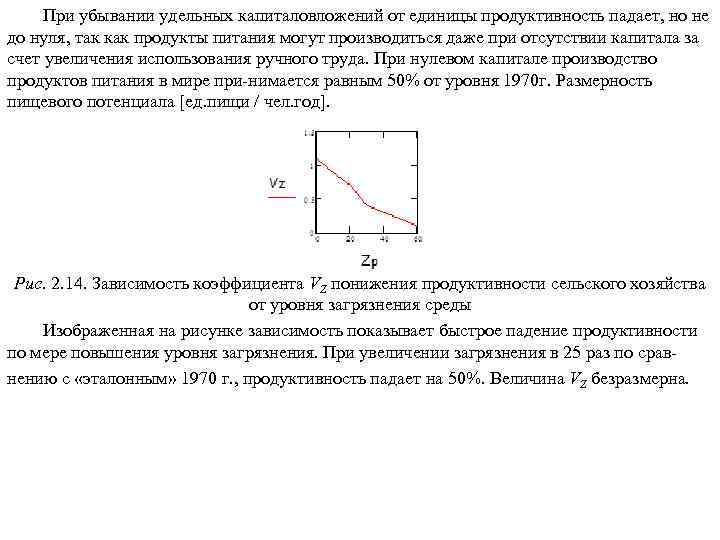При убывании удельных капиталовложений от единицы продуктивность падает, но не до нуля, так как продукты питания могут производиться даже при отсутствии капитала за счет увеличения использования ручного труда. При нулевом капитале производство продуктов питания в мире при-нимается равным 50% от уровня 1970 г. Размерность пищевого потенциала [ед. пищи / чел. год]. Рис. 2. 14. Зависимость коэффициента VZ понижения продуктивности сельского хозяйства от уровня загрязнения среды Изображенная на рисунке зависимость показывает быстрое падение продуктивности по мере повышения уровня загрязнения. При увеличении загрязнения в 25 раз по сравнению с «эталонным» 1970 г. , продуктивность падает на 50%. Величина VZ безразмерна.

Множитель влияния загрязнения среды на продуктивность сельского хозяйства VZ = VZ (ZP) - это графическая (табличная) зависимость. Относительный уровень загрязнения ZP =1 определяет загрязнение среды в 1970 г Удельное загрязнение природной среды ZP определяется как частное от деления уровня загрязнения Z на «стандартное» загрязнение Zc ZP = Z / Zc [ед. загрязнения] Множитель влияния плотности населения на продуктивность сельского хозяйства VP = VP (PP) - это графическая (табличная) унитарная зависимость. Плотность населения является одним из показателей процесса урбанизации. Растущее население занимает площади, ранее использовавшиеся или потенциально пригодные для сельскохозяйственного производства. Относительная плотность населения РР определяется как частное от деления численности населения планеты Р на площадь Земли S = 135 ∙ 10 6 км 2 и на нормальную плотность населения, которая в 1970 г. равнялась 26. 5 чел. / км 2. РР = Р / (S ∙ 26. 5) [чел. / км 2]. (2. 36) За единицу плотности населения принимается плотность, которая была в эталонном 1970 г. Рис. 2. 15. Зависимость коэффициента VP понижения продуктивности сельского хозяйства от плотности населения

Левый участок кривой описывает ситуацию, когда все сельхозугодия земли в 2. 4 раза превышают суммарную площадь существовавших в 1970 г. и пригодных для сельского хозяйства земель. На правом участке кривой плотность населения в 5 раз выше уровня 1970 г. Это должно привести к привлечению в сельскохозяйственное произво-дство менее продуктивных зе-мель с одновременным умень-шением площади плодородных земель за счет урбанизации. Величина VP безразмерная Удельная продуктивность сельского хозяйства WP. Это продуктивность хозяйства на душу населения. Она определяется как произведение трех сомножителей: пищевого потенциала основных сельскохозяйственных фондов FX, множитель влияния загрязнения среды на продуктивность VZ и множителя влияния плотности населения на продуктивность V P. WP = FX VZ VP [ед. пищи / чел. год]. (2. 37) Нормальная продуктивность сельского хозяйства W 0 - это удельная продуктивность сельского хозяйства, которая имела место в «эталонном» 1970 г. Она принимается равной единице W 0 = 1 [ед. пищи / чел. год]. (2. 38) Нормальная продуктивность вводится для того, чтобы уровень питания населения был безразмерной величиной. Уровень питания населения FP - это безразмерная величина, определяемая как отношение удельной продуктивности сельского хозяйства WP к нормальной продуктивности W 0 FP = WP / W 0 . (2. 39) Уровень питания определяет количество пищи на душу населения в единицах среднего мирового уровня питания на душу населения в «эталонном» 1970 г.

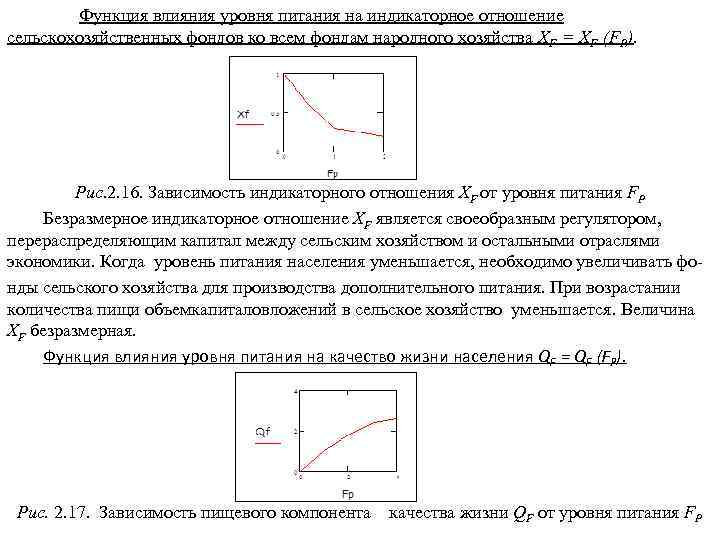Функция влияния уровня питания на индикаторное отношение сельскохозяйственных фондов ко всем фондам народного хозяйства XF = XF (FP). Рис. 2. 16. Зависимость индикаторного отношения XF от уровня питания FP Безразмерное индикаторное отношение XF является своеобразным регулятором, перераспределяющим капитал между сельским хозяйством и остальными отраслями экономики. Когда уровень питания населения уменьшается, необходимо увеличивать фонды сельского хозяйства для производства дополнительного питания. При возрастании количества пищи объемкапиталовложений в сельское хозяйство уменьшается. Величина XF безразмерная. Функция влияния уровня питания на качество жизни населения QF = QF (FP). Рис. 2. 17. Зависимость пищевого компонента качества жизни QF от уровня питания FP

Это графическая (табличная) унитарная зависимость. Качество жизни зависит от ряда факторов, среди которых уровень питания имеет наибольшее значение. Качество жизни вычисляется как произведение определяющих его факторов. Поэтому нулевое значение множителя QF понижает значение качества жизни до нуля независимо от значений других сомно-жителей. Однако при достаточно высоком уровне питания дальнейшее его увеличение вносит всё меньший вклад в качество жизни. Величина QF безразмерна. Функция влияния материального уровня на качество жизни QC = QC (C). Отношение «вещевой» и пищевой компонент качества жизни Q - это безразмерная величина как частное от деления «вещевой» QC и пищевой QF компонент жизни Рис. 2. 18. Зависимость «вещевой» компоненты качества жизни от материального уровня жизни населения Это графическая (табличная) унитарная зависимость. Значение функции QC = 1 имеет место при материальном уровне, характерном для 1970 г. Когда материальный уровень уменьшается до нуля, QC = 0. 2.

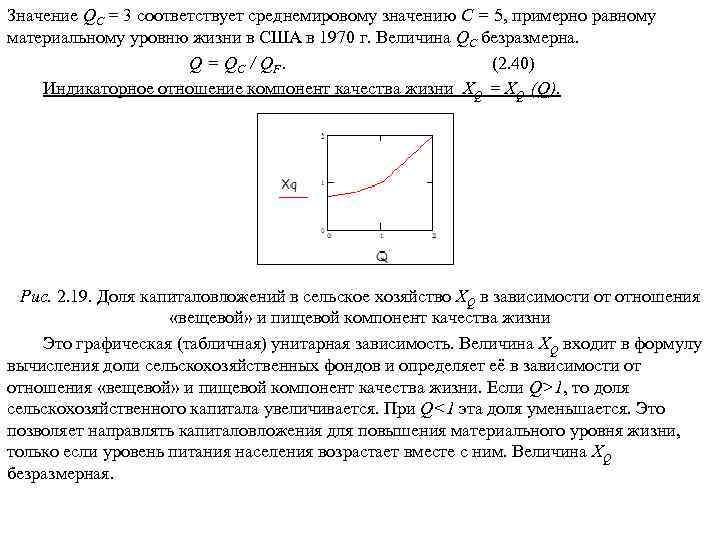Значение QC = 3 соответствует среднемировому значению С = 5, примерно равному материальному уровню жизни в США в 1970 г. Величина QC безразмерна. Q = QC / QF. (2. 40) Индикаторное отношение компонент качества жизни XQ = XQ (Q). Рис. 2. 19. Доля капиталовложений в сельское хозяйство XQ в зависимости от отношения «вещевой» и пищевой компонент качества жизни Это графическая (табличная) унитарная зависимость. Величина XQ входит в формулу вычисления доли сельскохозяйственных фондов и определяет её в зависимости от отношения «вещевой» и пищевой компонент качества жизни. Если Q>1, то доля сельскохозяйственного капитала увеличивается. При Q<1 эта доля уменьшается. Это позволяет направлять капиталовложения для повышения материального уровня жизни, только если уровень питания населения возрастает вместе с ним. Величина XQ безразмерная.

Скорость роста доли основных фондов сельского хозяйства Х 2 определяется как произведение индикаторного отношения сельскохозяйственных фондов XF и индикаторного отношения компонент качества жизни XQ, деленное на постоянную времени регулирования фондов Т 2: X 2 = XF ∙ XQ / T 2 [1 / год]. (2. 42) Время регулирования фондов Т 2 - это постоянная величина вводится для того, чтобы отразить в модели постепенный переход от реально существующих фондов в сельском хозяйстве к тому уровню, который определяется текущими условиями. Перераспределение фондов требует введения временной задержки, которая представляет собой срок, необходимый для изменения структуры капитала. Постоянная времени регулирования фондов принята равной 15 годам: Т 2 = 15 [год] . (2. 42) Скорость износа основных фондов сельского хозяйства Х 1 определяется как частное от деления текущего сельскохозяйственного капитала Х на время износа капитала, т. е. на время жизни основных фондов в сельском хозяйстве: Х 1 = Х / ТX [1 / год]. (2. 43) Время износа сельскохозяйственного капитала ТХ - эта постоянная величина принята равной постоянной регулирования фондов, т. е. 15 годам: ТХ = Т 2 = 15 [год] С учетом потоковой диаграммы, изображенной на рисунке 2. 13, и введенных обозначений, уравнение сельскохозяйственного сектора экономики записывается в виде: d. X / dt = (XF XQ - X) / TX . (2. 44)

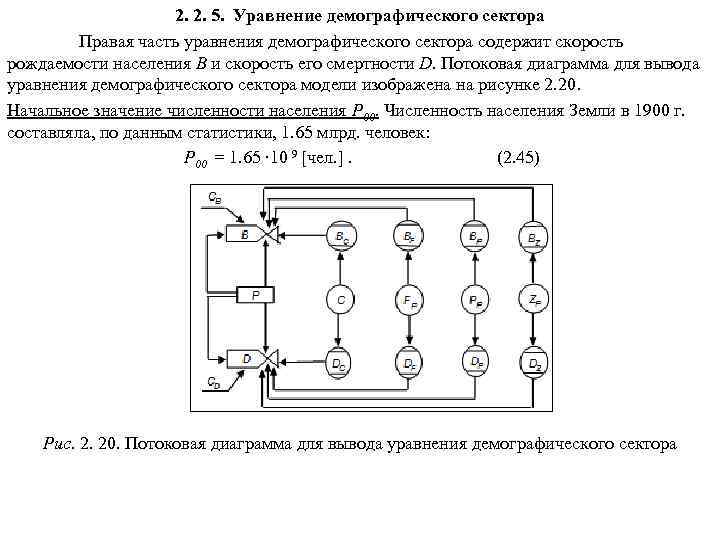2. 2. 5. Уравнение демографического сектора Правая часть уравнения демографического сектора содержит скорость рождаемости населения В и скорость его смертности D. Потоковая диаграмма для вывода уравнения демографического сектора модели изображена на рисунке 2. 20. Начальное значение численности населения Р 00. Численность населения Земли в 1900 г. составляла, по данным статистики, 1. 65 млрд. человек: Р 00 = 1. 65 ∙ 10 9 [чел. ]. (2. 45) Рис. 2. 20. Потоковая диаграмма для вывода уравнения демографического сектора

Текущая численность населения Р - это один из компонентов социальноэкологической системы, характеризующих её состояние. Численность населения связана с двумя потоками: скоростью рождаемости В и скоростью смертности D. Текущая численность населения определяется при численном интегрировании системы дифференциальных уравнений глобальной модели. Скорость рождаемости населения В определяется как произведение шести сомножителей: численности населения Р, коэффициента рождаемости СВ, множителя зависимости скорости рождаемости от материального уровня жизни ВС = ВС (С), множителя зависимости скорости рождаемости от уровня питания населения BF = BF (FP), множителя зависимости скорости рождаемости от плотности населения BP = BP (PP), множителя зависимости скорости рождаемости от загрязнения природной среды BZ = BZ (ZP). Таким образом: В = Р ∙ СВ ∙ ВС ∙ BF ∙ BP ∙ BZ [чел / год]. (2. 46) При нормальных условиях множители не должны изменять скорость рождаемости, т. е. они должны быть равными 1. Если условия оказываются более благоприятными, чем нормальные, то соответствующий множитель должен быть больше 1, а если менее благоприятными, то множитель должен быть меньше 1. За нормальные условия в модели приняты условия, существовавшие в мире в 1970 г. Коэффициент рождаемости СВ. Этот коэффициент определяется как отношение числа новорожденных N к среднегодовой численности населения Р¯ (Δt = 1 году): СВ = N / P¯ Δt [1/год]. Коэффициент СВ представляет собой, таким образом, интенсивность рождаемости. Для «эталонного» 1970 г. величина коэффициента рождаемости принята равной 0. 04: СВ = 0. 04 [1 / год]. (2. 47)

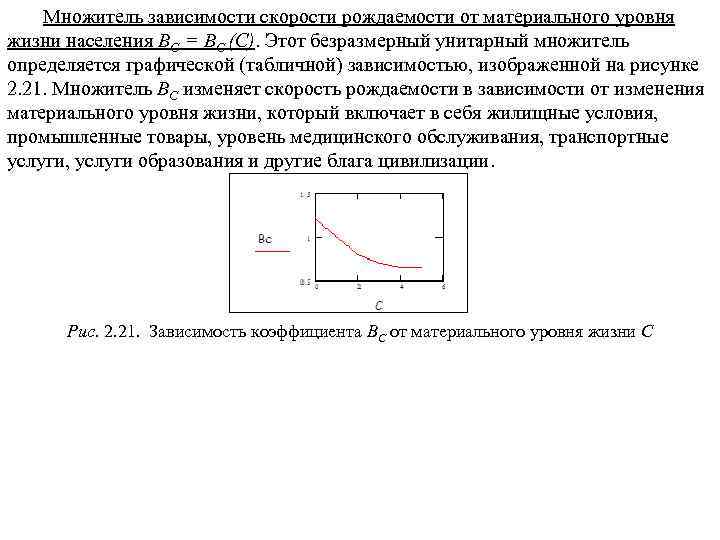Множитель зависимости скорости рождаемости от материального уровня жизни населения ВС = ВС (С). Этот безразмерный унитарный множитель определяется графической (табличной) зависимостью, изображенной на рисунке 2. 21. Множитель ВС изменяет скорость рождаемости в зависимости от изменения материального уровня жизни, который включает в себя жилищные условия, промышленные товары, уровень медицинского обслуживания, транспортные услуги, услуги образования и другие блага цивилизации. Рис. 2. 21. Зависимость коэффициента ВС от материального уровня жизни С

Множитель зависимости скорости рождаемости от уровня питания BF = BF (FP). Этот безразмерный унитарный множитель определяется графической (табличной) зависимостью, изображенной на рис. 2. 22. За единицу уровня питания принят уровень, существовавший в «эталонном» 1970 г. Значение FP = 2 следует понимать как удвоение уровня питания на душу населения по сравнению с уровнем 1970 г. Когда FP → 0, жизнь становится невозможной и скорость рождаемости – нулевой. При другом предельном значении уровня питания рождаемость удваивается. Рис. 2. 22. Зависимость коэффициента BF от уровня питания FP На заре цивилизации человечество существовало в таком неустойчивом состоянии, когда уровень питания регулировал скорость рождаемости и смертности таким образом, что население поддерживало свое существование при максимально возможной численности, определяемой уровнем производства продуктов питания.

Множитель зависимости скорости рождаемости от плотности населения ВР = ВР (РР). Этот безразмерный унитарный множитель определяется графической (табличной) зависимостью, изображенной на рис. 2. 24. Множитель имеет значение 1 для условий 1970 г. При уменьшении плотности населения происходит лишь небольшое увеличение скорости рождаемости. При пятикратном увеличении плотности по сравнению с 1970 г. происходит 50% снижение скорости рождаемости. Рис. 2. 23. Зависимость коэффициента ВР от плотности населения РР При оценке зависимости ВР = ВР (РР) следует иметь в виду, что по горизонтальной оси откладывается осредненная по всему миру плотность населения. Последствия высокой плотности весьма различны и при достижении экстремальной плотности в планетарном масштабе будут более неблагоприятными, чем те, что встречаются сегодня в урбанизированных регионах.

Множитель зависимости скорости рождаемости от загрязнения природной среды ВZ = ВZ (ZР). Это безразмерный унитарный множитель, определяемый графической (табличной) зависимостью, изображенной на рисунке 2. 24. Рис. 2. 24. Зависимость коэффициента BZ от загрязнения природной среды ZP Высокий уровень загрязнения будет оказывать влияние на рождаемость из-за ухудшения здоровья родителей. Кроме того, очень высокий уровень загрязнения может оказывать психологическое давление и вызывать конфликты между супругами. На рисунке загрязнение, равное 1, соответствует условиям 1970 г. При загрязнении ниже уровня 1970 г. степень его влияния на рождаемость незначительна. При экстремально высоком уровне загрязнения скорость рождаемости падает до 0. 1 от уровня 1970 г.

Скорость смертности населения D определяется как произведение шести сомножителей: численности населения Р, коэффициента смертности CD, множителя зависимости скорости смертности от материального уровня жизни DC = DC (C); множителя зависимости скорости смертности от уровня питания населения DF = DF (FР); множителя зависимости скорости смертности от плотности населения DР = DР (РР) и множителя зависимости скорости смертности от загрязнения природной среды DZ = DZ (ZР). Таким образом: D = P ∙ CD ∙ DC ∙ DF ∙ DP ∙ DF [чел / год]. (2. 48) В нормальных условиях 1970 г. множители не изменяют скорости смертности и равны 1. При улучшении или ухудшении условий значение соответствующего множителя должно быть меньше или больше 1. Коэффициент смертности СD определяется как отношение числа умерших М к среднегодовой численности населения Р¯ (Δt = 1 году): СD = М / Р¯∙ Δt [1 / год]. Коэффициент смертности, таким образом, представляет собой интенсивность смертности. Для «эталонного» 1970 г. величина коэффициента смертности принята равной 0. 028: CD = 0. 028 [1 / год]. Такая величина коэффициента смертности соответствует ожидаемой при рождении продолжительности жизни в 36 лет.

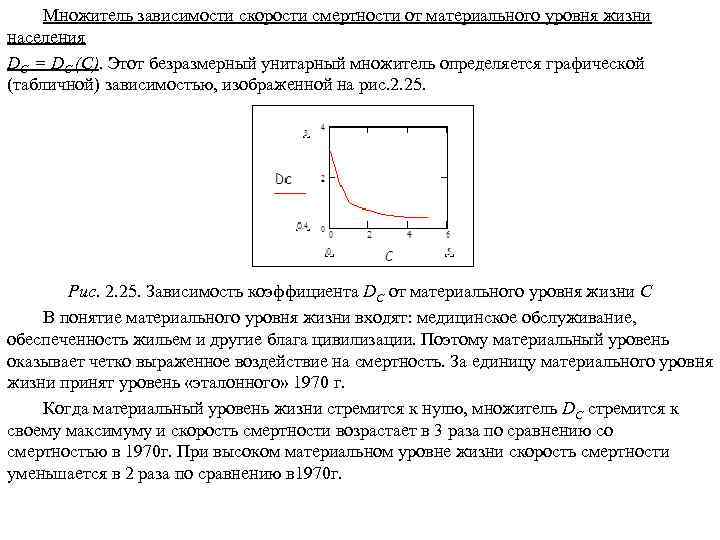Множитель зависимости скорости смертности от материального уровня жизни населения DC = DC (С). Этот безразмерный унитарный множитель определяется графической (табличной) зависимостью, изображенной на рис. 2. 25. Рис. 2. 25. Зависимость коэффициента DC от материального уровня жизни С В понятие материального уровня жизни входят: медицинское обслуживание, обеспеченность жильем и другие блага цивилизации. Поэтому материальный уровень оказывает четко выраженное воздействие на смертность. За единицу материального уровня жизни принят уровень «эталонного» 1970 г. Когда материальный уровень жизни стремится к нулю, множитель DC стремится к своему максимуму и скорость смертности возрастает в 3 раза по сравнению со смертностью в 1970 г. При высоком материальном уровне жизни скорость смертности уменьшается в 2 раза по сравнению в 1970 г.

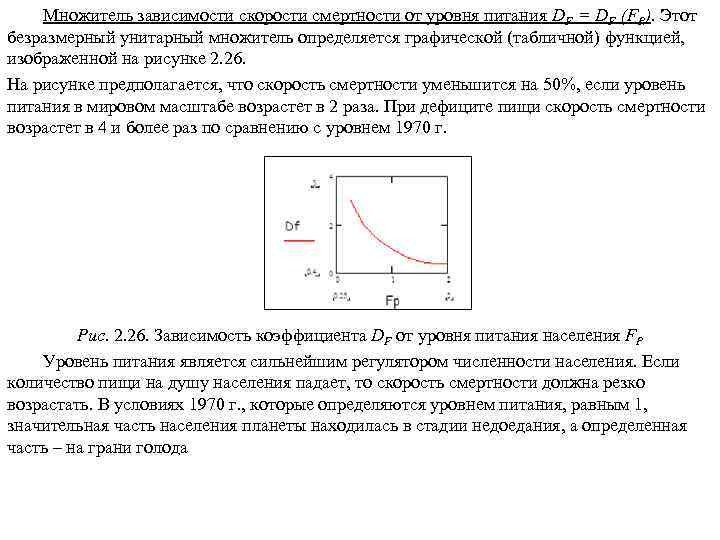Множитель зависимости скорости смертности от уровня питания DF = DF (FP). Этот безразмерный унитарный множитель определяется графической (табличной) функцией, изображенной на рисунке 2. 26. На рисунке предполагается, что скорость смертности уменьшится на 50%, если уровень питания в мировом масштабе возрастет в 2 раза. При дефиците пищи скорость смертности возрастет в 4 и более раз по сравнению с уровнем 1970 г. Рис. 2. 26. Зависимость коэффициента DF от уровня питания населения FP Уровень питания является сильнейшим регулятором численности населения. Если количество пищи на душу населения падает, то скорость смертности должна резко возрастать. В условиях 1970 г. , которые определяются уровнем питания, равным 1, значительная часть населения планеты находилась в стадии недоедания, а определенная часть – на грани голода

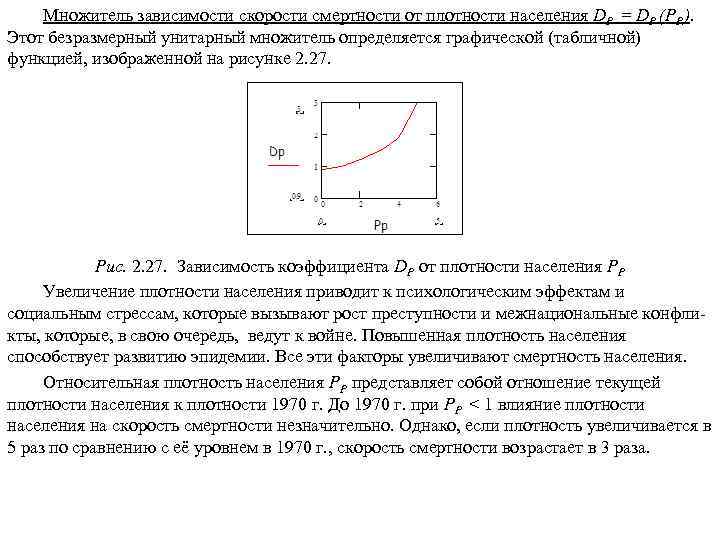Множитель зависимости скорости смертности от плотности населения DP = DP (PP). Этот безразмерный унитарный множитель определяется графической (табличной) функцией, изображенной на рисунке 2. 27. Рис. 2. 27. Зависимость коэффициента DP от плотности населения РР Увеличение плотности населения приводит к психологическим эффектам и социальным стрессам, которые вызывают рост преступности и межнациональные конфли- кты, которые, в свою очередь, ведут к войне. Повышенная плотность населения способствует развитию эпидемии. Все эти факторы увеличивают смертность населения. Относительная плотность населения РР представляет собой отношение текущей плотности населения к плотности 1970 г. До 1970 г. при РР < 1 влияние плотности населения на скорость смертности незначительно. Однако, если плотность увеличивается в 5 раз по сравнению с её уровнем в 1970 г. , скорость смертности возрастает в 3 раза.

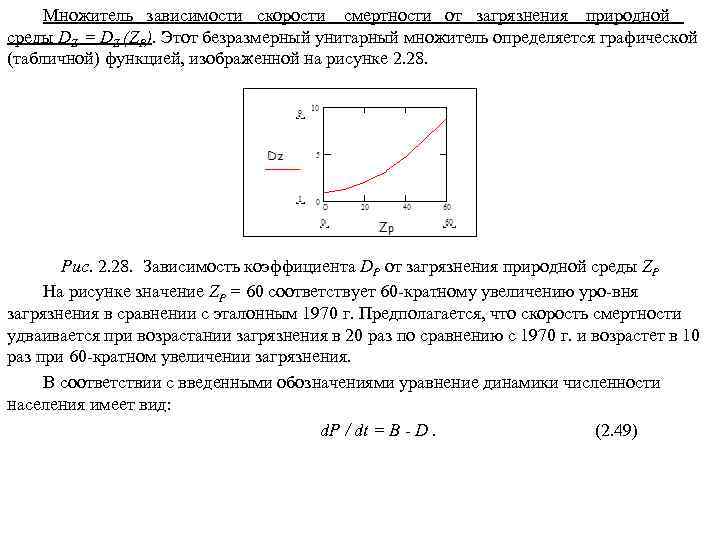Множитель зависимости скорости смертности от загрязнения природной среды DZ = DZ (ZP). Этот безразмерный унитарный множитель определяется графической (табличной) функцией, изображенной на рисунке 2. 28. Рис. 2. 28. Зависимость коэффициента DP от загрязнения природной среды ZP На рисунке значение ZP = 60 соответствует 60 -кратному увеличению уро-вня загрязнения в сравнении с эталонным 1970 г. Предполагается, что скорость смертности удваивается при возрастании загрязнения в 20 раз по сравнению с 1970 г. и возрастет в 10 раз при 60 -кратном увеличении загрязнения. В соответствии с введенными обозначениями уравнение динамики численности населения имеет вид: d. P / dt = B - D. (2. 49)

2. 2. 6. Качество жизни населения Качество жизни Qg используется как мера функционирования мировой системы. Эта безразмерная величина определяется как произведение стандартного качества жизни Q 0 на четыре множителя зависимости качества жизни от уровня питания QF, материального уровня жизни QC, уровня загрязнения природной среды QZ и плотности населения QP: Qg = Q 0 ∙ QC ∙ QP ∙ QF ∙ QZ . (2. 50) Стандартное качество жизни Q 0 – это постоянная величина, определяемая условиями жизни в эталонном 1970 г. , принимается равной 1: Q 0 = 1. (2. 51) Функция влияния удельного загрязнения природной среды на качество жизни QZ = QZ (ZP). Рис. 2. 29. Множитель зависимости качества жизни QZ от удельного загрязнения ZP Это графическая (табличная) зависимость. Изображенная на рисунке кривая показывает предполагаемую крутизну падения качества жизни при 30 -кратном возрастании загрязнения относительно уровня 1970 г. , принятого за единицу.

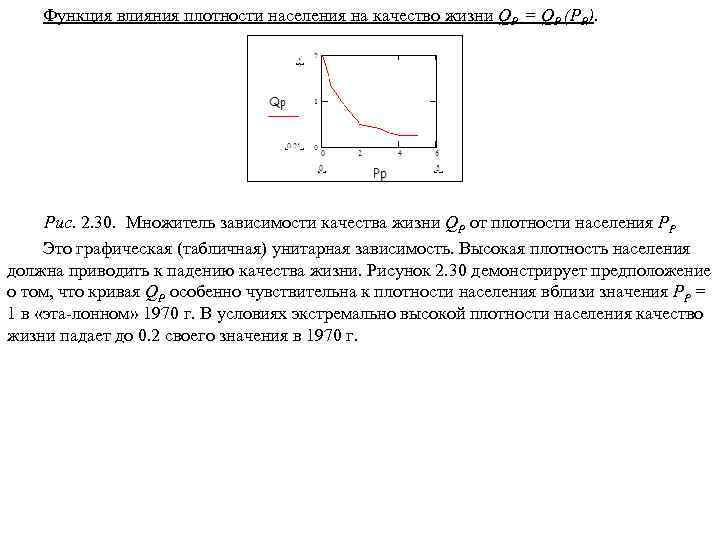Функция влияния плотности населения на качество жизни QP = QP (PP). Рис. 2. 30. Множитель зависимости качества жизни QP от плотности населения РР Это графическая (табличная) унитарная зависимость. Высокая плотность населения должна приводить к падению качества жизни. Рисунок 2. 30 демонстрирует предположение о том, что кривая QP особенно чувствительна к плотности населения вблизи значения РР = 1 в «эта-лонном» 1970 г. В условиях экстремально высокой плотности населения качество жизни падает до 0. 2 своего значения в 1970 г.

2. 2. 7. Начальные условия и реализация модели «Мир-2» на языке автоматического программирования Math. CAD Реализация модели «Мир-2» сводится к численному решению на ЭВМ задачи Коши для системы обыкновенных дифференциальных уравнений (2. 18); (2. 24); (2, 32); (2. 44); (2. 49) с соответствующими начальными условиями. В качестве начальных условий на момент времени t 00 ─ 1900 г в модели «Мир-2» приняты: P 00 = 1, 65 ∙ 10 9 чел. ; K 00 = 0, 4 ∙ 10 9 ед. капитала (принимается, что в 1900 г. на человека приходилось вчетверо меньше капитала, чем в 1970 г. ); X 00 = 0, 2; R 00 = 900 ∙ 10 9 ед. ресурсов (предполагается, что, начиная с 1900 г. , ресурсов хватило бы на 250 лет при скорости их потребления, существовавшей в 1970 г. ); Z 00 = 0, 2 ∙ 10 9 ед. загрязнения (считается, что в 1900 г. на душу населения приходилось в восемь раз меньше загрязнений, чем в 1970 г. ). Рассмотренный в этом разделе алгоритм модели реализован на язы-ке автоматического программирования Math. СAD доцентом В. П. Кулешом и дипломницей кафедры геоэкологии и природопользования М. С. Борисовой. Для численного интегрирования системы уравнений использован метод Рунге-Куута. Math. СAD ─ это мощная, гибкая универсальная система компьютерной математики, предназначенная для автоматизации решения массовых математических задач в самых разных областях знания. Помимо собственно вычислений, как численных, так и аналитических она позволяет решать сложные оформительские задачи, которые с трудом реализуются популярными текстовыми редакторами или электронными таблицами. А применение библиотек и пакетов расширения обеспечивает профессиональную ориентацию Math. СAD на любую область науки.

Отличительной чертой Math. СAD является работа с документами. Документы объединяют описание математического алгоритма решения задачи (или ряда задач) с текстовыми комментариями и результатами вычислений, заданными в форме символов, чисел, таблиц или графиков. Уникальное свойство Math. СAD ─ возможность описания математических алгоритмов в естественной математической форме с применением общепринятой символики для математических знаков, таких, например, как квадратный корень, знак деления в виде горизонтальной черты, знак интеграла и т. д. Это делает документ, представленный на экране дисплея, чрезвычайно похожим на странички текста из математических книг и научных статей. Такой подход значительно облегчает восприятие математической сущности задачи и избавляет пользователя от изучения некоторого промежуточного языка программирования, например, Фортран, Бейсик, Паскаль и др. Можно сказать, что в Math. СAD идея решения математических задач без их программирования доведена до совершенства: подавляющее большинство задач требует лишь корректного формульного описания и не нуждается в подготовке программ в их общепринятом виде. Разумеется, это не означает, что в системе нет своего языка программирования. В действительности он есть, но это математически ориентированный особый язык программирования сверхвысокого уровня, используемый, в основном, как входной язык для диалога с системой. В подавляющем большинстве расчетных задач этот язык позволяет задавать их решение в виде вводимых с помощью операторов и функций математических формул, и указывать форму выдачи результатов (таблицы или графики).

Специальные приемы введены лишь для задания циклического изменения переменных и создания так называемых ранжированных переменных – векторов. Результаты реализации модели «Мир-2» на Math. СAD на период 1900 - 2100 гг. иллюстрирует рисунок 2. 31. Сопоставление численных значений переменных, снятых с графика, приведенного в монографии Дж. Форрестера [1978], с соответствующими значениями, полученными при реализации модели на Math. СAD, показало их полную идентичность.

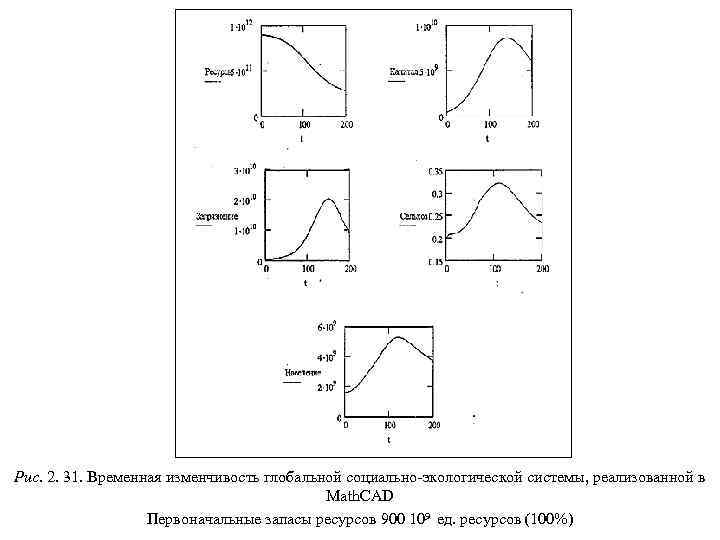Рис. 2. 31. Временная изменчивость глобальной социально-экологической системы, реализованной в Math. CAD Первоначальные запасы ресурсов 900 109 ед. ресурсов (100%)

2. 3. Прогнозные сценарии развития цивилизации при расширении ресурсноэнергетического потенциала Земли Ресурсно-энергетическим потенциалом, по аналогии с земельно-ресурсным, будем называть одну из составляющих природно-ресурсного потенциала ─ доступную при существующих технологических и социально-экономических отношениях совокупность невозобновляемых природных ресурсов. Расширение ресурсно-энергетического потенциала в будущем может быть достигнуто путем увеличения запасов топливных и минеральных ресурсов в процессе геологоразведки; использования малодоступных ресурсов, расположенных на шельфе, материковом склоне и ложе океана; развития ядерной энергетики, добычи углеводородного топлива из тонких пластов; использования битумных песков и низкокалорийных горючих сланцев, разработка которых сегодня считается нерентабельной. Казалось бы, увеличение запасов невозобновляемых природных ресурсов ─ благо для нашей цивилизации. Однако моделирование этого процесса показывает, что это не так. Не изменяя формулировки глобальной модели и функциональных зависимостей, ответственных за скорости протекания демографических, социально-экономических и экологических процессов, рассмотрим результаты моделирования развития нашей цивилизации по ряду сценариев, в которых первоначальные запасы невозобновляемых природных ресурсов увеличены на 60, 100 и 150%. Возможные варианты развития цивилизации рассмотрим на пятисотлетнем временном интервале 1900 – 2400 гг.

Сценарий 1 (рис. 2. 32). В этом сценарии количество первоначальных невозобновляемых природных ресурсов увеличено на 60% и составляет 1440 млрд. ед. ресурсов. При таком сценарии на протяжении 200 лет численность населения планеты трижды будет достигать максимальных значений: в 1987 г. – 5. 90 млрд. человек, в 2098 г. – 2. 98 млрд. человек и в 2189 г. – 3. 29 млрд. человек. Первая демографическая катастрофа настигнет нашу цивилизацию уже в 2036 г. Численность населения в это время составит 0. 4 млрд. человек. Вторая катастрофа произойдет на планете в 2133 г. Численность населения при этом будет 1. 06 млрд. человек. В период с 2189 по 2400 гг. численность населения будет снижаться и к концу периода достигнет 1. 54 млрд. человек. Согласно этого сценария, к 1987 г. должно было быть израсходовано 28% первоначальных невозобновляемых природных ресурсов, к 2098 г. – 64%, а к 2189 г. их останется только 19%. Уровень загрязнения окружающей среды дважды достигнет максимального значения: в 2013 г. он составит 1880 108 ед. загрязнения, а в 2118 г. – 1340 108 ед. загрязнения. Основные фонды экономики тоже будут иметь два экстремальных значения: в 2000 г. – 134 108 ед. капитала, а в 2104 г. – 99. 6 108 ед. капитала. Максимальные значения доли сельскохозяйственного капитала придутся на 2008 г. – 0. 79 и на 2118 г. – 0. 42.

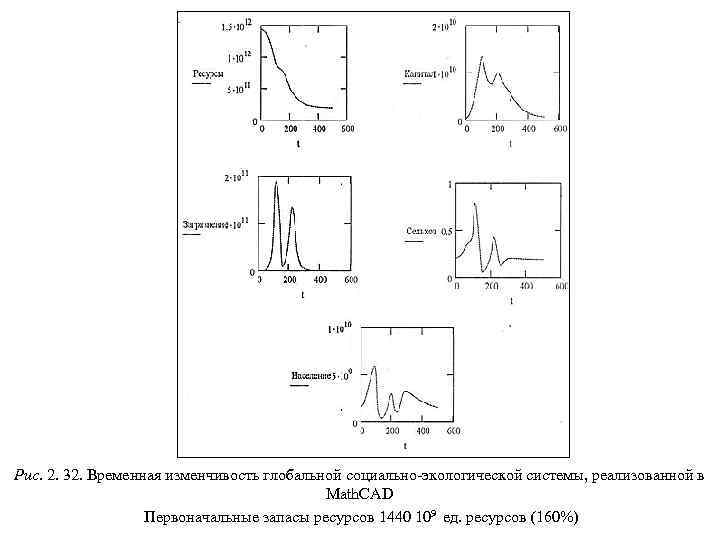Рис. 2. 32. Временная изменчивость глобальной социально-экологической системы, реализованной в Math. CAD Первоначальные запасы ресурсов 1440 109 ед. ресурсов (160%)

Сценарий 2 (рис. 2. 33). В этом сценарии количество первоначальных невозобновляемых природных ресурсов увеличено на 100% и составляет 1800 млрд. ед. ресурсов. В этом случае следует ожидать четырех пиков значений численности населения Земли: в 1972 г. -5. 81, в 2080 г. – 2. 67, в 2172 г. – 2. 88 и в 2258 г. – 3. 15 млрд. человек. Демографические катастрофы по этому сценарию должны иметь место трижды: в 2020 г. – 0. 36, в 2122 г. -0. 74 и в 2205 г. – 1. 18 млрд. человек. С 2258 г. численность населения планеты будет снижаться и к концу периода достигнет величины 1. 85 млрд. человек. К 1972 г. было бы израсходовано 22% первоначальных невозобновляемых природных ресурсов, к 2080 г. – 50%, к 2172 г. – 74%, а к 2258 г. их должно остаться 14% первоначальных запасов. Экологические катастрофы ожидают нашу цивилизацию трижды: в 1995 г. - 1980 108 , в 2101 г. – 1590 108 и в 2192 г. – 1240 108 ед. загрязнения. Основные фонды экономики будут иметь три максимальных значе-ния: в 1982 г. -141, 6 108 , в 2089 г. – 114 108 и в 2176 г. – 96 108 ед. капитала. Доля сельскохозяйственного капитала достигнет максимальных значений в 1988 г. – 0. 84, в 2099 г. – 0. 58 и в 2192 г. – 0. 36.

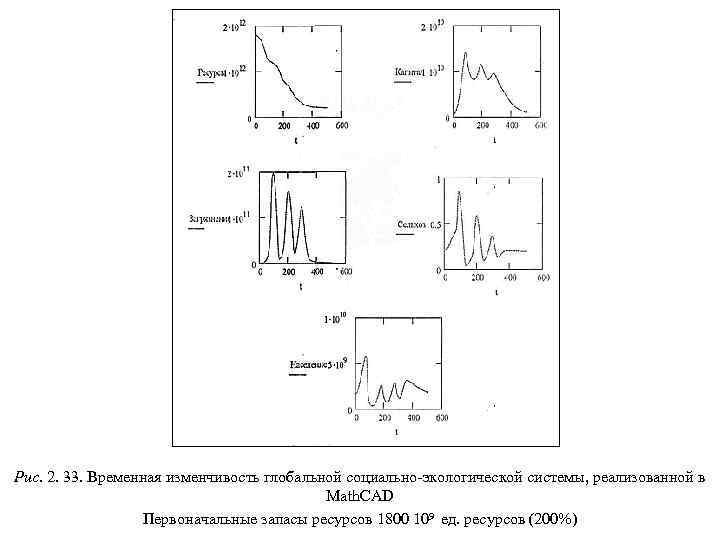Рис. 2. 33. Временная изменчивость глобальной социально-экологической системы, реализованной в Math. CAD Первоначальные запасы ресурсов 1800 109 ед. ресурсов (200%)

Сценарий 3 (рис. 2. 34). В этом случае количество первоначальных невозобновляемых природных ресурсов увеличено на 150% и составляет 2250 млрд. ед. ресурсов. Первый из четырех максимумов численности населения следовало бы ожидать уже в 1960 г. с численностью населения 5. 65 млрд. человек. Последующие пики численности должны произойти в 2069 г. – 2. 54, в 2166 г. – 2. 63 и в 2344 г. – 3. 06 млрд. человек. По сценарию мир потрясут четыре демографические катастрофы: в 2008 г. численность населения должна составить 0. 30, в 2115 г. – 0. 56, в 2209 г. – 0. 73 и в 2294 г. – 1. 29 млрд. человек. От 2344 г. к концу периода численность населения должна неуклонно снижаться и достигнуть 2. 25 млрд. человек. К 1960 г. должно было быть израсходовано 17% первоначальных невозобновляемых природных ресурсов, к 2069 г. – 39%, к 2166 г. – 61%, а к 2344 г. их должно остаться лишь 11%. Нашу цивилизацию по сценарию ожидают четыре экологические катастрофы: в 1982 г. – 2050 108, в 2092 г. – 1730 108, в 2188 г. – 1590 108 и в 2282 г. – 1150 108 ед. загрязнения. Основные фонды экономики должны иметь четыре максимальных значения: в 1968 г. – 148 108, в 2078 г. – 130 108, в 2175 г. – 117 108 и в 2262 г. - 92 108 ед. капитала. Доля сельскохозяйственного капитала тоже должна иметь четыре максимальных значения: в 1976 г. – 0. 88, в 2090 г. – 0. 64, в 2186 г. – 0. 58 и в 2324 г. – 0. 2.

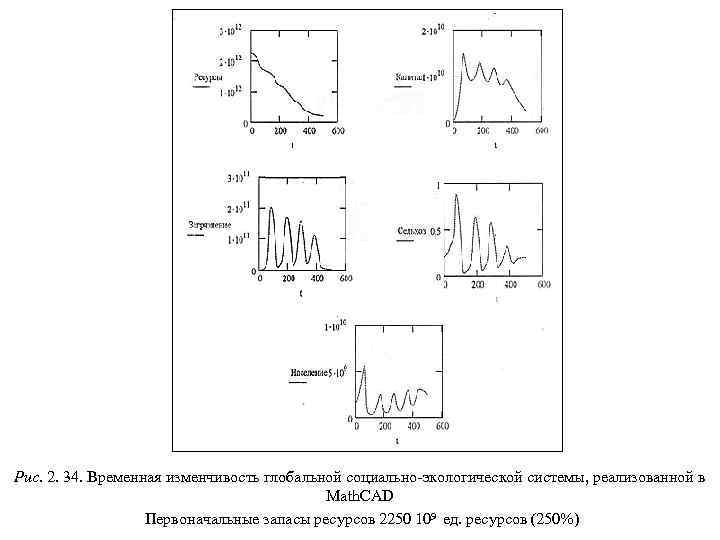Рис. 2. 34. Временная изменчивость глобальной социально-экологической системы, реализованной в Math. CAD Первоначальные запасы ресурсов 2250 109 ед. ресурсов (250%)

Анализ модельных сценариев свидетельствует, что по мере увеличения первоначальных запасов невозобновляемых природных ресурсов наша цивилизация столкнется со все возрастающим количеством демографических, экономических и экологических катастроф. Причем, чем большее виртуальное увеличение первоначальных запасов невозобновляемых природных ресурсов предполагает сценарий, тем раньше наступают катастрофы и тем они острее. При еще большем увеличении моделируемого периода (1900 – 2900 гг) численность населения планеты в каждом из сценариев выходит на уровень 1, 6 млрд. человек и дальше уже не меняется. Аналогичным образом стабилизируются остальные компоненты модели: капитал, доля сельскохозяйственного капитала, загрязнение окружающей среды. Заметим, что численность населения в 1, 6 млрд. человек, приходящаяся на начало XX столетия, соответствует принятому в биосферной концепции устойчивого развития цивилизации однопроцентному уровню потребления первичной продукции, который является предельно допустимым порогом возмущения природной среды. Таким образом, модельные расчеты показывают, что чем больше первоначальные запасы невозобновляемых природных ресурсов, тем больше времени требуется биосфере для принудительного снижения численности населения Земли до допустимого однопроцентного порога потребления населением продукции биоты. Рассмотренные модельные сценарии не следует воспринимать как долгосрочный прогноз поведения глобальной социально-экологической системы. Сценарии иллюстрируют лишь тенденции ее поведения в случае увеличения энергетической мощности нашей цивилизации.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА • • Араб-Оглы Э. А. Демографические и экологические прогнозы: Критика современных буржуазных концепций. – М. , 1978 – 319 с. Глобальная экологическая перспектива 3. Российский национальный комитет содействия ЮНЕП /Под ред. Г. Н. Голубева. – М. , Интер. Диалект= Дадаян В. С. Орбиты планетарной экономики. – М. , Наука, 1989 – 192 с. Егоров В. А. , Каллистов Ю. Н. , Митрофанов В. Б. , Пионтковский А. А. Математические модели глобального развития. – Л. , Гидрометео-издат, 1980. Скиннер Б. Хватит ли человечеству земных ресурсов? : Пер. с англ. М. , Мир. 1989 – 264 с. Форрестер Дж. Мировая динамика. – М. , Наука, 1978. Экодинамика и экологический мониторинг Санкт-Петербургского региона в контексте глобальных изменений. /Под ред. К. Я. Кондратьева и А. К. Фролова - СПб. , Наука, 1996 – 442 с.