1 Кафедра Инженерной графики и дизайна















- Размер: 1.1 Mегабайта
- Количество слайдов: 31
Описание презентации 1 Кафедра Инженерной графики и дизайна по слайдам
 1 Кафедра Инженерной графики и дизайна Раздел 1. Основы образования чертежа Лекция № 1 2008 Материал создан на базе кура лекций по Начертательной геометрии, разработанного зав. кафедрой ИГД МИСи. С Мокрецовой Л. О. — mok@misis. ru Автор: Доцент кафедры ИГД Головкина Валерия Борисовна – v. golovkina@bk. ru
1 Кафедра Инженерной графики и дизайна Раздел 1. Основы образования чертежа Лекция № 1 2008 Материал создан на базе кура лекций по Начертательной геометрии, разработанного зав. кафедрой ИГД МИСи. С Мокрецовой Л. О. — mok@misis. ru Автор: Доцент кафедры ИГД Головкина Валерия Борисовна – v. golovkina@bk. ru
 2 Что требуется для освоения дисциплины 1. Распечатать раздаточный материал к лекциям: • http : // misis. ru / • Институт ИТАСУ • Кафедра Инженерной графики и дизайна • Электронная библиотека • Опорный конспект 2. Подготовить рабочую тетрадь (задачи там же)
2 Что требуется для освоения дисциплины 1. Распечатать раздаточный материал к лекциям: • http : // misis. ru / • Институт ИТАСУ • Кафедра Инженерной графики и дизайна • Электронная библиотека • Опорный конспект 2. Подготовить рабочую тетрадь (задачи там же)
 3 Рекомендуемая литература Основная литература 1. Соломонов К. Н. , Чиченёва О. Н. , Бусыгина Е. Б. Основы начертательной геометрии. -М. : МИСи. С, 2003 2. Соломонов К. Н. , Чиченёва О. Н. , Бусыгина Е. Б. Основы технического черчения. – М. : МИСи. С, 2004 3. Сборник «Национальные стандарты» . ЕСКД. ГОСТ 2. 301 -68 2. 321 -84. -М. : ИПК Издательство Стандартов, 2004 4. Чекмарев А. А. Инженерная графика. М. : Высшая школа, 1998 5. Боголюбов С. К. Инженерная графика. – М. : Машиностроение 2000. – 352 с. Пособия 1. 1. №№ 1241 Головкина В. Б. , Мокрецова Л. О. и др. В. Начертательная геометрия и инженерная графика. Наглядные изображения: область применения и правила построения. Учебно-методическое пособие 2. 2. Курс лекций по Начертательной геометрии. Л. О. Мокрецова, Соломонов К. Н. , Чиченева О. Н. , В. Б. Головкина
3 Рекомендуемая литература Основная литература 1. Соломонов К. Н. , Чиченёва О. Н. , Бусыгина Е. Б. Основы начертательной геометрии. -М. : МИСи. С, 2003 2. Соломонов К. Н. , Чиченёва О. Н. , Бусыгина Е. Б. Основы технического черчения. – М. : МИСи. С, 2004 3. Сборник «Национальные стандарты» . ЕСКД. ГОСТ 2. 301 -68 2. 321 -84. -М. : ИПК Издательство Стандартов, 2004 4. Чекмарев А. А. Инженерная графика. М. : Высшая школа, 1998 5. Боголюбов С. К. Инженерная графика. – М. : Машиностроение 2000. – 352 с. Пособия 1. 1. №№ 1241 Головкина В. Б. , Мокрецова Л. О. и др. В. Начертательная геометрия и инженерная графика. Наглядные изображения: область применения и правила построения. Учебно-методическое пособие 2. 2. Курс лекций по Начертательной геометрии. Л. О. Мокрецова, Соломонов К. Н. , Чиченева О. Н. , В. Б. Головкина
 43. № 889 Информатика. Применение системы трехмерного геометрического моделирования КОМПАС. Дохновская И. В. , Мокрецова Л. О. , Чичинева О. Н. , Свирин В. В. , В. Б. Головкина Средства обеспечения освоения дисциплины • • Программный комплекс Компас 3 D • Курс лекций, созданный с использованием графического редактора « Power Point « и средств Internet.
43. № 889 Информатика. Применение системы трехмерного геометрического моделирования КОМПАС. Дохновская И. В. , Мокрецова Л. О. , Чичинева О. Н. , Свирин В. В. , В. Б. Головкина Средства обеспечения освоения дисциплины • • Программный комплекс Компас 3 D • Курс лекций, созданный с использованием графического редактора « Power Point « и средств Internet.
 5 Содержание курса лекций Предисловие. Введение. Раздел 1. Основы образования чертежа. Лекции 1. Лекция 2. Лекция 3. Раздел 2. Поверхности. Лекция 4. Раздел 3. Пересечение поверхностей. Лекция 5. Лекция 6. Лекция 7 Раздел 4. Аксонометрические проекции. Лекция 8.
5 Содержание курса лекций Предисловие. Введение. Раздел 1. Основы образования чертежа. Лекции 1. Лекция 2. Лекция 3. Раздел 2. Поверхности. Лекция 4. Раздел 3. Пересечение поверхностей. Лекция 5. Лекция 6. Лекция 7 Раздел 4. Аксонометрические проекции. Лекция 8.
 6 Пример выполнения курсовой работы в весеннем семестре
6 Пример выполнения курсовой работы в весеннем семестре
 7 ГАСПАР МОНЖ 1746 –
7 ГАСПАР МОНЖ 1746 –
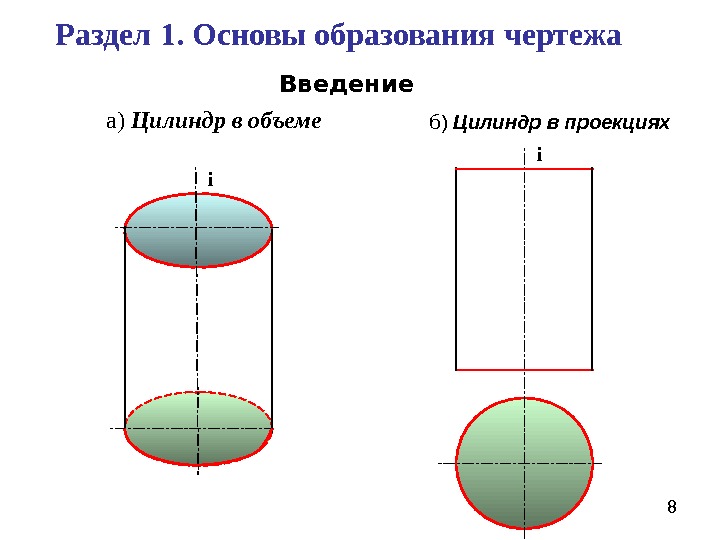
 8 iа) Цилиндр в объеме Раздел 1. Основы образования чертежа iб) Цилиндр в проекциях. Введение
8 iа) Цилиндр в объеме Раздел 1. Основы образования чертежа iб) Цилиндр в проекциях. Введение
 9 Метод проецирования • П 1 – плоскость проекций; • А – объект проецирования; • I – направление проецирования; • А 1 – проекция точки А; Проекция – в переводе с латинского слова projectio означает бросание вперед А 1 А П 1 I
9 Метод проецирования • П 1 – плоскость проекций; • А – объект проецирования; • I – направление проецирования; • А 1 – проекция точки А; Проекция – в переводе с латинского слова projectio означает бросание вперед А 1 А П 1 I
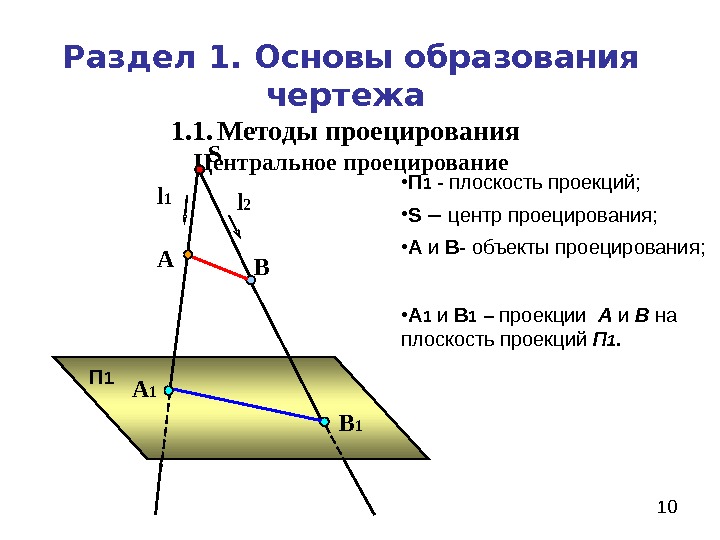
 10 Раздел 1. Основы образования чертежа 1. 1. Методы проецирования Центральное проецирование П 1 S l 1 A 1 А В В 1 l 2 • S – центр проецирования; • П 1 — плоскость проекций; • А и В- объекты проецирования; • А 1 и В 1 – проекции А и В на плоскость проекций П 1.
10 Раздел 1. Основы образования чертежа 1. 1. Методы проецирования Центральное проецирование П 1 S l 1 A 1 А В В 1 l 2 • S – центр проецирования; • П 1 — плоскость проекций; • А и В- объекты проецирования; • А 1 и В 1 – проекции А и В на плоскость проекций П 1.
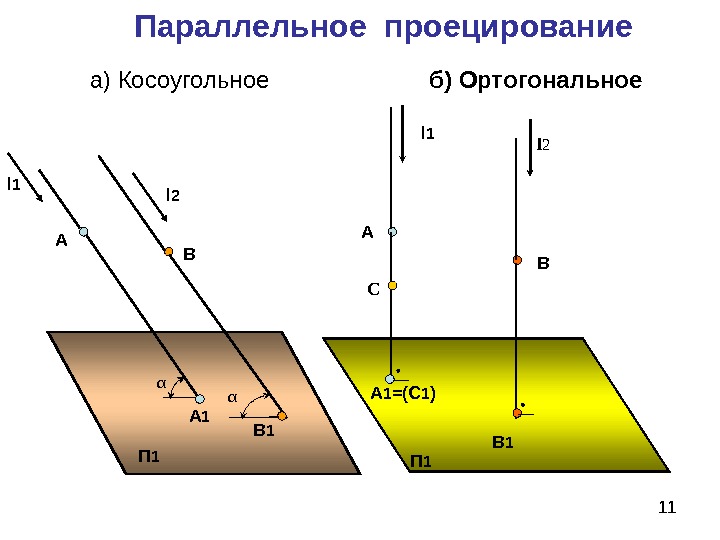
 11 Параллельное проецирование а) Косоугольное П 1 Аl 1 А 1 Вl 2 α В 1α б) Ортогональное П 1 А Вl 1 А 1 =(С 1 ) В 1 С l
11 Параллельное проецирование а) Косоугольное П 1 Аl 1 А 1 Вl 2 α В 1α б) Ортогональное П 1 А Вl 1 А 1 =(С 1 ) В 1 С l
 121. 1. Свойства параллельного проецирования П 1 А Вl 1 А 1=(С 1 ) В 1 С l 2 Выводы: 1. При параллельном проецировании происходит некоторое искажение объектов проецирования; 3. Конкурирующие точки лежат на одном проецирующем луче и служат для определения видимости точек и линий объектов проецирования на плоскости проекций; 2. Отрезок проецируется без искажения, если он параллелен плоскости проекций; 4. Точка принадлежит прямой, если одноименные проекции точки принадлежат одноименным проекциям прямой линии; 5. Равные отрезки прямых линии отображаются равными ; 6. Параллельность прямых на изображении сохраняется.
121. 1. Свойства параллельного проецирования П 1 А Вl 1 А 1=(С 1 ) В 1 С l 2 Выводы: 1. При параллельном проецировании происходит некоторое искажение объектов проецирования; 3. Конкурирующие точки лежат на одном проецирующем луче и служат для определения видимости точек и линий объектов проецирования на плоскости проекций; 2. Отрезок проецируется без искажения, если он параллелен плоскости проекций; 4. Точка принадлежит прямой, если одноименные проекции точки принадлежат одноименным проекциям прямой линии; 5. Равные отрезки прямых линии отображаются равными ; 6. Параллельность прямых на изображении сохраняется.
 131. 1. Комплексный чертеж Проецирование точки на две плоскости П 1 П 2 А l 1 А 1 l 2 Ах. Х Z А Y А А 2 0 АА 1 =А 2 Ах = Z А ; Х А Ах0 =Х А ; АА 2 =А 1 Ах = Y А ; А 2 –фронтальная проекция точки А. А 1 –горизонтальная проекция точки А;
131. 1. Комплексный чертеж Проецирование точки на две плоскости П 1 П 2 А l 1 А 1 l 2 Ах. Х Z А Y А А 2 0 АА 1 =А 2 Ах = Z А ; Х А Ах0 =Х А ; АА 2 =А 1 Ах = Y А ; А 2 –фронтальная проекция точки А. А 1 –горизонтальная проекция точки А;
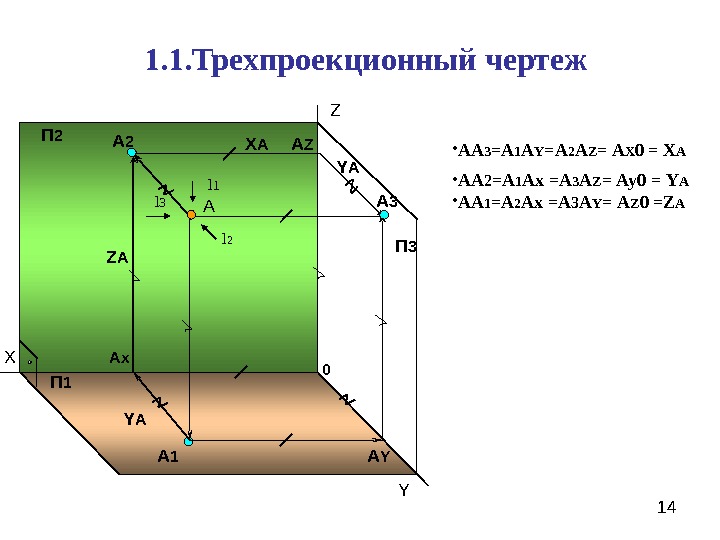
 14 Х Z Y 0 П 1 П 2 А А 1 Ах А 2 А YА Z А 3 Х А П 3 Y А Z А Y А 1. 1. Трехпроекционный чертеж • АА 3 =А 1 А Y =А 2 А Z = А Х 0 = Х А • АА 2 =А 1 Ах =А 3 А Z = Ау0 = Y А • АА 1 =А 2 Ах =А 3 А Y = А Z 0 = Z Аl 1 l 2 l
14 Х Z Y 0 П 1 П 2 А А 1 Ах А 2 А YА Z А 3 Х А П 3 Y А Z А Y А 1. 1. Трехпроекционный чертеж • АА 3 =А 1 А Y =А 2 А Z = А Х 0 = Х А • АА 2 =А 1 Ах =А 3 А Z = Ау0 = Y А • АА 1 =А 2 Ах =А 3 А Y = А Z 0 = Z Аl 1 l 2 l
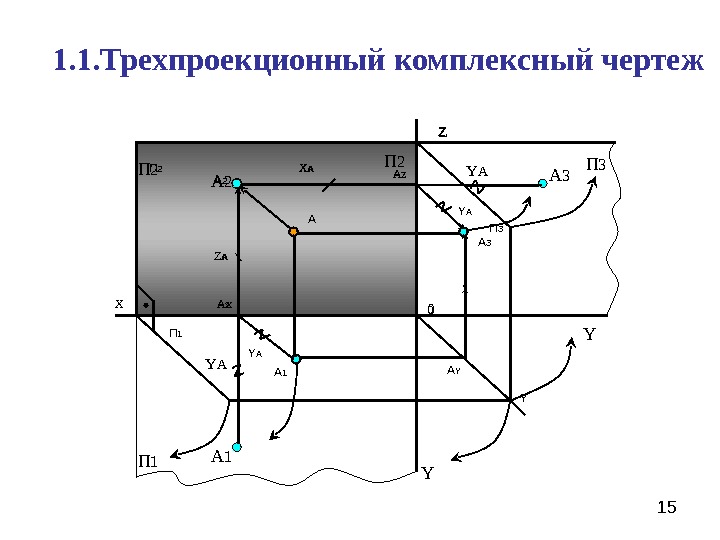
 15 Z Y 0 П 1 П 2 А А 1 А х. А 2 А YА Z А 3 Х А П 3 Y А Z А Y А Х YП 1 Y А П 3 А 1 Y АZ Х А 2 YZ АП 2 Ах А Z 0 Х А 1. 1. Трехпроекционный комплексный чертеж
15 Z Y 0 П 1 П 2 А А 1 А х. А 2 А YА Z А 3 Х А П 3 Y А Z А Y А Х YП 1 Y А П 3 А 1 Y АZ Х А 2 YZ АП 2 Ах А Z 0 Х А 1. 1. Трехпроекционный комплексный чертеж
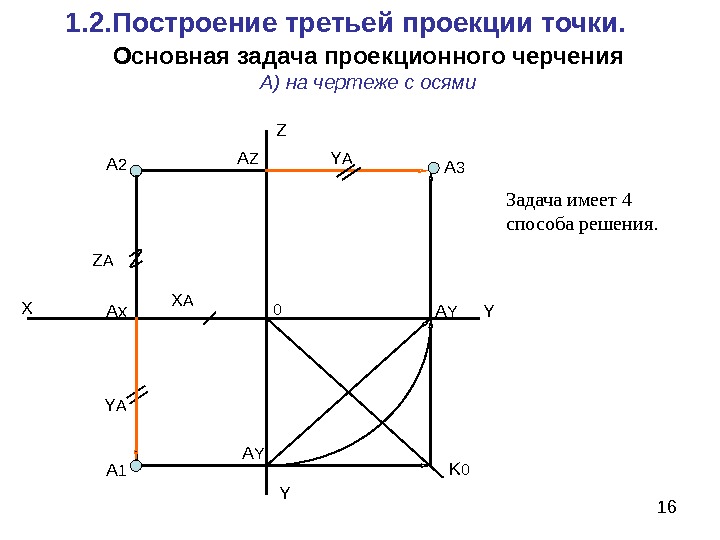
 16 Основная задача проекционного черчения А) на чертеже с осями 1. 2. Построение третьей проекции точки. X Z Y Y 0 A 2 A 1 Ax X A Y AZ A A Z A Y A 3 Y A A Y K 0 Задача имеет 4 способа решения.
16 Основная задача проекционного черчения А) на чертеже с осями 1. 2. Построение третьей проекции точки. X Z Y Y 0 A 2 A 1 Ax X A Y AZ A A Z A Y A 3 Y A A Y K 0 Задача имеет 4 способа решения.
 17 б) Безосный чертеж А 2 А 1 А 3 ∆ Y = Y A — Y B B 2 B 1 ∆ Y = Y A — Y B B 3 А 2 А 1 ; В 2 В 1 – вертикальные линии связи А 2 А 3 ; В 2 В 3 – горизонтальные линии связи
17 б) Безосный чертеж А 2 А 1 А 3 ∆ Y = Y A — Y B B 2 B 1 ∆ Y = Y A — Y B B 3 А 2 А 1 ; В 2 В 1 – вертикальные линии связи А 2 А 3 ; В 2 В 3 – горизонтальные линии связи
 18 Изображение отрезка прямой линии А 2 В 2 –фронтальная проекция отрезка АВ А 1 В 1 –горизонтальная проекция отрезка АВ А 3 В 3 – профильная проекция отрезка АВ А 3 А 2 А 1∆ Y A-B B 2 B 1 ∆ Y A-B B 3 Соединяем одноименные проекции точек А и В АВ — отрезок общего положения, не параллелен и не перпендикулярен ни одной из плоскостей проекций й.
18 Изображение отрезка прямой линии А 2 В 2 –фронтальная проекция отрезка АВ А 1 В 1 –горизонтальная проекция отрезка АВ А 3 В 3 – профильная проекция отрезка АВ А 3 А 2 А 1∆ Y A-B B 2 B 1 ∆ Y A-B B 3 Соединяем одноименные проекции точек А и В АВ — отрезок общего положения, не параллелен и не перпендикулярен ни одной из плоскостей проекций й.
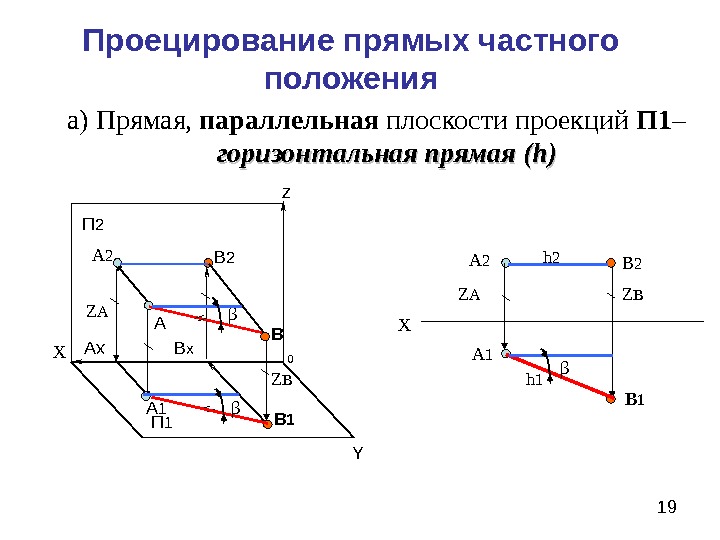
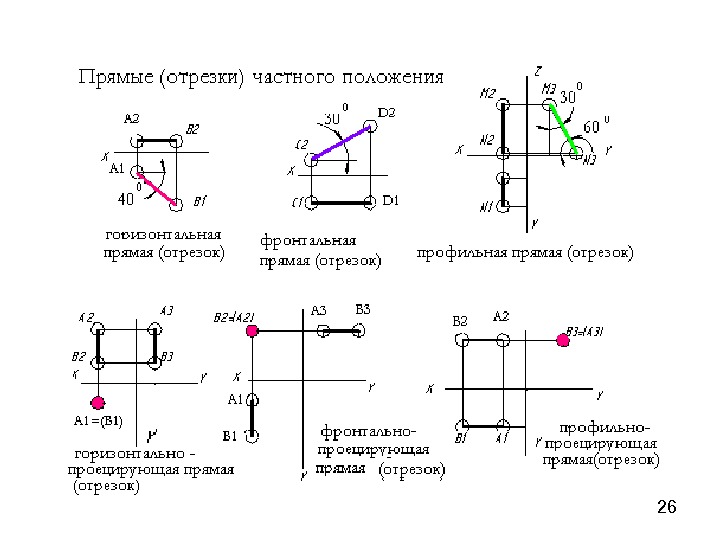
 19 П 1 П 2 z Y 0 Х Проецирование прямых частного положения а) Прямая, параллельная плоскости проекций П 1 – горизонтальная прямая ( h)h) А А 1 Ах В 1 ВВ 2 ββА 2 Х А 2 В 2 А 1 В 1βZ А Z В Z Вh 2 h
19 П 1 П 2 z Y 0 Х Проецирование прямых частного положения а) Прямая, параллельная плоскости проекций П 1 – горизонтальная прямая ( h)h) А А 1 Ах В 1 ВВ 2 ββА 2 Х А 2 В 2 А 1 В 1βZ А Z В Z Вh 2 h
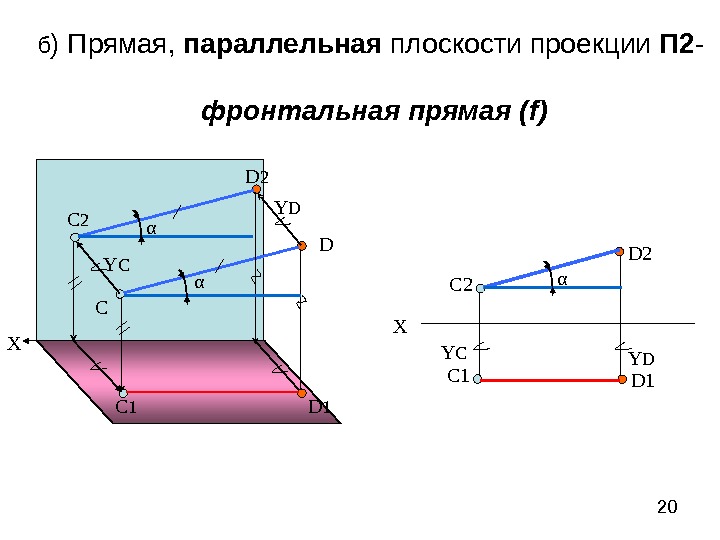
 20 б ) Прямая, параллельная плоскости проекции П 2 — фронтальная прямая ( f ) Х С DС 2 D 2 C 1 D 1αα Y D Y C Х С 2 С 1 D 2 D 1α Y C Y
20 б ) Прямая, параллельная плоскости проекции П 2 — фронтальная прямая ( f ) Х С DС 2 D 2 C 1 D 1αα Y D Y C Х С 2 С 1 D 2 D 1α Y C Y
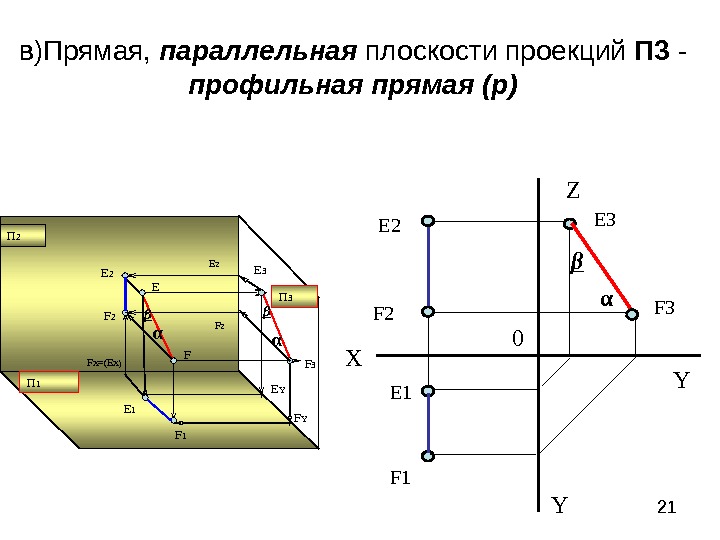
 21 в)Прямая, параллельная плоскости проекций П 3 — профильная прямая (р) П 2 F 3 Х Z Y Y 0 F 1 E 1 F 2 E 3 F 3β α П 1 П 3 E F E 3 F Y F 1 E Y E 1 F 2 E 2 F Х = (E Х ) E Z F Z αα β β
21 в)Прямая, параллельная плоскости проекций П 3 — профильная прямая (р) П 2 F 3 Х Z Y Y 0 F 1 E 1 F 2 E 3 F 3β α П 1 П 3 E F E 3 F Y F 1 E Y E 1 F 2 E 2 F Х = (E Х ) E Z F Z αα β β
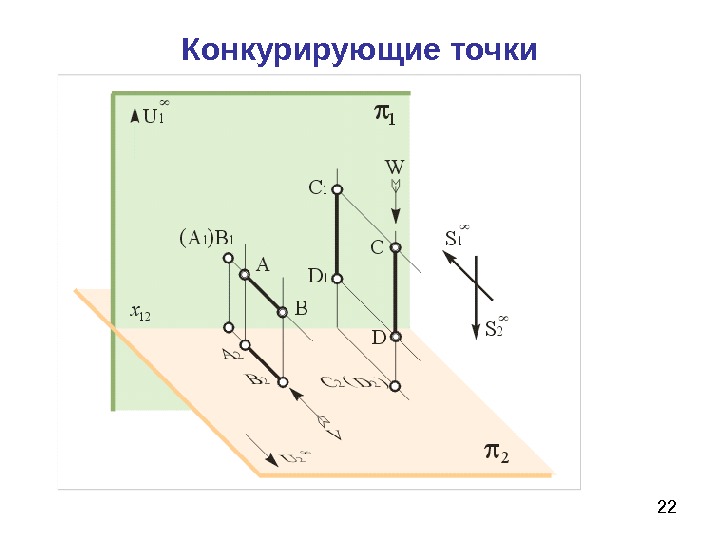
 22 Конкурирующие точки
22 Конкурирующие точки
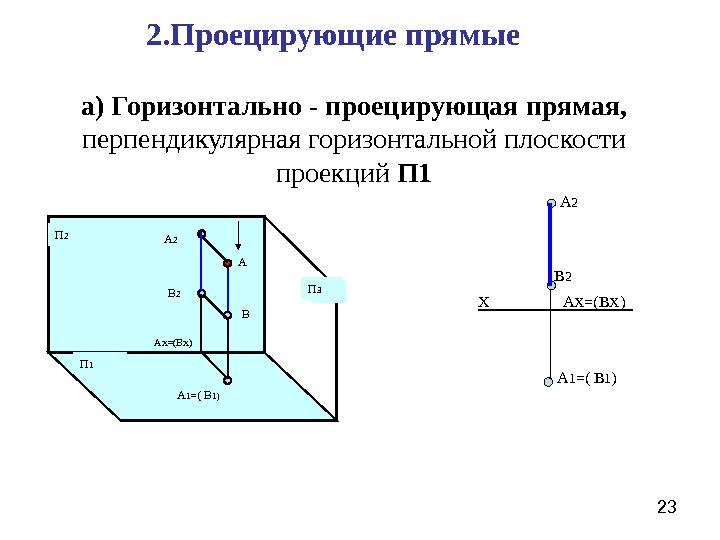
 232. Проецирующие прямые а) Горизонтально — проецирующая прямая, перпендикулярная горизонтальной плоскости проекций П 1 Х А 2 В 2 А 1 =( В 1 )П 1 П 2 П 3 А В А 1 =( В 1)А 2 В 2 А Х = (В Х )
232. Проецирующие прямые а) Горизонтально — проецирующая прямая, перпендикулярная горизонтальной плоскости проекций П 1 Х А 2 В 2 А 1 =( В 1 )П 1 П 2 П 3 А В А 1 =( В 1)А 2 В 2 А Х = (В Х )
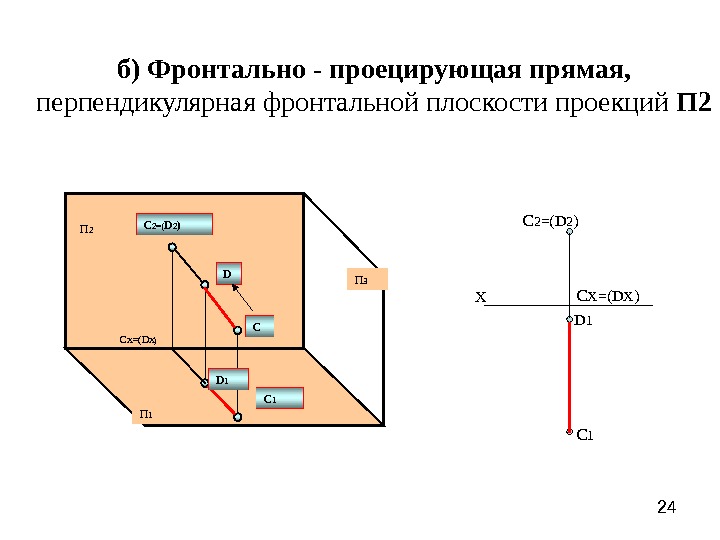
 24 б) Фронтально — проецирующая прямая, перпендикулярная фронтальной плоскости проекций П 2 ХП 2 П 1 П 3 СD C 1 D 1 C 2 =( D 2 ) D 1 C 1 С Х =( D Х) С Х =( D Х )
24 б) Фронтально — проецирующая прямая, перпендикулярная фронтальной плоскости проекций П 2 ХП 2 П 1 П 3 СD C 1 D 1 C 2 =( D 2 ) D 1 C 1 С Х =( D Х) С Х =( D Х )
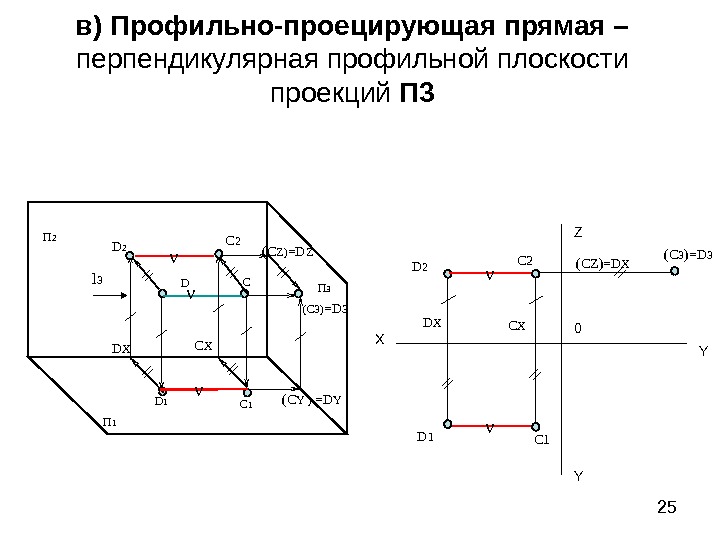
 25 в) Профильно-проецирующая прямая – перпендикулярная профильной плоскости проекций П 3 П 2 П 1 П 3 С D C 1 D 1 D 2 D Х С 2 ( C Z ) =D Z ( С Y ) = D Y(C 3) =D 3 C Х Х Z Y Y 0 D 2 D 1 D Х C 1 C Х ( CZ ) =D ХС 2 (C 3 )=D 3 l 3 ν νν ν ν
25 в) Профильно-проецирующая прямая – перпендикулярная профильной плоскости проекций П 3 П 2 П 1 П 3 С D C 1 D 1 D 2 D Х С 2 ( C Z ) =D Z ( С Y ) = D Y(C 3) =D 3 C Х Х Z Y Y 0 D 2 D 1 D Х C 1 C Х ( CZ ) =D ХС 2 (C 3 )=D 3 l 3 ν νν ν ν

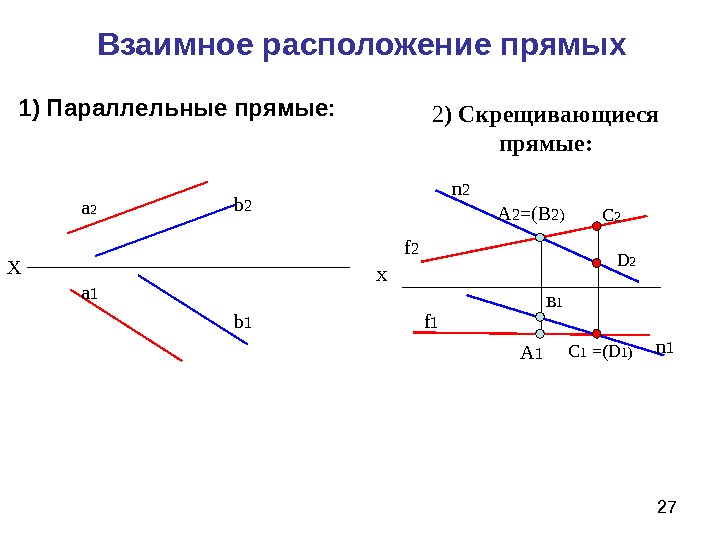
 27 Взаимное расположение прямых 1 ) Параллельные прямые: Х а 2 b 2 a 1 b 1 2 ) Скрещивающиеся прямые: Х f 2 f 1 n 2 n 1 A 2 =(B 2) A 1 B 1 C 1 =(D 1)
27 Взаимное расположение прямых 1 ) Параллельные прямые: Х а 2 b 2 a 1 b 1 2 ) Скрещивающиеся прямые: Х f 2 f 1 n 2 n 1 A 2 =(B 2) A 1 B 1 C 1 =(D 1)
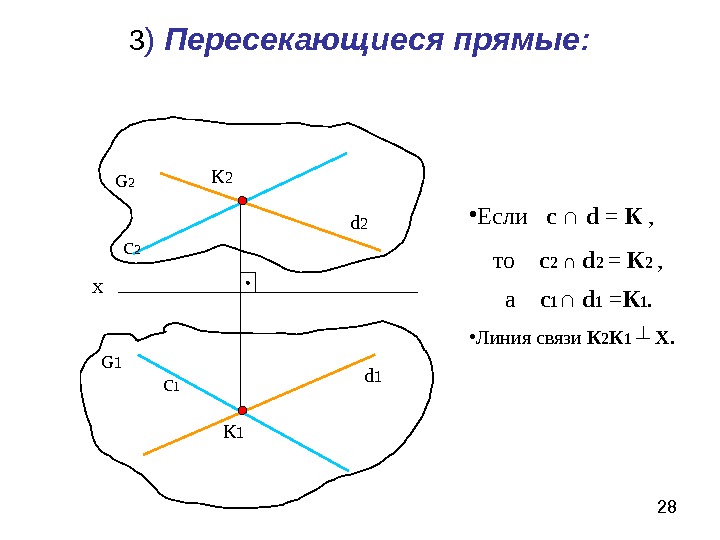
 283 ) Пересекающиеся прямые: Х с 2 с 1 К 2 К 1 d 2 d 1 • Если с ∩ d = К , то с 2 ∩ d 2 = К 2 , а с 1 ∩ d 1 = К 1. • Линия связи К 2 К 1 ┴ Х. G 2 G
283 ) Пересекающиеся прямые: Х с 2 с 1 К 2 К 1 d 2 d 1 • Если с ∩ d = К , то с 2 ∩ d 2 = К 2 , а с 1 ∩ d 1 = К 1. • Линия связи К 2 К 1 ┴ Х. G 2 G
 29 Теорема о проецировании прямого угла Х h 2 h 1 а 2 К 1 а 1 < ( a ∩ h ) = 90 °
29 Теорема о проецировании прямого угла Х h 2 h 1 а 2 К 1 а 1 < ( a ∩ h ) = 90 °
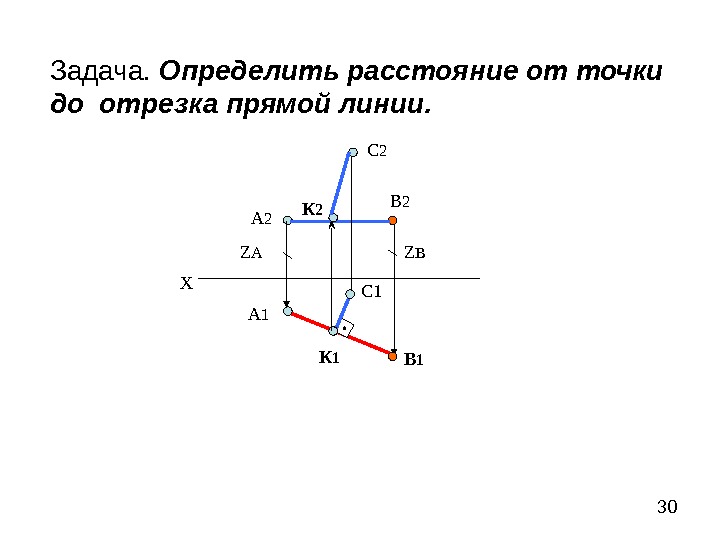
 30 Задача. Определить расстояние от точки до отрезка прямой линии. Х А 2 В 2 А 1 В 1 Z А Z В К 1 К 2 С 1 С
30 Задача. Определить расстояние от точки до отрезка прямой линии. Х А 2 В 2 А 1 В 1 Z А Z В К 1 К 2 С 1 С
 31 СПАСИБО ЗА ВНИМАНИЕ !
31 СПАСИБО ЗА ВНИМАНИЕ !

