1 К. К. Лихарев, Одноэлектроника, В мире









































- Размер: 11.8 Mегабайта
- Количество слайдов: 105
Описание презентации 1 К. К. Лихарев, Одноэлектроника, В мире по слайдам
 1 К. К. Лихарев, Одноэлектроника, В мире науки , n. 8, 1992, c. 42 К. К. Likharev , Correlated discrete transfer of single electrons in ultra small tunnel junctions, IBM J. Res. Development, Vol. 32, N 0. 1, 1988, p. 144 -158. К. К. Likharev , Tord Claeson, Single Electronics, Scientific American, June 1992, p. 80 -85 К. К. Likharev , Single-Electron Devices and Their Applications, Proceedings of the IEEE, Vol. 87, No. 4, 1999, p. 606 -632 Теория описанных явлений создавалась усилиями многих ученых, но решающий вклад в нее внесли московские физики Д. А. Аверин и К. К. Лихарев. Сделанные ими расчеты и предсказания необходимо было проверить на эксперименте. Первыми эту проверку в январе 1987 года осуществили сотрудники физического факультета МГУ кандидат физико-математических наук Л. С. Кузьмин и доктор физико-математических наук К. К. Лихарев. Емкость С : Δ V = e/C, S ~ 0. 1 x 0. 1 mm 2 , С ~ 10 -10 F , Δ V~10 -9 V; S ≤ 0. 1 μ m 2 , C ≤ 10 -15 F, Δ V~10 -4 V Δ V ↔ V T = k. T/e ; T = 300 K, V T = 3· 10 -2 V; T = 1 K, V T ~ 10 -4 V ~ Δ V [C~10 -15 F] Одноэлектроника Теория: 1985 -1988 гг. — Лихарев К. К. , Аверин Д. В. , Зорин А. Б. , Widom Эксп. : 1987 -88 гг. – Кузьмин Л. С. , Лихарев К. К. ; Fulton & Dolan; Barner & Ruggiero
1 К. К. Лихарев, Одноэлектроника, В мире науки , n. 8, 1992, c. 42 К. К. Likharev , Correlated discrete transfer of single electrons in ultra small tunnel junctions, IBM J. Res. Development, Vol. 32, N 0. 1, 1988, p. 144 -158. К. К. Likharev , Tord Claeson, Single Electronics, Scientific American, June 1992, p. 80 -85 К. К. Likharev , Single-Electron Devices and Their Applications, Proceedings of the IEEE, Vol. 87, No. 4, 1999, p. 606 -632 Теория описанных явлений создавалась усилиями многих ученых, но решающий вклад в нее внесли московские физики Д. А. Аверин и К. К. Лихарев. Сделанные ими расчеты и предсказания необходимо было проверить на эксперименте. Первыми эту проверку в январе 1987 года осуществили сотрудники физического факультета МГУ кандидат физико-математических наук Л. С. Кузьмин и доктор физико-математических наук К. К. Лихарев. Емкость С : Δ V = e/C, S ~ 0. 1 x 0. 1 mm 2 , С ~ 10 -10 F , Δ V~10 -9 V; S ≤ 0. 1 μ m 2 , C ≤ 10 -15 F, Δ V~10 -4 V Δ V ↔ V T = k. T/e ; T = 300 K, V T = 3· 10 -2 V; T = 1 K, V T ~ 10 -4 V ~ Δ V [C~10 -15 F] Одноэлектроника Теория: 1985 -1988 гг. — Лихарев К. К. , Аверин Д. В. , Зорин А. Б. , Widom Эксп. : 1987 -88 гг. – Кузьмин Л. С. , Лихарев К. К. ; Fulton & Dolan; Barner & Ruggiero
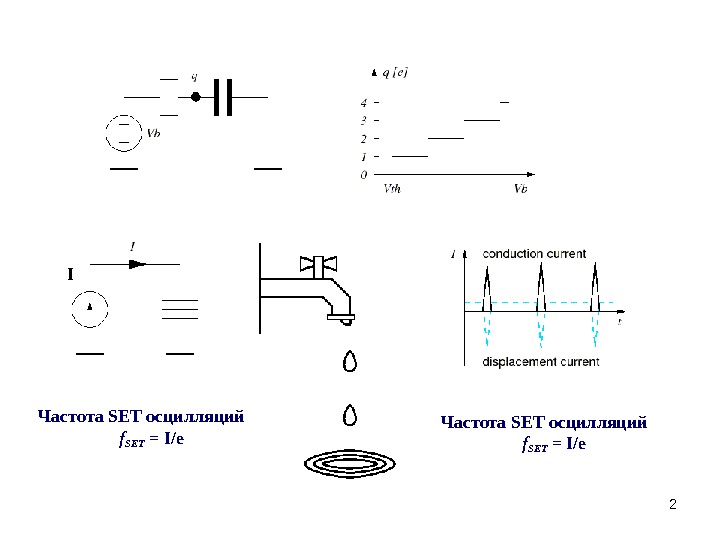
 2 Частота SET осцилляций f SET = I/e. I
2 Частота SET осцилляций f SET = I/e. I
 3 Когда же будет достигнут предел миниатюризации обычной электроники? Уже сейчас микроэлектронной промышленностью в опытном порядке создаются транзисторы с размером рабочих элементов 20– 30 нм. Они еще способны работать с обычными электрическими сигналами, однако при дальнейшем уменьшении размеров очень быстро нарастают проблемы, о которых говорилось выше. Область от 30 нм до 5 нм (так называемая область мезоструктур) следует считать переходной от классической твердотельной электроники к квантовой. Промышленность вплотную подошла к этой области и уже столкнулась с рядом трудностей. В соответствии с законом Мура, полное освоение области мезоэлектроники ожидается примерно через десять лет. Таким образом, мезотранзисторы — это последний рубеж существования обычных транзисторов, за которым последует поколение нанотранзисторов. Закон Мура: 19 апреля 1965 г. , в журнале «Electronics» (vol. 39, № 8) вышла ныне всемирно знаменитая статья Гордона Мура (Gordon Moore) «Cramming more components i nto integrated circuits» (Объединение большего количества компонентов в интегральных схемах). В этой статье Мур (будущий сооснователь корпорации Intel), работавший тогда директором отдела разработок компании Fairchild Semiconductors, дал прогноз развития микроэлектроники на ближайшие десять лет на основании анализа шестилетнего развития микроэлектроники, предсказав, что количество элементов на кристаллах электронных микросхем будет и далее удваиваться каждый год.
3 Когда же будет достигнут предел миниатюризации обычной электроники? Уже сейчас микроэлектронной промышленностью в опытном порядке создаются транзисторы с размером рабочих элементов 20– 30 нм. Они еще способны работать с обычными электрическими сигналами, однако при дальнейшем уменьшении размеров очень быстро нарастают проблемы, о которых говорилось выше. Область от 30 нм до 5 нм (так называемая область мезоструктур) следует считать переходной от классической твердотельной электроники к квантовой. Промышленность вплотную подошла к этой области и уже столкнулась с рядом трудностей. В соответствии с законом Мура, полное освоение области мезоэлектроники ожидается примерно через десять лет. Таким образом, мезотранзисторы — это последний рубеж существования обычных транзисторов, за которым последует поколение нанотранзисторов. Закон Мура: 19 апреля 1965 г. , в журнале «Electronics» (vol. 39, № 8) вышла ныне всемирно знаменитая статья Гордона Мура (Gordon Moore) «Cramming more components i nto integrated circuits» (Объединение большего количества компонентов в интегральных схемах). В этой статье Мур (будущий сооснователь корпорации Intel), работавший тогда директором отдела разработок компании Fairchild Semiconductors, дал прогноз развития микроэлектроники на ближайшие десять лет на основании анализа шестилетнего развития микроэлектроники, предсказав, что количество элементов на кристаллах электронных микросхем будет и далее удваиваться каждый год.
 4 Выступая в 1975 г. на конференции International Electron Devices Meeting, Гордон Мур отметил, что за прошедшее десятилетие количество элементов на кристаллах действительно удваивалось каждый год, однако в будущем, когда сложность чипов возрастет, удвоение числа транзисторов в микросхемах будет происходить несколько медленнее – каждые два года. Это новое предсказание также сбылось, и закон Мура продолжает в этом виде (удвоение за два года) действовать поныне (то есть в течение почти тридцати лет!), в последнее время немного ускорившись до удвоения за 18 месяцев, что можно наглядно проследить на примере деятельности лидера современной полупроводниковой индустрии корпорации Intel. Существует несколько интерпретаций закона Мура: • наиболее выгодное число транзисторов на кристалле удваивается каждый год; • число транзисторов в производимых чипах удваивается каждые два года; • технологически возможное число транзисторов на кристалле микропроцессора удваивается каждые два года; • производительность микропроцессоров удваивается каждые 18 мес. ; • тактовая частота микропроцессоров удваивается каждые 18 мес. ; • вычислительная мощность компьютера удваивается каждые 18 мес. ; • доступная вычислительная мощность удваивается каждые 18 мес. ; • плотность транзисторов на чипе удваивается каждые 18 мес. ; • вычислительная мощность, доступная за $1, удваивается каждые 18 мес. ; • стоимость чипа падает вдвое каждые 18 мес.
4 Выступая в 1975 г. на конференции International Electron Devices Meeting, Гордон Мур отметил, что за прошедшее десятилетие количество элементов на кристаллах действительно удваивалось каждый год, однако в будущем, когда сложность чипов возрастет, удвоение числа транзисторов в микросхемах будет происходить несколько медленнее – каждые два года. Это новое предсказание также сбылось, и закон Мура продолжает в этом виде (удвоение за два года) действовать поныне (то есть в течение почти тридцати лет!), в последнее время немного ускорившись до удвоения за 18 месяцев, что можно наглядно проследить на примере деятельности лидера современной полупроводниковой индустрии корпорации Intel. Существует несколько интерпретаций закона Мура: • наиболее выгодное число транзисторов на кристалле удваивается каждый год; • число транзисторов в производимых чипах удваивается каждые два года; • технологически возможное число транзисторов на кристалле микропроцессора удваивается каждые два года; • производительность микропроцессоров удваивается каждые 18 мес. ; • тактовая частота микропроцессоров удваивается каждые 18 мес. ; • вычислительная мощность компьютера удваивается каждые 18 мес. ; • доступная вычислительная мощность удваивается каждые 18 мес. ; • плотность транзисторов на чипе удваивается каждые 18 мес. ; • вычислительная мощность, доступная за $1, удваивается каждые 18 мес. ; • стоимость чипа падает вдвое каждые 18 мес.
 5 Логические элементы, срабатывающие на определенную величину зарядового пакета, как, например, в случае КМОП-схем, будут слишком часто ошибаться, если пакет окажется недостаточно велик. Так, при кодировании логической единицы пакетом из десяти зарядов с порогом срабатывания в пять зарядов логический элемент будет неправильно срабатывать примерно в 3% случаев. Иначе говоря, согласно пуассоновской статистике, в трех случаях из ста мы обнаружим в зарядовом пакете менее пяти электронов. При этом существенно увеличить избыточный заряд, хранимый в структуре нанометрового размера, невозможно. Например, на сферическом кластере радиусом 2– 3 нм можно разместить без проблем лишь несколько лишних электронов. Кроме эффекта квантования электрического заряда, на малых расстояниях начинают сказываться волновые свойства частиц. Длина когерентности электронной волны в твердом теле при обычной температуре составляет величину порядка единиц нанометров. Поэтому на расстояниях, меньших 1 нм, начинают проявляться волновые свойства электронов. Выражается это в том, что когда вещество берется в малых количествах, его не всегда можно однозначно отнести к изоляторам, проводникам или полупроводникам. Например, некоторые химические элементы, взятые в количестве, допустим, 20, 50 и 100 атомов, будут последовательно проходить стадию изолятора, полупроводника и проводника соответственно. Все сказанное иллюстрирует тот факт, что использование ресурсов вещества, пространства, времени, энергии и информации в наномире строго регламентируется особыми правилами, основывающимися на законах квантовой механики. Мало того что конструирование нанотранзисторов превращается в сложную квантовомеханическую задачу, овеществление квантовомеханических схем и «чертежей» требует разработки сложнейших технологических процессов. Итак, нанотранзистор — это существенно квантовомеханический прибор. Однако он вовсе не обязан работать только с квантовой информацией. Доказано, что в базисе нанотранзисторов возможна реализация устройств обычной классической логики. Более того, разработка промышленных технологий создания нанометровых приборов классической логики — главная задача современной наноэлектроники. На ее решение брошены огромные финансовые ресурсы в крупнейших научных центрах мира.
5 Логические элементы, срабатывающие на определенную величину зарядового пакета, как, например, в случае КМОП-схем, будут слишком часто ошибаться, если пакет окажется недостаточно велик. Так, при кодировании логической единицы пакетом из десяти зарядов с порогом срабатывания в пять зарядов логический элемент будет неправильно срабатывать примерно в 3% случаев. Иначе говоря, согласно пуассоновской статистике, в трех случаях из ста мы обнаружим в зарядовом пакете менее пяти электронов. При этом существенно увеличить избыточный заряд, хранимый в структуре нанометрового размера, невозможно. Например, на сферическом кластере радиусом 2– 3 нм можно разместить без проблем лишь несколько лишних электронов. Кроме эффекта квантования электрического заряда, на малых расстояниях начинают сказываться волновые свойства частиц. Длина когерентности электронной волны в твердом теле при обычной температуре составляет величину порядка единиц нанометров. Поэтому на расстояниях, меньших 1 нм, начинают проявляться волновые свойства электронов. Выражается это в том, что когда вещество берется в малых количествах, его не всегда можно однозначно отнести к изоляторам, проводникам или полупроводникам. Например, некоторые химические элементы, взятые в количестве, допустим, 20, 50 и 100 атомов, будут последовательно проходить стадию изолятора, полупроводника и проводника соответственно. Все сказанное иллюстрирует тот факт, что использование ресурсов вещества, пространства, времени, энергии и информации в наномире строго регламентируется особыми правилами, основывающимися на законах квантовой механики. Мало того что конструирование нанотранзисторов превращается в сложную квантовомеханическую задачу, овеществление квантовомеханических схем и «чертежей» требует разработки сложнейших технологических процессов. Итак, нанотранзистор — это существенно квантовомеханический прибор. Однако он вовсе не обязан работать только с квантовой информацией. Доказано, что в базисе нанотранзисторов возможна реализация устройств обычной классической логики. Более того, разработка промышленных технологий создания нанометровых приборов классической логики — главная задача современной наноэлектроники. На ее решение брошены огромные финансовые ресурсы в крупнейших научных центрах мира.
 6 Пусть емкость такой системы есть С. Тогда энергия данной системы, т. е. , по сути, конденсатора, составляет E = Q 2 /2 C , (1) где Q — заряд на обкладках конденсатора. Так как заряд электрона является дискретной величиной, то минимальная величина изменения энергии Δ Е составит Δ Е = e 2 /2 C , (2) где е — элементарный заряд электрона. Для наблюдения эффектов необходимо, чтобы минимальное изменение энергии было больше температурных флуктуаций, т. е e 2 /2 C >> k. T , (3) где k– постоянная Больцмана, а Т – температура. Кроме этого, необходимо, чтобы данное изменение превышало энергию квантовых флуктуации Δ Е >> h. G/C , (4) где G = max (Gs, Gi), Gi — проводимость туннельного перехода, Gs — проводимость, шунтирующая переход. Исходя из (4) можно записать, что G <> RQ, (5) где R Q — квантовое сопротивление R Q =h/4 e 2 =6, 45 к. Ом. Одно из важнейших предположений теории одноэлектронного туннелирования заключалось в том, что начальный заряд Q 0 , на туннельном переходе может быть отличен от 0, и, более того, может принимать значения, не кратные целому числу электронов. Данный факт объясняется тем, что начальный заряд может создаваться поляризацией близлежащих электродов, заряженных примесей и т. д. и, таким образом, иметь любое значение. Тогда заряд Q в уравнении (1) будет иметь вид Q=Q 0 –е. Из всего вышесказанного вытекает, что, если Q лежит в пределах от -е/2 до +е/2, добавление или вычитание целого числа электронов будет увеличивать энергию (1), т. е. является энергетически невыгодным. Данный вывод иллюстрируется на рис. 1.
6 Пусть емкость такой системы есть С. Тогда энергия данной системы, т. е. , по сути, конденсатора, составляет E = Q 2 /2 C , (1) где Q — заряд на обкладках конденсатора. Так как заряд электрона является дискретной величиной, то минимальная величина изменения энергии Δ Е составит Δ Е = e 2 /2 C , (2) где е — элементарный заряд электрона. Для наблюдения эффектов необходимо, чтобы минимальное изменение энергии было больше температурных флуктуаций, т. е e 2 /2 C >> k. T , (3) где k– постоянная Больцмана, а Т – температура. Кроме этого, необходимо, чтобы данное изменение превышало энергию квантовых флуктуации Δ Е >> h. G/C , (4) где G = max (Gs, Gi), Gi — проводимость туннельного перехода, Gs — проводимость, шунтирующая переход. Исходя из (4) можно записать, что G <> RQ, (5) где R Q — квантовое сопротивление R Q =h/4 e 2 =6, 45 к. Ом. Одно из важнейших предположений теории одноэлектронного туннелирования заключалось в том, что начальный заряд Q 0 , на туннельном переходе может быть отличен от 0, и, более того, может принимать значения, не кратные целому числу электронов. Данный факт объясняется тем, что начальный заряд может создаваться поляризацией близлежащих электродов, заряженных примесей и т. д. и, таким образом, иметь любое значение. Тогда заряд Q в уравнении (1) будет иметь вид Q=Q 0 –е. Из всего вышесказанного вытекает, что, если Q лежит в пределах от -е/2 до +е/2, добавление или вычитание целого числа электронов будет увеличивать энергию (1), т. е. является энергетически невыгодным. Данный вывод иллюстрируется на рис. 1.
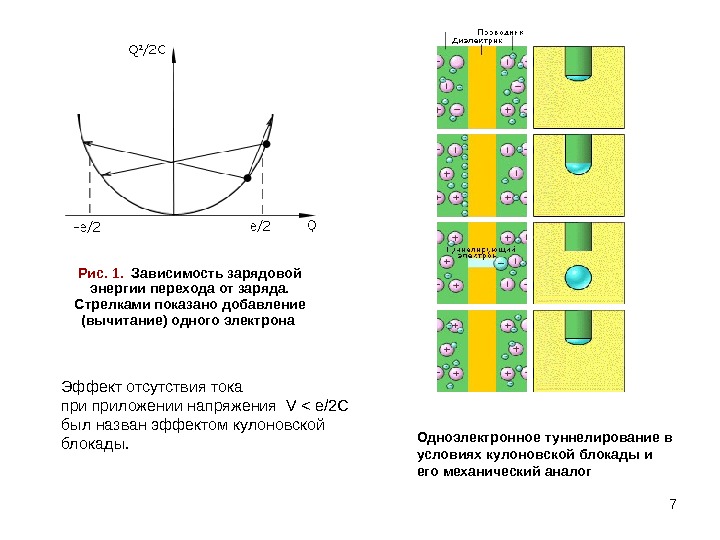
 7 Рис. 1. Зависимость зарядовой энергии перехода от заряда. Стрелками показано добавление (вычитание) одного электрона Эффект отсутствия тока приложении напряжения V < e/2 C был назван эффектом кулоновской блокады. Одноэлектронное туннелирование в условиях кулоновской блокады и его механический аналог
7 Рис. 1. Зависимость зарядовой энергии перехода от заряда. Стрелками показано добавление (вычитание) одного электрона Эффект отсутствия тока приложении напряжения V < e/2 C был назван эффектом кулоновской блокады. Одноэлектронное туннелирование в условиях кулоновской блокады и его механический аналог
 8 Figure 1. 1: The left side shows, that the electron cloud shift against the lattice of atoms is not quantized. The right side shows an accumulation of electrons at a tunnel junction.
8 Figure 1. 1: The left side shows, that the electron cloud shift against the lattice of atoms is not quantized. The right side shows an accumulation of electrons at a tunnel junction.
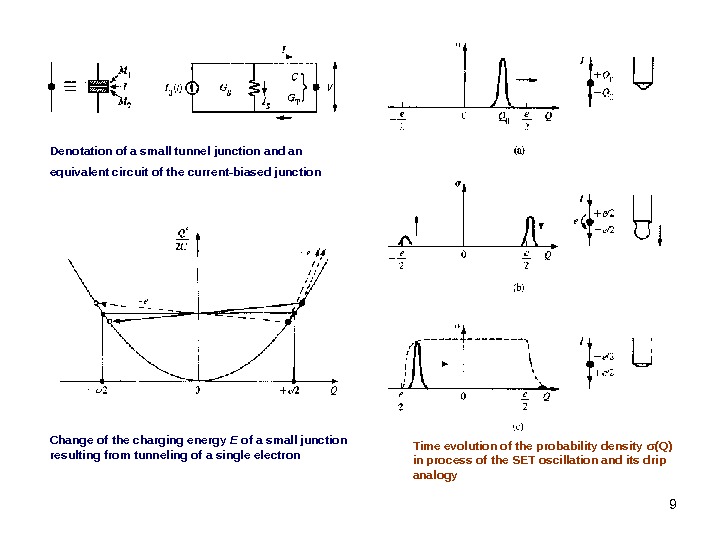
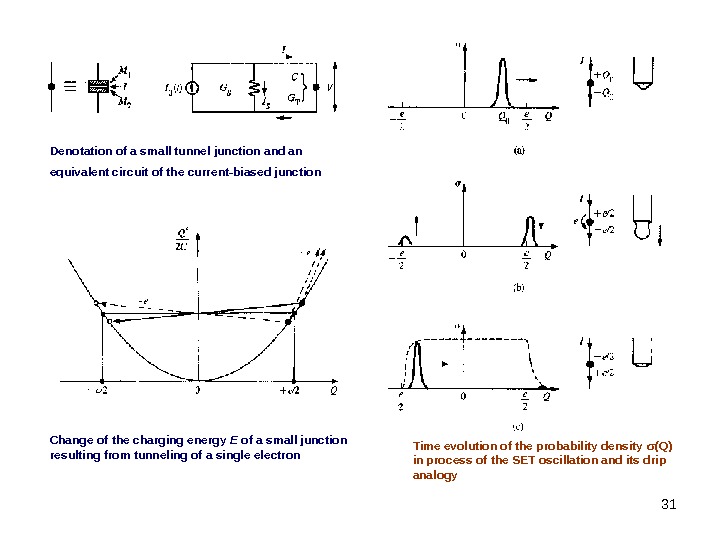
 9 Denotation of a small tunnel junction and an equivalent circuit of the current-biased junction Change of the charging energy E of a small junction resulting from tunneling of a single electron Time evolution of the probability density σ (Q) in process of the SET oscillation and its drip analogy
9 Denotation of a small tunnel junction and an equivalent circuit of the current-biased junction Change of the charging energy E of a small junction resulting from tunneling of a single electron Time evolution of the probability density σ (Q) in process of the SET oscillation and its drip analogy
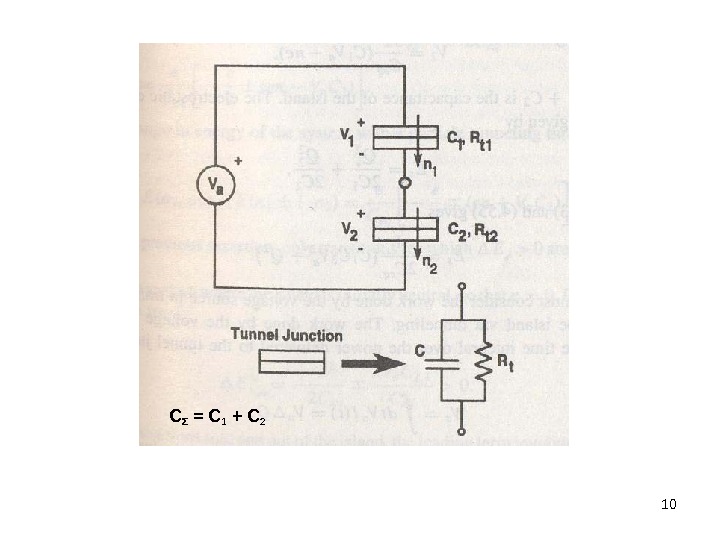
 10 C Σ = C 1 +
10 C Σ = C 1 +
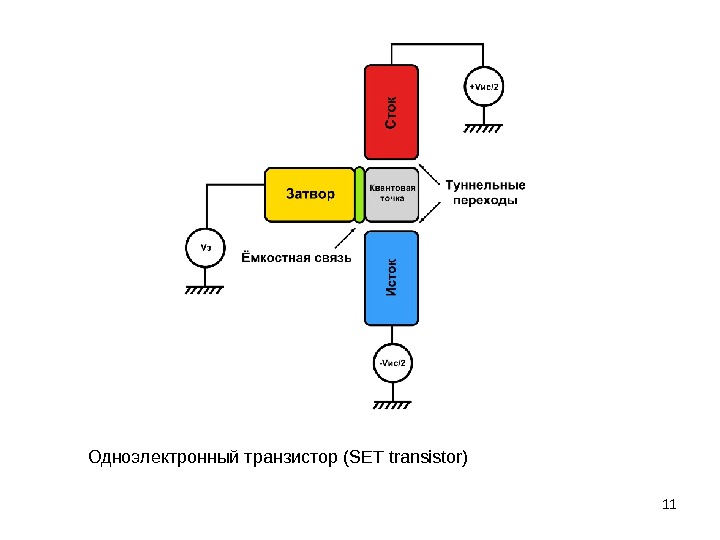
 11 Одноэлектронный транзистор ( SET transistor)
11 Одноэлектронный транзистор ( SET transistor)
 12 Одноэлектронный транзистор с подводящими контактами из ниобия и алюминиевым островом. Created by Torsten Henning and published in Charging effects in niobium nanostructures , Ph. D thesis, Mikroelektronik och Nanovetenskap, Chalmers Tekniska Högskola AB och Göteborgs Universitet, Göteborg 1999.
12 Одноэлектронный транзистор с подводящими контактами из ниобия и алюминиевым островом. Created by Torsten Henning and published in Charging effects in niobium nanostructures , Ph. D thesis, Mikroelektronik och Nanovetenskap, Chalmers Tekniska Högskola AB och Göteborgs Universitet, Göteborg 1999.
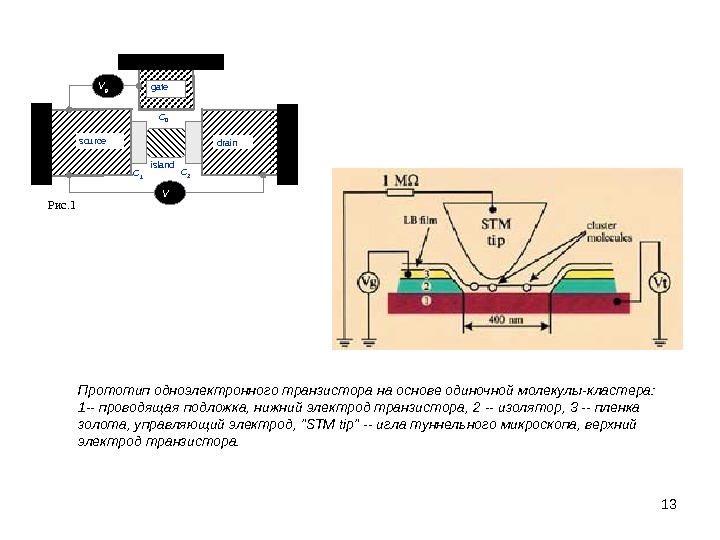
 13 Прототип одноэлектронного транзистора на основе одиночной молекулы-кластера: 1 — проводящая подложка, нижний электрод транзистора, 2 — изолятор, 3 — пленка золота, управляющий электрод, «STM tip» — игла туннельного микроскопа, верхний электрод транзистора. source drain island C 1 C 2 C 0 V g V gate Рис.
13 Прототип одноэлектронного транзистора на основе одиночной молекулы-кластера: 1 — проводящая подложка, нижний электрод транзистора, 2 — изолятор, 3 — пленка золота, управляющий электрод, «STM tip» — игла туннельного микроскопа, верхний электрод транзистора. source drain island C 1 C 2 C 0 V g V gate Рис.
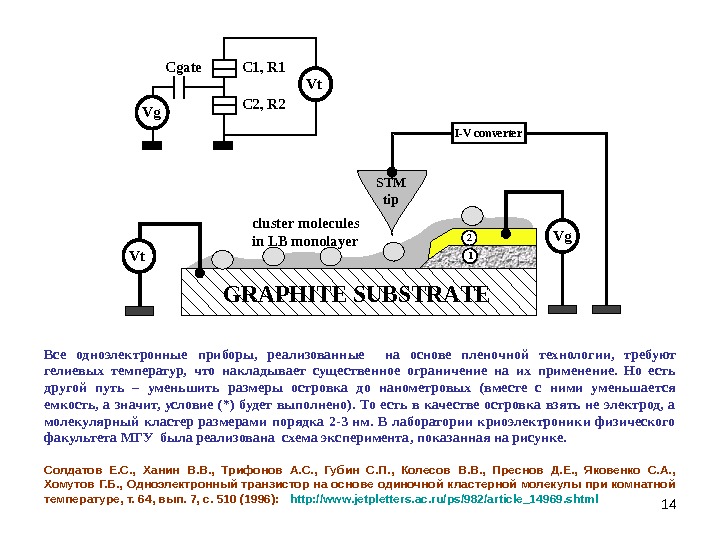
 14 I-V converter Vg Vt GRAPHITE SUBSTRATE cluster molecules in LB monolayer 1 2 Vt Vg C 1, R 1 C 2, R 2 Cgate STM tip. Все одноэлектронные приборы , реализованные на основе пленочной технологии, требуют гелиевых температур, что накладывает существенное ограничение на их применение. Но есть другой путь – уменьшить размеры островка до нанометровых (вместе с ними уменьшается емкость, а значит, условие (*) будет выполнено). То есть в качестве островка взять не электрод, а молекулярный кластер размерами порядка 2 -3 нм. В лаборатории криоэлектроники физического факультета МГУ была реализована схема эксперимента , показанная на рисунке. Солдатов Е. С. , Ханин В. В. , Трифонов А. С. , Губин С. П. , Колесов В. В. , Преснов Д. Е. , Яковенко С. А. , Хомутов Г. Б. , Одноэлектронный транзистор на основе одиночной кластерной молекулы при комнатной температуре, т. 64, вып. 7, с. 510 (1996): http: //www. jetpletters. ac. ru/ps/982/article_14969. shtml
14 I-V converter Vg Vt GRAPHITE SUBSTRATE cluster molecules in LB monolayer 1 2 Vt Vg C 1, R 1 C 2, R 2 Cgate STM tip. Все одноэлектронные приборы , реализованные на основе пленочной технологии, требуют гелиевых температур, что накладывает существенное ограничение на их применение. Но есть другой путь – уменьшить размеры островка до нанометровых (вместе с ними уменьшается емкость, а значит, условие (*) будет выполнено). То есть в качестве островка взять не электрод, а молекулярный кластер размерами порядка 2 -3 нм. В лаборатории криоэлектроники физического факультета МГУ была реализована схема эксперимента , показанная на рисунке. Солдатов Е. С. , Ханин В. В. , Трифонов А. С. , Губин С. П. , Колесов В. В. , Преснов Д. Е. , Яковенко С. А. , Хомутов Г. Б. , Одноэлектронный транзистор на основе одиночной кластерной молекулы при комнатной температуре, т. 64, вып. 7, с. 510 (1996): http: //www. jetpletters. ac. ru/ps/982/article_14969. shtml
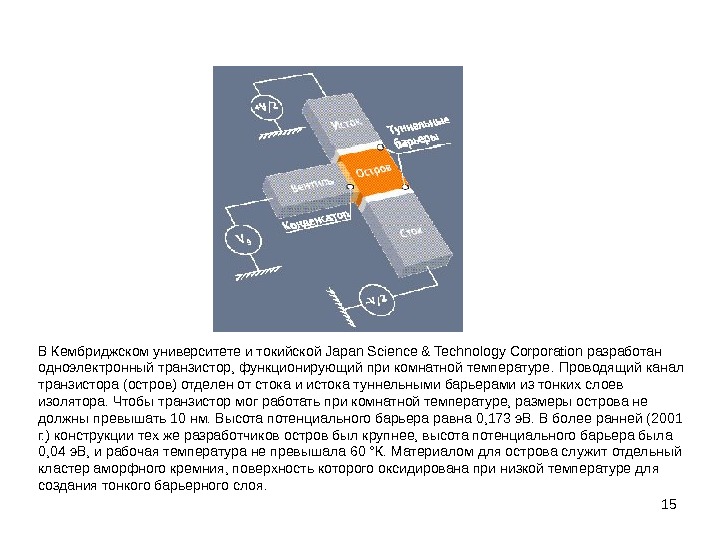
 15 В Кембриджском университете и токийской Japan Science & Technology Corporation разработан одноэлектронный транзистор, функционирующий при комнатной температуре. Проводящий канал транзистора (остров) отделен от стока и истока туннельными барьерами из тонких слоев изолятора. Чтобы транзистор мог работать при комнатной температуре, размеры острова не должны превышать 10 нм. Высота потенциального барьера равна 0, 173 э. В. В более ранней (2001 г. ) конструкции тех же разработчиков остров был крупнее, высота потенциального барьера была 0, 04 э. В, и рабочая температура не превышала 60 °К. Материалом для острова служит отдельный кластер аморфного кремния, поверхность которого оксидирована при низкой температуре для создания тонкого барьерного слоя.
15 В Кембриджском университете и токийской Japan Science & Technology Corporation разработан одноэлектронный транзистор, функционирующий при комнатной температуре. Проводящий канал транзистора (остров) отделен от стока и истока туннельными барьерами из тонких слоев изолятора. Чтобы транзистор мог работать при комнатной температуре, размеры острова не должны превышать 10 нм. Высота потенциального барьера равна 0, 173 э. В. В более ранней (2001 г. ) конструкции тех же разработчиков остров был крупнее, высота потенциального барьера была 0, 04 э. В, и рабочая температура не превышала 60 °К. Материалом для острова служит отдельный кластер аморфного кремния, поверхность которого оксидирована при низкой температуре для создания тонкого барьерного слоя.
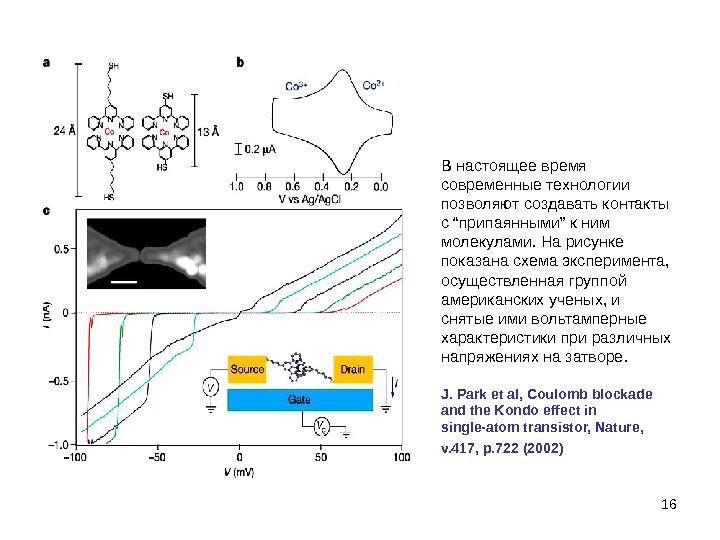
 16 В настоящее время современные технологии позволяют создавать контакты с “припаянными” к ним молекулами. На рисунке показана схема эксперимента, осуществленная группой американских ученых, и снятые ими вольтамперные характеристики при различных напряжениях на затворе. J. Park et al, Coulomb blockade and the Kondo effect in single-atom transistor, Nature, v. 417, p. 722 (2002)
16 В настоящее время современные технологии позволяют создавать контакты с “припаянными” к ним молекулами. На рисунке показана схема эксперимента, осуществленная группой американских ученых, и снятые ими вольтамперные характеристики при различных напряжениях на затворе. J. Park et al, Coulomb blockade and the Kondo effect in single-atom transistor, Nature, v. 417, p. 722 (2002)
 17 Ортодоксальная теория. 0 — D модель В используемой модели пренебрегается 1) размером и формой туннельного перехода, 2) конечным временем туннелирования (операторы С+ и С для одного и того же момента времени), 3) конечным временем перераспределения электрического заряда в электродах, 4) квантованием энергии в электродах и шунте, 5) квантовой природой тока I 0( t ), – полагается классической функцией. Гамильтониан системы: IHHH C Q Hs. T ˆˆˆ 2 ˆ 0 2 , ˆˆˆ , , 21, , 0 kq kkqkkkq. Hk. Hbb. Ecc. EH 2, 1 k — энергетические состояния в 1 -м электроде q — энергетические состояния во 2 -м электроде bcˆ, ˆ — операторы рождения bc ˆ , ˆ — операторы уничтожения , ˆˆˆ , , * HHbc. Tcb. TH qk qkqkkqkq. T , ˆˆ HHsssk. HHˆˆ , 2 constcccc e Q kq qqkk , )()(ˆHe. QFQFH i. Q ]ˆ , ˆ [
17 Ортодоксальная теория. 0 — D модель В используемой модели пренебрегается 1) размером и формой туннельного перехода, 2) конечным временем туннелирования (операторы С+ и С для одного и того же момента времени), 3) конечным временем перераспределения электрического заряда в электродах, 4) квантованием энергии в электродах и шунте, 5) квантовой природой тока I 0( t ), – полагается классической функцией. Гамильтониан системы: IHHH C Q Hs. T ˆˆˆ 2 ˆ 0 2 , ˆˆˆ , , 21, , 0 kq kkqkkkq. Hk. Hbb. Ecc. EH 2, 1 k — энергетические состояния в 1 -м электроде q — энергетические состояния во 2 -м электроде bcˆ, ˆ — операторы рождения bc ˆ , ˆ — операторы уничтожения , ˆˆˆ , , * HHbc. Tcb. TH qk qkqkkqkq. T , ˆˆ HHsssk. HHˆˆ , 2 constcccc e Q kq qqkk , )()(ˆHe. QFQFH i. Q ]ˆ , ˆ [
 18 Qˆˆи. HT — не коммутируют, Qˆˆ0 и. H — коммутируют (“примерно”), если e. QN/2, 1 s. Hˆ — коммутирует со всеми операторами в гамильтониане; , Vdt CQV / Для сверхпроводящих ( S ) электродов джозефсоновская фаза , )2/(conste Формально такая фаза может быть введена и для т нормальных ( N ) электродов. Выражение для туннельного тока (случай большой емкости) , ˆˆˆ0 THHH , ˆˆˆ210 q. Hk. HH, ˆ , , 0 q qqqkk k kbb. Ecc. EH ; ˆ , , * qk qkqkkqkq. Tbc. Tcb. TH Коммутационные соотношения: . 0, 0, »»»’ kkkkkkkcccccc )](), ([ 1 )](), ([)(ˆt. Ht. A i t. At. H i t. A , 2 , 1ˆ, ˆ q qq k kkbb. Ncc. N, 0 ˆ 1 N IIˆ Электрический ток ]ˆ , ˆ [ˆ ˆ 111 THNe i. Ne. I , , *ˆ qk qkqkqkkqbc. T e i. I
18 Qˆˆи. HT — не коммутируют, Qˆˆ0 и. H — коммутируют (“примерно”), если e. QN/2, 1 s. Hˆ — коммутирует со всеми операторами в гамильтониане; , Vdt CQV / Для сверхпроводящих ( S ) электродов джозефсоновская фаза , )2/(conste Формально такая фаза может быть введена и для т нормальных ( N ) электродов. Выражение для туннельного тока (случай большой емкости) , ˆˆˆ0 THHH , ˆˆˆ210 q. Hk. HH, ˆ , , 0 q qqqkk k kbb. Ecc. EH ; ˆ , , * qk qkqkkqkq. Tbc. Tcb. TH Коммутационные соотношения: . 0, 0, »»»’ kkkkkkkcccccc )](), ([ 1 )](), ([)(ˆt. Ht. A i t. At. H i t. A , 2 , 1ˆ, ˆ q qq k kkbb. Ncc. N, 0 ˆ 1 N IIˆ Электрический ток ]ˆ , ˆ [ˆ ˆ 111 THNe i. Ne. I , , *ˆ qk qkqkqkkqbc. T e i. I
 19 Зная оператор тока, можно вычислить среднее значение тока по формуле Кубо как поправку к равновесному значению, равному нолю, за счет возмущения H T : )]( ~ )( ~ [ˆ»t. It. Hdt i IT t Здесь E F 1 и E F 2 – химические потенциалы, которые, однако, с огромной точностью, особенно при Т → 0, равны энергии Ферми. Также считаем, что H Т → e εt H T , где ε → +0 , для описания адиабатического включения, чтобы избежать «встряски» и последующего переходного процесса. Знак «тильда» здесь означает представление взаимодействия, например, Усреднение проводится по большому ансамблю Гиббса ( N – переменное число частиц): 221100 ˆˆˆˆNENEHHFF. . . , ~ , ˆ )(~ 00 ˆˆ t. Ei kkt. Ei qqt. Hi kq eccebbe. Iet. I Вводим обозначение Вычисление тока по формуле Кубо и выполняем преобразования: /)(kqqk. EE. )]( ~ ), ( ~ [ , , 1, 1 * 111 * , 1, , 1 * 111 *’ 1 »1′ 11’1′ qkk kk titi qkkq qqk qq titi kqkq. T cce. TT e i bbe. TT e it. It. H qkqk kqqk
19 Зная оператор тока, можно вычислить среднее значение тока по формуле Кубо как поправку к равновесному значению, равному нолю, за счет возмущения H T : )]( ~ )( ~ [ˆ»t. It. Hdt i IT t Здесь E F 1 и E F 2 – химические потенциалы, которые, однако, с огромной точностью, особенно при Т → 0, равны энергии Ферми. Также считаем, что H Т → e εt H T , где ε → +0 , для описания адиабатического включения, чтобы избежать «встряски» и последующего переходного процесса. Знак «тильда» здесь означает представление взаимодействия, например, Усреднение проводится по большому ансамблю Гиббса ( N – переменное число частиц): 221100 ˆˆˆˆNENEHHFF. . . , ~ , ˆ )(~ 00 ˆˆ t. Ei kkt. Ei qqt. Hi kq eccebbe. Iet. I Вводим обозначение Вычисление тока по формуле Кубо и выполняем преобразования: /)(kqqk. EE. )]( ~ ), ( ~ [ , , 1, 1 * 111 * , 1, , 1 * 111 *’ 1 »1′ 11’1′ qkk kk titi qkkq qqk qq titi kqkq. T cce. TT e i bbe. TT e it. It. H qkqk kqqk
( 20 Усредняем по большому ансамблю Гиббса: )()(2 , , 0 ''' )()]( ~ )(](/docs//noc-single-electronics_images/noc-single-electronics_19.jpg) 20 Усредняем по большому ансамблю Гиббса: )()(2 , , 0 »’ )()]( ~ )( ~ [ ttitti kq qk kq. T qkqkeenn. T e it. It. H )()(2)(ˆ2 , , )(‘)(‘2 , , 2 »» kqkq qk kq tttti kq qk kq. EEnn. Teedtedtnn. Te. Iqkqk При этом были использованы следующие соотношения : 11 kkkkkncc 0)()(»’ i i ededttittttiqkqk )(2)()( 11 i P i ii i e. VEE e n FF Tk EEq Tk EEk B Fq B Fk 21;
20 Усредняем по большому ансамблю Гиббса: )()(2 , , 0 »’ )()]( ~ )( ~ [ ttitti kq qk kq. T qkqkeenn. T e it. It. H )()(2)(ˆ2 , , )(‘)(‘2 , , 2 »» kqkq qk kq tttti kq qk kq. EEnn. Teedtedtnn. Te. Iqkqk При этом были использованы следующие соотношения : 11 kkkkkncc 0)()(»’ i i ededttittttiqkqk )(2)()( 11 i P i ii i e. VEE e n FF Tk EEq Tk EEk B Fq B Fk 21;
 21 Итак, )()( 2ˆ2 , , kqqk qk kq. EEnn. T e I Можно использовать другую форму записи, если перейти к отсчету энергии от уровня Ферми: qkqk. FFqkq. Fqk. Fke. VEEEE 2121, )( 11 112 ˆ 212 , , e. V ee. Te I qk Tk EE qk kq B Fk С учетом суммирования по спину: )( 1 14ˆ 21 2 , e. V ee T e I qk Tk EE qk kq B Fk
21 Итак, )()( 2ˆ2 , , kqqk qk kq. EEnn. T e I Можно использовать другую форму записи, если перейти к отсчету энергии от уровня Ферми: qkqk. FFqkq. Fqk. Fke. VEEEE 2121, )( 11 112 ˆ 212 , , e. V ee. Te I qk Tk EE qk kq B Fk С учетом суммирования по спину: )( 1 14ˆ 21 2 , e. V ee T e I qk Tk EE qk kq B Fk
 22 Плотность состояний Уравнение Шредингера для свободной частицы )()( 22 2 2 22 r. Er zyxm kkk В случае ограниченного объема в виде куба со стороной L решение будет представлять собой стоячую волну z L n y L n x L n Arzyx n sinsinsin)( Поэтому удобно ввести волновые функции, удовлетворяющие периодическим гран. условиям: . . ), , , (), , ( дтиzyxzy. Lx Это будут бегущие плоские волны: . . . , 4 , 2 , 0. ; . . , 4 , 2 , 0, )( )( LLk LLker zyxrki k Подставляя это выражение в уравнение Шредингера, получим: 2, 22 22 kkkk m E zyxk )()()(ˆrkrirpkkk Эти волновые функции являются также собств. волн. функциями оператора импульса с собственными значениями ipˆ k , поскольку 22 2 , / FFk m Emk. V
22 Плотность состояний Уравнение Шредингера для свободной частицы )()( 22 2 2 22 r. Er zyxm kkk В случае ограниченного объема в виде куба со стороной L решение будет представлять собой стоячую волну z L n y L n x L n Arzyx n sinsinsin)( Поэтому удобно ввести волновые функции, удовлетворяющие периодическим гран. условиям: . . ), , , (), , ( дтиzyxzy. Lx Это будут бегущие плоские волны: . . . , 4 , 2 , 0. ; . . , 4 , 2 , 0, )( )( LLk LLker zyxrki k Подставляя это выражение в уравнение Шредингера, получим: 2, 22 22 kkkk m E zyxk )()()(ˆrkrirpkkk Эти волновые функции являются также собств. волн. функциями оператора импульса с собственными значениями ipˆ k , поскольку 22 2 , / FFk m Emk. V
 23 zyxkkk, , Из условий для вытекает, что каждому разрешенному вектору k тройке квантовых чисел zyxkkk, , отвечает объем в k -пространстве величиной 3/2 L, т. е. каждой Поэтому в сфере объемом 3 3 3 4 Fk число точек, описывающих разрешенные состояния, равно числу ячеек объемом 3/2 L , и поэтому число разрешенных состояний (число электронов) 3 23 3 3)/2( 3/4 2 F Fk V L k N Таким образом: 3/1 23 V N k. F 3/2 2 2 3 2 V N m EF 2/3 22 2 3 Fm. EV N 3/1 23 V N m VF FF FF E N Em. V d. E d. N En 2 3 2)( 2/13 32 — плотность состояний: Число состояний в левом металле: kk. Lkk. Fkdnd. Em V d )(2 2/1 3 32 Это выражение написано с учетом спина (фактор 2), а также с учетом интегрирования по углам , , kk что дало фактор 4 π. При переходе к единичному телесному углу необходимо число состояний поделить на 4 π : 4/dd
23 zyxkkk, , Из условий для вытекает, что каждому разрешенному вектору k тройке квантовых чисел zyxkkk, , отвечает объем в k -пространстве величиной 3/2 L, т. е. каждой Поэтому в сфере объемом 3 3 3 4 Fk число точек, описывающих разрешенные состояния, равно числу ячеек объемом 3/2 L , и поэтому число разрешенных состояний (число электронов) 3 23 3 3)/2( 3/4 2 F Fk V L k N Таким образом: 3/1 23 V N k. F 3/2 2 2 3 2 V N m EF 2/3 22 2 3 Fm. EV N 3/1 23 V N m VF FF FF E N Em. V d. E d. N En 2 3 2)( 2/13 32 — плотность состояний: Число состояний в левом металле: kk. Lkk. Fkdnd. Em V d )(2 2/1 3 32 Это выражение написано с учетом спина (фактор 2), а также с учетом интегрирования по углам , , kk что дало фактор 4 π. При переходе к единичному телесному углу необходимо число состояний поделить на 4 π : 4/dd
 24)( 1 1 4 )( 4ˆ)(2 e. V ee T d nd e II qk Tk e. V Tkkqq qqk kk B k dddsin Введем обозначение для среднего значения матричного элемента: 212 2 , , 44 FFkqq k qqkk. Td d T d ee Tnn e I Tk e. V Tk. RL BB 1)( 12 11 )0()0( 4 Выражение для тока: Можно показать, что интеграл в этом выражении всегда равен e. V. В случае, когда Т = 0, интеграл сводится к вычитанию двух ступенек, что сразу дает величину e. V. При Т ≠ 0 и при выполнении условия e. V << k B T подинтегральное выражение можно разложить по параметру e. V / k B T , и тогда легко увидеть, что интеграл равен e. V. Для рассмотрения этого интеграла в общем случае можно сделать замену , /Tkz. B которая позволяет записать рассматриваемый интеграл в виде — uzz 1 e 1 (u), , )(dz Tk e. V uгдеu. Tk B B , uzx Выполнив замену )()( uu убеждаемся, что
24)( 1 1 4 )( 4ˆ)(2 e. V ee T d nd e II qk Tk e. V Tkkqq qqk kk B k dddsin Введем обозначение для среднего значения матричного элемента: 212 2 , , 44 FFkqq k qqkk. Td d T d ee Tnn e I Tk e. V Tk. RL BB 1)( 12 11 )0()0( 4 Выражение для тока: Можно показать, что интеграл в этом выражении всегда равен e. V. В случае, когда Т = 0, интеграл сводится к вычитанию двух ступенек, что сразу дает величину e. V. При Т ≠ 0 и при выполнении условия e. V << k B T подинтегральное выражение можно разложить по параметру e. V / k B T , и тогда легко увидеть, что интеграл равен e. V. Для рассмотрения этого интеграла в общем случае можно сделать замену , /Tkz. B которая позволяет записать рассматриваемый интеграл в виде — uzz 1 e 1 (u), , )(dz Tk e. V uгдеu. Tk B B , uzx Выполнив замену )()( uu убеждаемся, что
 25 T RL R V VTnn e I 2 )0()0( 4 (закон Ома (!) ) 2 )0()0(4 Tnne G RLT 1 2)0()0( 4 Tnn e RRLT Закон Ома указывает на диссипацию энергии протекании туннельного тока (!) u. . , 1 )1(10 22 ет s ds dz e e du d uz uz. С другой стороны, Это означает, что рассматриваемый интеграл равен e. V. Таким образом, — Диссипация энергии при одном акте туннелирования
25 T RL R V VTnn e I 2 )0()0( 4 (закон Ома (!) ) 2 )0()0(4 Tnne G RLT 1 2)0()0( 4 Tnn e RRLT Закон Ома указывает на диссипацию энергии протекании туннельного тока (!) u. . , 1 )1(10 22 ет s ds dz e e du d uz uz. С другой стороны, Это означает, что рассматриваемый интеграл равен e. V. Таким образом, — Диссипация энергии при одном акте туннелирования
 26 Учет изменения электростатической энергии при туннелировании 22 )( 2 22 e Q c e EEE C e. Q E CQ qkqk Закон сохранения энергии при туннелировании электрона : . ) 2 ()( e Q C e EEEEqkqk Вероятность туннельного скачка в единицу времени с уменьшением заряда на е. e. QQ 2 exp 1 21 )( 2 e Q CT e e Q C e Re Q T 1 2 exp 21 )( 2 e Q CT e e Q C e Re Q T .
26 Учет изменения электростатической энергии при туннелировании 22 )( 2 22 e Q c e EEE C e. Q E CQ qkqk Закон сохранения энергии при туннелировании электрона : . ) 2 ()( e Q C e EEEEqkqk Вероятность туннельного скачка в единицу времени с уменьшением заряда на е. e. QQ 2 exp 1 21 )( 2 e Q CT e e Q C e Re Q T 1 2 exp 21 )( 2 e Q CT e e Q C e Re Q T .
 27 Рассмотрим систему (х – совокупность ее координат), являющуюся частью замкнутой системы ( q – совокупность остальных координат замкнутой системы). Поскольку { x } – система не является замкнутой и взаимодействует с остальной частью общей замкнутой системы, то Матрица плотности (статистическая матрица). )()(), ( 21 qxxq Пусть F – физическая величина, которая относится только к рассматриваемой системе, то есть оператор действует только на координаты { x }. . ), (ˆ), (* dqdxxq. F , ), ‘(xx Введем функцию называемую матрицей плотности: , ), (), ‘(* dqxqxqxx которая обладает свойством эрмитовости: , ), ‘()’, (*xxxx т. е. Диагональные элементы матрицы плотности определяют распределение вероятности для координат рассматриваемой системы: . ), (2 dqxqxx Среднее значение физической величины F , записанное с помощью матрицы плотности: . )’. (ˆ ‘dxxx. FFxx Fˆ Оператор действует только на переменные x в матрице , после чего нужно положить x ’= x. Описание с помощью матрицы плотности является более общим. Описание с помощью волновой функции является частным случаем, отвечающим матрице плотности . )()'(), ‘( * xxxx
27 Рассмотрим систему (х – совокупность ее координат), являющуюся частью замкнутой системы ( q – совокупность остальных координат замкнутой системы). Поскольку { x } – система не является замкнутой и взаимодействует с остальной частью общей замкнутой системы, то Матрица плотности (статистическая матрица). )()(), ( 21 qxxq Пусть F – физическая величина, которая относится только к рассматриваемой системе, то есть оператор действует только на координаты { x }. . ), (ˆ), (* dqdxxq. F , ), ‘(xx Введем функцию называемую матрицей плотности: , ), (), ‘(* dqxqxqxx которая обладает свойством эрмитовости: , ), ‘()’, (*xxxx т. е. Диагональные элементы матрицы плотности определяют распределение вероятности для координат рассматриваемой системы: . ), (2 dqxqxx Среднее значение физической величины F , записанное с помощью матрицы плотности: . )’. (ˆ ‘dxxx. FFxx Fˆ Оператор действует только на переменные x в матрице , после чего нужно положить x ’= x. Описание с помощью матрицы плотности является более общим. Описание с помощью волновой функции является частным случаем, отвечающим матрице плотности . )()'(), ‘( * xxxx
 28 Если предположить, что рассматриваемая подсистема находится в некотором полно описанном состоянии с волновой функцией ψ (это было бы «чистое» состояние), которое тогда можно разложить по полной системе функций ψ n ( х ): , n nnc тогда среднее значение nm nmmn. Fcc. F, * dx. FFmnnmˆ* (матр. элемент оператора) Переход к неполному квантово-механическому описанию подсистемы можно рассматривать (в некотором смысле) как усреднение по ее различным ψ – состояниям. То есть от одинарного набора коэффичиентов { cn } переходим к двойному (по двум индексам) набору коэффициентов { Wmn } : (*) , n m nmmn FWF Совокупность { Wmn } (эти элементы могут быть функциями времени) и есть матрица плотности в энергетическом представлении, или статистическая матрица. n nmmn. FW Поскольку — диагональный матричный элемент произведения операторов. FWˆˆ , тогда m mm. FWSp. FWFˆˆˆˆ Итак, , * mnmn. Wcc то есть вероятность, что подсистема находится в n -ом состоянии будет равна 0 nnn. WW диагональному элементу (вместо квадрата модуля С * n C n ) , для которого выполняется условие нормировки: n n. WWSp 1)ˆ( Усреднение (*) с помощью статистической матрицы имеет двоякую природу. Оно включает в себя ( i ) усреднение, связанное с вероятностным характером квантовомеханического описания (даже наиболее полного), и ( ii ) статистическое усреднение, связанное с неполнотой сведений об объекте. Статистическая матрица в квантовой статистике заменяет функцию распределения в классической статистике.
28 Если предположить, что рассматриваемая подсистема находится в некотором полно описанном состоянии с волновой функцией ψ (это было бы «чистое» состояние), которое тогда можно разложить по полной системе функций ψ n ( х ): , n nnc тогда среднее значение nm nmmn. Fcc. F, * dx. FFmnnmˆ* (матр. элемент оператора) Переход к неполному квантово-механическому описанию подсистемы можно рассматривать (в некотором смысле) как усреднение по ее различным ψ – состояниям. То есть от одинарного набора коэффичиентов { cn } переходим к двойному (по двум индексам) набору коэффициентов { Wmn } : (*) , n m nmmn FWF Совокупность { Wmn } (эти элементы могут быть функциями времени) и есть матрица плотности в энергетическом представлении, или статистическая матрица. n nmmn. FW Поскольку — диагональный матричный элемент произведения операторов. FWˆˆ , тогда m mm. FWSp. FWFˆˆˆˆ Итак, , * mnmn. Wcc то есть вероятность, что подсистема находится в n -ом состоянии будет равна 0 nnn. WW диагональному элементу (вместо квадрата модуля С * n C n ) , для которого выполняется условие нормировки: n n. WWSp 1)ˆ( Усреднение (*) с помощью статистической матрицы имеет двоякую природу. Оно включает в себя ( i ) усреднение, связанное с вероятностным характером квантовомеханического описания (даже наиболее полного), и ( ii ) статистическое усреднение, связанное с неполнотой сведений об объекте. Статистическая матрица в квантовой статистике заменяет функцию распределения в классической статистике.
 29 Если внешний ток I 0 ( t ), туннельный ток I и ток через шунт достаточно малы и не нарушают равновесия внутренних степеней свободы металлов и шунта, эти воздействия можно рассматривать как возмущения и пользоваться матрицей плотности: . ˆ), ‘, (, , WSp. Spt. QQsqksqk Эволюция матрицы плотности описывается уравнением фон Неймана ( von Neumann ): , TSIFFF Где F I , F S , F T (вклады от токов I 0 , I S , I T ) могут быть вычислены независимо в 1 -м приближении теории возмущений: ‘, 0 ‘)()(), ()(1 QQQQII QQt. It. Fttt. I i. F , )'(), (‘ 1 )(, , , 2, t TSTSTSsqk. TSftt. HTrdtt. F где TSTTSSf. HHIH, , , температурно-равновесные матрицы плотности шунта и элктродов соответственно. При малых значениях проводимостей G T и G S воздействия F T и F I не могут порождать новых диагональных элементов матрицы плотности, а воздействие F S ведет к «распаду» недиагональных элементов с характерным временем τ s = C / G s , если G s <<1/ R T. Следовательно матрица плотности станет диагональной и будет оставаться таковой : )(), ()(, QQt. QQ ), (t. Q — плотность вероятности величины заряда Q.
29 Если внешний ток I 0 ( t ), туннельный ток I и ток через шунт достаточно малы и не нарушают равновесия внутренних степеней свободы металлов и шунта, эти воздействия можно рассматривать как возмущения и пользоваться матрицей плотности: . ˆ), ‘, (, , WSp. Spt. QQsqksqk Эволюция матрицы плотности описывается уравнением фон Неймана ( von Neumann ): , TSIFFF Где F I , F S , F T (вклады от токов I 0 , I S , I T ) могут быть вычислены независимо в 1 -м приближении теории возмущений: ‘, 0 ‘)()(), ()(1 QQQQII QQt. It. Fttt. I i. F , )'(), (‘ 1 )(, , , 2, t TSTSTSsqk. TSftt. HTrdtt. F где TSTTSSf. HHIH, , , температурно-равновесные матрицы плотности шунта и элктродов соответственно. При малых значениях проводимостей G T и G S воздействия F T и F I не могут порождать новых диагональных элементов матрицы плотности, а воздействие F S ведет к «распаду» недиагональных элементов с характерным временем τ s = C / G s , если G s <<1/ R T. Следовательно матрица плотности станет диагональной и будет оставаться таковой : )(), ()(, QQt. QQ ), (t. Q — плотность вероятности величины заряда Q.
 30 Для плотности вероятности можно получить уравнение, используя уравнение Фоккера-Планка для процесса х( t ), заданного обыкновенным дифференциальным уравнением, линейный или нелинейные коэффициенты которого или его правая часть являются случайными δ-коррелированными функциями. Наиболее простой случай такого дифференциального уравнения: )(, 0, )()()(Dгдеtxbxax Уравнение Фоккера-Планка: , )( 2 1 )(22 2 1 k xt . . )()0, (, )(2, , )()()(0 2 21 условиеначxxx. Dbk dx db b. Dxbxbxak. )()(I)()(IQ 00 ffs s f. SSVQb. Qat. VGQ C G t. IIt. 22, )(02 201 Tk. G G Tk Gk. Q C G t. Ikb. Bs s B s s Equation. Master. FQ Q TCk QC G Q t. I t TBs )( 0 . )()()()( QQQe. Qe. QQF T
30 Для плотности вероятности можно получить уравнение, используя уравнение Фоккера-Планка для процесса х( t ), заданного обыкновенным дифференциальным уравнением, линейный или нелинейные коэффициенты которого или его правая часть являются случайными δ-коррелированными функциями. Наиболее простой случай такого дифференциального уравнения: )(, 0, )()()(Dгдеtxbxax Уравнение Фоккера-Планка: , )( 2 1 )(22 2 1 k xt . . )()0, (, )(2, , )()()(0 2 21 условиеначxxx. Dbk dx db b. Dxbxbxak. )()(I)()(IQ 00 ffs s f. SSVQb. Qat. VGQ C G t. IIt. 22, )(02 201 Tk. G G Tk Gk. Q C G t. Ikb. Bs s B s s Equation. Master. FQ Q TCk QC G Q t. I t TBs )( 0 . )()()()( QQQe. Qe. QQF T
 31 Denotation of a small tunnel junction and an equivalent circuit of the current-biased junction Change of the charging energy E of a small junction resulting from tunneling of a single electron Time evolution of the probability density σ (Q) in process of the SET oscillation and its drip analogy
31 Denotation of a small tunnel junction and an equivalent circuit of the current-biased junction Change of the charging energy E of a small junction resulting from tunneling of a single electron Time evolution of the probability density σ (Q) in process of the SET oscillation and its drip analogy
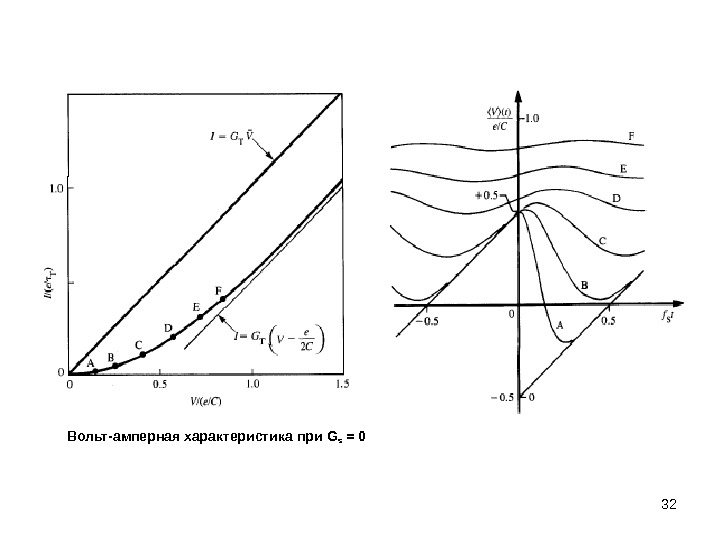
 32 Вольт-амперная характеристика при G s =
32 Вольт-амперная характеристика при G s =
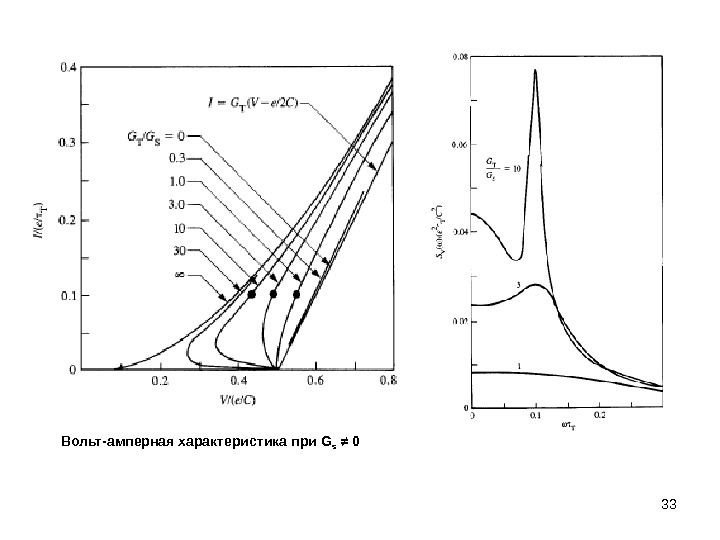
 33 Вольт-амперная характеристика при G s ≠
33 Вольт-амперная характеристика при G s ≠
 34 SIS туннельный переход. Туннелирование куперовских пар Будем рассматривать случай, когда среднее напряжение на переходе много меньше щелевого напряжения . /)()(21 e. TTV В этом случае справедливо «адиабатическое» приближение : , pq. THHH. )(cos. Jp. EH где Тогда: , }{}{}{22110 IHk. Hk. HHHqss где , }{)(0 ssk. It. II. 2/, )/2(cos 2/00 2 0 eh. ECQHJ. 2 , i t Qi. Q При малых значениях G T , G S , и I 0 . 0 HH . )()(0 Возможные аналогии: (1) Квантовомеханический плоский маятник: В этом случае имеем набор дискретных энергетических уровней. (2) Одномерное движение частицы массой Ce 2)2/( Qe )2/( и моментом вдоль φ-оси в поле с периодическим потенциалом . )(JU При этом волновые функции будут Блоховскими волновыми функциями: , )()(0 /0 nknk ik nk. UUe. U где число k может быть как целым, так и реальным, поэтому . )()(0 Энергетический спектр состоит из зон (полос): n = 0, 1, 2, 3, ….
34 SIS туннельный переход. Туннелирование куперовских пар Будем рассматривать случай, когда среднее напряжение на переходе много меньше щелевого напряжения . /)()(21 e. TTV В этом случае справедливо «адиабатическое» приближение : , pq. THHH. )(cos. Jp. EH где Тогда: , }{}{}{22110 IHk. Hk. HHHqss где , }{)(0 ssk. It. II. 2/, )/2(cos 2/00 2 0 eh. ECQHJ. 2 , i t Qi. Q При малых значениях G T , G S , и I 0 . 0 HH . )()(0 Возможные аналогии: (1) Квантовомеханический плоский маятник: В этом случае имеем набор дискретных энергетических уровней. (2) Одномерное движение частицы массой Ce 2)2/( Qe )2/( и моментом вдоль φ-оси в поле с периодическим потенциалом . )(JU При этом волновые функции будут Блоховскими волновыми функциями: , )()(0 /0 nknk ik nk. UUe. U где число k может быть как целым, так и реальным, поэтому . )()(0 Энергетический спектр состоит из зон (полос): n = 0, 1, 2, 3, ….
 35 При s >> 1 (сильное джозефсоновское взаимодействие) ширина нижней зоны . 0/8 exp 2//32 4/1 0 QJJQJ EEEEEE Зоны разделены энергетической щелью: . 1, 8 n. EE QJpn При s << 1 энергетические зоны значительно шире: , /E 1/2)m-(q/2 e , 2/)2()(J 2 Qn. Eдля. Cemqq. E. )()2/1(2/qsigneq. Intm И разделены узкой энергетической щелью: . , 2 1 n n. Js. E Рассмотрим случай малых флуктуаций: . , , max. QSSQTTSQTQBJRGRGEETk. E В этом случае система находится внутри нижней зоны ( n =0), кроме того, при 0 QTTRG (**), )()( 2 2 00 q Dq. V q G q t. I t S . , )(, 0 0 q. Q dqd. E q. VTk. GD BS Если 1, 2 1, / )( max. V , dq, 0/ 0 0 t 0 00 s e. E s. Ce dq qd. E IETk. B Уравнение имеет стационарное решение : I 0 = 0, | V | I t , имеем движение q вдоль энергетической зоны E 0 ( k ).
35 При s >> 1 (сильное джозефсоновское взаимодействие) ширина нижней зоны . 0/8 exp 2//32 4/1 0 QJJQJ EEEEEE Зоны разделены энергетической щелью: . 1, 8 n. EE QJpn При s << 1 энергетические зоны значительно шире: , /E 1/2)m-(q/2 e , 2/)2()(J 2 Qn. Eдля. Cemqq. E. )()2/1(2/qsigneq. Intm И разделены узкой энергетической щелью: . , 2 1 n n. Js. E Рассмотрим случай малых флуктуаций: . , , max. QSSQTTSQTQBJRGRGEETk. E В этом случае система находится внутри нижней зоны ( n =0), кроме того, при 0 QTTRG (**), )()( 2 2 00 q Dq. V q G q t. I t S . , )(, 0 0 q. Q dqd. E q. VTk. GD BS Если 1, 2 1, / )( max. V , dq, 0/ 0 0 t 0 00 s e. E s. Ce dq qd. E IETk. B Уравнение имеет стационарное решение : I 0 = 0, | V | I t , имеем движение q вдоль энергетической зоны E 0 ( k ).
 36 В туннельном SIS переходе при изменении Ф на Ф 0 источник тока совершает работу . )(0 t. IE Кроме того, в качестве источника тока можно представить себе сверхпроводящую катушку с индуктивностью L >> Ф 0 / I , тогда изменение φ на 2π приведет к изменению магнитного потока в этой катушке на Ф 0 . s s ks kiks ks k. UUe. Udk. C, )()2(, )( )()()( ks. , , 2, 1, 0 )()(s k. U Для того, чтобы найти волновые функции и собственные значения энергии , )()(k. Es необходимо решить уравнение Шредингера с Гамильтогианом: . 2/, cos )2/( 2 2 2 0 CQJq. ECe. EEEH Это будет как раз хорошо известное уравнение Матье (!). Свойства спектра энергии: периодическая зависимость внутри каждой зоны: . 2, )()1( )()( квазизарядekqk. E nn Аналогия между малым туннельным SIS переходом и электроном в кристаллической решетке нарушается по мере появления слабого взаимодействия I q (за счет тока квазичастиц) с термостатом, которое приводит к установлению равновесного статистического распределения по энергиям E ( s ) ( k ). В отличие от ансамбля электронов в кристаллической решетке, для которых справедлива статистика Ферми-Дирака, одиночный переход как одиночный объект представляет собой статистический ансамбль, который описывается статистическим распределением Гиббса: . , /)(exp)( 0 )( )(1)( )( n Tk k. E B nndke. ZTkk. EZk. Ef. B n Если , min)0()1()0(EETkk. B то переход находится в состоянии n = 0 как в отсутствие тока, так и при малом токе I. Введем параметр , /2/1 QJEEs который сильно влияет на )()(k. En
36 В туннельном SIS переходе при изменении Ф на Ф 0 источник тока совершает работу . )(0 t. IE Кроме того, в качестве источника тока можно представить себе сверхпроводящую катушку с индуктивностью L >> Ф 0 / I , тогда изменение φ на 2π приведет к изменению магнитного потока в этой катушке на Ф 0 . s s ks kiks ks k. UUe. Udk. C, )()2(, )( )()()( ks. , , 2, 1, 0 )()(s k. U Для того, чтобы найти волновые функции и собственные значения энергии , )()(k. Es необходимо решить уравнение Шредингера с Гамильтогианом: . 2/, cos )2/( 2 2 2 0 CQJq. ECe. EEEH Это будет как раз хорошо известное уравнение Матье (!). Свойства спектра энергии: периодическая зависимость внутри каждой зоны: . 2, )()1( )()( квазизарядekqk. E nn Аналогия между малым туннельным SIS переходом и электроном в кристаллической решетке нарушается по мере появления слабого взаимодействия I q (за счет тока квазичастиц) с термостатом, которое приводит к установлению равновесного статистического распределения по энергиям E ( s ) ( k ). В отличие от ансамбля электронов в кристаллической решетке, для которых справедлива статистика Ферми-Дирака, одиночный переход как одиночный объект представляет собой статистический ансамбль, который описывается статистическим распределением Гиббса: . , /)(exp)( 0 )( )(1)( )( n Tk k. E B nndke. ZTkk. EZk. Ef. B n Если , min)0()1()0(EETkk. B то переход находится в состоянии n = 0 как в отсутствие тока, так и при малом токе I. Введем параметр , /2/1 QJEEs который сильно влияет на )()(k. En
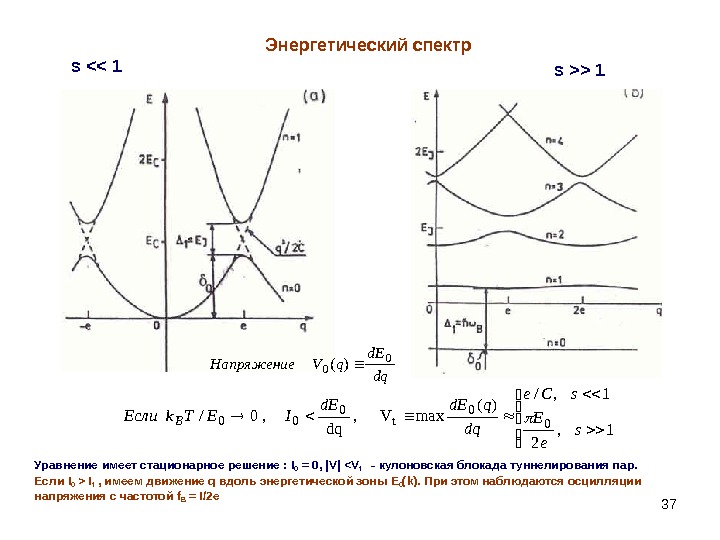
 37 Энергетический спектр s <> 1 dqd. E q. VНапряжение 0 0 )( 1, 2 1, / )( max. V , dq, 0/0 0 t 0 00 s e. E s. Ce dq qd. E IETk. Если. B Уравнение имеет стационарное решение : I 0 = 0, | V | I t , имеем движение q вдоль энергетической зоны E 0 ( k ). При этом наблюдаются осцилляции напряжения с частотой f B = I/2 e
37 Энергетический спектр s <> 1 dqd. E q. VНапряжение 0 0 )( 1, 2 1, / )( max. V , dq, 0/0 0 t 0 00 s e. E s. Ce dq qd. E IETk. Если. B Уравнение имеет стационарное решение : I 0 = 0, | V | I t , имеем движение q вдоль энергетической зоны E 0 ( k ). При этом наблюдаются осцилляции напряжения с частотой f B = I/2 e
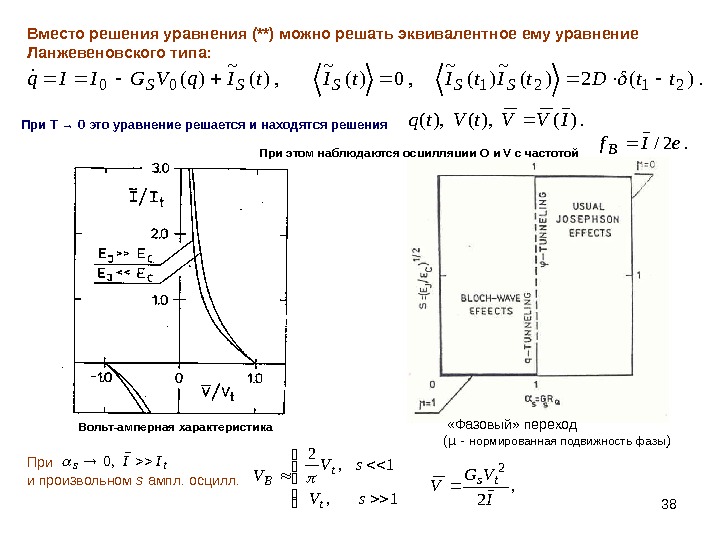
 38 Вместо решения уравнения (**) можно решать эквивалентное ему уравнение Ланжевеновского типа: . )(2)(~ , 0)(~ , )(~ )( 212100 tt. Dt. It. Iq. VGIIq SSSSS При Т → 0 это уравнение решается и находятся решения . )(), (IVVt. Vtq При этом наблюдаются осцилляции Q и V с частотой . 2/e. If. B Вольт-амперная характеристика «Фазовый» переход ( µ — нормированная подвижность фазы ) При ts. II, 0 и произвольном s ампл. осцилл. 1, 1, 2 s. V V t t B , 2 2 I VG Vts
38 Вместо решения уравнения (**) можно решать эквивалентное ему уравнение Ланжевеновского типа: . )(2)(~ , 0)(~ , )(~ )( 212100 tt. Dt. It. Iq. VGIIq SSSSS При Т → 0 это уравнение решается и находятся решения . )(), (IVVt. Vtq При этом наблюдаются осцилляции Q и V с частотой . 2/e. If. B Вольт-амперная характеристика «Фазовый» переход ( µ — нормированная подвижность фазы ) При ts. II, 0 и произвольном s ампл. осцилл. 1, 1, 2 s. V V t t B , 2 2 I VG Vts
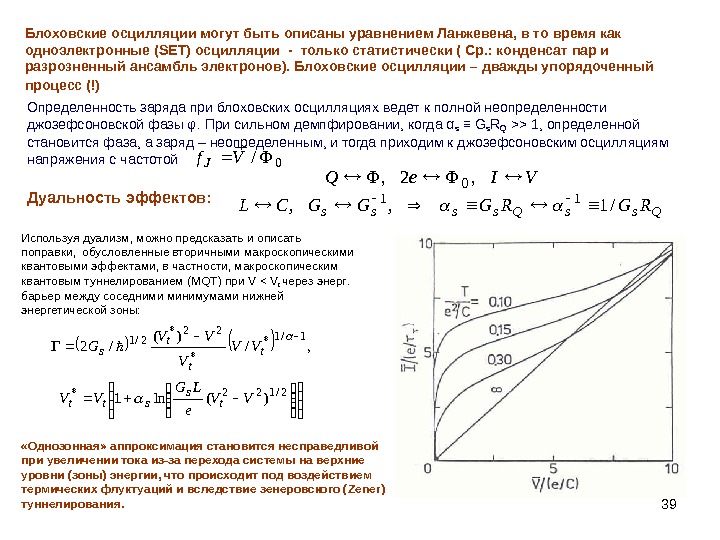
 39 Блоховские осцилляции могут быть описаны уравнением Ланжевена, в то время как одноэлектронные ( SET ) осцилляции — только статистически ( Ср. : конденсат пар и разрозненный ансамбль электронов). Блоховские осцилляции – дважды упорядоченный процесс (!) Определенность заряда при блоховских осцилляциях ведет к полной неопределенности джозефсоновской фазы φ. При сильном демпфировании, когда α s ≡ G s R Q >> 1, определенной становится фаза, а заряд – неопределенным, и тогда приходим к джозефсоновским осцилляциям напряжения с частотой 0/Vf. J Дуальность эффектов: VIe. Q, 2, 0 Qssss. RGRGGGCL/1, , 11 Используя дуализм, можно предсказать и описать поправки, обусловленные вторичными макроскопическими квантовыми эффектами, в частности, макроскопическим квантовым туннелированием ( MQT ) при V < V t через энерг. барьер между соседними минимумами нижней энергетической зоны: 2/122* 1/1* * 22* 2/1 )(ln 1 , / )( /2 VV e LG VV VV G t s stt t s «Однозонная» аппроксимация становится несправедливой при увеличении тока из-за перехода системы на верхние уровни (зоны) энергии, что происходит под воздействием термических флуктуаций и вследствие зенеровского ( Zener) туннелирования.
39 Блоховские осцилляции могут быть описаны уравнением Ланжевена, в то время как одноэлектронные ( SET ) осцилляции — только статистически ( Ср. : конденсат пар и разрозненный ансамбль электронов). Блоховские осцилляции – дважды упорядоченный процесс (!) Определенность заряда при блоховских осцилляциях ведет к полной неопределенности джозефсоновской фазы φ. При сильном демпфировании, когда α s ≡ G s R Q >> 1, определенной становится фаза, а заряд – неопределенным, и тогда приходим к джозефсоновским осцилляциям напряжения с частотой 0/Vf. J Дуальность эффектов: VIe. Q, 2, 0 Qssss. RGRGGGCL/1, , 11 Используя дуализм, можно предсказать и описать поправки, обусловленные вторичными макроскопическими квантовыми эффектами, в частности, макроскопическим квантовым туннелированием ( MQT ) при V < V t через энерг. барьер между соседними минимумами нижней энергетической зоны: 2/122* 1/1* * 22* 2/1 )(ln 1 , / )( /2 VV e LG VV VV G t s stt t s «Однозонная» аппроксимация становится несправедливой при увеличении тока из-за перехода системы на верхние уровни (зоны) энергии, что происходит под воздействием термических флуктуаций и вследствие зенеровского ( Zener) туннелирования.
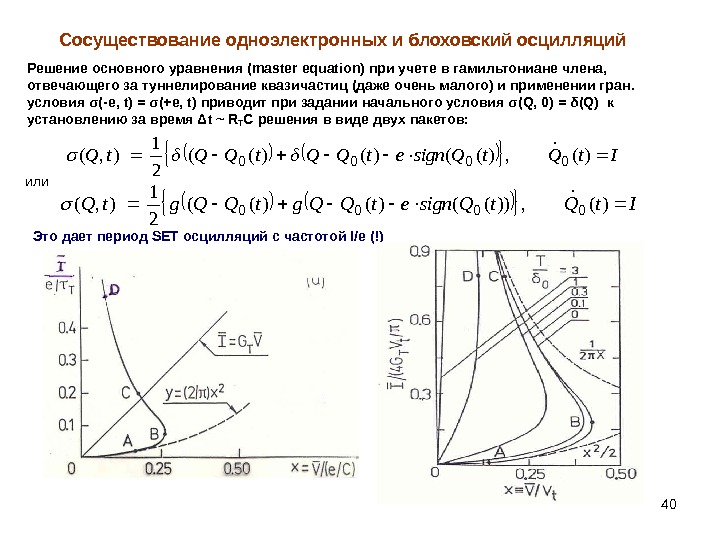
 40 Сосуществование одноэлектронных и блоховский осцилляций Решение основного уравнения ( master equation) при учете в гамильтониане члена, отвечающего за туннелирование квазичастиц (даже очень малого) и применении гран. условия σ (-е , t) = σ (+e, t) приводит при задании начального условия σ ( Q, 0) = δ (Q) к установлению за время Δ t ~ R T C решения в виде двух пакетов: It. Qsignet. QQt. Q )(, )(()()(( 21 ), ( 0000 или It. Qsignet. QQgt. Q)(, ))(()()(( 2 1 ), (0000 Это дает период SET осцилляций c частотой I/e (!)
40 Сосуществование одноэлектронных и блоховский осцилляций Решение основного уравнения ( master equation) при учете в гамильтониане члена, отвечающего за туннелирование квазичастиц (даже очень малого) и применении гран. условия σ (-е , t) = σ (+e, t) приводит при задании начального условия σ ( Q, 0) = δ (Q) к установлению за время Δ t ~ R T C решения в виде двух пакетов: It. Qsignet. QQt. Q )(, )(()()(( 21 ), ( 0000 или It. Qsignet. QQgt. Q)(, ))(()()(( 2 1 ), (0000 Это дает период SET осцилляций c частотой I/e (!)
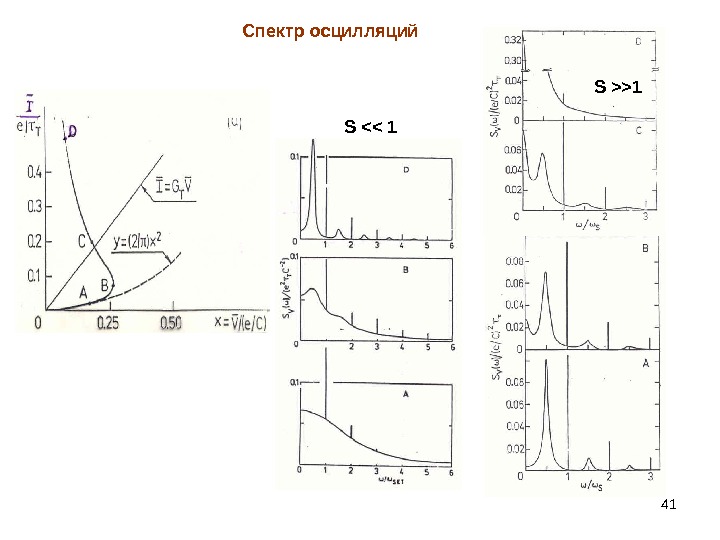
 41 Спектр осцилляций S <>
41 Спектр осцилляций S <>
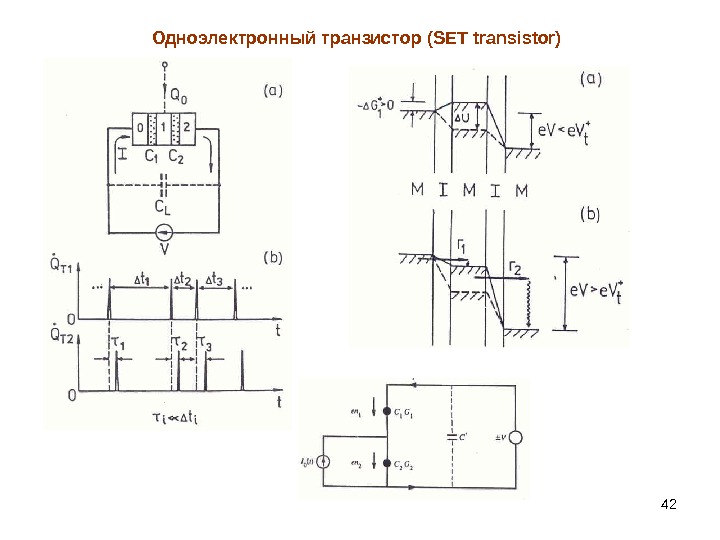
 42 Одноэлектронный транзистор ( SET transistor)
42 Одноэлектронный транзистор ( SET transistor)
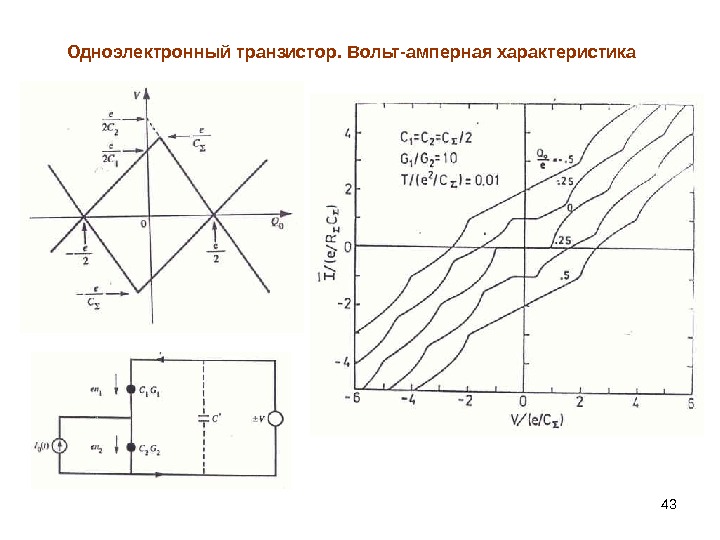
 43 Одноэлектронный транзистор. Вольт-амперная характеристика
43 Одноэлектронный транзистор. Вольт-амперная характеристика
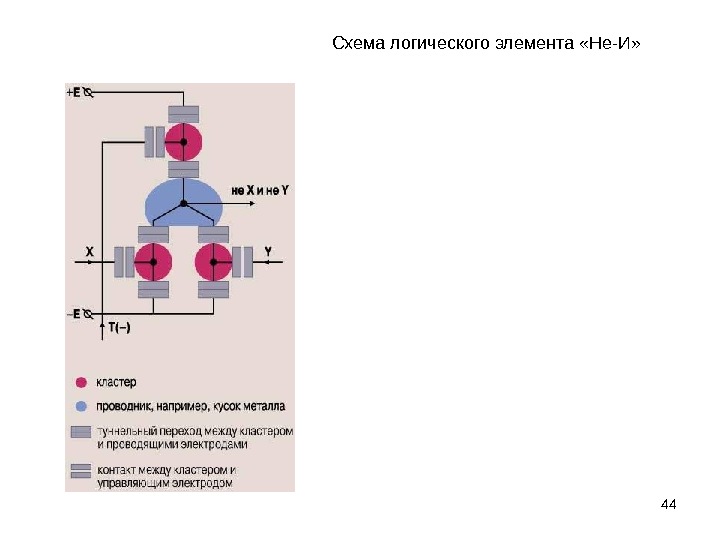
 44 Схема логического элемента «Не-И»
44 Схема логического элемента «Не-И»
 45 Синхронизация одноэлектронных и блоховских колебаний
45 Синхронизация одноэлектронных и блоховских колебаний
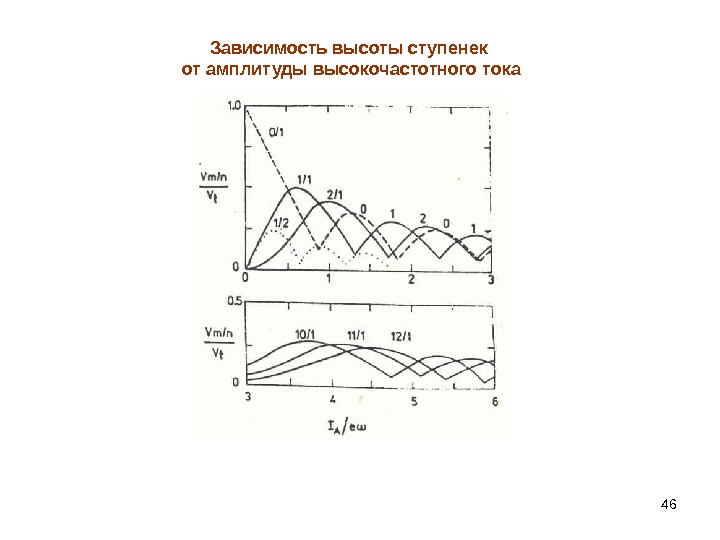
 46 Зависимость высоты ступенек от амплитуды высокочастотного тока
46 Зависимость высоты ступенек от амплитуды высокочастотного тока
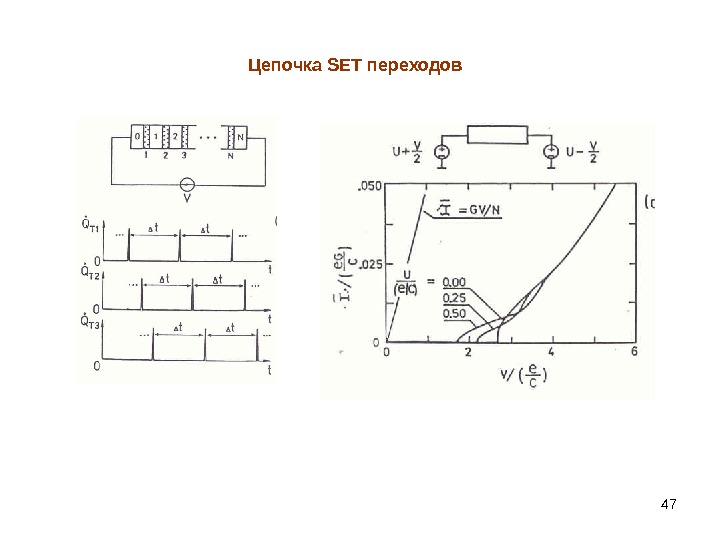
 47 Цепочка SET переходов
47 Цепочка SET переходов
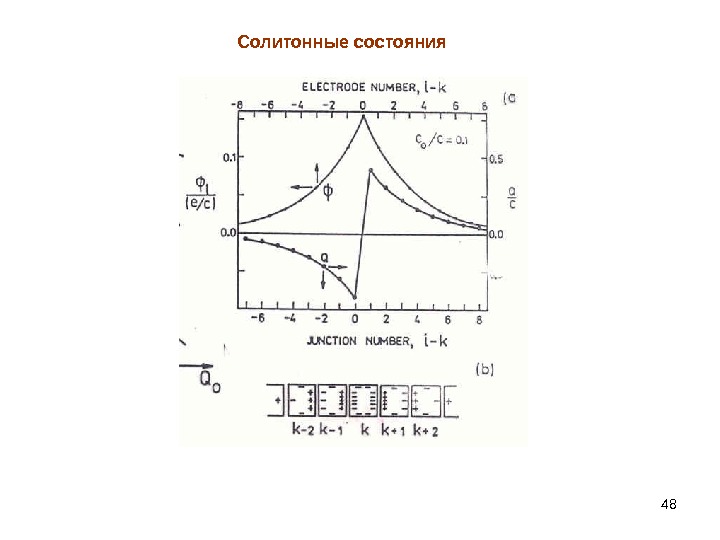
 48 Солитонные состояния
48 Солитонные состояния
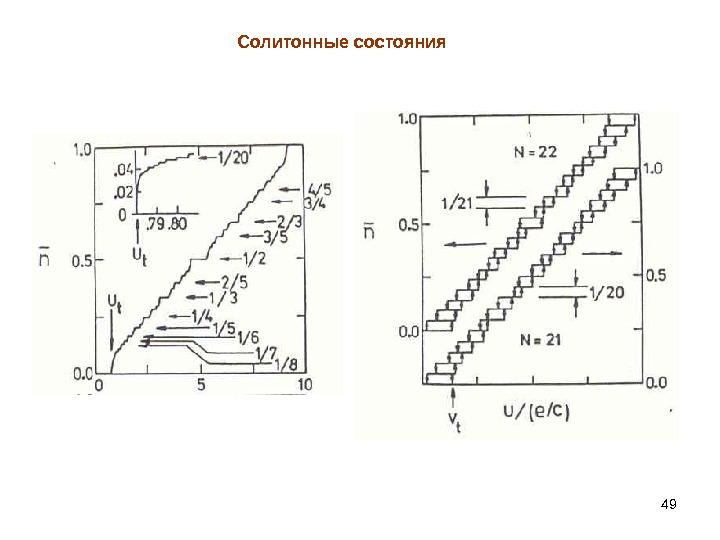
 49 Солитонные состояния
49 Солитонные состояния
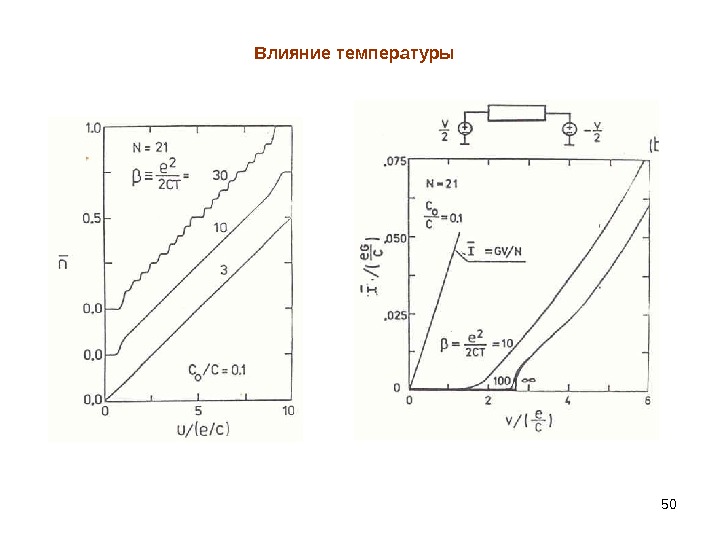
 50 Влияние температуры
50 Влияние температуры
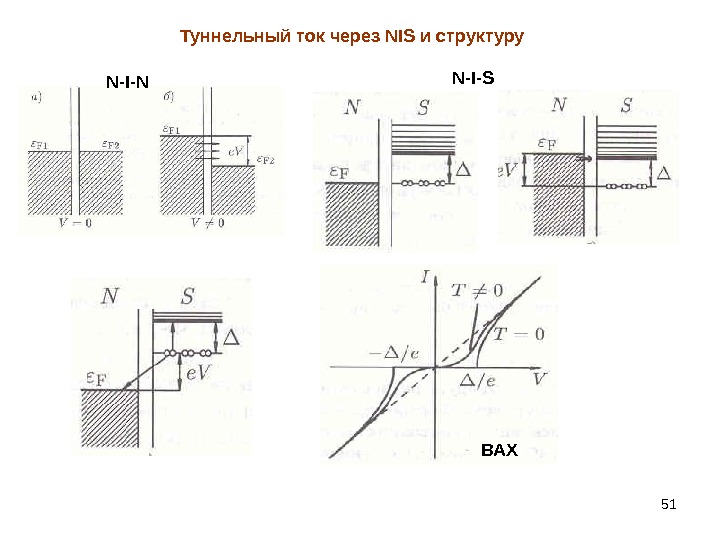
 51 Туннельный ток через NIS и структуру N-I-N N-I-S BAX
51 Туннельный ток через NIS и структуру N-I-N N-I-S BAX
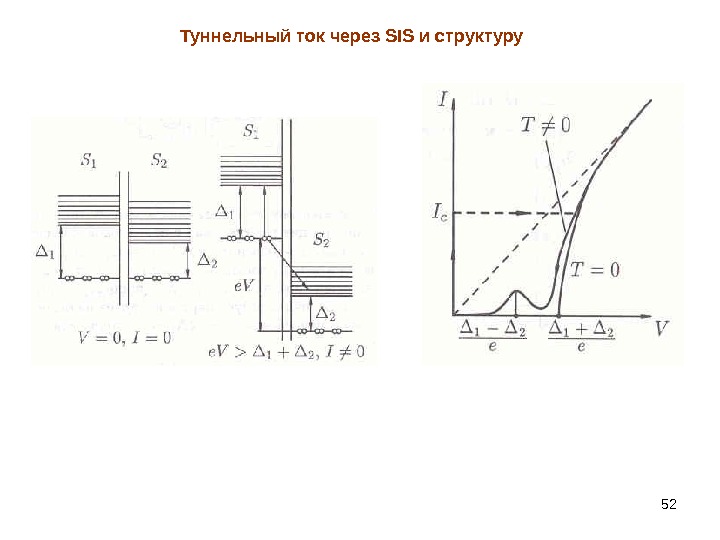
 52 Туннельный ток через SIS и структуру
52 Туннельный ток через SIS и структуру
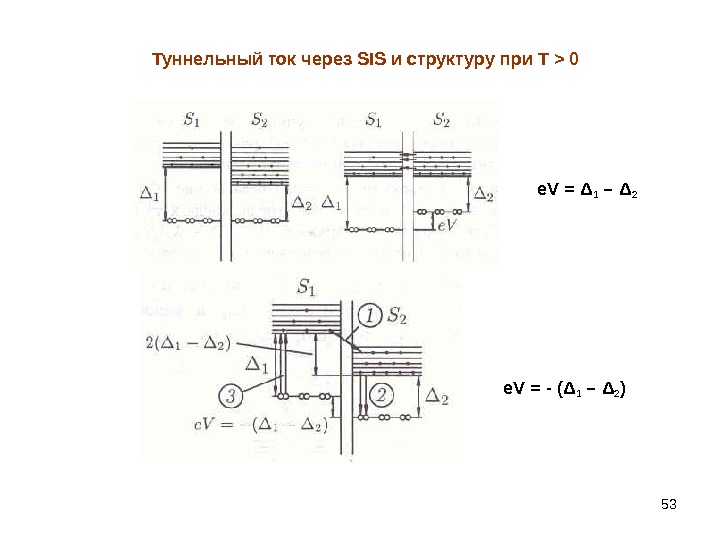
 53 Туннельный ток через SIS и структуру при Т > 0 e. V = Δ 1 – Δ 2 e. V = — ( Δ 1 – Δ 2 )
53 Туннельный ток через SIS и структуру при Т > 0 e. V = Δ 1 – Δ 2 e. V = — ( Δ 1 – Δ 2 )
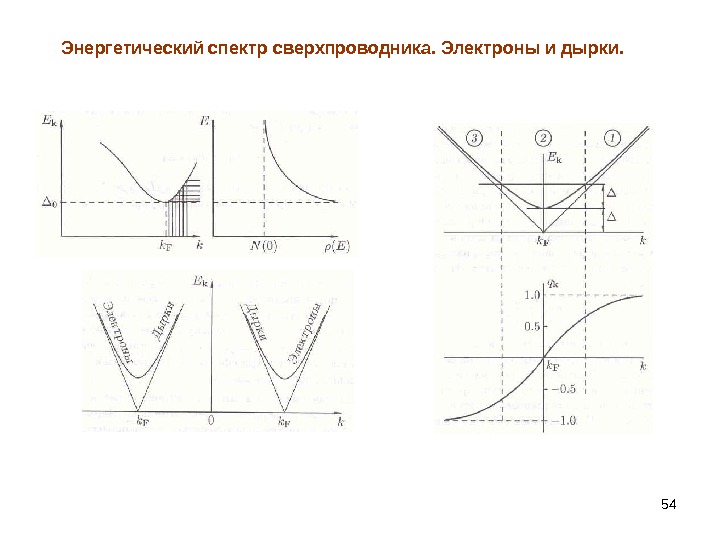
 54 Энергетический спектр сверхпроводника. Электроны и дырки.
54 Энергетический спектр сверхпроводника. Электроны и дырки.
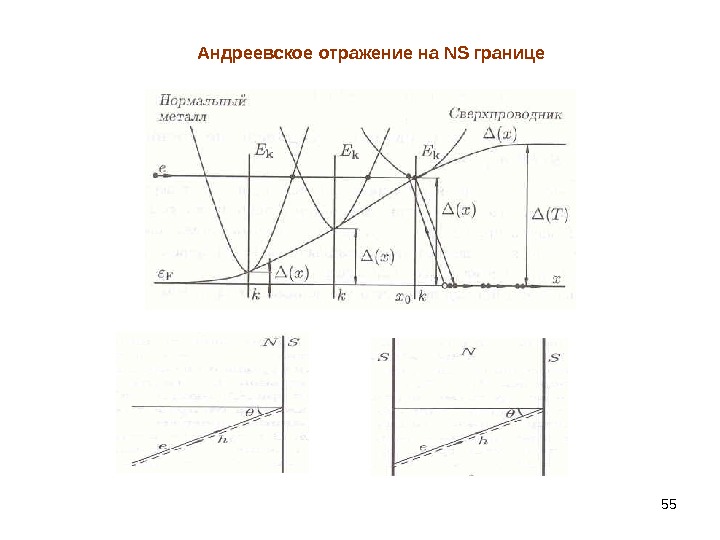
 55 Андреевское отражение на NS границе
55 Андреевское отражение на NS границе
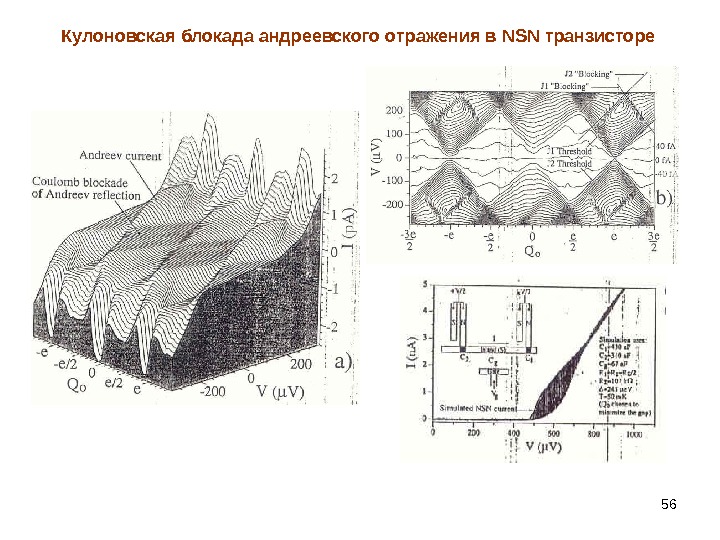
 56 Кулоновская блокада андреевского отражения в NSN транзисторе
56 Кулоновская блокада андреевского отражения в NSN транзисторе
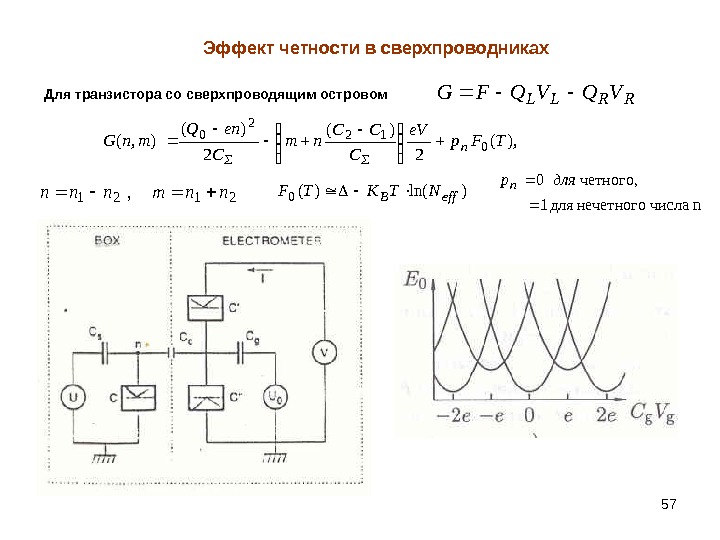
 57 Эффект четности в сверхпроводниках RRLL VQVQFG Для транзистора со сверхпроводящим островом 2121, nnmnnn ), ( 2 )( ), (0 12 2 0 TFp e. V C CC nm C en. Q mn. Gn n числа нечетного для 1 , четного 0 дляp n )ln()(0 eff. BNTKT
57 Эффект четности в сверхпроводниках RRLL VQVQFG Для транзистора со сверхпроводящим островом 2121, nnmnnn ), ( 2 )( ), (0 12 2 0 TFp e. V C CC nm C en. Q mn. Gn n числа нечетного для 1 , четного 0 дляp n )ln()(0 eff. BNTKT

 59 • Классические вычисления классические алгоритмы; классические биты ( « 0» и « 1» ) «Закон» Мура ( элементы микросхем уменьшаются вдвое каждые полтора года ) и перспективы использования эффективных квантовых алгоритмов • Квантовые вычисления квантовые алгоритмы; принцип суперпозиции и квантовый параллелизм; квантовые биты – кубиты (суперпозиция « 0» и « 1» ) Полупроводниковая элементная база Квантовый компьютер — физическое устройство, выполняющее логические операции над квантовыми состояниями путем унитарных преобразований, не нарушающих квантовые суперпозиции в процессе вычислений. Необходима новая элементная база для создания базовых ячеек квантового компьютера – кубитов. Регистр из L кубитов может хранить до 2 L чисел.
59 • Классические вычисления классические алгоритмы; классические биты ( « 0» и « 1» ) «Закон» Мура ( элементы микросхем уменьшаются вдвое каждые полтора года ) и перспективы использования эффективных квантовых алгоритмов • Квантовые вычисления квантовые алгоритмы; принцип суперпозиции и квантовый параллелизм; квантовые биты – кубиты (суперпозиция « 0» и « 1» ) Полупроводниковая элементная база Квантовый компьютер — физическое устройство, выполняющее логические операции над квантовыми состояниями путем унитарных преобразований, не нарушающих квантовые суперпозиции в процессе вычислений. Необходима новая элементная база для создания базовых ячеек квантового компьютера – кубитов. Регистр из L кубитов может хранить до 2 L чисел.
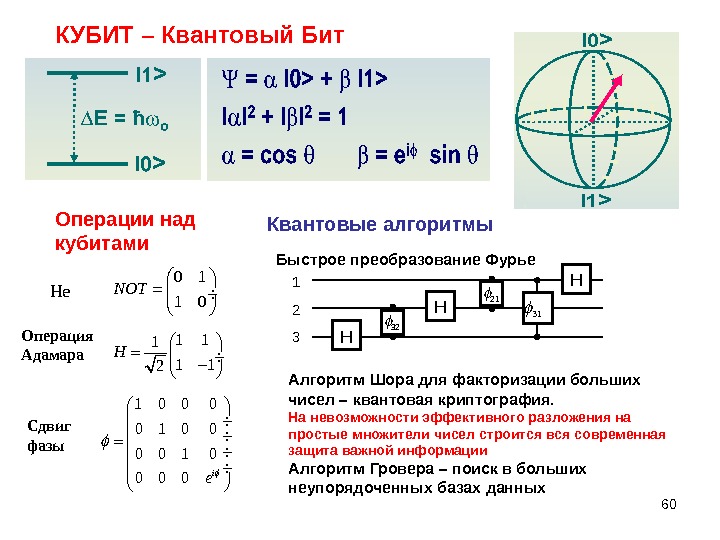
 600 1 1 0 NOT КУБИТ – Квантовый Бит Операции над кубитами Квантовые алгоритмы Не 1 11 1 12 H Операция Адамара 1 0 0 0 0 1 0 0 i e Сдвиг фазы Быстрое преобразование Фурье 1 2 3 H Н 31 32 21 Н Алгоритм Шора для факторизации больших чисел – квантовая криптография. На невозможности эффективного разложения на простые множители чисел строится вся современная защита важной информации Алгоритм Гровера – поиск в больших неупорядоченных базах данных
600 1 1 0 NOT КУБИТ – Квантовый Бит Операции над кубитами Квантовые алгоритмы Не 1 11 1 12 H Операция Адамара 1 0 0 0 0 1 0 0 i e Сдвиг фазы Быстрое преобразование Фурье 1 2 3 H Н 31 32 21 Н Алгоритм Шора для факторизации больших чисел – квантовая криптография. На невозможности эффективного разложения на простые множители чисел строится вся современная защита важной информации Алгоритм Гровера – поиск в больших неупорядоченных базах данных
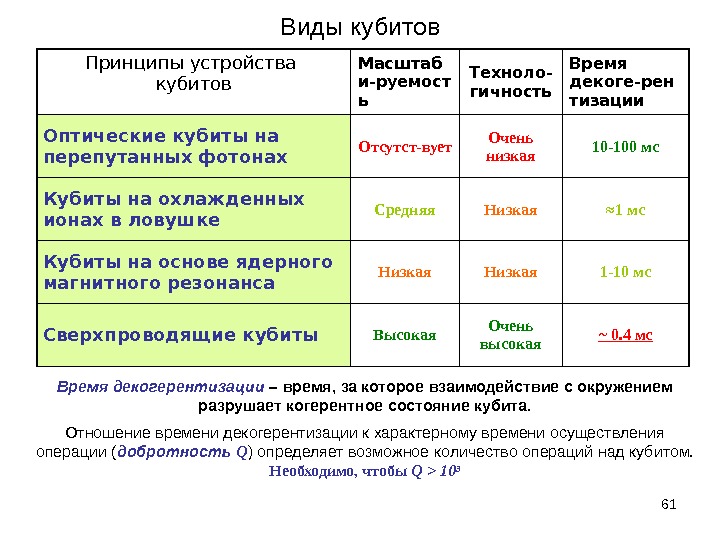
 61 Виды кубитов Принципы устройства кубитов Масштаб и-руемост ь Техноло- гичность Время декоге-рен тизации Оптические кубиты на перепутанных фотонах Отсутст-вует Очень низкая 10 -100 мс Кубиты на охлажденных ионах в ловушке Средняя Низкая ≈ 1 мс Кубиты на основе ядерного магнитного резонанса Низкая 1 -10 мс Сверхпроводящие кубиты Высокая Очень высокая ~ 0. 4 мс Время декогерентизации – время, за которое взаимодействие с окружением разрушает когерентное состояние кубита. Отношение времени декогерентизации к характерному времени осуществления операции ( добротность Q ) определяет возможное количество операций над кубитом. Необходимо, чтобы Q >
61 Виды кубитов Принципы устройства кубитов Масштаб и-руемост ь Техноло- гичность Время декоге-рен тизации Оптические кубиты на перепутанных фотонах Отсутст-вует Очень низкая 10 -100 мс Кубиты на охлажденных ионах в ловушке Средняя Низкая ≈ 1 мс Кубиты на основе ядерного магнитного резонанса Низкая 1 -10 мс Сверхпроводящие кубиты Высокая Очень высокая ~ 0. 4 мс Время декогерентизации – время, за которое взаимодействие с окружением разрушает когерентное состояние кубита. Отношение времени декогерентизации к характерному времени осуществления операции ( добротность Q ) определяет возможное количество операций над кубитом. Необходимо, чтобы Q >
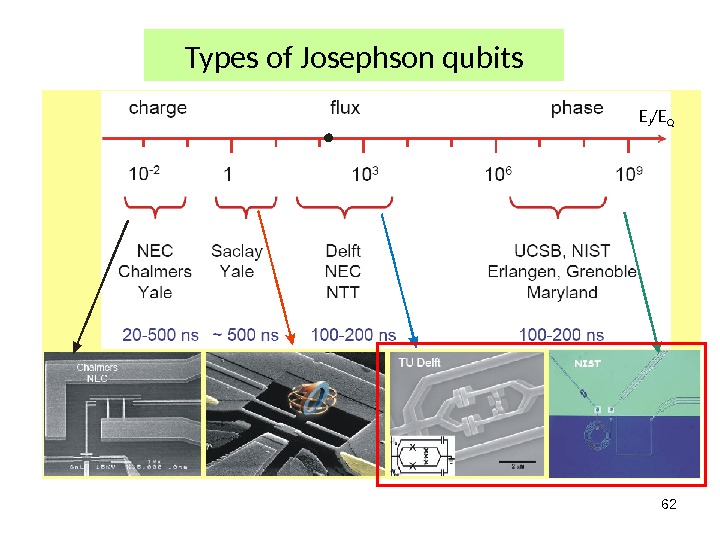
 62 Types of Josephson qubits E J /E Q
62 Types of Josephson qubits E J /E Q
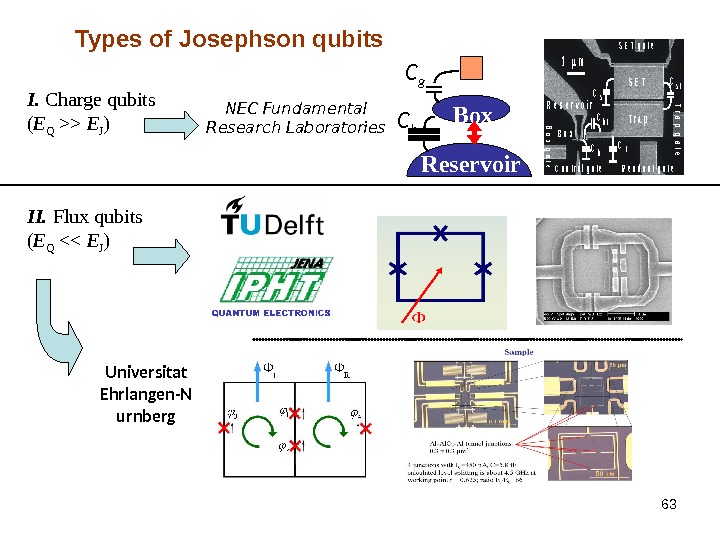
 63 Types of Josephson qubits I. Charge qubits ( E Q >> E J ) NEC Fundamental Research Laboratories Reservoir Box C b. C g II. Flux qubits ( E Q << E J )C C C CC s t b t s bt S E T T r a p R e s e r v o i r R e a d o u t g a t e S E T g a t e C o n t r o l g a t e B o x 1 m Trap gate Box gate Universitat Ehrlangen-N urnberg
63 Types of Josephson qubits I. Charge qubits ( E Q >> E J ) NEC Fundamental Research Laboratories Reservoir Box C b. C g II. Flux qubits ( E Q << E J )C C C CC s t b t s bt S E T T r a p R e s e r v o i r R e a d o u t g a t e S E T g a t e C o n t r o l g a t e B o x 1 m Trap gate Box gate Universitat Ehrlangen-N urnberg
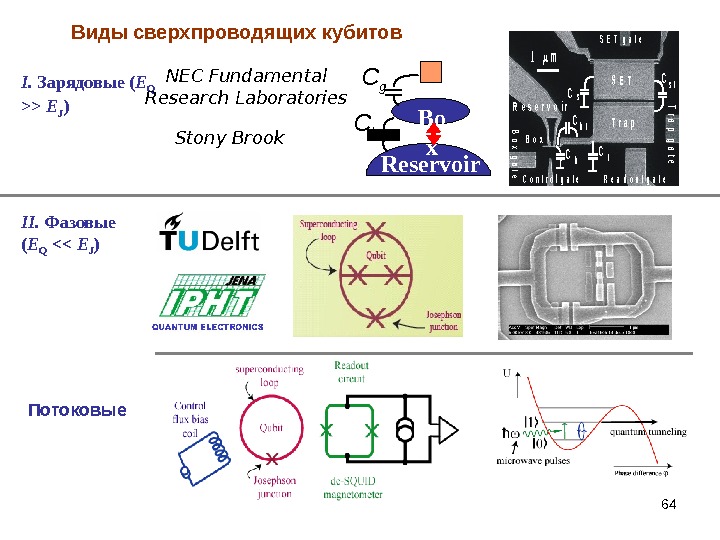
 64 Виды сверхпроводящих кубитов I. Зарядовые ( E Q >> E J ) NEC Fundamental Research Laboratories Reservoir Bo x. C b. C g II. Фазовые ( E Q << E J )C C C CC s t b t s bt S E T T r a p R e s e r v o i r R e a d o u t g a t e S E T g a t e C o n t r o l g a t e B o x 1 m Trap gate Box gate Потоковые Stony Brook
64 Виды сверхпроводящих кубитов I. Зарядовые ( E Q >> E J ) NEC Fundamental Research Laboratories Reservoir Bo x. C b. C g II. Фазовые ( E Q << E J )C C C CC s t b t s bt S E T T r a p R e s e r v o i r R e a d o u t g a t e S E T g a t e C o n t r o l g a t e B o x 1 m Trap gate Box gate Потоковые Stony Brook
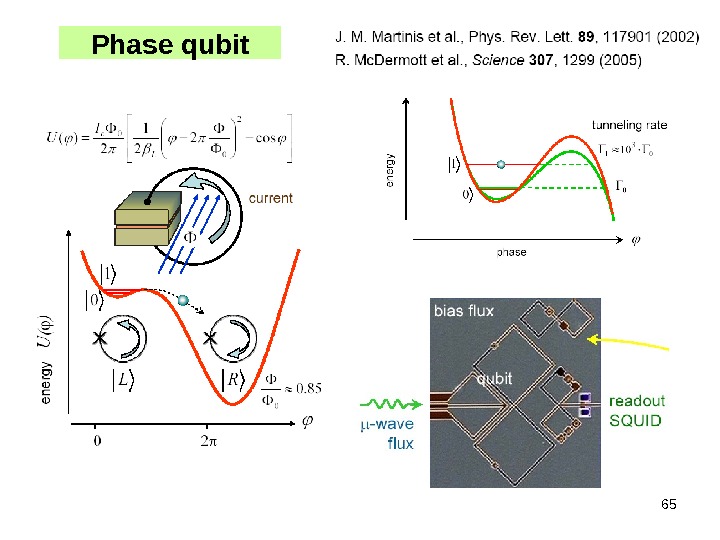
 65 Phase qubit
65 Phase qubit
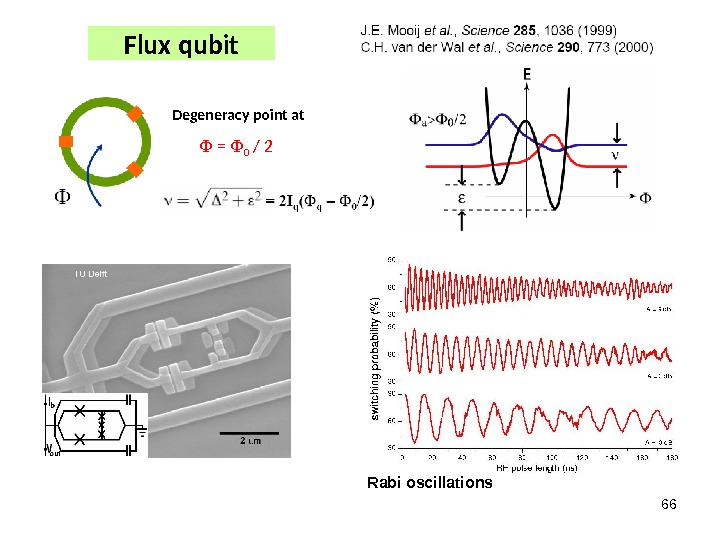
 66 Flux qubit Degeneracy point at = 0 / 2 Rabi oscillations
66 Flux qubit Degeneracy point at = 0 / 2 Rabi oscillations
 67 Quantronium (Saclay) Operation at optimal point (saddle) — minimizes noise effects — voltage fluctuations couple transversely — flux fluctuations couple quadratically 2 ch J 2 g x J xg z 0 xx xg 2 oxo 1 1 1 V 2 2 4 E E V H E ( )δV δ σσσ -1€€€€€ 2 0 1€€€€€ 2 1 -0. 25 0. 5 -1€€€€€ 2 0 1€€€€€ 2 V g x / 0 0. 5 1 -1 E 1 E 0 E C ≈ E J z xhx. Jgc 1 2σE)Vσ(HE)( Charge-phase qubit
67 Quantronium (Saclay) Operation at optimal point (saddle) — minimizes noise effects — voltage fluctuations couple transversely — flux fluctuations couple quadratically 2 ch J 2 g x J xg z 0 xx xg 2 oxo 1 1 1 V 2 2 4 E E V H E ( )δV δ σσσ -1€€€€€ 2 0 1€€€€€ 2 1 -0. 25 0. 5 -1€€€€€ 2 0 1€€€€€ 2 V g x / 0 0. 5 1 -1 E 1 E 0 E C ≈ E J z xhx. Jgc 1 2σE)Vσ(HE)( Charge-phase qubit
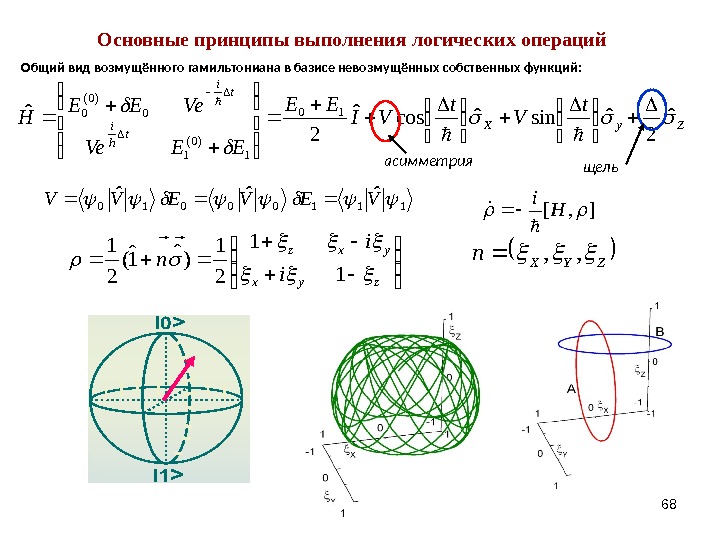
 68 Основные принципы выполнения логических операций 11100010 ˆˆˆVEVEVV Общий вид возмущённого гамильтониана в базисе невозмущённых собственных функций: zyx yxz i i n 11 21 )ˆ 1 ˆ ( 21 ZYXn, , ], [ Hi Zy. X t h i ti t Vt VIEE EEVe Ve. EE Н ˆ 2ˆ sinˆ cosˆ 2ˆ 10 1)0( 10)0( 0 асимметрия щель
68 Основные принципы выполнения логических операций 11100010 ˆˆˆVEVEVV Общий вид возмущённого гамильтониана в базисе невозмущённых собственных функций: zyx yxz i i n 11 21 )ˆ 1 ˆ ( 21 ZYXn, , ], [ Hi Zy. X t h i ti t Vt VIEE EEVe Ve. EE Н ˆ 2ˆ sinˆ cosˆ 2ˆ 10 1)0( 10)0( 0 асимметрия щель
 69 JJE E 3 3 )2 cos()cos(2 2 1ˆ2 22 2 JJQ EEEH энергиявскаяджозефсоно IIIII энергияякулоновска I UVWH 2 coscosˆ 2 2 Гамильтонианы кубитов на основе 2 -ч- и 3 -х-контактных интерферометров. 0)2 cos(2»qa )2 cos()cos(2)1( 21 ˆ 3 22 1 33 JJQ EEEH Гамильтониан двухконтактного кубита: Гамильтониан трёхконтактного кубита: Общий метод решения уравнений Шредингера — использование теории возмущений, где « 0» -приближение – чётные и нечётные решения уравнения Матье: Общий вид: 2, 1 2 AB «барьер»
69 JJE E 3 3 )2 cos()cos(2 2 1ˆ2 22 2 JJQ EEEH энергиявскаяджозефсоно IIIII энергияякулоновска I UVWH 2 coscosˆ 2 2 Гамильтонианы кубитов на основе 2 -ч- и 3 -х-контактных интерферометров. 0)2 cos(2»qa )2 cos()cos(2)1( 21 ˆ 3 22 1 33 JJQ EEEH Гамильтониан двухконтактного кубита: Гамильтониан трёхконтактного кубита: Общий метод решения уравнений Шредингера — использование теории возмущений, где « 0» -приближение – чётные и нечётные решения уравнения Матье: Общий вид: 2, 1 2 AB «барьер»
![70]], [, [ 2 ], [AA k H i Уравнение для матрицы плотности (уравнение 70]], [, [ 2 ], [AA k H i Уравнение для матрицы плотности (уравнение](/docs//noc-single-electronics_images/noc-single-electronics_69.jpg) 70]], [, [ 2 ], [AA k H i Уравнение для матрицы плотности (уравнение Линдблада) 21 Ta. Tk Запутанность (энтропия фон Неймана) ))(ˆlog)(ˆ()(2 tt. Sp. E Декогеренция – процесс увеличения запутанности с окружением. 2* *2)0(ˆ 2/10 02/1 )(10 «жёсткость» измерения А – оператор измеряемой наблюдаемой ρ – редуцированная матрица плотности Решение этого уравнения дает эволюцию ρ ( t ) от ρ (0) до ρ (∞): B. M. Mensky, Quantum measurements and decoherence: models and phenomenology, 2000.
70]], [, [ 2 ], [AA k H i Уравнение для матрицы плотности (уравнение Линдблада) 21 Ta. Tk Запутанность (энтропия фон Неймана) ))(ˆlog)(ˆ()(2 tt. Sp. E Декогеренция – процесс увеличения запутанности с окружением. 2* *2)0(ˆ 2/10 02/1 )(10 «жёсткость» измерения А – оператор измеряемой наблюдаемой ρ – редуцированная матрица плотности Решение этого уравнения дает эволюцию ρ ( t ) от ρ (0) до ρ (∞): B. M. Mensky, Quantum measurements and decoherence: models and phenomenology, 2000.
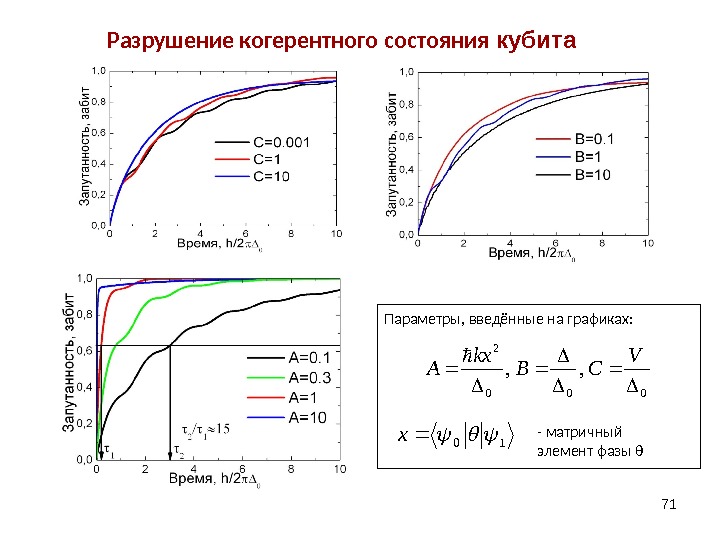
 71 Разрушение когерентного состояния кубита Параметры, введённые на графиках: 000 2 , , V CBkx A 10 x — матричный элемент фазы θ
71 Разрушение когерентного состояния кубита Параметры, введённые на графиках: 000 2 , , V CBkx A 10 x — матричный элемент фазы θ
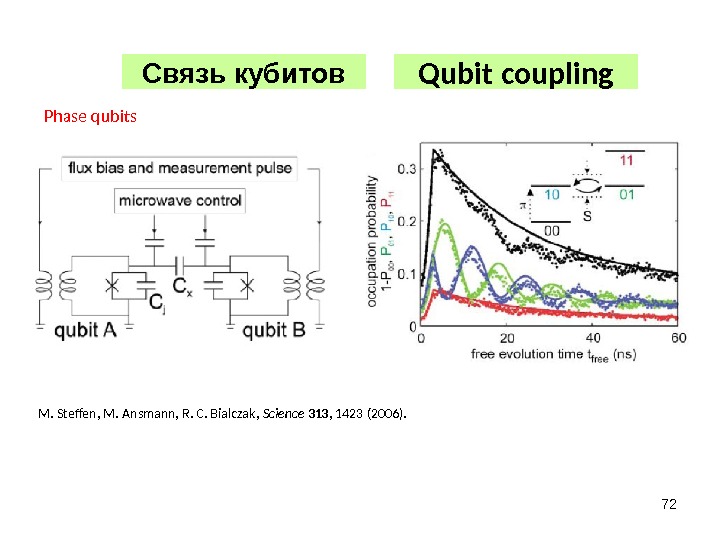
 72 Qubit coupling M. Steffen, M. Ansmann, R. C. Bialczak, Science 313 , 1423 (2006). Phase qubits Связь кубитов
72 Qubit coupling M. Steffen, M. Ansmann, R. C. Bialczak, Science 313 , 1423 (2006). Phase qubits Связь кубитов
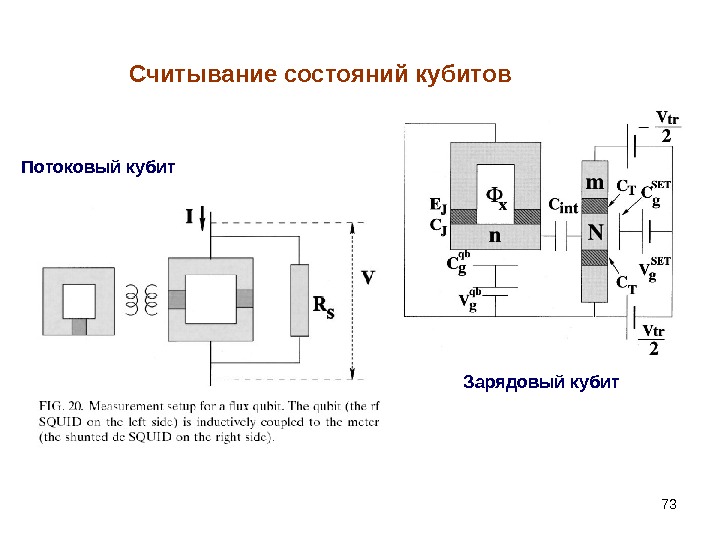
 73 Считывание состояний кубитов Потоковый кубит Зарядовый кубит
73 Считывание состояний кубитов Потоковый кубит Зарядовый кубит
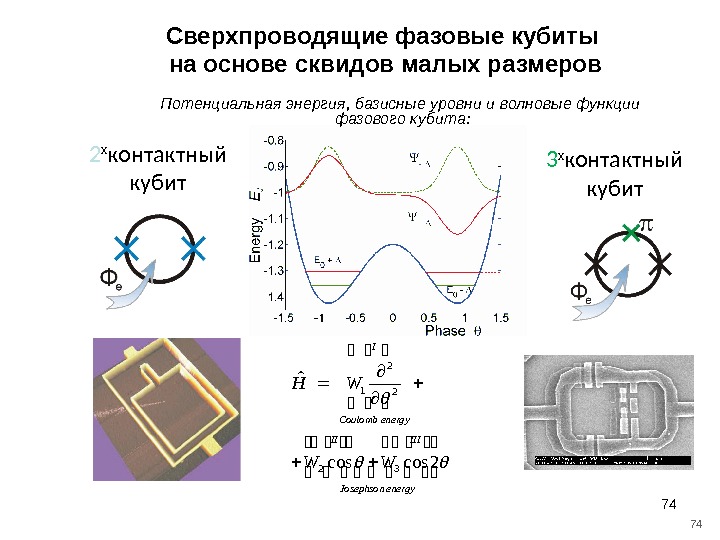
 74 74 Сверхпроводящие фазовые кубиты на основе сквидов малых размеров Потенциальная энергия, базисные уровни и волновые функции фазового кубита: 2 х контактный кубит 3 х контактный кубит energy. Josephson IIIII ergy. Coulomb en I WW WH 32 2 2 1 2 coscos ˆ
74 74 Сверхпроводящие фазовые кубиты на основе сквидов малых размеров Потенциальная энергия, базисные уровни и волновые функции фазового кубита: 2 х контактный кубит 3 х контактный кубит energy. Josephson IIIII ergy. Coulomb en I WW WH 32 2 2 1 2 coscos ˆ
 75 Круговой ток в кольце кубита как функция приложенного к нему магнитного потока в состояниях 0 и 1. сплошные линии — 2 -х-контактный кубит, пунктирные линии — 3 -х-контактный кубит Считывание состояния кубита с использованием RSFQ цепей: Воздействие магнитного поля тока в кубите на перемещающийся по JTL квант потока будет приводить или к ускорению или к запаздыванию кванта в зависимости от направления тока в кубите. Считывание состояния кубита
75 Круговой ток в кольце кубита как функция приложенного к нему магнитного потока в состояниях 0 и 1. сплошные линии — 2 -х-контактный кубит, пунктирные линии — 3 -х-контактный кубит Считывание состояния кубита с использованием RSFQ цепей: Воздействие магнитного поля тока в кубите на перемещающийся по JTL квант потока будет приводить или к ускорению или к запаздыванию кванта в зависимости от направления тока в кубите. Считывание состояния кубита













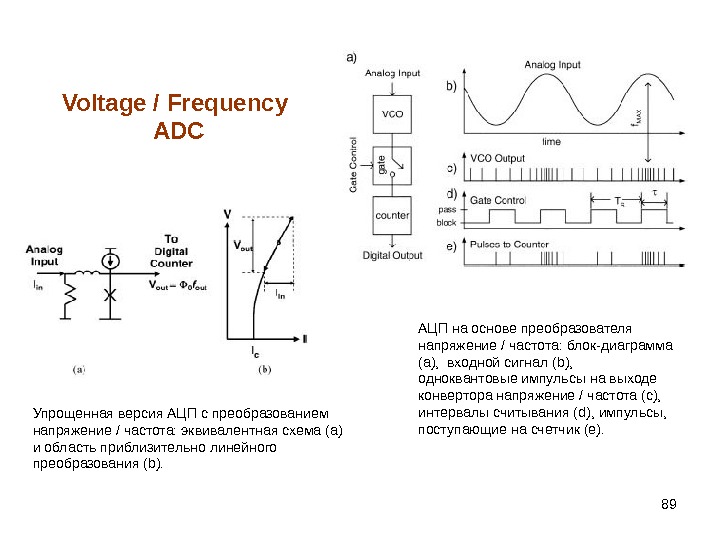
 89 Voltage / Frequency ADC Упрощенная версия АЦП с преобразованием напряжение / частота: эквивалентная схема (а) и область приблизительно линейного преобразования ( b). АЦП на основе преобразователя напряжение / частота: блок-диаграмма (а), входной сигнал ( b), одноквантовые импульсы на выходе конвертора напряжение / частота (с), интервалы считывания ( d), импульсы, поступающие на счетчик (е).
89 Voltage / Frequency ADC Упрощенная версия АЦП с преобразованием напряжение / частота: эквивалентная схема (а) и область приблизительно линейного преобразования ( b). АЦП на основе преобразователя напряжение / частота: блок-диаграмма (а), входной сигнал ( b), одноквантовые импульсы на выходе конвертора напряжение / частота (с), интервалы считывания ( d), импульсы, поступающие на счетчик (е).
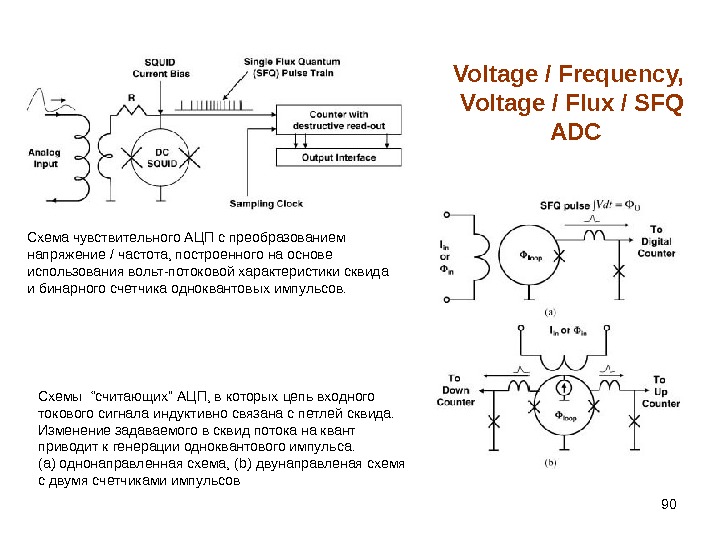
 90 Voltage / Frequency, Voltage / Flux / SFQ ADC Схема чувствительного АЦП с преобразованием напряжение / частота, построенного на основе использования вольт-потоковой характеристики сквида и бинарного счетчика одноквантовых импульсов. Схемы “ считающих ” АЦП, в которых цепь входного токового сигнала индуктивно связана с петлей сквида. Изменение задаваемого в сквид потока на квант приводит к генерации одноквантового импульса. (а) однонаправленная схема, ( b ) двунаправленая схемя с двумя счетчиками импульсов
90 Voltage / Frequency, Voltage / Flux / SFQ ADC Схема чувствительного АЦП с преобразованием напряжение / частота, построенного на основе использования вольт-потоковой характеристики сквида и бинарного счетчика одноквантовых импульсов. Схемы “ считающих ” АЦП, в которых цепь входного токового сигнала индуктивно связана с петлей сквида. Изменение задаваемого в сквид потока на квант приводит к генерации одноквантового импульса. (а) однонаправленная схема, ( b ) двунаправленая схемя с двумя счетчиками импульсов
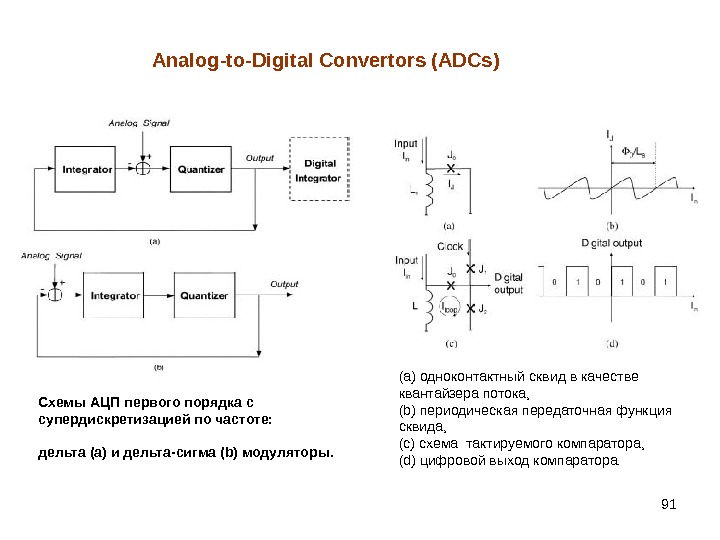
 91 Analog-to-Digital Convertors (ADCs) Схемы АЦП первого порядка с супердискретизацией по частоте: дельта ( a ) и дельта-сигма ( b ) модуляторы. (а) одноконтактный сквид в качестве квантайзера потока, ( b ) периодическая передаточная функция сквида, (с) схема тактируемого компаратора, (d) цифровой выход компаратора.
91 Analog-to-Digital Convertors (ADCs) Схемы АЦП первого порядка с супердискретизацией по частоте: дельта ( a ) и дельта-сигма ( b ) модуляторы. (а) одноконтактный сквид в качестве квантайзера потока, ( b ) периодическая передаточная функция сквида, (с) схема тактируемого компаратора, (d) цифровой выход компаратора.
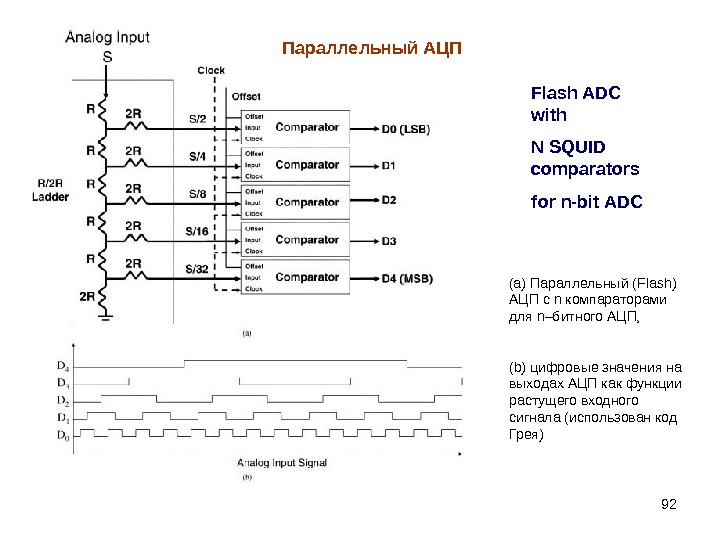
 92 Flash ADC with N SQUID comparators for n-bit ADC (а) Параллельный ( Flash) АЦП с n компараторами для n –битного АЦП, ( b) цифровые значения на выходах АЦП как функции растущего входного сигнала (использован код Грея) Параллельный АЦП
92 Flash ADC with N SQUID comparators for n-bit ADC (а) Параллельный ( Flash) АЦП с n компараторами для n –битного АЦП, ( b) цифровые значения на выходах АЦП как функции растущего входного сигнала (использован код Грея) Параллельный АЦП
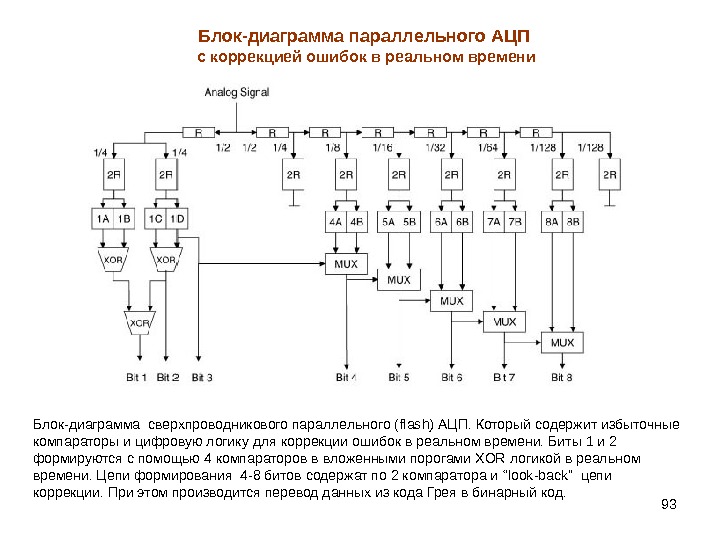
 93 Блок-диаграмма сверхпроводникового параллельного ( flash) АЦП. Который содержит избыточные компараторы и цифровую логику для коррекции ошибок в реальном времени. Биты 1 и 2 формируются с помощью 4 компараторов в вложенными порогами XOR логикой в реальном времени. Цепи формирования 4 -8 битов содержат по 2 компаратора и “look-back” цепи коррекции. При этом производится перевод данных из кода Грея в бинарный код. Блок-диаграмма параллельного АЦП с коррекцией ошибок в реальном времени
93 Блок-диаграмма сверхпроводникового параллельного ( flash) АЦП. Который содержит избыточные компараторы и цифровую логику для коррекции ошибок в реальном времени. Биты 1 и 2 формируются с помощью 4 компараторов в вложенными порогами XOR логикой в реальном времени. Цепи формирования 4 -8 битов содержат по 2 компаратора и “look-back” цепи коррекции. При этом производится перевод данных из кода Грея в бинарный код. Блок-диаграмма параллельного АЦП с коррекцией ошибок в реальном времени
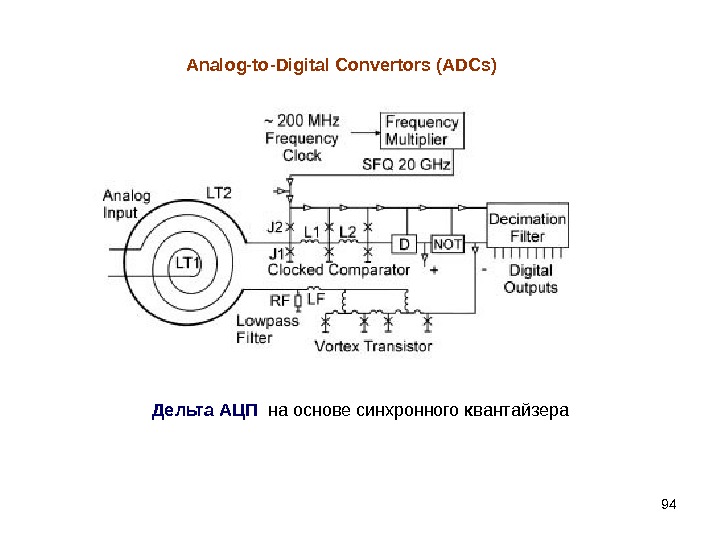
 94 Analog-to-Digital Convertors (ADCs) Дельта АЦП на основе синхронного к вантайзера
94 Analog-to-Digital Convertors (ADCs) Дельта АЦП на основе синхронного к вантайзера
 95 Analog-to-Digital Convertors (ADCs) Чип 5 х 5 мм, содержащий дельта АЦП с дельта модулятором и цифровым фильтром (для децимации ) , который разбит на 3 части для размещения на чипе.
95 Analog-to-Digital Convertors (ADCs) Чип 5 х 5 мм, содержащий дельта АЦП с дельта модулятором и цифровым фильтром (для децимации ) , который разбит на 3 части для размещения на чипе.








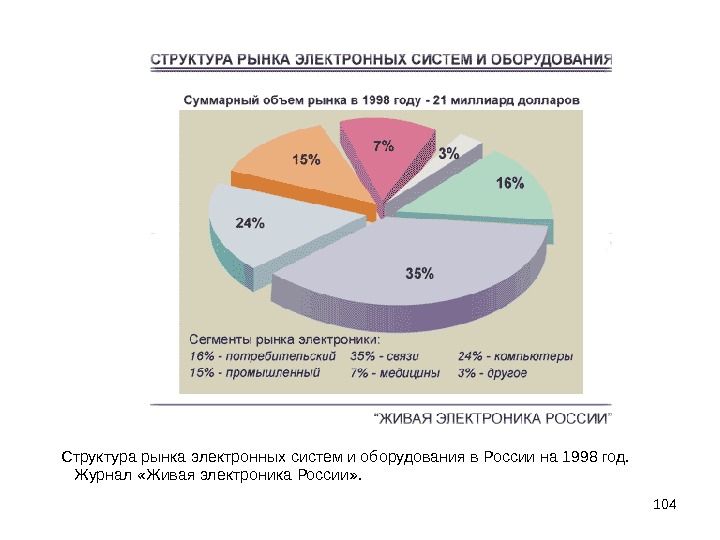
 104 Структура рынка электронных систем и оборудования в России на 1998 год. Журнал «Живая электроника России» .
104 Структура рынка электронных систем и оборудования в России на 1998 год. Журнал «Живая электроника России» .
 105 Министерство обороны США, например, финансирует программу создания “Smart dust” — умной пыли, т. е. большого семейства микророботов, размером в пылинку, которые смогут, рассыпавшись над территорией противника, проникать во все щели, каналы связи, создавать свою сеть, собирать и передавать оперативную информацию, проводить спецоперации и т. д. Есть и более гуманистические проекты: создать специальные микророботы-“доктора”, которые будут сочетать функции диагноста, терапевта и хирурга, перемещаясь по кровеносной, лимфатической или другой системе человека. Уже изготовлены образцы таких роботов, имеющих все функциональные узлы и размеры около 1 мм, и существует реальная перспектива уменьшения их размеров до микронного и субмикронного уровня. Ключевые технологии и материалы всегда играли большую роль в истории цивилизации, выполняя не только узко производственные функции, но и социальные. Достаточно вспомнить, как сильно отличались каменный и бронзовый века, век пара и век электричества, атомной энергии и компьютеров. По мнению многих экспертов, XXI в. будет веком нанонауки и нанотехнологий, которые и определят его лицо. Воздействие нанотехнологий на жизнь обещает иметь всеобщий характер, изменить экономику и затронуть все стороны быта, работы, социальных отношений. С помощью нанотехнологий мы сможем экономить время, получать больше благ за меньшую цену, постоянно повышать уровень и качество жизни. Прогноз развития рынка продукции нанотехнологии на 2015 г. Вот как формулирует грядущие благодаря нанотехнологиям перемены сотрудник Института глобального прогнозирования (Institute For Global Future, USA) Дж. Кэнтон: – наноэнергетика сделает мир более чистым в результате разработки новых типов двигателей, топливных элементов и транспортных средств; – сформируется новая экономика, основанная на нанотехнологиях и нанопродуктах. E-бизнес (электронно-информационный) уступит лидирующие позиции NT-бизнесу (нанотехнологическому); – быстрое развитие нанопромышленности потребует коренной перестройки системы образования на всех уровнях; – потребительские и промышленные товары станут более долговечными, качественными и компактными, а вместе с тем и более дешевыми; – медицинское обслуживание будет более доступным и эффективным. Появятся новые лекарственные препараты и диагностические средства. Нанобиотехнология сделает жизнь людей более здоровой и продолжительной; – новые подключенные к Интернету устройства, объединяющие функции телефона, телевизора и компьютера, образуют глобальную систему связи, которая объединит всех, везде и всегда;
105 Министерство обороны США, например, финансирует программу создания “Smart dust” — умной пыли, т. е. большого семейства микророботов, размером в пылинку, которые смогут, рассыпавшись над территорией противника, проникать во все щели, каналы связи, создавать свою сеть, собирать и передавать оперативную информацию, проводить спецоперации и т. д. Есть и более гуманистические проекты: создать специальные микророботы-“доктора”, которые будут сочетать функции диагноста, терапевта и хирурга, перемещаясь по кровеносной, лимфатической или другой системе человека. Уже изготовлены образцы таких роботов, имеющих все функциональные узлы и размеры около 1 мм, и существует реальная перспектива уменьшения их размеров до микронного и субмикронного уровня. Ключевые технологии и материалы всегда играли большую роль в истории цивилизации, выполняя не только узко производственные функции, но и социальные. Достаточно вспомнить, как сильно отличались каменный и бронзовый века, век пара и век электричества, атомной энергии и компьютеров. По мнению многих экспертов, XXI в. будет веком нанонауки и нанотехнологий, которые и определят его лицо. Воздействие нанотехнологий на жизнь обещает иметь всеобщий характер, изменить экономику и затронуть все стороны быта, работы, социальных отношений. С помощью нанотехнологий мы сможем экономить время, получать больше благ за меньшую цену, постоянно повышать уровень и качество жизни. Прогноз развития рынка продукции нанотехнологии на 2015 г. Вот как формулирует грядущие благодаря нанотехнологиям перемены сотрудник Института глобального прогнозирования (Institute For Global Future, USA) Дж. Кэнтон: – наноэнергетика сделает мир более чистым в результате разработки новых типов двигателей, топливных элементов и транспортных средств; – сформируется новая экономика, основанная на нанотехнологиях и нанопродуктах. E-бизнес (электронно-информационный) уступит лидирующие позиции NT-бизнесу (нанотехнологическому); – быстрое развитие нанопромышленности потребует коренной перестройки системы образования на всех уровнях; – потребительские и промышленные товары станут более долговечными, качественными и компактными, а вместе с тем и более дешевыми; – медицинское обслуживание будет более доступным и эффективным. Появятся новые лекарственные препараты и диагностические средства. Нанобиотехнология сделает жизнь людей более здоровой и продолжительной; – новые подключенные к Интернету устройства, объединяющие функции телефона, телевизора и компьютера, образуют глобальную систему связи, которая объединит всех, везде и всегда;

