5128b35adb4e2f9f3293dce1c331d18a.ppt
- Количество слайдов: 65
 1 Information Security Chapter 2: Cryptography Lecture #1 -Week 3 Dr. Khalid, Dr. Mohannad CIT 460 Information Security Dr. Khalid, Dr. Mohannad
1 Information Security Chapter 2: Cryptography Lecture #1 -Week 3 Dr. Khalid, Dr. Mohannad CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 2 Block Cipher Modes of Operation and Stream Ciphers CIT 460 Information Security Dr. Khalid, Dr. Mohannad
2 Block Cipher Modes of Operation and Stream Ciphers CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 3 Outline We will discuss How to use block ciphers? RC 4: a widely used stream cipher Problems with WEP’s use of RC 4 CIT 460 Information Security Dr. Khalid, Dr. Mohannad
3 Outline We will discuss How to use block ciphers? RC 4: a widely used stream cipher Problems with WEP’s use of RC 4 CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 4 How to use a block cipher? Block ciphers encrypt fixed-size blocks e. g. DES encrypts 64 -bit blocks We need some way to encrypt a message of arbitrary length e. g. a message of 1000 bytes NIST defines several ways to do it called modes of operation CIT 460 Information Security Dr. Khalid, Dr. Mohannad
4 How to use a block cipher? Block ciphers encrypt fixed-size blocks e. g. DES encrypts 64 -bit blocks We need some way to encrypt a message of arbitrary length e. g. a message of 1000 bytes NIST defines several ways to do it called modes of operation CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 5 Five Modes of Operation Electronic codebook mode (ECB) Cipher block chaining mode (CBC) – most popular Output feedback mode (OFB) Cipher feedback mode (CFB) Counter mode (CTR) CIT 460 Information Security Dr. Khalid, Dr. Mohannad
5 Five Modes of Operation Electronic codebook mode (ECB) Cipher block chaining mode (CBC) – most popular Output feedback mode (OFB) Cipher feedback mode (CFB) Counter mode (CTR) CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 6 Message Padding The plaintext message is broken into blocks, P 1, P 2, P 3, . . . The last block may be short of a whole block and needs padding. Possible padding: Known non-data values (e. g. nulls) Or a number indicating the size of the pad Or a number indicating the size of the plaintext The last two schemes may require an extra block. CIT 460 Information Security Dr. Khalid, Dr. Mohannad
6 Message Padding The plaintext message is broken into blocks, P 1, P 2, P 3, . . . The last block may be short of a whole block and needs padding. Possible padding: Known non-data values (e. g. nulls) Or a number indicating the size of the pad Or a number indicating the size of the plaintext The last two schemes may require an extra block. CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 7 Electronic Code Book (ECB) The plaintext is broken into blocks, P 1, P 2, P 3, . . . Each block is encrypted independently: Ci = EK(Pi) For a given key, this mode behaves like we have a gigantic codebook, in which each plaintext block has an entry, hence the name Electronic Code Book CIT 460 Information Security Dr. Khalid, Dr. Mohannad
7 Electronic Code Book (ECB) The plaintext is broken into blocks, P 1, P 2, P 3, . . . Each block is encrypted independently: Ci = EK(Pi) For a given key, this mode behaves like we have a gigantic codebook, in which each plaintext block has an entry, hence the name Electronic Code Book CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 8 Remarks on ECB Strength: it’s simple. Weakness: Repetitive information contained in the plaintext may show in the ciphertext, if aligned with blocks. If the same message (e. g. , an SSN) is encrypted (with the same key) and sent twice, their ciphertexts are the same. Typical application: secure transmission of short pieces of information (e. g. a temporary encryption key) CIT 460 Information Security Dr. Khalid, Dr. Mohannad
8 Remarks on ECB Strength: it’s simple. Weakness: Repetitive information contained in the plaintext may show in the ciphertext, if aligned with blocks. If the same message (e. g. , an SSN) is encrypted (with the same key) and sent twice, their ciphertexts are the same. Typical application: secure transmission of short pieces of information (e. g. a temporary encryption key) CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 9 Cipher Block Chaining (CBC) CIT 460 Information Security Dr. Khalid, Dr. Mohannad
9 Cipher Block Chaining (CBC) CIT 460 Information Security Dr. Khalid, Dr. Mohannad
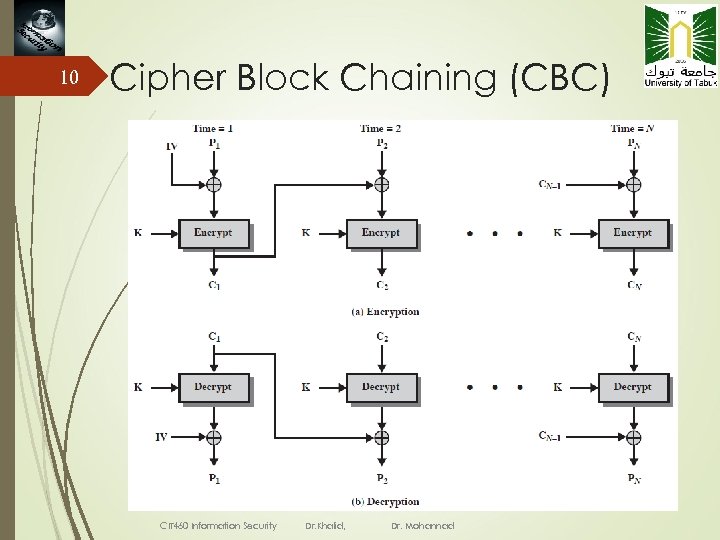 10 Cipher Block Chaining (CBC) CIT 460 Information Security Dr. Khalid, Dr. Mohannad
10 Cipher Block Chaining (CBC) CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 11 Remarks on CBC The encryption of a block depends on the current and all blocks before it. So, repeated plaintext blocks are encrypted differently. Initialization Vector (IV) Must be known to both the sender & receiver Typically, IV is either a fixed value or is sent encrypted in ECB mode before the rest of ciphertext. CIT 460 Information Security Dr. Khalid, Dr. Mohannad
11 Remarks on CBC The encryption of a block depends on the current and all blocks before it. So, repeated plaintext blocks are encrypted differently. Initialization Vector (IV) Must be known to both the sender & receiver Typically, IV is either a fixed value or is sent encrypted in ECB mode before the rest of ciphertext. CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 12 Information Security Chapter 2: Cryptography Lecture #2 -Week 3 Dr. Khalid, Dr. Mohannad CIT 460 Information Security Dr. Khalid M. O Nahar
12 Information Security Chapter 2: Cryptography Lecture #2 -Week 3 Dr. Khalid, Dr. Mohannad CIT 460 Information Security Dr. Khalid M. O Nahar
 13 Public-Key Cryptography. Asymmetric Encryption probably most significant advance in the 3000 year history of cryptography uses two keys – a public & a private key asymmetric since parties are not equal uses clever application of number theoretic concepts to function complements rather than replaces private key crypto
13 Public-Key Cryptography. Asymmetric Encryption probably most significant advance in the 3000 year history of cryptography uses two keys – a public & a private key asymmetric since parties are not equal uses clever application of number theoretic concepts to function complements rather than replaces private key crypto
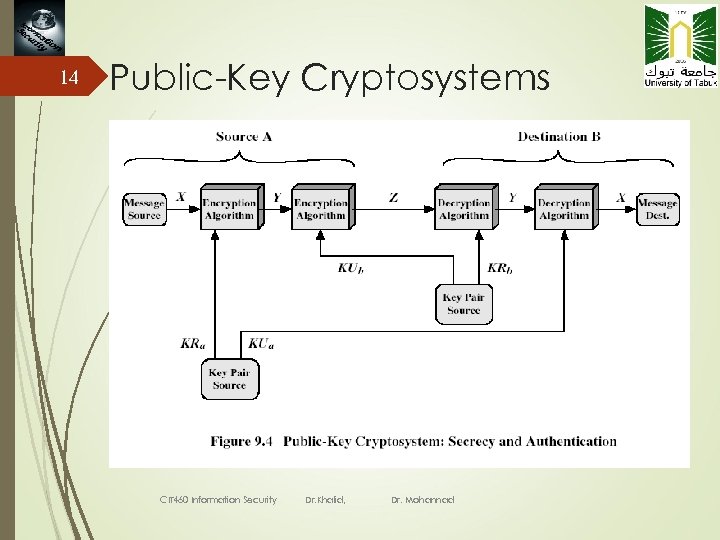 14 Public-Key Cryptosystems CIT 460 Information Security Dr. Khalid, Dr. Mohannad
14 Public-Key Cryptosystems CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 15 Public-Key Applications can classify uses into 3 categories: encryption/decryption (provide secrecy) digital signatures (provide authentication) key exchange (of session keys) some algorithms are suitable for all uses, others are specific to one CIT 460 Information Security Dr. Khalid, Dr. Mohannad
15 Public-Key Applications can classify uses into 3 categories: encryption/decryption (provide secrecy) digital signatures (provide authentication) key exchange (of session keys) some algorithms are suitable for all uses, others are specific to one CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 16 Security of Public Key Schemes like private key schemes brute force exhaustive search attack is always theoretically possible but keys used are too large (>512 bits) security relies on a large enough difference in difficulty between easy (en/decrypt) and hard (cryptanalysis) problems more generally the hard problem is known, its just made too hard to do in practise requires the use of very large numbers hence is slow compared to secret key schemes CIT 460 Information Security Dr. Khalid, Dr. Mohannad
16 Security of Public Key Schemes like private key schemes brute force exhaustive search attack is always theoretically possible but keys used are too large (>512 bits) security relies on a large enough difference in difficulty between easy (en/decrypt) and hard (cryptanalysis) problems more generally the hard problem is known, its just made too hard to do in practise requires the use of very large numbers hence is slow compared to secret key schemes CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 17 Public key encryption algorithms Requirements: 1 . B + need K ( ) and K ( ) such that - + B B K (K (m)) = m + 2 given public key KB , it should be impossible to compute private key KB RSA: Rivest, Shamir, Adelson algorithm CIT 460 Information Security Dr. Khalid, Dr. Mohannad
17 Public key encryption algorithms Requirements: 1 . B + need K ( ) and K ( ) such that - + B B K (K (m)) = m + 2 given public key KB , it should be impossible to compute private key KB RSA: Rivest, Shamir, Adelson algorithm CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 18 RSA: Choosing keys 1. Choose two large prime numbers p, q. (e. g. , 1024 bits each) 2. Compute n = pq, z = (p-1)(q-1) 3. Choose e (with e
18 RSA: Choosing keys 1. Choose two large prime numbers p, q. (e. g. , 1024 bits each) 2. Compute n = pq, z = (p-1)(q-1) 3. Choose e (with e
 19 RSA: Encryption, decryption 0. Given (n, e) and (n, d) as computed above 1. To encrypt bit pattern, m, compute e mod n (i. e. , remainder when m e is divided by n) c=m 2. To decrypt received bit pattern, c, compute d m = c d mod n (i. e. , remainder when c is divided by n) Magic d m = (m e mod n) mod n happens! c CIT 460 Information Security Dr. Khalid, Dr. Mohannad
19 RSA: Encryption, decryption 0. Given (n, e) and (n, d) as computed above 1. To encrypt bit pattern, m, compute e mod n (i. e. , remainder when m e is divided by n) c=m 2. To decrypt received bit pattern, c, compute d m = c d mod n (i. e. , remainder when c is divided by n) Magic d m = (m e mod n) mod n happens! c CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 20 RSA example: Hani chooses p=5, q=7. Then n=35, z=24. e=5 (so e, z relatively prime). d=29 (so ed-1 exactly divisible by z. Encrypt: m c = me mod n me letter l 12 1524832 17 Decrypt: c 17 d c 48196857210675091411825223071697 CIT 460 Information Security Dr. Khalid, Dr. Mohannad m = cd mod n letter 12 l
20 RSA example: Hani chooses p=5, q=7. Then n=35, z=24. e=5 (so e, z relatively prime). d=29 (so ed-1 exactly divisible by z. Encrypt: m c = me mod n me letter l 12 1524832 17 Decrypt: c 17 d c 48196857210675091411825223071697 CIT 460 Information Security Dr. Khalid, Dr. Mohannad m = cd mod n letter 12 l
 21 RSA: Why is that d m = (m e mod n) mod n Useful number theory result: If p, q prime and n = pq, then: y y mod (p-1)(q-1) x mod n = x mod n e (m mod n) d mod n = med mod n = m ed mod (p-1)(q-1) mod n (using number theory result above) 1 = m mod n CIT 460 Information Security Dr. Khalid, Dr. Mohannad (since we chose ed to be divisible by (p-1)(q-1) with remainder 1 ) = m
21 RSA: Why is that d m = (m e mod n) mod n Useful number theory result: If p, q prime and n = pq, then: y y mod (p-1)(q-1) x mod n = x mod n e (m mod n) d mod n = med mod n = m ed mod (p-1)(q-1) mod n (using number theory result above) 1 = m mod n CIT 460 Information Security Dr. Khalid, Dr. Mohannad (since we chose ed to be divisible by (p-1)(q-1) with remainder 1 ) = m
 22 What We Have Covered So Far Symmetric encryption Public encryption Data Integrity Digital Signature Key distribution CIT 460 Information Security Dr. Khalid, Dr. Mohannad
22 What We Have Covered So Far Symmetric encryption Public encryption Data Integrity Digital Signature Key distribution CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 23 Information Security Chapter 2: Cryptography Lecture #2 -Week 3 cont. Dr. Khalid, Dr. Mohannad CIT 460 Information Security Dr. Khalid, Dr. Mohannad
23 Information Security Chapter 2: Cryptography Lecture #2 -Week 3 cont. Dr. Khalid, Dr. Mohannad CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 24 Hash Algorithms see similarities in the evolution of hash functions & block ciphers increasing power of brute-force attacks leading to evolution in algorithms from DES to AES in block ciphers from MD 4 & MD 5 to SHA-1 & RIPEMD 160 in hash algorithms likewise tend to use common iterative structure as do block ciphers CIT 460 Information Security Dr. Khalid, Dr. Mohannad
24 Hash Algorithms see similarities in the evolution of hash functions & block ciphers increasing power of brute-force attacks leading to evolution in algorithms from DES to AES in block ciphers from MD 4 & MD 5 to SHA-1 & RIPEMD 160 in hash algorithms likewise tend to use common iterative structure as do block ciphers CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 25 Data integrity is the data security service by which the data are protected from unauthorized or accidental modification. Hash function is a cryptographic tool that is used to ensure the integrity of data. It is also called a Manipulation Detection Code (MDC, for short). CIT 460 Information Security Dr. Khalid, Dr. Mohannad
25 Data integrity is the data security service by which the data are protected from unauthorized or accidental modification. Hash function is a cryptographic tool that is used to ensure the integrity of data. It is also called a Manipulation Detection Code (MDC, for short). CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 26 Properties of Hash function (A) Compression function Hash function is a function h: M Y that has, as a minimum, two properties: it compresses a sequence m M of bits of arbitrary length, including the empty sequence, into a sequence h(m) Y of the constant (fixed) length, for any m M it is easy to compute h(m). CIT 460 Information Security Dr. Khalid, Dr. Mohannad
26 Properties of Hash function (A) Compression function Hash function is a function h: M Y that has, as a minimum, two properties: it compresses a sequence m M of bits of arbitrary length, including the empty sequence, into a sequence h(m) Y of the constant (fixed) length, for any m M it is easy to compute h(m). CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 (B) Collision resistance 27 Apart from the property of compression and ease of computation a hash function should have additionally other potential properties: one-way – for almost all y Y it is computationally infeasible to find any input m M such that h(m)=y; weak collision resistance – for a given m it is computationally infeasible to find a second input m' such that h(m)= h(m'); strong collision resistance – it is computationally infeasible to find any two distinct inputs m and m' such that h(m)= h(m'). CIT 460 Information Security Dr. Khalid, Dr. Mohannad
(B) Collision resistance 27 Apart from the property of compression and ease of computation a hash function should have additionally other potential properties: one-way – for almost all y Y it is computationally infeasible to find any input m M such that h(m)=y; weak collision resistance – for a given m it is computationally infeasible to find a second input m' such that h(m)= h(m'); strong collision resistance – it is computationally infeasible to find any two distinct inputs m and m' such that h(m)= h(m'). CIT 460 Information Security Dr. Khalid, Dr. Mohannad
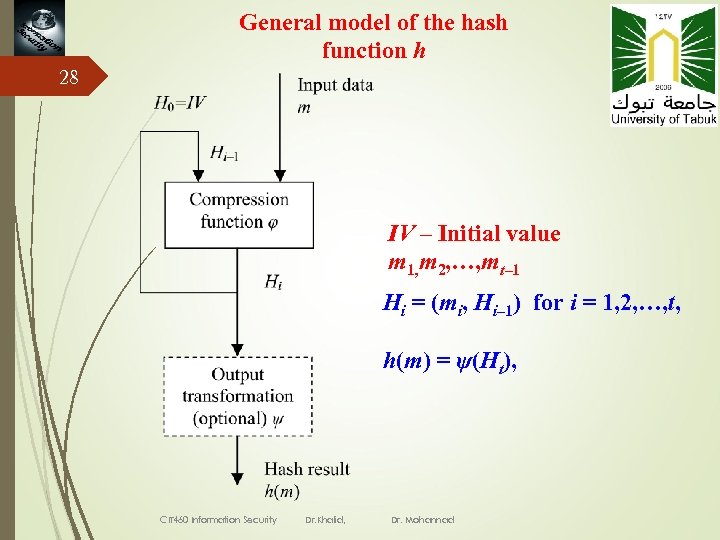 General model of the hash function h 28 IV – Initial value m 1, m 2, …, mt– 1 Hi = (mi, Hi– 1) for i = 1, 2, …, t, h(m) = ψ(Ht), CIT 460 Information Security Dr. Khalid, Dr. Mohannad
General model of the hash function h 28 IV – Initial value m 1, m 2, …, mt– 1 Hi = (mi, Hi– 1) for i = 1, 2, …, t, h(m) = ψ(Ht), CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 Computational complexity theory 29 P: computationally feasible problem means a decision problem which can be resolved (computed) in polynomial time by means of a deterministic device (machine). NP: computationally infeasible problem can be resolved in polynomial time by the use of a nondeterministic device or in exponential time using a deterministic device P NP One way Function CIT 460 Information Security Dr. Khalid, Dr. Mohannad
Computational complexity theory 29 P: computationally feasible problem means a decision problem which can be resolved (computed) in polynomial time by means of a deterministic device (machine). NP: computationally infeasible problem can be resolved in polynomial time by the use of a nondeterministic device or in exponential time using a deterministic device P NP One way Function CIT 460 Information Security Dr. Khalid, Dr. Mohannad
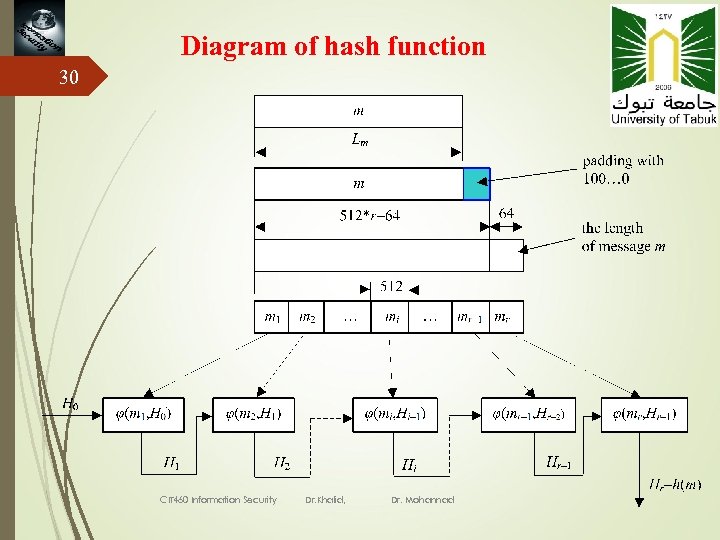 Diagram of hash function 30 CIT 460 Information Security Dr. Khalid, Dr. Mohannad
Diagram of hash function 30 CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 31 MD 5 designed by Ronald Rivest (the R in RSA) latest in a series of MD 2, MD 4 produces a 128 -bit hash value until recently was the most widely used hash algorithm in recent times have both brute-force & cryptanalytic concerns specified as Internet standard RFC 1321 CIT 460 Information Security Dr. Khalid, Dr. Mohannad
31 MD 5 designed by Ronald Rivest (the R in RSA) latest in a series of MD 2, MD 4 produces a 128 -bit hash value until recently was the most widely used hash algorithm in recent times have both brute-force & cryptanalytic concerns specified as Internet standard RFC 1321 CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 32 Secure Hash Algorithm (SHA-1) SHA was designed by NIST & NSA in 1993, revised 1995 as SHA-1 US standard for use with DSA signature scheme standard is FIPS 180 -1 1995, also Internet RFC 3174 nb. the algorithm is SHA, the standard is SHS produces 160 -bit hash values now the generally preferred hash algorithm based on design of MD 4 with key differences CIT 460 Information Security Dr. Khalid, Dr. Mohannad
32 Secure Hash Algorithm (SHA-1) SHA was designed by NIST & NSA in 1993, revised 1995 as SHA-1 US standard for use with DSA signature scheme standard is FIPS 180 -1 1995, also Internet RFC 3174 nb. the algorithm is SHA, the standard is SHS produces 160 -bit hash values now the generally preferred hash algorithm based on design of MD 4 with key differences CIT 460 Information Security Dr. Khalid, Dr. Mohannad
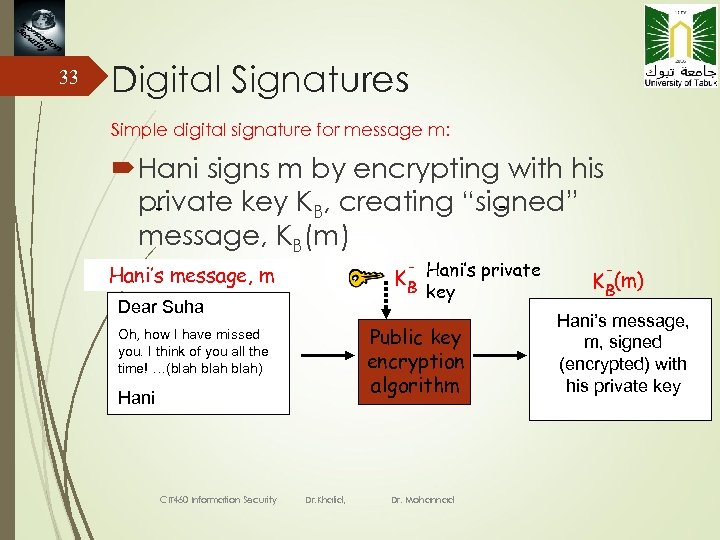 33 Digital Signatures Simple digital signature for message m: Hani signs m by encrypting with his private key KB, creating “signed” message, KB(m) - Hani’s private KB key Hani’s message, m Dear Suha Public key encryption algorithm Oh, how I have missed you. I think of you all the time! …(blah) Hani CIT 460 Information Security Dr. Khalid, Dr. Mohannad - K B(m) Hani’s message, m, signed (encrypted) with his private key
33 Digital Signatures Simple digital signature for message m: Hani signs m by encrypting with his private key KB, creating “signed” message, KB(m) - Hani’s private KB key Hani’s message, m Dear Suha Public key encryption algorithm Oh, how I have missed you. I think of you all the time! …(blah) Hani CIT 460 Information Security Dr. Khalid, Dr. Mohannad - K B(m) Hani’s message, m, signed (encrypted) with his private key
 34 Digital Signatures (more) - Suppose Suha receives msg m, digital signature KB(m) Suha verifies m signed by Hani by applying Hani’s public + + key KB to KB(m) then checks KB(KB(m) ) = m. + If KB(KB(m) ) = m, whoever signed m must have used Hani’s private key. Suha thus verifies that: ü Hani signed m. ü No one else signed m. ü Hani signed m and not m’. Non-repudiation: ü Suha can take m, and signature KB(m) to court and prove that Hani signed m. CIT 460 Information Security Dr. Khalid, Dr. Mohannad
34 Digital Signatures (more) - Suppose Suha receives msg m, digital signature KB(m) Suha verifies m signed by Hani by applying Hani’s public + + key KB to KB(m) then checks KB(KB(m) ) = m. + If KB(KB(m) ) = m, whoever signed m must have used Hani’s private key. Suha thus verifies that: ü Hani signed m. ü No one else signed m. ü Hani signed m and not m’. Non-repudiation: ü Suha can take m, and signature KB(m) to court and prove that Hani signed m. CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 Digital Signatures (more) 35 Introduction Definition of digital signature Main goals of digital signature Symmetric key signature Asymmetric key signature Message digits signature Some problems Solutions Main components of DS Conclusions CIT 460 Information Security Dr. Khalid, Dr. Mohannad
Digital Signatures (more) 35 Introduction Definition of digital signature Main goals of digital signature Symmetric key signature Asymmetric key signature Message digits signature Some problems Solutions Main components of DS Conclusions CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 What is digital signature? 36 A digital signature is the electronic equivalent of a handwritten signature, verifying the authenticity of electronic documents. In fact, digital signatures provide even more security than their handwritten counterparts. CIT 460 Information Security Dr. Khalid, Dr. Mohannad
What is digital signature? 36 A digital signature is the electronic equivalent of a handwritten signature, verifying the authenticity of electronic documents. In fact, digital signatures provide even more security than their handwritten counterparts. CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 37 Algorithm Conditions The receiver can verify the claimed identity of the sender The sender cannot later deny the content of the message The receiver himself cannot have the possible of falsify the message. CIT 460 Information Security Dr. Khalid, Dr. Mohannad
37 Algorithm Conditions The receiver can verify the claimed identity of the sender The sender cannot later deny the content of the message The receiver himself cannot have the possible of falsify the message. CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 38 More benefits of using Digital Signature It insures by means of verification and validation that the user is whom he/she claims to be. Digital certificates insure data Integrity giving the user piece of mind that the message or transaction has not been accidentally or maliciously altered. CIT 460 Information Security Dr. Khalid, Dr. Mohannad
38 More benefits of using Digital Signature It insures by means of verification and validation that the user is whom he/she claims to be. Digital certificates insure data Integrity giving the user piece of mind that the message or transaction has not been accidentally or maliciously altered. CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 39 More benefits cont. Digital certificates ensure confidentiality and ensure that messages can only be read by authorized intended recipients. Digital certificates also verify date and time so that senders or recipients can not dispute if the message was actually sent or received. CIT 460 Information Security Dr. Khalid, Dr. Mohannad
39 More benefits cont. Digital certificates ensure confidentiality and ensure that messages can only be read by authorized intended recipients. Digital certificates also verify date and time so that senders or recipients can not dispute if the message was actually sent or received. CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 40 Symmetric key signature Suha’s key Suha Han i CIT 460 Information Security Dr. Khalid, Hani’s key Dr. Mohannad
40 Symmetric key signature Suha’s key Suha Han i CIT 460 Information Security Dr. Khalid, Hani’s key Dr. Mohannad
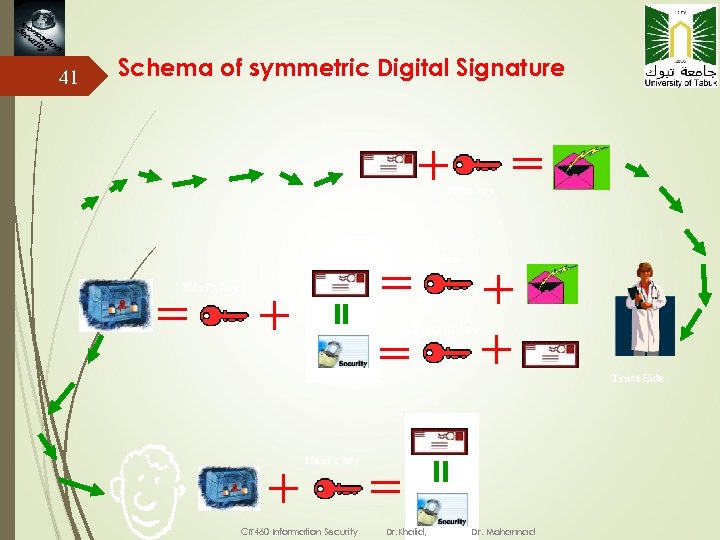 41 Schema of symmetric Digital Signature Suha key Hani’s key Trust Side Hani’s key CIT 460 Information Security Dr. Khalid, Dr. Mohannad
41 Schema of symmetric Digital Signature Suha key Hani’s key Trust Side Hani’s key CIT 460 Information Security Dr. Khalid, Dr. Mohannad
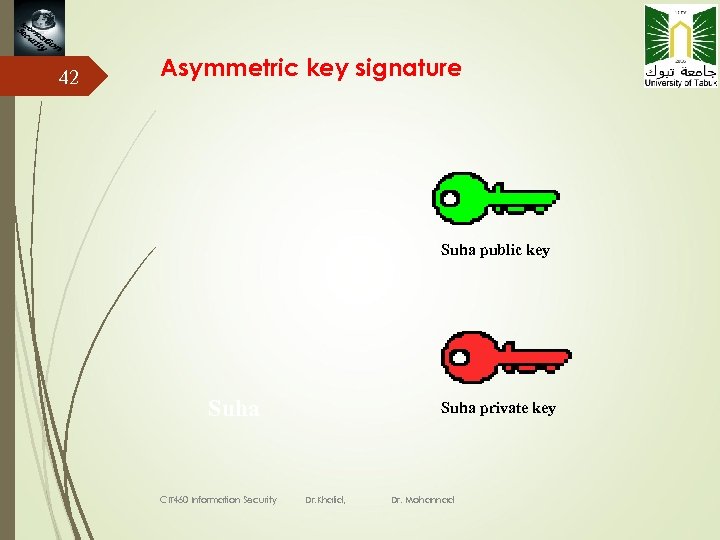 42 Asymmetric key signature Suha public key Suha CIT 460 Information Security Suha private key Dr. Khalid, Dr. Mohannad
42 Asymmetric key signature Suha public key Suha CIT 460 Information Security Suha private key Dr. Khalid, Dr. Mohannad
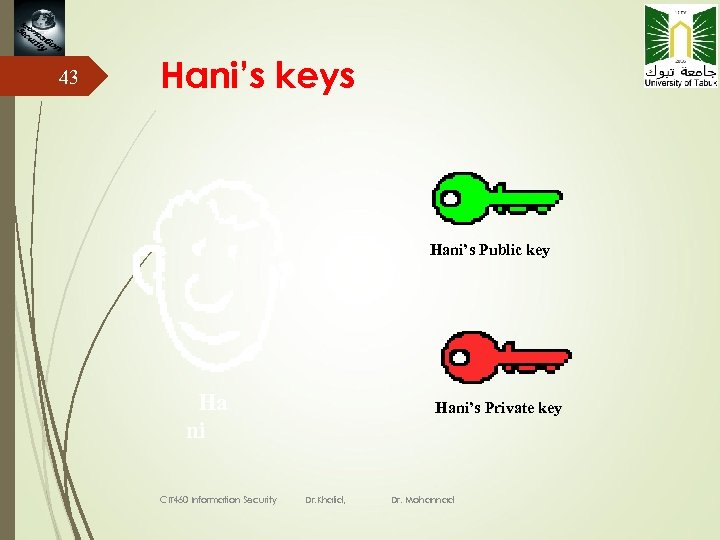 43 Hani’s keys Hani’s Public key Ha ni CIT 460 Information Security Hani’s Private key Dr. Khalid, Dr. Mohannad
43 Hani’s keys Hani’s Public key Ha ni CIT 460 Information Security Hani’s Private key Dr. Khalid, Dr. Mohannad
 44 Sending message from Suha to Hani by using digital signature Suha private key Hani’s Public key CIT 460 Information Security Dr. Khalid, Dr. Mohannad
44 Sending message from Suha to Hani by using digital signature Suha private key Hani’s Public key CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 45 Hani verify the message Hani’s private key Suha’s Public key CIT 460 Information Security Dr. Khalid, Dr. Mohannad
45 Hani verify the message Hani’s private key Suha’s Public key CIT 460 Information Security Dr. Khalid, Dr. Mohannad
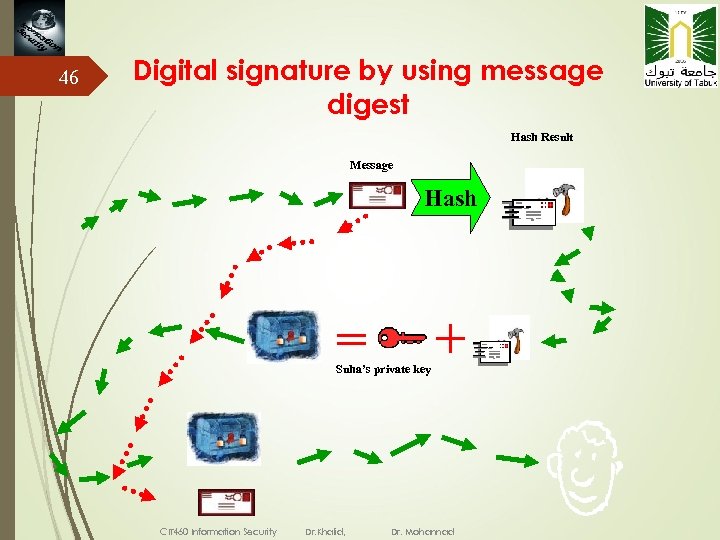 46 Digital signature by using message digest Hash Result Message Hash Suha’s private key CIT 460 Information Security Dr. Khalid, Dr. Mohannad
46 Digital signature by using message digest Hash Result Message Hash Suha’s private key CIT 460 Information Security Dr. Khalid, Dr. Mohannad
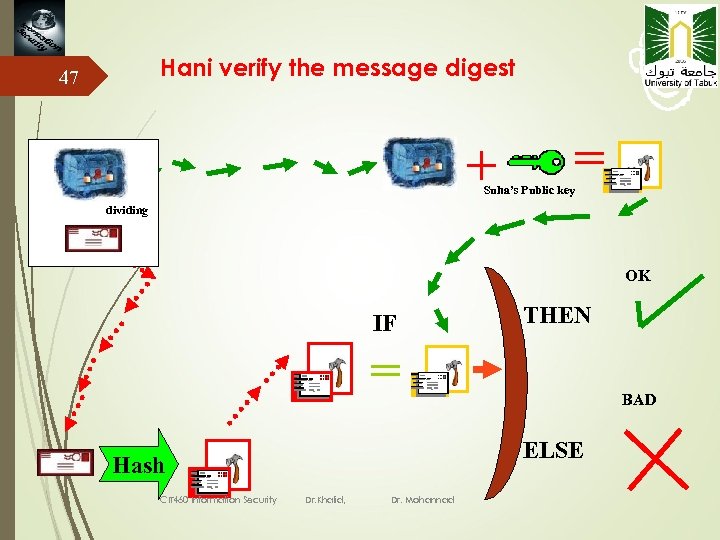 Hani verify the message digest 47 Suha’s Public key dividing OK IF THEN BAD ELSE Hash CIT 460 Information Security Dr. Khalid, Dr. Mohannad
Hani verify the message digest 47 Suha’s Public key dividing OK IF THEN BAD ELSE Hash CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 48 Some problems Replying of the same message Fresh less of the message Responding of the receiver CIT 460 Information Security Dr. Khalid, Dr. Mohannad
48 Some problems Replying of the same message Fresh less of the message Responding of the receiver CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 49 Solutions Generating a pseudo number for every sent message Time stamping The receiver must do the operation that the sender did. CIT 460 Information Security Dr. Khalid, Dr. Mohannad same
49 Solutions Generating a pseudo number for every sent message Time stamping The receiver must do the operation that the sender did. CIT 460 Information Security Dr. Khalid, Dr. Mohannad same
 50 Components that a digital signature Your public key, private key Receiver public, private key Your name and e-mail address Name of receiver and email address Expiration date of the public key Name of the company Serial number of the Digital ID Digital signature of the CA (certification Authority) Time stamping CIT 460 Information Security Dr. Khalid, Dr. Mohannad
50 Components that a digital signature Your public key, private key Receiver public, private key Your name and e-mail address Name of receiver and email address Expiration date of the public key Name of the company Serial number of the Digital ID Digital signature of the CA (certification Authority) Time stamping CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 51 How long do digital signatures remain valid? Normally, a key expires after some period of time, such as one year, and a document signed with an expired key should not be accepted. However, there are many cases where it is necessary for signed documents to be regarded as legally valid for much longer than two years; long-term leases and contracts are examples. By registering the contract with a digital time-stamping service at the time it is signed, the signature can be validated even after the key expires. CIT 460 Information Security Dr. Khalid, Dr. Mohannad
51 How long do digital signatures remain valid? Normally, a key expires after some period of time, such as one year, and a document signed with an expired key should not be accepted. However, there are many cases where it is necessary for signed documents to be regarded as legally valid for much longer than two years; long-term leases and contracts are examples. By registering the contract with a digital time-stamping service at the time it is signed, the signature can be validated even after the key expires. CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 52 Conclusion Authentication. Asymmetric DS is more common than symmetric ones. We have two general methods of DS: Secret without using message digest Overt by using message digest CIT 460 Information Security Dr. Khalid, Dr. Mohannad
52 Conclusion Authentication. Asymmetric DS is more common than symmetric ones. We have two general methods of DS: Secret without using message digest Overt by using message digest CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 53 Key Distribution symmetric schemes require both parties to share a common secret key issue is how to securely distribute this key often secure system failure due to a break in the key distribution scheme CIT 460 Information Security Dr. Khalid, Dr. Mohannad
53 Key Distribution symmetric schemes require both parties to share a common secret key issue is how to securely distribute this key often secure system failure due to a break in the key distribution scheme CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 54 Key Distribution given parties A and B have various key distribution alternatives: 1. A can select key and physically deliver to B 2. third party can select & deliver key to A & B 3. if A & B have communicated previously can use previous key to encrypt a new key 4. if A & B have secure communications with a third party C, C can relay key between A & B CIT 460 Information Security Dr. Khalid, Dr. Mohannad
54 Key Distribution given parties A and B have various key distribution alternatives: 1. A can select key and physically deliver to B 2. third party can select & deliver key to A & B 3. if A & B have communicated previously can use previous key to encrypt a new key 4. if A & B have secure communications with a third party C, C can relay key between A & B CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 55 Trusted Intermediaries Symmetric key problem: Public key problem: How do two entities establish shared secret key over network? When Suha obtains Hani’s public key (from web site, e-mail, diskette), how does she know it is Hani’s public key, not Trudy’s? Solution: trusted key distribution center (KDC) acting as intermediary between entities Solution: trusted certification authority (CA) CIT 460 Information Security Dr. Khalid, Dr. Mohannad
55 Trusted Intermediaries Symmetric key problem: Public key problem: How do two entities establish shared secret key over network? When Suha obtains Hani’s public key (from web site, e-mail, diskette), how does she know it is Hani’s public key, not Trudy’s? Solution: trusted key distribution center (KDC) acting as intermediary between entities Solution: trusted certification authority (CA) CIT 460 Information Security Dr. Khalid, Dr. Mohannad
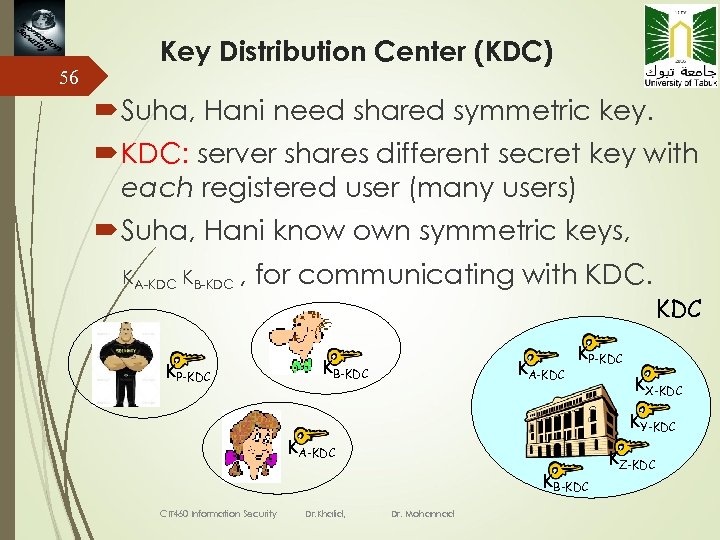 56 Key Distribution Center (KDC) Suha, Hani need shared symmetric key. KDC: server shares different secret key with each registered user (many users) Suha, Hani know own symmetric keys, KA-KDC KB-KDC , for communicating with KDC. KP-KDC KB-KDC KA-KDC KP-KDC KY-KDC KA-KDC KB-KDC CIT 460 Information Security Dr. Khalid, KX-KDC Dr. Mohannad KZ-KDC
56 Key Distribution Center (KDC) Suha, Hani need shared symmetric key. KDC: server shares different secret key with each registered user (many users) Suha, Hani know own symmetric keys, KA-KDC KB-KDC , for communicating with KDC. KP-KDC KB-KDC KA-KDC KP-KDC KY-KDC KA-KDC KB-KDC CIT 460 Information Security Dr. Khalid, KX-KDC Dr. Mohannad KZ-KDC
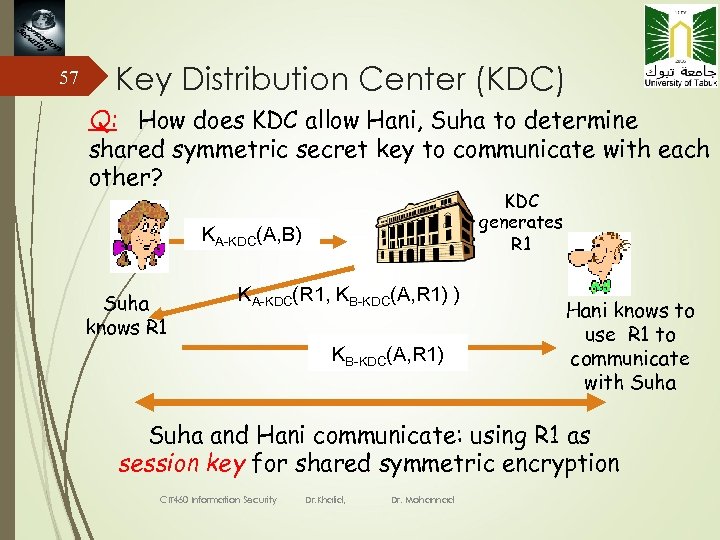 57 Key Distribution Center (KDC) Q: How does KDC allow Hani, Suha to determine shared symmetric secret key to communicate with each other? KDC generates R 1 KA-KDC(A, B) Suha knows R 1 KA-KDC(R 1, KB-KDC(A, R 1) ) KB-KDC(A, R 1) Hani knows to use R 1 to communicate with Suha and Hani communicate: using R 1 as session key for shared symmetric encryption CIT 460 Information Security Dr. Khalid, Dr. Mohannad
57 Key Distribution Center (KDC) Q: How does KDC allow Hani, Suha to determine shared symmetric secret key to communicate with each other? KDC generates R 1 KA-KDC(A, B) Suha knows R 1 KA-KDC(R 1, KB-KDC(A, R 1) ) KB-KDC(A, R 1) Hani knows to use R 1 to communicate with Suha and Hani communicate: using R 1 as session key for shared symmetric encryption CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 58 Distribution of Public Keys can be considered as using one of: Public announcement Publicly available directory Public-key authority Public-key certificates CIT 460 Information Security Dr. Khalid, Dr. Mohannad
58 Distribution of Public Keys can be considered as using one of: Public announcement Publicly available directory Public-key authority Public-key certificates CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 59 Public Announcement users distribute public keys to recipients or broadcast to community at large eg. append PGP keys to email messages or post to news groups or email list major weakness is forgery anyone can create a key claiming to be someone else and broadcast it until forgery is discovered can masquerade as claimed user CIT 460 Information Security Dr. Khalid, Dr. Mohannad
59 Public Announcement users distribute public keys to recipients or broadcast to community at large eg. append PGP keys to email messages or post to news groups or email list major weakness is forgery anyone can create a key claiming to be someone else and broadcast it until forgery is discovered can masquerade as claimed user CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 60 Publicly Available Directory can obtain greater security by registering keys with a public directory must be trusted with properties: contains {name, public-key} entries participants register securely with directory participants can replace key at any time directory is periodically published directory can be accessed electronically still vulnerable to tampering or forgery CIT 460 Information Security Dr. Khalid M. O Nahar
60 Publicly Available Directory can obtain greater security by registering keys with a public directory must be trusted with properties: contains {name, public-key} entries participants register securely with directory participants can replace key at any time directory is periodically published directory can be accessed electronically still vulnerable to tampering or forgery CIT 460 Information Security Dr. Khalid M. O Nahar
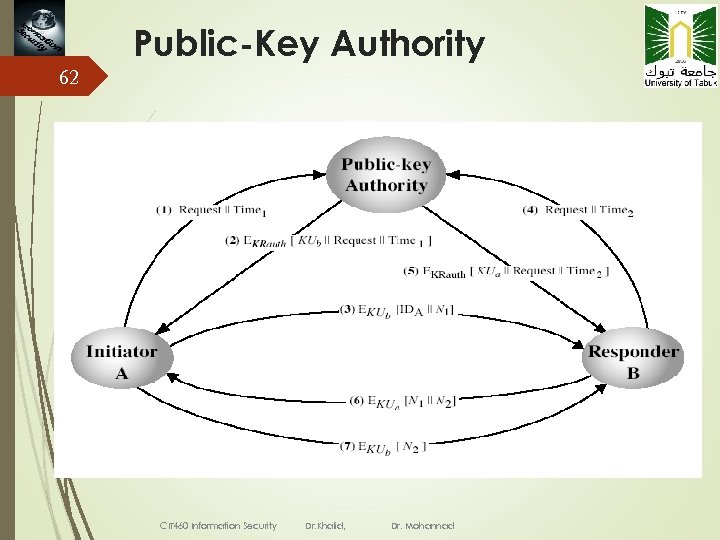
 61 Public-Key Authority improve security by tightening control over distribution of keys from directory has properties of directory and requires users to know public key for the directory then users interact with directory to obtain any desired public key securely does require real-time access to directory when keys are needed CIT 460 Information Security Dr. Khalid M. O Nahar
61 Public-Key Authority improve security by tightening control over distribution of keys from directory has properties of directory and requires users to know public key for the directory then users interact with directory to obtain any desired public key securely does require real-time access to directory when keys are needed CIT 460 Information Security Dr. Khalid M. O Nahar
 Public-Key Authority 62 CIT 460 Information Security Dr. Khalid, Dr. Mohannad
Public-Key Authority 62 CIT 460 Information Security Dr. Khalid, Dr. Mohannad
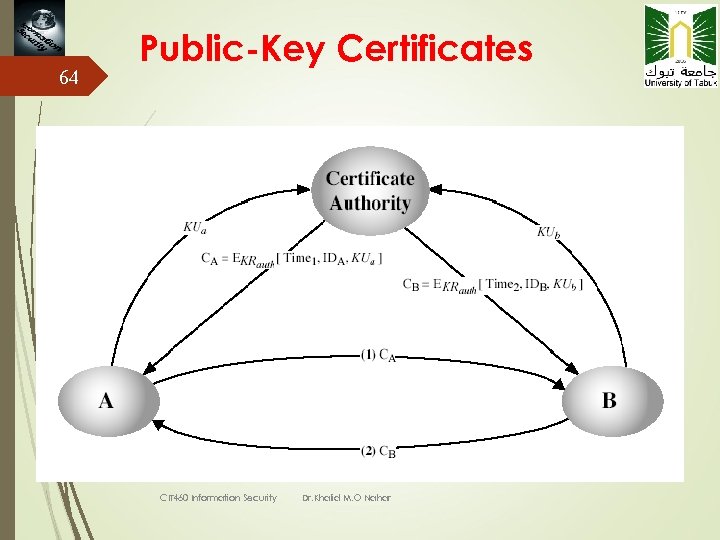
 63 Public-Key Certificates certificates allow key exchange without real-time access to public-key authority a certificate binds identity to public key usually with other info such as period of validity, rights of use etc with all contents signed by a trusted Public -Key or Certificate Authority (CA) can be verified by anyone who knows the public-key authorities public-key CIT 460 Information Security Dr. Khalid, Dr. Mohannad
63 Public-Key Certificates certificates allow key exchange without real-time access to public-key authority a certificate binds identity to public key usually with other info such as period of validity, rights of use etc with all contents signed by a trusted Public -Key or Certificate Authority (CA) can be verified by anyone who knows the public-key authorities public-key CIT 460 Information Security Dr. Khalid, Dr. Mohannad
 64 Public-Key Certificates CIT 460 Information Security Dr. Khalid M. O Nahar
64 Public-Key Certificates CIT 460 Information Security Dr. Khalid M. O Nahar
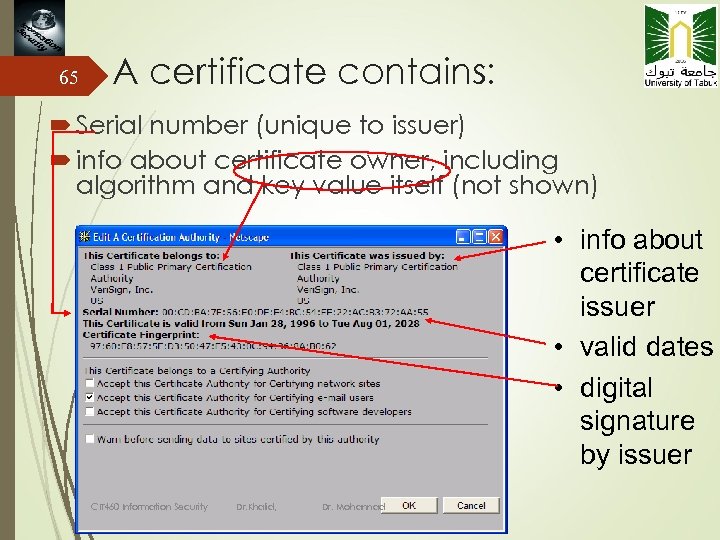 65 A certificate contains: Serial number (unique to issuer) info about certificate owner, including algorithm and key value itself (not shown) • info about certificate issuer • valid dates • digital signature by issuer CIT 460 Information Security Dr. Khalid, Dr. Mohannad
65 A certificate contains: Serial number (unique to issuer) info about certificate owner, including algorithm and key value itself (not shown) • info about certificate issuer • valid dates • digital signature by issuer CIT 460 Information Security Dr. Khalid, Dr. Mohannad


