1 I Particle Physics II II III V

Скачать презентацию 1 I Particle Physics II II III V

2431fdd262508c231b6dd349f3c44305.ppt

Количество слайдов: 87

1 I. Particle Physics II II. III. V. IV. • • • Introduction, history & overview (2) Concepts (3): Units (h=c=1) Relativistic kinematics Cross section, lifetime, decay width, … Symmetries (quark model, …) Quantum Electro Dynamics: QED (6 -7) Spin 0 electrodynamics (Klein-Gordon) Spin ½ electrodynamics (Dirac) Experimental highlights: “g-2”, e e , … Quantum Chromo Dynamics: QCD (3 -4) Colour concept and partons High q 2 strong interaction SB Structure functions Experimental highlights: s, e p, … VI. VIII. • • • Quantum Flavour Dynamics: QFD (4) Low q 2 weak interaction High q 2 weak interaction Electro-weak interaction Experimental highlights: LEP Origin of mass? (2) Symmetry breaking Higgs particle: in e e and in pp Origin of matter? (6) K 0 -K 0, oscillations B 0 -B 0 oscillations Jvd. B Neutrino oscillations Fantasy land (2) File on “paling”: z 66/Power. Point/ED_Master/Concepts. ppt II. Concepts Particle Physics 2002/2003 Part of the “Particle and Astroparticle Physics” Master’s Curriculum

2 Units (h=c=1)

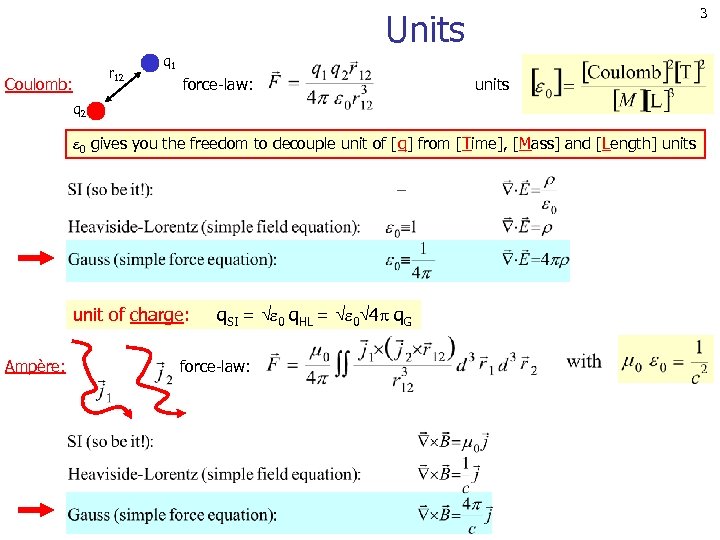3 Units r 12 q 1 Coulomb: force-law: units q 2 0 gives you the freedom to decouple unit of [q] from [Time], [Mass] and [Length] units unit of charge: q. SI = 0 q. HL = 0 4 q. G Ampère: force-law:

4 Natural units: h=c=1 Fundamental quantities: Units: Length [L] Time [T] Mass [M] h 1. 0566 10 34 Js c 299792458 m/s (1 Js=1 kg m 2/s) (definition of the length unit) Simplify life by setting: c 1 h 1 [L]=[T] [M]=[L] =[T] Remaining freedom: pick one unit Energy! [E]=e. V, ke. V, Me. V, Ge. V, Te. V, … Energy [E] Mass [M] Momentum Lenght [L] Time [T] Ge. V/c 2 (via E=1/2 mv 2) Ge. V/c (via p=mv) Ge. V 1 hc (via 1=[hc]=Jm and [E] Ge. V) Ge. V 1 h (via 1=[h]=Js and [E] Ge. V) e (Gaussian units!) potential energy of electron in Hydrogen rest energy of an electron +e the fine-structure constant, , sets the strength of the e. m. interaction

Maxwell equations in Gaussian units 5 In vacuum; d. w. z. vrijwel altijd: = 0 en j = 0 (In particle physics we do not need to worry about e. m. behavior in matter!) Cross section: area m 2 Ge. V 2 typical cross sections 1 b = 10 24 cm 2 1 nb = 10 33 cm 2 1 pb = 10 36 cm 2 1 fb = 10 39 cm 2 Physics! (this course) LEP: 10+31 cm 2 s 1= 0. 1 nb 1 s 1 100 pb 1 year 1 “B-factory”: 10+33 cm 2 s 1= 100 nb 1 s 1 10 fb 1 year 1 LHC: 10+34 cm 2 s 1= 0. 1 pb 1 s 1 100 fb 1 year 1 Lifetime: time s Ge. V 1 typical “luminosities” Technology! (other course)

6 Relativistic kinematics

Lorentz-transformations Co-moving coordinate systems S’ S v x x’’ Lorentzcontractie: Lengteverkorting gezien vanuit bewegend stelsel Events: S: @ t=0: (0, 0) & (0, L) transform to S 0: L 0= L L= L 0/ Tijdsdilatatie: Tijdsverlenging gezien vanuit bewegend stelsel Events: S 0: @ z 0=0: (0, 0) & (t 0, 0) transform to S: t= t 0 Voorbeeld: Muonen, 2 10 -6 s, m 106 Me. V in kosmische straling p =10 Ge. V l v 60 km i. p. v. 600 m 7

4 -vector Notation: Invariant (“boosts”, rotations, …): Introduce metric: Contra-variant 4 -vector Co-variant 4 -vector Generally for 4 -vectors a and b : Lorentz-invariant formulate in terms of scalars, 4 -vectors, … 8

Lorentz-transformations: Rotations Lorentz-transformaties: These matrices must obey: For infinitesimal transformations you find: Because: 0 1 2 3 Rotation Z-axis: 0 1 2 3 Finite rotation around Z-axis yields: S S’ 9

Infinitesimal macroscopic: 10

Lorentz-transformations: Boosts Boost along Z-axis: Finite boost along Z-axis yields: De relatie tussen x 0=ct, x 3=z en x’ 0=ct’, x’ 3=z’ is: De relatie tussen en de snelheid v/c is: Oftewel: Dus: 11

Lorentz group: Generators Lorentz-group parameters: Dus: 4 x 4 – 10 = 6 parameters: 3 rotaties: around X-, Y- & Z- axis 3 boosts: around X-, Y- & Z-axis Generators for infinitesimal transformations: Commutation-relations: Representations: spin j and mass m 2 12

The velocity 4 -vector 13 S Standaard definitie van snelheid: x/ t: Gezien vanuit S: snelheid u= x/ t Gezien vanuit S’: snelheid u’= x’/ t’ En dus Dit is geen goede keus i. v. m. Lorentz invariantie Betere definitie van snelheid ( t= ): Definieer nu de impuls als p =m =(E/c, px, py, pz), dan: Waarom p 0 E/c? Deeltjes met m=0: u x

Derivatives Afgeleiden: en Een contra-variante vector transformeert als: Een co-variante vector transformeert als: Het invariante product: voor de afgeleide analoog voor Covariante producten: 14

15 Transformatie naar zwaartepunts systeem m 1 m 2 m 3 m 4 m 5 Systeem van N deeltjes; transformeer naar het c. m. Lorentz boost met Dan inderdaad: Lab-frame

16 Verval van deeltjes m. B m. A m. C c. m. frame Met volgt m 140 Me. V m 106 Me. V me 0. 511 Me. V Voorbeelden: E Ee Ee 53 Me. V 3 deeltjes

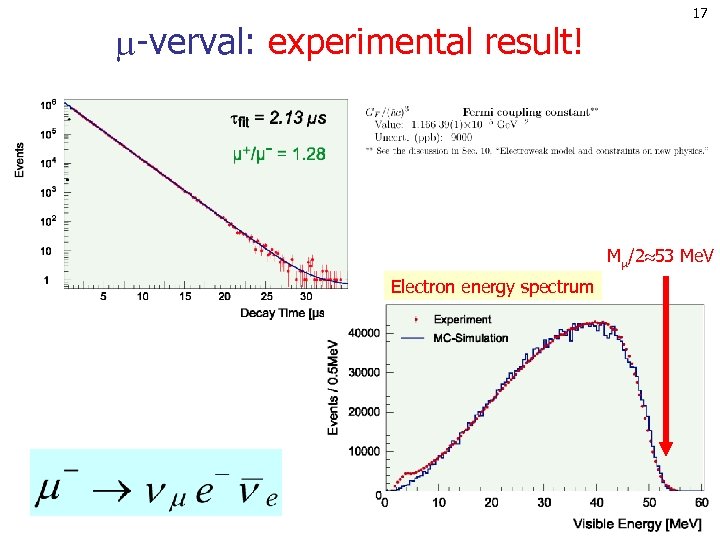-verval: experimental result! 17 M /2 53 Me. V Electron energy spectrum

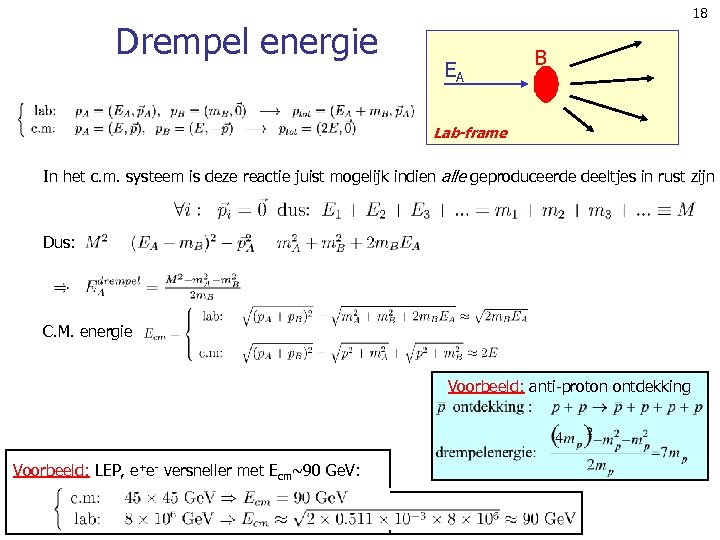Drempel energie 18 EA B Lab-frame In het c. m. systeem is deze reactie juist mogelijk indien alle geproduceerde deeltjes in rust zijn Dus: C. M. energie Voorbeeld: anti-proton ontdekking Voorbeeld: LEP, e+e- versneller met Ecm~90 Ge. V:

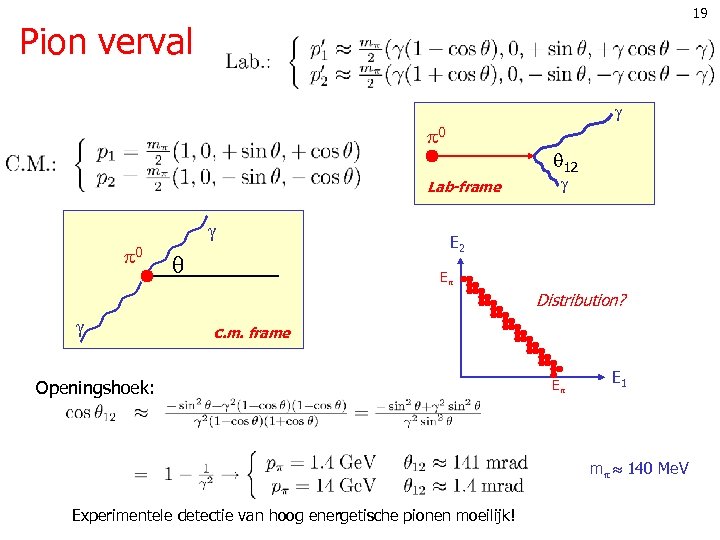19 Pion verval 0 12 Lab-frame 0 E 2 E Distribution? c. m. frame Openingshoek: E E 1 m 140 Me. V Experimentele detectie van hoog energetische pionen moeilijk!

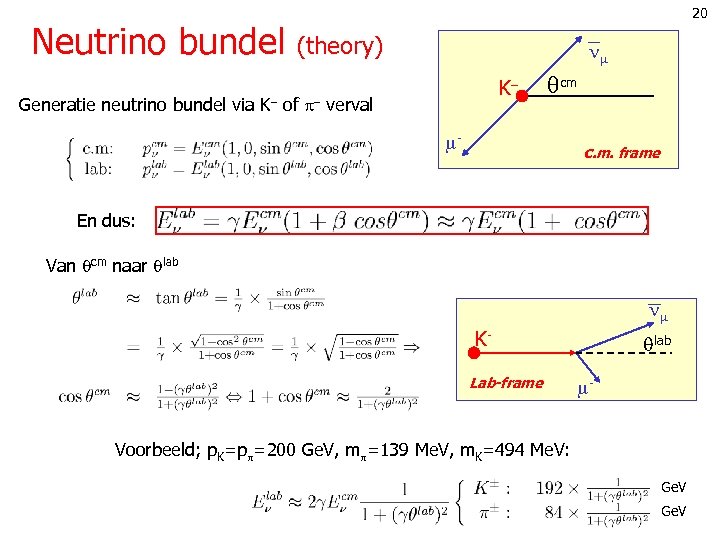20 Neutrino bundel (theory) K Generatie neutrino bundel via K of verval cm - c. m. frame En dus: Van cm naar lab KLab-frame lab - Voorbeeld; p. K=p =200 Ge. V, m =139 Me. V, m. K=494 Me. V: Ge. V

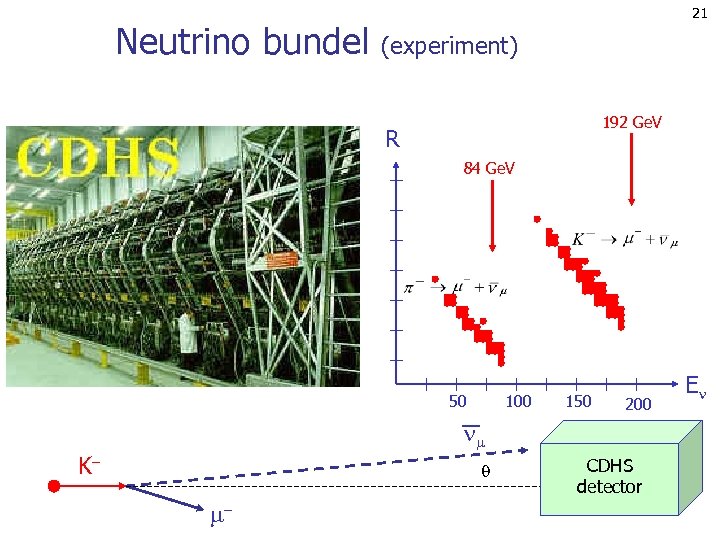21 Neutrino bundel (experiment) 192 Ge. V R 84 Ge. V 50 100 150 200 K CDHS detector E

Compton verstrooiing Foton verstrooiing: licht op elektronen Als h en c weer teruggestopt worden: 22 P’ , E k Lab-frame P ’, E’ k’ ’ 0. 06 0. 04 Compton’s original data 0. 02 0. 00 0

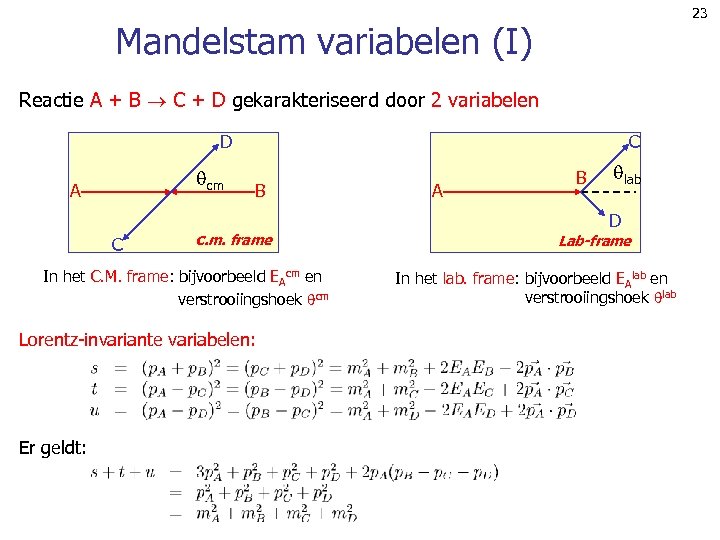23 Mandelstam variabelen (I) Reactie A + B C + D gekarakteriseerd door 2 variabelen C D cm A C B c. m. frame In het C. M. frame: bijvoorbeeld EAcm en verstrooiingshoek cm Lorentz-invariante variabelen: Er geldt: A B lab D Lab-frame In het lab. frame: bijvoorbeeld EAlab en verstrooiingshoek lab

24 Mandelstam variabelen (II) Handige uitdrukkingen in termen van s, t & u: Lab. frame: Energie van A: C. M. frame: C. M. energie: Energie van A: Want: A Voor A + A, in het c. m. frame geldt: A A c. m. frame A

25 Cross section, lifetime, decay width, …

26 Levensduur Bijna alle elementaire deeltjes vervallen! d. w. z. Levensduur: Vertakkingsverhouding Eenheden b. v. m. B m. C m. A c. m. frame verschillende vervalskanalen, b. v.

27 Werkzame doorsnede Ingrediënten om de telsnelheid A + B C + D te bepalen: 1. De overgangswaarschijnlijkheid Wfi De kans op een i f overgang per tijdseenheid per volume eenheid W wordt bepaald door de dynamica! 2. De experimentele omstandigheden (flux factor) a) Bundel intensiteit # per tijdseenheid per oppervlakte eenheid b) Dichtheid van het target # per volume eenheid 3. De fase-ruimte n W geeft de kans voor exact gedefinieerde toestanden i en f. Omdat niet elke toestand gemeten kan worden wordt over enkele (bijna identieke) toestanden geïntegreerd. Voor A + B C + D: [ ]=oppervlakte

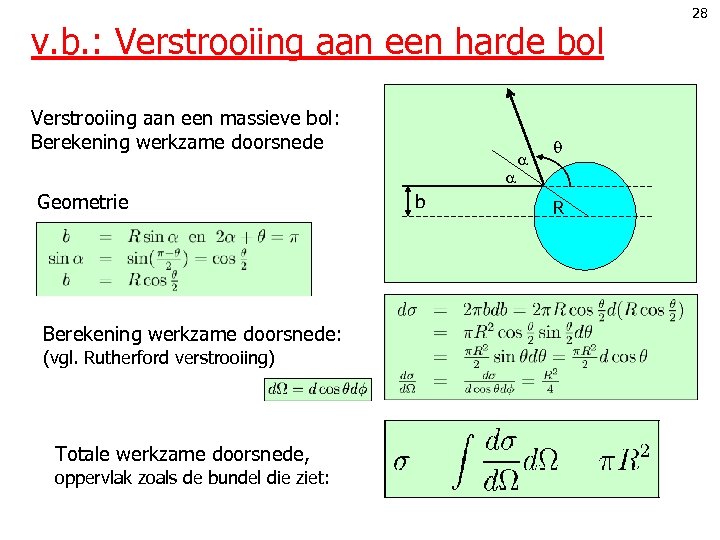v. b. : Verstrooiing aan een harde bol Verstrooiing aan een massieve bol: Berekening werkzame doorsnede Geometrie Berekening werkzame doorsnede: (vgl. Rutherford verstrooiing) Totale werkzame doorsnede, oppervlak zoals de bundel die ziet: b R 28

29 Fermi’s ‘golden rule’ (klassiek) Storingsrekening: Schrödinger vergelijking ‘ongestoorde’ toestanden Veronderstel: selecteer toestand af(t) Dan volgt voor da(t)/dt: kies alleen n=i En voor a(t) (laagste orde): De overgangsamplitude: met f i Voor een tijdsonafhankelijke storing:

30 Fermi’s golden rule Geeft |Tfi|2 de kans voor i f overgang? Neen! De overgangswaarschijnlijkheid per tijdseenheid wordt dan: i. h. a. : - welgedefinieerde begintoestand (bepaal jij!) - scala van eindtoestanden (bepaalt de natuur!) Fermi’s ‘golden rule’:

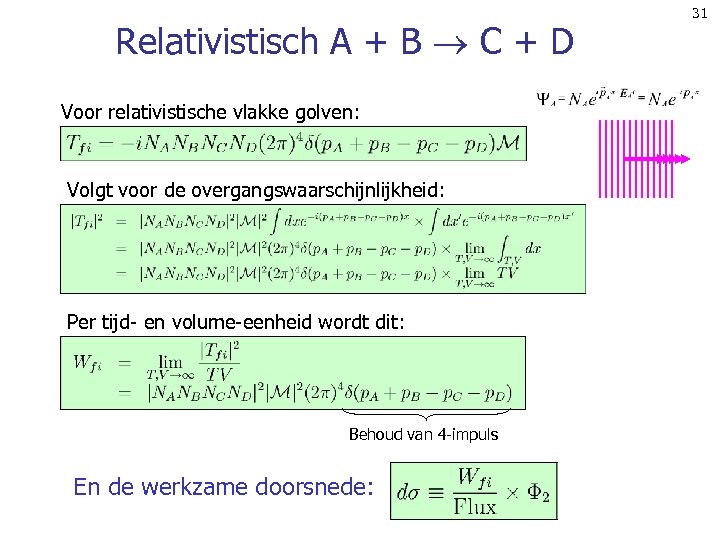Relativistisch A + B C + D Voor relativistische vlakke golven: Volgt voor de overgangswaarschijnlijkheid: Per tijd- en volume-eenheid wordt dit: Behoud van 4 -impuls En de werkzame doorsnede: 31

N-particle phase-space 32 Klein-Gordon: (volgende college) Dus voor het geheel in een doos Lx. L=V: take this simplest Faseruimte voor 1 deeltje Faseruimte voor 2 Ec en 2 ED deeltjes: Wfi met gekozen normalisatie: gebruik periode randvoorwaarden: pi=2 ni /L

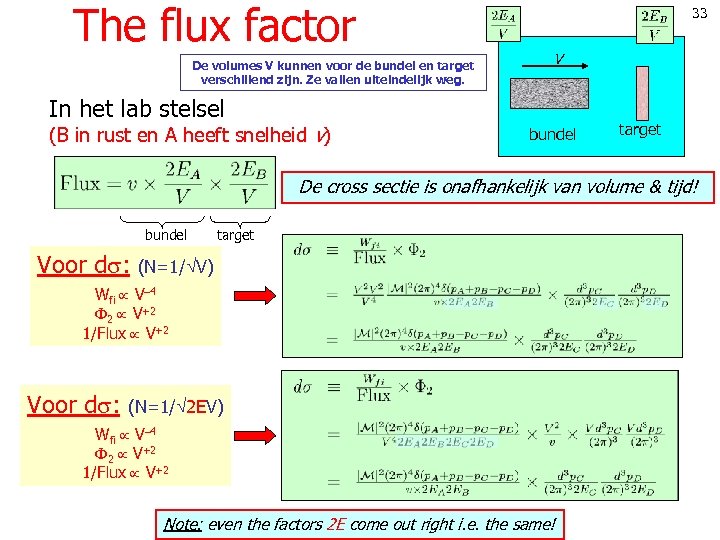The flux factor De volumes V kunnen voor de bundel en target verschillend zijn. Ze vallen uiteindelijk weg. 33 v In het lab stelsel (B in rust en A heeft snelheid v) bundel target De cross sectie is onafhankelijk van volume & tijd! bundel target Voor d : (N=1/ V) Wfi V 4 2 V+2 1/Flux V+2 Voor d : (N=1/ 2 EV) Wfi V 4 2 V+2 1/Flux V+2 Note: even the factors 2 E come out right i. e. the same!

Lorentz invariant form 34

Flux factor voor A + B … c. m. stelsel: P 1=(E 1, +p) P 2=(E 2, p) lab stelsel: P 1=(E, p) P 2=(m 2, 0) 35

Generic Expressions: and verstroooiing A A + B C + D werkzame doorsnede A B A 36 D B C B verval A C + D vervalsbreedte C D A

37 Faseruimte 2 deeltjes Bepaling van de faseruimte met impulsbehoud Doe de integraal over de 3 -momenta van p 4 m. b. v. de -functie Merk op dat E 4 niet onafhankelijk is: Herschrijf in bol-coördinaten, d 3 p 3=|p 3|2 d dp 3 Dus: In cm stelsel geldt E 3 d. E 3=E 4 d. E 4=pdp Met E’=E 3+E 4 nog niet gelijk aan E E 1+E 2 Note: 6 vrijheidsgraden waarvan er 4 vastgelegd worden door impulsbehoud: 2 over

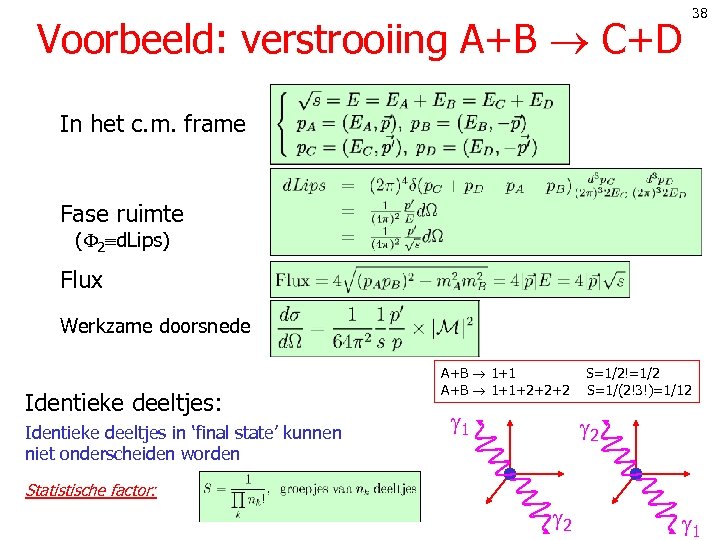38 Voorbeeld: verstrooiing A+B C+D In het c. m. frame Fase ruimte ( 2 d. Lips) Flux Werkzame doorsnede Identieke deeltjes: Identieke deeltjes in ‘final state’ kunnen niet onderscheiden worden A+B 1+1 S=1/2!=1/2 A+B 1+1+2+2+2 S=1/(2!3!)=1/12 1 2 Statistische factor: 2 1

Voorbeeld: verval A C+D 39 In het c. m. frame (gelijk lab frame) Fase ruimte Flux Voorbeeld: 0 Note S=1/2 u u Schatting: geeft: 10 -17 s, terwijl PDG geeft: =8. 7 10 -17 s

40 Toy-model: ABC theory

Feynman regels 41 Berekening van de amplitude M: Hiervoor is de dynamica van wisselwerking nodig. In het vervolg zullen we de amplitudes berekenen voor elektromagnetische, sterke en zwakke wisselwerkingen. Om een idee te krijgen eerst de amplitude voor een hypothetisch model, 3 toy-model: Feynman regels ABC theorie: p 2 p 1 A ig B p 3 C B p 1 p 2 A q ig C ig p 3 B p 4 A

42 Levensduur ( 3 toy-model) B The matrix element A is simply [g]=[Ge. V] g C De vervalsbreedte wordt met Fermi’s regel: 8 En de levensduur 8 van deeltje A is dus De impuls van B (of C) kan bepaald worden, in c. m. systeem: 8

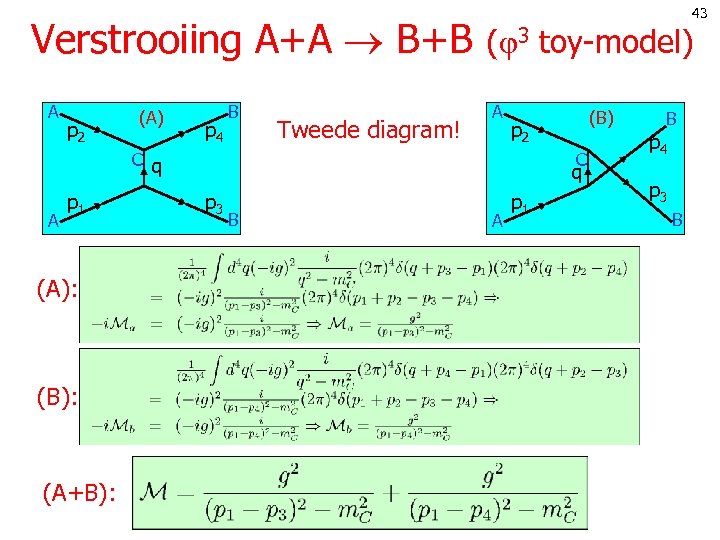43 Verstrooiing A+A B+B ( 3 toy-model) A p 2 (A) p 4 B Tweede diagram! A p 2 C q A p 1 (A): (B): (A+B): (B) C q p 3 B A p 1 B p 4 p 3 B

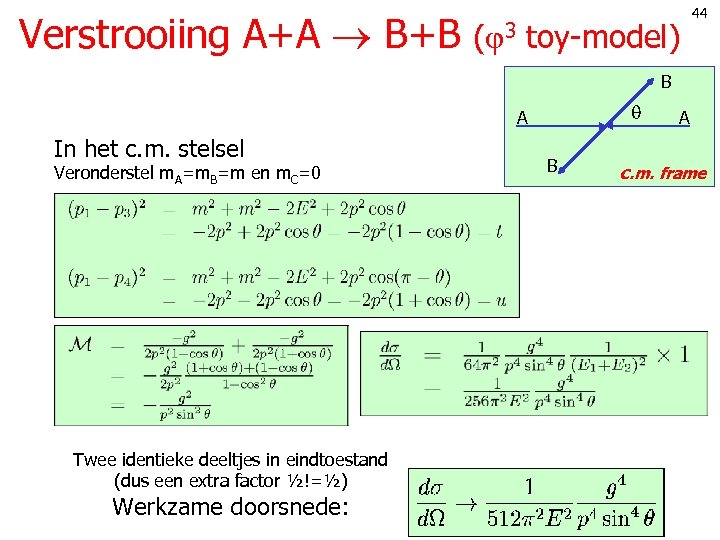Verstrooiing A+A B+B ( 3 toy-model) 44 B A In het c. m. stelsel Veronderstel m. A=m. B=m en m. C=0 Twee identieke deeltjes in eindtoestand (dus een extra factor ½!=½) Werkzame doorsnede: B A c. m. frame

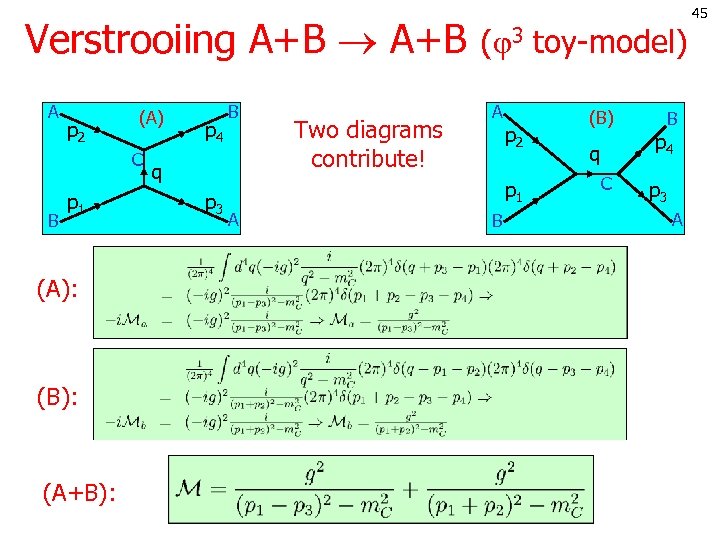Verstrooiing A+B ( 3 toy-model) A p 2 (A) C B p 1 (A): (B): (A+B): p 4 B q p 3 Two diagrams contribute! A p 2 p 1 A B (B) B p 4 q C p 3 A 45

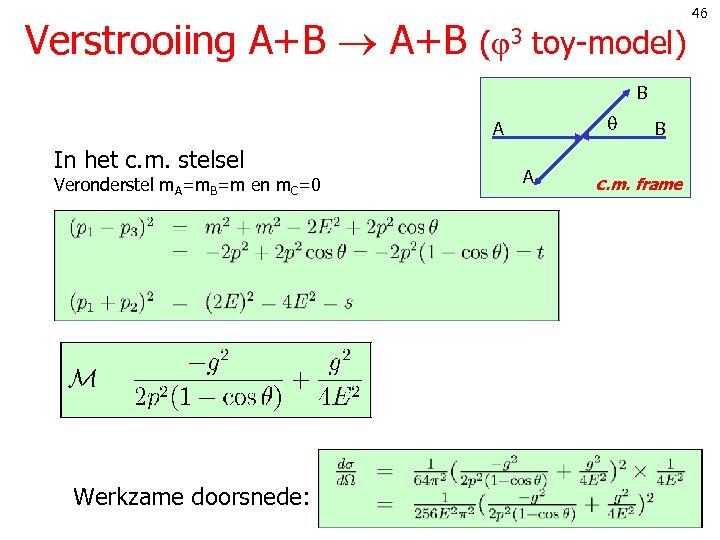Verstrooiing A+B ( 3 toy-model) B A In het c. m. stelsel Veronderstel m. A=m. B=m en m. C=0 Werkzame doorsnede: A B c. m. frame 46

47 Symmetries (…, quark model) • • Symmetry conserved quantity & classification of states Mathematical background: groups & representations Examples Quark model: Baryons & Mesons

Symmetry conserved quantity 48 classification of states Imagine Hamiltonian invariant under some kind of (coordinate) transformation Physics invariant 1=U+U U+=U 1 x x’ Rx (x) ’(x’) U (x) For matrix elements Hamiltonian H: (H=H’) Via de Schrödinger equation: conserved quantity U For an infinitesimal transformation, one can write: Operator O hermitean and commutes with H use eigenvalues to classify states!

Continuous space-time symmetries Space: physics invariant under x x’ x+ (if possible always study infinitesimal transformations) Space: physics invariant under r r’ (x y, y+ x, z) Time: physics invariant under t t’ t+ 49

inversion reflection y z x y Coordinates: z x Coordinates: Operators: Vectors: Pseudo-vectors: 50

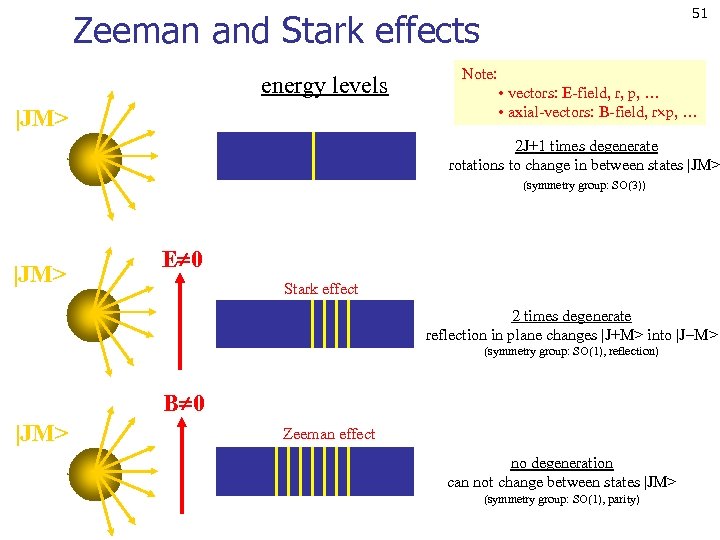51 Zeeman and Stark effects energy levels |JM> Note: • vectors: E-field, r, p, … • axial-vectors: B-field, r p, … 2 J+1 times degenerate rotations to change in between states |JM> (symmetry group: SO(3)) |JM> E 0 Stark effect 2 times degenerate reflection in plane changes |J+M> into |J M> (symmetry group: SO(1), reflection) B 0 |JM> Zeeman effect no degeneration can not change between states |JM> (symmetry group: SO(1), parity)

52 Is physics mirror P invariant?

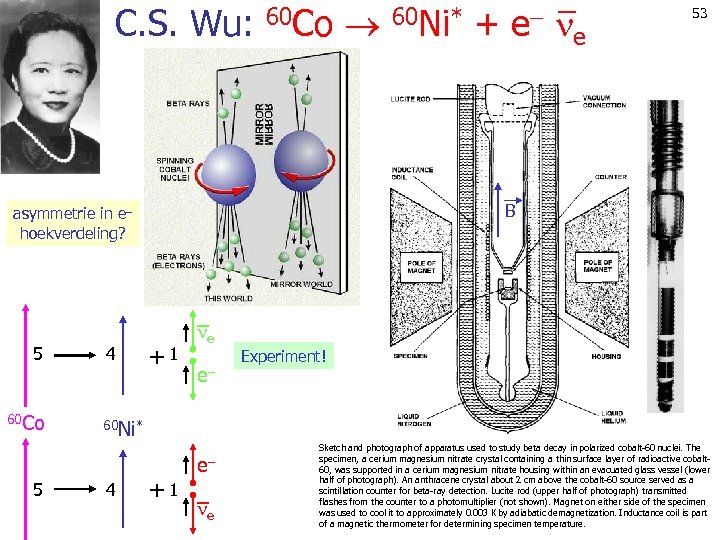C. S. Wu: 60 Co 60 Ni* + e 60 Co 5 4 e B asymmetrie in e hoekverdeling? 5 53 +1 e e Experiment! 60 Ni* 4 +1 e e Sketch and photograph of apparatus used to study beta decay in polarized cobalt-60 nuclei. The specimen, a cerium magnesium nitrate crystal containing a thin surface layer of radioactive cobalt 60, was supported in a cerium magnesium nitrate housing within an evacuated glass vessel (lower half of photograph). An anthracene crystal about 2 cm above the cobalt-60 source served as a scintillation counter for beta-ray detection. Lucite rod (upper half of photograph) transmitted flashes from the counter to a photomultiplier (not shown). Magnet on either side of the specimen was used to cool it to approximately 0. 003 K by adiabatic demagnetization. Inductance coil is part of a magnetic thermometer for determining specimen temperature.

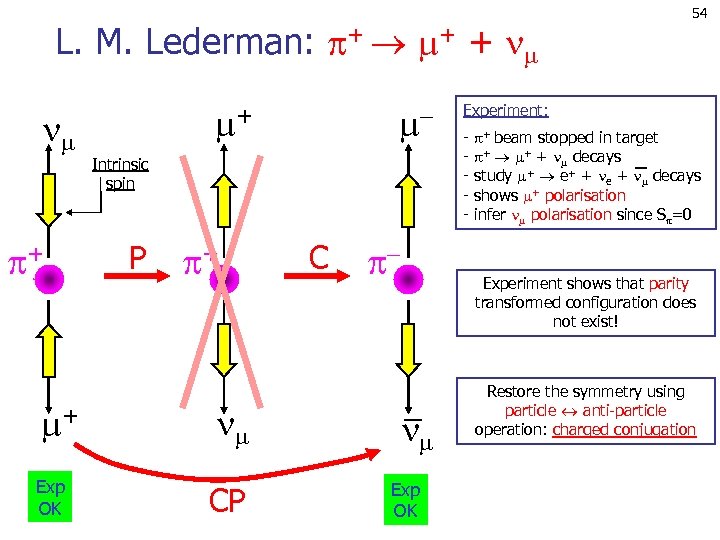L. M. Lederman: + + Exp OK + Intrinsic spin P + CP C 54 Experiment: - + beam stopped in target - + + + decays - study + e+ + e + decays - shows + polarisation - infer polarisation since S =0 Experiment shows that parity transformed configuration does not exist! Exp OK Restore the symmetry using particle anti-particle operation: charged conjugation

December 27, 1956: Fall of Parity Conservation 55 Symmetries have long played a crucial role in physics. Since 1925, physicists had assumed that our world is indistinguishable from its mirror image - a notion known as parity conservation - and prevailing scientific theory reflected that assumption. Until a series of pivotal experiments at the National Bureau of Standards in 1956 (now the National Institute of Standards and Technology), parity conservation enjoyed exalted status among the most fundamental laws of physics, including conservation of energy, momentum and electric charge. But as with relativity, Nature once again demonstrated that it is not always obliged to follow the rules of "common sense". Parity conservation implies that Nature is symmetrical and makes no distinction between right- and left-handed rotations, or between opposite sides of a subatomic particle. For example, two similar radioactive particles spinning in opposite directions about a vertical axis should emit their decay products with the same intensity upwards and downwards. Yet although there were many experiments that established parity conservation in strong interactions, the assumption had never been experimentally verified for weak interactions. Indeed, when the weak force was first postulated to explain disintegration of elementary particles, it seemed inconceivable that parity would not hold there as well. All that changed in the 1950 s, when high-energy physicists began observing phenomena that could not be explained by existing theories, most notably the decays of K mesons emitted in the collision of a high-energy proton with an atomic nucleus. The K meson appeared in two distinct versions, decaying into either two or three pi mesons, (which necessarily had opposite parity), although in all other characteristics they seemed identical. In June of 1956, theoretical physicists Chen Ning Yang and Tsung Dao Lee submitted a short paper to the Physical Review raising the question of whether parity is conserved in weak interactions, and suggesting several experiments to decide the issue. Lee and Yang's paper did not immediately spark more than passing curiosity among physicists when it appeared in October 1956. Freeman Dyson later admitted that while he thought the paper was interesting, "I had not the imagination to say, 'By golly, if this is true, it opens up a whole new branch of physics!' And I think other physicists, with very few exceptions, at that time were as unimaginative as I. " Richard Feynman pronounced the notion of parity violation "unlikely, but possible, and a very exciting possibility, " but later made a $50 bet with a friend that parity would not be violated. One of the simplest proposed experiments involved measuring the directional intensity of beta radiation from cobalt-60 nuclei oriented with a strong magnetic field so that their spins aligned in the same direction. Parity conservation demands that the emitted beta rays be equally distributed between the two poles. If more beta particles emerged from one pole than the other, it would be possible to distinguish the mirror image nuclei from their counterparts, which would be tantamount to parity violation. Between Christmas of 1956 and New Year's, NBS scientists set about performing beta decay experiments. The team was led by Columbia Professor C. S. Wu. Professor Wu had been born in China in 1912, had received her Ph. D from the University of California in 1940, and had worked on the Manhattan Project during World War II. In 1975 she would serve as the first woman president of the APS. When the results were in, the NBS team arrived at a startling conclusion: the emission of beta particles is greater in the direction opposite to that of the nuclear spin. Thus, since the beta emission distribution is not identical to the mirror image of the spinning cobalt-60 nucleus, parity was unequivocally shown not to be conserved. Leon Lederman, who at the time worked with Columbia University's cyclotron, performed an independent test of parity with that equipment, involving the decay of pi and mu mesons, and also obtained distinct evidence for parity violation. In short, Nature is a semi-ambidextrous southpaw. And Feynman lost his bet. The result shattered a fundamental concept of nuclear physics that had been universally accepted for 30 years, thus clearing the way for a reconsideration of physical theories and leading to new, far-reaching discoveries - most notably a better understanding of the characteristics of elementary particles, and a more unified theory of the fundamental forces. Further Reading: S. Weinberg, Reviews of Modern Physics, 52, 515 (1980); A. Salam, p. 525; S. L. Glashow, p. 539.

56 Is physics CP invariant?

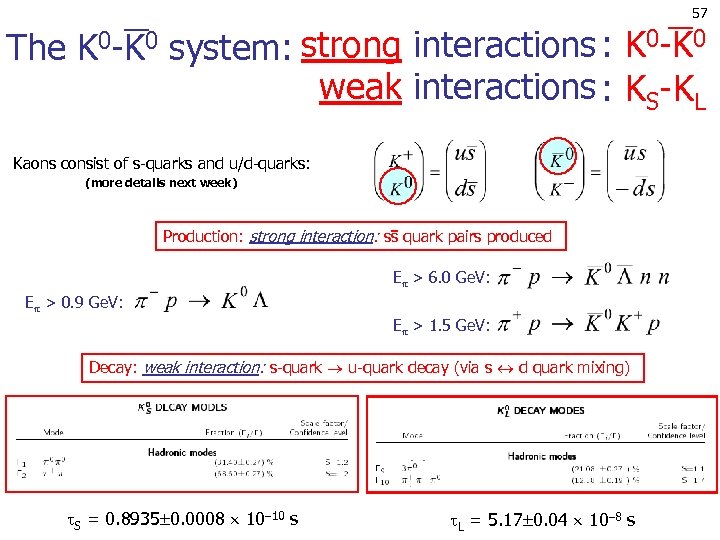57 The K 0 -K 0 system: strong interactions : K 0 -K 0 weak interactions : KS-KL Kaons consist of s-quarks and u/d-quarks: (more details next week) Production: strong interaction: ss quark pairs produced E > 6. 0 Ge. V: E > 0. 9 Ge. V: E > 1. 5 Ge. V: Decay: weak interaction: s-quark u-quark decay (via s d quark mixing) S = 0. 8935 0. 0008 10 10 s L = 5. 17 0. 04 10 8 s

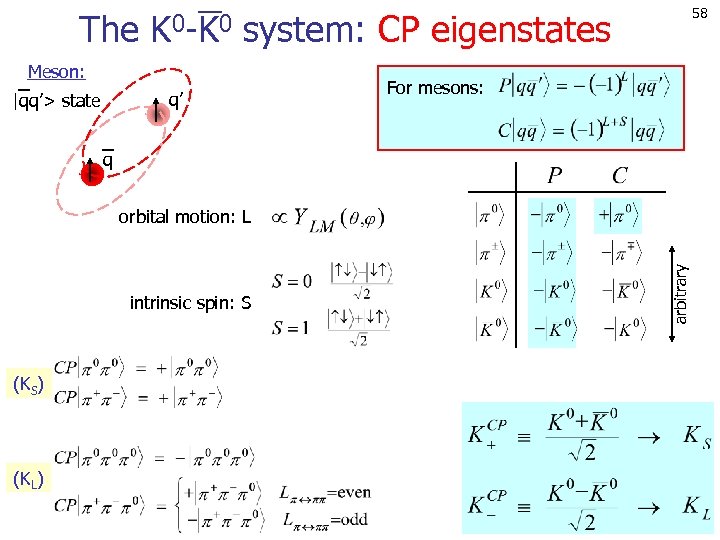58 The K 0 -K 0 system: CP eigenstates Meson: q’ |qq’> state For mesons: q intrinsic spin: S (KS) (KL) arbitrary orbital motion: L

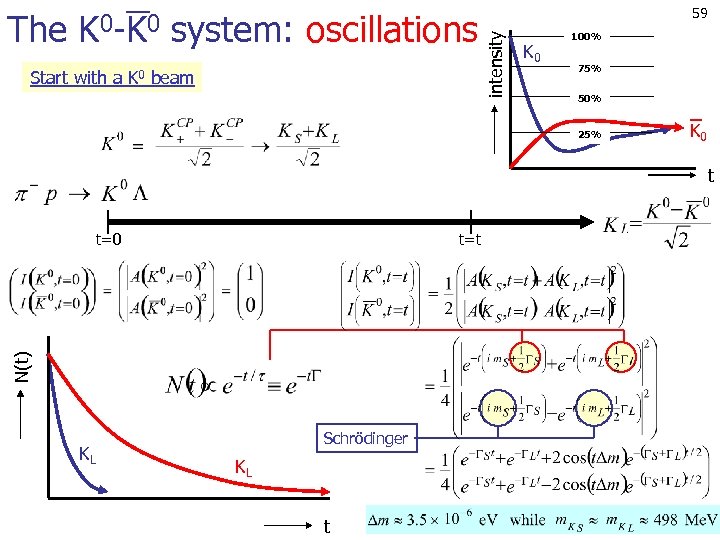Start with a K 0 beam 59 intensity The K 0 -K 0 system: oscillations K 0 100% 75% 50% 25% K 0 t t=t N(t) t=0 KL Schrödinger KL t

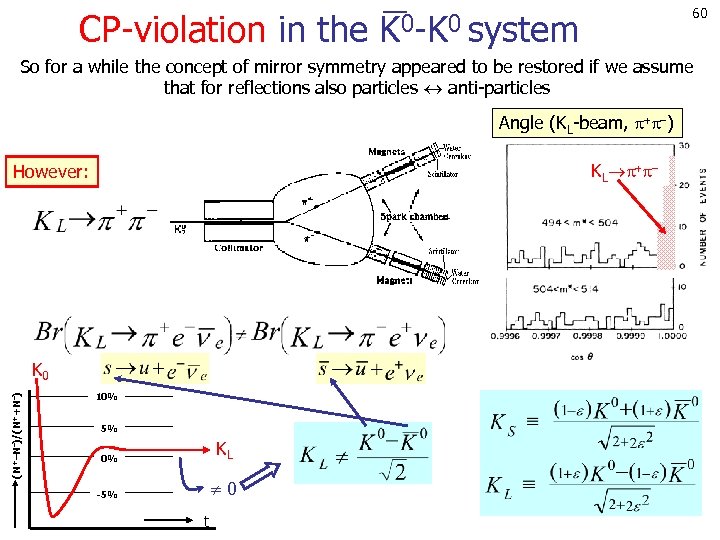60 CP-violation in the K 0 -K 0 system So for a while the concept of mirror symmetry appeared to be restored if we assume that for reflections also particles anti-particles Angle (KL-beam, ) KL However: (N+ N )/(N++N ) K 0 10% 5% 0% KL -5% 0 t

61 Physics is CPT invariant!

Symmetries in (particle) physics n Space-time n n n n Permutations identical particles n n n Fermions anti-symmetric under interchange Bosons symmetric under interchange Internal symmetries n n Space translations conservation of momentum Time translations conservation of energy Rotations conservation of angular momentum Boosts Space reflections parity conservation (violated in weak interactions!) Time reversal SU(2), SU(3) Gauge symmetries n n Global conservation of charges Local interactions 62

Groups & representations Group (in mathematics) set transformations G obeying: Closure: a, b in G c ab in G Identity: 1 in G with ( a) 1 a=a 1=a Inverse: a in G exists a 1 with aa 1=a 1 a=1 Associative: a, b, c in G: (ab)c=a(bc) Commutative: a, b in G: ab=ba (Abelian) 1. 2. 3. 4. 5. Finite: o {1, a} with a 2=1 o Permutations of N elements: SN Infinite: o Translations in 3 dimensions T(3) o Rotations in 3 dimensions SO(3) o Boosts in 3 D space-time Representation: mapping of elements of G onto matrices obeying Mc=Ma. Mb once c=ab Ma a b c=ab Mb Mc=Ma. Mb d G matrices If all the matrices can not be broken down into blocks of smaller dimensional matrices the representation is called: irreducible 63 Example: group {1, a} two representations: 1 (+1) and a ( 1) Example: group S 3 three representations:

64 Rotation group SO(3) Always the same questions: Specific for SO(3): 1. J 1, J 2 & J 3 for rot. x-, y- & z-ax [Ji, Jj]=i ijk. Jk and [Ji, J 2]=0 spin j (J 2) and projection m (J 3) multiplicity 2 j+1 2. 3. Find generators infinitesimal transformations and their commutation relations (i. e. Lie algebra) Find quantum numbers with which to label states Find irreducible representations multiplet structure |j+j> |jm+p> J+ |jm+1> |jm 1> 2 j must be an integer! Note: phase convention required! J |j j> |jm q>

65 SO(3) representations & SU(2) symmetry SU(2) SO(3) Addition of angular momenta (j 1 j 2): j 1 j 2= j 1 j 2+1 j 2+2 …… j 1+j 2 1 j 1+j 2 Example:

Clebsch-Gordon coefficients 66

67 Constructing the SO(3) representations General principle: • Start with infinitesimal transformations: x-, y- and z-axis rotations: • Find the matrices corresponding to these infinitesimal rotations

68 Constructing the SO(3) representations • Construct the macroscopic rotations via exponentiation:

69 Isospin Heisenberg (1932): 1. proton & neutron states of one particle: the nucleon 2. physics invariant under p n transformation i. e. an internal SU(2) symmetry All this: strong interaction only! Name: “isospin” analogous to the normal (Euclidean) spin Isospin multiplets: I=1/2 I=1 I=3/2 nucleon (mp=938. 28 Me. V, mn =939. 57 Me. V): pions (m 0=135 Me. V, m =140 Me. V): -baryons: (m 1232 Me. V):

70 Isopin examples Two nucleon system: Only stable 2 -nucleon system: deuterium 2 H What is the isospin of deuterium? this corresponds to deuterium: I=0: Iz= 1 Energy levels in “mirror” nuclei: nuclei with same total number of nucleons but differences in number of protons/neutrons What can you say about the isospin of these levels? Branching ratio’s: Iz=0 Iz=+1 4+ 4+ 4+ I 1 2+ 2+ 2+ I 1 0+ 0+ 0+ I 1 18 O 1+ 18 Ne I 0 67% 18 F What can you say about the relative occurrence of: p 0 and 33% n + decays?

71 Charge conjugation particle anti-particle Define operation “C” which converts a particle into its anti-particle: particle doublet: anti-particle doublet: Group with two elements because C 2=1 C=C 1=C† C hermitean eigenvalues +1 and 1 1 C C C C 2=1 Not often particle = anti-particle. Exceptions: photon: particle/anti-particle bound states C = With this choice Particles and anti-particles transform alike under rotations in iso-space e. g. rotation of around x-axis

72 Isospin at the quark level: u-quark & d-quark (flavors) Messy situation in the sixties (compare pre-Mendeleev chaos atomic elements): Many particles: p, n, , , , …… e p too often large angle scatterings proton has sub-structure Progress: 1. Theory: ordering in terms of quark sub-structure: u-, d- and s-quarks (flavors) 2. Experiment: a. Discovery of sub-structure in the nucleon (compare Rutherford atom) b. Discovery of a fourth quark flavor in 1974: charm Copy isospin to u- and d-quarks:

“Eightfold way”: u-quark, d-quark & s-quark (flavors) 73 Gelmann & Zweig (1963): 1. hadrons built with three constituents: u-, d-, & s-quarks: 1. 2. Mesons: qq Baryons: qqq physics invariant under uds transformation i. e. an internal SU(3) symmetry Note: do not carry this beyond uds since the mass differences between the quarks become way too large All this: strong interaction only! What does this buy you? 1. 2. Order in the zoo of particles; compare p and n as two states of the nucleon Expression of properties (masses, magnetic moments, …) in terms of a few parameters 3. 4. But realize: SU(3) flavor is badly broken (mu md ms) and applies only to strong interaction This opposed to exact color SU(3) symmetry of strong interactions we will encounter later!

74 SU(3) symmetry For SU(2): ØMultiplets |jm>, 2 j+1 states; one traceless generator: J 3 ØStep operators within multiplet: J J 1 i. J 2 ØBuild all representations from 2 D (j=1/2) representation J j=1/2 1/2 j=0 j=1 For SU(3): ØThree SU(2) sub-groups; two traceless generator: 3 and 8 ØThree step operator sets; 1 i 2 4 i 5 6 i 7 ØBuild all representations from 3 D (“ 3 and 3”) representations

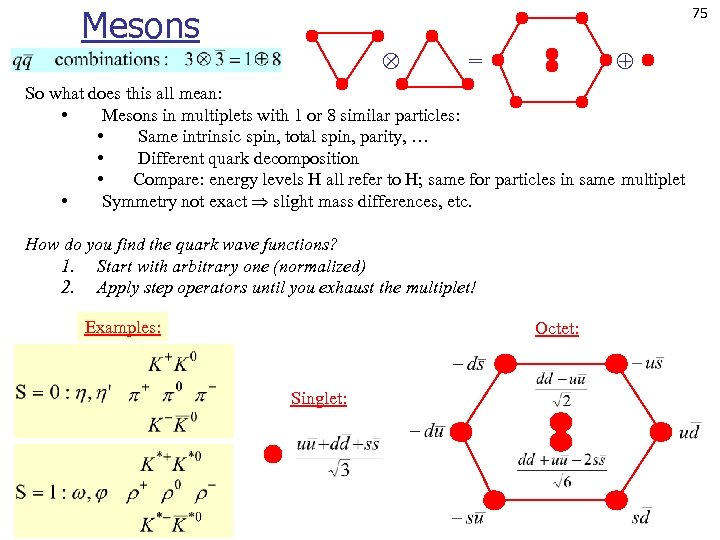Mesons 75 = So what does this all mean: • Mesons in multiplets with 1 or 8 similar particles: • Same intrinsic spin, total spin, parity, … • Different quark decomposition • Compare: energy levels H all refer to H; same for particles in same multiplet • Symmetry not exact slight mass differences, etc. How do you find the quark wave functions? 1. Start with arbitrary one (normalized) 2. Apply step operators until you exhaust the multiplet! Examples: Octet: Singlet:

76 Meson masses If SU(3) would be exact all particle masses within a multiplet identical SU(3) symmetry broken by: 1. u-, d- and s-quark mass differences (singlet+octet mixed “nonet”) In addition binding energy has contribution from quark spin-spin interaction Fit this mu=md=310 Me. V and ms=483 Me. V Meson nonet S=0 fit mass exp mass Meson nonet S=1 fit mass exp mass (3) 140 138 (3) 780 776 K (2 x 2) 484 496 K (2 x 2) 896 892 (1) 559 549 (1) 780 783 ’ (1) --- 958 (1) 1032 1020

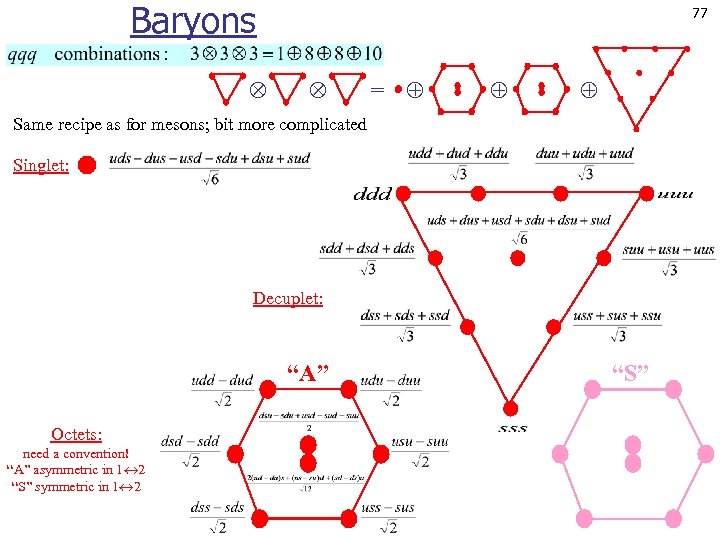Baryons 77 = Same recipe as for mesons; bit more complicated Singlet: Decuplet: “A” Octets: need a convention! “A” asymmetric in 1 2 “S”

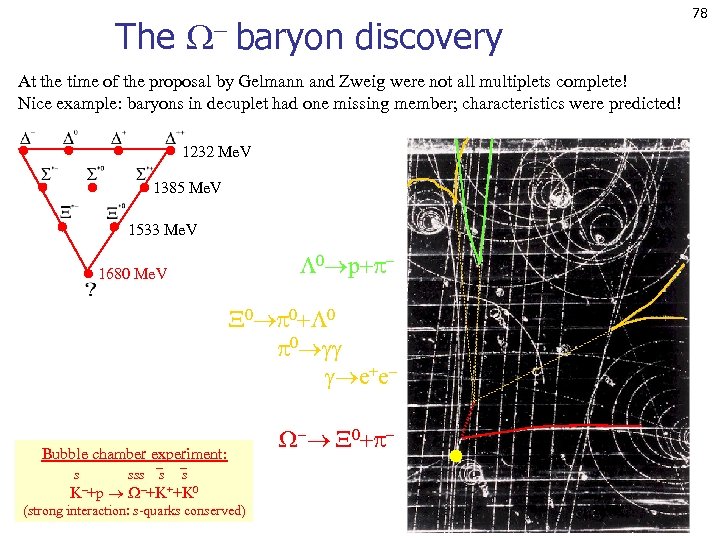The baryon discovery At the time of the proposal by Gelmann and Zweig were not all multiplets complete! Nice example: baryons in decuplet had one missing member; characteristics were predicted! 1232 Me. V 1385 Me. V 1533 Me. V 0 p 1680 Me. V 0 0 e+e Bubble chamber experiment: s sss s s K +p +K++K 0 (strong interaction: s-quarks conserved) 0 78

79 Adding the intrinsic spin Mesons: S=0 S=1 Baryons: Symmetric 10 3/2 8 A 1/2 A+8 S 1/2 S S=3/2 S=1/2 Anti-symmetric 1 3/2 8 A 1/2 S+8 S 1/2 A S=1/2 Remark: of course this only refers to the intrinsic spin (S) of a hadron. In addition any hadron (meson and baryon) will have orbital spin (L) due to the quark motions.

80 Restoring anti-symmetry: color little problem: ++ s s s u u u particle with half-integer spin obey Fermi-Dirac statistics must be anti-symmetric brute force solution: invent hidden degree of freedom: color physics: 1. 2. 3. 4. q q invariant under color (RGB) transitions; exact SU(3) symmetry 2 3 compare the color charge and the electromagnetic charge instead of the photon now eight force carriers: gluons: RB, RG, BG, RR, BB, GG hypothesis: all hadrons in color singlet state: baryons: multiply with: (RGB RBG GRB BGR+BRG+GBR)/ 6 mesons: multiply with: (RR+BB+GG)/ 3 (symmetric in color) (anti-symmetric in color)

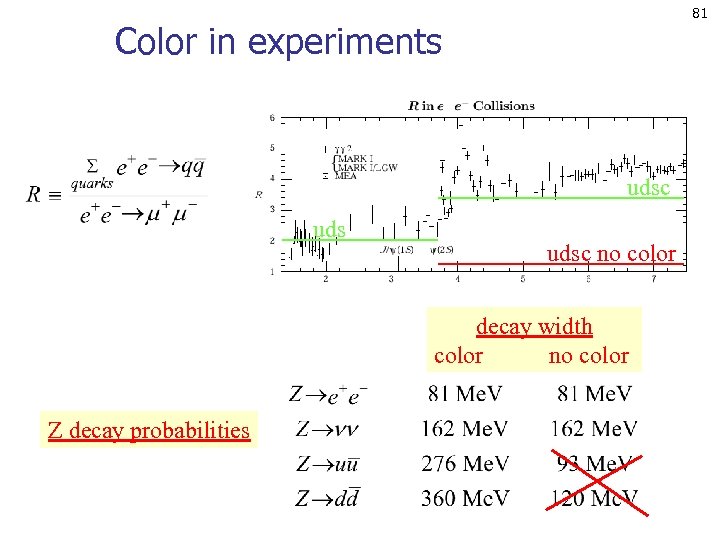81 Color in experiments udsc no color decay width color no color Z decay probabilities

Example: , p , and n wave functions Conventions: Wave functions full (123) symmetry Complete wave function: multiply with: quark with spin up: q Q quark with spin down: q q (RGB RBG GRB BGR +BRG +GBR)/ 6 82

Baryon magnetic moments 83 Magnetic moment of a particle is obtained using: For a S=1/2 point (Dirac) particle with mass m and electric charge q one finds: With the quark-flavour wave functions one can calculate magnetic moments of mesons and baryons with as only unknown parameters the u-, d- and s-quark masses! Proton: Assume now: Neutron (simply u d): ü mu md m u=e/3 m and d= e/6 m