1 Гидродинамика

1 Гидродинамика зернистых материалов Лекция № 5 1. Неподвижный зернистый слой 2. Псевдоожиженный слой твердого зернистого материала

2 1. Движение жидкости через зернистый слой твердого материала В химической технологии широко применяются аппараты, в которых жидкость протекает через слой сыпучего материала. Этот случай можно рассматривать как течение через пористую среду, в которой жидкость движется по каналам (порам) между отдельными частицами сыпучего материала.

3 Неподвижный зернистый слой • Форма и размеры элементов зернистых слоев весьма разнообразны: частицы слоев осадка на фильтрах, гранулы, таблетки, кусочки катализаторов или адсорбентов, насадочные тела абсорбционных и ректификационных колонн. • При этом зернистые слои могут быть монодисперсными или полидисперсными в зависимости от того, одинаковы или различны по размеру частицы зернистого слоя.

4 Основные характеристики зернистых материалов Основными характеристиками зернистого материала являются : • Удельная поверхность – поверхность частиц материала, приходящаяся на единицу объема, занятого слоем (f, м 2/ м 3) • Порозность – относительная объемная доля пустот (ε ) • Размер частиц (d) и их форма

5 Порозность • Если в объеме зернистого слоя V содержится Vт плотного материала, то • Или через плотности зернистого материала и плотного материала:

6 Удельная поверхность • В случае монодисперсного слоя сферических частиц диаметром d количество их в 1 м 3 слоя равно : • Отсюда удельная поверхность слоя найдется как:

7 Эквивалентный (гидравлический) радиус канала • Течение жидкости в слое происходит в межчастичном пространстве - каналах слоя, конфигурация которых довольно сложна. • Основной характеристики каналов является их гидравлический радиус или эквивалентный диаметр.

8 Эквивалентный (гидравлический) радиус канала • В слое зерен, поперечное сечение и высота которого соответственно равны S и H, сумма равная поверхность всех каналов =суммарной поверхности всех частиц и составляет : SHf = Vf, • Их суммарное живое сечение равно εS • Эквивалентный (гидравлический) диаметр канала выразится как:

9 Гидравлическое сопротивление зернистого слоя Для определения гидравлического сопротивления (перепада давлений ∆Р) зернистого слоя высотой Н и площадью поперечного сечения S можно воспользоваться известным выражением : (1) • здесь l −длина каналов; wи −средняя скорость движения жидкости (газа) в каналах слоя.

10 Гидравлическое сопротивление зернистого слоя • Длину каналов выразим через высоту слоя, введя поправку на извилистость (кривизну) каналов l = причем 1 Н, > • Истинную скорость течения жидкости в каналах так же целесообразно заменить через фиктивную скорость (w ), равную средней cкорости течения и рассчитанную на полное сечение аппарата. • В этом случае истинная и средняя скорость связаны между собой посредством величины порозности слоя: wи = w/ε

11 Гидравлическое сопротивление зернистого слоя Подставив полученные значения для l, d, wи в формулу (1) получим: (2)

12 Коэффициент гидравлического сопротивления • Величина коэффициента гидравлического сопротивления λ является функцией режима течения (Re). • Специфической особенностью процессов гидродинамики жидкостей при их течении в зернистых слоях, является то, что в подавляющем большинстве случаев жидкость движется в ламинарном режиме (из-за сравнительно малых значений величины диаметра твердых частиц и диаметра каналов)

13 Коэффициент гидравлического сопротивления (ламинарный режим) • для ламинарного режима уравнение для расчета гидравлического сопротивления слоя зерен можно представить как: • Уравнение (2) приобретает вид:

14 Коэффициент гидравлического сопротивления (турбулентный режим) • Для турбулентного режима аналитически выразить величину коэффициента сопротивления λ практически не представляется возможным. • На практике часто используется универсальное полуэмпирическое уравнение:

15 2. Псевдоожиженный слой зернистых материалов Взвешенный слой - то такое состояние слоя зернистого материала, при пропускании через который газа или жидкости вес частиц уравновешивается силой гидродинамического потока, в результате чего частицы получают свободу относительного перемещения. Взвешенный слой называется еще псевдоожиженным, кипящим слоем. Аппараты с кипящим или взвешенным слоем нашли применение во многих отраслях промышленности: там, где необходимо провести процессы взаимодействия между мелко раздробленными твердыми телами и газом или жидкостями. Аппараты со взвешенным слоем могут применяться для смешивания сыпучих материалов, классификации материалов по крупности.

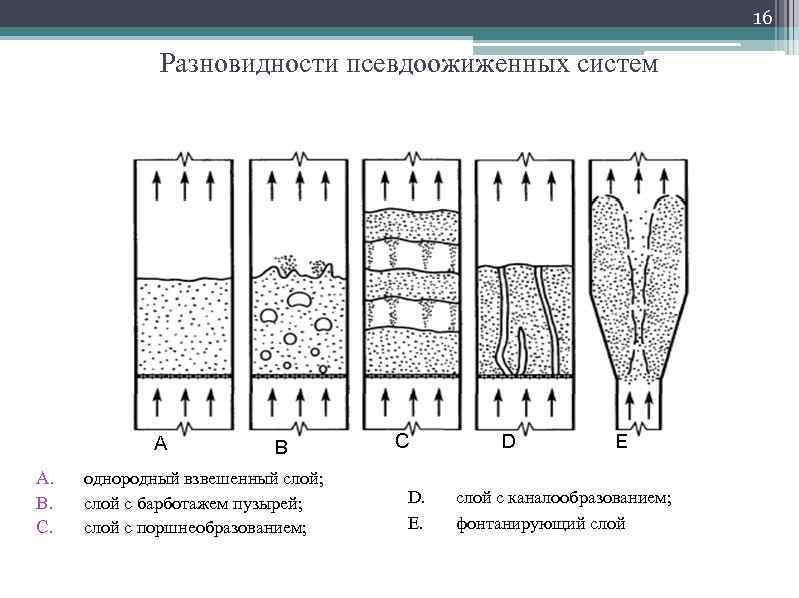
16 Разновидности псевдоожиженных систем A B C D E A. однородный взвешенный слой; B. слой с барботажем пузырей; D. слой с каналообразованием; C. слой с поршнеобразованием; E. фонтанирующий слой

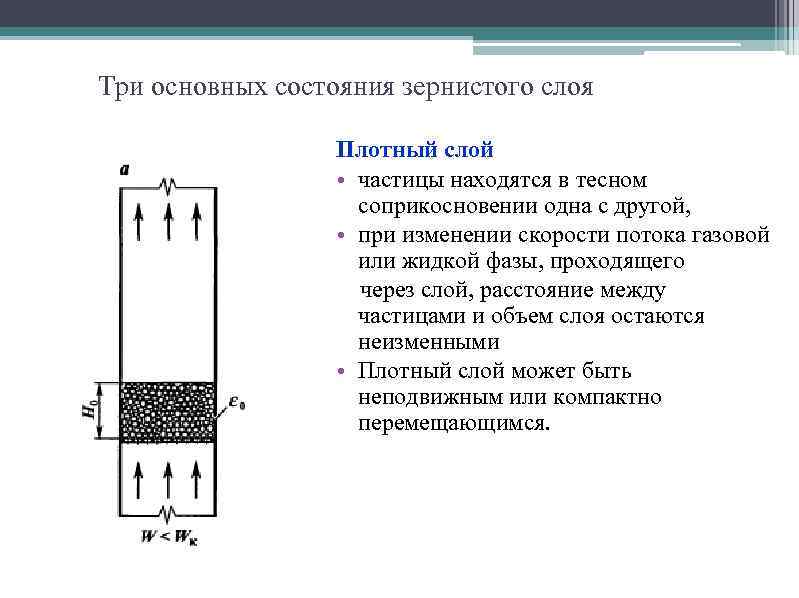
Три основных состояния зернистого слоя Плотный слой • частицы находятся в тесном соприкосновении одна с другой, • при изменении скорости потока газовой или жидкой фазы, проходящего через слой, расстояние между частицами и объем слоя остаются неизменными • Плотный слой может быть неподвижным или компактно перемещающимся. 17

Три основных состояния зернистого слоя Взвешенный, псевдоожиженный или кипящий слой • Частицы в результате воздействия движущейся через слой газовой или жидкой фазы находятся в хаотическом движении в пределах слоя, напоминая кипящую жидкость. • Расстояние между частицами и объем слоя изменяются в зависимости от скорости потока, проходящего через слой. 18

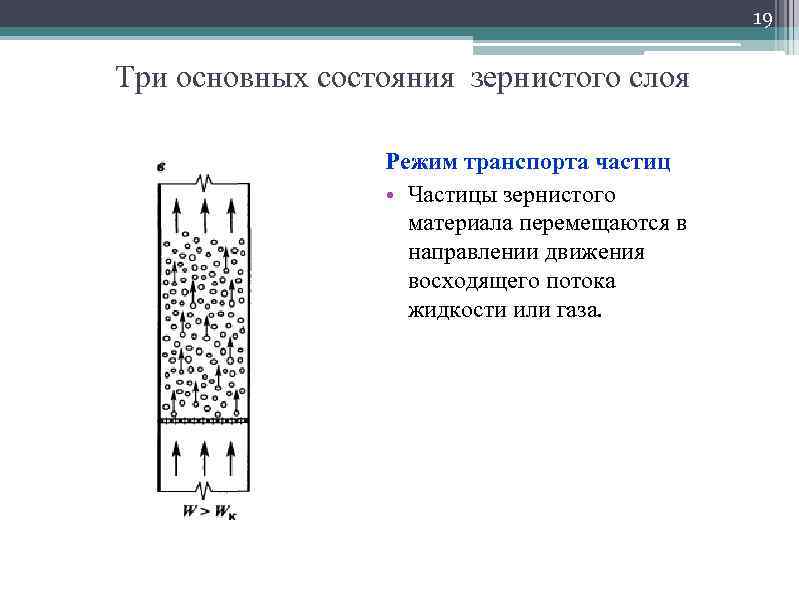
19 Три основных состояния зернистого слоя Режим транспорта частиц • Частицы зернистого материала перемещаются в направлении движения восходящего потока жидкости или газа.

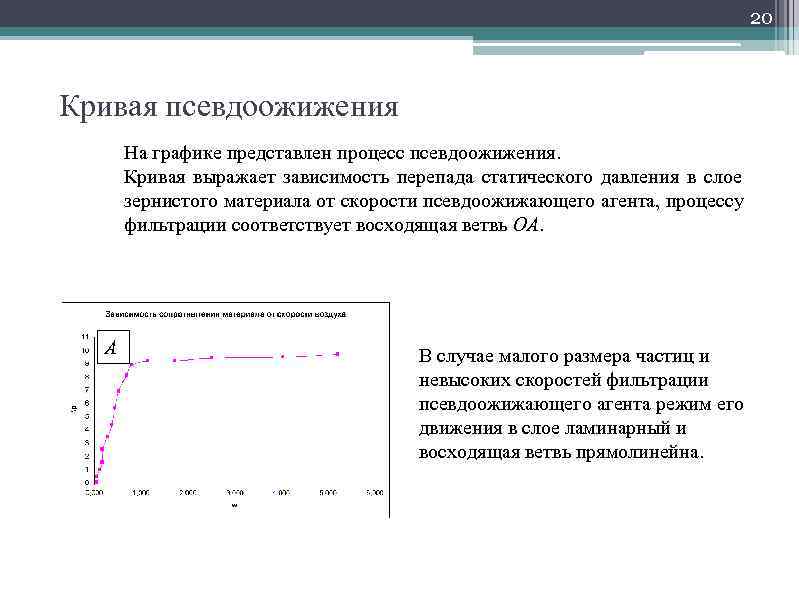
20 Кривая псевдоожижения На графике представлен процесс псевдоожижения. Кривая выражает зависимость перепада статического давления в слое зернистого материала от скорости псевдоожижающего агента, процессу фильтрации соответствует восходящая ветвь ОА. А В случае малого размера частиц и невысоких скоростей фильтрации псевдоожижающего агента режим его движения в слое ламинарный и восходящая ветвь прямолинейна.

21 Режим псевдоожижения Переход от режима фильтрации к режиму псевдоожижения соответствует на кривой псевдоожижения критической скорости wкр (точка А, ), называемой скоростью начала псевдоожижения wпс. В момент начала псевдоожижения вес зернистого материала, приходящийся на единицу площади поперечного сечения аппарата, уравновешивается силой гидравлического сопротивления слоя: ΔРсл = (ρТ – ρв)(1 - ε 0)h 0 g, где ΔРсл – сопротивление слоя зернистого материала, Па; h 0 – высота неподвижного слоя, м; ρТ и ρв – плотности твердых частиц и воздуха (псевдоожижающего агента), кг/м 3; ε 0 – порозность неподвижного слоя материала. Отношение рабочей скорости газа к критической есть число псевдоожижения Wp/Wкр = К.

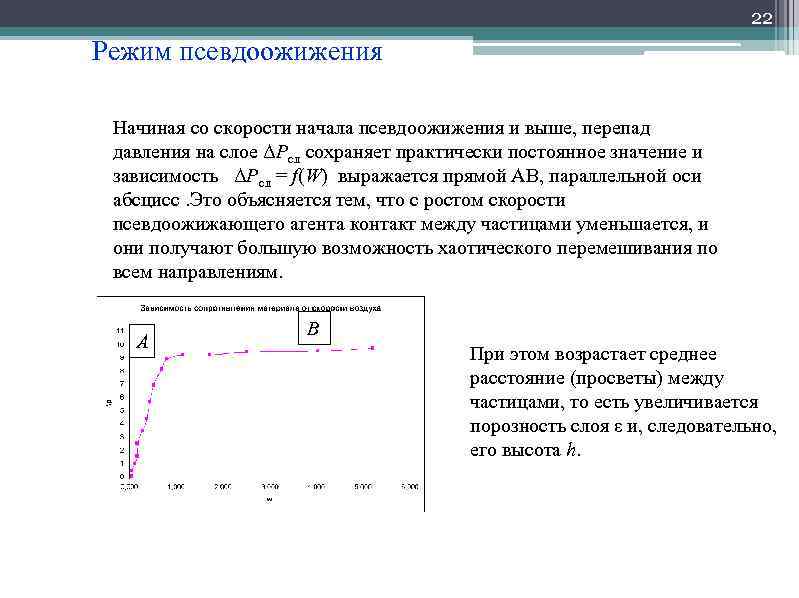
22 Режим псевдоожижения Начиная со скорости начала псевдоожижения и выше, перепад давления на слое ΔРсл сохраняет практически постоянное значение и зависимость ΔРсл = f(W) выражается прямой АВ, параллельной оси абсцисс. Это объясняется тем, что с ростом скорости псевдоожижающего агента контакт между частицами уменьшается, и они получают большую возможность хаотического перемешивания по всем направлениям. В А При этом возрастает среднее расстояние (просветы) между частицами, то есть увеличивается порозность слоя ε и, следовательно, его высота h.

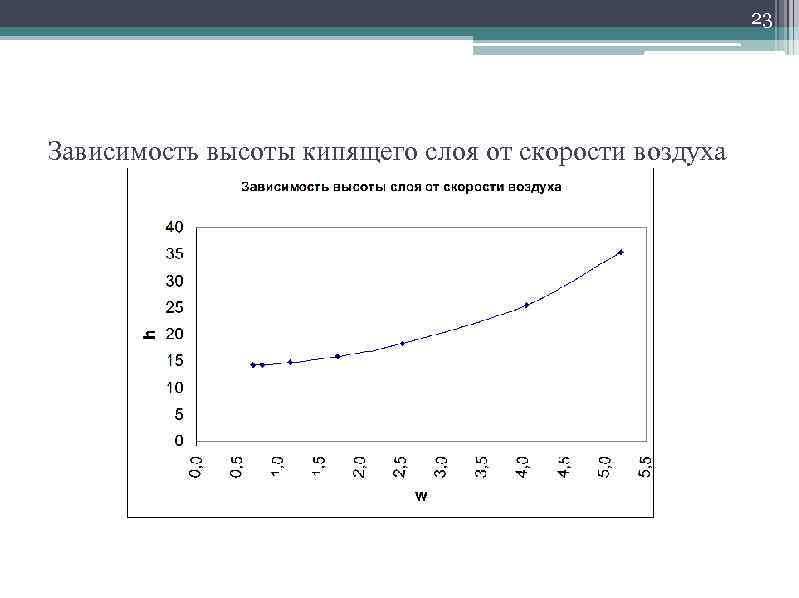
23 Зависимость высоты кипящего слоя от скорости воздуха

24 Определение высоты кипящего слоя Так как перепад давления в псевдоожиженном слое ΔРсл остается практически постоянным, высоту кипящего слоя можно определить из следующего условия: ΔРсл = (ρТ – ρв)(1 - ε 0)h 0 g = (ρТ – ρв)(1 - ε)hg, откуда где ε – порозность кипящего слоя материала, находится по формуле: где h. Т – высота твердой фазы материала (без внутренних и внешних пустот), м; H – средняя высота кипящего слоя материала, м. Высота твердой фазы материала находится по формуле: где М – масса слоя зернистого материала, кг; ρТ – плотность твердой фазы материала, кг/м 3; F – площадь основания колонны с зернистым материалом, м 2:

25 Скорость псевдоожижения w 0 можно найти, приравняв уравнение сопротивления псевдоожиженного слоя сопротивлению зернистого слоя. после преобразований можно получить следующие расчетные уравнения: Re 0 –модифицированный критерий Рейнольдса , который соответствует скорости псевдоожижения w 0. при ·ψ·Ar<18500 при ·ψ·Ar=18500 -1, 1· 108. при ·ψ·Ar>1, 1· 108 критерий Архимеда.

26 Определение скорости витания Скорость витания Re vit можно приближенно определить по полуэмпирической зависимости Аэрова – Тодеса , при ε=1 и Обобщением опытных данных при промежуточных значениях порозности ε была получена формула По этой формуле можно вычислить скорость, необходимую для достижения заданной доли свободного объема слоя.

27 Определение порозности слоя при заданной скорости Для расчета ε при данном значении скорости выражение приводится к виду: При расчете необходимо привести параметры среды к рабочим условиям процесса.