
1. Гармонические колебания О x
О x
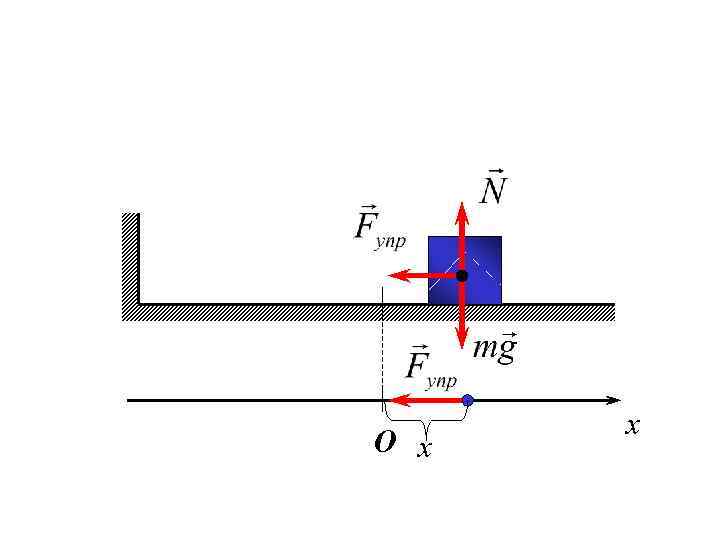
О x x
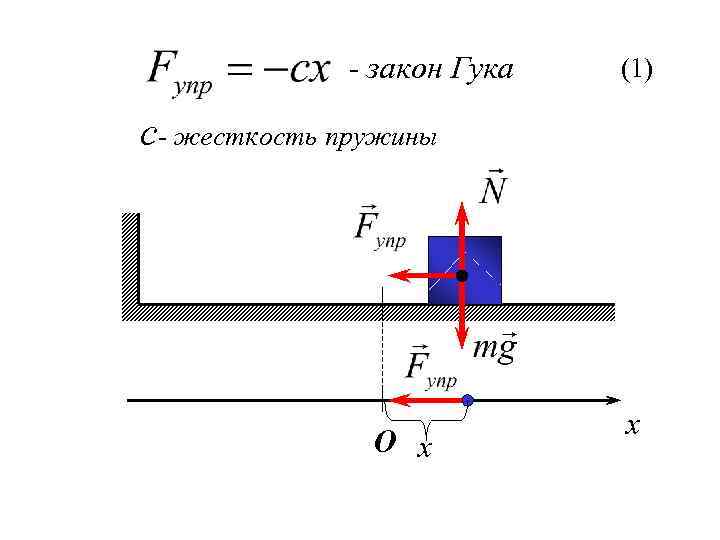
- закон Гука (1) с- жесткость пружины О x x
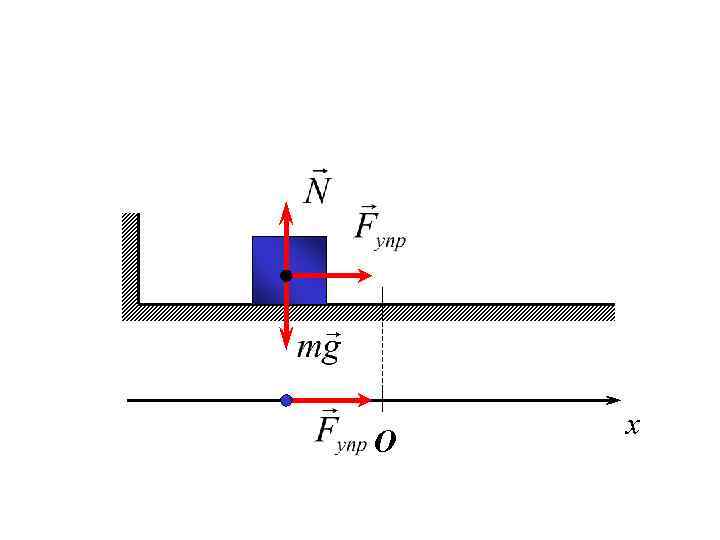
О x

Составим дифференциальное уравнение движения: (2)

Составим дифференциальное уравнение движения: (2) или (3) где

Общее решение уравнения (3) имеет вид: (4) где А – амплитуда колебаний, - начальная фаза

Общее решение уравнения (3) имеет вид: (4) где А – амплитуда колебаний, - начальная фаза Начальные условия движения: (5)

(6)
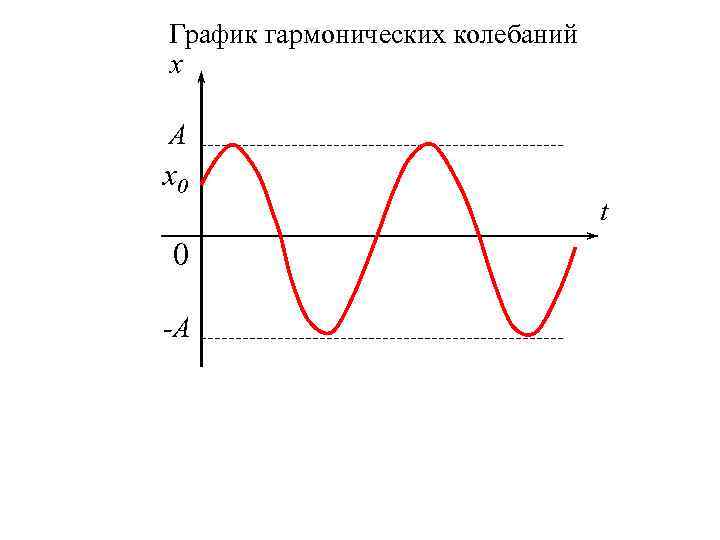
График гармонических колебаний x A x 0 0 -A t
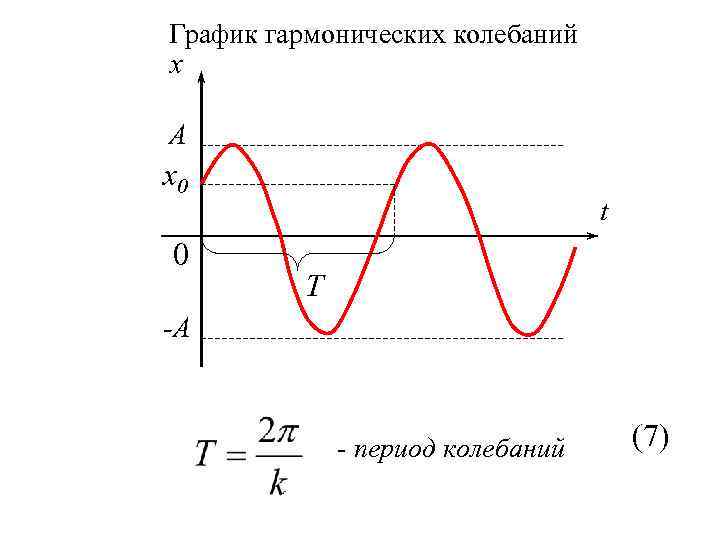
График гармонических колебаний x A x 0 0 t T -A - период колебаний (7)
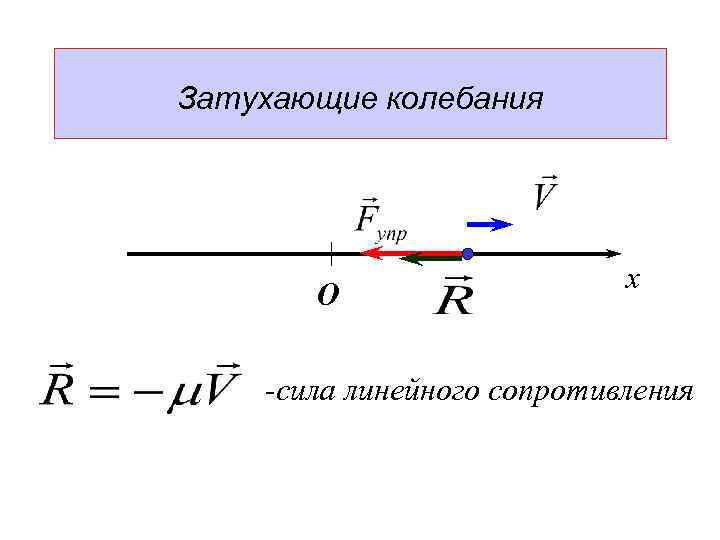
Затухающие колебания О x -сила линейного сопротивления
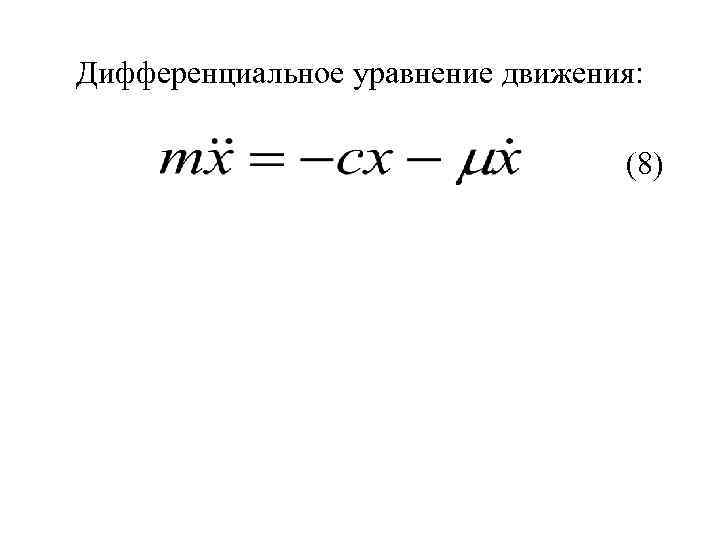
Дифференциальное уравнение движения: (8)

Дифференциальное уравнение движения: (8) (9) где

Характеристическое уравнение: (10) Корни: Случаи:

В случаях 1) и 2) – движение носит апериодический характер. В случае 3)- возникают затухающие колебания с частотой (11)

В случаях 1) и 2) – движение носит апериодический характер. В случае 3)- возникают затухающие колебания с частотой (11) Решение уравнения (10) в этом случае имеет вид: (12)
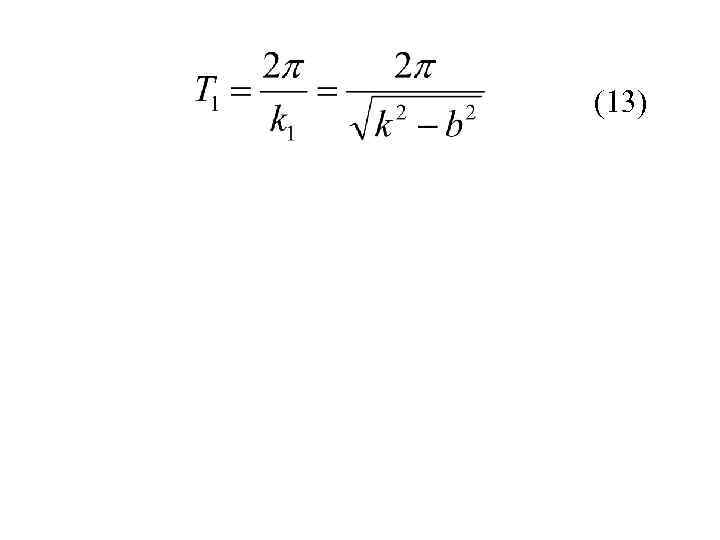
(13)
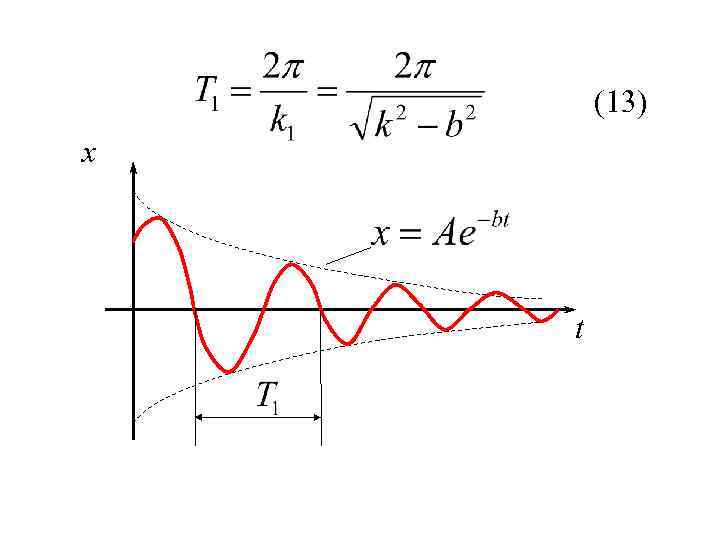
(13) x t

3. Вынужденные колебания точки О x - вынуждающая сила

Дифференциальное уравнение движения: (14)

Дифференциальное уравнение движения: (14) (15) где

Ищем решение уравнения (15) в виде: (16)

Ищем решение уравнения (15) в виде: (16) (17) (18)

Общее решение неоднородного уравнения (15): (19) -амплитуда вынужденных колебаний

Случай:

Случай: (20)

Общее решение уравнения (15) при (21)
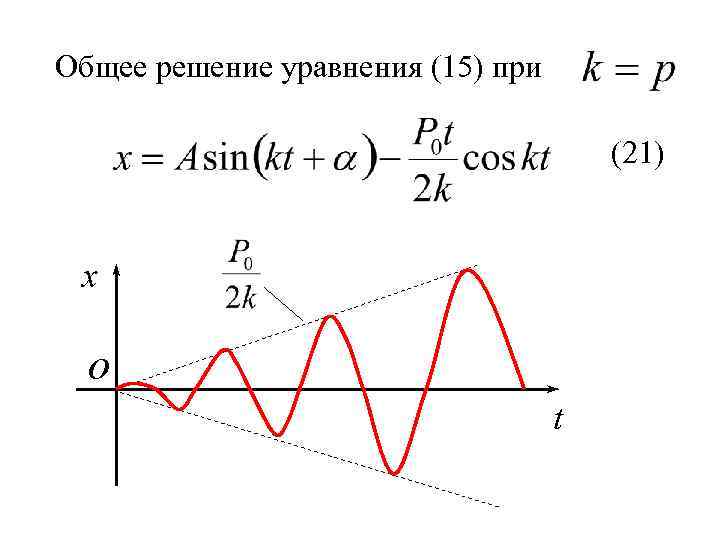
Общее решение уравнения (15) при (21) x o t
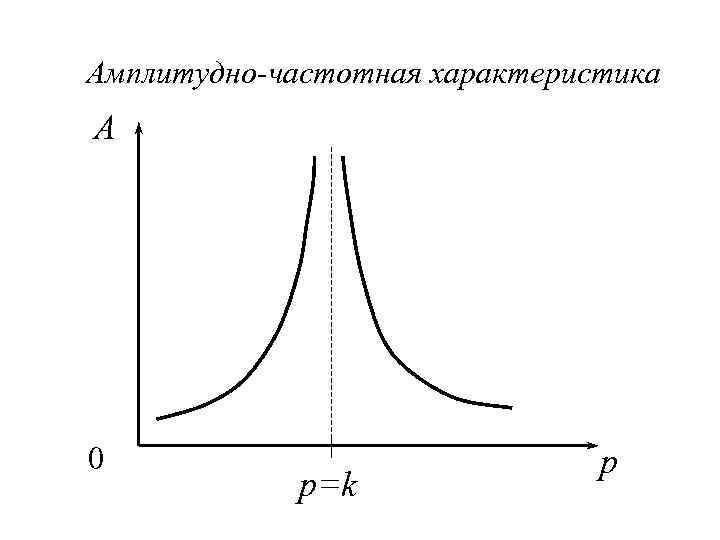
Амплитудно-частотная характеристика A 0 p=k p
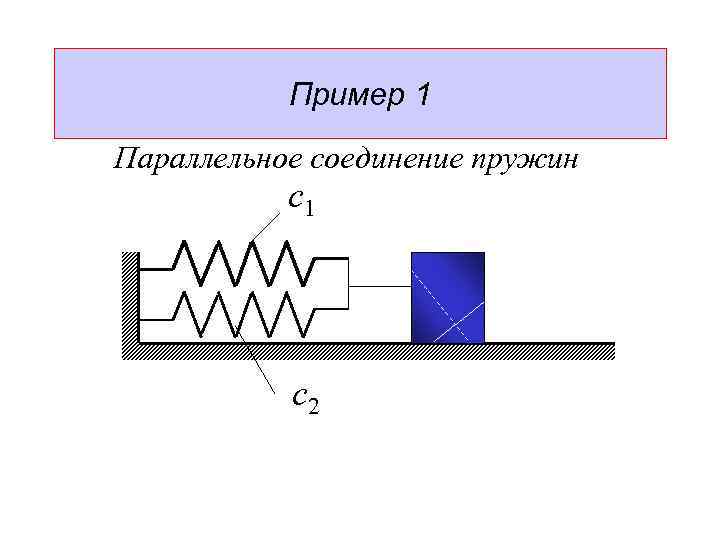
Пример 1 Параллельное соединение пружин с1 с2
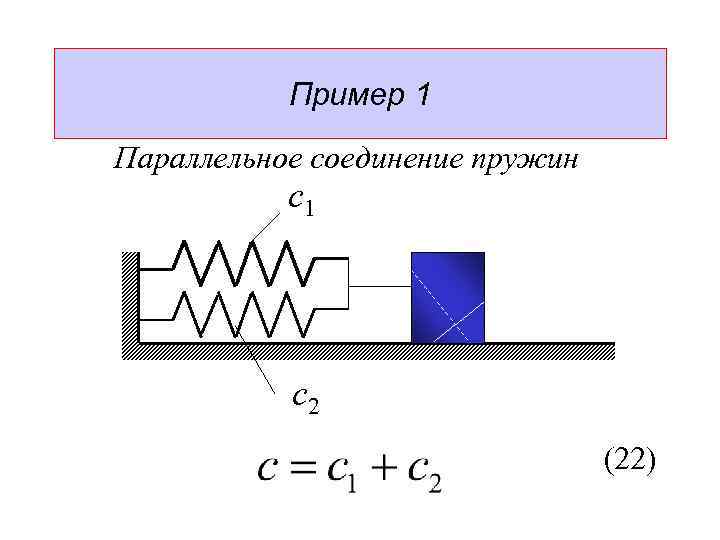
Пример 1 Параллельное соединение пружин с1 с2 (22)
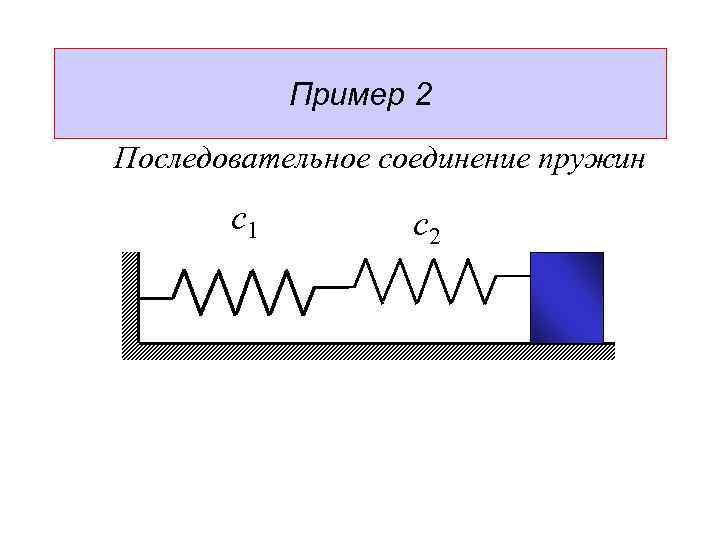
Пример 2 Последовательное соединение пружин с1 с2
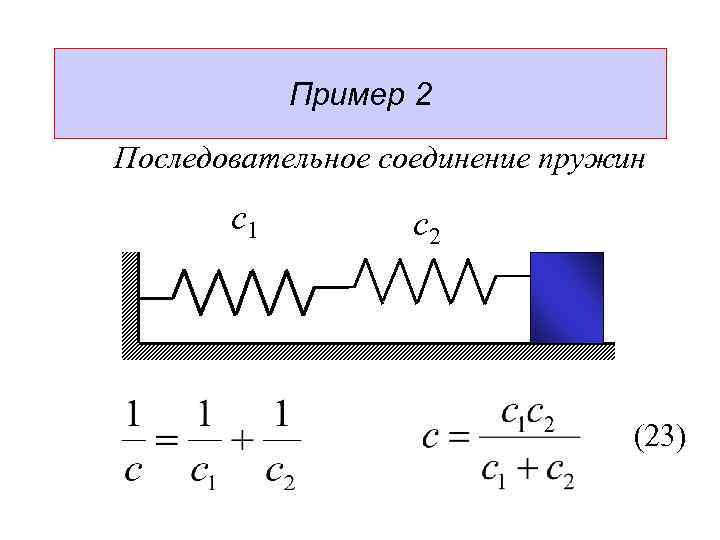
Пример 2 Последовательное соединение пружин с1 с2 (23)