1 Функция y = log x, её

1

Функция y = log x, её свойства и график. a 2

Работа устно: № a b 1 2 4 Е Н c d 3 Е Р П 3

Джон Непер John Napier Дата рождения: 1550 год Место рождения: замок Мерчистон, в те годы предместье Эдинбурга Дата смерти: 4 апреля 1617 Место смерти: Эдинбург Научная сфера: математика Альма-матер: Сент-Эндрюсский университет Известен как: изобретатель логарифмов 4

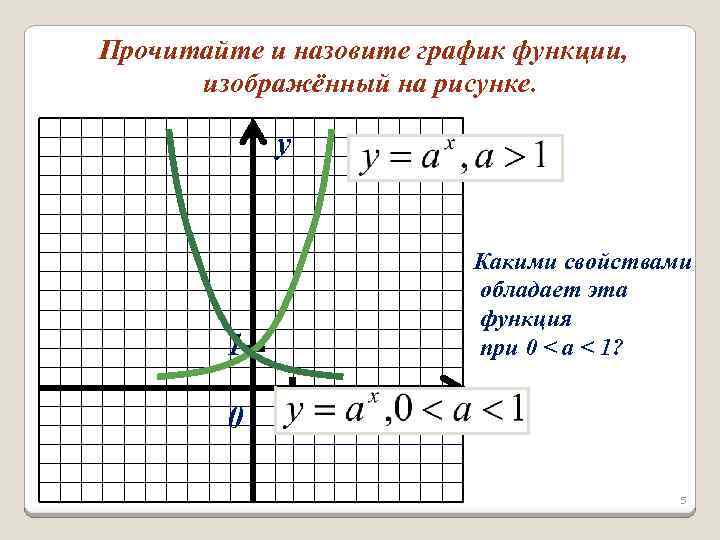Прочитайте и назовите график функции, изображённый на рисунке. y Какими свойствами обладает эта функция при 0 < a < 1? 1 0 1 x 5

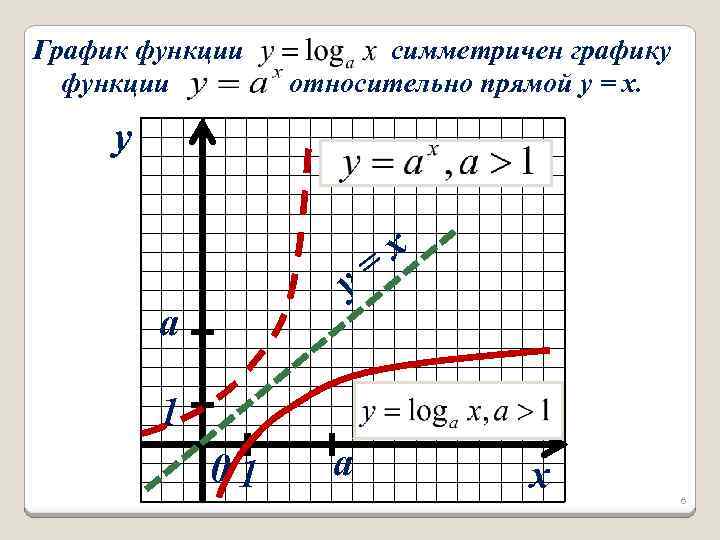График функции симметричен графику относительно прямой y = x. y = y a x 1 01 a x 6

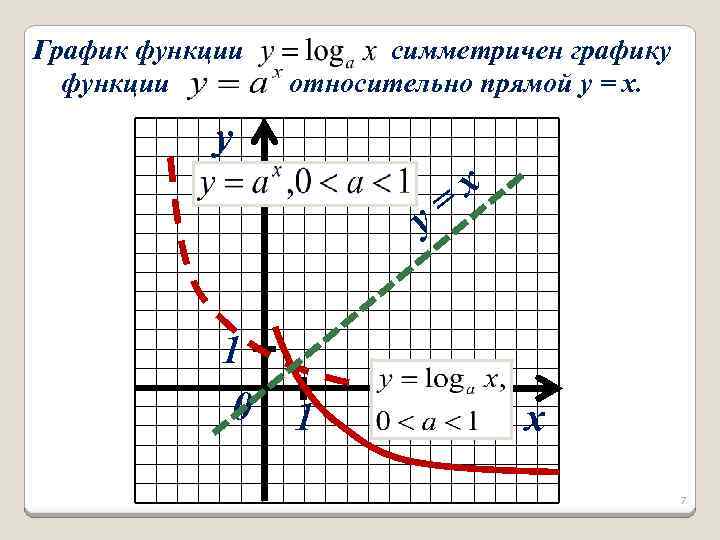График функции симметричен графику относительно прямой y = x. y = y 1 0 1 x x 7

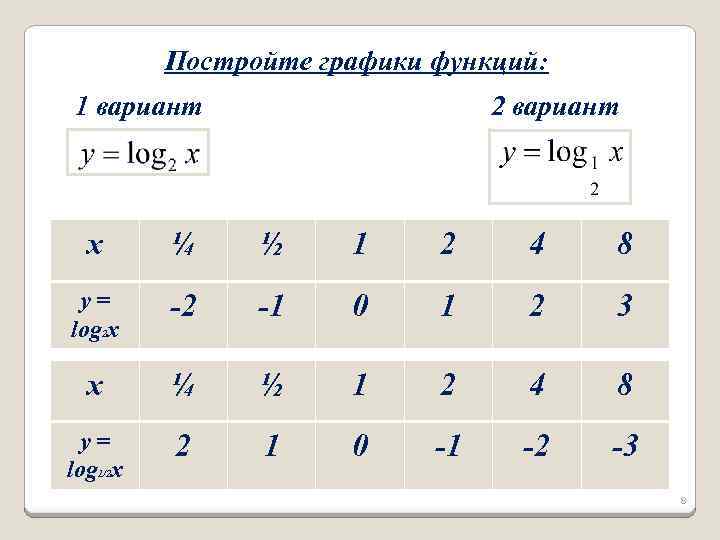Постройте графики функций: 1 вариант 2 вариант x ¼ ½ 1 2 4 8 y= log 2 x -2 -1 0 1 2 3 x ¼ ½ 1 2 4 8 y= log 1/2 x 2 1 0 -1 -2 -3 8

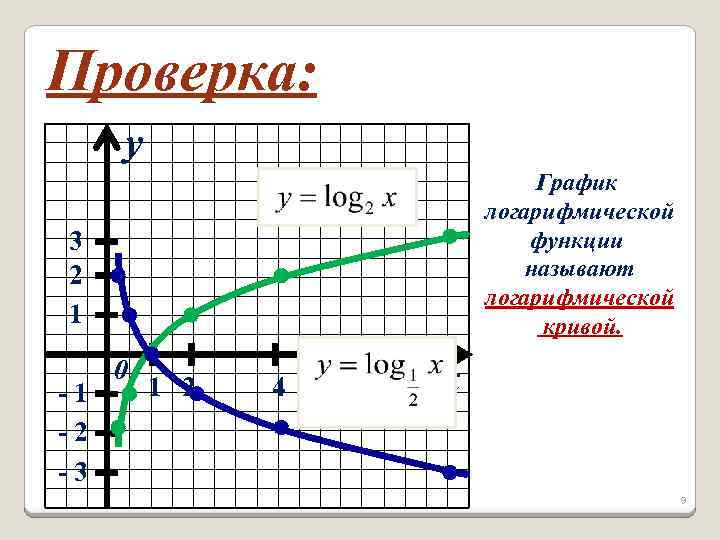Проверка: y График логарифмической функции называют логарифмической кривой. 3 2 1 -1 -2 -3 0 1 2 4 8 x 9

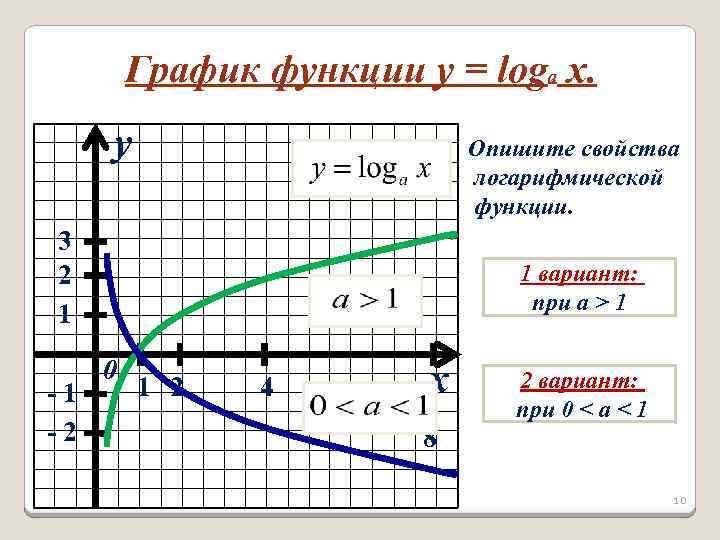График функции y = loga x. y Опишите свойства логарифмической функции. 3 2 1 -1 -2 1 вариант: при a > 1 0 1 2 4 x 8 2 вариант: при 0 < a < 1 10

Свойства функции у = loga x, a > 1. у 1) D(f) = (0, + ∞); 2) не является ни чётной, ни нечётной; 0 х 3) возрастает на (0, + ∞); 4)не ограничена сверху, не ограничена снизу; 5)не имеет ни наибольшего, ни наименьшего значений; 6) непрерывна; 7) E(f) = (- ∞, + ∞); 8) выпукла вверх. 11

Свойства функции у = loga x, 0 < a < 1. у 1) D(f) = (0, + ∞); 2) не является ни чётной, ни нечётной; х 0 3) убывает на (0, + ∞); 4)не ограничена сверху, не ограничена снизу; 5)не имеет ни наибольшего, ни наименьшего значений; 6) непрерывна; 7) E(f) = (- ∞, + ∞); 8) выпукла вниз. 12

Основные свойства логарифмической функции № a>1 0

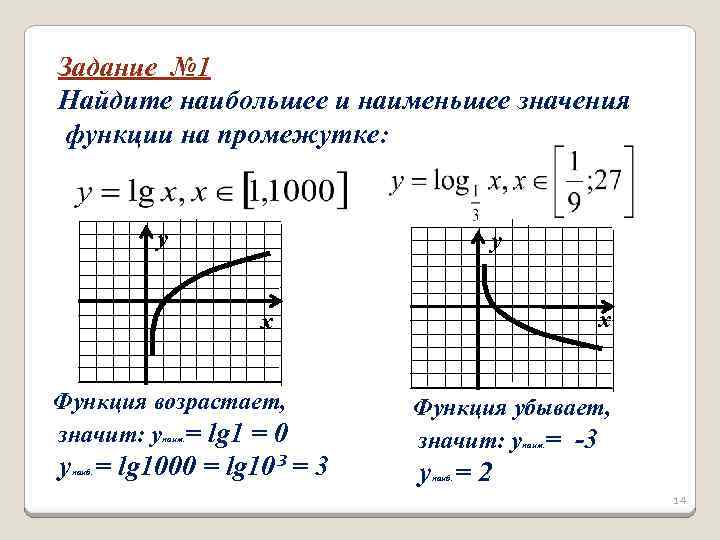Задание № 1 Найдите наибольшее и наименьшее значения функции на промежутке: у у х х Функция возрастает, значит: y = lg 1 = 0 наим. y = lg 1000 = lg 10³ = 3 наиб. Функция убывает, значит: y = -3 наим. y =2 наиб. 14

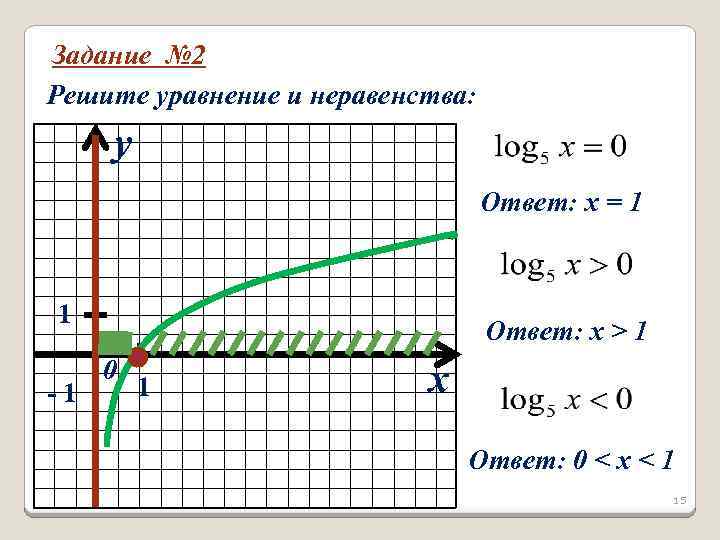Задание № 2 Решите уравнение и неравенства: y Ответ: х = 1 1 -1 Ответ: х > 1 0 1 x Ответ: 0 < х < 1 15

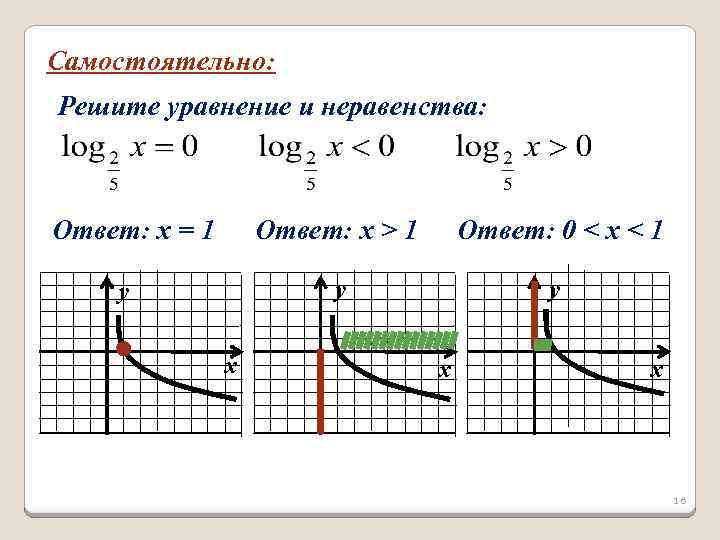Самостоятельно: Решите уравнение и неравенства: Ответ: х = 1 Ответ: х > 1 у у х Ответ: 0 < х < 1 у х х 16

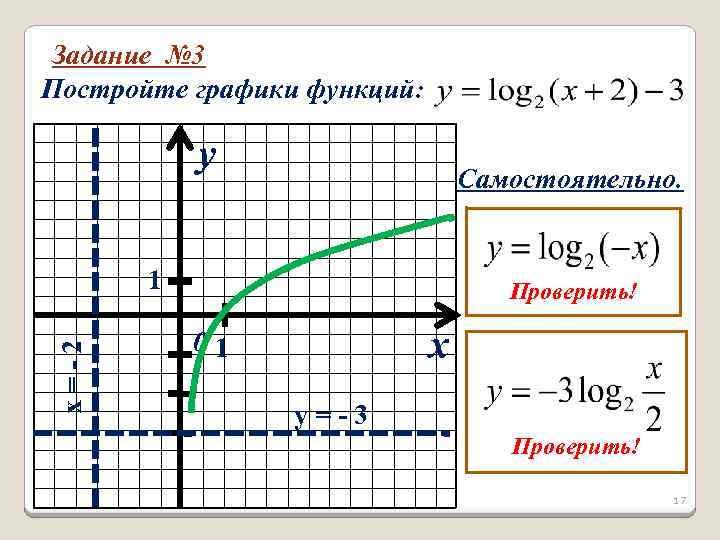Задание № 3 Постройте графики функций: y Самостоятельно. x=-2 1 Проверить! x 01 y=-3 Проверить! 17

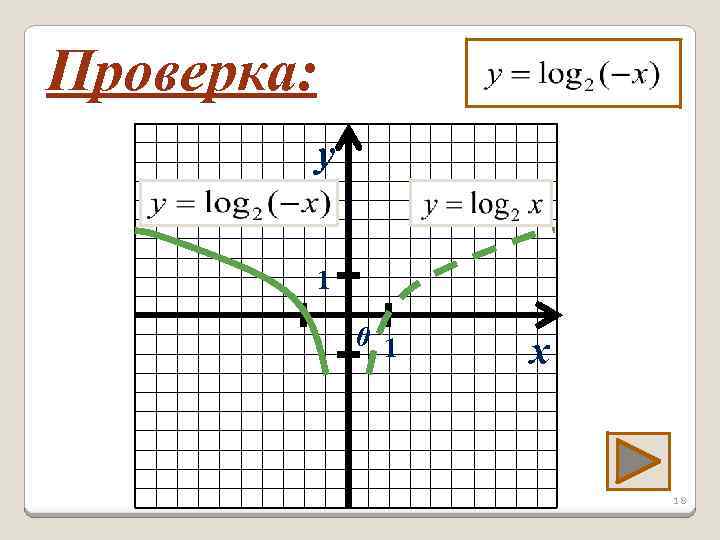Проверка: y 1 0 1 x 18

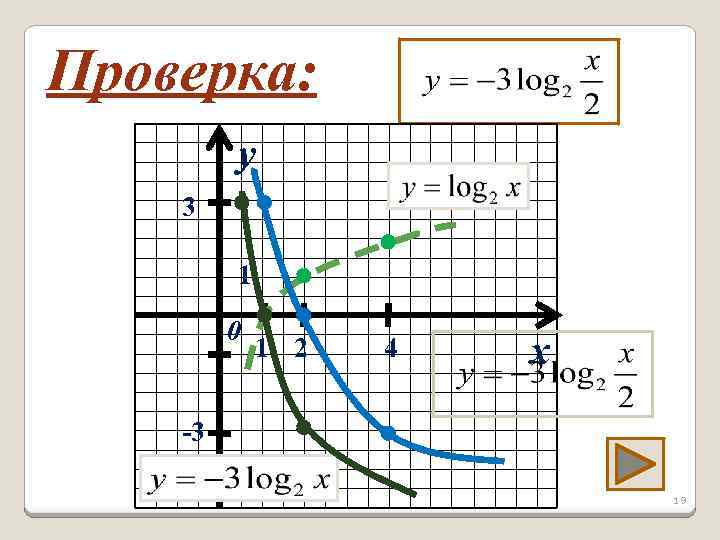Проверка: y 3 1 0 1 2 4 x -3 19

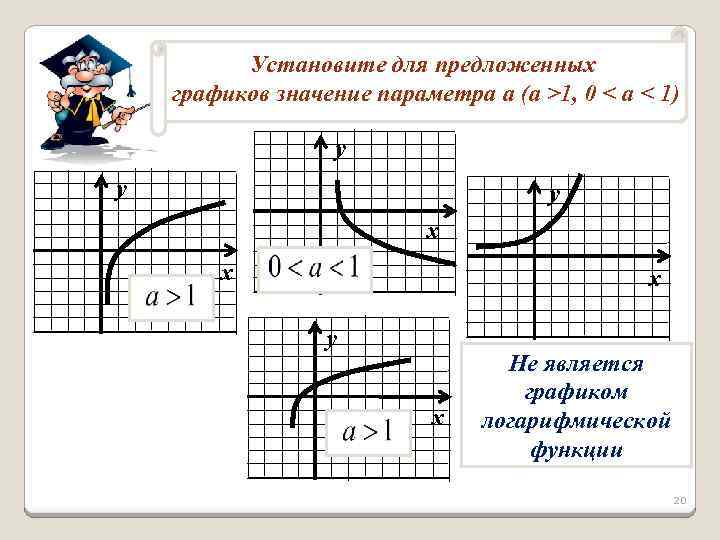Установите для предложенных графиков значение параметра a (a >1, 0 < a < 1) у у у х х х у х Не является графиком логарифмической функции 20