339f958596b3665661cfa8316a8078c5.ppt
- Количество слайдов: 37
 1 Fundamentals of Corporate Finance Second Canadian Edition prepared by: Carol Edwards BA, MBA, CFA Instructor, Finance British Columbia Institute of Technology copyright © 2003 Mc. Graw Hill Ryerson Limited
1 Fundamentals of Corporate Finance Second Canadian Edition prepared by: Carol Edwards BA, MBA, CFA Instructor, Finance British Columbia Institute of Technology copyright © 2003 Mc. Graw Hill Ryerson Limited
 2 Chapter 10 Risk, Return and Capital Budgeting Chapter Outline Measuring Market Risk þ Risk and Return þ Capital Budgeting and Project Risk þ copyright © 2003 Mc. Graw Hill Ryerson Limited
2 Chapter 10 Risk, Return and Capital Budgeting Chapter Outline Measuring Market Risk þ Risk and Return þ Capital Budgeting and Project Risk þ copyright © 2003 Mc. Graw Hill Ryerson Limited
 3 Measuring Market Risk • The Ø Market Portfolio We learned in the last chapter that we should be interested in market risk. ü Market risk is a result of macroeconomic events which affect almost all companies and the returns on almost all stocks. Ø Ø We can easily measure market risk by tracking the performance of a market portfolio of all securities. But, in this chapter, we want to define and measure the relevant risk on an individual stock, not a portfolio of stocks. copyright © 2003 Mc. Graw Hill Ryerson Limited
3 Measuring Market Risk • The Ø Market Portfolio We learned in the last chapter that we should be interested in market risk. ü Market risk is a result of macroeconomic events which affect almost all companies and the returns on almost all stocks. Ø Ø We can easily measure market risk by tracking the performance of a market portfolio of all securities. But, in this chapter, we want to define and measure the relevant risk on an individual stock, not a portfolio of stocks. copyright © 2003 Mc. Graw Hill Ryerson Limited
 4 Measuring Market Risk • The Ø Ø Market Portfolio Since we now know that unique risk is not of concern to investors, what we want to measure is the market risk of an individual stock. We will measure a stock’s market risk by comparing the sensitivity of the stock’s returns to fluctuations in the market portfolio. ü We will call this measure of sensitivity beta ( ). copyright © 2003 Mc. Graw Hill Ryerson Limited
4 Measuring Market Risk • The Ø Ø Market Portfolio Since we now know that unique risk is not of concern to investors, what we want to measure is the market risk of an individual stock. We will measure a stock’s market risk by comparing the sensitivity of the stock’s returns to fluctuations in the market portfolio. ü We will call this measure of sensitivity beta ( ). copyright © 2003 Mc. Graw Hill Ryerson Limited
 5 Measuring Market Risk • The Ø Market Portfolio In theory, the market portfolio should contain all the assets in the world economy. ü Not just stocks, but bonds, foreign securities, real estate, etc. Ø In reality, financial analysts use indexes of the stock market, such as the TSE 300 as proxies for the market portfolio. copyright © 2003 Mc. Graw Hill Ryerson Limited
5 Measuring Market Risk • The Ø Market Portfolio In theory, the market portfolio should contain all the assets in the world economy. ü Not just stocks, but bonds, foreign securities, real estate, etc. Ø In reality, financial analysts use indexes of the stock market, such as the TSE 300 as proxies for the market portfolio. copyright © 2003 Mc. Graw Hill Ryerson Limited
 6 Measuring Market Risk • Measuring Beta Ø We measure beta by: 1. Collecting data on the returns on the market 2. 3. 4. 5. portfolio over a specified time period. Collecting data on the returns on a stock over the same time period. Graphing the returns on the stock against the returns on the market. Drawing a regression line through the points and measuring its slope. The slope of the regression line is the stock’s beta. copyright © 2003 Mc. Graw Hill Ryerson Limited
6 Measuring Market Risk • Measuring Beta Ø We measure beta by: 1. Collecting data on the returns on the market 2. 3. 4. 5. portfolio over a specified time period. Collecting data on the returns on a stock over the same time period. Graphing the returns on the stock against the returns on the market. Drawing a regression line through the points and measuring its slope. The slope of the regression line is the stock’s beta. copyright © 2003 Mc. Graw Hill Ryerson Limited
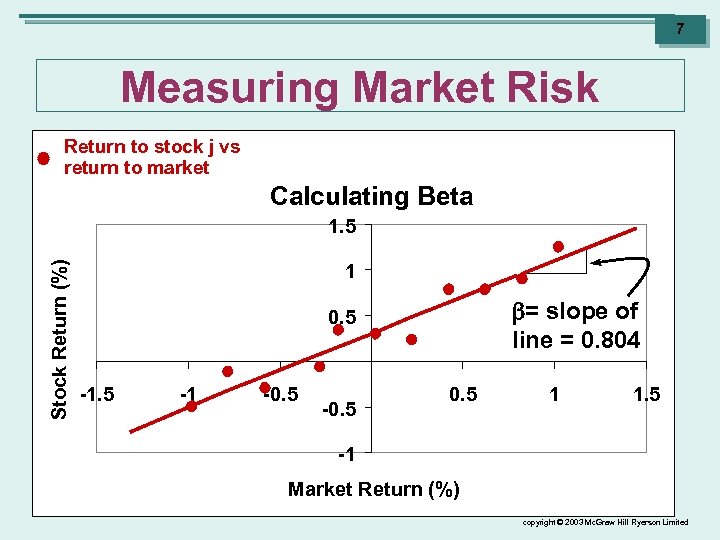 7 Measuring Market Risk Return to stock j vs return to market Calculating Beta Stock Return (%) 1. 5 1 = slope of line = 0. 804 0. 5 -1 -0. 5 1 1. 5 -1 Market Return (%) copyright © 2003 Mc. Graw Hill Ryerson Limited
7 Measuring Market Risk Return to stock j vs return to market Calculating Beta Stock Return (%) 1. 5 1 = slope of line = 0. 804 0. 5 -1 -0. 5 1 1. 5 -1 Market Return (%) copyright © 2003 Mc. Graw Hill Ryerson Limited
 8 Measuring Market Risk • Measuring Ø Beta We can also measure beta if we know: ü The correlation of the stock’s return with the market’s return ( jm) ü The standard deviation of the stock and the market ( j , m). Beta of Stockj = jm j m copyright © 2003 Mc. Graw Hill Ryerson Limited
8 Measuring Market Risk • Measuring Ø Beta We can also measure beta if we know: ü The correlation of the stock’s return with the market’s return ( jm) ü The standard deviation of the stock and the market ( j , m). Beta of Stockj = jm j m copyright © 2003 Mc. Graw Hill Ryerson Limited
 9 Measuring Market Risk • Measuring Ø Beta Lastly, we can measure beta if we know: ü The covariance of the stock’s return with the market’s return (covjm) ü The standard deviation of the market ( m). jm = cov(rjrm ) / j m Beta of Stockj = cov(rjrm) 2 m copyright © 2003 Mc. Graw Hill Ryerson Limited
9 Measuring Market Risk • Measuring Ø Beta Lastly, we can measure beta if we know: ü The covariance of the stock’s return with the market’s return (covjm) ü The standard deviation of the market ( m). jm = cov(rjrm ) / j m Beta of Stockj = cov(rjrm) 2 m copyright © 2003 Mc. Graw Hill Ryerson Limited
 10 Measuring Market Risk • Measuring Ø Beta For example, you know: ü The correlation of the stock’s return with the market’s return ( jm) = 0. 70 ü The covariance of the stock’s return with the market’s return (covjm) = 420 ü The standard deviation of the market ( m) = 20%. standard deviation of the stock ( j) = 30%. What is the beta of the stock? copyright © 2003 Mc. Graw Hill Ryerson Limited
10 Measuring Market Risk • Measuring Ø Beta For example, you know: ü The correlation of the stock’s return with the market’s return ( jm) = 0. 70 ü The covariance of the stock’s return with the market’s return (covjm) = 420 ü The standard deviation of the market ( m) = 20%. standard deviation of the stock ( j) = 30%. What is the beta of the stock? copyright © 2003 Mc. Graw Hill Ryerson Limited
 11 Measuring Market Risk • Measuring Beta of Stockj = jm j m 0. 7(30) = cov(rjrm) 2 m = 20 420 = 20 2 = 1. 05 copyright © 2003 Mc. Graw Hill Ryerson Limited
11 Measuring Market Risk • Measuring Beta of Stockj = jm j m 0. 7(30) = cov(rjrm) 2 m = 20 420 = 20 2 = 1. 05 copyright © 2003 Mc. Graw Hill Ryerson Limited
 12 Measuring Market Risk • Sample Ø Ø Betas If you look at Table 10. 1 on page 308 of your text, you will see the betas for some selected Canadian common stocks. Suppose you had invested 50% of your money in Inco and 50% of your money in Westcoast Energy. What would be the beta of the portfolio? copyright © 2003 Mc. Graw Hill Ryerson Limited
12 Measuring Market Risk • Sample Ø Ø Betas If you look at Table 10. 1 on page 308 of your text, you will see the betas for some selected Canadian common stocks. Suppose you had invested 50% of your money in Inco and 50% of your money in Westcoast Energy. What would be the beta of the portfolio? copyright © 2003 Mc. Graw Hill Ryerson Limited
 13 Measuring Market Risk • Beta Ø of a Portfolio The portfolio beta will be the weighted average of the betas of the individual assets. ü The weight will be equal to the proportion of the portfolio invested in each asset. v Thus the weights will be 50% on Inco and 50% on Westcoast. ü The beta of Inco is 1. 33 (from Table 10. 1). ü The beta of Westcoast Energy is 0. 48 (from Table 10. 1). copyright © 2003 Mc. Graw Hill Ryerson Limited
13 Measuring Market Risk • Beta Ø of a Portfolio The portfolio beta will be the weighted average of the betas of the individual assets. ü The weight will be equal to the proportion of the portfolio invested in each asset. v Thus the weights will be 50% on Inco and 50% on Westcoast. ü The beta of Inco is 1. 33 (from Table 10. 1). ü The beta of Westcoast Energy is 0. 48 (from Table 10. 1). copyright © 2003 Mc. Graw Hill Ryerson Limited
 14 Measuring Market Risk • Beta of a Portfolio of Two Assets: Portfolio Beta ( ( = fraction of portfolio x beta of in 1 st asset + fraction of portfolio x beta of in 2 nd asset ) ) = (0. 5 x 1. 33) + (0. 5 X 0. 48) = 0. 905 copyright © 2003 Mc. Graw Hill Ryerson Limited
14 Measuring Market Risk • Beta of a Portfolio of Two Assets: Portfolio Beta ( ( = fraction of portfolio x beta of in 1 st asset + fraction of portfolio x beta of in 2 nd asset ) ) = (0. 5 x 1. 33) + (0. 5 X 0. 48) = 0. 905 copyright © 2003 Mc. Graw Hill Ryerson Limited
 15 Risk and Return • Benchmark Ø The return on a t-bill is fixed and unaffected by what happens in the market. ü Thus, Ø Betas its beta is zero. A portfolio with average market risk is by definition set at a beta of one. ü Its expected return equals the return on a t-bill plus the normal market risk premium of 7%. Ø Given these two benchmarks, is it possible to calculate the return on an asset, or portfolio, with a beta other than zero or one? copyright © 2003 Mc. Graw Hill Ryerson Limited
15 Risk and Return • Benchmark Ø The return on a t-bill is fixed and unaffected by what happens in the market. ü Thus, Ø Betas its beta is zero. A portfolio with average market risk is by definition set at a beta of one. ü Its expected return equals the return on a t-bill plus the normal market risk premium of 7%. Ø Given these two benchmarks, is it possible to calculate the return on an asset, or portfolio, with a beta other than zero or one? copyright © 2003 Mc. Graw Hill Ryerson Limited
 16 Risk and Return • Measuring Ø Return Given Beta For example, what is the expected return on a stock with a beta of 0. 5 if: üA t-bill returns 4% ü The the market returns 11%. v As a result: Market risk premium = rm - rf = 11% - 4% = 7% copyright © 2003 Mc. Graw Hill Ryerson Limited
16 Risk and Return • Measuring Ø Return Given Beta For example, what is the expected return on a stock with a beta of 0. 5 if: üA t-bill returns 4% ü The the market returns 11%. v As a result: Market risk premium = rm - rf = 11% - 4% = 7% copyright © 2003 Mc. Graw Hill Ryerson Limited
 17 Risk and Return • Capital Ø Asset Pricing Model (CAPM) The CAPM says the relationship between an asset’s beta and its expected return is: Expected Return = risk-free rate + risk premium rj = rf + (rm - rf) Thus, for our example: Expected Return = rj = rf + (rm - rf) = 4% + 0. 5 (11% - 4%) = 7. 5% copyright © 2003 Mc. Graw Hill Ryerson Limited
17 Risk and Return • Capital Ø Asset Pricing Model (CAPM) The CAPM says the relationship between an asset’s beta and its expected return is: Expected Return = risk-free rate + risk premium rj = rf + (rm - rf) Thus, for our example: Expected Return = rj = rf + (rm - rf) = 4% + 0. 5 (11% - 4%) = 7. 5% copyright © 2003 Mc. Graw Hill Ryerson Limited
 18 Risk and Return • Capital Ø Ø Ø Asset Pricing Model (CAPM) The CAPM says that given the risk-free rate is 4% and the market risk premium is 7%, an asset with a beta of 0. 5 will have an expected return of 7. 5% This relationship is graphed on the next slide. Note that on this graph: ü The v Expected return = 4% + 0. 0 x(11% - 7%) = 4% ü The v beta of a t-bill is zero. beta is 1. 0 for a market risk portfolio. Expected return = 4% + 1. 0 x(11% - 7%) = 11% copyright © 2003 Mc. Graw Hill Ryerson Limited
18 Risk and Return • Capital Ø Ø Ø Asset Pricing Model (CAPM) The CAPM says that given the risk-free rate is 4% and the market risk premium is 7%, an asset with a beta of 0. 5 will have an expected return of 7. 5% This relationship is graphed on the next slide. Note that on this graph: ü The v Expected return = 4% + 0. 0 x(11% - 7%) = 4% ü The v beta of a t-bill is zero. beta is 1. 0 for a market risk portfolio. Expected return = 4% + 1. 0 x(11% - 7%) = 11% copyright © 2003 Mc. Graw Hill Ryerson Limited
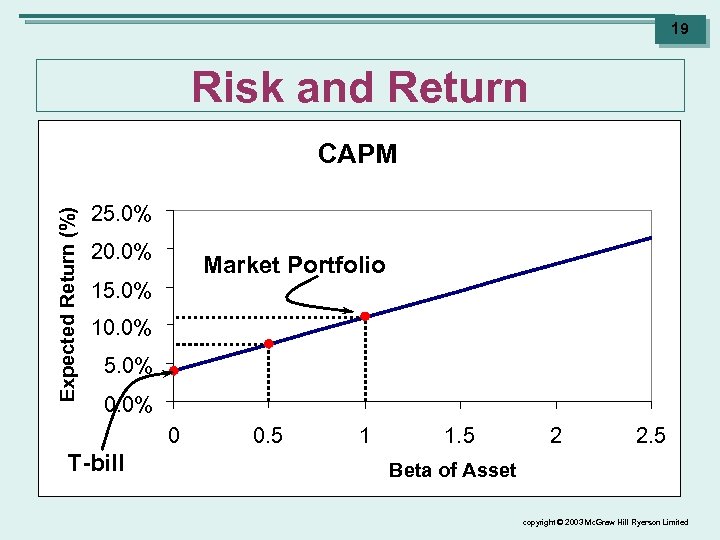 19 Risk and Return Expected Return (%) CAPM 25. 0% 20. 0% Market Portfolio 15. 0% 10. 0% 5. 0% 0 T-bill 0. 5 1 1. 5 2 2. 5 Beta of Asset copyright © 2003 Mc. Graw Hill Ryerson Limited
19 Risk and Return Expected Return (%) CAPM 25. 0% 20. 0% Market Portfolio 15. 0% 10. 0% 5. 0% 0 T-bill 0. 5 1 1. 5 2 2. 5 Beta of Asset copyright © 2003 Mc. Graw Hill Ryerson Limited
 20 Risk and Return • Security Ø Ø Market Line (SML) On the graph, the blue line which shows the relationship between the risk of the security (its beta) and the return on the security is called the Security Market Line (SML). The SML sets the standard for other investments. ü Investors will hold other investments only if they offer equally good prospects. copyright © 2003 Mc. Graw Hill Ryerson Limited
20 Risk and Return • Security Ø Ø Market Line (SML) On the graph, the blue line which shows the relationship between the risk of the security (its beta) and the return on the security is called the Security Market Line (SML). The SML sets the standard for other investments. ü Investors will hold other investments only if they offer equally good prospects. copyright © 2003 Mc. Graw Hill Ryerson Limited
 21 Risk and Return • Security Ø For example, you are looking at investing in security with a beta of 2. 3 and an expected return of 16%. ü Is Ø Market Line (SML) this pricing information sustainable? Clue: ü Look at the graph on the next slide. copyright © 2003 Mc. Graw Hill Ryerson Limited
21 Risk and Return • Security Ø For example, you are looking at investing in security with a beta of 2. 3 and an expected return of 16%. ü Is Ø Market Line (SML) this pricing information sustainable? Clue: ü Look at the graph on the next slide. copyright © 2003 Mc. Graw Hill Ryerson Limited
 22 Risk and Return Expected Return (%) CAPM 25. 0% 20. 0% 15. 0% 10. 0% 5. 0% Proposed Holding 0. 0% 0 0. 5 1 1. 5 2 2. 3 Beta of Asset copyright © 2003 Mc. Graw Hill Ryerson Limited
22 Risk and Return Expected Return (%) CAPM 25. 0% 20. 0% 15. 0% 10. 0% 5. 0% Proposed Holding 0. 0% 0 0. 5 1 1. 5 2 2. 3 Beta of Asset copyright © 2003 Mc. Graw Hill Ryerson Limited
 23 Risk and Return • Security Ø Market Line (SML) If you look at the graph, you will see that an asset with a beta of 2. 3 should yield about 20%. ü This security is yielding only 16%. ü No one would buy it because the expected return is insufficient for the risk. ü The result: The security’s price would drop, causing the expected return to rise. v The price would fall until the security’s expected return was pushed up to 20%. v At that price and expected return the CAPM holds. v copyright © 2003 Mc. Graw Hill Ryerson Limited
23 Risk and Return • Security Ø Market Line (SML) If you look at the graph, you will see that an asset with a beta of 2. 3 should yield about 20%. ü This security is yielding only 16%. ü No one would buy it because the expected return is insufficient for the risk. ü The result: The security’s price would drop, causing the expected return to rise. v The price would fall until the security’s expected return was pushed up to 20%. v At that price and expected return the CAPM holds. v copyright © 2003 Mc. Graw Hill Ryerson Limited
 24 Risk and Return • Security Market Line (SML) The reasoning we have just gone through holds for any asset with any level of risk. Ø The expected return on an asset should reflect its relevant risk, which is measured by its beta. Ø ü If the expected return does not reflect the security’s risk properly, then the price of the asset should adjust up, or down. ü The price will adjust until the asset generates the return required by the market given the security’s risk level. copyright © 2003 Mc. Graw Hill Ryerson Limited
24 Risk and Return • Security Market Line (SML) The reasoning we have just gone through holds for any asset with any level of risk. Ø The expected return on an asset should reflect its relevant risk, which is measured by its beta. Ø ü If the expected return does not reflect the security’s risk properly, then the price of the asset should adjust up, or down. ü The price will adjust until the asset generates the return required by the market given the security’s risk level. copyright © 2003 Mc. Graw Hill Ryerson Limited
 25 Risk and Return • How Well Does the CAPM Work? Studies have found the CAPM is too simple to capture exactly how stock markets work. Ø However the CAPM does capture two fundamental financial principals in a simple way: Ø ü Investors require extra return for taking on risk. ü Investors appear to be concerned primarily with the market risk they cannot eliminate by diversification. Ø Thus the CAPM is a good rule of thumb for pricing assets. copyright © 2003 Mc. Graw Hill Ryerson Limited
25 Risk and Return • How Well Does the CAPM Work? Studies have found the CAPM is too simple to capture exactly how stock markets work. Ø However the CAPM does capture two fundamental financial principals in a simple way: Ø ü Investors require extra return for taking on risk. ü Investors appear to be concerned primarily with the market risk they cannot eliminate by diversification. Ø Thus the CAPM is a good rule of thumb for pricing assets. copyright © 2003 Mc. Graw Hill Ryerson Limited
 26 Risk and Return • Using the CAPM to Estimate Project Returns Ø You can use the CAPM to estimate the discount rate for new capital projects. Ø For example, Biomira has a beta of 1. 25. ü Thus: Expected Return = 4% + 1. 25 x(11% - 4%) = 12. 75% Ø If Biomira were proposing an expansion project, you would discount its estimated cash flows at 12. 75%. copyright © 2003 Mc. Graw Hill Ryerson Limited
26 Risk and Return • Using the CAPM to Estimate Project Returns Ø You can use the CAPM to estimate the discount rate for new capital projects. Ø For example, Biomira has a beta of 1. 25. ü Thus: Expected Return = 4% + 1. 25 x(11% - 4%) = 12. 75% Ø If Biomira were proposing an expansion project, you would discount its estimated cash flows at 12. 75%. copyright © 2003 Mc. Graw Hill Ryerson Limited
 27 Capital Budgeting and Project Risk • Company Ø Ø vs Project Risk On the previous slide we estimated the company cost of capital for Biomira. The company cost of capital is the expected rate of return demanded by investors in that company. ü It is determined by the average risk of the company’s assets and operations. Ø The company cost of capital may be used to discount the cash flows of a project under certain conditions. copyright © 2003 Mc. Graw Hill Ryerson Limited
27 Capital Budgeting and Project Risk • Company Ø Ø vs Project Risk On the previous slide we estimated the company cost of capital for Biomira. The company cost of capital is the expected rate of return demanded by investors in that company. ü It is determined by the average risk of the company’s assets and operations. Ø The company cost of capital may be used to discount the cash flows of a project under certain conditions. copyright © 2003 Mc. Graw Hill Ryerson Limited
 28 Capital Budgeting and Project Risk • Company Ø vs Project Risk Biomira is considering 3 projects: Project 1 is an expansion project with the same overall risk as the company itself. ü Project 2 involves the introduction of a new product line and its risk exceeds that of the company itself. ü Project 3 has no risk and involves the sale of a guaranteed amount of product to the government at a guaranteed price. ü Ø For which of these projects should you use the company cost of capital in analyzing the forecasted cash flows? copyright © 2003 Mc. Graw Hill Ryerson Limited
28 Capital Budgeting and Project Risk • Company Ø vs Project Risk Biomira is considering 3 projects: Project 1 is an expansion project with the same overall risk as the company itself. ü Project 2 involves the introduction of a new product line and its risk exceeds that of the company itself. ü Project 3 has no risk and involves the sale of a guaranteed amount of product to the government at a guaranteed price. ü Ø For which of these projects should you use the company cost of capital in analyzing the forecasted cash flows? copyright © 2003 Mc. Graw Hill Ryerson Limited
 29 Capital Budgeting and Project Risk • Company Ø vs Project Risk Remember that the discount rate should reflect the risk of the project’s cash flows. ü Only Project 1 has the same risk as Biomira. ü Thus, only Project 1’s cash flows should be discounted at 12. 75%, the company’s cost of capital. Ø You must use a different cost of capital for the other two projects. copyright © 2003 Mc. Graw Hill Ryerson Limited
29 Capital Budgeting and Project Risk • Company Ø vs Project Risk Remember that the discount rate should reflect the risk of the project’s cash flows. ü Only Project 1 has the same risk as Biomira. ü Thus, only Project 1’s cash flows should be discounted at 12. 75%, the company’s cost of capital. Ø You must use a different cost of capital for the other two projects. copyright © 2003 Mc. Graw Hill Ryerson Limited
 30 Capital Budgeting and Project Risk • Company Ø vs Project Risk Project 3 has no risk. ü You should recognize that its cash flows would be discounted at the current t-bill rate. Ø Project 2 is more risky than the company itself, so we know its discount rate should be greater than 12. 75%. copyright © 2003 Mc. Graw Hill Ryerson Limited
30 Capital Budgeting and Project Risk • Company Ø vs Project Risk Project 3 has no risk. ü You should recognize that its cash flows would be discounted at the current t-bill rate. Ø Project 2 is more risky than the company itself, so we know its discount rate should be greater than 12. 75%. copyright © 2003 Mc. Graw Hill Ryerson Limited
 31 Capital Budgeting and Project Risk • Company Ø vs Project Risk This leads to another fundamental principal of finance: üA project’s required rate of return depends on the project’s risk. ü Discount a project at the project cost of capital. v This is the minimum acceptable rate of return on a project given its risk level. copyright © 2003 Mc. Graw Hill Ryerson Limited
31 Capital Budgeting and Project Risk • Company Ø vs Project Risk This leads to another fundamental principal of finance: üA project’s required rate of return depends on the project’s risk. ü Discount a project at the project cost of capital. v This is the minimum acceptable rate of return on a project given its risk level. copyright © 2003 Mc. Graw Hill Ryerson Limited
 32 Capital Budgeting and Project Risk • Determinants Ø of Project Risk You now know that a company’s cost of capital is the correct discount rate for projects that have the same risk as the company’s existing business. ü It is not appropriate for projects which are safer or riskier than the company’s average. Ø How can you estimate a project’s risk level? copyright © 2003 Mc. Graw Hill Ryerson Limited
32 Capital Budgeting and Project Risk • Determinants Ø of Project Risk You now know that a company’s cost of capital is the correct discount rate for projects that have the same risk as the company’s existing business. ü It is not appropriate for projects which are safer or riskier than the company’s average. Ø How can you estimate a project’s risk level? copyright © 2003 Mc. Graw Hill Ryerson Limited
 33 Capital Budgeting and Project Risk • Determinants Ø of Project Risk Here a few things to bear in mind: ü Operating leverage increases the risk of a project. v High fixed cost projects tend to have high betas. ü Only market risk is important. v Ignore unique risk, that is, those risks which are specific only to that particular project. v Look for those risks in the project which reflect macroeconomic factors. v That is, cyclical companies tend to have high betas. copyright © 2003 Mc. Graw Hill Ryerson Limited
33 Capital Budgeting and Project Risk • Determinants Ø of Project Risk Here a few things to bear in mind: ü Operating leverage increases the risk of a project. v High fixed cost projects tend to have high betas. ü Only market risk is important. v Ignore unique risk, that is, those risks which are specific only to that particular project. v Look for those risks in the project which reflect macroeconomic factors. v That is, cyclical companies tend to have high betas. copyright © 2003 Mc. Graw Hill Ryerson Limited
 34 Capital Budgeting and Project Risk • Determinants ü See of Project Risk if you can find a proxy for the project. Sometimes you can find a company which is exclusively involved in the type of project your firm is proposing. v You can use its beta as a proxy for the project’s beta. v This approach is known as a pure play approach. v copyright © 2003 Mc. Graw Hill Ryerson Limited
34 Capital Budgeting and Project Risk • Determinants ü See of Project Risk if you can find a proxy for the project. Sometimes you can find a company which is exclusively involved in the type of project your firm is proposing. v You can use its beta as a proxy for the project’s beta. v This approach is known as a pure play approach. v copyright © 2003 Mc. Graw Hill Ryerson Limited
 35 Summary of Chapter 10 Ø Only market risk is relevant in measuring the risk of an asset or project. ü Unique Ø risk should be ignored. We measure market risk by calculating the beta of the asset. ü By definition, 1. 0 is the average beta of a market portfolio of common stocks. Individual assets with a beta of more than 1. 0 are particularly sensitive to market fluctuations. v Assets with a beta of less than 1. 0 are not so sensitive to such movements. v copyright © 2003 Mc. Graw Hill Ryerson Limited
35 Summary of Chapter 10 Ø Only market risk is relevant in measuring the risk of an asset or project. ü Unique Ø risk should be ignored. We measure market risk by calculating the beta of the asset. ü By definition, 1. 0 is the average beta of a market portfolio of common stocks. Individual assets with a beta of more than 1. 0 are particularly sensitive to market fluctuations. v Assets with a beta of less than 1. 0 are not so sensitive to such movements. v copyright © 2003 Mc. Graw Hill Ryerson Limited
 36 Summary of Chapter 10 Ø The CAPM shows the relationship between the expected return on a security and its risk level, or beta: Expected Return = risk-free rate + risk premium rj = rf + (rm - rf) Ø The Security Market Line (SML) is a graphical representation of the CAPM. copyright © 2003 Mc. Graw Hill Ryerson Limited
36 Summary of Chapter 10 Ø The CAPM shows the relationship between the expected return on a security and its risk level, or beta: Expected Return = risk-free rate + risk premium rj = rf + (rm - rf) Ø The Security Market Line (SML) is a graphical representation of the CAPM. copyright © 2003 Mc. Graw Hill Ryerson Limited
 37 Summary of Chapter 10 Ø You can calculate the opportunity cost of capital for a project. ü If the project has the same risk as the company itself, calculate the company cost of capital. v Use it to discount the project’s cash flows. ü If the project is more, or less, risky than the company itself, calculate the project cost of capital. v Use it to discount the project’s cash flows. copyright © 2003 Mc. Graw Hill Ryerson Limited
37 Summary of Chapter 10 Ø You can calculate the opportunity cost of capital for a project. ü If the project has the same risk as the company itself, calculate the company cost of capital. v Use it to discount the project’s cash flows. ü If the project is more, or less, risky than the company itself, calculate the project cost of capital. v Use it to discount the project’s cash flows. copyright © 2003 Mc. Graw Hill Ryerson Limited
