1 FINANCIAL RISK MANAGEMENT Types of Financial

1 FINANCIAL RISK MANAGEMENT

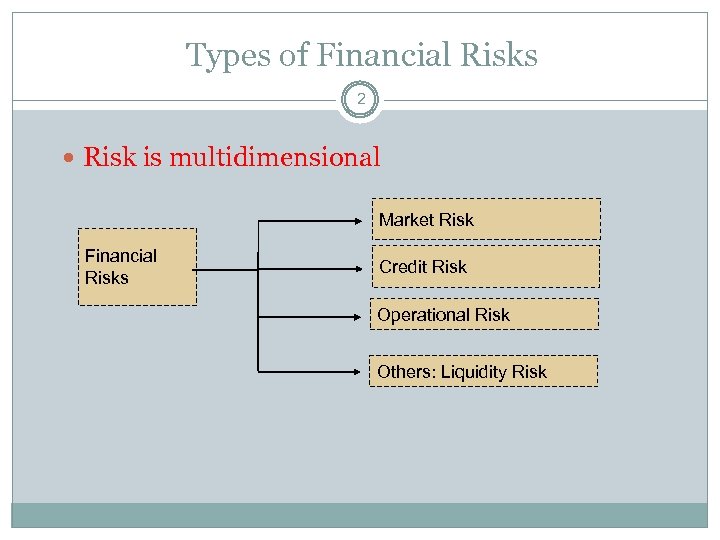Types of Financial Risks 2 Risk is multidimensional Market Risk Financial Risks Credit Risk Operational Risk Others: Liquidity Risk

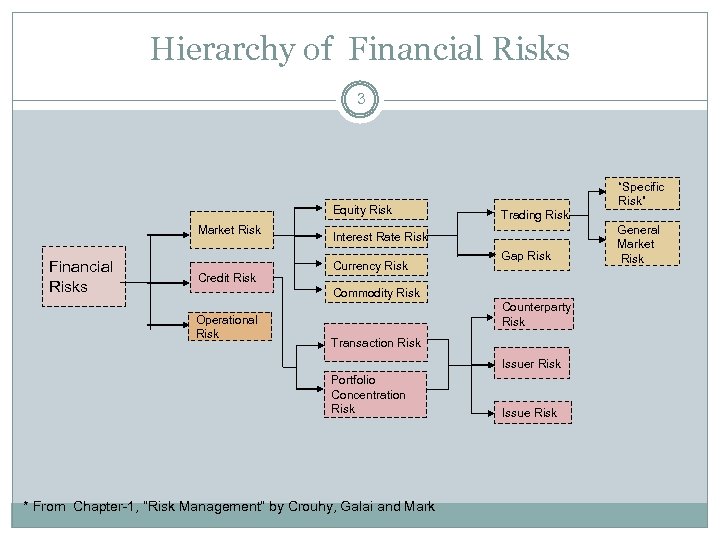Hierarchy of Financial Risks 3 Equity Risk Market Risk Financial Risks Credit Risk “Specific Risk” Trading Risk Interest Rate Risk Currency Risk Gap Risk Commodity Risk Operational Risk Counterparty Risk Transaction Risk Issuer Risk Portfolio Concentration Risk * From Chapter-1, “Risk Management” by Crouhy, Galai and Mark Issue Risk General Market Risk

Response to Financial Risk 4 Market response-introduce new products (derivatives) Equity futures Foreign currency futures Currency swaps Equity Options

Evolution of Regulatory environment: Basel 5 Basel I in 1988, the Basel Committee on Banking Supervision (BCBS) in Basel, Switzerland, published a set of minimum capital requirements for banks. is also known as the 1988 Basel Accord Basel- II was published in June 2004 was implemented in the years prior to 2008 Basel- III was agreed upon by the members of the Basel Committee on Banking Supervision in 2010– 11 was scheduled to be introduced from 2013 until 2015

Basel-I 6 Two minimum standards Asset to capital multiple Risk based capital ratio (Cooke ratio) A ratio that calculates the amount of capital a bank should have as a percentage of its total risk-adjusted assets. Scope is limited Portfolio effects missing- a well diversified portfolio is much less likely to suffer massive credit losses Netting is absent Focus on credit risk, no market or operational risk

Basel-II 7 This version aims at: Ensuring that capital allocation is more risk sensitive; Enhance disclosure requirements which would allow market participants to assess the capital adequacy of an institution; Ensuring that credit risk, operational risk and market risk are quantified based on data and formal techniques;

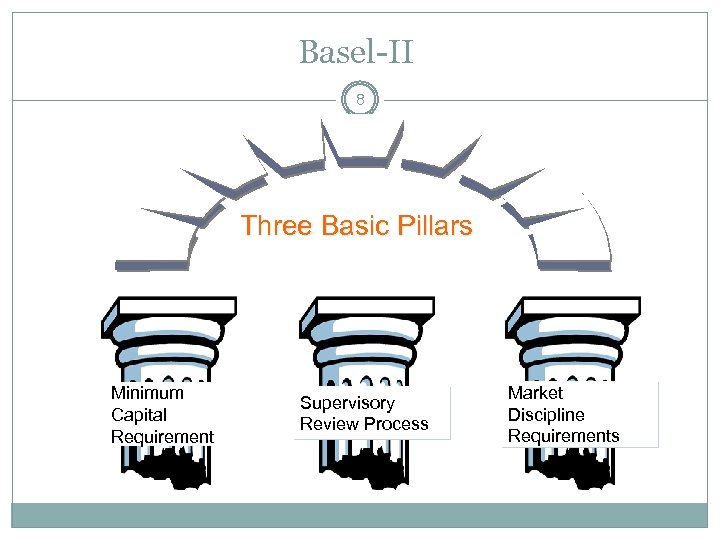Basel-II 8 Three Basic Pillars Minimum Capital Requirement Supervisory Review Process Market Discipline Requirements

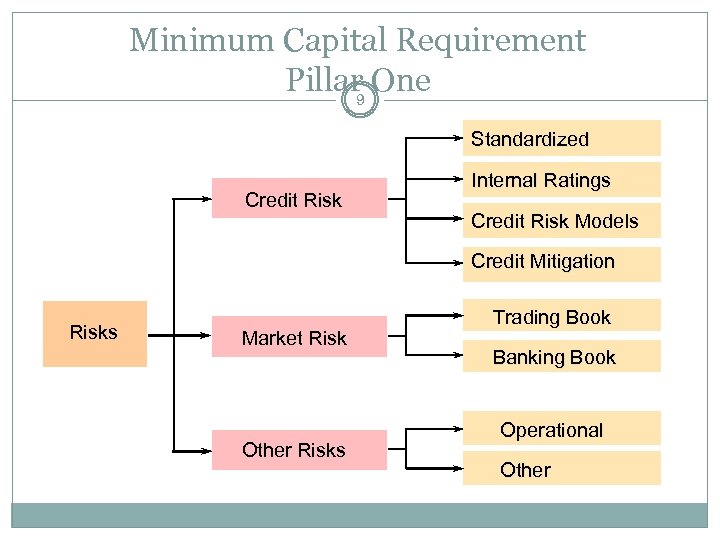Minimum Capital Requirement Pillar One 9 Standardized Credit Risk Internal Ratings Credit Risk Models Credit Mitigation Risks Market Risk Other Risks Trading Book Banking Book Operational Other

Basel III (or the Third Basel Accord) 10 Basel III (or the Third Basel Accord) is a global, voluntary regulatory framework on bank capital adequacy, stress testing and market liquidity risk. It was agreed upon by the members of the Basel Committee on Banking Supervision in 2010– 11, and was scheduled to be introduced from 2013 until 2015 It builds on the Basel I and Basel II documents and was developed in response to the deficiencies in financial regulation revealed by the financial crisis of 2007– 08. Basel III was supposed to strengthen bank capital requirements by increasing bank liquidity and decreasing bank leverage.

Basel III (or the Third Basel Accord) 11 Capital requirements The original Basel III rule from 2010 required banks to hold 4. 5% of Common Equity Tier 1 (CET 1) ratio (up from 2% in Basel II). A mandatory "capital conservation buffer", equivalent to 2. 5% of risk-weighted assets. Considering the 4. 5% CET 1 capital ratio required, banks have to hold a total of 7% CET 1 capital Leverage ratio Basel III introduced a minimum "leverage ratio". The banks are expected to maintain a leverage ratio in excess of 3% under Basel III. Tier 1 capital/Total exposure >=3%

CHAPTER 1 12 THE TYPES OF TRADES AND VALUATION

Introduction 13 Market risk: the possibility of losses resulting from unfavorable market movements. It is the risk of losing money because the perceived value of an instrument has changed. The difference between credit risk and market risk In credit risk there needs to be a default or failure by a counterparty to fulfill an obligation In market risk, we deal simply with changes in the prices that investors are prepared to pay

Introduction 14 Before launching into the mathematics of risk measurement, it is necessary to have a reasonable understanding of the types of trades and instruments that give rise to the risk This chapter will discuss the main instruments that banks trade—along with an explanation of how to value each of the instruments Valuation is very important in risk measurement because risk is all about potential changes in value

Introduction 15 Typically, a bank trades the following instruments: Debt instruments, also known as fixed income or bonds Forward rate agreements Equities, also known as stocks Foreign exchange, also known as FX or currency Forwards and futures Swaps Options

DEBT INSTRUMENTS 16 Debt instruments are securities that provide interest payments but no ownership claim on the issuer Four important features for debt instruments: Maturity Issuer credit rating Payment structure Currency

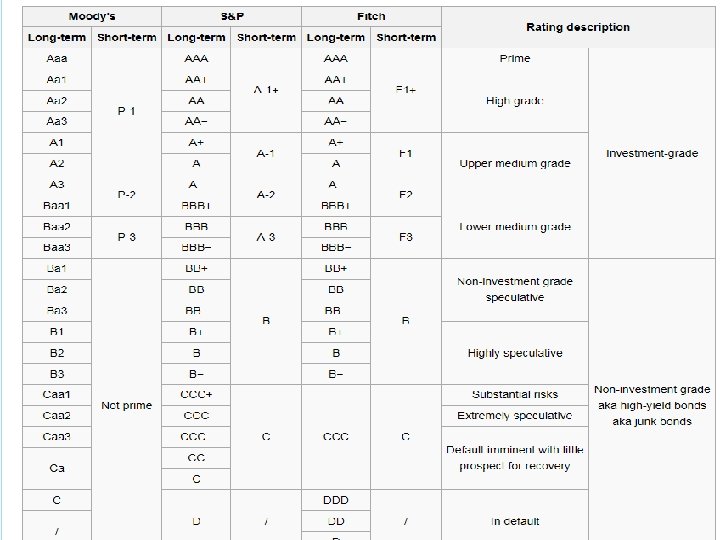
DEBT INSTRUMENTS 17 Maturity the time left until final payment Issuer Credit Ratings the credit risk of most bonds is rated by a third-party company called a rating agency, such as Standard & Poor's The ratings generally correspond to probabilities of default Bonds with high probabilities of default trade at lower prices than risk-free bonds

18

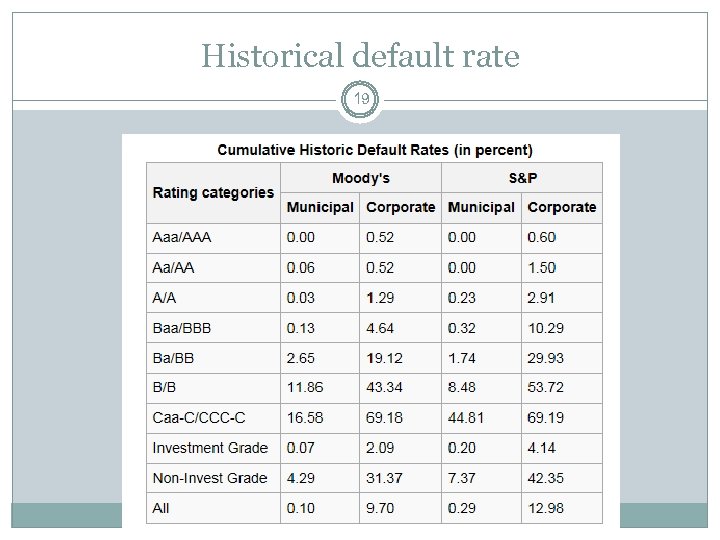Historical default rate 19

DEBT INSTRUMENTS 20 As we discus later in the chapter, a lower price implies a higher interest rate The difference between the interest rate for a risky bond and the interest rate for a risk-free bond of the same maturity is called the credit spread

DEBT INSTRUMENTS 21 Payment Structure The payments of interest on a bond are called coupons and are either fixed or floating Fixed-rate bonds pay the same percentage every time, and the rate is fixed when the bond is first issued Floating-rate bonds pay a variable percentage and the interest rate is reset periodically to a prevailing market rate Currency Debt instruments can be denominated in any currency

The Valuation of Bonds 22 A Single Payment Any bond promising to pay a certain amount at a future point in time has a value The value of a bond is the price that investors are prepared to pay today to own that bond If we consider a bond that promises to make a single payment, at time t, then the current value of the bond and the future payment amount can be used to define a discount factor (DF):

The Valuation of Bonds 23 The discount factor will be less than one, as it is almost always better to have cash now than the same amount promised in the future The discount factor includes all the effects that cause the value to be less than the promised amount, including the effects of inflation and the possibility of default. If the cash flow is certain (e. g. , a fixed-rate government bond), then the discount is called the risk-free discount

The Valuation of Bonds 24 If the cash flow is risky, e. g. , if there is a possibility of default, the value will be less, and therefore, the discount factor will be smaller The discount factor for a given maturity, t, can be used to define a discount rate, rt, which is more familiarly known as an interest rate. The usual expression for the discount rate is as follows:

Zero-coupon bonds 25 Zero-coupon bonds are bonds that do not pay interest explicitly. The bond is sold at a discount to face value, with the difference between the face value and the sale price implicitly being the interest payment. The value of a risk-free zero-coupon bond is simply the amount of the payment multiplied by the risk-free discount factor:

Coupon-paying bonds 26 Coupon-paying bonds have a series of fixed- intermediate-interest payments. The value of a coupon-paying bond is the sum of the value of the individual payments:

Example-1 27 Bond Par Amount: $1, 000 Bond Coupon: 8% Coupon Frequency: Annual Market Discount Rate: 6% Bond Maturity: 2 years Ans: $1, 036. 67

Measuring Interest Rate Sensitivity Using Duration 28 Duration is a measure of the interest rate sensitivity of the value of a bond or loan. This is useful because once we know the duration and the possible movement of interest rates, we have a measure of how much value the bank could lose in its bond portfolio If a bond had a duration of seven, it would mean that value of the instrument would decline by seven percent if interest rates rose one percent

Macaulay duration 29 There are two types of duration: Macaulay duration and modified duration Macaulay duration is easier to calculate, but modified duration is more accurate Macaulay duration is simply the average time for cash flows, weighted by their present values:

Example-2 30 Follow Example 1 Calculate Macaulay Duration $75. 47 x 1 +$ 71. 20 x 2 + $890. 00 x 2 = $1997. 86 / $1036. 67 = 1. 93 years

Modified duration 31

Example-3 32 Follow Example 1 Calculate Modified Duration =(Macaulay Duration)/(1+r) 1. 93 / (1+. 06) = 1. 82 percentage

Duration dollars 33 If we had not divided by V, we would have had the absolute price sensitivity, which is called duration dollars:

Duration dollars 34

Example-4 35 Follow Example 1 Calculate dollars duration =(Modified Duration)*Bond price 1. 82 percentage*1997. 86=36. 36 dollars

Durations 36 The unit of duration is time This may seem strange, but it is because duration is the sensitivity with respect to interest rates, and interest rates are in units of increase per time period Therefore, since duration is change in percentage value per change in interest rate, the unit of duration is time

Durations 37 Why we bother with duration rather than just using the derivative directly? The simple answer is that it is market custom. Many bank financial reports will give "duration, " but few will give "the derivative of value with respect to interest rates. “ Therefore, it is necessary to understand the meaning of duration

Limitations of Durations 38 Duration has significant limitations as a measure of risk. It is the first derivative of value with respect to rates. As such, it is a linear measure and only describes changes in the value of a bond based on small parallel shifts in the yield curve. It does not describe the value changes that could result from the convexity of bond prices or complex shifts in the yield curve

Limitations of Durations 39 Convexity is the nonlinear relationship between the price of a bond and its yield, as illustrated in Figure 4 -2. As duration is a linear description of value changes, it becomes increasingly inaccurate as the rate change becomes larger To account for convexity, we need to give up the linear approximation of duration and use full bond valuation.

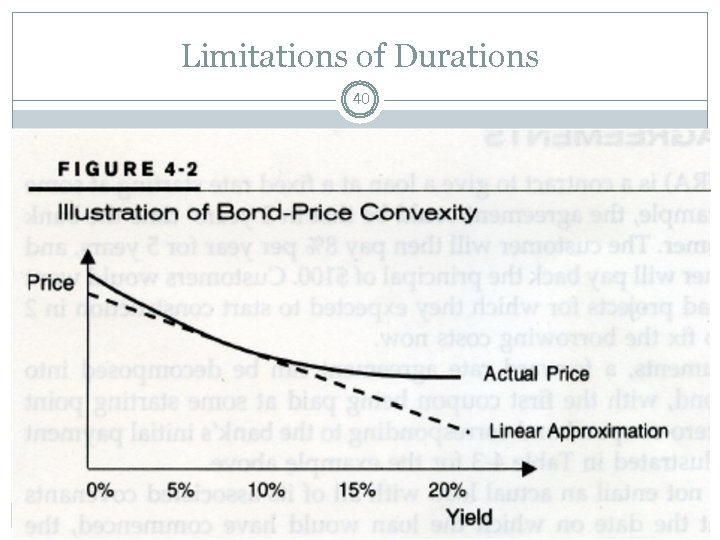
Limitations of Durations 40

OPTIONS 41 An option is a type of derivative contract An option gives the holder the right but not the obligation to buy or sell an underlying asset at a future time, at a predetermined price The predetermined price is called the strike price. The party holding the right to choose is said to be long the option, and the counterparty who sold or wrote the option is said to be short the option

OPTIONS 42 Options can be categorized according to the rights given to the holder: Puts: A put option gives the holder the right to sell the underlying security and receive a predetermined strike price. Calls: A call option gives the holder the right to buy the underlying security by paying a predetermined strike price.

OPTIONS 43 Options are similar to futures, but with one important difference: the holder can choose whether to exercise the option at the time of contract expiration Options can be difficult to value There are many option classifications

The Black-Scholes Equation 44 The Black-Scholes equation was developed by two professors who were later awarded a Nobel Prize for their accomplishment. The Black-Scholes equation calculates the current value of holdingan option on a stock The equation assumes that the option can only be exercised at maturity (European option), and that there are no dividends or transaction costs It also assumes that the percentage change in the stock price has Normal distribution

The Black-Scholes Equation 45 With these restrictions, the value of a call option on a stock is a function of the following five variables S = Spot price of the underlying security T = Time left to maturity of the option X = Strike price of option r = Risk-free interest rate to the time of option expiration σ= Annual volatility for the underlying security.

The Black-Scholes Equation 46

Greeks 47 Delta: measures the rate of change of theoretical option value with respect to changes in the underlying asset's price. Delta is the first derivative of the value of the option with respect to the underlying instrument's price. For a vanilla option, delta will be a number between 0. 0 and 1. 0 for a long call (or a short put) and 0. 0 and − 1. 0 for a long put (or a short call);

Greeks 48 Gamma: measures the rate of change in the delta with respect to changes in the underlying price. Gamma is the second derivative of the value function with respect to the underlying price. Vega: measures sensitivity to volatility. Vega is the derivative of the option value with respect to the volatility of the underlying asset. Theta: measures the sensitivity of the value of the derivative to the passage of time (see Option time value): the "time decay. "

Greeks 49 Rho: measures sensitivity to the interest rate: it is the derivative of the option value with respect to the risk free interest rate (for the relevant outstanding term).