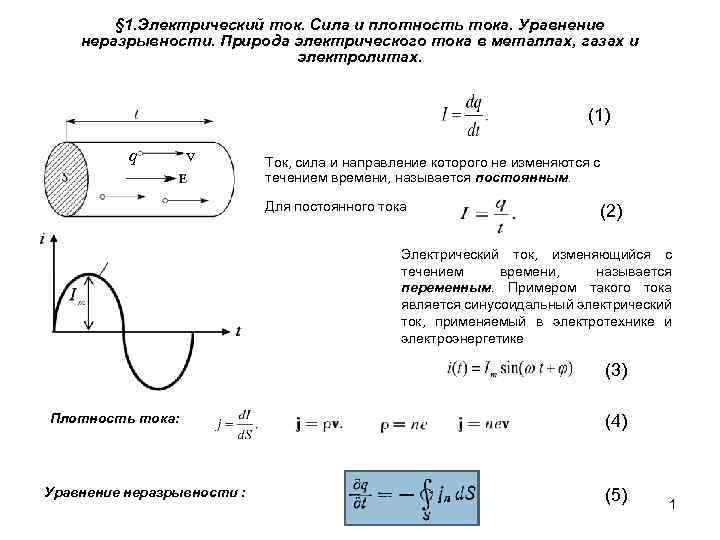
1 Электрический ток Сила и плотность тока

§ 1. Электрический ток. Сила и плотность тока. Уравнение неразрывности. Природа электрического тока в металлах, газах и электролитах. (1) q v Ток, сила и направление которого не изменяются с течением времени, называется постоянным. Для постоянного тока (2) Электрический ток, изменяющийся с течением времени, называется переменным. Примером такого тока является синусоидальный электрический ток, применяемый в электротехнике и электроэнергетике (3) Плотность тока: Уравнение неразрывности : (4) (5) 1

§ 2. Классическая электронная теория металлов. 2

§ 3. Подвижность носителей заряда. Проводимость. Закон Ома в локальной форме. 3

§ 3. Подвижность носителей заряда. Проводимость. Закон Ома в локальной форме. (2) 4

§ 4. Закон Джоуля-Ленца в локальной и интегральной формах. 5

6

§ 5. Закон Видемана-Франца. 7

§ 6. Трудности классической электронной теории металлов. 8

§ 7. Расчет разветвленных цепей постоянного тока. Правила Кирхгофа. 9

10

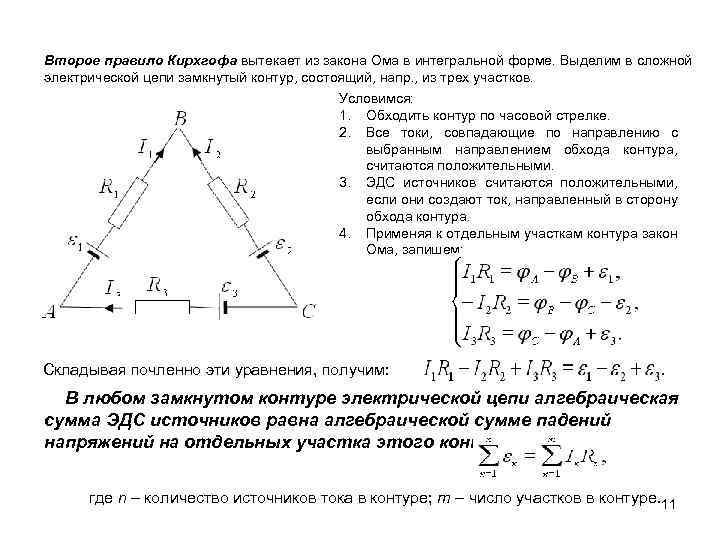Второе правило Кирхгофа вытекает из закона Ома в интегральной форме. Выделим в сложной электрической цепи замкнутый контур, состоящий, напр. , из трех участков. Условимся: 1. Обходить контур по часовой стрелке. 2. Все токи, совпадающие по направлению с выбранным направлением обхода контура, считаются положительными. 3. ЭДС источников считаются положительными, если они создают ток, направленный в сторону обхода контура. 4. Применяя к отдельным участкам контура закон Ома, запишем: Складывая почленно эти уравнения, получим: В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС источников равна алгебраической сумме падений напряжений на отдельных участка этого контура, т. е. где n – количество источников тока в контуре; m – число участков в контуре. 11