1 Эйлер, Ляпунов, Навье и Стокс 2 Что

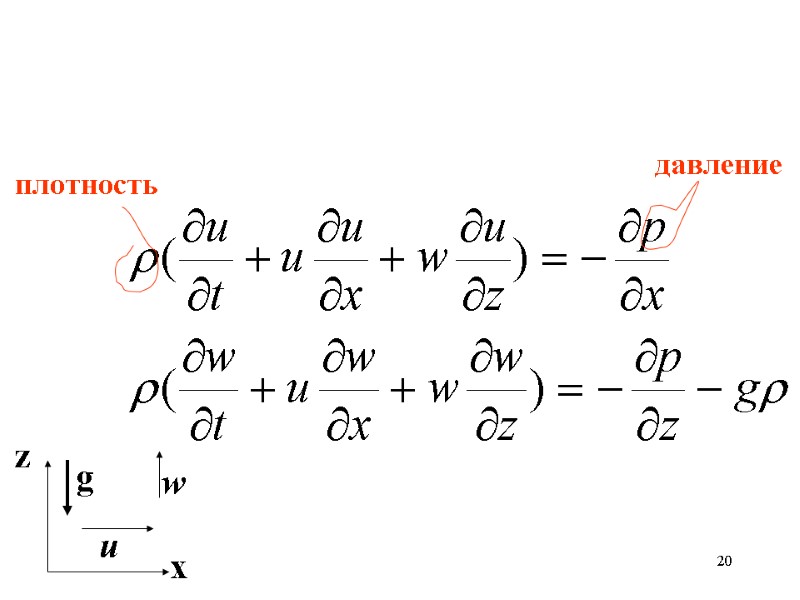
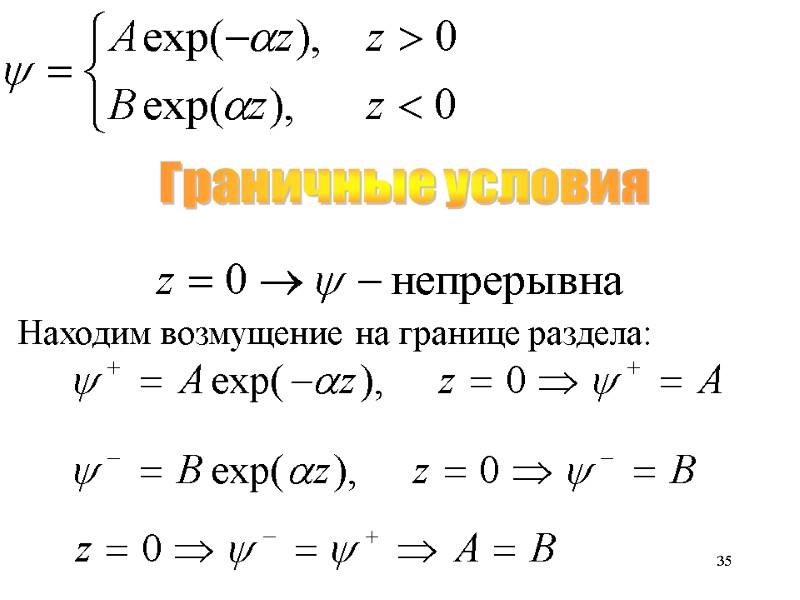
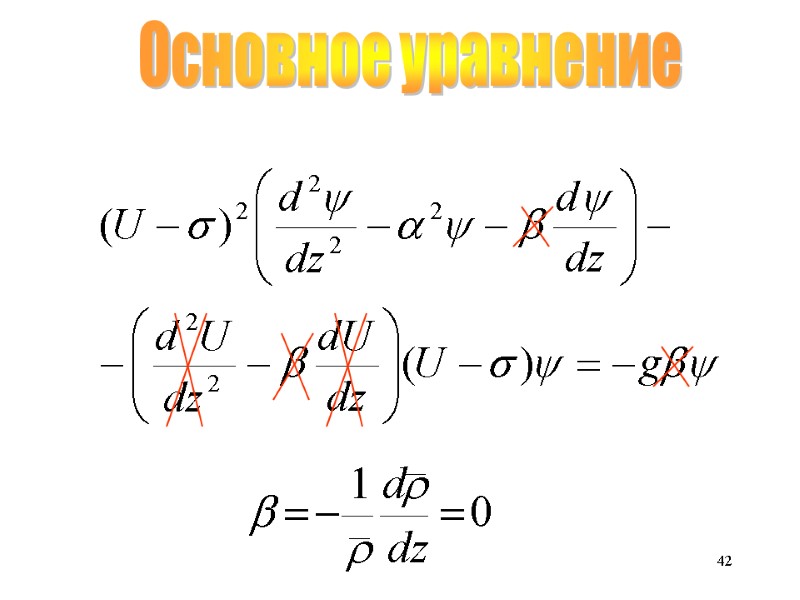
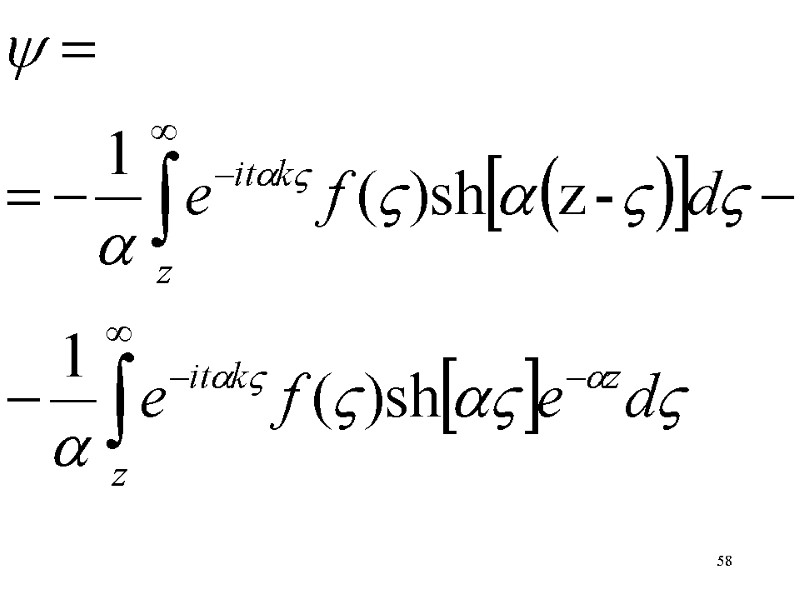
1 Эйлер, Ляпунов, Навье и Стокс

2 Что надо понимать под устойчивостью? Устойчивость решений уравнений по Ляпунову: Пусть имеется возможность как-то измерять отклонение одного решения от другого, какая-то мера этого отклонения. Устойчивость означает, что каково бы ни было >0, всегда можно найти такое >0, что если начальные условия изменить не более, чем на , то решение в любой момент времени изменится не более, чем на , то есть это есть устойчивость по возмущениям начальных данных.

3 Пусть мы перешли к линеаризованной системе уравнений. Для линейной системы понятие устойчивости обычно другое. Здесь неустойчивые решения неограниченно растут, а устойчивые остаются ограниченными одной константой для всех моментов времени. Допустим, что мы показали неустойчивость некоторого решения в линейном приближении. Решение неограниченно растет, то есть становится сколь угодно большим, с какого бы малого значения мы его не начинали.

4 Как в таком случае должно вести себя решение нелинейных уравнений? Когда решение еще мало, оно довольно хорошо следует за решением линейной системы, по самому смыслу линейной аппроксимации. Но когда оно становится достаточно большим, линейное приближение перестает действовать. Как правило, в таких случаях решение за счет нелинейных членов уравнения остается ограниченным (это бывает следствием, например, ограниченности общей энергии в системе) и доходит до некоторого конечного предела.

5 Пусть теперь мы взяли в начальный момент меньшие по значению начальные условия. Пока действует линейное приближение, решение растет пропорционально прежнему. Теперь оно позже выйдет из зоны действия линейного приближения, но для таких же значений амплитуды, что и прежде. В конечном итоге оно, хотя и позже, подойдет к тем же предельным значениям, которые окажутся, таким образом, независимыми от начальных условий.

6 Если начальные условия стремятся к нулю, то решение для каждого момента времени стремится к нулю, но неравномерно относительно всех моментов времени, то есть нет устойчивости по Ляпунову. Итак, если доказана неустойчивость в линейном приближении, то есть неустойчивость и в точном смысле.

7 Устойчивость движения идеальной жидкости

8 Задача на устойчивость Пусть основное (невозмущенное) движение жидкости определяется полем скорости u(x,y,z) Пример: плоскопараллельное движение со сдвигом скорости u(y) y x u0

9 Осредненная во времени величина возмущений отлична от нуля: В потоке жидкости существуют возмущения скорости:

10 Основное течение и возмущения должны удовлетворять уравнениям движения, неразрывности и граничным условиям. Хаотические возмущения оставляем теории турбулентности

11 Линейное уравнение - опускаем произведения малых величин и малые величины в степени выше первой Решаем линейную задачу на устойчивость основного движения жидкости к малым возмущениям.

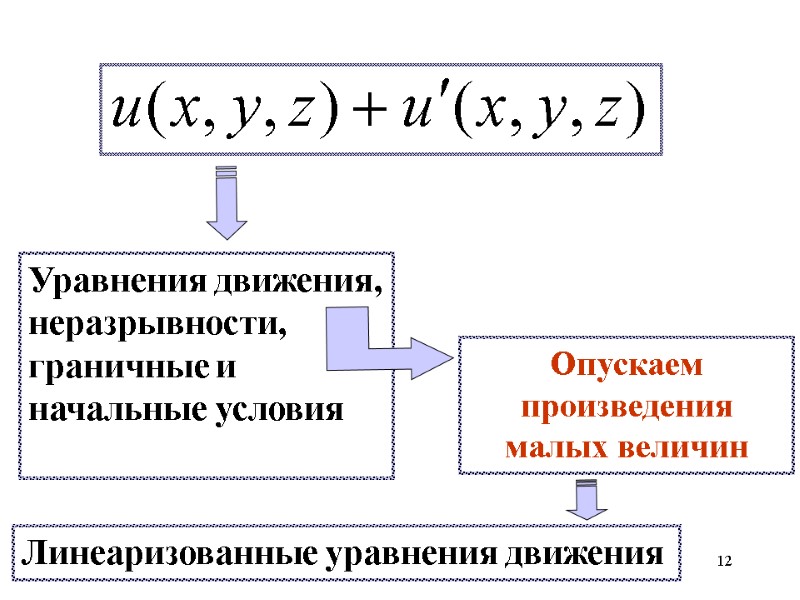
12 Уравнения движения, неразрывности, граничные и начальные условия Опускаем произведения малых величин Линеаризованные уравнения движения

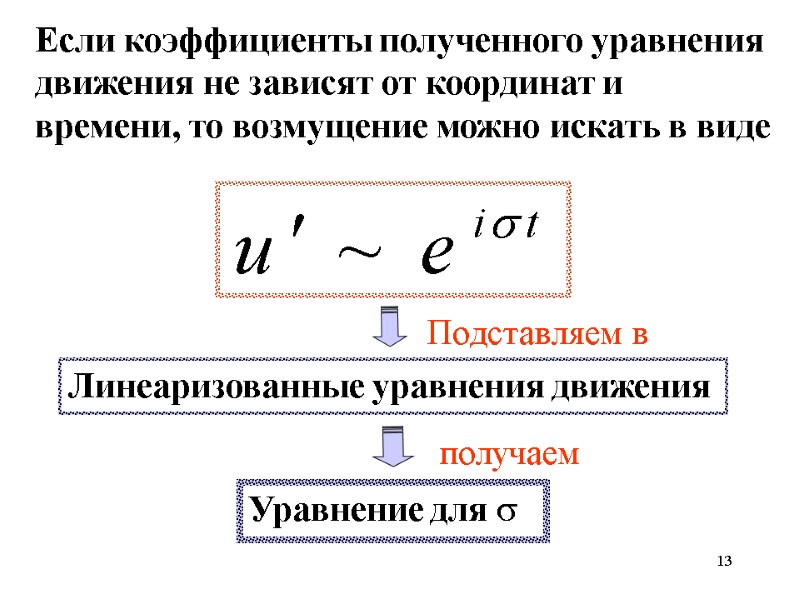
13 Линеаризованные уравнения движения Если коэффициенты полученного уравнения движения не зависят от координат и времени, то возмущение можно искать в виде Уравнение для  Подставляем в получаем

14 действительные  - нет потери устойчивости основного течения Если коэффициент  - действительный, то возмущение периодически меняется во времени, оставаясь малой величиной - имеют место нейтральные колебания Если  - действительная величина

15 мнимые  - потеря устойчивости основного течения Если коэффициент  - мнимый, то имеются решения, амплитуда которых экспоненциально растет со временем. Основное течение теряет устойчивость  - мнимая величина

16 Решение линейной задачи на устойчивость основного течения к бесконечно малым возмущениям позволяет выявить факт потери устойчивости основного движения: экспоненциальный рост амплитуды возмущений говорит о неустойчивости основного течения к малым возмущениям . Однако вид нового течения остается неизвестным.

17 Действительно, линейные уравнения справедливы лишь для бесконечно малых возмущений. Когда эти возмущения становятся конечными, следует переходить к нелинейным уравнениям. Вид нового течения можно получить, решая задачу на устойчивость основного течения к возмущениям конечной амплитуды (нелинейную задачу).

18 Линейная задача идеальная жидкость стационарное основное течение

19 Рассмотрим течение идеальной жидкости (без вязкости) в вертикальной плоскости (х,z). Движение описывается уравнениями Эйлера:

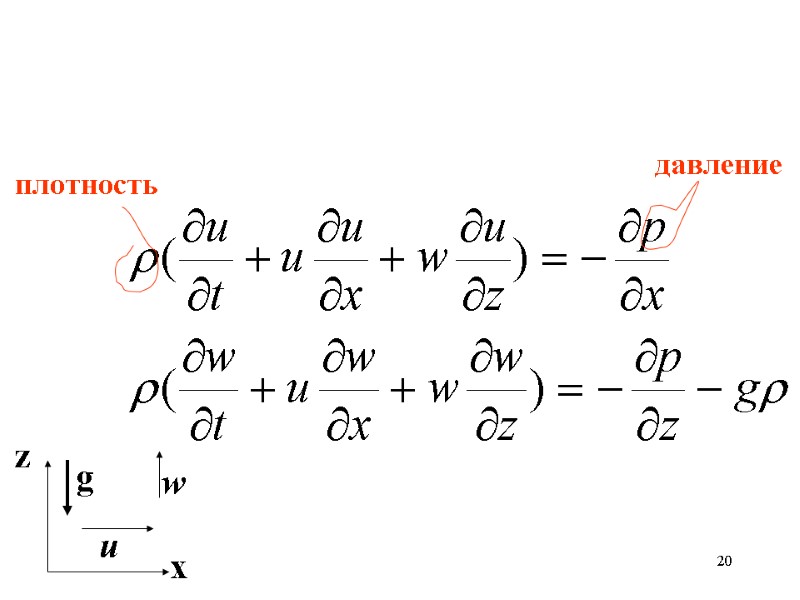20 x z g u w давление плотность

21 Предполагаем, что жидкость является несжимаемой:

22 Основное стационарное течение, устойчивость которого исследуется, направлено по оси Ох и его скорость зависит только от вертикальной координаты U(z). Скорость возмущенного течения: возмущения По оси Ох По оси Оz только возмущения

23 Остальные переменные имеют основную стационарную составляющую и возмущение: давление плотность

24 Опускаем произведения малых величин - получаем линеаризованные уравнения

25 Вводим функцию тока для возмущений Вводим вертикальный градиент плотности в виде

26 К левой и правой частям уравнений движения применяем операцию rot , в результате, исчезает градиент давления Применение операции rot сужает класс решений: теряются решения, обусловленные градиентом давления rot rot rot rot

27 Основное уравнение

28 Если коэффициенты полученного уравнения движения не зависят от координаты х и времени t, то возмущение можно искать в виде нормальных волн где  - волновое число в направлении оси Ох, - фазовая скорость волны

29 Основное уравнение

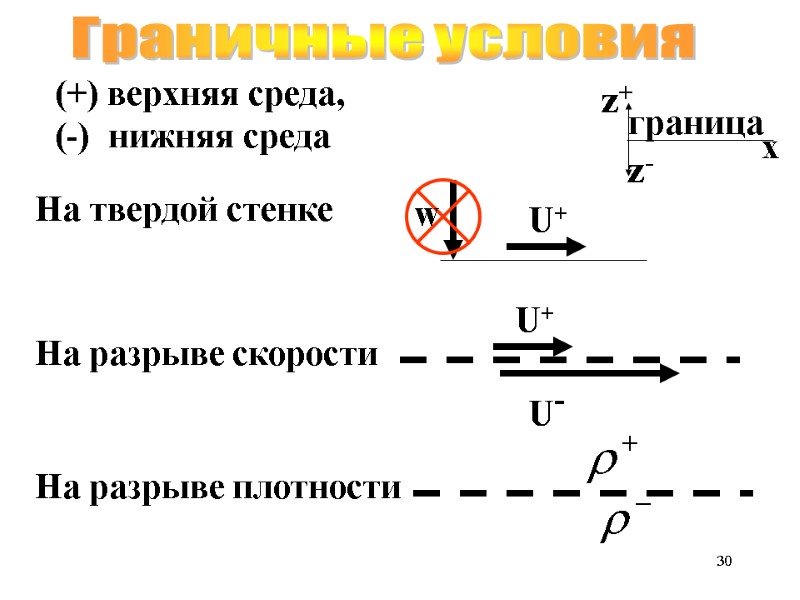
30 Граничные условия На твердой стенке На разрыве скорости На разрыве плотности U+ U- U+ w (+) верхняя среда, (-) нижняя среда

31 На твердой стенке Граничные условия На разрыве скорости На разрыве плотности

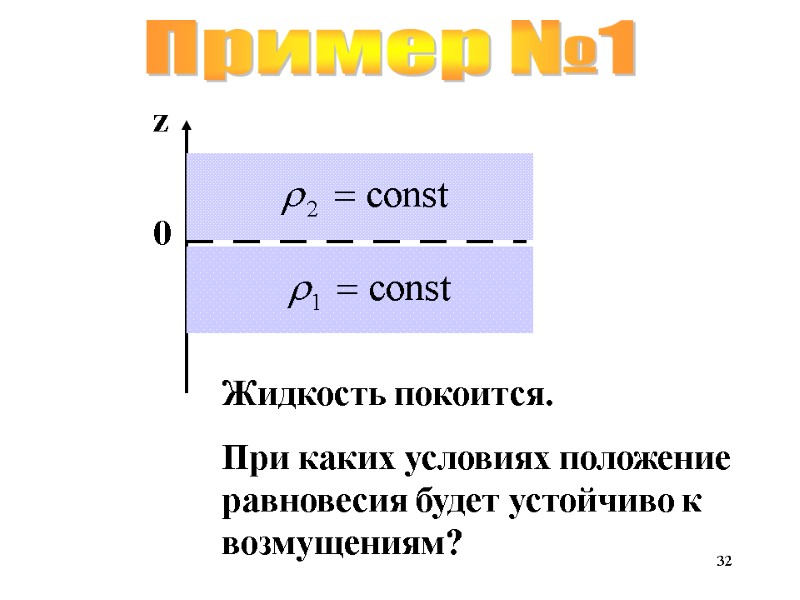
32 Пример №1 z 0 Жидкость покоится. При каких условиях положение равновесия будет устойчиво к возмущениям?

33 Основное уравнение

34 Основное уравнение Решение

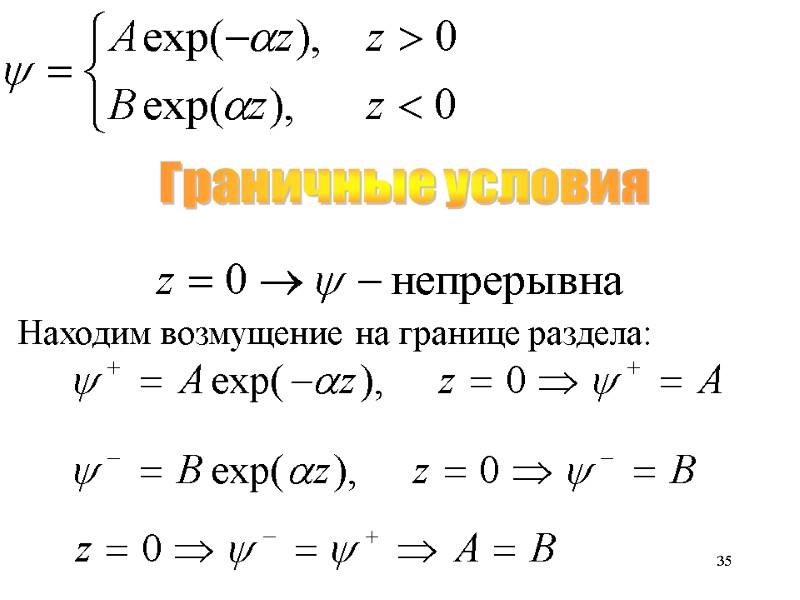35 Граничные условия Находим возмущение на границе раздела:

36 Граничные условия На разрыве плотности

37 В полученное условие подставляем возмущение  в верхней и нижней среде получаем

38 - действительная величина - мнимая величина

39 Нейтральные малые колебания Возмущение экспоненциально растет со временем

40 z 0 Статическая или тейлоровская неустойчивость Состояние системы абсолютно неустойчиво к возмущениям. Какое движение возникает реально?

41 Пример №3 Разрыв скорости U+=const U-= const Переходим к системе координат, движущейся со скоростью средней между U+ и U- +U -U x z

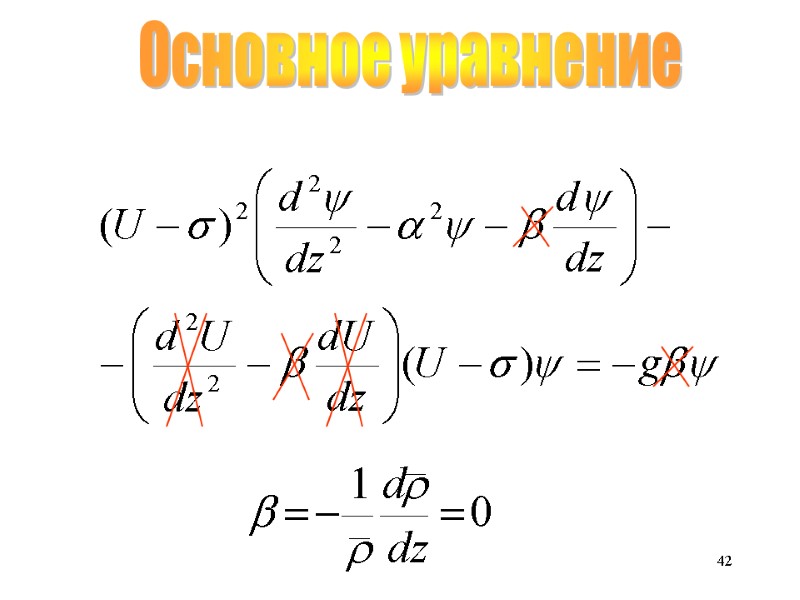42 Основное уравнение

43 Основное уравнение

44 Решения:

45 Граничные условия На разрыве скорости

46 Граничные условия На разрыве плотности

47 Подставляем решение в граничные условия Течение с разрывом скорости абсолютно неустойчиво к возмущениям

48 Решение линейной задачи не позволяет ответить на вопрос: какое новое движение возникает в жидкости при потере устойчивости? Ответ можно получить либо экспериментальным путем, либо решая нелинейную задачу, учитывающую нелинейные граничные условия.

49

50 Вопросы 1. Что такое основное течение и возмущения? 2. Должны ли возмущения удовлетворять уравнениям движения и граничным условиям? 3. Как получить линейные уравнения движения и граничные условия? 4. Почему решение для возмущенного течения ищется в виде экспоненциальных функций параметров задачи (нормальных волн)?

51 5. Для каких значений фазовой скорости возмущений обнаруживается потеря устойчивости основного потока к бесконечно малым возмущениям? 6. Какое заключение об устойчивости основного течения к бесконечно малым возмущениям дает решение линейной задачи с линейными граничными условиями?

52 Параллельные течения

53 Пусть жидкость заполняет полупространство z>0, плотность постоянна во все время движения, а скорость растет линейно с координатой z: U=kz. x z U Пример №4

54 Уравнение движения можно записать в этом случае: Зависимость от z продолжаем считать гармонической: exp(iz). Полученное уравнение нужно решать при начальных и граничных условиях: - ограничено при

55 Полученное уравнение интегрируем по t: Произвольная функция f(z) определяется начальным условием:

56 Осталось решить дифференциальное уравнение второго порядка по z при заданных краевых условиях. Решение находим методом вариации произвольного постоянного:

57 Нужно сделать какие-либо предположения о начальных условиях 0(z) , чтобы этот интеграл сходился. Например, можно предположить, что эти начальные условия отличны от нуля лишь в конечной области изменения z. Константы С1 и С2 должны быть найдены из условия ограниченности на бесконечности и обращения в нуль при z=0.

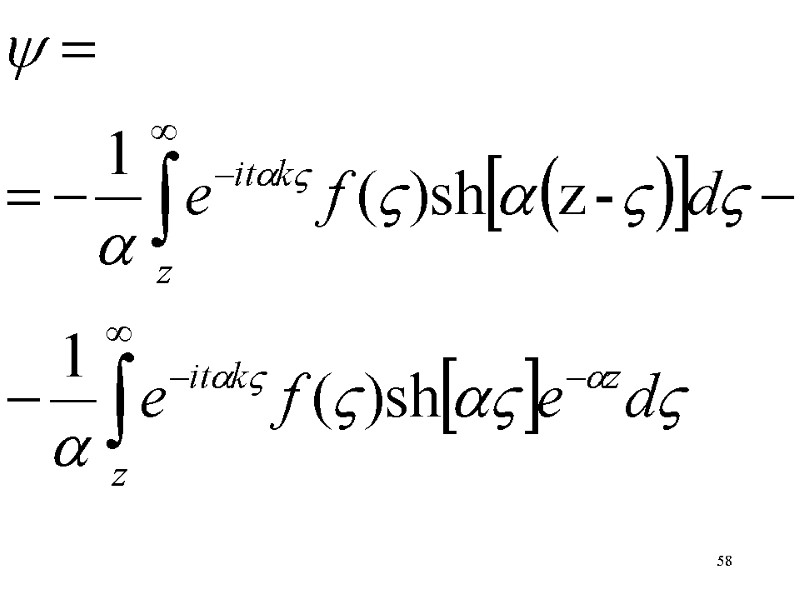58

59 Можно показать, что это выражение ограничено при и не превосходит величины:

60 x y u Малые возмущения остаются все время ограниченными по своей амплитуде. Вывод: движение параллельного потока жидкости при линейном вертикальном профиле скорости абсолютно устойчиво. u y x Свободная поверхность

61 Почти параллельные течения

62 Существуют строго параллельные течения, например течение Пуазейля-Куэтта в кольцевой трубе со скользящими относительно друг друга стенками. В природе в основном встречаются «почти» параллельные течения. Это такие течения, у которых производные параметров вдоль потока малы по сравнению с производными в поперечном направлении Свободная поверхность u y x

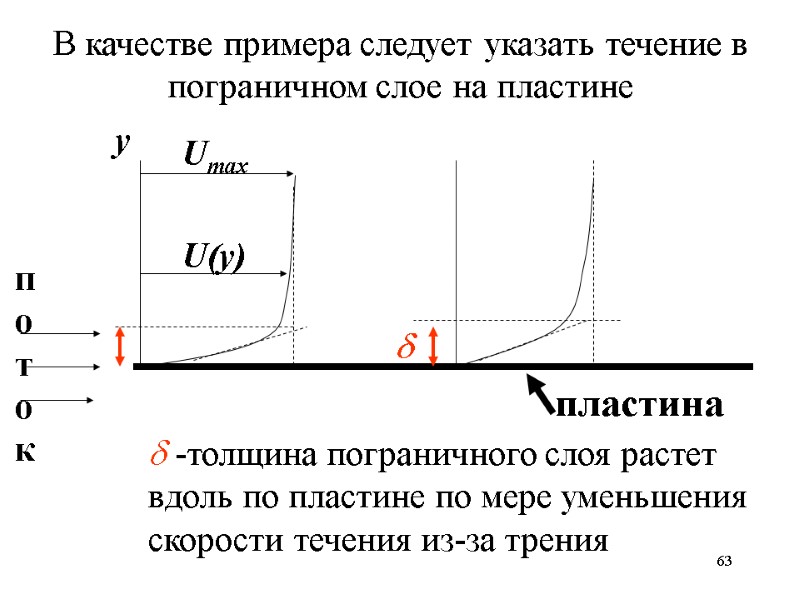
63 у U(у)   -толщина пограничного слоя растет вдоль по пластине по мере уменьшения скорости течения из-за трения поток пластина Umax В качестве примера следует указать течение в пограничном слое на пластине

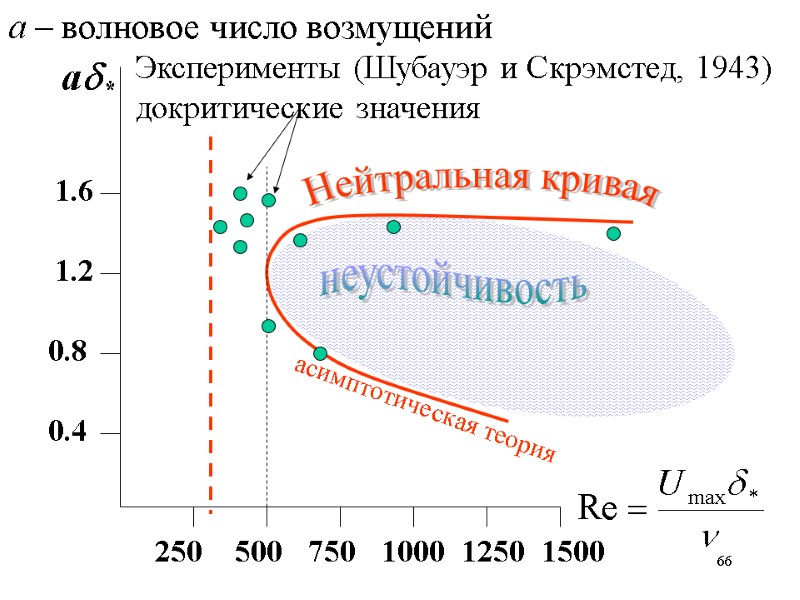
64 Асимптотическая теория (б.м.возмущения, линейная задача) была впервые дана Толмином (1929) и позднее развита Шлихтингом (1935), Линем (1945) и Шеном (1964). Пока возмущения малы, результаты асимптотической теории хорошо согласуются с экспериментом. В экспериментах Шубауэра и Скрэмстеда и в целом ряде других экспериментов были приняты значительные усилия для подавления возмущений на пластине. Если такие возмущения присутствуют, то неустойчивость пограничного слоя возникает при меньших докритических значениях числа Рейнольдса

65 Толщина слоя вытеснения:

66 а* 250 500 750 1000 1250 1500 0.4 0.8 1.2 1.6 Эксперименты (Шубауэр и Скрэмстед, 1943) докритические значения Нейтральная кривая неустойчивость а – волновое число возмущений асимптотическая теория

67 Максимальные отличия расчетных и экспериментальных данных наблюдаются вблизи минимального критического числа Рейнольдса Re=500. Численные результаты для конечных возмущений, полученные в рамках приближения «параллельного» течения, согласуются с экспериментом существенно хуже, особенно вблизи критического значения числа Рейнольдса .

68 Все попытки аппроксимировать “почти” параллельные течения строго параллельными течениями для того, чтобы применить уравнение Орра-Зоммерфельда с разделяющимися переменными, потерпели неудачу. Новые возможности в решении проблемы дало применение численных методов с использованием быстродействующих мощных компьютеров, позволивших исследовать непараллельное течение.

69 Фазель и Конзельман (1990) решали уравнения Навье-Стокса для двухмерного потока несжимаемой жидкости без упрощений, используя адекватную численную схему. Эта работа позволила исследовать устойчивость пограничного слоя к различным возмущениям, в том числе и двухмерным. Встал вопрос об определении наиболее опасного возмущения для потери устойчивости.

70 . Наиболее опасным возмущениям соответствует минимальное докритическое значение числа Рейнольдса Во многих экспериментах возмущения различной амплитуды и формы вносились искусственно, чтобы убедиться в истинности полученных наименьших значений критического числа Рейнольдса.

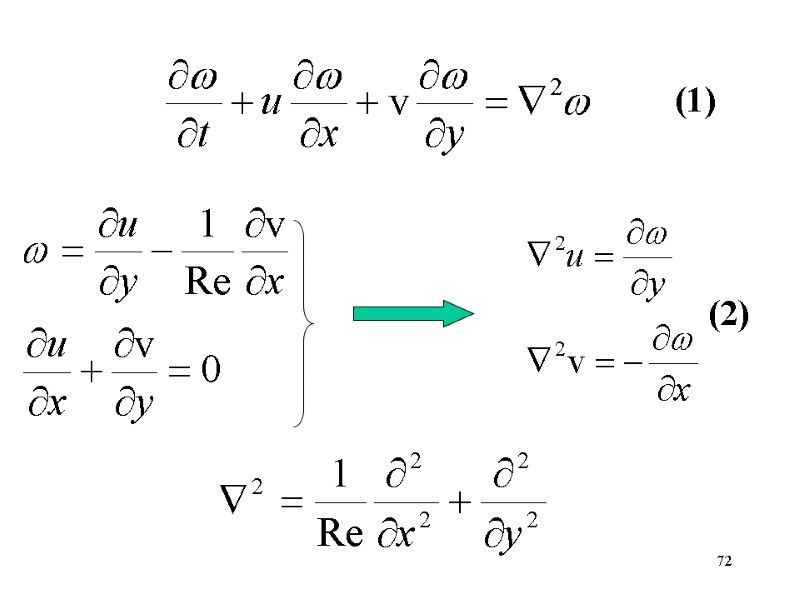
71 Уравнение Навье-Стокса решалось в безразмерном виде в формулировке для вихря скорости: Масштаб длины Начало координат

72 (1) (2)

73 Уравнения (1)-(2) решаются со следующими начальными и граничными условиями: где начальное поле параметров получено с помощью численного решения задачи (1)-(2) для стационарного пограничного слоя, то есть без члена в уравнении (1).

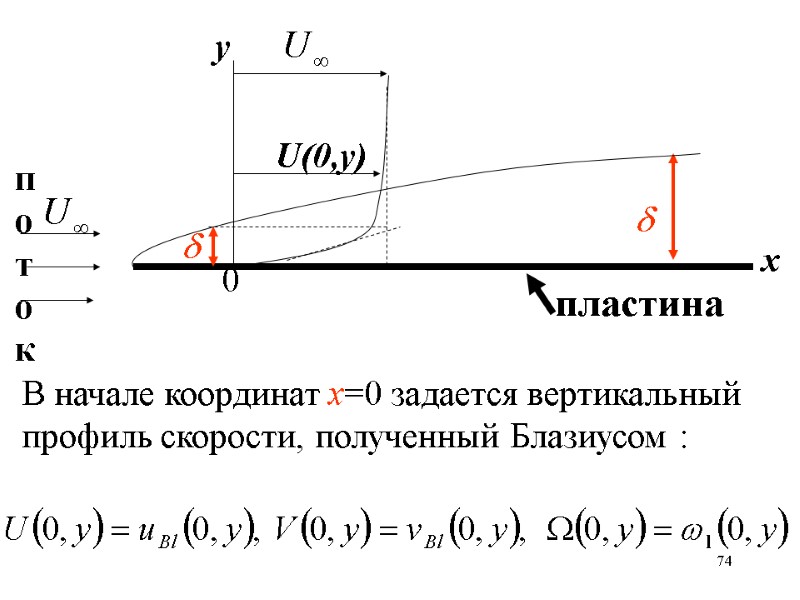
74 у U(0,у)  поток пластина 0 х В начале координат х=0 задается вертикальный профиль скорости, полученный Блазиусом : 

75 Вода течет со скоростью 9 см/с. Число Рейнольдса, рассчитанное по расстоянию сечения от передней кромки, равно 500, a толщина вытеснения равна примерно 5 мм. Фото F. X. Wortmann Профиль Блазиуса

76 Для нестационарной задачи на профиль Блазиуса накладываются периодические возмущения:

77 Возмущения uпер, v пер, пер получены из решения задачи на собственные значения для уравнений Орра-Зоммерфельда, когда эффектами не-параллельности можно пренебречь. В ходе решения оказалось, что влияние этих эффектов на собственные функции задачи так малы, что их действительно можно получить для возмущающих функций из простой задачи Орра-Зоммерфельда с разделяющимися переменными для обыкновенных дифференциальных уравнений.

78 В результате, удается генерировать вполне реалистичные возмущения типа волн Толмина-Шлихтинга, которые усиливаются или затухают при распространении вниз по потоку в зависимости от числа Рейнольдса.

79 При рассчитанном по длине числе Рейнольдса Re=20 000 (верхний снимок) пограничный слой на пластинке, помещенной вдоль потока, ламинарен. При Re=100 000 (нижний снимок) появляются двумерные волны Толлмина-Шлихтинга, видимые благодаря подкрашенной жидкости. Фото ONERA. [Werle, 1980] Неустойчивость пограничного слоя на пластинке

80 Переход, возникающий вниз по потоку от волн Толлмина-Шлихтинга. В левой части снимка волны двумерные; они становятся трехмерными ниже по течению. Линии были получены подкрашиванием воды. Число Рейнольдса, рассчитанное по длине, равно 400 000. [Wortmann, 1977]

81 Этот подход соответствует действиям экспериментаторов, которые для снижения числа Рейнольдса до минимального значения (300-400) вводят возмущения искусственным образом с помощью волнопродукторов, колеблющейся ленты и др. (Шубауэр и Срэмстад, Росс, Качанов, Козлов и Левченко). Если возмущения не вносятся, минимальное критическое число Рейнольдса получается более высоким.

82 Еще один возможный способ возбуждения возмущений представляет собой периодическую подачу и отсос жидкости через узкую прорезь, проделанную поперек пластины вдоль оси z (Липман 1982). В этом случае периодически возникают вертикальные перепады скорости над прорезью, формирующие вихревые образования в пограничном слое.

83 На пластине ставятся следующие граничные условия для стационарного потока: и для нестационарного потока:

84 Условие для вихря получены из уравнений (2) для вертикальной компоненты скорости возмущений. В граничных условиях принято условие периодического появления вертикальной составляющей скорости при периодической подаче и отсосе жидкости через узкую прорезь. 0 х1 х2 хс

85 Функция возмущений f задавалась в следующем виде: , где  - частота возмущений , а функция fх задавалась: х1 х2 хс fх

86 На выходе расчетной области, имеющей координату Х, для стационарного потока имеем:

87 Для нестационарного потока (штрихи обозначают возмущенные величины,  - локальное волновое число волны возмущений =2/,  - длина волны) :

88 На верхней границе расчетной области задается максимальное значение горизонтальной скорости, нулевые условия для вертикального градиента вертикальной скорости и вихря скорости. Для выполнения этих условий достаточно взять высоту расчетного слоя в 6-14 раз превышающую толщину слоя вытеснения. Компоненты скорости возмущений полагаются затухающими по экспоненте с высотой. Однако для верхней границы домена они не равны нулю.

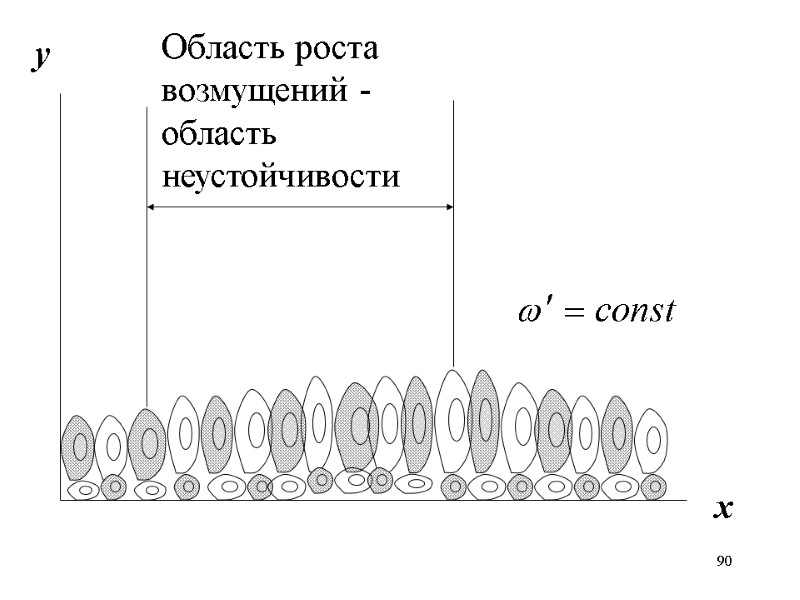
89 Изменение начальных возмущений вдоль пластины, полученное в результате численного решения здачи приведено на рисунке на следующем слайде. Возмущения представлены как линии равной завихренности. Область отрицательной завихренности закрашена. Область роста возмущений - область неустойчивости, область затухания возмущений - область устойчивости.

90 у х Область роста возмущений - область неустойчивости

91