bac988bc258d40aaed90f68754cebe78.ppt
- Количество слайдов: 32

1 Dummy Variables

Topics for This Chapter 1. Intercept Dummy Variables 2. Slope Dummy Variables 3. Different Intercepts & Slopes 4. Testing Qualitative Effects 5. Are Two Regressions Equal? 6. Interaction Effects 2

Dummy variables 3 Ø Dummy variables, often called binary or dichotomous variables, are explanatory variables that only take two values, usually 0 and 1. Ø These simple variables are a very powerful tool for capturing qualitative characteristics of individuals, such as gender, race, geographic region of residence. Ø In general, we use dummy variables to describe any event that has only two possible outcomes.

Intercept Dummy Variables 4 Dummy variables are binary (0, 1) yt = 1 + 2 Xt + 3 Dt + εt yt = speed of car in miles per hour Xt = age of car in years Dt = 1 if red car, Dt = 0 otherwise. Police: red cars travel faster. H 0: 3 = 0 H 1: 3 > 0
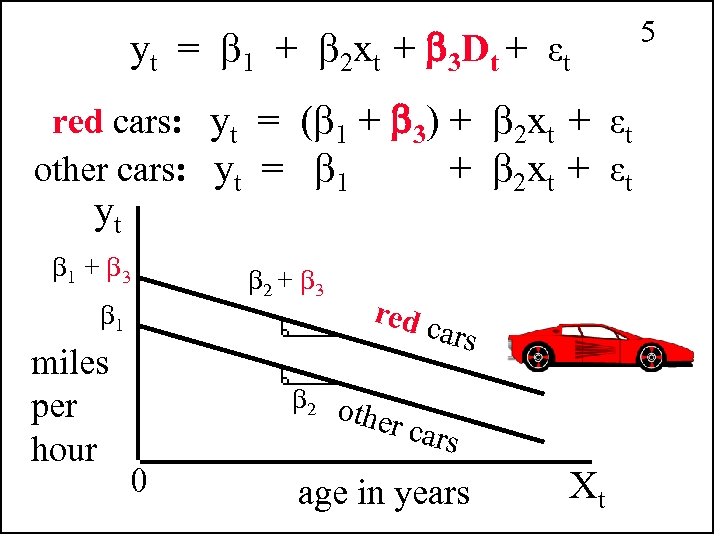
yt = 1 + 2 xt + 3 Dt + εt 5 red cars: yt = ( 1 + 3) + 2 xt + εt other cars: yt = 1 + 2 xt + εt yt 1 + 3 1 miles per hour 2 + 3 red c ars 2 ot her c ars 0 age in years Xt
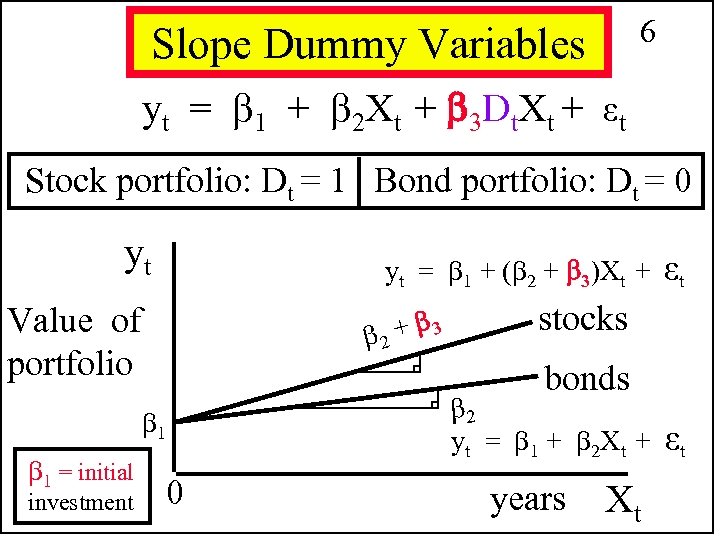
6 Slope Dummy Variables yt = 1 + 2 Xt + 3 Dt. Xt + εt Stock portfolio: Dt = 1 Bond portfolio: Dt = 0 yt yt = 1 + ( 2 + 3)Xt + εt Value of portfolio 2 + 3 bonds 1 1 = initial investment stocks 0 2 yt = 1 + 2 Xt + εt years Xt
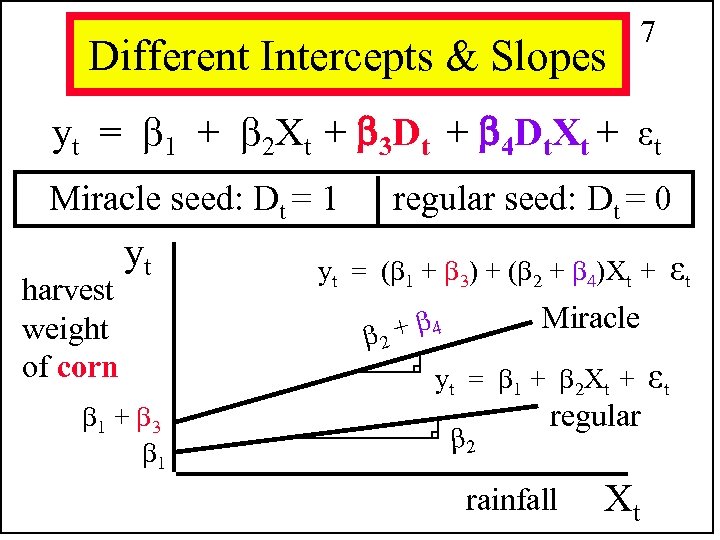
Different Intercepts & Slopes 7 yt = 1 + 2 Xt + 3 Dt + 4 Dt. Xt + εt Miracle seed: Dt = 1 regular seed: Dt = 0 harvest weight of corn yt 1 + 3 1 yt = ( 1 + 3) + ( 2 + 4)Xt + εt Miracle 2 + 4 yt = 1 + 2 Xt + εt 2 regular rainfall Xt
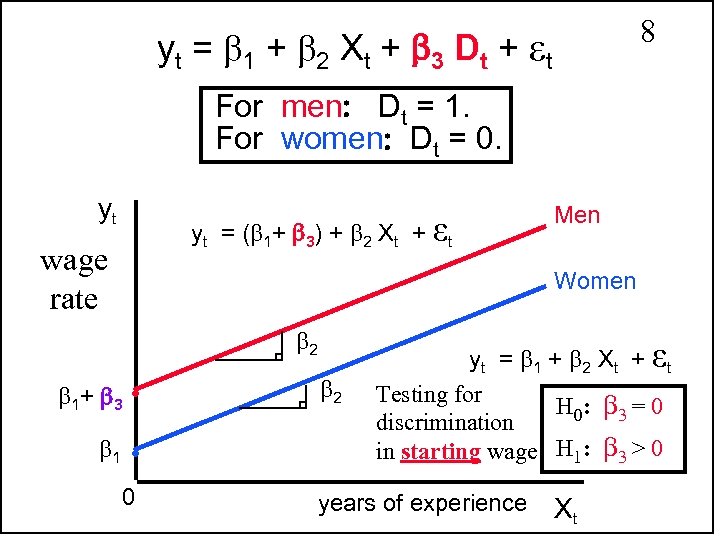
8 yt = 1 + 2 Xt + 3 Dt + εt For men Dt = 1. For women Dt = 0. yt yt = ( 1+ 3) + 2 Xt + εt wage rate Women 2 1+ 3 1 Men . . 0 2 yt = 1 + 2 Xt + εt Testing for H 0: 3 = 0 discrimination in starting wage H 1: 3 > 0 years of experience Xt
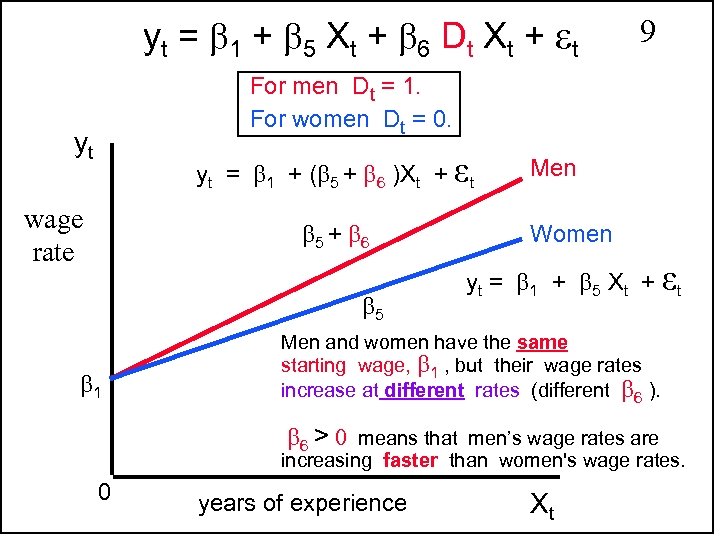
yt = 1 + 5 Xt + 6 Dt Xt + εt 9 For men Dt = 1. For women Dt = 0. yt yt = 1 + ( 5 + 6 )Xt + εt wage rate 5 + 6 5 1 Men Women yt = 1 + 5 Xt + εt Men and women have the same starting wage, 1 , but their wage rates increase at different rates (different 6 ). 6 > means that men’s wage rates are increasing faster than women's wage rates. 0 years of experience Xt
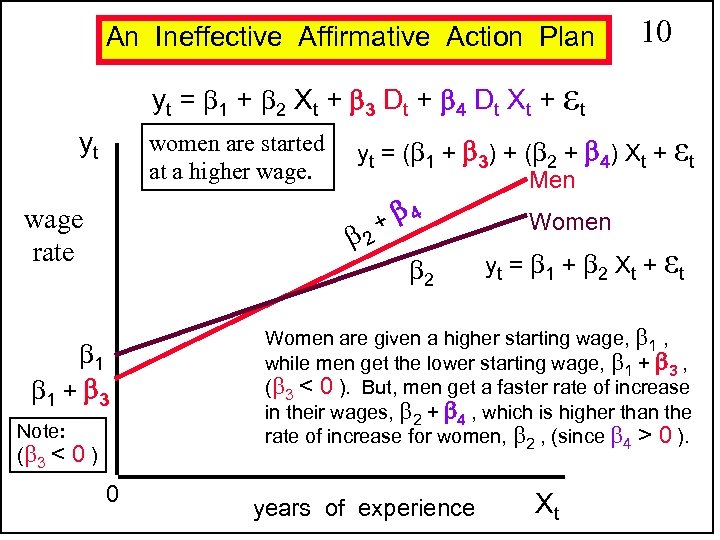
An Ineffective Affirmative Action Plan 10 yt = 1 + 2 Xt + 3 Dt + 4 Dt Xt + εt yt women are started at a higher wage rate yt = ( 1 + 3) + ( 2 + 4) Xt + εt Men 2 1 1 + 3 Note: ( 3 < 0 ) 0 + 4 2 Women yt = 1 + 2 Xt + εt Women are given a higher starting wage, 1 , while men get the lower starting wage, 1 + 3 , ( 3 < 0 ). But, men get a faster rate of increase in their wages, 2 + 4 , which is higher than the rate of increase for women, 2 , (since 4 > 0 ). years of experience Xt

Testing Qualitative Effects 11 1. Test for differences in intercept. 2. Test for differences in slope. 3. Test for differences in both intercept and slope.

men: Dt = 1 ; women: Dt = 0 12 Yt Xt 3 Dt Dt Xt εt 1 2 4 H 0: vs 1: Testing for discrimination in starting wage. b 3 Est. Var b 3 H 0: vs 1: Testing for discrimination in wage increases. intercept b 4 Est. Var b 4 t T 4 slope t T 4

13 Ho: H 1 : otherwise Testing SSE R SSE U 2 SSE U T 4 F , T 4 T SSE U yt b 1 b Xt b Dt Xt and t 1 SSE R T t 1 intercept and slope yt b 1 b 2 X t 2 2

The University Effect on House Prices 14 Ø A real estate economist collects data on two similar neighborhoods, one bordering a large state university, and one that is a neighborhood about 3 miles from the university. Ø Records 1000 observations Ø Dependent Variable: House prices are given in $; Ø Independent Variables: Ø SQFT is the number of square feet of living area. Ø AGE are the house age (years) Ø UTOWN = 1 for homes near the university, 0 otherwise Ø USQFT = SQFT UTOWN Ø POOL = 1 if a pool is present, 0 otherwise Ø FPLACE = 1 is a fireplace is present, 0 otherwise
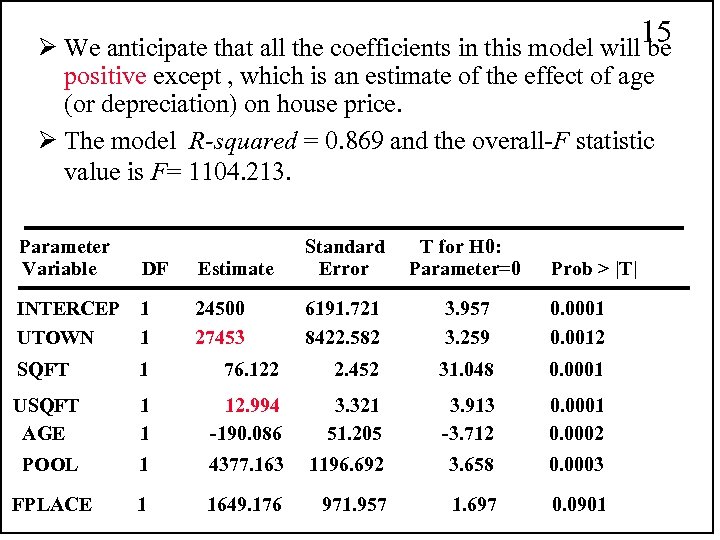
15 Ø We anticipate that all the coefficients in this model will be positive except , which is an estimate of the effect of age (or depreciation) on house price. Ø The model R-squared = 0. 869 and the overall-F statistic value is F= 1104. 213. Parameter Standard T for H 0: Variable DF Estimate Error Parameter=0 Prob > |T| INTERCEP 1 24500 6191. 721 3. 957 0. 0001 UTOWN 1 27453 8422. 582 3. 259 0. 0012 SQFT 1 76. 122 2. 452 31. 048 0. 0001 USQFT 1 12. 994 3. 321 3. 913 0. 0001 AGE 1 -190. 086 51. 205 -3. 712 0. 0002 POOL 1 4377. 163 1196. 692 3. 658 0. 0003 FPLACE 1 1649. 176 971. 957 1. 697 0. 0901

Based on these regression estimates, 16 what do we conclude? Ø We estimate the location premium, for lots near the university, to be $27, 453 Ø We estimate the price per square foot to be $89. 11 (= $76. 122 + $12. 994) for houses near the university, and $76. 12 for houses in other areas. Ø We estimate that houses depreciate $190. 09 per year Ø We estimate that a pool increases the value of a home by $4377. 16 Ø We estimate that a fireplace increases the value of a home by $1649. 17

Are Two Regressions Equal? 17 Chow Test (there are two alternative ways) I. Restricted versus Unrestricted Models men: Dt = 1 ; women: Dt = 0 yt = 1 + 2 Xt + 3 Dt + 4 Dt Xt + εt H 0: 3 = 4 = 0 yt = wage rate vs. H 1: otherwise Xt = years of experience

18 II. Get SSEU separately (running three regressions) Forcing men and women to have same 1, 2. Everyone: yt = 1 + 2 Xt + εt SSER Allowing men and women to be different. Men only: ytm = 1 + 2 Xtm + εtm SSEm Women only: ytw = 1 + 2 Xtw + εtw SSEw (SSER SSEU)/J J = # restrictions F = SSEU /(T K) K=unrestricted coefs. J = 2 K = 4 where SSEU = SSEm + SSEw

19 Interaction Variables 1. Interaction Dummies 2. Polynomial Terms (special case of continuous interaction) 3. Interaction Among Continuous Variables

Interactions Between Qualitative Factors 20 Ø Suppose we are estimating a wage equation, in which an individual’s wages are explained as a function of their experience, skill, and other factors related to productivity. Ø It is customary to include dummy variables for race and gender in such equations. Ø Including just race and gender dummies will not capture interactions between these qualitative factors. Special wage treatment for being “white” and “male” is not captured by separate race and gender dummies. Ø To allow for such a possibility consider the following specification, where for simplicity we use only experience (EXP) as a productivity measure

21 Wage = 1 + 2 EXP + 1 RACE + 2 SEX + (RACE SEX) + ε where 1 measures the effect of race 2 measures the effect of gender measures the effect of being “white” and “male. ”

1. Interaction Dummies 22 Wage Gap between Men and Women yt = wage rate; Xt = experience For men Mt = 1. For women Mt = 0. For black Bt = 1. For nonblack Bt = 0. No Interaction: wage gap assumed the same: yt = 1 + 2 Xt + 3 Mt + 4 Bt + εt Interaction: wage gap depends on race: yt = 1 + 2 X t + 3 M t + 4 B t + 5 M t B t + ε t

23 2. Polynomial Terms Polynomial Regression yt = income; Xt = age Linear in parameters but nonlinear in variables: 2 3 yt = 1 + 2 X t + 3 X t + 4 X t + εt yt 20 30 40 50 60 70 80 90 People retire at different ages or not at all. Xt

Polynomial Regression yt = income; Xt = age yt = 1 + 2 X t + 3 X 2 t + 4 X 3 t + εt Rate income is changing as we age: yt 2 = 2 + 2 3 X t + 3 4 X t Xt Slope changes as X t changes. 24

3. Continuous Interaction 25 Exam grade = f(sleep: Zt , study time: Bt) yt = 1 + 2 Zt + 3 Bt + 4 Zt Bt + εt Sleep and study time do not act independently. More study time will be more effective when combined with more sleep and less effective when combined with less sleep.

continuous interaction 26 Exam grade = f(sleep: Zt , study time: Bt) yt = 1 + 2 Zt + 3 Bt + 4 Zt Bt + εt Your studying is more effective with more sleep. yt = 2 + 4 Zt Bt yt Your mind sorts = 2 + 4 Bt Zt things out while you sleep (when you have things to sort out. )

Exam grade = f(sleep: Zt , study time: Bt) 27 If Zt + Bt = 24 hours, then Bt = (24 Zt) yt = 1 + 2 Zt + 3 Bt + 4 Zt Bt + εt yt = 1+ 2 Zt + 3(24 Zt) + 4 Zt (24 Zt) + εt 2 yt = ( 1+24 3) + ( 2 3+24 4)Zt 4 Z t + εt 2 yt = 1 + 2 Zt + 3 Z t + εt Sleep needed to maximize your exam grade: 2 yt = 2 + 2 3 Zt = 0 Zt = 3 Zt where 2 > 0 and 3 < 0

Qualitative Variables with Several Categories 28 Ø Many qualitative factors have more than two categories. Ø Examples are region of the country (North, South, East, West) and level of educational attainment (less than high school, college, postgraduate). Ø For each category we create a separate binary dummy variable. Ø To illustrate, let us again use a wage equation as an example, and focus only on experience and level of educational attainment (as a proxy for skill) as explanatory variables.

29 Define dummies for educational attainment as follows: Specify the wage equation as Wage = 1 + 2 EXP + 1 E 1 + 2 E 2 + 3 E 3 + ε

Ø First notice that we have not included all the 30 dummy variables for educational attainment. Doing so would have created a model in which exact collinearity exists. Ø Since the educational categories are exhaustive, the sum of the education dummies is equal to 1. Thus the “intercept variable, ” is an exact linear combination of the education dummies. Ø The usual solution to this problem is to omit one dummy variable, which defines a reference group, as we shall see by examining the regression function,

31 Ø 1 measures the expected wage differential between workers who have a high school diploma and those who do not. Ø 2 measures the expected wage differential between workers who have a college degree and those who did not graduate from high school, and so on.

32 Ø The omitted dummy variable, E 0, identifies those who did not graduate from high school. The coefficients of the dummy variables represent expected wage differentials relative to this group. Ø The intercept parameter 1 represents the base wage for a worker with no experience and no high school diploma. Ø Mathematically it does NOT matter which dummy variable is omitted, although the choice of E 0 is convenient in the example above. Ø If we are estimating an equation using geographic dummy variables, N, S, E and W, identifying regions of the country, the choice of which dummy variable to omit is arbitrary.
bac988bc258d40aaed90f68754cebe78.ppt