1 Доцент кафедры радиотехнических систем А С

1

Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Базовые методы модуляции гармонической несущей. Источники: 1) Акулиничев Ю. П. Теория электрической связи. Учебное пособие. – Томск, ТУСУР. – 2007. Разделы 2. 8 - 2. 10 2) Системы и сети передачи информации: Учеб. пособие для вузов / М. В. Гаранин, В. И. Журавлев, СВ. Кунегин. -М. : Радио и связь, 2001. Глава 2 2

Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ ИСТОЧНИКИ 1. Теория электрической связи: учебное пособие/ Ю. П. Акулиничев. - Томск : Томск. гос. ун-т систем упр. и радиоэлектроники, 2007, 214 с. , или Акулиничев Ю. П. Теория электрической связи. Часть 1. Учебнометодическое пособие. – Томск, ТМЦДО. – 2005. – и Часть 2. 2. Акулиничев Ю. П. , Дроздова В. И. Сборник задач по теории информации. – Томск: ТГУ, 1976. – 146 с. 3. Гаранин М. В. , Журавлев В. И. , Кунегин С. В. Системы и сети передачи информации: Учеб. пособие для вузов. – М. : Радио и связь, 2001. – 336 с. 4. Современные технологии цифровых оптоволоконных сетей связи (ATM, PDH, SONET и WDM): производственнопрактическое издание/ Николай Николаевич Слепов. - М. : Радио и связь, 2000. 3

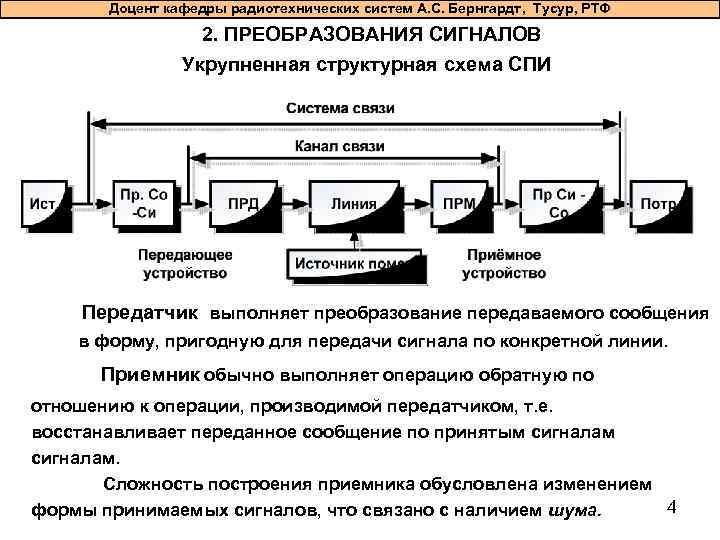Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ 2. ПРЕОБРАЗОВАНИЯ СИГНАЛОВ Укрупненная структурная схема СПИ Передатчик выполняет преобразование передаваемого сообщения в форму, пригодную для передачи сигнала по конкретной линии. Приемник обычно выполняет операцию обратную по отношению к операции, производимой передатчиком, т. е. восстанавливает переданное сообщение по принятым сигналам. Сложность построения приемника обусловлена изменением 4 формы принимаемых сигналов, что связано с наличием шума.

Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ 2. ПРЕОБРАЗОВАНИЯ СИГНАЛОВ Схема цифровой системы передачи непрерывных сообщений m(t) Источник непрерывных сообщений Исходный цифровой (двоичный) поток Аналогоцифровое Преобразование Кодер канала Модулятор Цифроаналоговое Преобразование Форматирование Декодер источника Кодек источника Декодер канала Кодек канала S(t) Линия связи (среда) Принятый цифровой (двоичный) поток m(t) Получатель Кодер источника Демодулятор Модем Ŝ (t) 5

Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ КОДИРОВАНИЕ ЛИНИИ СВЯЗИ (МОДУЛЯЦИЯ). Состоит в таком преобразовании сообщения, чтобы его можно было передать через среду передачи. Обычно это перенос спектра сигналов из низкочастотной области в выделенную для их передачи область высоких частот. 6

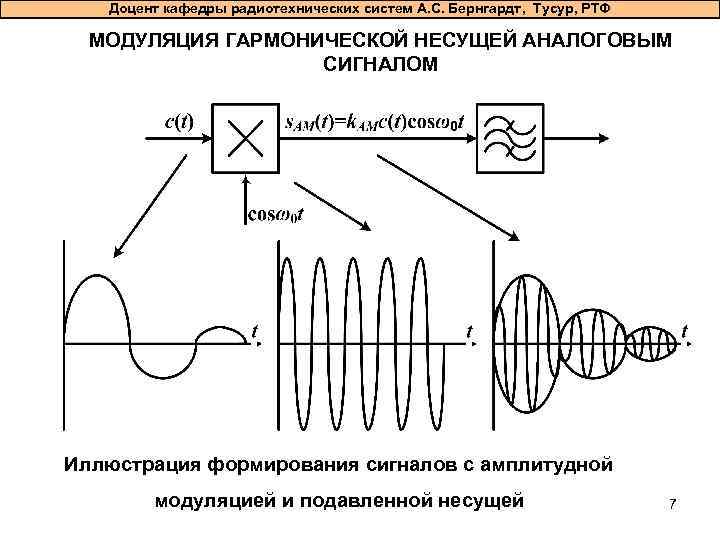Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ МОДУЛЯЦИЯ ГАРМОНИЧЕСКОЙ НЕСУЩЕЙ АНАЛОГОВЫМ СИГНАЛОМ Иллюстрация формирования сигналов с амплитудной модуляцией и подавленной несущей 7

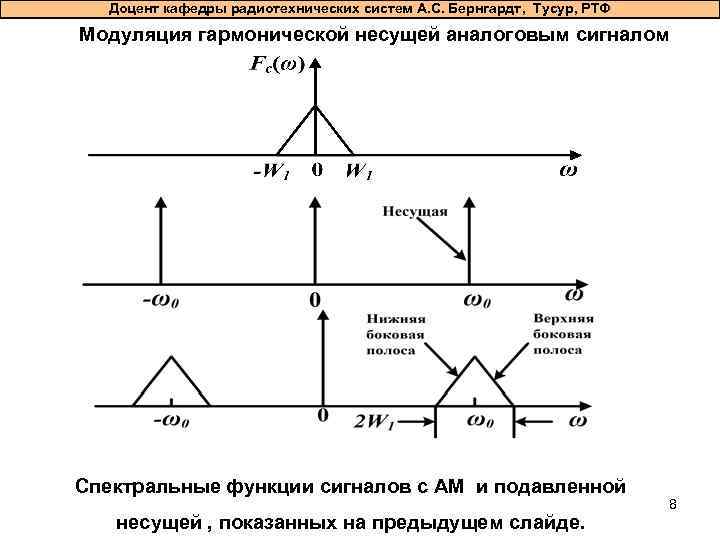Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Модуляция гармонической несущей аналоговым сигналом Спектральные функции сигналов с АМ и подавленной несущей , показанных на предыдущем слайде. 8

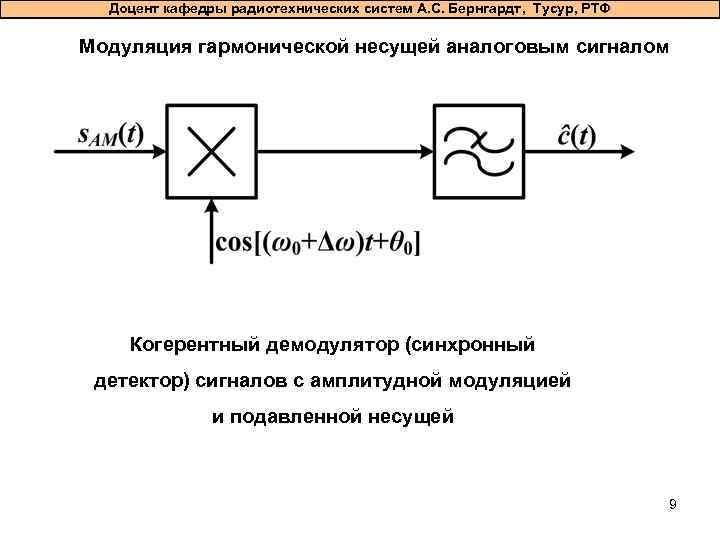Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Модуляция гармонической несущей аналоговым сигналом Когерентный демодулятор (синхронный детектор) сигналов с амплитудной модуляцией и подавленной несущей 9

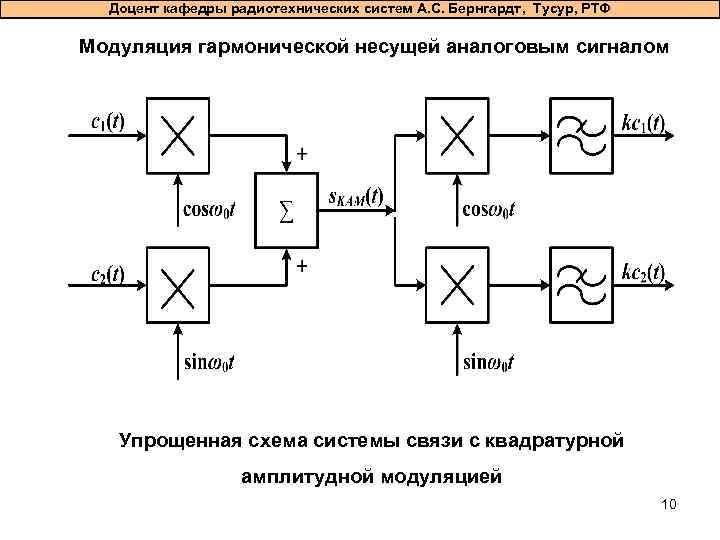Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Модуляция гармонической несущей аналоговым сигналом Упрощенная схема системы связи с квадратурной амплитудной модуляцией 10

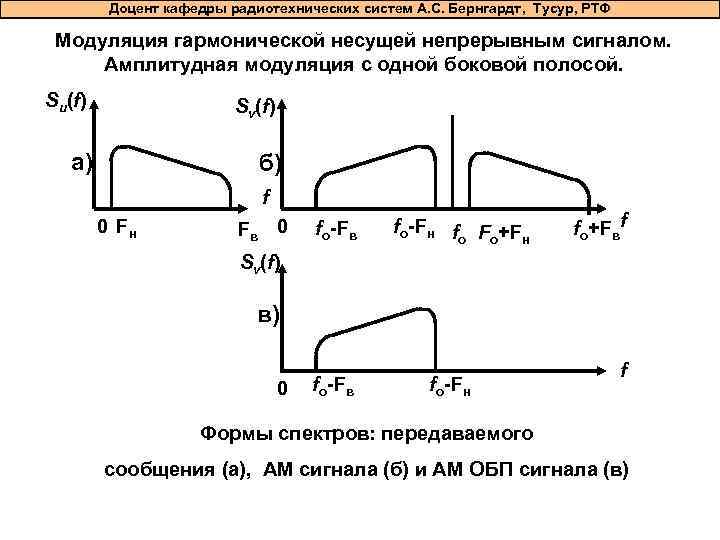Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Модуляция гармонической несущей непрерывным сигналом. Амплитудная модуляция с одной боковой полосой. Su(f) Sv(f) а) б) f 0 Fн Fв 0 fo-Fв fo-Fн f F +F o o н fo+Fвf Sv(f) в) 0 fo-Fв fo-Fн f Формы спектров: передаваемого сообщения (а), АМ сигнала (б) и АМ ОБП сигнала (в)

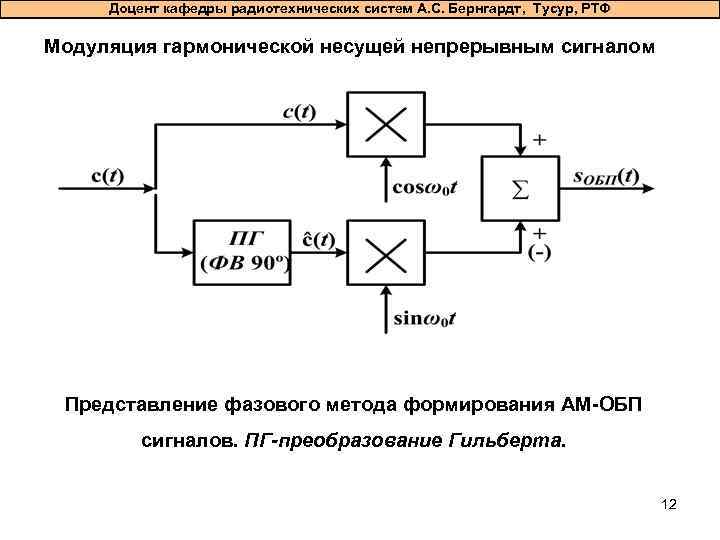Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Модуляция гармонической несущей непрерывным сигналом Представление фазового метода формирования АМ-ОБП сигналов. ПГ-преобразование Гильберта. 12

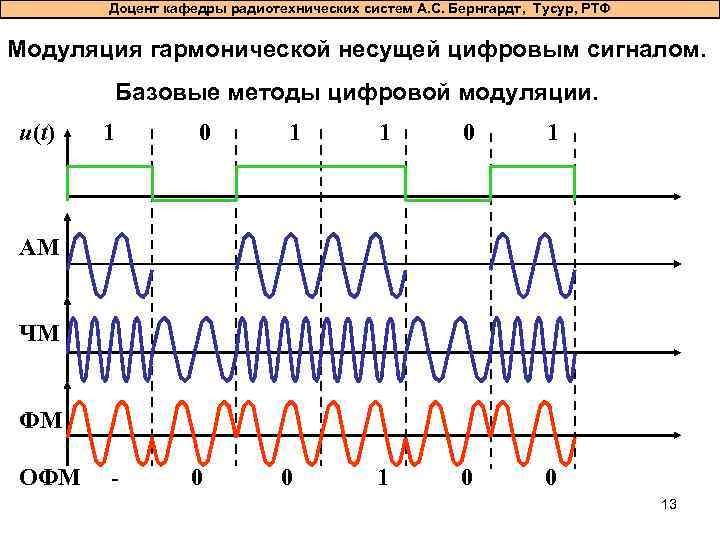Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Модуляция гармонической несущей цифровым сигналом. Базовые методы цифровой модуляции. u(t) 1 0 1 1 0 0 АМ ЧМ ФМ ОФМ - 0 0 13

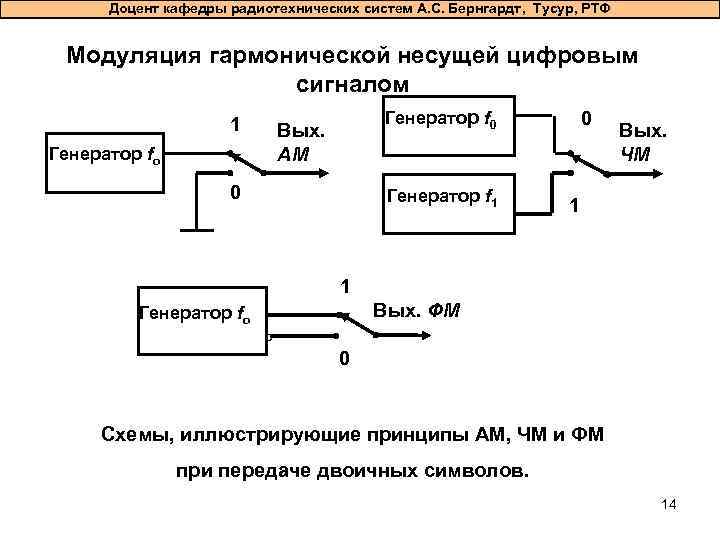Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Модуляция гармонической несущей цифровым сигналом 1 Генератор f 0 Вых. АМ Генератор fо 0 Генератор f 1 0 Вых. ЧМ 1 1 Вых. ФМ Генератор fо о 0 Схемы, иллюстрирующие принципы АМ, ЧМ и ФМ при передаче двоичных символов. 14

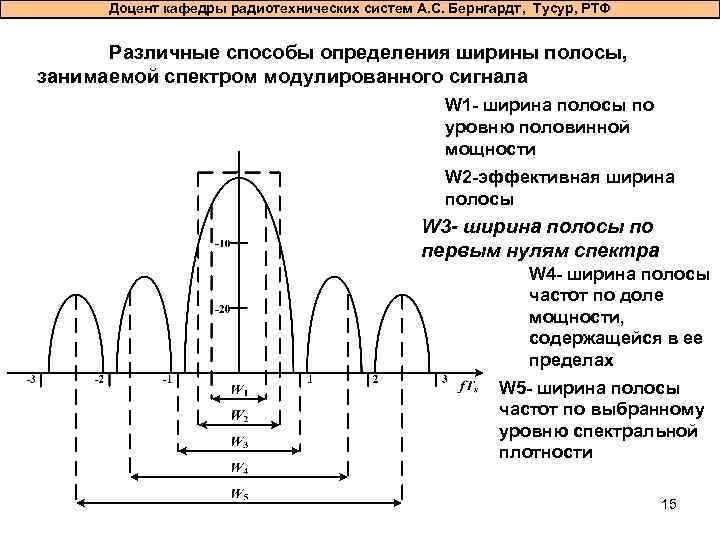Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Различные способы определения ширины полосы, занимаемой спектром модулированного сигнала W 1 - ширина полосы по уровню половинной мощности W 2 -эффективная ширина полосы W 3 - ширина полосы по первым нулям спектра W 4 - ширина полосы частот по доле мощности, содержащейся в ее пределах W 5 - ширина полосы частот по выбранному уровню спектральной плотности 15

Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Следует подчеркнуть, что целесообразность использования того или иного определения ширины полосы частот в значительной мере определяется спецификой решаемой задачи В дальнейшем при сравнении различных видов модуляции будет использоваться определение ширины полосы частот по первым нулям спектральной функции W 3. 16

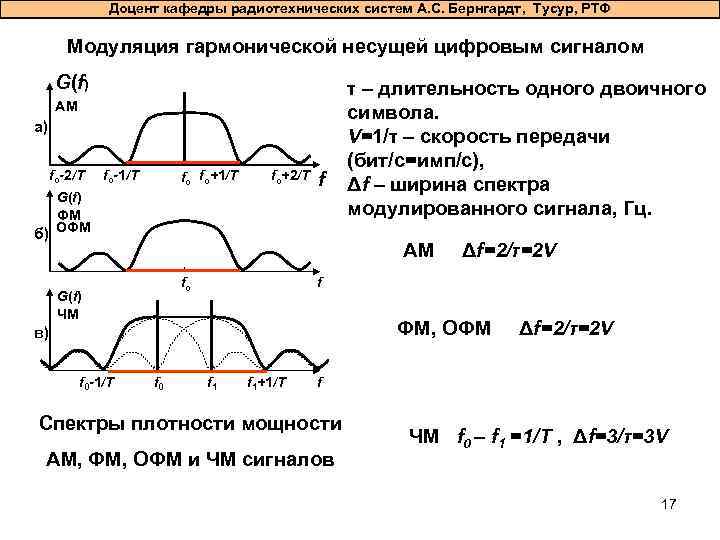Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Модуляция гармонической несущей цифровым сигналом G(f) АМ а) fo-2/Т б) fo-1/Т fo fo+1/Т fo+2/Т G(f) ФМ ОФМ f τ – длительность одного двоичного символа. V=1/τ – скорость передачи (бит/с=имп/с), Δf – ширина спектра модулированного сигнала, Гц. АМ f fo G(f) ЧМ ФМ, ОФМ в) f 0 -1/Т Δf=2/τ=2 V f 0 f 1+1/Т Δf=2/τ=2 V f Спектры плотности мощности АМ, ФМ, ОФМ и ЧМ сигналов ЧМ f 0 – f 1 =1/Т , Δf=3/τ=3 V 17

Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Многопозиционные методы модуляции цифровым сигналом. Для повышения спектральной эффективности (уменьшение f при неизменном значении V) используют многопозиционные методы модуляции/ Многопозиционная модуляция, предполагает переход от двоичного алфавита символов дискретного сообщения к М - ичному: где k- длина преобразуемых последовательностей двоичных символов, М- объем алфавита. Каждый символ из М-ичного алфавита модулирует один или несколько параметров гармонического колебания конечной длительности: амплитуду, частоту, фазу. 18

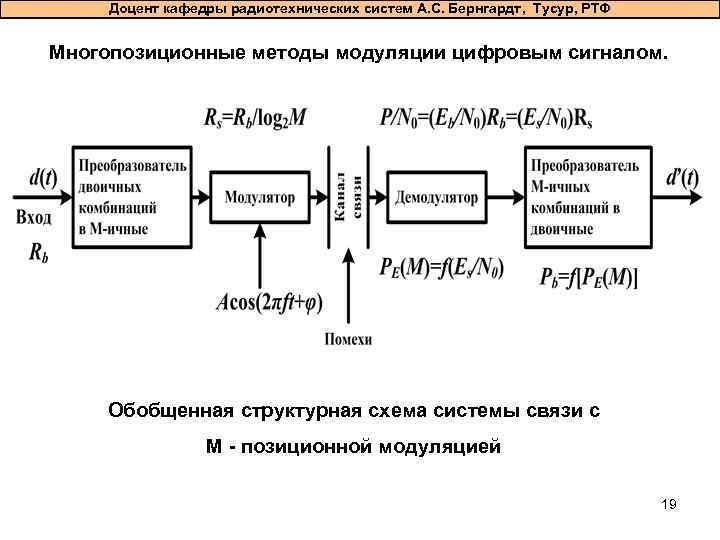Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Многопозиционные методы модуляции цифровым сигналом. Обобщенная структурная схема системы связи с М - позиционной модуляцией 19

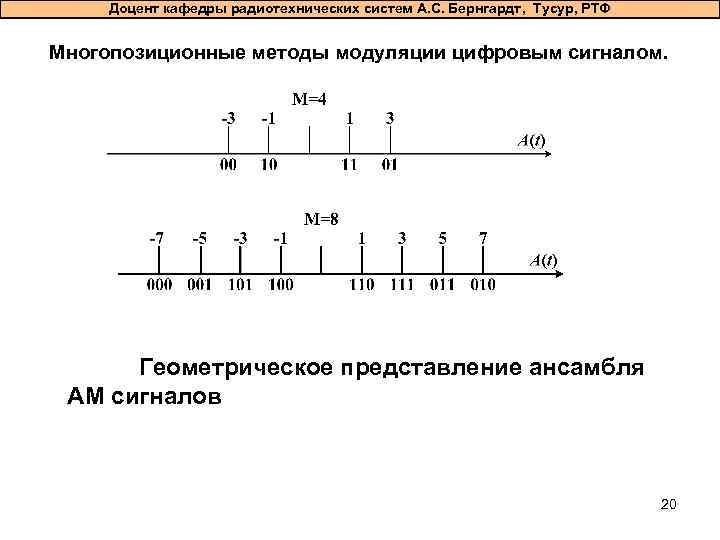Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Многопозиционные методы модуляции цифровым сигналом. Геометрическое представление ансамбля AM сигналов 20

Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Многопозиционные методы модуляции цифровым сигналом. а) k=1, M=2, ФМ-2 (BPSK) 0 1 б) k=2, M=4, ФМ-4, QPSK 1→ 01 2→ 10 0→ 00 3→ 11 в) k=3, M=8, ФМ-8. 2→ 010 1→ 001 3→ 011 0→ 000 4→ 100 5→ 101 6→ 110 7→ 111 Векторное представление колебаний при многократной ФМ 21

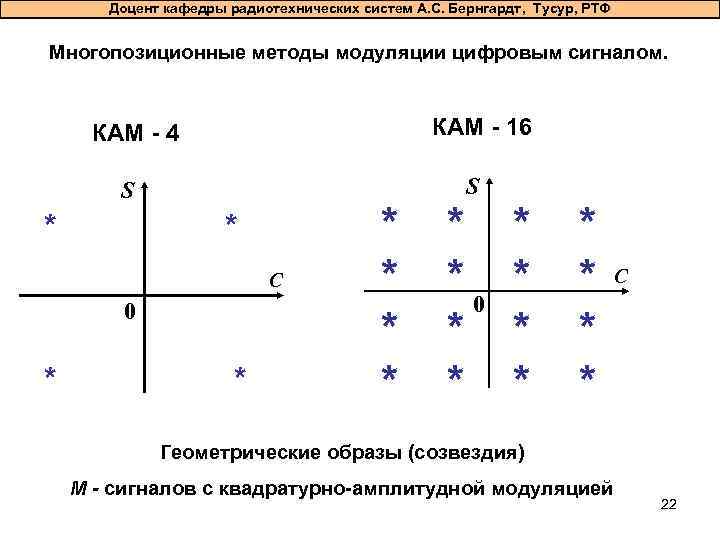Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Многопозиционные методы модуляции цифровым сигналом. КАМ - 16 КАМ - 4 S * * C 0 * * * S * *0 * * * * * C Геометрические образы (созвездия) М - сигналов с квадратурно-амплитудной модуляцией 22

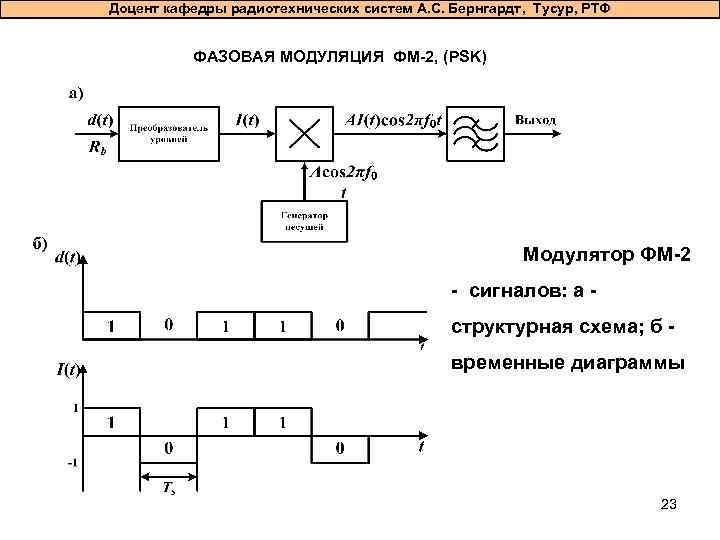Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ ФАЗОВАЯ МОДУЛЯЦИЯ ФМ-2, (PSK) Модулятор ФМ-2 - сигналов: а структурная схема; б временные диаграммы 23

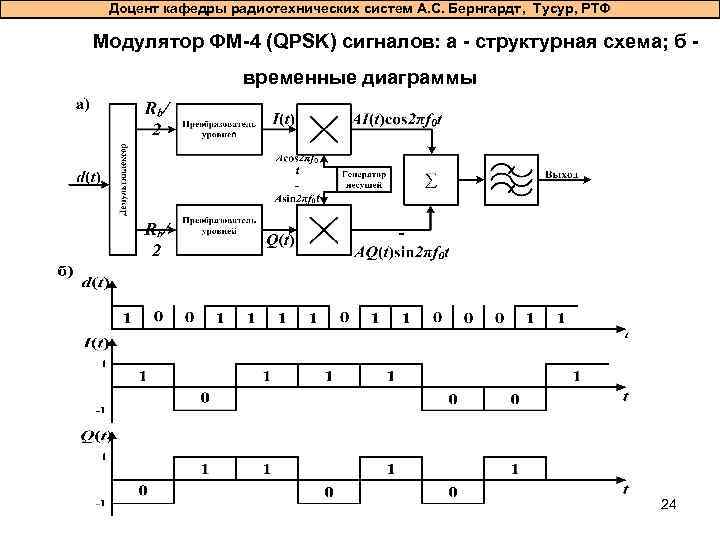Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Модулятор ФМ-4 (QPSK) сигналов: а - структурная схема; б временные диаграммы 24

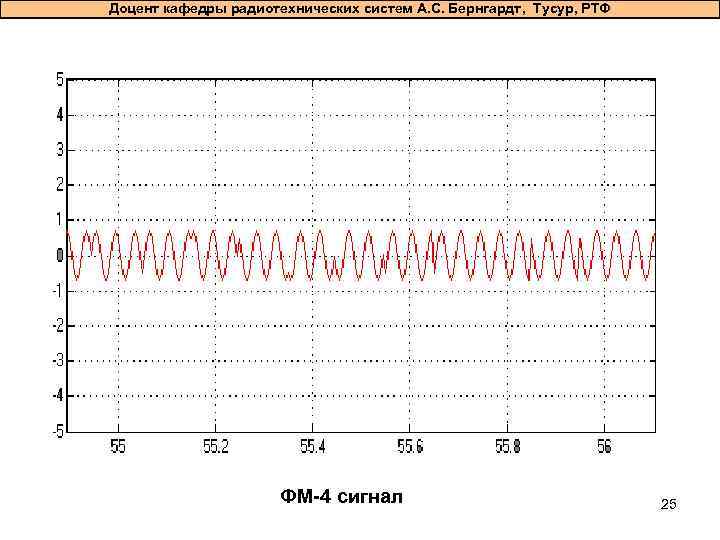Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ ФМ-4 сигнал 25

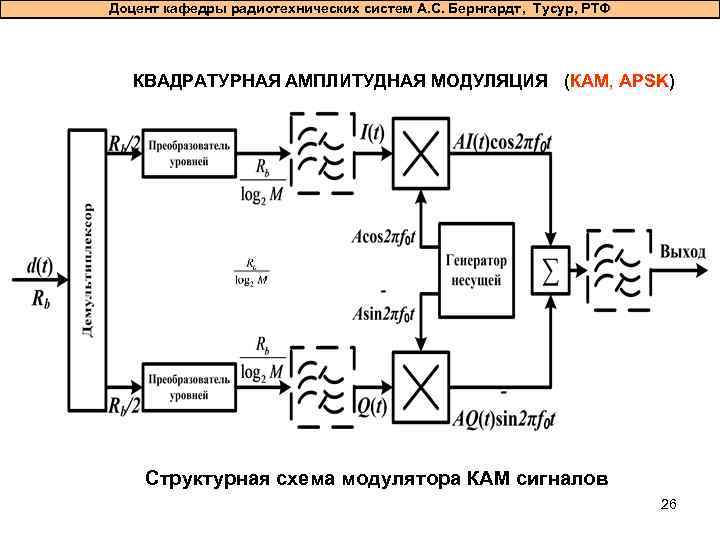Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ КВАДРАТУРНАЯ АМПЛИТУДНАЯ МОДУЛЯЦИЯ (КАМ, APSK) Структурная схема модулятора КАМ сигналов 26

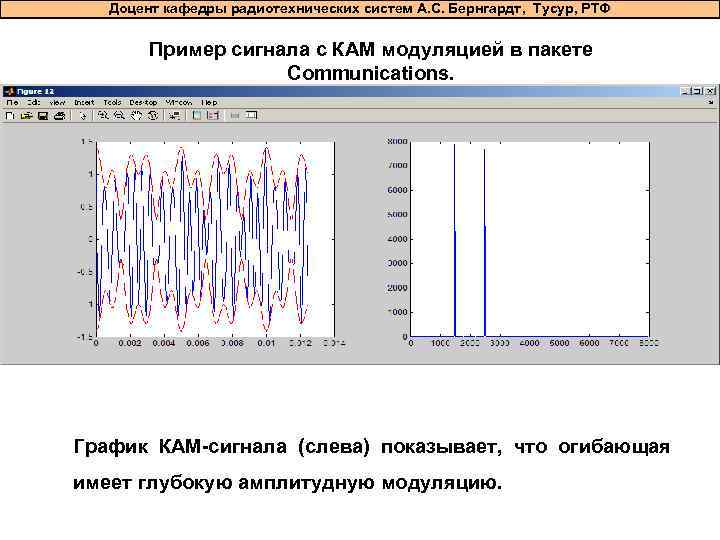Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Пример сигнала с КАМ модуляцией в пакете Communications. График КАМ-сигнала (слева) показывает, что огибающая имеет глубокую амплитудную модуляцию.

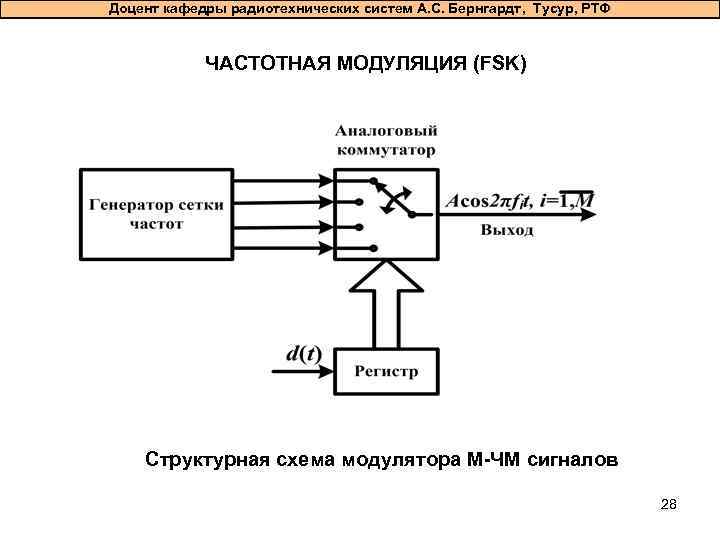Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ ЧАСТОТНАЯ МОДУЛЯЦИЯ (FSK) Структурная схема модулятора М-ЧМ сигналов 28

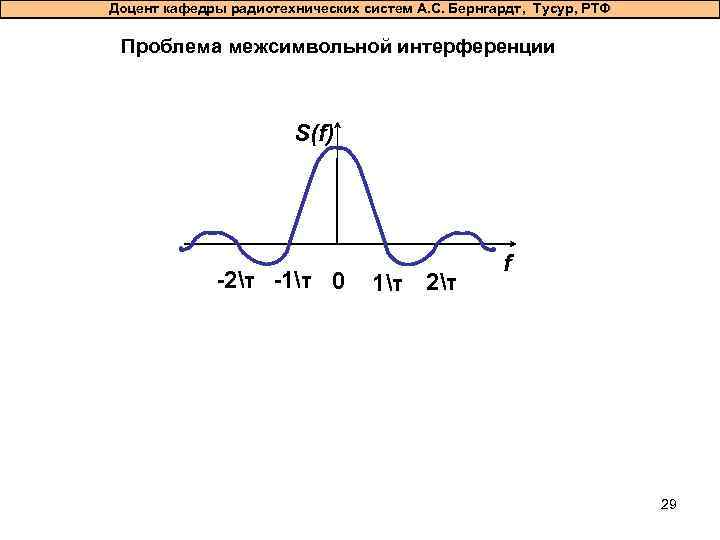Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Проблема межсимвольной интерференции S(f) -2τ -1τ 0 1τ 2τ f 29

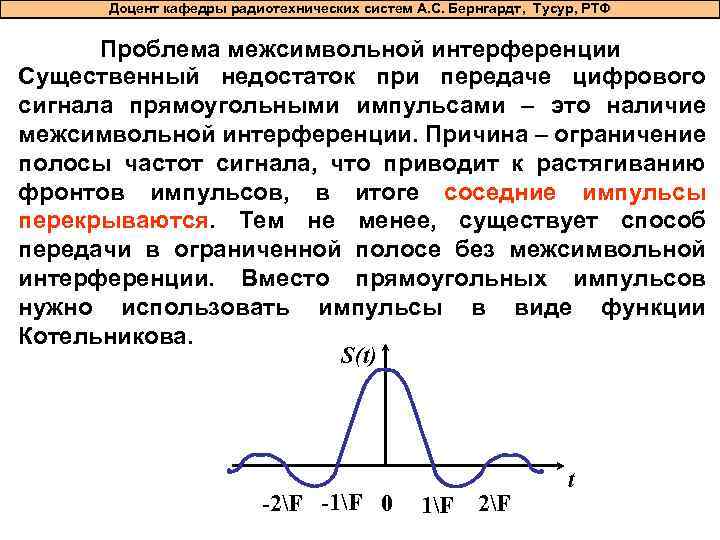Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Проблема межсимвольной интерференции Существенный недостаток при передаче цифрового сигнала прямоугольными импульсами – это наличие межсимвольной интерференции. Причина – ограничение полосы частот сигнала, что приводит к растягиванию фронтов импульсов, в итоге соседние импульсы перекрываются. Тем не менее, существует способ передачи в ограниченной полосе без межсимвольной интерференции. Вместо прямоугольных импульсов нужно использовать импульсы в виде функции Котельникова. S(t) -2F -1F 0 1F 2F t

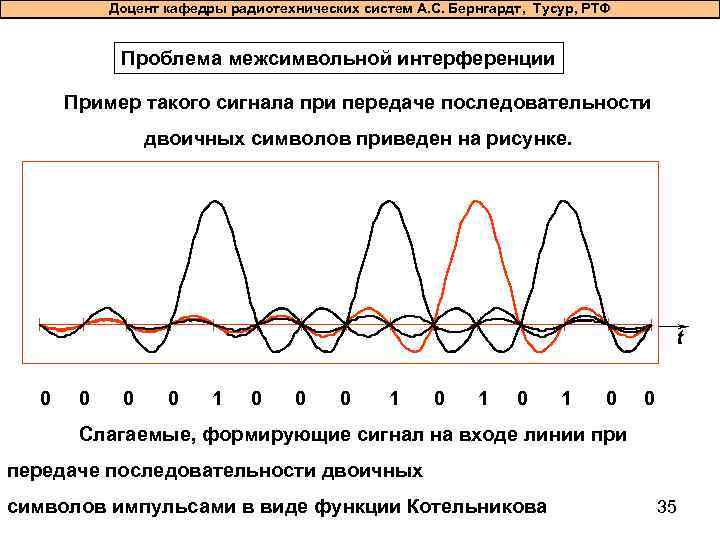
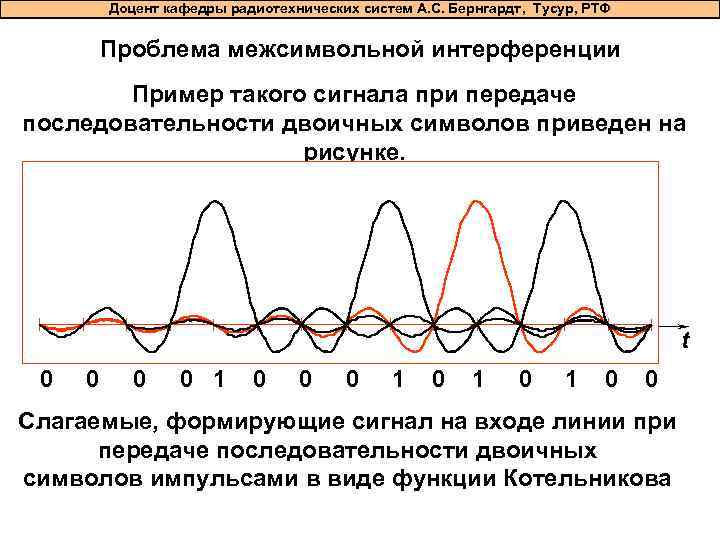Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Проблема межсимвольной интерференции Пример такого сигнала при передаче последовательности двоичных символов приведен на рисунке. t 0 0 1 0 1 0 0 Слагаемые, формирующие сигнал на входе линии при передаче последовательности двоичных символов импульсами в виде функции Котельникова

Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Проблема межсимвольной интерференции Существует метод передачи с использованием ортогональных частотно-разделенных сигналов (Orthogonal Frequency-Division Multiplexing (OFDM)). Для его реализации в полосе частот Δf = 1/τ, минимально необходимой для последовательной передачи радиоимпульсов длительности τ, организуют n гармонических поднесущих с шагом по частоте, равным Δf /n. Символы комбинации передают одновременно на этих поднесущих, используя один из методов манипуляции (обычно ОФМ или КАМ). В каждом субканале передаются радиоимпульсы прямоугольной формы, при этом форму спектра каждого из них задает функция Котельникова, сдвинутая по оси частот.

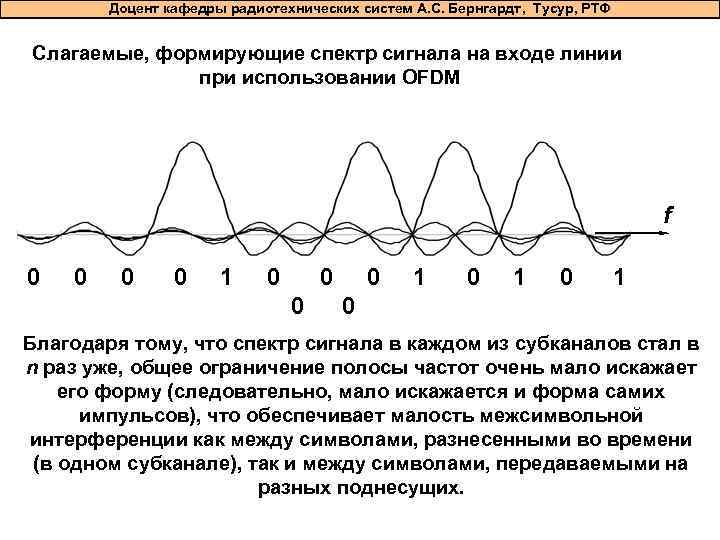Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Слагаемые, формирующие спектр сигнала на входе линии при использовании OFDM f 0 0 0 0 1 0 1 0 Благодаря тому, что спектр сигнала в каждом из субканалов стал в n раз уже, общее ограничение полосы частот очень мало искажает его форму (следовательно, мало искажается и форма самих импульсов), что обеспечивает малость межсимвольной интерференции как между символами, разнесенными во времени (в одном субканале), так и между символами, передаваемыми на разных поднесущих.

Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Спектральная плотность мощности OFDM сигнала.

Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Проблема межсимвольной интерференции Пример такого сигнала при передаче последовательности двоичных символов приведен на рисунке. t 0 0 1 0 1 0 0 Слагаемые, формирующие сигнал на входе линии при передаче последовательности двоичных символов импульсами в виде функции Котельникова 35

Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Проблема межсимвольной интерференции Существует также метод передачи с использованием ортогональных частотно-разделенных сигналов (Orthogonal Frequency-Division Multiplexing (OFDM)). Для его реализации в полосе частот Δf = 1/τ, минимально необходимой для последовательной передачи радиоимпульсов длительности T, организуют n гармонических поднесущих с шагом по частоте, равным Δf /n, частота к-й поднесущей равна к/n. T. Символы комбинации передают одновременно на этих поднесущих, используя один из методов манипуляции (обычно ОФМ или КАМ). Следовательно, длительность каждого символа в n раз больше. В каждом субканале передаются радиоимпульсы прямоугольной формы, при этом форму спектра каждого из них задает функция 36 Котельникова, сдвинутая по оси частот.

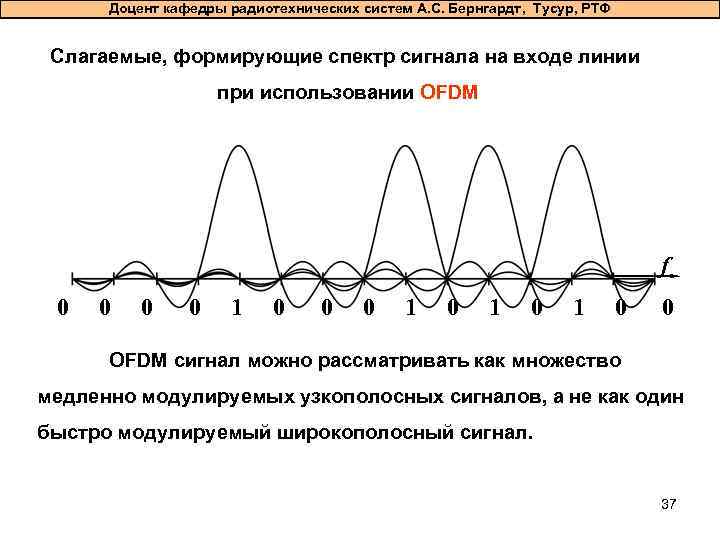Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Слагаемые, формирующие спектр сигнала на входе линии при использовании OFDM f 0 0 1 0 1 0 0 OFDM сигнал можно рассматривать как множество медленно модулируемых узкополосных сигналов, а не как один быстро модулируемый широкополосный сигнал. 37

Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Слагаемые, формирующие спектр сигнала на входе линии при использовании OFDM Благодаря тому, что спектр сигнала в каждом из субканалов стал в n раз уже, общее ограничение полосы частот очень мало искажает его форму (следовательно, мало искажается и форма самих импульсов), что обеспечивает малость межсимвольной интерференции как между символами, разнесенными во времени (в одном субканале), так и между символами, передаваемыми на разных поднесущих. 38

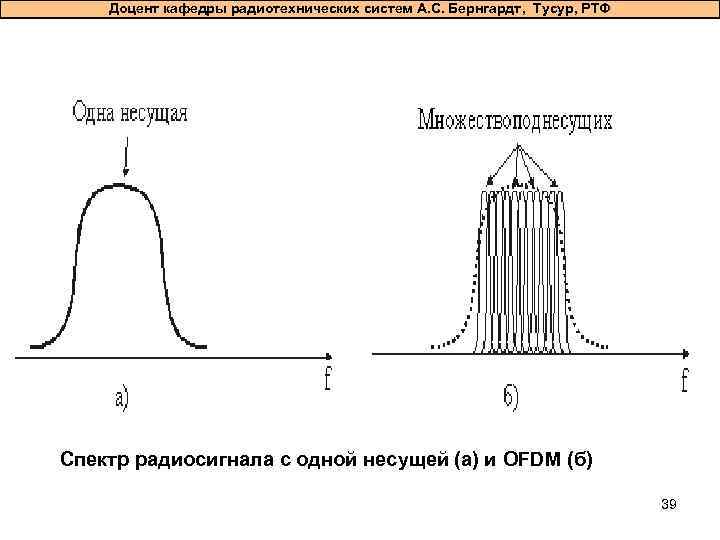Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Спектр радиосигнала с одной несущей (а) и OFDM (б) 39

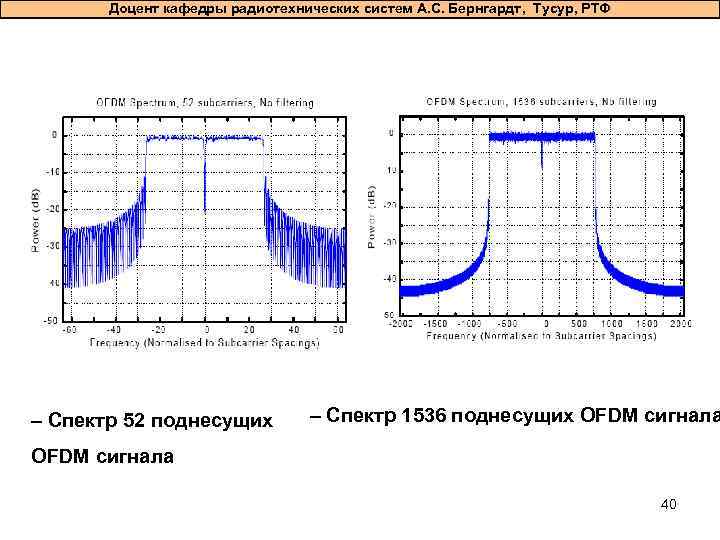Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ – Спектр 52 поднесущих – Спектр 1536 поднесущих OFDM сигнала 40

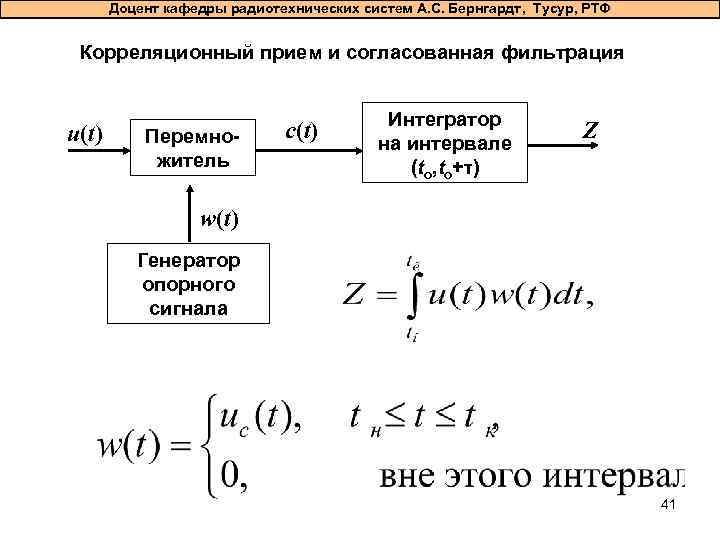Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Корреляционный прием и согласованная фильтрация u(t) Перемножитель c(t) Интегратор на интервале (to, to+τ) Z w(t) Генератор опорного сигнала 41

Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Корреляционный прием и согласованная фильтрация Линейный фильтр с постоянными параметрами, согласованный с сигналом uc(t), имеет импульсную характеристику В момент окончания сигнала uc( tk ) имеем Отношение сигнал/шум по мощности на выходе q=2 Ес/N 0, где N 0 – спектральная плотность мощности белого шума, а Ес - энергия сигнала. 42

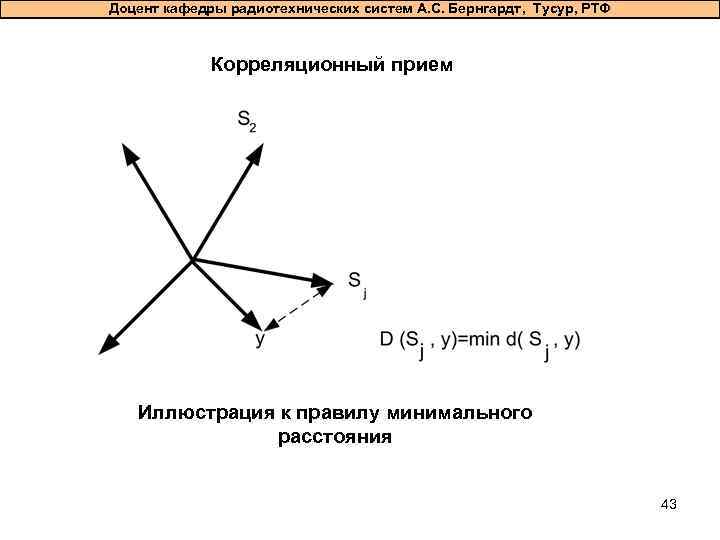Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Корреляционный прием Иллюстрация к правилу минимального расстояния 43

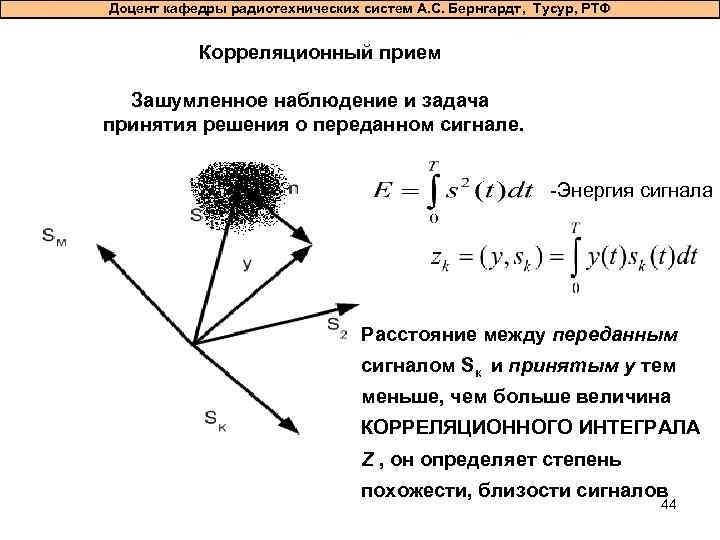Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Корреляционный прием Зашумленное наблюдение и задача принятия решения о переданном сигнале. -Энергия сигнала Расстояние между переданным сигналом Sк и принятым у тем меньше, чем больше величина КОРРЕЛЯЦИОННОГО ИНТЕГРАЛА Z , он определяет степень похожести, близости сигналов 44

Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ Корреляционный приемник двоичного сигнала АМ ЧМ, ФМ Решается задача обнаружения импульса u(t) на фоне шума, при этом Решается задача различения сигналов u 0(t) и u 0(t) на фоне шума, при этом 45

Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ 46

Доцент кафедры радиотехнических систем А. С. Бернгардт, Тусур, РТФ 47