Скачать презентацию 1 COMP 3503 Automated Discovery and Clustering Methods Скачать презентацию 1 COMP 3503 Automated Discovery and Clustering Methods

f6261347a30650e91a7039ab87387593.ppt

  • Количество слайдов: 57

1 COMP 3503 Automated Discovery and Clustering Methods Daniel L. Silver Cog. Nova Technologies 1 COMP 3503 Automated Discovery and Clustering Methods Daniel L. Silver Cog. Nova Technologies

2 Agenda q Automated Exploration/Discovery (unsupervised clustering methods) q K-Means Clustering Method q Kohonen 2 Agenda q Automated Exploration/Discovery (unsupervised clustering methods) q K-Means Clustering Method q Kohonen Self Organizing Maps (SOM) Cog. Nova Technologies

3 Overview of Modeling Methods q Automated Exploration/Discovery • • q Prediction/Classification • • 3 Overview of Modeling Methods q Automated Exploration/Discovery • • q Prediction/Classification • • • q e. g. . discovering new market segments distance and probabilistic clustering algorithmsx 2 • • B x 1 e. g. . forecasting gross sales given current factors statistics (regression, K-nearest neighbour) artificial neural networks, genetic algorithms f(x) Explanation/Description • A e. g. . characterizing customers by demographics inductive decision trees/rules rough sets, Bayesian belief nets if age > 35 x and income < $35 k then. . . Cog. Nova Technologies

4 Automated Exploration/Discovery Through Unsupervised Learning Objective: To induce a model without use of 4 Automated Exploration/Discovery Through Unsupervised Learning Objective: To induce a model without use of a target (supervisory) variable such that similar examples are grouped into selforganized clusters or catagories. This can be considered a method of unsupervised concept learning. C A There is no explicit teaching B x 2 signal. x 1 Cog. Nova Technologies

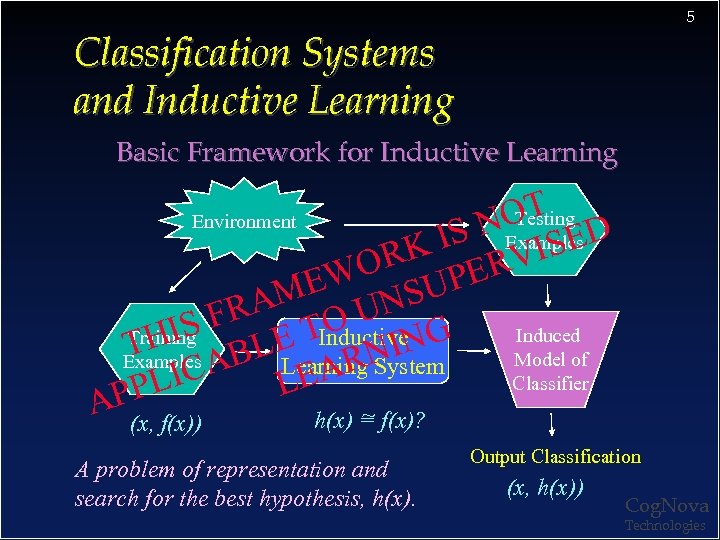5 Classification Systems and Inductive Learning Basic Framework for Inductive Learning Testing OT D 5 Classification Systems and Inductive Learning Basic Framework for Inductive Learning Testing OT D N Examples IS VISE RK ER WO UP ME UNS RA O IS F LE T Induced Training Inductive. NG H T NI Model of Examples AB Learning System R EA Classifier LIC L P AP ~ Environment (x, f(x)) h(x) = f(x)? A problem of representation and search for the best hypothesis, h(x). Output Classification (x, h(x)) Cog. Nova Technologies

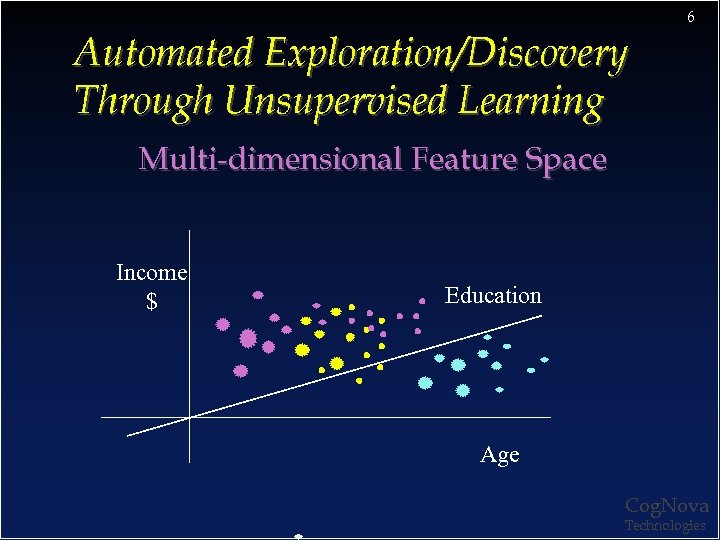6 Automated Exploration/Discovery Through Unsupervised Learning Multi-dimensional Feature Space Income $ Education Age Cog. 6 Automated Exploration/Discovery Through Unsupervised Learning Multi-dimensional Feature Space Income $ Education Age Cog. Nova Technologies

7 Automated Exploration/Discovery Through Unsupervised Learning Common Uses q Market segmentation q Population catagorization 7 Automated Exploration/Discovery Through Unsupervised Learning Common Uses q Market segmentation q Population catagorization q Product/service catagorization q Automated subject indexing (WEBSOM) q Multi-variable (vector) quantization • reduce several variables to one Cog. Nova Technologies

WHF 3. 6 & 4. 8 Clustering techniques apply when there is no class WHF 3. 6 & 4. 8 Clustering techniques apply when there is no class to be predicted ●Aim: divide instances into “natural” groups ● Clusters can be: ● disjoint vs. overlapping ●deterministic vs. probabilistic ●flat vs. hierarchical ● Cog. Nova Technologies

Representing clusters I Simple 2 -D representation 9 Venn diagram Overlapping clusters Cog. Nova Representing clusters I Simple 2 -D representation 9 Venn diagram Overlapping clusters Cog. Nova Technologies

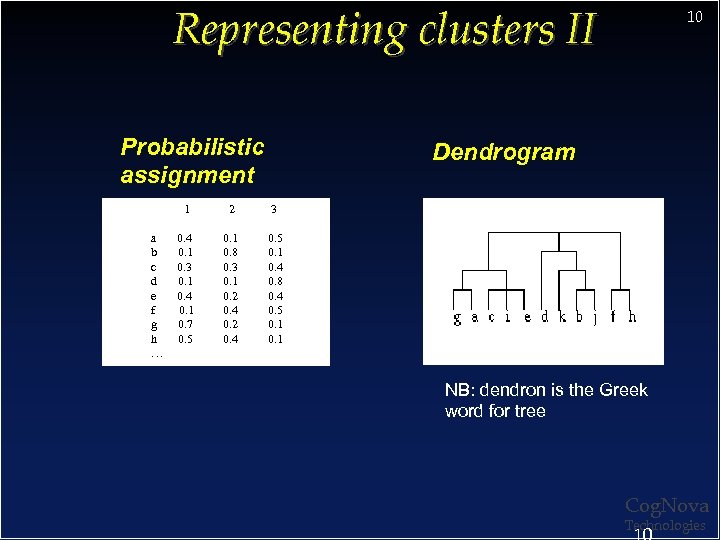Representing clusters II Probabilistic assignment 1 Dendrogram 2 3 a 0. 4 b 0. Representing clusters II Probabilistic assignment 1 Dendrogram 2 3 a 0. 4 b 0. 1 c 0. 3 d 0. 1 e 0. 4 f 0. 1 g 0. 7 h 0. 5 … 10 0. 1 0. 5 0. 8 0. 1 0. 3 0. 4 0. 1 0. 8 0. 2 0. 4 0. 5 0. 2 0. 1 0. 4 0. 1 NB: dendron is the Greek word for tree Cog. Nova Technologies

3. 6 & 4. 8 Clustering 11 The classic clustering algorithm -- k-means clusters 3. 6 & 4. 8 Clustering 11 The classic clustering algorithm -- k-means clusters are disjoint, deterministic, and flat ● Cog. Nova Technologies

12 K-Means Clustering Method q Consider m examples each with 2 attributes [x, y] 12 K-Means Clustering Method q Consider m examples each with 2 attributes [x, y] in a 2 D input space q Method depends on storing all examples q Set number of clusters, K q Centroid of clusters is initially the average coordinates of first K examples or randomly chosen coordinates Cog. Nova Technologies

13 K-Means Clustering Method q Until cluster boundaries stop changing • Assign each example 13 K-Means Clustering Method q Until cluster boundaries stop changing • Assign each example to the cluster who’s centroid is nearest - using some distance measure (e. g. Euclidean distance) • Recalculate centroid of each cluster: e. g. [mean(x), mean(y)] for all examples currently in cluster K Cog. Nova Technologies

3. 6 & 4. 8 Clustering DEMO: http: //home. dei. polimi. it/matteucc/Clustering/tutorial_ht ml/Applet. KM. 3. 6 & 4. 8 Clustering DEMO: http: //home. dei. polimi. it/matteucc/Clustering/tutorial_ht ml/Applet. KM. html 14 Cog. Nova Technologies

15 K-Means Clustering Method q Advantages: • simple algorithm to implement • can form 15 K-Means Clustering Method q Advantages: • simple algorithm to implement • can form very interesting groupings • clusters can be characterized by attributes / values • sequential learning method q Disadvantages: • • all variables must be ordinal in nature problems transforming categorical variables requires lots of memory, computation time does poorly for large numbers of attributes (curse of dimensionality) Cog. Nova Technologies

Discussion 16 Algorithm minimizes squared distance to cluster centers ●Result can vary significantly based Discussion 16 Algorithm minimizes squared distance to cluster centers ●Result can vary significantly based on initial choice of seeds ●Can get trapped in local minimum initial Example: ● cluster centres instances To increase chance of finding global optimum: restart with different random seeds ●Can we applied recursively with k = 2 ● Cog. Nova Technologies

17 Kohonen SOM (Self Organizing Feature Map) Implements a version of K-Means q Two 17 Kohonen SOM (Self Organizing Feature Map) Implements a version of K-Means q Two layer feed-forward neural network q Input layer fully connected to an output layer of N outputs arranged in 2 D; weights initialized to small random values q Objective is to arrange the outputs into a map which is topologically organized according to the features presented in the data q Cog. Nova Technologies

18 Kohonen SOM The Training Algorithm Present an example to the inputs q The 18 Kohonen SOM The Training Algorithm Present an example to the inputs q The winning output is that whose weights are “closest” to the input values (e. g. Euclidean dist. ) q Adjust the winners weights slightly to make it more like the example q Adjust the weights of the neighbouring output nodes relative to proximity to chosen output node q Reduce the neighbourhood size q Repeated for I iterations through examples Cog. Nova Technologies

19 SOM Demos q q http: //www. eee. metu. edu. tr/~alatan/Courses/Dem o/Kohonen. htm http: 19 SOM Demos q q http: //www. eee. metu. edu. tr/~alatan/Courses/Dem o/Kohonen. htm http: //davis. wpi. edu/~matt/courses/soms/applet. html Cog. Nova Technologies

20 Kohonen SOM In the end, the network effectively quantizes the input vector of 20 Kohonen SOM In the end, the network effectively quantizes the input vector of each example to a single output node q The weights to that node indicate the feature values that characterize the cluster q Topology of map shows association/ proximity of clusters q Biological justification - evidence of localized topological mapping in neocortex q Cog. Nova Technologies

21 Faster distance calculations Can we use k. D-trees or ball trees to speed 21 Faster distance calculations Can we use k. D-trees or ball trees to speed up the process? Yes: ● First, build tree, which remains static, for all the data points ●At each node, store number of instances and sum of all instances ●In each iteration, descend tree and find out which cluster each node belongs to ● Can stop descending as soon as we find out that a node belongs entirely to a particular cluster ●Use statistics stored at the nodes to compute new cluster centers ● Cog. Nova Technologies

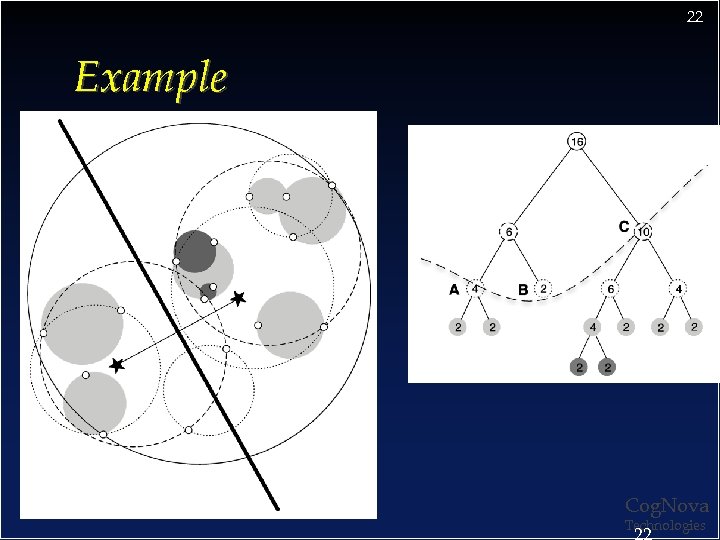22 Example Cog. Nova Technologies 22 Example Cog. Nova Technologies

23 6. 8 Clustering: how many clusters? How to choose k in k-means? Possibilities: 23 6. 8 Clustering: how many clusters? How to choose k in k-means? Possibilities: ● Choose k that minimizes cross-validated squared distance to cluster centers ●Use penalized squared distance on the training data ( eg. using an MDL criterion) ●Apply k-means recursively with k = 2 and use stopping criterion (eg. based on MDL) ● Seeds for subclusters can be chosen by seeding along direction of greatest variance in cluster (one standard deviation away in each direction from cluster center of parent cluster) ●Implemented in algorithm called X-means (using Bayesian Information Criterion instead of MDL) ● Cog. Nova Technologies

24 Hierarchical clustering ● Recursively splitting clusters produces a hierarchy that can be represented 24 Hierarchical clustering ● Recursively splitting clusters produces a hierarchy that can be represented as a dendogram Could also be represented as a Venn diagram of sets and subsets (without intersections) Height of each node in the dendogram can be made proportional to the dissimilarity between its children Cog. Nova Technologies

25 Agglomerative clustering ● ● Bottom-up approach Simple algorithm Requires a distance/similarity measure Start 25 Agglomerative clustering ● ● Bottom-up approach Simple algorithm Requires a distance/similarity measure Start by considering each instance to be a cluster Find the two closest clusters and merge them Continue merging until only one cluster is left The record of mergings forms a hierarchical clustering structure – a binary dendogram Cog. Nova Technologies

26 Distance measures ● ● Single-linkage Minimum distance between the two clusters Distance between 26 Distance measures ● ● Single-linkage Minimum distance between the two clusters Distance between the clusters closest two members Can be sensitive to outliers Complete-linkage Maximum distance between the two clusters Two clusters are considered close only if all instances in their union are relatively similar Also sensitive to outliers Seeks compact clusters Cog. Nova Technologies

27 Distance measures cont. ● ● Compromise between the extremes of minimum and maximum 27 Distance measures cont. ● ● Compromise between the extremes of minimum and maximum distance Represent clusters by their centroid, and use distance between centroids – centroid linkage ● ● Works well for instances in multidimensional Euclidean space Not so good if all we have is pairwise similarity between instances Calculate average distance between each pair of members of the two clusters – average-linkage Technical deficiency of both: results depend on the numerical scale on which distances are measured Cog. Nova Technologies

28 More distance measures ● Group-average clustering ● Uses the average distance between all 28 More distance measures ● Group-average clustering ● Uses the average distance between all members of the merged cluster Differs from average-linkage because it includes pairs from the same original cluster Ward's clustering method Calculates the increase in the sum of squares of the distances of the instances from the centroid before and after fusing two clusters Minimize the increase in this squared distance at each clustering step All measures will produce the same result if the clusters Cog. Nova are compact and well separated ● Technologies

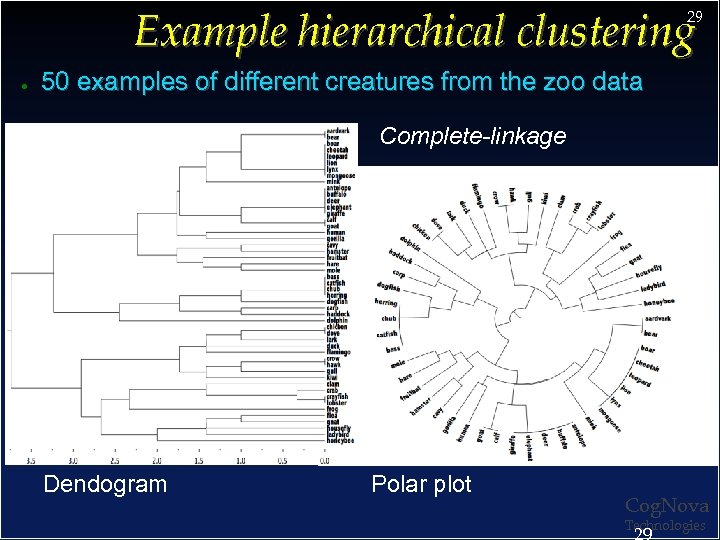Example hierarchical clustering 29 ● 50 examples of different creatures from the zoo data Example hierarchical clustering 29 ● 50 examples of different creatures from the zoo data Complete-linkage Dendogram Polar plot Cog. Nova Technologies

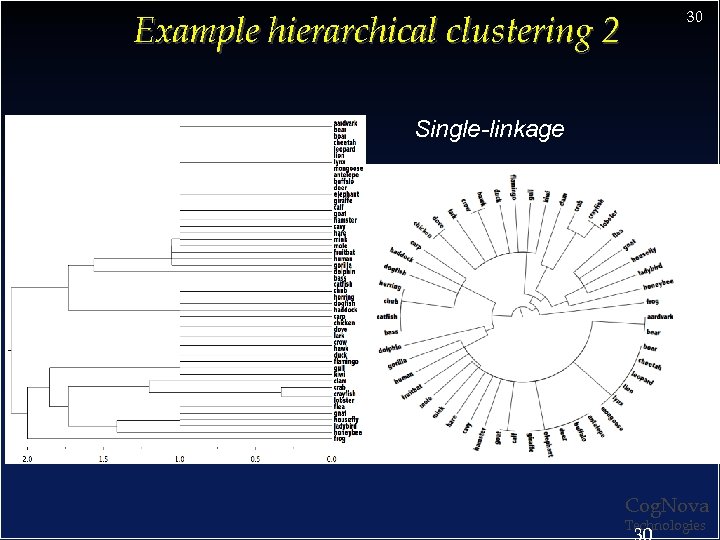Example hierarchical clustering 2 30 Single-linkage Cog. Nova Technologies Example hierarchical clustering 2 30 Single-linkage Cog. Nova Technologies

Incremental clustering 31 Heuristic approach (COBWEB/CLASSIT) ●Form a hierarchy of clusters incrementally ●Start: ● Incremental clustering 31 Heuristic approach (COBWEB/CLASSIT) ●Form a hierarchy of clusters incrementally ●Start: ● tree consists of empty root node ● Then: ● add instances one by one ●update tree appropriately at each stage ● to update, find the right leaf for an instance ●May involve restructuring the tree ● Base update decisions on category utility ● Cog. Nova Technologies

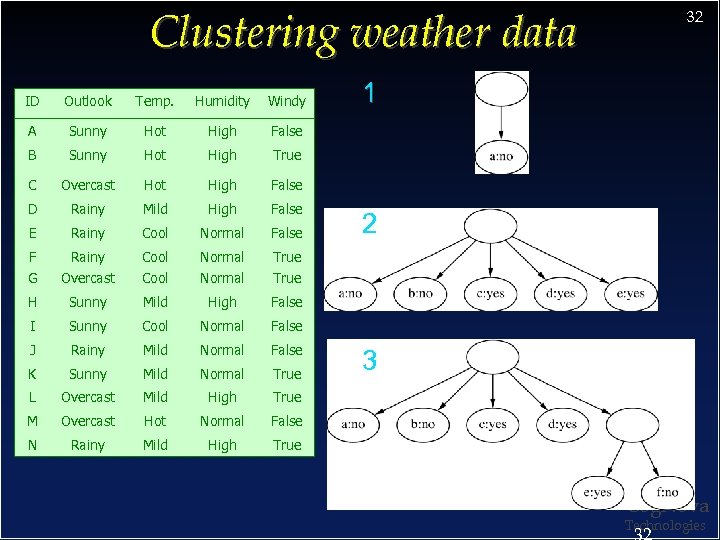Clustering weather data ID Outlook Temp. Humidity Windy A Sunny Hot High True C Clustering weather data ID Outlook Temp. Humidity Windy A Sunny Hot High True C Overcast Hot High False D Rainy Mild High False E Rainy Cool Normal False F Rainy Cool Normal True G Overcast Cool Normal True H Sunny Mild High False I Sunny Cool Normal False J Rainy Mild Normal False K Sunny Mild Normal True L Overcast Mild High True M Overcast Hot Normal False N Rainy Mild High 1 False B 32 True 2 3 Cog. Nova Technologies

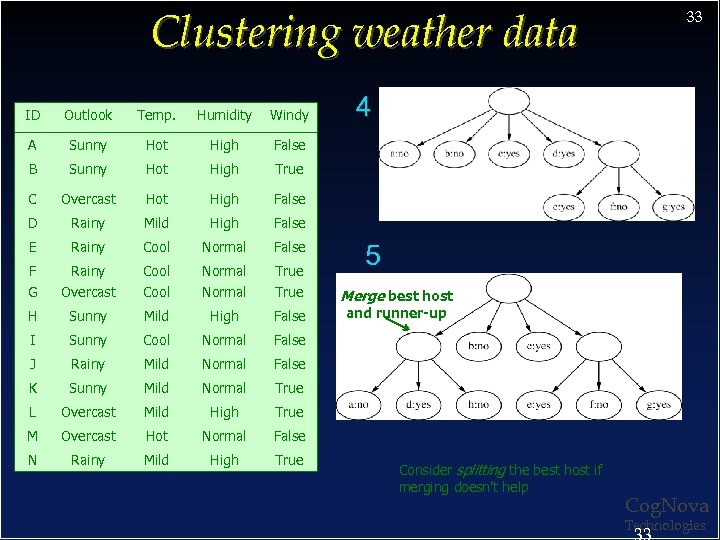Clustering weather data ID Outlook Temp. Humidity Windy A Sunny Hot High True C Clustering weather data ID Outlook Temp. Humidity Windy A Sunny Hot High True C Overcast Hot High False D Rainy Mild High False E Rainy Cool Normal False F Rainy Cool Normal True G Overcast Cool Normal True H Sunny Mild High False I Sunny Cool Normal False J Rainy Mild Normal False K Sunny Mild Normal True L Overcast Mild High True M Overcast Hot Normal False N Rainy Mild High True 4 False B 33 5 Merge best host and runner-up 3 Consider splitting the best host if merging doesn’t help Cog. Nova Technologies

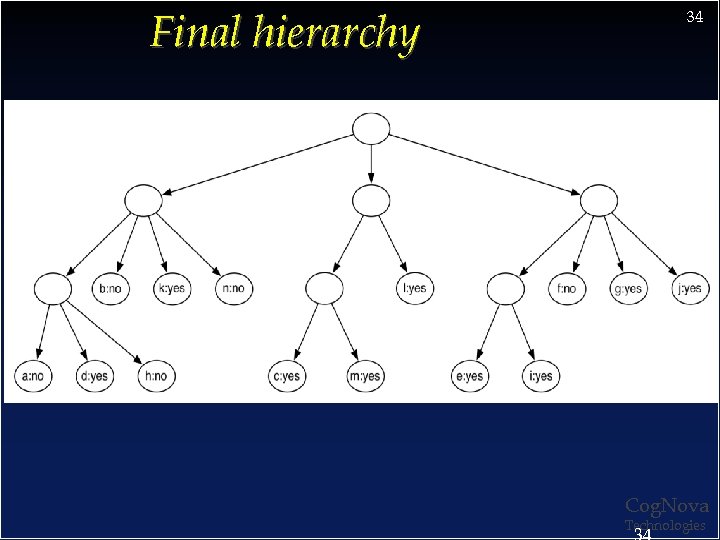Final hierarchy 34 Cog. Nova Technologies Final hierarchy 34 Cog. Nova Technologies

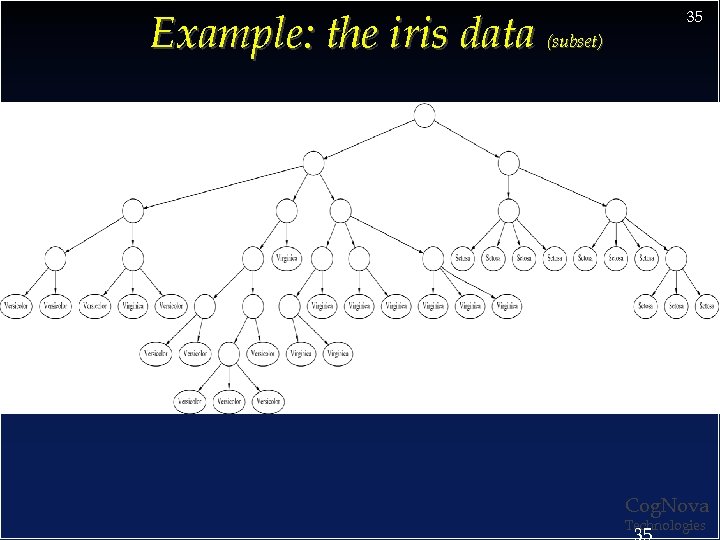Example: the iris data (subset) 35 Cog. Nova Technologies Example: the iris data (subset) 35 Cog. Nova Technologies

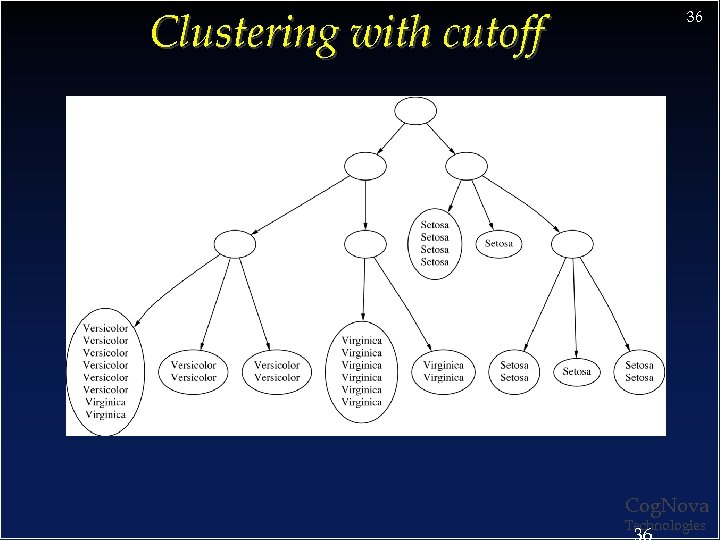Clustering with cutoff 36 Cog. Nova Technologies Clustering with cutoff 36 Cog. Nova Technologies

Category utility 37 Category utility: quadratic loss function defined on conditional probabilities: ● Every Category utility 37 Category utility: quadratic loss function defined on conditional probabilities: ● Every instance in different category numerator becomes ● maximum number of attributes Cog. Nova Technologies

Numeric attributes 38 Cog. Nova Technologies Numeric attributes 38 Cog. Nova Technologies

Probability-based clustering 39 Problems with heuristic approach: ● Division by k? ●Order of examples? Probability-based clustering 39 Problems with heuristic approach: ● Division by k? ●Order of examples? ●Are restructuring operations sufficient? ●Is result at least local minimum of category utility? ● Probabilistic perspective seek the most likely clusters given the data ●Also: instance belongs to a particular cluster with a certain probability ● Cog. Nova Technologies

Finite mixtures 40 Model data using a mixture of distributions ●One cluster, one distribution Finite mixtures 40 Model data using a mixture of distributions ●One cluster, one distribution ● governs probabilities of attribute values in that cluster ● Finite mixtures : finite number of clusters ●Individual distributions are normal (Gaussian) ●Combine distributions using cluster weights ● Cog. Nova Technologies

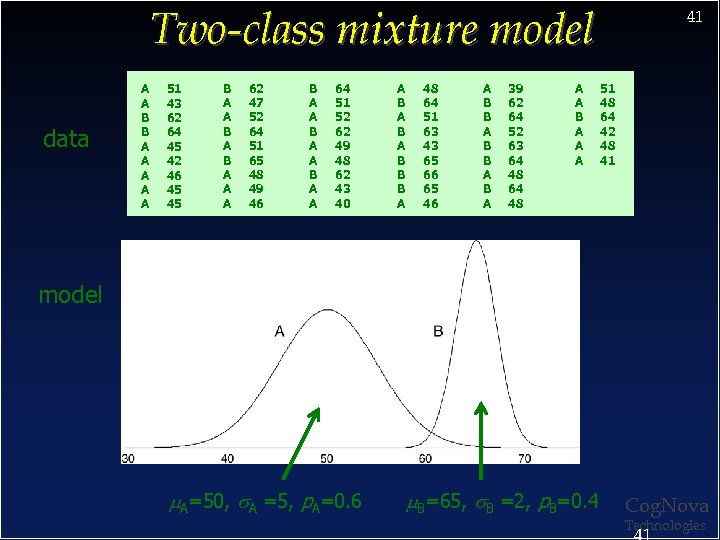Two-class mixture model data A A B B A A A 51 43 62 Two-class mixture model data A A B B A A A 51 43 62 64 45 42 46 45 45 B A A A 62 47 52 64 51 65 48 49 46 B A A 64 51 52 62 49 48 62 43 40 A B A B B B A 48 64 51 63 43 65 66 65 46 A B B A B A 39 62 64 52 63 64 48 A A B A A A 41 51 48 64 42 48 41 model A=50, A =5, p. A=0. 6 B=65, B =2, p. B=0. 4 Cog. Nova Technologies

Using the mixture model 42 Cog. Nova Technologies Using the mixture model 42 Cog. Nova Technologies

Learning the clusters 43 Assume: ● we know there are k clusters ● Learn Learning the clusters 43 Assume: ● we know there are k clusters ● Learn the clusters ● determine their parameters ●I. e. means and standard deviations ● Performance criterion: ● probability of training data given the clusters ● EM algorithm ● finds a local maximum of the likelihood ● Cog. Nova Technologies

EM algorithm 44 EM = Expectation-Maximization ● Generalize k-means to probabilistic setting ● Iterative EM algorithm 44 EM = Expectation-Maximization ● Generalize k-means to probabilistic setting ● Iterative procedure: ● E “expectation” step: Calculate cluster probability for each instance ●M “maximization” step: Estimate distribution parameters from cluster probabilities ● Store cluster probabilities as instance weights ●Stop when improvement is negligible ● Cog. Nova Technologies

More on EM 45 Estimate parameters from weighted instances ● Stop when log-likelihood saturates More on EM 45 Estimate parameters from weighted instances ● Stop when log-likelihood saturates ● Log-likelihood: ● Cog. Nova Technologies

Extending the mixture model 46 More then two distributions: easy ●Several attributes: easy—assuming independence! Extending the mixture model 46 More then two distributions: easy ●Several attributes: easy—assuming independence! ●Correlated attributes: difficult ● Joint model: bivariate normal distribution with a (symmetric) covariance matrix ●n attributes: need to estimate n + n (n+1)/2 parameters ● Cog. Nova Technologies

More mixture model extensions 47 Nominal attributes: easy if independent ●Correlated nominal attributes: difficult More mixture model extensions 47 Nominal attributes: easy if independent ●Correlated nominal attributes: difficult ● Two correlated attributes v 1 v 2 parameters ● Missing values: easy ●Can use other distributions than normal: ● “log-normal” if predetermined minimum is given ●“log-odds” if bounded from above and below ●Poisson for attributes that are integer counts ● Use cross-validation to estimate k ! ● Cog. Nova Technologies

Bayesian clustering 48 Problem: many parameters EM overfits ●Bayesian approach : give every parameter Bayesian clustering 48 Problem: many parameters EM overfits ●Bayesian approach : give every parameter a prior probability distribution ● Incorporate prior into overall likelihood figure ●Penalizes introduction of parameters ● Eg: Laplace estimator for nominal attributes ●Can also have prior on number of clusters! ●Implementation: NASA’s AUTOCLASS ● Cog. Nova Technologies

Discussion 49 Can interpret clusters by using supervised learning ● post-processing step ● Decrease Discussion 49 Can interpret clusters by using supervised learning ● post-processing step ● Decrease dependence between attributes? ● pre-processing step ●E. g. use principal component analysis ● Can be used to fill in missing values ●Key advantage of probabilistic clustering: ● Can estimate likelihood of data ●Use it to compare different models objectively ● Cog. Nova Technologies

WEKA Tutroial 50 K-means, EM and Cobweb and the Weather data http: //www. cs. WEKA Tutroial 50 K-means, EM and Cobweb and the Weather data http: //www. cs. ccsu. edu/~markov/ccsu_courses/Data. Mining-Ex 3. html Cog. Nova Technologies

51 Cog. Nova Technologies 51 Cog. Nova Technologies

Semisupervised learning ● Semisupervised learning: attempts to use unlabeled data as well as labeled Semisupervised learning ● Semisupervised learning: attempts to use unlabeled data as well as labeled data ● 52 The aim is to improve classification performance Why try to do this? Unlabeled data is often plentiful and labeling data can be expensive Web mining: classifying web pages Text mining: identifying names in text Video mining: classifying people in the news ● Leveraging the large pool of unlabeled examples would be very attractive Cog. Nova Technologies

Clustering for classification 53 Idea: use naïve Bayes on labeled examples and then apply Clustering for classification 53 Idea: use naïve Bayes on labeled examples and then apply EM ● First, build naïve Bayes model on labeled data ●Second, label unlabeled data based on class probabilities (“expectation” step) ●Third, train new naïve Bayes model based on all the data (“maximization” step) nd and 3 rd step until convergence ●Fourth, repeat 2 ● Essentially the same as EM for clustering with fixed cluster membership probabilities for labeled data and #clusters = #classes ● Cog. Nova Technologies

Comments 54 Has been applied successfully to document classification ● Certain phrases are indicative Comments 54 Has been applied successfully to document classification ● Certain phrases are indicative of classes ●Some of these phrases occur only in the unlabeled data, some in both sets ●EM can generalize the model by taking advantage of cooccurrence of these phrases ● Refinement 1: reduce weight of unlabeled data ●Refinement 2: allow multiple clusters per class ● Cog. Nova Technologies

Co-training 55 Method for learning from multiple views (multiple sets of attributes), eg: ● Co-training 55 Method for learning from multiple views (multiple sets of attributes), eg: ● First set of attributes describes content of web page ●Second set of attributes describes links that link to the web page ● Step 1: build model from each view ●Step 2: use models to assign labels to unlabeled data ● Step 3: select those unlabeled examples that were most confidently predicted (ideally, preserving ratio of classes) ●Step 4: add those examples to the training set ● Step 5: go to Step 1 until data exhausted ●Assumption: views are independent ● Cog. Nova Technologies

EM and co-training 56 Like EM for semisupervised learning, but view is switched in EM and co-training 56 Like EM for semisupervised learning, but view is switched in each iteration of EM ● Uses all the unlabeled data (probabilistically labeled) for training ● Has also been used successfully with support vector machines ● Using logistic models fit to output of SVMs ● Co-training also seems to work when views are chosen randomly! ● Why? Possibly because co-trained classifier is more robust ● Cog. Nova Technologies

57 THE END danny. silver@acadiau. ca Cog. Nova Technologies 57 THE END danny. silver@acadiau. ca Cog. Nova Technologies