ac2acb24442fdb9c38db85fca0e8c523.ppt
- Количество слайдов: 43
 1 Chapter 6: The Time Value of Money Part II Investments Copyright © 1999 Addison Wesley Longman
1 Chapter 6: The Time Value of Money Part II Investments Copyright © 1999 Addison Wesley Longman
 CHAPTER The Time Value of Money Copyright © 1999 Addison Wesley Longman 6
CHAPTER The Time Value of Money Copyright © 1999 Addison Wesley Longman 6
 3 Chapter 6: The Time Value of Money Objectives 1. 2. 3. 4. Compute FV of Lump Sum Compute PV of Lump Sum Compute FV of Annuity Apply TVM Concepts Copyright © 1999 Addison Wesley Longman
3 Chapter 6: The Time Value of Money Objectives 1. 2. 3. 4. Compute FV of Lump Sum Compute PV of Lump Sum Compute FV of Annuity Apply TVM Concepts Copyright © 1999 Addison Wesley Longman
 Chapter 6: The Time Value of Money 4 THE TIME VALUE OF MONEY The time value of money is the return required to induce a saver to defer current consumption with the expectation of increased future wealth. The time value of money embodies the first fundamental tenant of finance: A dollar today is worth more than a dollar to be received in the future. Copyright © 1999 Addison Wesley Longman
Chapter 6: The Time Value of Money 4 THE TIME VALUE OF MONEY The time value of money is the return required to induce a saver to defer current consumption with the expectation of increased future wealth. The time value of money embodies the first fundamental tenant of finance: A dollar today is worth more than a dollar to be received in the future. Copyright © 1999 Addison Wesley Longman
 Chapter 6: The Time Value of Money 5 FUTURE VALUE u What an amount of money today will be worth at some point in the future at given rate of interest. 1. Compounding is the process of accumulating interest on interest making the balance grow at a geometric rate 2. Compound interest is interest earned on both the initial principal and the interest reinvested from prior periods Copyright © 1999 Addison Wesley Longman
Chapter 6: The Time Value of Money 5 FUTURE VALUE u What an amount of money today will be worth at some point in the future at given rate of interest. 1. Compounding is the process of accumulating interest on interest making the balance grow at a geometric rate 2. Compound interest is interest earned on both the initial principal and the interest reinvested from prior periods Copyright © 1999 Addison Wesley Longman
 6 Chapter 6: The Time Value of Money One Period Model FV 1 = PV 0 (1 + i) FV 1 = 100 (1. 05) = 105 Copyright © 1999 Addison Wesley Longman
6 Chapter 6: The Time Value of Money One Period Model FV 1 = PV 0 (1 + i) FV 1 = 100 (1. 05) = 105 Copyright © 1999 Addison Wesley Longman
 Chapter 6: The Time Value of Money 7 Calculating Future Value FV = PV(1 + i/k)nk FV = future value of money n periods into the future PV = present value of money today i = nominal interest rate n = # of years investment is to be held k = # of compounding periods in a year (# of times interest is calculated and credited to account) i/k = periodic rate Copyright © 1999 Addison Wesley Longman
Chapter 6: The Time Value of Money 7 Calculating Future Value FV = PV(1 + i/k)nk FV = future value of money n periods into the future PV = present value of money today i = nominal interest rate n = # of years investment is to be held k = # of compounding periods in a year (# of times interest is calculated and credited to account) i/k = periodic rate Copyright © 1999 Addison Wesley Longman
 Chapter 6: The Time Value of Money 8 Example: Place $1000 into a savings account for 5 years at 10% compounded annually. What will be the future value of the account upon withdrawal in 5 years? FV = PV(1 + i/k)nk 0 1 2 3 4 5 |---------------|---------------|--------| $1, 000 ? Copyright © 1999 Addison Wesley Longman
Chapter 6: The Time Value of Money 8 Example: Place $1000 into a savings account for 5 years at 10% compounded annually. What will be the future value of the account upon withdrawal in 5 years? FV = PV(1 + i/k)nk 0 1 2 3 4 5 |---------------|---------------|--------| $1, 000 ? Copyright © 1999 Addison Wesley Longman
 9 Chapter 6: The Time Value of Money Using the Calculator 1. Set up the TVM template [N] = [I/Y] = [PV] = [PMT] = [FV] = 2. Make sure your calculator is set to the financial mode for time value of money calculations. 3. Make sure calculator is set to 1 payment per year [P/Y]. Copyright © 1999 Addison Wesley Longman
9 Chapter 6: The Time Value of Money Using the Calculator 1. Set up the TVM template [N] = [I/Y] = [PV] = [PMT] = [FV] = 2. Make sure your calculator is set to the financial mode for time value of money calculations. 3. Make sure calculator is set to 1 payment per year [P/Y]. Copyright © 1999 Addison Wesley Longman
![10 Chapter 6: The Time Value of Money 4. To obtain [N], multiply the 10 Chapter 6: The Time Value of Money 4. To obtain [N], multiply the](https://present5.com/presentation/ac2acb24442fdb9c38db85fca0e8c523/image-10.jpg) 10 Chapter 6: The Time Value of Money 4. To obtain [N], multiply the # of years (n) quoted in the problem by the # of payments per year or compounding periods per year (k). 5. To enter [I/Y], divide the interest rate by the # of payments per year (k). 6. To enter [PMT], enter the amount of the payment. If there is no payment, enter a 0. 7. To enter [PV] or [FV], enter the amount and press the key. Copyright © 1999 Addison Wesley Longman
10 Chapter 6: The Time Value of Money 4. To obtain [N], multiply the # of years (n) quoted in the problem by the # of payments per year or compounding periods per year (k). 5. To enter [I/Y], divide the interest rate by the # of payments per year (k). 6. To enter [PMT], enter the amount of the payment. If there is no payment, enter a 0. 7. To enter [PV] or [FV], enter the amount and press the key. Copyright © 1999 Addison Wesley Longman
 11 Chapter 6: The Time Value of Money 8. To solve for the missing variable a. TI-BA press [CPT] & b. HP press [? ] Copyright © 1999 Addison Wesley Longman [? ]
11 Chapter 6: The Time Value of Money 8. To solve for the missing variable a. TI-BA press [CPT] & b. HP press [? ] Copyright © 1999 Addison Wesley Longman [? ]
 12 Chapter 6: The Time Value of Money As the Number of Compounding Periods Increases, the Future Balance Increases FV of $2000 10 years from now at a rate of 6% Annual Compunding = $3, 581. 69 Semi-Annual Compounding = $3, 612. 22 Copyright © 1999 Addison Wesley Longman
12 Chapter 6: The Time Value of Money As the Number of Compounding Periods Increases, the Future Balance Increases FV of $2000 10 years from now at a rate of 6% Annual Compunding = $3, 581. 69 Semi-Annual Compounding = $3, 612. 22 Copyright © 1999 Addison Wesley Longman
 13 Chapter 6: The Time Value of Money FIGURE 6. 1 Effect of Different Compounding Frequencies on Future Value Copyright © 1999 Addison Wesley Longman
13 Chapter 6: The Time Value of Money FIGURE 6. 1 Effect of Different Compounding Frequencies on Future Value Copyright © 1999 Addison Wesley Longman
 Chapter 6: The Time Value of Money 14 Present Value What an amount of money to be received in the future is worth today discounted at a certain rate of interest. A. Discounting • The process of deducting or taking out interest income or the expected increase in an investments value over time to determine the current (present) value of an asset • The reverse of compunding B. The discount rate The rate that you expect to receive on similar investments of comparable risk. Copyright © 1999 Addison Wesley Longman
Chapter 6: The Time Value of Money 14 Present Value What an amount of money to be received in the future is worth today discounted at a certain rate of interest. A. Discounting • The process of deducting or taking out interest income or the expected increase in an investments value over time to determine the current (present) value of an asset • The reverse of compunding B. The discount rate The rate that you expect to receive on similar investments of comparable risk. Copyright © 1999 Addison Wesley Longman
 15 Chapter 6: The Time Value of Money Calculating Present Value PV = FV [1/ (1 + i/k)nk] FV PV i n k i/k = = = future value of money n periods into the future present value of money today nominal interest rate # of years investment is to be held # of compounding periods in a year (# of times interest is calculated and credited to account) = periodic rate Copyright © 1999 Addison Wesley Longman
15 Chapter 6: The Time Value of Money Calculating Present Value PV = FV [1/ (1 + i/k)nk] FV PV i n k i/k = = = future value of money n periods into the future present value of money today nominal interest rate # of years investment is to be held # of compounding periods in a year (# of times interest is calculated and credited to account) = periodic rate Copyright © 1999 Addison Wesley Longman
 16 Chapter 6: The Time Value of Money Example: Your new company will reimburse your total education costs of $10, 000 after you have been with the firm for 5 years. If your discount rate is 8% compounded monthly (probably the rate you are paying on your student loans), what is the present value of the $10, 000 reimbursement? 0 1 2 3 4 5 |---------------|---------------|--------| ? $10, 000 Using the calculator [N] [I/Y] [PV] [PMT] [FV] = = = Copyright © 1999 Addison Wesley Longman
16 Chapter 6: The Time Value of Money Example: Your new company will reimburse your total education costs of $10, 000 after you have been with the firm for 5 years. If your discount rate is 8% compounded monthly (probably the rate you are paying on your student loans), what is the present value of the $10, 000 reimbursement? 0 1 2 3 4 5 |---------------|---------------|--------| ? $10, 000 Using the calculator [N] [I/Y] [PV] [PMT] [FV] = = = Copyright © 1999 Addison Wesley Longman
 17 Chapter 6: The Time Value of Money Comparing Interest Rates A. Annual Percentage Rate (APR) 1. the periodic rate times the number of compounding periods 2. rate stated by banks in advertising B. Effective (equivalent) Annual Rate (EAR) The annual rate which provides the same return on money compounded at some periodic rate k times a year. 1. The "true" rate 2. used to compare rates when compounding periods differ 3. EAR = (1 + i/k)k - 1 Copyright © 1999 Addison Wesley Longman
17 Chapter 6: The Time Value of Money Comparing Interest Rates A. Annual Percentage Rate (APR) 1. the periodic rate times the number of compounding periods 2. rate stated by banks in advertising B. Effective (equivalent) Annual Rate (EAR) The annual rate which provides the same return on money compounded at some periodic rate k times a year. 1. The "true" rate 2. used to compare rates when compounding periods differ 3. EAR = (1 + i/k)k - 1 Copyright © 1999 Addison Wesley Longman
 18 Chapter 6: The Time Value of Money Example: You place $5, 000 into a CD for 3 years paying a nominal rate of 8% compounded quarterly. What is the effective annual rate for this CD? In other words, at what annual compounding rate would you have the same amount of money? EAR = (1 + i/k)k - 1 Copyright © 1999 Addison Wesley Longman
18 Chapter 6: The Time Value of Money Example: You place $5, 000 into a CD for 3 years paying a nominal rate of 8% compounded quarterly. What is the effective annual rate for this CD? In other words, at what annual compounding rate would you have the same amount of money? EAR = (1 + i/k)k - 1 Copyright © 1999 Addison Wesley Longman
 19 Chapter 6: The Time Value of Money Checking your answer Obtain the terminal value of the CD at the 8% with quarterly compounding and at the EAR using annual compounding Quarterly compounding Annual compounding [N] = [I/Y] = [PV] = [PMT] = [FV] = Copyright © 1999 Addison Wesley Longman
19 Chapter 6: The Time Value of Money Checking your answer Obtain the terminal value of the CD at the 8% with quarterly compounding and at the EAR using annual compounding Quarterly compounding Annual compounding [N] = [I/Y] = [PV] = [PMT] = [FV] = Copyright © 1999 Addison Wesley Longman
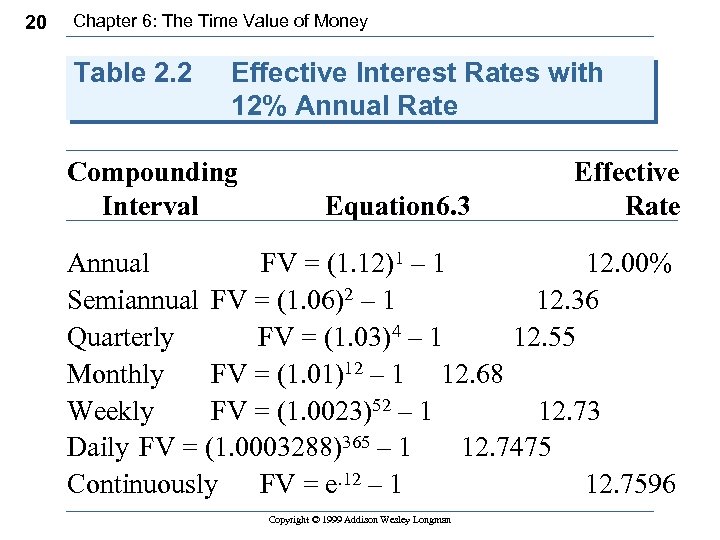 20 Chapter 6: The Time Value of Money Table 2. 2 Effective Interest Rates with 12% Annual Rate Compounding Effective Interval Equation 6. 3 Rate Annual FV = (1. 12)1 – 1 12. 00% Semiannual FV = (1. 06)2 – 1 12. 36 Quarterly FV = (1. 03)4 – 1 12. 55 Monthly FV = (1. 01)12 – 1 12. 68 Weekly FV = (1. 0023)52 – 1 12. 73 Daily FV = (1. 0003288)365 – 1 12. 7475 Continuously FV = e. 12 – 1 12. 7596 Copyright © 1999 Addison Wesley Longman
20 Chapter 6: The Time Value of Money Table 2. 2 Effective Interest Rates with 12% Annual Rate Compounding Effective Interval Equation 6. 3 Rate Annual FV = (1. 12)1 – 1 12. 00% Semiannual FV = (1. 06)2 – 1 12. 36 Quarterly FV = (1. 03)4 – 1 12. 55 Monthly FV = (1. 01)12 – 1 12. 68 Weekly FV = (1. 0023)52 – 1 12. 73 Daily FV = (1. 0003288)365 – 1 12. 7475 Continuously FV = e. 12 – 1 12. 7596 Copyright © 1999 Addison Wesley Longman
 21 Chapter 6: The Time Value of Money Annuities An annuity is a series of equal payments made at fixed intervals for a specified number of years or indefinitely. A. Types of Annuities 1. Ordinary annuity Series of equal payments made at the end of each period for a fixed number of periods. 0 1 2 3 4 5 |---------------|---------------|--------| $100 $100 Copyright © 1999 Addison Wesley Longman
21 Chapter 6: The Time Value of Money Annuities An annuity is a series of equal payments made at fixed intervals for a specified number of years or indefinitely. A. Types of Annuities 1. Ordinary annuity Series of equal payments made at the end of each period for a fixed number of periods. 0 1 2 3 4 5 |---------------|---------------|--------| $100 $100 Copyright © 1999 Addison Wesley Longman
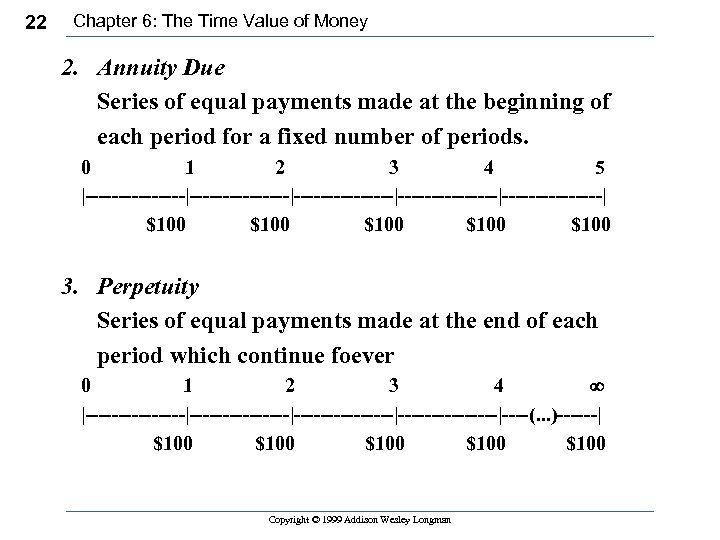 22 Chapter 6: The Time Value of Money 2. Annuity Due Series of equal payments made at the beginning of each period for a fixed number of periods. 0 1 2 3 4 5 |---------------|---------------|--------| $100 $100 3. Perpetuity Series of equal payments made at the end of each period which continue foever 0 1 2 3 4 ¥ |---------------|---------------|----(. . . )------| $100 $100 Copyright © 1999 Addison Wesley Longman
22 Chapter 6: The Time Value of Money 2. Annuity Due Series of equal payments made at the beginning of each period for a fixed number of periods. 0 1 2 3 4 5 |---------------|---------------|--------| $100 $100 3. Perpetuity Series of equal payments made at the end of each period which continue foever 0 1 2 3 4 ¥ |---------------|---------------|----(. . . )------| $100 $100 Copyright © 1999 Addison Wesley Longman
 23 Chapter 6: The Time Value of Money Future Value of an Annuity 1. The future value of an ordinary annuity where i=10% 0 1 2 3 4 5 |---------------|---------------|--------| $100 $100 Copyright © 1999 Addison Wesley Longman
23 Chapter 6: The Time Value of Money Future Value of an Annuity 1. The future value of an ordinary annuity where i=10% 0 1 2 3 4 5 |---------------|---------------|--------| $100 $100 Copyright © 1999 Addison Wesley Longman
![24 Chapter 6: The Time Value of Money Using a calculator [N] = [I/Y] 24 Chapter 6: The Time Value of Money Using a calculator [N] = [I/Y]](https://present5.com/presentation/ac2acb24442fdb9c38db85fca0e8c523/image-24.jpg) 24 Chapter 6: The Time Value of Money Using a calculator [N] = [I/Y] = [PV] = [PMT] = [FV] = Copyright © 1999 Addison Wesley Longman
24 Chapter 6: The Time Value of Money Using a calculator [N] = [I/Y] = [PV] = [PMT] = [FV] = Copyright © 1999 Addison Wesley Longman
 25 Chapter 6: The Time Value of Money 2. The future value of an annuity due where i=10% 0 1 2 3 4 5 |---------------|---------------|--------| $100 $100 Copyright © 1999 Addison Wesley Longman
25 Chapter 6: The Time Value of Money 2. The future value of an annuity due where i=10% 0 1 2 3 4 5 |---------------|---------------|--------| $100 $100 Copyright © 1999 Addison Wesley Longman
![26 Chapter 6: The Time Value of Money Using a calculator [N] = [I/Y] 26 Chapter 6: The Time Value of Money Using a calculator [N] = [I/Y]](https://present5.com/presentation/ac2acb24442fdb9c38db85fca0e8c523/image-26.jpg) 26 Chapter 6: The Time Value of Money Using a calculator [N] = [I/Y] = [PV] = [PMT] = [FV] = Copyright © 1999 Addison Wesley Longman
26 Chapter 6: The Time Value of Money Using a calculator [N] = [I/Y] = [PV] = [PMT] = [FV] = Copyright © 1999 Addison Wesley Longman
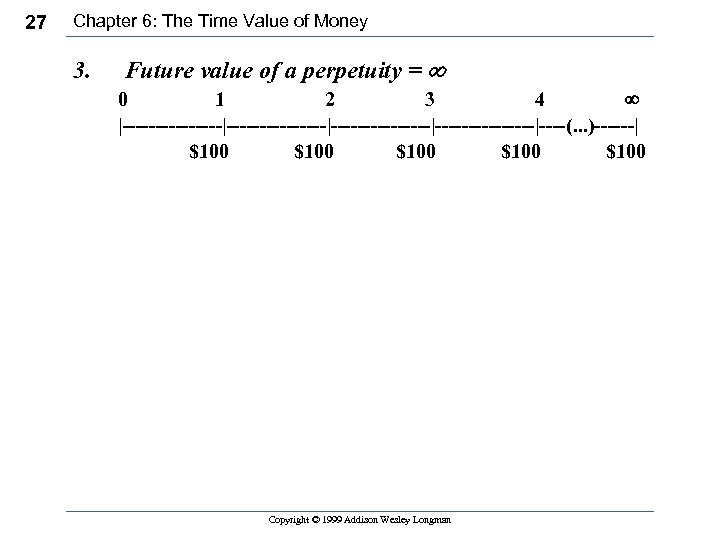 27 Chapter 6: The Time Value of Money 3. Future value of a perpetuity = ¥ 0 1 2 3 4 ¥ |---------------|---------------|----(. . . )------| $100 $100 Copyright © 1999 Addison Wesley Longman
27 Chapter 6: The Time Value of Money 3. Future value of a perpetuity = ¥ 0 1 2 3 4 ¥ |---------------|---------------|----(. . . )------| $100 $100 Copyright © 1999 Addison Wesley Longman
 28 Chapter 6: The Time Value of Money Present Value of an Annuity The present value of all annuity payments discounted at your discount rate. 1. the present value of an ordinary annuity where i=10% 0 1 2 3 4 5 |--------------|---------------|--------| $100 $100 Copyright © 1999 Addison Wesley Longman
28 Chapter 6: The Time Value of Money Present Value of an Annuity The present value of all annuity payments discounted at your discount rate. 1. the present value of an ordinary annuity where i=10% 0 1 2 3 4 5 |--------------|---------------|--------| $100 $100 Copyright © 1999 Addison Wesley Longman
![29 Chapter 6: The Time Value of Money Using a calculator [N] = [I/Y] 29 Chapter 6: The Time Value of Money Using a calculator [N] = [I/Y]](https://present5.com/presentation/ac2acb24442fdb9c38db85fca0e8c523/image-29.jpg) 29 Chapter 6: The Time Value of Money Using a calculator [N] = [I/Y] = [PV] = [PMT] = [FV] = Copyright © 1999 Addison Wesley Longman
29 Chapter 6: The Time Value of Money Using a calculator [N] = [I/Y] = [PV] = [PMT] = [FV] = Copyright © 1999 Addison Wesley Longman
 30 Chapter 6: The Time Value of Money 2. the present value of an annuity due where i=10% 0 1 2 3 4 5 |---------------|---------------|--------| $100 $100 3. the present value of a perpetuity where i=10% 0 1 2 3 4 ¥ |---------------|---------------|----(. . . )------| $100 $100 Copyright © 1999 Addison Wesley Longman
30 Chapter 6: The Time Value of Money 2. the present value of an annuity due where i=10% 0 1 2 3 4 5 |---------------|---------------|--------| $100 $100 3. the present value of a perpetuity where i=10% 0 1 2 3 4 ¥ |---------------|---------------|----(. . . )------| $100 $100 Copyright © 1999 Addison Wesley Longman
![31 Chapter 6: The Time Value of Money Using a calculator [N] = [I/Y] 31 Chapter 6: The Time Value of Money Using a calculator [N] = [I/Y]](https://present5.com/presentation/ac2acb24442fdb9c38db85fca0e8c523/image-31.jpg) 31 Chapter 6: The Time Value of Money Using a calculator [N] = [I/Y] = [PV] = [PMT] = [FV] = Copyright © 1999 Addison Wesley Longman
31 Chapter 6: The Time Value of Money Using a calculator [N] = [I/Y] = [PV] = [PMT] = [FV] = Copyright © 1999 Addison Wesley Longman
 32 Chapter 6: The Time Value of Money Example: Deferred Annuities What is the PV of the following cash flow stream? 100 10% |------ |----- - | 0 1 2 3 4 5 Copyright © 1999 Addison Wesley Longman
32 Chapter 6: The Time Value of Money Example: Deferred Annuities What is the PV of the following cash flow stream? 100 10% |------ |----- - | 0 1 2 3 4 5 Copyright © 1999 Addison Wesley Longman
 33 Chapter 6: The Time Value of Money Uneven Cash Flows A series of Cash flows in which the payment amount varies from period to period. A. Future Value of an uneven cash flow stream where i=10% 0 1 2 3 4 5 |--------------|--------------|-------| $100 $200 $-50 $300 $100 Copyright © 1999 Addison Wesley Longman
33 Chapter 6: The Time Value of Money Uneven Cash Flows A series of Cash flows in which the payment amount varies from period to period. A. Future Value of an uneven cash flow stream where i=10% 0 1 2 3 4 5 |--------------|--------------|-------| $100 $200 $-50 $300 $100 Copyright © 1999 Addison Wesley Longman
 34 Chapter 6: The Time Value of Money B. Present Value of an uneven cash flow stream where i=10% 0 1 2 3 4 5 |---------------|---------------|--------| $100 $200 $-50 $300 $100 Copyright © 1999 Addison Wesley Longman
34 Chapter 6: The Time Value of Money B. Present Value of an uneven cash flow stream where i=10% 0 1 2 3 4 5 |---------------|---------------|--------| $100 $200 $-50 $300 $100 Copyright © 1999 Addison Wesley Longman
 35 Chapter 6: The Time Value of Money Amortized Loans Characteristics 1. Repay the loan in equal payments for each period over the life of the loan. 2. Each payment includes both principal and interest. Copyright © 1999 Addison Wesley Longman
35 Chapter 6: The Time Value of Money Amortized Loans Characteristics 1. Repay the loan in equal payments for each period over the life of the loan. 2. Each payment includes both principal and interest. Copyright © 1999 Addison Wesley Longman
 36 Chapter 6: The Time Value of Money Example: You buy a car for $10, 000 and finance it for 5 years at 10% APR with payments at the end of each month. What is the amount of each payment if you fully amortize the loan? [N] [I/Y] [PV] [PMT] [FV] = = = Copyright © 1999 Addison Wesley Longman
36 Chapter 6: The Time Value of Money Example: You buy a car for $10, 000 and finance it for 5 years at 10% APR with payments at the end of each month. What is the amount of each payment if you fully amortize the loan? [N] [I/Y] [PV] [PMT] [FV] = = = Copyright © 1999 Addison Wesley Longman
 37 Chapter 6: The Time Value of Money The Amortization Schedule 1. Repayment schedule of amortized loan 2. Breaks payments into interest and principal components 3. As the loan is paid off the proportion of interest being paid declines and the proportion of principal being paid off increases Copyright © 1999 Addison Wesley Longman
37 Chapter 6: The Time Value of Money The Amortization Schedule 1. Repayment schedule of amortized loan 2. Breaks payments into interest and principal components 3. As the loan is paid off the proportion of interest being paid declines and the proportion of principal being paid off increases Copyright © 1999 Addison Wesley Longman
 38 Chapter 6: The Time Value of Money Example: Given the above car loan, provide an amortization schedule for the first year. Month Beginning Payment Interest Principal Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec Balance $10, 000 $ 9, 871 $ 9, 741 _______ _______ _______ Per Payment $212. 47 $83. 33 $129. 14 $212. 47 $82. 26 $130. 21 _______ ________ _______ _______ ________ _______ _______ ________ Copyright © 1999 Addison Wesley Longman
38 Chapter 6: The Time Value of Money Example: Given the above car loan, provide an amortization schedule for the first year. Month Beginning Payment Interest Principal Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec Balance $10, 000 $ 9, 871 $ 9, 741 _______ _______ _______ Per Payment $212. 47 $83. 33 $129. 14 $212. 47 $82. 26 $130. 21 _______ ________ _______ _______ ________ _______ _______ ________ Copyright © 1999 Addison Wesley Longman
 39 Chapter 6: The Time Value of Money Growth Rates u u u To compute the compounded growth rate use the FV equation. The beginning value is the PV. The ending value is the FV. Copyright © 1999 Addison Wesley Longman
39 Chapter 6: The Time Value of Money Growth Rates u u u To compute the compounded growth rate use the FV equation. The beginning value is the PV. The ending value is the FV. Copyright © 1999 Addison Wesley Longman
 40 Chapter 6: The Time Value of Money Example: You bought stock for $15. 00 per share 5 years ago. It is currently selling for $45. 00 per share. What is the compounded average growth rate? FV = PV (1 + g)N Copyright © 1999 Addison Wesley Longman
40 Chapter 6: The Time Value of Money Example: You bought stock for $15. 00 per share 5 years ago. It is currently selling for $45. 00 per share. What is the compounded average growth rate? FV = PV (1 + g)N Copyright © 1999 Addison Wesley Longman
 41 Chapter 6: The Time Value of Money FV = PV (1 + g)N Using a calculator [N] = [I/Y] = [PV] = [PMT] = [FV] = Copyright © 1999 Addison Wesley Longman
41 Chapter 6: The Time Value of Money FV = PV (1 + g)N Using a calculator [N] = [I/Y] = [PV] = [PMT] = [FV] = Copyright © 1999 Addison Wesley Longman
 42 Chapter 6: The Time Value of Money Review of FV & PV 1 2 Use future value to find the balance resulting from an interest-earning deposit. Use future value of an annuity to find the payment needed to achieve a known future balance. Copyright © 1999 Addison Wesley Longman
42 Chapter 6: The Time Value of Money Review of FV & PV 1 2 Use future value to find the balance resulting from an interest-earning deposit. Use future value of an annuity to find the payment needed to achieve a known future balance. Copyright © 1999 Addison Wesley Longman
 43 Chapter 6: The Time Value of Money 3 Use either present or future value (without an annuity) to compute growth rates. 4 Use present value on all loan calculations. 5 Use present value to value assets. 6 Use present value to evaluate investments. Copyright © 1999 Addison Wesley Longman
43 Chapter 6: The Time Value of Money 3 Use either present or future value (without an annuity) to compute growth rates. 4 Use present value on all loan calculations. 5 Use present value to value assets. 6 Use present value to evaluate investments. Copyright © 1999 Addison Wesley Longman


