Математика в компьютерной графике(Лекция1).ppt
- Количество слайдов: 37
 1 CG Math Математика в компьютерной графике URL: http: //www. school 30. spb. ru/cgsg/cgc/ E-mail: CGSG@yandex. ru Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
1 CG Math Математика в компьютерной графике URL: http: //www. school 30. spb. ru/cgsg/cgc/ E-mail: CGSG@yandex. ru Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 2 Базовые понятия CG Math • свободные векторы, радиус векторы, операции с векторами, скалярное и векторное произведение векторов (vector dot & cross production) • базис, координаты, декартова система координат • матрицы, операции с матрицами, обращение матриц Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
2 Базовые понятия CG Math • свободные векторы, радиус векторы, операции с векторами, скалярное и векторное произведение векторов (vector dot & cross production) • базис, координаты, декартова система координат • матрицы, операции с матрицами, обращение матриц Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 3 Преобразования transformations) ( CG Math § Аффинные § Перспективные § Билинейные Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
3 Преобразования transformations) ( CG Math § Аффинные § Перспективные § Билинейные Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 4 Аффинные преобразования CG Math • Параллельный перенос (translation) Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
4 Аффинные преобразования CG Math • Параллельный перенос (translation) Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
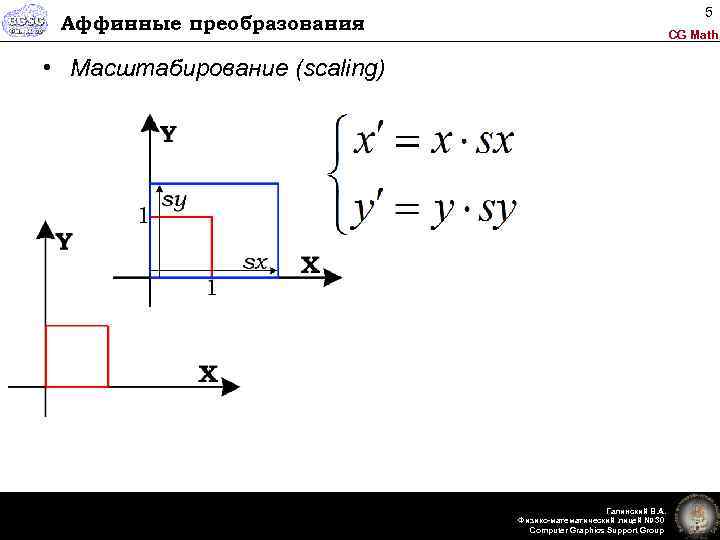 5 Аффинные преобразования CG Math • Масштабирование (scaling) Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
5 Аффинные преобразования CG Math • Масштабирование (scaling) Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
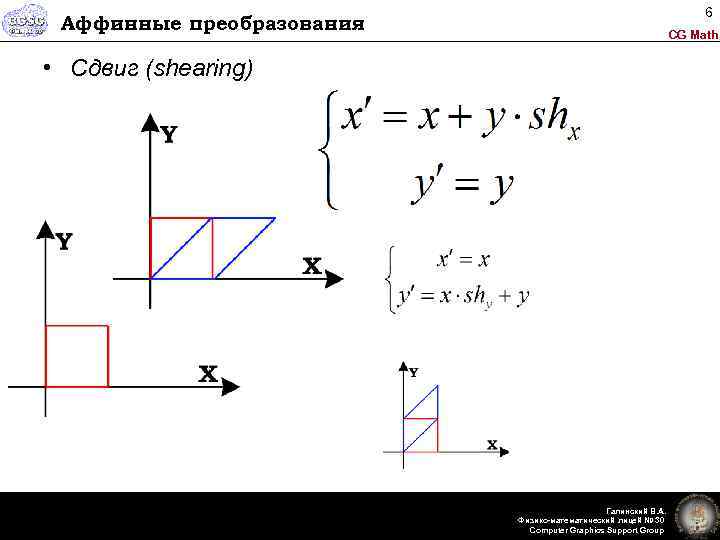 6 Аффинные преобразования CG Math • Сдвиг (shearing) Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
6 Аффинные преобразования CG Math • Сдвиг (shearing) Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
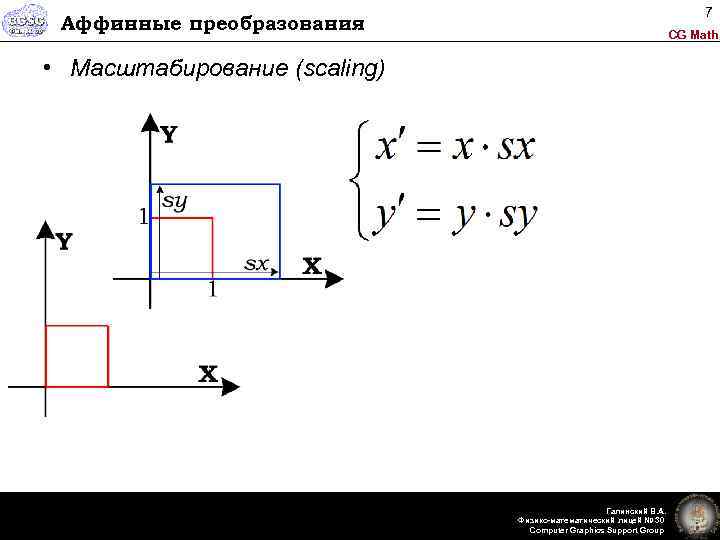 7 Аффинные преобразования CG Math • Масштабирование (scaling) Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
7 Аффинные преобразования CG Math • Масштабирование (scaling) Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 8 Аффинные преобразования CG Math • Поворот относительно начала координат (rotation) r Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
8 Аффинные преобразования CG Math • Поворот относительно начала координат (rotation) r Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 Матричная запись аффинных преобразований • Перепишем в матричном виде общую запись аффинных преобразований: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 9 CG Math
Матричная запись аффинных преобразований • Перепишем в матричном виде общую запись аффинных преобразований: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 9 CG Math
 10 Однородные координаты ( homogeneous ) CG Math • представим координаты на плоскости (2 D) трехкомпонентной вектор - строкой: • будем полагать w = 1 • перепишем преобразование в общем виде: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
10 Однородные координаты ( homogeneous ) CG Math • представим координаты на плоскости (2 D) трехкомпонентной вектор - строкой: • будем полагать w = 1 • перепишем преобразование в общем виде: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 Матричный вид аффинных преобразований ~ translation ~ scaling ~ translation shear by x ~ rotation ~ shear by y Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 11 CG Math
Матричный вид аффинных преобразований ~ translation ~ scaling ~ translation shear by x ~ rotation ~ shear by y Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 11 CG Math
 12 Композиция преобразований CG Math • подвергнем точку последовательным преобразованиям системы координат: • перепишем: • в силу ассоциативности: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
12 Композиция преобразований CG Math • подвергнем точку последовательным преобразованиям системы координат: • перепишем: • в силу ассоциативности: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 13 Обратные аффинные преобразования CG Math Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
13 Обратные аффинные преобразования CG Math Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 Преобразование точек, векторов и нормалей • точка (радиус-вектор) (p): • вектор (v) и нормаль (n) (только направление): • преобразования: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 14 CG Math
Преобразование точек, векторов и нормалей • точка (радиус-вектор) (p): • вектор (v) и нормаль (n) (только направление): • преобразования: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 14 CG Math
 15 Преобразование нормалей CG Math Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
15 Преобразование нормалей CG Math Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 16 Нотации записи: столбец или строка CG Math Одно преобразование: Композиция преобразований: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
16 Нотации записи: столбец или строка CG Math Одно преобразование: Композиция преобразований: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 17 Пример: привязка систем координат CG Math • заданы точки соответствия • найти «матрицу перехода» Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
17 Пример: привязка систем координат CG Math • заданы точки соответствия • найти «матрицу перехода» Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 18 Пример: привязка систем координат CG Math Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
18 Пример: привязка систем координат CG Math Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 19 Пример: преобразование изображений CG Math => Прямое отображение (direct mapping) => Поворот и масштабирование <= Обратное отображение (inverse mapping) <= Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
19 Пример: преобразование изображений CG Math => Прямое отображение (direct mapping) => Поворот и масштабирование <= Обратное отображение (inverse mapping) <= Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
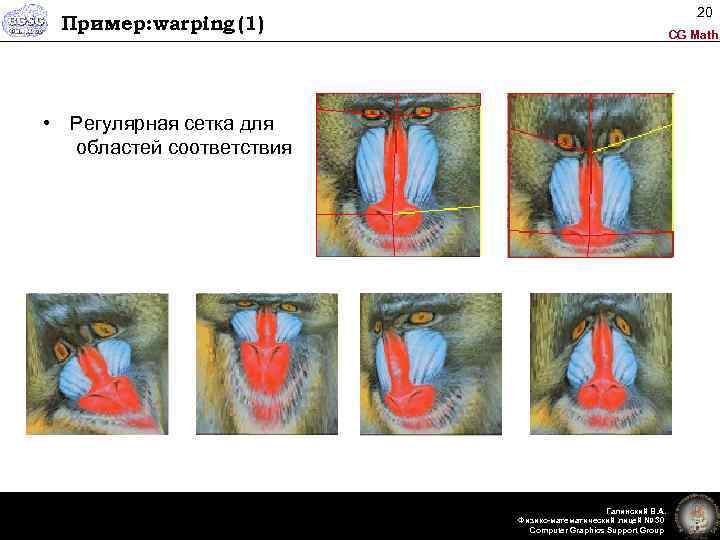 20 Пример: warping (1) CG Math • Регулярная сетка для областей соответствия Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
20 Пример: warping (1) CG Math • Регулярная сетка для областей соответствия Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
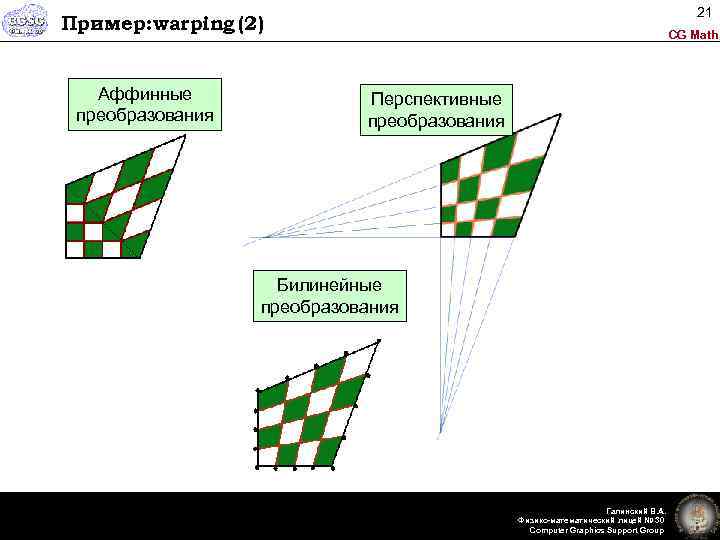 21 Пример: warping (2) Аффинные преобразования CG Math Перспективные преобразования Билинейные преобразования Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
21 Пример: warping (2) Аффинные преобразования CG Math Перспективные преобразования Билинейные преобразования Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
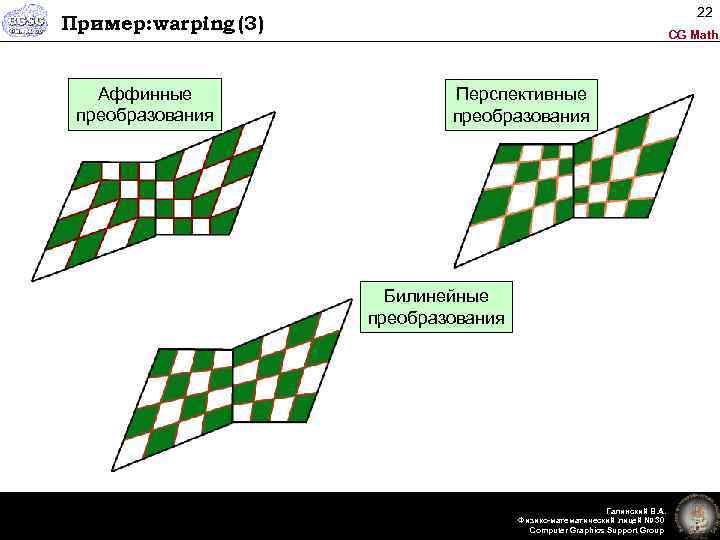 22 Пример: warping (3) Аффинные преобразования CG Math Перспективные преобразования Билинейные преобразования Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
22 Пример: warping (3) Аффинные преобразования CG Math Перспективные преобразования Билинейные преобразования Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
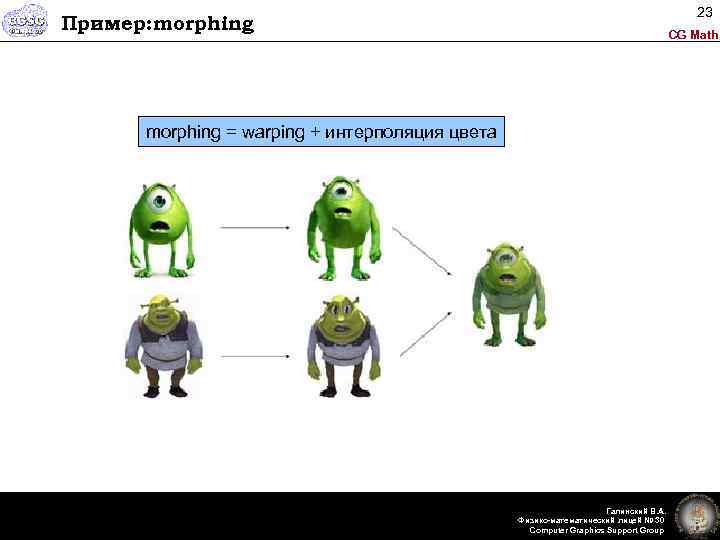 23 Пример: morphing CG Math morphing = warping + интерполяция цвета Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
23 Пример: morphing CG Math morphing = warping + интерполяция цвета Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 24 Перспективные преобразования CG Math Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
24 Перспективные преобразования CG Math Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 Привязка с перспективным преобразованием (1) • общая формула: • прямое отображение: • полагаем w=1, итоговая формула для координат: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 25 CG Math
Привязка с перспективным преобразованием (1) • общая формула: • прямое отображение: • полагаем w=1, итоговая формула для координат: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 25 CG Math
 Привязка с перспективным преобразованием (2) • получаем матрицу обратного отображения • определитель присутствует и в числителе и в знаменателе – вычислять не нужно: • находим присоединенную матрицу: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 26 CG Math
Привязка с перспективным преобразованием (2) • получаем матрицу обратного отображения • определитель присутствует и в числителе и в знаменателе – вычислять не нужно: • находим присоединенную матрицу: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 26 CG Math
 Привязка с перспективным преобразованием (3) 27 CG Math • Задача привязки: по 4 точкам соответствия определить матрицу перехода: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Привязка с перспективным преобразованием (3) 27 CG Math • Задача привязки: по 4 точкам соответствия определить матрицу перехода: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 Привязка с перспективным преобразованием (4) • запишем зависимость (выразим координаты x и y): • выпишем в матричной форме 8 уравнений: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 28 CG Math
Привязка с перспективным преобразованием (4) • запишем зависимость (выразим координаты x и y): • выпишем в матричной форме 8 уравнений: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 28 CG Math
 Привязка с перспективным преобразованием (5) • для упрощения задачи переход ищем из единичного квадрата: • получаем: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 29 CG Math
Привязка с перспективным преобразованием (5) • для упрощения задачи переход ищем из единичного квадрата: • получаем: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 29 CG Math
 Привязка с перспективным преобразованием (6) • обозначаем: • и находим решение: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 30 CG Math
Привязка с перспективным преобразованием (6) • обозначаем: • и находим решение: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 30 CG Math
 Аффинные преобразования в пространстве • Аналогично случаю 2 D вводим однородные координаты: • и преобразования в общем случае: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 31 CG Math
Аффинные преобразования в пространстве • Аналогично случаю 2 D вводим однородные координаты: • и преобразования в общем случае: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 31 CG Math
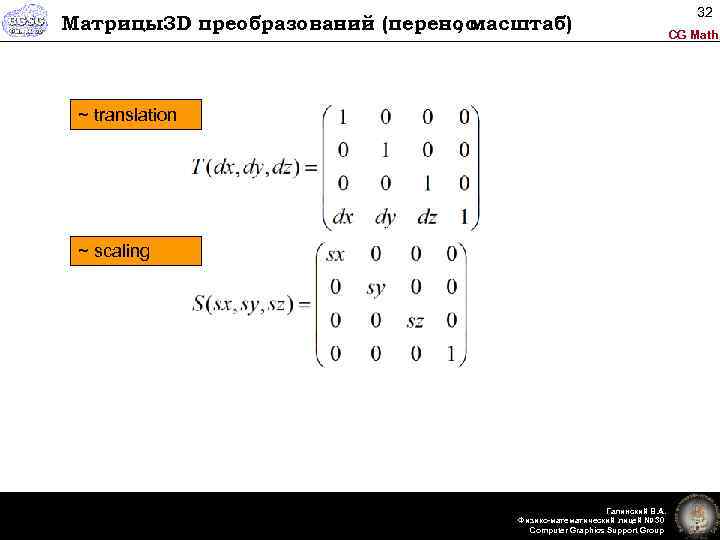 Матрицы3 D преобразований (перенос , масштаб) ~ translation ~ scaling Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 32 CG Math
Матрицы3 D преобразований (перенос , масштаб) ~ translation ~ scaling Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 32 CG Math
 Матрицы3 D преобразований (поворот вокруг осей) ~ rotation Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 33 CG Math
Матрицы3 D преобразований (поворот вокруг осей) ~ rotation Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 33 CG Math
 Матрицы3 D преобразований (поворот вокруг оси) • Поворот вокруг произвольной оси, проходящей через начало координат. Ось задается нормированным радиус вектором. ~ rotation Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 34 CG Math
Матрицы3 D преобразований (поворот вокруг оси) • Поворот вокруг произвольной оси, проходящей через начало координат. Ось задается нормированным радиус вектором. ~ rotation Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 34 CG Math
 Пример: построение матрицы камеры (1) • камера задается: позиция С и векторы направление «вверх» V, «вправо» U и вперед N. • ищем преобразование в виде «перенос+поворот» : где Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 35 CG Math
Пример: построение матрицы камеры (1) • камера задается: позиция С и векторы направление «вверх» V, «вправо» U и вперед N. • ищем преобразование в виде «перенос+поворот» : где Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 35 CG Math
 Пример: построение матрицы камеры (2) • после преобразования вектора отобразятся: т. е. Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 36 CG Math
Пример: построение матрицы камеры (2) • после преобразования вектора отобразятся: т. е. Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 36 CG Math
 Пример: построение матрицы камеры (3) • зная находим Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 37 CG Math
Пример: построение матрицы камеры (3) • зная находим Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group 37 CG Math


