ce06908db95de9232d1a016466aa035a.ppt
- Количество слайдов: 22

1 An Efficient and Easily Parallelizable Algorithm for Pricing Weather Derivatives Yusaku Yamamoto Dept. of Computational Science & Engineering Nagoya University LSSC’ 05,Sozopol June 6 -10, 2005

2 Outline of the talk 1. 2. 3. 4. 5. 6. Introduction Problem formulation A new pricing algorithm based on the fast Gauss transform Parallelization Numerical results Conclusion

3 1. Introduction • Weather conditions greatly affect business activities. Excessive heat in summer Electronics companies: larger sales of air conditioners Little snow In winter Local governments: decrease of costs for removing snow Department stores: increase of air conditioning costs Hotels in ski areas: decrease of revenues Variation of revenues due to weather conditions = weather risks = Financial products to reduce weather risks and stabilize the revenues Weather derivatives

4 What is a weather derivative? • Definition – A financial contract which allows the holder to receive a certain amount of money if predetermined weather conditions are met. • Example of a temperature derivative – “The holder will receive $10, 000 for one day in July for which the maximum temperature is under 20 C” A manufacturer of air conditioners can use this derivative to compensate for a possible loss of revenues due to cool summer. • Market of weather derivatives – $11 billion in Europe and the USA (in year 2002)
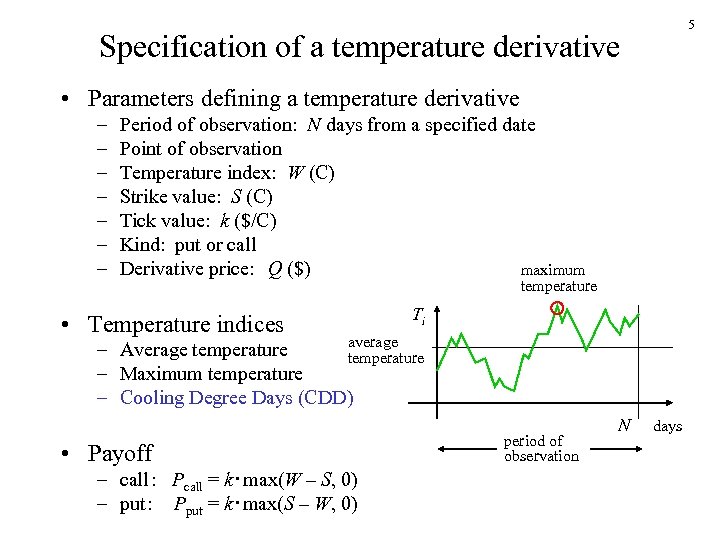
5 Specification of a temperature derivative • Parameters defining a temperature derivative – – – – Period of observation: N days from a specified date Point of observation Temperature index: W (C) Strike value: S (C) Tick value: k ($/C) Kind: put or call Derivative price: Q ($) maximum • Temperature indices temperature Ti average – Average temperature – Maximum temperature – Cooling Degree Days (CDD) • Payoff – call: Pcall = k・max(W – S, 0) – put: Pput = k・max(S – W, 0) period of observation N days
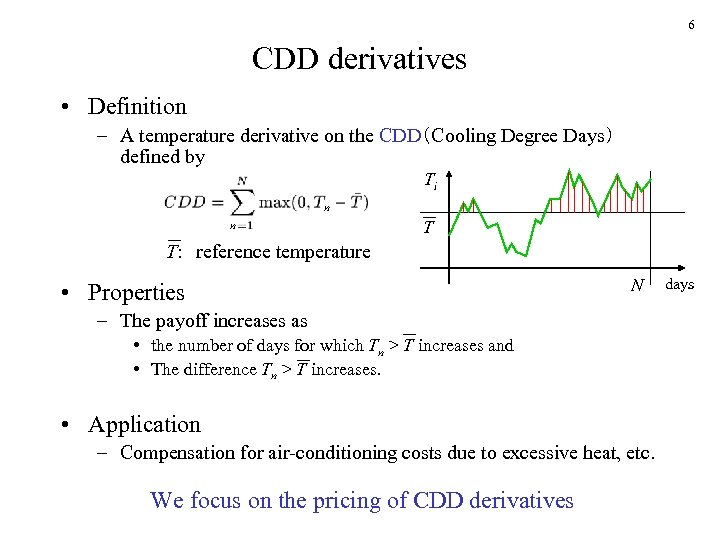
6 CDD derivatives • Definition – A temperature derivative on the CDD(Cooling Degree Days) defined by Ti n n T T: reference temperature • Properties N – The payoff increases as • the number of days for which Tn > T increases and • The difference Tn > T increases. • Application – Compensation for air-conditioning costs due to excessive heat, etc. We focus on the pricing of CDD derivatives days

7 2. Problem formulation • Principles for pricing – Construct a stochastic model describing the daily air temperature {T 1, T 2, … , TN} during the period of observation. – Compute the expectation value of the payoff Pcall under the stochastic model. – Add premium e to the result to get the derivative price: Q = E[Pcall] + e. • Stochastic models for daily air temperature – Historical model (Zeng, 2000) • Determines Tn by random sampling from the past data – Dischel model (Dischel, 1999) • Tn is assuemd to follow a non-stationary autoregressive model of order 1. – GARCH models (Cao & Wei, 1999) – Long-term memory models

8 The Dischel model • The model – Tn follows a non-stationary autoregressive model of order 1. Tn = (1 – β)Θn + βTn– 1 + εn n: Θ temperature of the n-th day in an average year ~ N [μ,σ2], i. i. d. εn – Widely used for pricing as a simple yet effective model. • Determination of the parameters – Parameters b, m and s are determined from the past data by least squares fitting. – It is also possible to adjust b, m and s to incorporate the long-term weather prediction (Egi et al. , 2003).
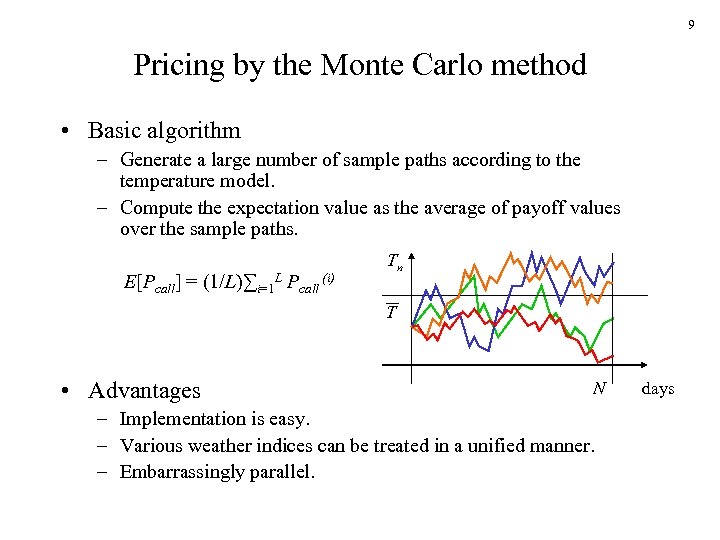
9 Pricing by the Monte Carlo method • Basic algorithm – Generate a large number of sample paths according to the temperature model. – Compute the expectation value as the average of payoff values over the sample paths. E[Pcall] = (1/L)∑i=1 L Pcall (i) Tn T • Advantages N – Implementation is easy. – Various weather indices can be treated in a unified manner. – Embarrassingly parallel. days

10 Problems with the MC method • Slow convergence – Requires 108 sample paths to compute the price to 3 -digit accuracy. – The computation takes about 10 min on an average PC. • Circumstances where the MC method is too slow – Real-time pricing – Pricing of a portfolio consisting of hundreds of derivatives • Objectives of our research – To develop a pricing algorithm for the CDD derivatives that is • orders of magnitude faster than the MC method, and • easily parallelizable

11 3. A new pricing algorithm based on the fast Gauss transform • The basic idea (Yamamoto & Egi, 2004) – Define the partial CDD Cn as follows: Cn = ∑ i=1 n max(0, Ti – T ) – Compute the joint probability distribution function pn (Tn, Cn) of (Tn, Cn) by a recursion formula. – Compute the expected payoff from p. N (TN, CN). • The joint pdf for the 1 st day

12 Computing the joint pdf by a recursion formula • Transition pdf from pn– 1 (Tn– 1, Cn– 1 ) to pn (Tn, Cn) ( ) When , we have from Cn = Cn– 1 + (Tn – T ), The transition pdf for can be computed similarly.

Computing the joint pdf by a recursion formula 13 • The recursion formula for pn (Tn, Cn) When , Convolution of a function with the Gaussian distribution Similarly, the recursion formula for can be expressed as a convolution of a function with the Gaussian distribution. • Computational work (assuming M grid points for both Tn and Cn directions) • O(M 2) for each convolution • O(M 3) for computing pn(Tn, Cn) for all values of Tn and Cn

14 Computing the expected payoff • The expected payoff can be computed from p. N (TN, CN) by simple integrations:

15 Acceleration by the fast Gauss transform • Computational work of the present method – O(M 3) work to compute M convolutions at each time step. • The fast Gauss transform(Greengard & Strain, 1991) – Expand the Gaussian in the convolution with Hermite functions. – Reduces the computational work from O(M 2) to O(M). – Proved useful to construct fast and accurate pricing algorithms for various financial derivatives (Broadie & Yamamoto, 2003). • Effect of using the FGT – The computational work at each time step can be reduced from O(M 3) to O(M 2).

16 Convergence of the proposed method • Computational work – O(M 2) for each step (thanks to the use of the FGT) • Accuracy – The pricing error can be shown to decrease as O(1/M 2). The error decreases as E = O(1/τ) with the computational timeτ. • Comparison with the Monte Carlo method – For the MC method, E = O(1/√τ). Asymptotically, our method converges faster than the MC method.

17 4. Parallelization • The recursion formulas at each time step When Tn < T, ) When Tn ≧T, The computation of pn (Tn, Cn) for different values of Cn can be done independently. Easily parallelizable by partitioning the array of pn (Tn, Cn) in the Cn direction and allocating each partial array to one processor.
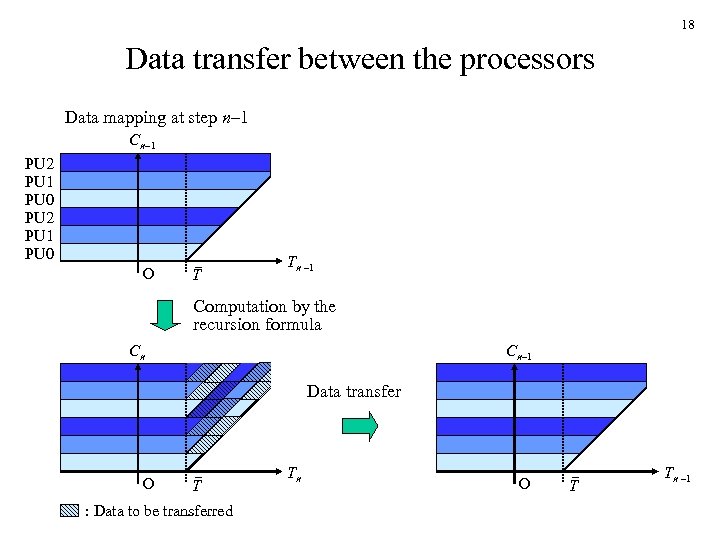
18 Data transfer between the processors Data mapping at step n– 1 Cn– 1 PU 2 PU 1 PU 0 O T Tn – 1 Computation by the recursion formula Cn– 1 Cn Data transfer O T : Data to be transferred Tn O T Tn – 1

19 5. Numerical results • Target problem – CDD call derivatives under the Dischel model • Numerical methods – Monte Carlo method – Our method • Parameters – – – Period of observation: N days from July 7 th (N = 10 or 20) Place of observation: Tokyo Index: CDD (T = 24 C) Strike value: K= 20 or 40 C b = – 0. 56, m = – 0. 01, s = 1. 83, Qk = 20 • Computing environments – Alpha workstation with g 77 compiler
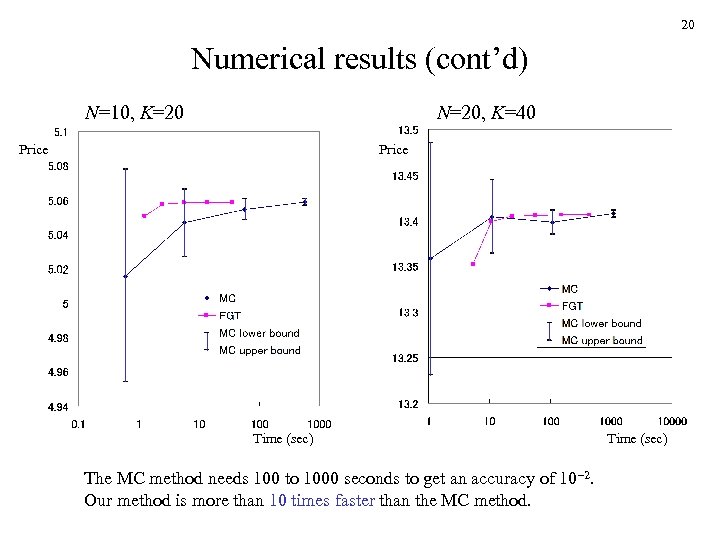
20 Numerical results (cont’d) N=10, K=20 N=20, K=40 Price Time (sec) The MC method needs 100 to 1000 seconds to get an accuracy of 10– 2. Our method is more than 10 times faster than the MC method. Time (sec)
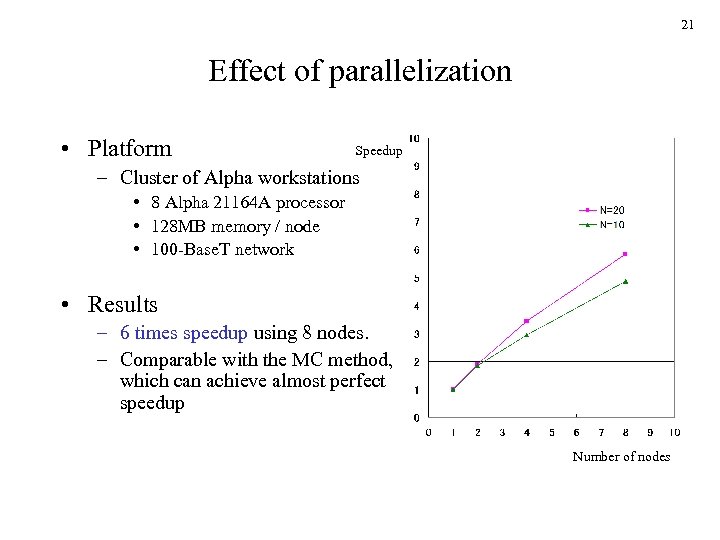
21 Effect of parallelization • Platform Speedup – Cluster of Alpha workstations • 8 Alpha 21164 A processor • 128 MB memory / node • 100 -Base. T network • Results – 6 times speedup using 8 nodes. – Comparable with the MC method, which can achieve almost perfect speedup Number of nodes

22 6. Conclusion • Conclusion – We developed a fast and an easily parallelizable algorithm for pricing CDD weather derivatives based on the fast Gauss transform. – Our algorithm is more than 10 times faster than the MC method when computing the price of a CDD derivative with 5 to 20 monitoring dates. – Also, it can achieve 6 times speedup on a WS cluster with 8 nodes. • Future work – Application to other types of temperature derivatives – Application to the pricing of a portfolio consisting of a large number of derivatives
ce06908db95de9232d1a016466aa035a.ppt