2015-2016. ИСТ. Лекция_2.Алгоритмы.ppt
- Количество слайдов: 22
 1
1
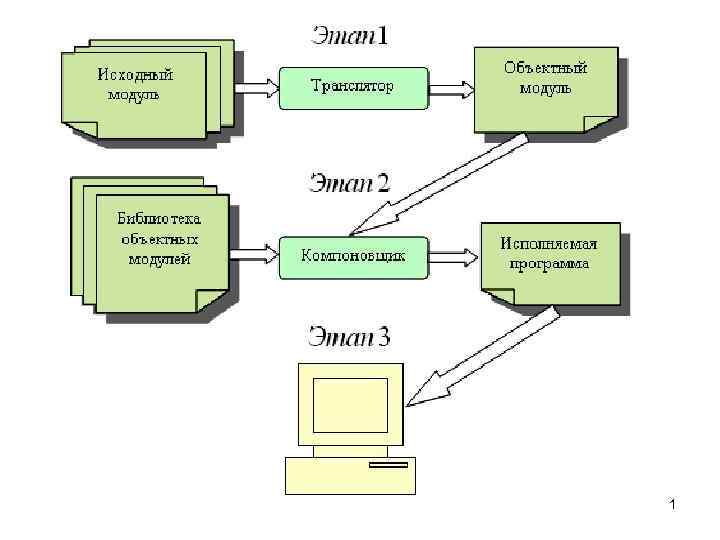
 Алгоритмы вычислительных процессов. Алгоритм – точное предписание, определяющее вычислительный процесс, ведущий от варьируемых начальных данных к искомому результату. Таким образом, алгоритм должен содержать конечную последовательность шагов или операций, однозначно определяющих процесс переработки исходных и промежуточных 2 данных в искомый результат.
Алгоритмы вычислительных процессов. Алгоритм – точное предписание, определяющее вычислительный процесс, ведущий от варьируемых начальных данных к искомому результату. Таким образом, алгоритм должен содержать конечную последовательность шагов или операций, однозначно определяющих процесс переработки исходных и промежуточных 2 данных в искомый результат.
 Алгоритмы и их свойства. Дискретность. Весь вычислительный процесс разбит на мелкие этапы (шаги, дискреты). И решение задачи сводится к решению простых задач, при этом каждое действие выполняется только после того, как закончится исполнение предыдущего. 3
Алгоритмы и их свойства. Дискретность. Весь вычислительный процесс разбит на мелкие этапы (шаги, дискреты). И решение задачи сводится к решению простых задач, при этом каждое действие выполняется только после того, как закончится исполнение предыдущего. 3
 • Детерминированность (определённость), которая заключается в том, что чётко определён порядок выполнения алгоритма. Это обеспечивает однозначность результата при заданных исходных данных. • Результативность. Получение вполне определённого результата за определённое число шагов. 4
• Детерминированность (определённость), которая заключается в том, что чётко определён порядок выполнения алгоритма. Это обеспечивает однозначность результата при заданных исходных данных. • Результативность. Получение вполне определённого результата за определённое число шагов. 4
 • Конечность. При работе с численными методами строится бесконечный, сходящийся к искомому решению процесс. Процесс обрывается, когда очередное приближённое решение достигает заданной точности. Таким образом, за конечное число шагов получается решение задачи. 5
• Конечность. При работе с численными методами строится бесконечный, сходящийся к искомому решению процесс. Процесс обрывается, когда очередное приближённое решение достигает заданной точности. Таким образом, за конечное число шагов получается решение задачи. 5
 • Массовость. С помощью выбранного алгоритма можно получать вполне определённый результат при различных исходных данных для некоторого класса задач. • Формальность. Исполнитель, незнакомый с содержанием алгоритма, но правильно выполнивший его предписание, получает искомый результат. 6
• Массовость. С помощью выбранного алгоритма можно получать вполне определённый результат при различных исходных данных для некоторого класса задач. • Формальность. Исполнитель, незнакомый с содержанием алгоритма, но правильно выполнивший его предписание, получает искомый результат. 6
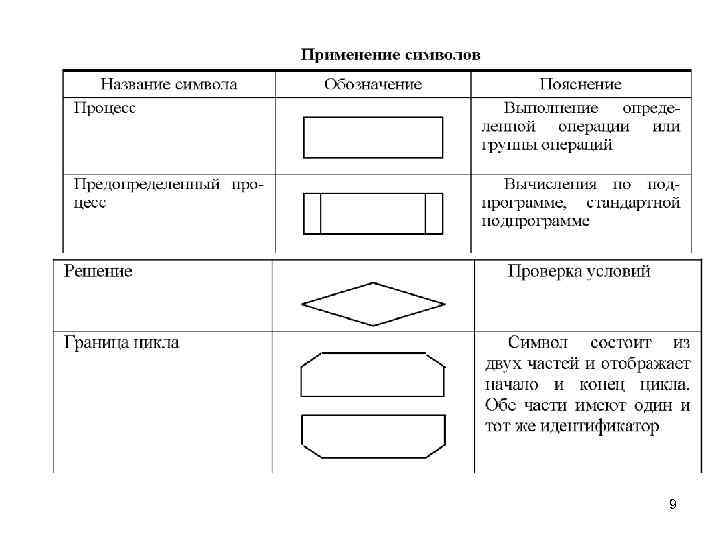
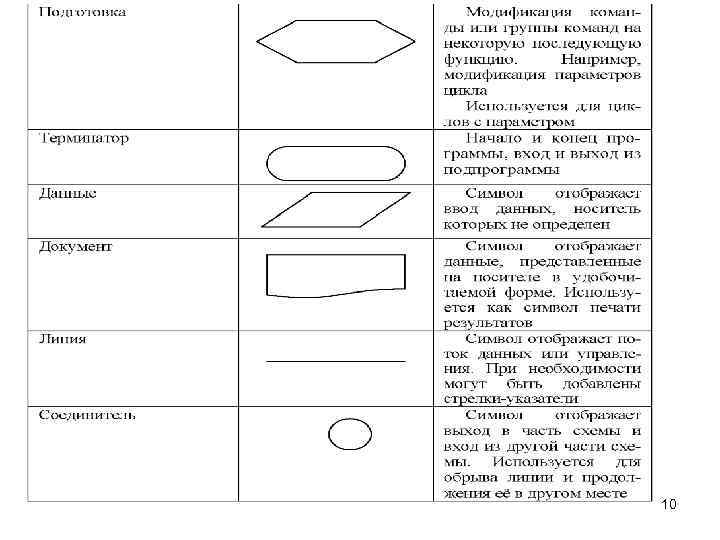
 Способы описания алгоритмов • словесная запись; • псевдокод; • схемы. Задача. Заданы координаты двух точек. Координаты 1 -й точки - XI, Y 1, координаты 2 -й точки -Х 2, Y 2. Определить, какая из точек наиболее удалена от начала координат. 7
Способы описания алгоритмов • словесная запись; • псевдокод; • схемы. Задача. Заданы координаты двух точек. Координаты 1 -й точки - XI, Y 1, координаты 2 -й точки -Х 2, Y 2. Определить, какая из точек наиболее удалена от начала координат. 7
 Решение. 1. Вычисляем расстояние 1 -й точки до начала координат: 2. Вычисляем расстояние 2 -й точки до начала координат: 3. Определяем большее из расстояний. Если R 1 больше R 2, то переход к следующему пункту, если R 1 меньше, то переход к п. 5. 4. Печать сообщения «Первая точка лежит ближе к началу координат» . Переход к п. 6. 5. Печать сообщения «Вторая точка лежит ближе к началу координат» . 6. Конец алгоритма. 8
Решение. 1. Вычисляем расстояние 1 -й точки до начала координат: 2. Вычисляем расстояние 2 -й точки до начала координат: 3. Определяем большее из расстояний. Если R 1 больше R 2, то переход к следующему пункту, если R 1 меньше, то переход к п. 5. 4. Печать сообщения «Первая точка лежит ближе к началу координат» . Переход к п. 6. 5. Печать сообщения «Вторая точка лежит ближе к началу координат» . 6. Конец алгоритма. 8
 9
9
 10
10
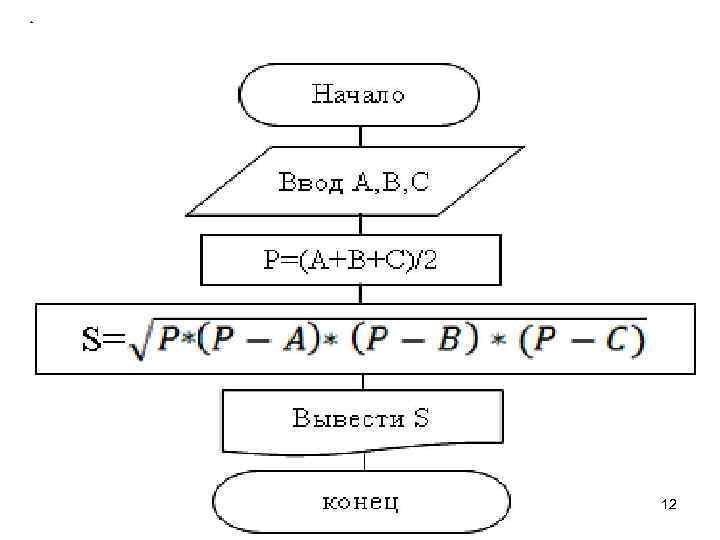
 Типовые структуры алгоритмов Линейный алгоритм Составить алгоритм вычисления площади треугольника со сторонами A, B, C по формуле Герона: 11
Типовые структуры алгоритмов Линейный алгоритм Составить алгоритм вычисления площади треугольника со сторонами A, B, C по формуле Герона: 11
 12
12
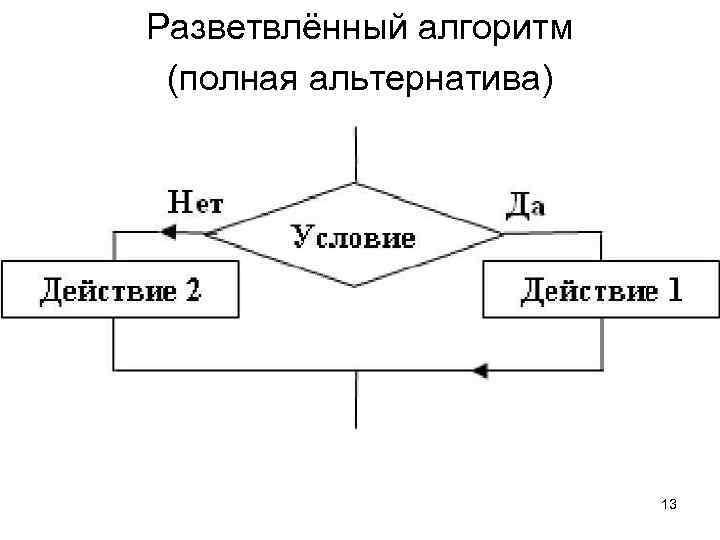 Разветвлённый алгоритм (полная альтернатива) 13
Разветвлённый алгоритм (полная альтернатива) 13
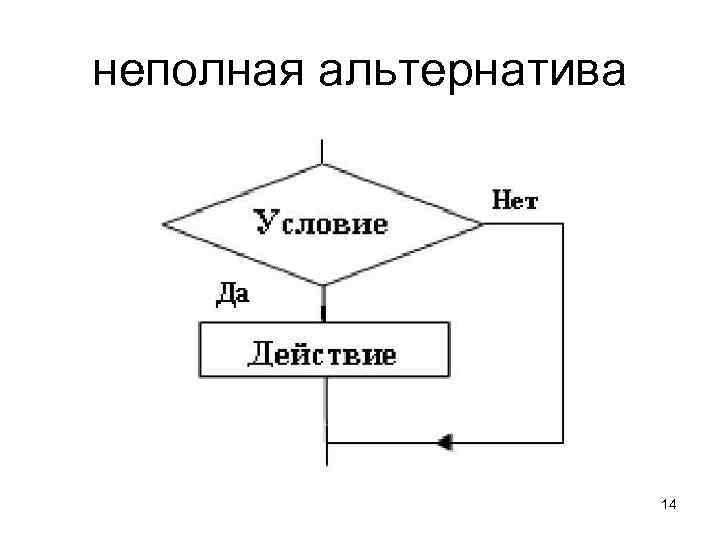 неполная альтернатива 14
неполная альтернатива 14
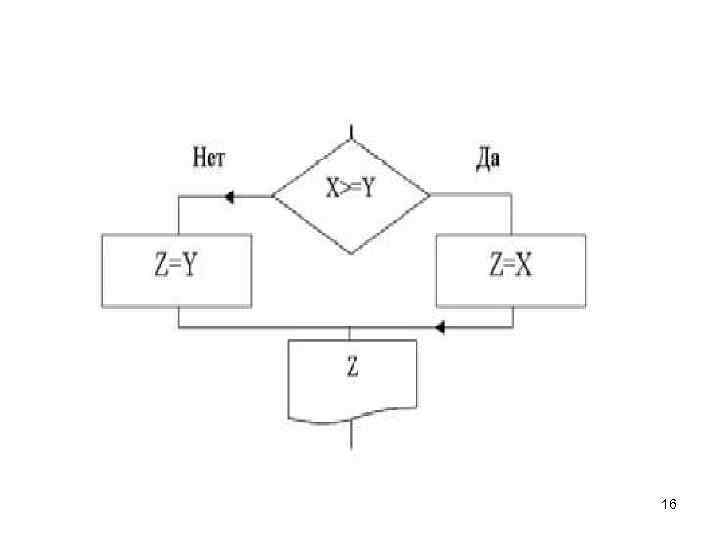
 Даны два числа X и У. Составить схему алгоритма для нахождения наибольшего. 15
Даны два числа X и У. Составить схему алгоритма для нахождения наибольшего. 15
 16
16
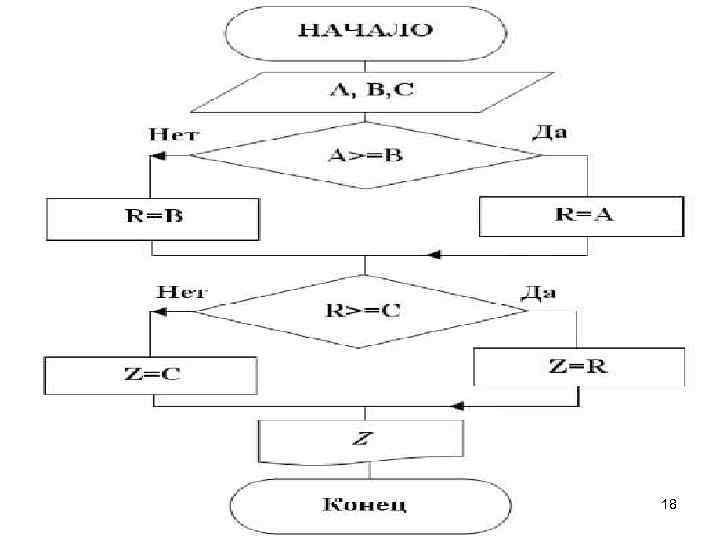
 Даны три числа А, В, С. Составить схему алгоритма вычисления Z = тах(А, В, С). R = max(A, B), Z = max(R, C). 17
Даны три числа А, В, С. Составить схему алгоритма вычисления Z = тах(А, В, С). R = max(A, B), Z = max(R, C). 17
 18
18
 Циклический алгоритм • Алгоритмом циклической структуры называется алгоритм, в котором предусмотрено неоднократное выполнение одной и той же последовательности действий при различных значениях входящих в них величин. • Многократно повторяющиеся участки называются циклами или телом цикла. • Переменная алгоритма, которая при каждом выполнении цикла принимает новое значение, называется параметром цикла (или переменной цикла). 19
Циклический алгоритм • Алгоритмом циклической структуры называется алгоритм, в котором предусмотрено неоднократное выполнение одной и той же последовательности действий при различных значениях входящих в них величин. • Многократно повторяющиеся участки называются циклами или телом цикла. • Переменная алгоритма, которая при каждом выполнении цикла принимает новое значение, называется параметром цикла (или переменной цикла). 19
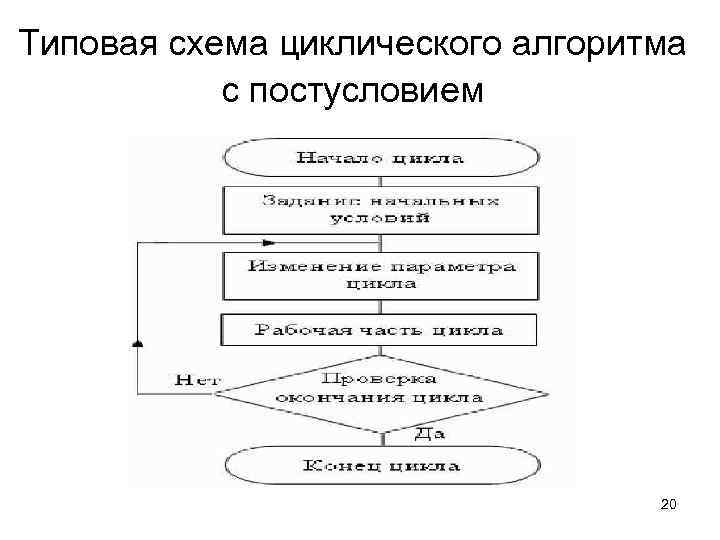 Типовая схема циклического алгоритма с постусловием 20
Типовая схема циклического алгоритма с постусловием 20
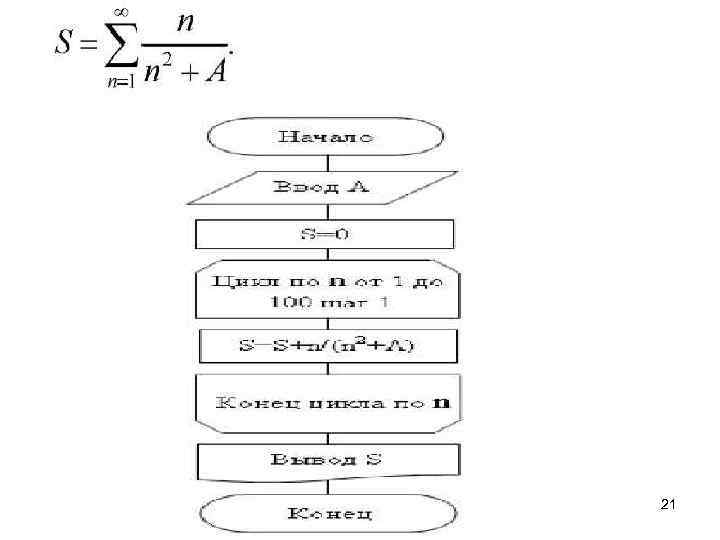 21
21
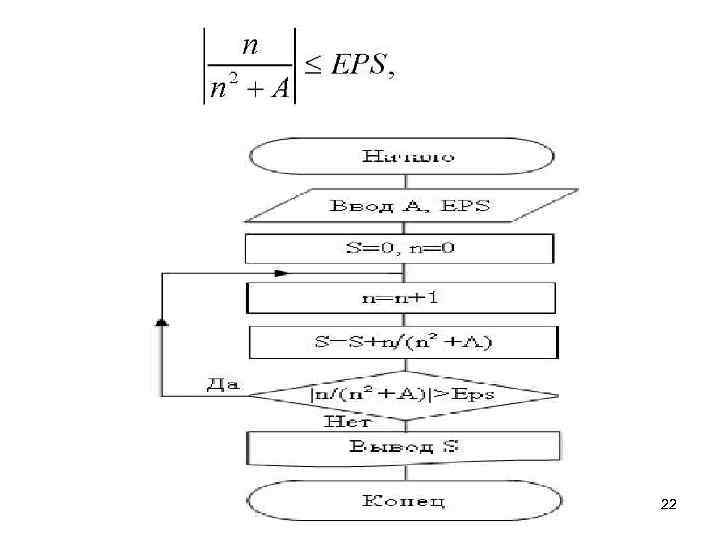 22
22


