Скачать презентацию 1 — A Presentation the eductive Скачать презентацию 1 — A Presentation the eductive

0c4277caf49be0d28bc72d3989860c41.ppt

  • Количество слайдов: 23

1 - A Presentation : the « eductive » viewpoint. Rationalizability and the stability 1 - A Presentation : the « eductive » viewpoint. Rationalizability and the stability of expectations. 1

A simple game. n The rules of the game : n n Lessons : A simple game. n The rules of the game : n n Lessons : n n n 0 is the unique Nash equilibrium. It is a rather « reasonable » predictor of what happens. Change the game : n n n write a number : [0, 100] Winner : 10 Euros : closest to 2/3 of the mean (of others) What happens in this game ? See Nagel (1995) Announce : [0, + infinity) [0, 100]. . . 3/2 instead of 2/3. « Eductive » or « evolutive » explanation 2

Expectational Stability A first theoretical perspective. 3 Expectational Stability A first theoretical perspective. 3

The approach. n General inspiration : n n n Expectational coordination is more or The approach. n General inspiration : n n n Expectational coordination is more or less stable. Find criteria with « eductive » flavour. Classify : type 2/3 or. . . 1/2, or 3/2 n n n Situations, economies ? global Equilibria : local The above argument is captured by rationnalisability ideas n n n Iterated elimination of dominated strategies Old wine : Luce Raiffa, Farqhason, Moulin. New bottles : Bernheim, Pearce (1984). 4

Rationalizable solutions in games. n Game in normal form n n n n A Rationalizable solutions in games. n Game in normal form n n n n A number of technical variations : n n n S(i), s(i), u(i, s(i), s(-i)) Iterative elimination of non best response strategies : S(0, i) =S(i) S(1, i) = {S(0, i) strategies in S(0, i) non BR to some srategy in j[ S(0, j)]}. . S( , i) = {S( -1, i) s(i) in S( - 1, i) non BR to j[ (S( -1, j)]} R = [ i( (S( , i)] Correlated or independant rationalizability. Curb set, correlated equilibria, p-minimal sets Note R contains N ! 5

Rationalizable solutions in games. n The « 2/3 of the mean » game. n Rationalizable solutions in games. n The « 2/3 of the mean » game. n n n n S(i)={0, 100}, u(i, s(i), s(-i))=…. . ; Iterative elimination of non best response strategies : S(0, i) = {0, 100}, S(1, i) = {0, 6666…}. . S( , i) = {0, (2/3) 100} 0 is n n the unique Nash equilibrium. The unique « rationalizable » outcome. n n n Dominant solvable Nash outcome Strongly rational equilibrium, « edcutively » stable We have « strategic complementarities » 6

n Rationalizability and expectational coordination. Rationalizability consequence of n n The viewpoint taken here. n Rationalizability and expectational coordination. Rationalizability consequence of n n The viewpoint taken here. n n n Strongly Rational if it can be guessed through the mental process. There are several equilibria n n n Economic models. No « market power » : a continuum of agents. Nash equilibria are Rational Expectations Equilibria The equilibrium is unique. n n CK of the game, CK of rationality, (Tan, Werlang) A local viewpoint on the mental process. Locally strongly rational. Terminology : « eductively stable ? 7

Strategic complementarities : 1. First insights. 8 Strategic complementarities : 1. First insights. 8

One-dimensional aggregate : strategic complementarities. n The specialized model. n n n A continuum One-dimensional aggregate : strategic complementarities. n The specialized model. n n n A continuum of (small) agents; Each is concerned by his own action and an aggregate of actions of others : a(i), A= a(i)di Case 1 : the aggregate is one dimensional. n n Strategic complementarities Muth etc The aggregate is not one dimensional. Strategic complementarities : n the best response a(i) increases with the (expected) A. 9

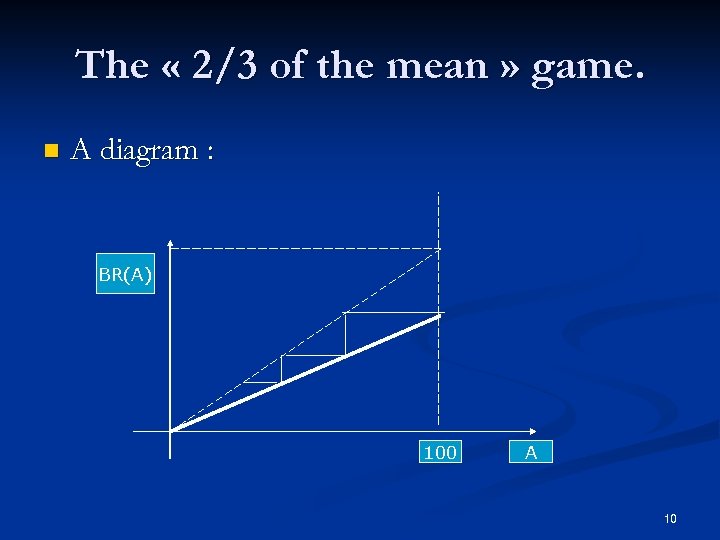The « 2/3 of the mean » game. n A diagram : BR(A) 100 The « 2/3 of the mean » game. n A diagram : BR(A) 100 A 10

Strategic Complementarities : a simple model. n The model : n n n Population Strategic Complementarities : a simple model. n The model : n n n Population agents a : Individual Costs c, F(c. ), Profitability = da Strategic complementarities. Equilibria n n n Three or One ? How flat is the distribution. 11

n Draw n n n One dimensional aggregate strategic complementarities. aggregate = f((point) expectations n Draw n n n One dimensional aggregate strategic complementarities. aggregate = f((point) expectations of the aggregate) Example : planned production as a function of expected production (keynesian situation) This function is increasing. SC Possibly with jumps. Equilibrium n n Fixed point. unique. or not What does rationalizability bring ? max S(2) min S(1) 12

One-dimensional aggregate strategic complementarities n The unique equilibrium is Strongly Rational. n n n One-dimensional aggregate strategic complementarities n The unique equilibrium is Strongly Rational. n n n The argument. The Graal !… In case of multiplicity n n The rationalizable set. Some equilibria are locally strongly rational. max S(2) min R S(1) 13

Local Strong Rationality. n The local viewpoint n n n Hypothetical Common Knowledge of Local Strong Rationality. n The local viewpoint n n n Hypothetical Common Knowledge of the nbhd. If slope >1, the hypothetical CK is dismissed. n Locally eductively stable equilibrium Question : n Is there a nbhd, distinct from the equilibrium s. t. the fact that evby believes in that the outcome is in the nbd implies surely that it will be ? It is CK That Q V 14

1 -C Expectational coordination in a simple partial equilibrium context The Muth model : 1 -C Expectational coordination in a simple partial equilibrium context The Muth model : strategic substitutabilities. 15

A simple partial equilibrium model n Very simple framework (Muth, 1961) : n Sellers A simple partial equilibrium model n Very simple framework (Muth, 1961) : n Sellers : firms) or farmers n n Buyers will buy to-morrow. n n n décide to-day about production (wheat). Cost C(f, q) ( =q 2/2 c(f) ) Many : demand curve : A-Bp « Walras, Marshall » partial equilibrium : n Notional supply n n Quadratic case : Maxq [pq - q 2/2 c(f)] S(p, f) = c(f)p S(p) = Cp Equilibrium : n n S(p) = A-Bp héraut walrassien ? Is it Strongly Rational. 16

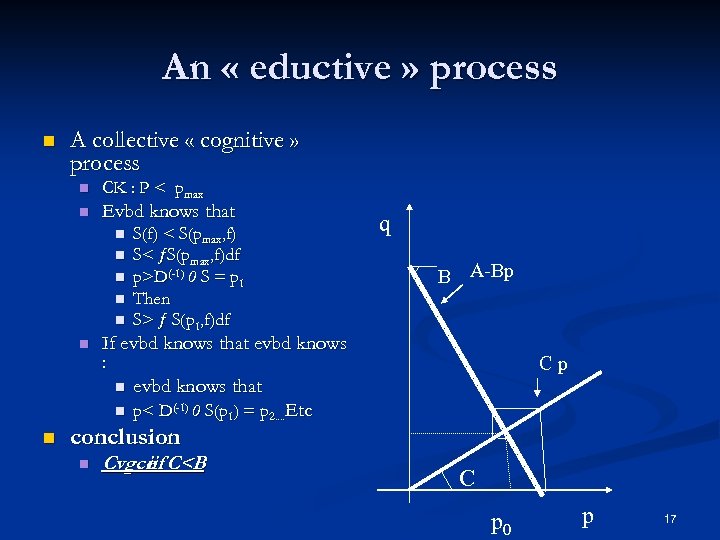An « eductive » process n A collective « cognitive » process n n An « eductive » process n A collective « cognitive » process n n CK : P < pmax Evbd knows that n n n n S(f) < S(pmax, f) S< S(pmax, f)df p>D(-1) 0 S = p 1 Then S> S(p 1, f)df q B A-Bp If evbd knows that evbd knows : n evbd knows that n p< D(-1) 0 S(p 1) = p 2. . Etc Cp conclusion n Cvgce C

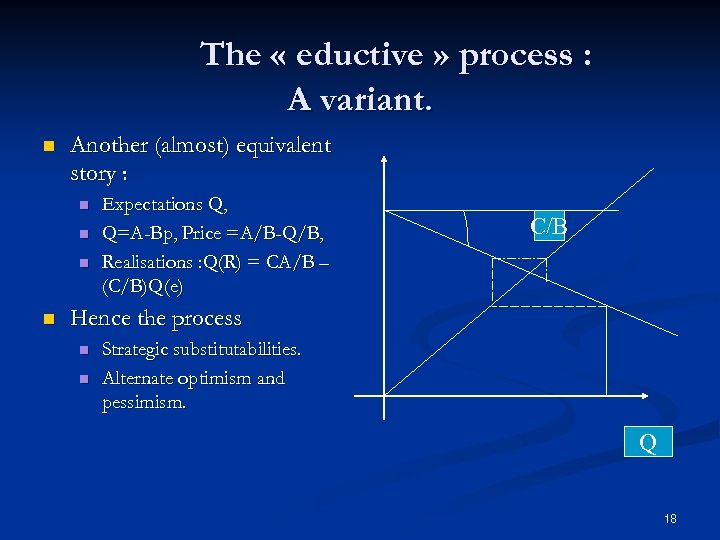The « eductive » process : A variant. n Another (almost) equivalent story : The « eductive » process : A variant. n Another (almost) equivalent story : n n Expectations Q, Q=A-Bp, Price =A/B-Q/B, Realisations : Q(R) = CA/B – (C/B)Q(e) C/B Hence the process n n Strategic substitutabilities. Alternate optimism and pessimism. Q 18

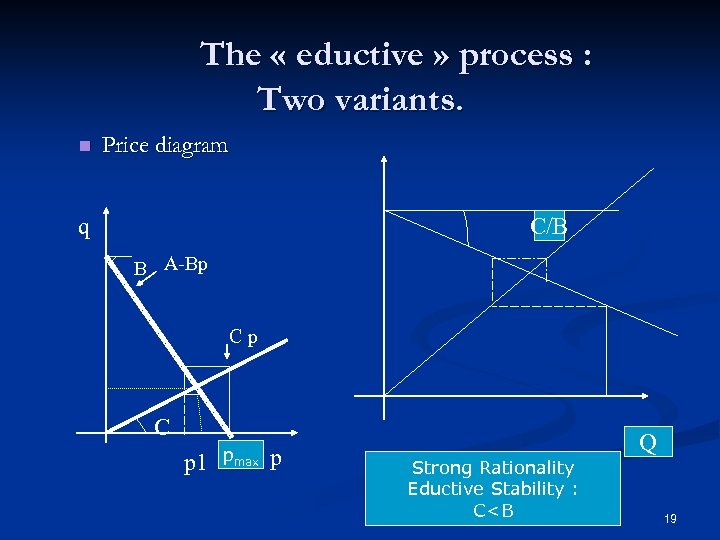The « eductive » process : Two variants. n Price diagram C/B q B The « eductive » process : Two variants. n Price diagram C/B q B A-Bp Cp C p 1 pmax p Q Strong Rationality Eductive Stability : C

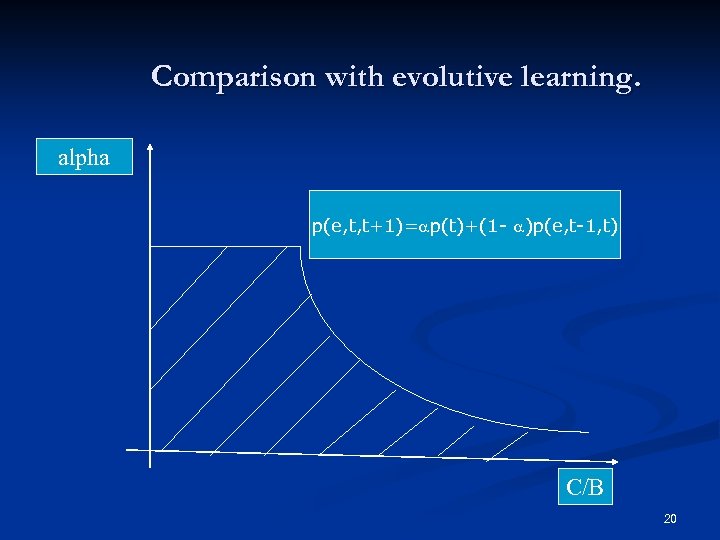Comparison with evolutive learning. alpha p(e, t, t+1)= p(t)+(1 - )p(e, t-1, t) C/B Comparison with evolutive learning. alpha p(e, t, t+1)= p(t)+(1 - )p(e, t-1, t) C/B 20

An insight into the algebra. n The equations : n n n n Learning An insight into the algebra. n The equations : n n n n Learning equations : a= p(e, t, t+1)=ap(t)+(1 -a)p(e, t-1, t) Equilibrium equations. A-Bp(t)=Cp(e, t-1, t) p(t)=(1/B)(A-C p(e, t-1, t)) p(e, t, t+1)=. . [-a(C/B)+(1 -a)]p(e, t-1, t) A(C/B) +a -1<1 Conclusions. n n n Small a is good. (inf. learning process) Small C/B is good. (inf system) =captured by the «eductive » viewpoint 21

The «eductive » viewpoint. n A « high-tech » formal (global) definition. n Definition The «eductive » viewpoint. n A « high-tech » formal (global) definition. n Definition (with a continuum of small agents) n Let E* (in some vector space ) be an (Rat. Exp. ) equilibrium. Assertion A : It is CK that E (rationality and the model are CK) n Assertion B : It is CK that E=E* n n n If A B, the equ. is (globally) Strongly Rational. A « high-tech » formal (local) definition. n Let V(E*} be some non trivial neighbourhood n Assertion It is CK that A : E is in V(E*) Assertion B : It is CK that E=E* n n n Same definition as before if V is the whole set of states. E* is locally, (vis-à-vis V), Strongly Rational. 22

The «eductive » stability criterion. n Remarks on the generality. n n Remarks on The «eductive » stability criterion. n Remarks on the generality. n n Remarks on the requirements. n n n Potentially general. Requires « rational » agents with some Common Knowledge on the (working of) the system. A « hyper-rationalistic » view of coordination. A « Low-tech » interpretation and alternative intuition. n n Local Expectational viewpoint. n n Can wefinda non-trivial of equilibrium ifeverybody nbd s. t believes the state bein tha will it, it willsurely …. ? be A Connection with « evolutive learning » (asymptotic stability of…) Too demanding ? 23