1.6. Работа сил электростатического поля Сила, действующая на

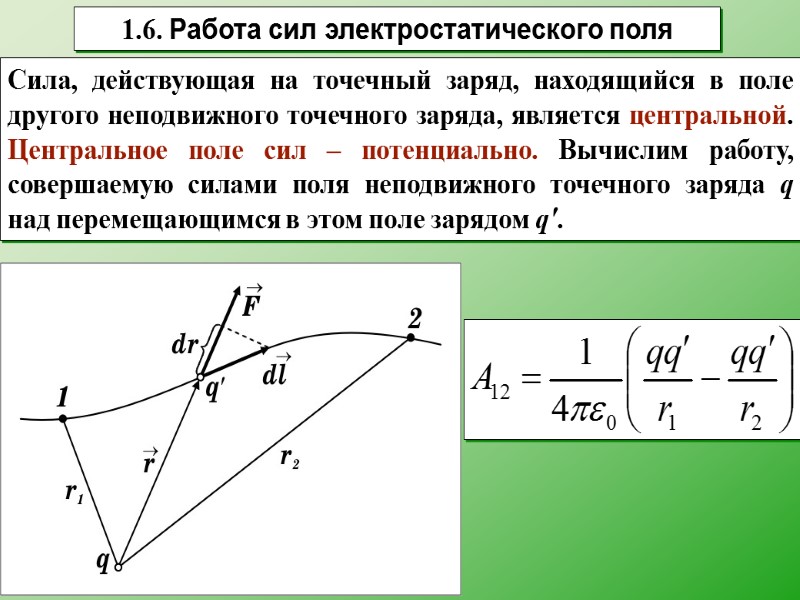
1.6. Работа сил электростатического поля Сила, действующая на точечный заряд, находящийся в поле другого неподвижного точечного заряда, является центральной. Центральное поле сил – потенциально. Вычислим работу, совершаемую силами поля неподвижного точечного заряда q над перемещающимся в этом поле зарядом q'.

Работа не зависит от пути, по которому перемещался в электрическом поле заряд q', а зависит только от начального и конечного положений этого заряда. Следовательно, силы, действующие на заряд q' в поле неподвижного заряда q, являются потенциальными. Этот вывод легко распространяется па поле любой системы неподвижных зарядов. Работа потенциальных сил по замкнутому контуру равна нулю. Циркуляция вектора напряженности по любому замкнутому контуру равна нулю – теорема о циркуляции вектора E. Это характерно только для электростатического поля.

1.7. Потенциал Тело, находящееся в потенциальном поле сил, обладает потенциальной энергией, за счет которой совершается работа силами поля. Работа может быть представлена как разность значений потенциальной энергии, которыми обладал заряд q' в точках 1 и 2 поля заряда q: Потенциальная энергия заряда q' Значение сonst выбирается т.о., чтобы при удалении от заряда на бесконечность потенциальная энергия обращалась в нуль.

φ называется потенциалом поля в данной точке и используется для описания электрических полей. Потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. – потенциал поля точечного заряда.
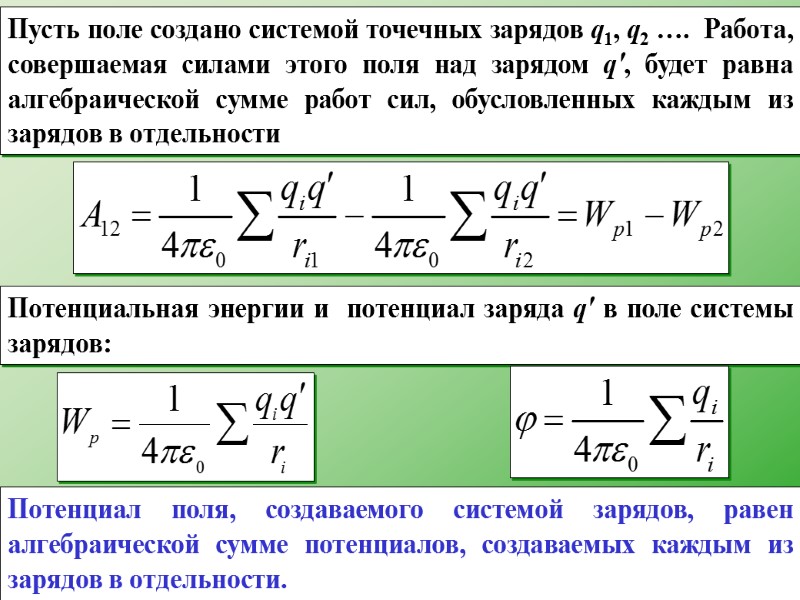
Пусть поле создано системой точечных зарядов q1, q2 …. Работа, совершаемая силами этого поля над зарядом q', будет равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности Потенциальная энергии и потенциал заряда q' в поле системы зарядов: Потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.

Потенциальную энергию точечного заряда Работа, совершаемая над точечным зарядом силами поля, равна произведению величины заряда на разность потенциалов в начальной и конечной точках. 1.8. Связь между, напряженностью электрического поля и потенциалом Электрическое поле можно описать либо с помощью векторной величины Е, либо с помощью скалярной величины φ. Связь между этими величинами должна быть аналогична, связи между потенциальной энергией и силой.

где l – произвольно выбранное направление в пространстве. По известным значениям φ можно найти Е в каждой точке. Можно решить и обратную задачу. Интеграл в правой части можно брать по любой линии, соединяющей точки 1 и 2, так как работа не зависит от пути.
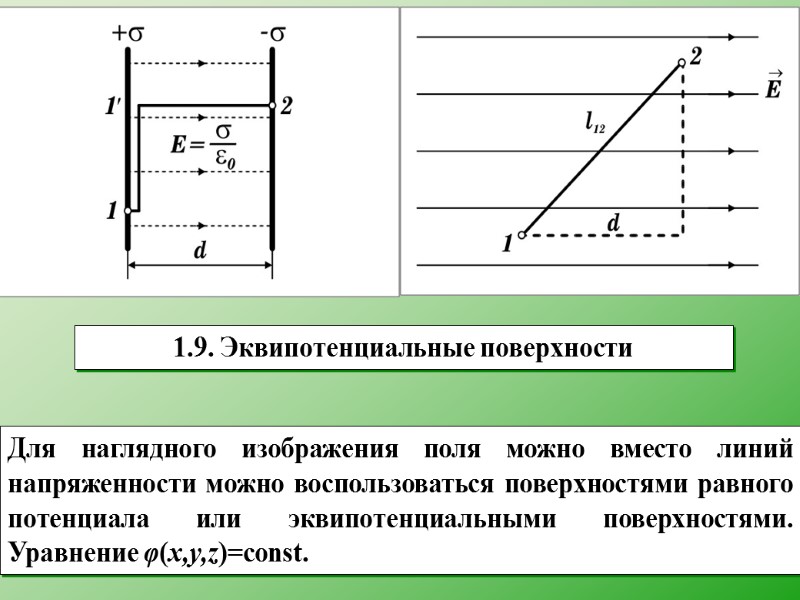
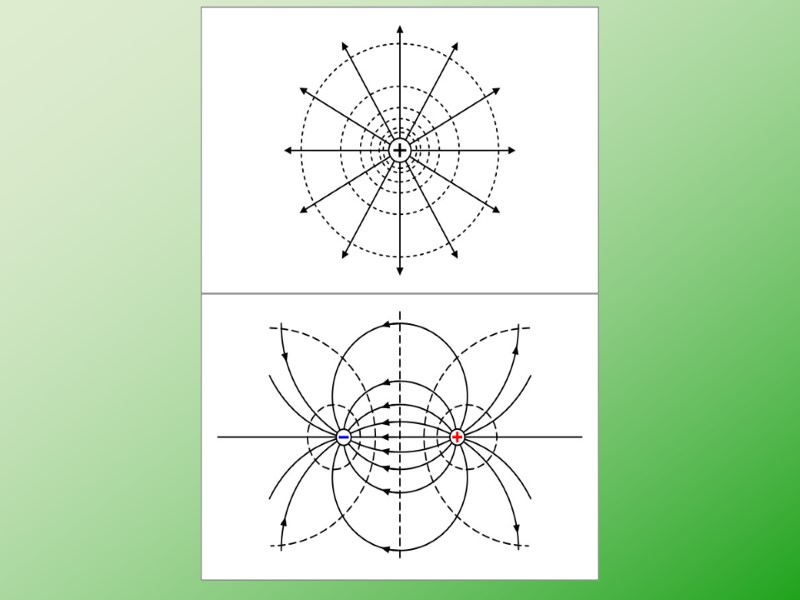
1.9. Эквипотенциальные поверхности Для наглядного изображения поля можно вместо линий напряженности можно воспользоваться поверхностями равного потенциала или эквипотенциальными поверхностями. Уравнение φ(x,y,z)=const.
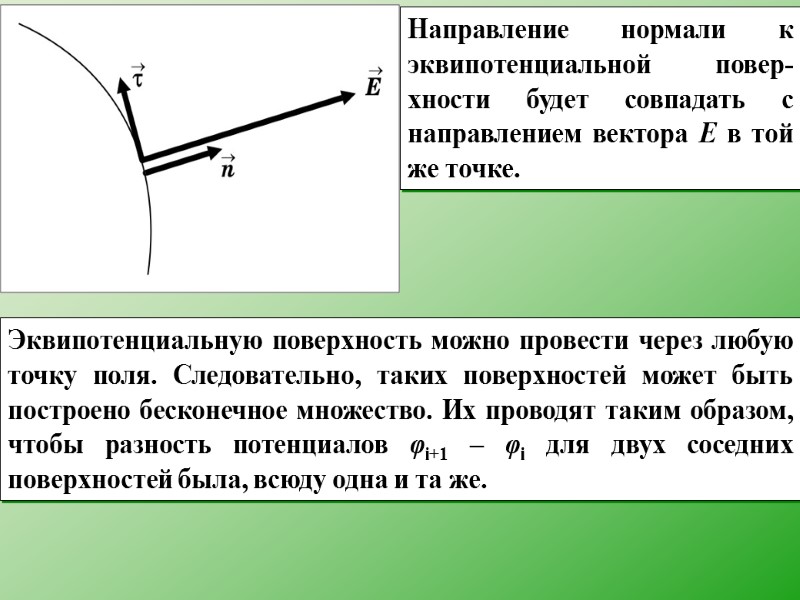
Направление нормали к эквипотенциальной повер-хности будет совпадать с направлением вектора Е в той же точке. Эквипотенциальную поверхность можно провести через любую точку поля. Следовательно, таких поверхностей может быть построено бесконечное множество. Их проводят таким образом, чтобы разность потенциалов φi+1 – φi для двух соседних поверхностей была, всюду одна и та же.

2. Во многих случаях оказывается, что для нахождения напряженности электрического поля легче сначала подсчитать потенциал и затем взять градиент от него. Для вычисления φ нужно взять один интеграл, а для вычисления — E три. Кроме того, обычно интегралы для определения φ проще, чем для Ex, Ey, Ez.
4886-lektsi3_rabota_sil_pol.ppt
- Количество слайдов: 11

