
1. 5. Расчет резьбы на прочность 1
Расчет резьбы на прочность 2

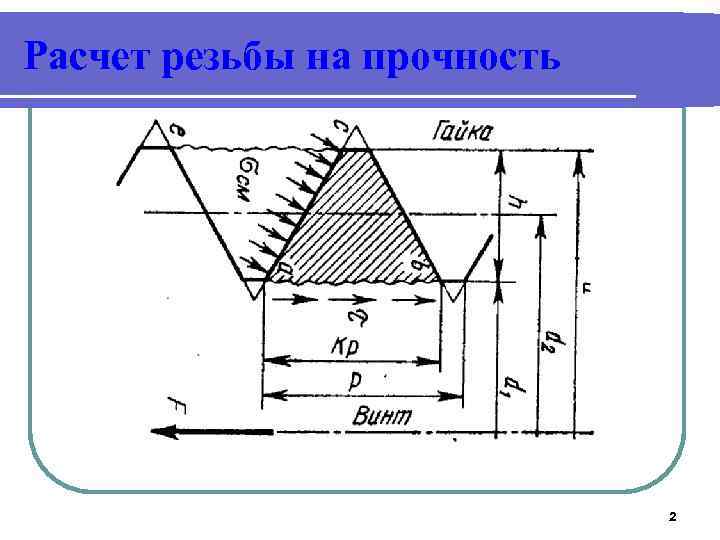
Расчет резьбы на прочность Основные виды разрушения резьб: крепежных — срез витков, ходовых — износ витков. В соответствии с этим основными критериями работоспособности и расчета для крепежных резьб являются прочность, связанная с напряжениями среза т, а для ходовых резьб — износостойкость, связанная с напряжениями смятия о см, рис. 1. 17. l Условия прочности резьбы по напряжениям среза: l l l для винта, для гайки(1. 12) 3

Расчет резьбы на прочность l где H — высота гайки или глубина завинчивания винта в деталь; К = аb/р или К = се/р — коэффициент полноты резьбы; Кm — коэффициент неравномерности нагрузки по виткам резьбы. 4

Расчет резьбы на прочность l Для треугольной резьбы К 0, 87, для прямоугольной К 0, 5 для трапецеидальной К 0, 65; Km (0, 6. . . 0, 7) —большие значения при вв/ вг > 1, 3, где вв—предел прочности материала болта, а вг —гайки. Это связано с тем. что увеличение относительной прочности материала винта позволяет в большей степени использовать пластические деформации в резьбе для выравнивания распределения нагрузки по виткам резьбы. 5

Расчет резьбы на прочность l Если материалы винта и гайки одинаковы, то по напряжениям среза рассчитывают только резьбу винта, так как d 1<d. Условие износостойкости ходовой резьбы по напряжениям смятия: l l (1. 13) где z = H/p — число рабочих витков (например, число витков гайки). 6

Расчет резьбы на прочность l Формула (1. 13)—общая для винта и гайки. Коэффициент Кm здесь принят равным единице, с учетом приработки ходовых резьб и при условии, что допускаемые напряжения принимают согласно с накопленным опытом эксплуатации. 7

Расчет резьбы на прочность Высота гайки и глубина завинчивания. l Равнопрочность резьбы и стержня винта является одним из условий назначения высоты стандартных гаек. Так, например, приняв в качестве предельных напряжений пределы текучести материала на растяжение и сдвиг и учитывая, что T = 0, 6 T, запишем условия равнопрочности резьбы на срез и стержня винта на растяжение в виде: 8

Расчет резьбы на прочность Высота гайки и глубина завинчивания. откуда при K = 0, 87 и Km 0, 6 получаем: l H Q, 8 d 1. (1. 14) l Здесь F/[( /4)d 12] — напряжение растяжения в стержне винта, рассчитанное приближенно по внутреннему диаметру резьбы d 1. l В соответствии с этим высоту нормальных стандартных гаек крепежных изделий принимают l H O, 8 d. (1. 15) l Кроме нормальных стандартом предусмотрены высокие H 1, 2 d низкие H 0, 5 d гайки. l 9

Расчет резьбы на прочность Высота гайки и глубина завинчивания. Так как d > d 1 (например, для основной крепежной резьбы d 1, 2 d 1, то прочность резьбы при нормальных и высоких гайках превышает прочность стержня винта. l По тем же соображениям устанавливают глубину завинчивания винтов и шпилек в детали: в стальные детали H 1 = d, в чугунные и силуминовые H 1 1, 5 d. l Стандартные высоты гаек (за исключением низких) и глубины завинчивания исключают необходимость расчета на прочность резьбы стандартных крепежных деталей l 10

Расчет резьбы на прочность Расчет на прочность стержня винта (болта) при различных случаях нагружения l Стержень винта нагружен только внешней растягивающей силой. Примером служит нарезанный участок крюка для подвешивания груза (рис. 1. 18). Рис. 1. 18 11

Расчет резьбы на прочность Расчет на прочность стержня винта (болта) при различных случаях нагружения l Опасным является сечение, ослабленное нарезкой. Площадь этого сечения оценивают приближенно по внутреннему диаметру d 1 резьбы. Условие прочности по напряжениям растяжения в стержне: l l (1. 16) Допускаемые напряжения см. справочную литературу. 12

Расчет резьбы на прочность Расчет на прочность стержня винта (болта) при различных случаях нагружения l Болт затянут, внешняя нагрузка отсутствует. Примером служат болты для крепления ненагруженных герметичных крышек и люков корпусов машин (рис. 1. 19). рис. 1. 19 13

Расчет резьбы на прочность Расчет на прочность стержня винта (болта) при различных случаях нагружения l. В этом случае стержень болта растягивается осевой силой Fзат возникающей от затяжки болта, и закручивается моментом сил в резьбе Тр— см. формулу (1. 5), где F равна Fзат. Напряжение растяжения от силы Fзат, 14

Расчет резьбы на прочность Расчет на прочность стержня винта (болта) при различных случаях нагружения l Напряжение кручения от момента ТР Требуемое значение силы затяжки Fзат = А см l где А — площадь стыка деталей, приходящаяся на один болт, см — напряжение смятия в стыке деталей, значение которого выбирают по условиям герметичности. l 15

Расчет резьбы на прочность Расчет на прочность стержня винта (болта) при различных случаях нагружения l Прочность болта определяют эквивалентному напряжению: по l l (1. 18) l Вычисления показывают, что для стандартных метрических резьб, экв= 1, 3 . 16

Расчет резьбы на прочность Расчет на прочность стержня винта (болта) при различных случаях нагружения l Это позволяет рассчитывать прочность болтов по упрощенной формуле: l l (1. 19) 17

Расчет резьбы на прочность Расчет на прочность стержня винта (болта) при различных случаях нагружения l Расчетами и практикой установлено, что болты с резьбой меньше M 10. . М 12 можно разрушить при недостаточно квалифицированной затяжке. Например, болт с резьбой М 8 разрушается при силе на ключе, равной 45 Н; болт с резьбой М 12 — при силе 180 H 18

Расчет резьбы на прочность Расчет на прочность стержня винта (болта) при различных случаях нагружения l Поэтому в среднем и тяжелом машиностроении не рекомендуют применять болты малых диаметров (меньше М 8). На некоторых заводах для затяжки болтов используют специальные ключи предельного момента. Эти ключи не позволяют приложить при затяжке момент больше установленного. В таком случае отпадает необходимость ограничивать применение болтов малых диаметров (при условии, что ключи предельного момента применяют и в эксплуатации). 19

Расчет резьбы на прочность Болтовое соединение нагружено силами, сдвигающими детали в стыке 20

Расчет резьбы на прочность Болтовое соединение нагружено силами, сдвигающими детали в стыке Условием надежности соединения является отсутствие сдвига деталей в стыке. Конструкция может быть выполнена в двух вариантах. l Болт поставлен с зазором (рис. 1. 20). При этом внешнюю нагрузку F уравновешивают силами трения в стыке, которые образуются от затяжки болта. Без затяжки болтов детали могут сдвигаться на значение зазора, что не допустимо l 21

Расчет резьбы на прочность Болтовое соединение нагружено силами, сдвигающими детали в стыке Рассматривая равновесие детали 2, получим условие отсутствия сдвига деталей: l F i F TP = i Fзат f, (1. 20) l или l Fзат= K F/(i f); l где i—число плоскостей стыка деталей (на рис. 1. 20—i = 2; при соединении только двух деталей i = 1); f — коэффициент трения в стыке (f = 0, 15. . . 0, 20 для сухих чугунных и стальных поверхностей); l 22

Расчет резьбы на прочность Болтовое соединение нагружено силами, сдвигающими детали в стыке l. К —коэффициент запаса (K =1, 3. . . 1. 5 при статической нагрузке, K = 1, 8. . . 2 при переменной нагрузке). l Прочность болта оценивают по эквивалентному напряжению — формула (1. 19). 23

Расчет резьбы на прочность Болтовое соединение нагружено силами, сдвигающими детали в стыке l Отметим, что в соединении, в котором болт поставлен с зазором. внешняя нагрузка не передается на болт. Поэтому болт рассчитывают только на статическую прочность по силе затяжки даже при переменной внешней нагрузке. Влияние переменной нагрузки учитывают путем выбора повышенных значений коэффициента запаса. 24

Расчет резьбы на прочность Болтовое соединение нагружено силами, сдвигающими детали в стыке l Болт поставлен без зазора (рис. 1. 21). В этом случае отверстие калибруют разверткой, а диаметр стержня болта выполняют с допуском, обеспечивающим беззазорную посадку. При расчете прочности соединения не учитывают силы трения в стыке, так как затяжка болта необязательна. В общем случае болт можно заменить штифтом. 25

Расчет резьбы на прочность Болтовое соединение нагружено силами, сдвигающими детали в стыке l Стержень болта рассчитывают по напряжениям среза и смятия. Условие прочности по напряжениям среза: l l (1. 21) l где i — число плоскостей среза (на рис. 1. 21, a i = 2; при соединении только двух деталей — рис. 1. 21, б i = 1). 26

Расчет резьбы на прочность Болтовое соединение нагружено силами, сдвигающими детали в стыке l Закон распределения напряжений смятия по цилиндрической поверхности контакта болта и детали (рис. 1. 22) трудно установить точно. 27

Расчет резьбы на прочность Болтовое соединение нагружено силами, сдвигающими детали в стыке l. В значительной степени это зависит от точности размеров и формы деталей соединения. Поэтому расчет на смятие производят по условным напряжениям. Эпюру действительного распределения напряжений (рис. 1. 22, а) заменяют условной с равномерным распределением напряжений (рис. 1. 22, б). 28

Расчет резьбы на прочность Болтовое соединение нагружено силами, сдвигающими детали в стыке l При этом для средней детали (и при соединении только двух деталей) l l или 29

Расчет резьбы на прочность Болтовое соединение нагружено силами, сдвигающими детали в стыке l для крайней детали 30

Расчет резьбы на прочность Болтовое соединение нагружено силами, сдвигающими детали в стыке l Формулы (1. 22) справедливы для болта и деталей. Из двух значений cм в этих формулах расчет прочности выполняют по наибольшему, а допускаемое напряжение определяют по более слабому материалу болта или детали. 31

Расчет резьбы на прочность Болтовое соединение нагружено силами, сдвигающими детали в стыке l Сравнивая варианты установки болтов с зазором и без зазора (см. рис. 1. 20 и 1. 21), следует отметить, что первый вариант дешевле второго, так как не требует точных размеров болта и отверстия. Однако условия работы болта, поставленного с зазором, хуже, чем без зазора. 32

Расчет резьбы на прочность Болтовое соединение нагружено силами, сдвигающими детали в стыке l Так, например, приняв коэффициент трения в стыке деталей f 0, 2, K=1, 5 и i = 1, из формулы (1. 20) получим Fзат= 7, 5 F. l Следовательно, расчетная нагрузка болта с зазором в 7, 5 раз превышает внешнюю нагрузку. Кроме того, вследствие нестабильности коэффициента трения и трудности контроля затяжки работа таких соединений при сдвигающей нагрузке недостаточно надежна. 33
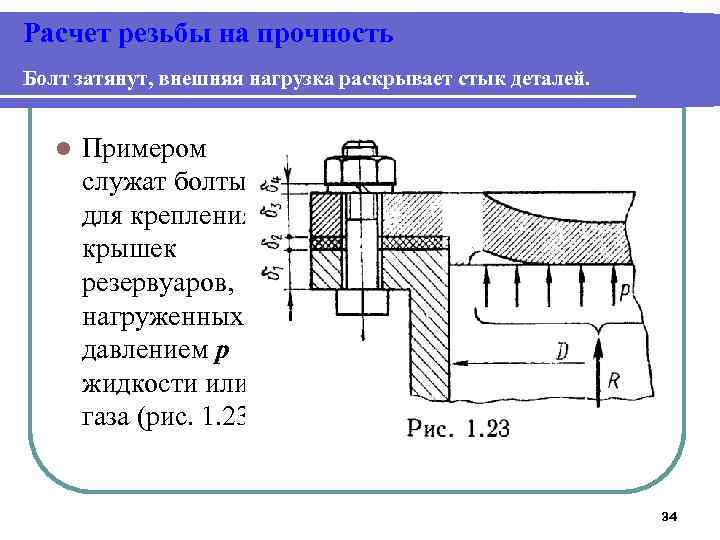
Расчет резьбы на прочность Болт затянут, внешняя нагрузка раскрывает стык деталей. l Примером служат болты для крепления крышек резервуаров, нагруженных давлением p жидкости или газа (рис. 1. 23). 34

Расчет резьбы на прочность Болт затянут, внешняя нагрузка раскрывает стык деталей. l Затяжка болтов должна обеспечить герметичность соединения или нераскрытие стыка под нагрузкой. Задача о распределении нагрузки между элементами такого соединения статически неопределима и решается с учетом деформаций этих элементов. Обозначим: Fзат — сила затяжки болта; F=R/z — внешняя нагрузка соединения, приходящаяся на один болт (z — число болтов). 35

Расчет резьбы на прочность Болт затянут, внешняя нагрузка раскрывает стык деталей. l После приложения внешней нагрузки к затянутому соединении; болт дополнительно растянется на некоторую величину , а деформация сжатия деталей уменьшится на ту же величину. l Для простоты можно сказать, что только часть внешней нагрузки дополнительно нагружает болт, а другая часть идет на разгрузку стыка. 36

Расчет резьбы на прочность Болт затянут, внешняя нагрузка раскрывает стык деталей. обозначим — коэффициент внешней нагрузки (учитывает; приращение нагрузки болта в долях от силы F, то дополнительна нагрузка болта равна F, а уменьшение затяжки стыка — (1— )F l Если 37

Расчет резьбы на прочность Болт затянут, внешняя нагрузка раскрывает стык деталей. l Значение коэффициента определяют по условию равенства дополнительных деформаций болта и деталей (условие совместности деформаций): l (1. 23); l где б — податливость болта, равная его деформации при единично нагрузке; д — суммарная податливость соединяемых деталей 38

Расчет резьбы на прочность Болт затянут, внешняя нагрузка раскрывает стык деталей. l. Из равенства (1. 23) l l Далее (1. 24) получим приращение нагрузки на болт l (1. 25) 39

Расчет резьбы на прочность Болт затянут, внешняя нагрузка раскрывает стык деталей. l расчетную (суммарную) нагрузку болта l (1. 26) lи остаточную затяжку стыка от одного болта l (1. 27) 40

Расчет резьбы на прочность Анализ полученных решений и выбор затяжки соединений. . С увеличением податливости болта и уменьшением податливости деталей д уменьшается и приращение нагрузки болта F (формулу (1. 25). Эту зависимость выгодно используют на практике особенно при переменной внешней нагрузке F. l 1. 41

Расчет резьбы на прочность Анализ полученных решений и выбор затяжки соединений. . l. Например, при изменении внешней нагрузки Fб от нуля до максимума (рис. 1. 24) в суммарной нагрузке болта Fp изменяется только составляющая Fб (по тому же закону, что и F). Как правило д, значительно меньше б , поэтому Fб. значительно меньше F. От переменной составляющей Fб зависит сопротивление болта усталости. 42

Расчет резьбы на прочность Анализ полученных решений и выбор затяжки соединений. . l Применение упругих болтов (рис. 1. 25) является хорошей защитой от усталостного разрушения 43

Расчет резьбы на прочность Анализ полученных решений и выбор затяжки соединений. . l Опасным сечением для прочности стержня является сечение по внутреннему диаметру резьбы d 1 —см. формулу (1. 16). Учитывая отсутствие концентрации напряжений в ненарезанной части стержня, ее диаметр можно выполнить меньше d 1 (рис. 1. 25, а) или просверлить здесь отверстие (рис. 1. 25, б). При этом болт будет равнопрочным, а его податливость увеличится. 44

Расчет резьбы на прочность Анализ полученных решений и выбор затяжки соединений. . l 2. С уменьшением Fзат при постоянной F уменьшается Fост см. формулу (1. 27). При Fзат (1 - )F сила Fост становится равной нулю, в стыке появляется зазор. Образование зазора в стыке недопустимо, так как при этом нарушается плотность соединения, а при переменной нагрузке появляются удары в стыке, от которых соединение быстро разрушается. 45

Расчет резьбы на прочность Анализ полученных решений и выбор затяжки соединений. l Таким образом, достаточная предварительная затяжка Fзат, обеспечивающая нераскрытие стыка деталей, является необходимым условием надежности и герметичности соединения. Условие нераскрытия стыка: Fост>0. l Практически нераскрытие стыка зависит не только от значения затяжки Fзат но и от сохранения ее в эксплуатации. 46

Расчет резьбы на прочность Анализ полученных решений и выбор затяжки соединений. l l l Последнее определяется следующими факторами: качеством обработки поверхностей стыка. При большей шероховатости поверхности ее неровности постепенно сминаются, что приводит к ослаблению затяжки. Для ответственных соединений поверхности стыка деталей рекомендуют шлифовать; числом поверхностей стыков. Чем больше поверхностей, тем хуже сохраняется затяжка (на рис. 1. 23 число поверхностей стыка равно пяти, считая поверхности под гайкой и головкой болта); качеством поверхности и точностью резьбы. Грубая резьба сминается и уменьшает силу затяжки. В ответственных соединениях рекомендуют применять гайки, увеличивающие равномерность распределения нагрузки по виткам резьбы. надежностью способа стопорения резьбы. качеством прокладок. Упругие прокладки в стыке лучше сохраняют затяжку. (Отметим, что пружинная шайба (см. рис. 1. 23) в этом смысле также выполняет роль упругой прокладки. ) 47

Расчет резьбы на прочность Анализ полученных решений и выбор затяжки соединений. В зависимости от перечисленных факторов, трудно поддающихся учету, а также ввиду опасности раскрытия стыка деталей целесообразно применять высокую затяжку соединений, особенно при переменных нагрузках. Это положение подтверждается практикой эксплуатации резьбовых соединений. На практике рекомендуют принимать: l Fзат= Kзат F (1. 28) l где Kзат — коэффициент затяжки l 48

Расчет резьбы на прочность Анализ полученных решений и выбор затяжки соединений. l По условию нераскрытия стыка при постоянной нагрузке Kзат = (1 , 25. . . 2), при переменной нагрузке Kзат = (2, 5. . . 4), l По условию герметичности: при мягкой прокладке Kзат = (1, 3. . . 2, 5) при металлической фасонной прокладке Kзат = (2. . . 3, 5), при металлической плоской прокладке Kзат = (3. . . 5). 49

Расчет резьбы на прочность Прочность болта при статических нагрузках. l При статических нагрузках прочность болта в соединении типа рис. 1. 23 оценивают по формуле l l l (1. 32) Здесь коэффициент 1, 3 по-прежнему учитывает напряжения кручения, которые могут возникнуть при затяжке соединения под нагрузкой (как правило, это не рекомендуют). 50

Расчет резьбы на прочность Прочность болта при переменных нагрузках. l При переменных нагрузках [см. рис. 1. 24 и формулы (1. 25) и (1. 26)] полное напряжение в болте можно разделить на постоянное: 51

Расчет резьбы на прочность Прочность болта при переменных нагрузках. lи переменное с амплитудой l (1. 33) 52

Расчет резьбы на прочность Прочность болта при переменных нагрузках. l Запас прочности по переменным напряжениям подсчитывают по формуле (см. курс механика материалов) l l (1. 34) 53

Расчет резьбы на прочность Прочность болта при переменных нагрузках. l где а—предел выносливости материала болта. К —эффективный коэффициент концентрации напряжений в резьбе (определяют при испытании затянутой резьбовой пары, а не просто стержня с резьбой). =0, 1—коэффициент чувствительности к асимметрии цикла напряжений. 54
Расчет резьбы на прочность Эффект эксцентричного нагружения болта 55

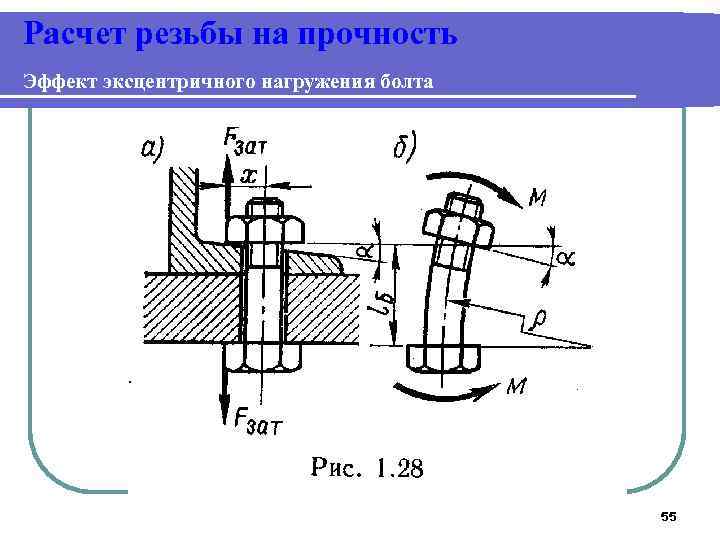
Расчет резьбы на прочность Эффект эксцентричного нагружения болта l Эксцентричное нагружение болта возникает из-за непараллельности опорных поверхностей детали и гайки или головки болта, например вследствие уклона полки швеллера, погрешностей изготовления деталей, болтов, гаек и т. д. Во всех этих случаях кроме напряжений растяжения в стержне болта появляются напряжения изгиба. 56

Расчет резьбы на прочность Эффект эксцентричного нагружения болта l Например, для болта на рис. 1. 28, а напряжение растяжения в стержне: 57

Расчет резьбы на прочность Эффект эксцентричного нагружения болта lа напряжения изгиба при больших значениях , не ограничивающих деформацию болта 58

Расчет резьбы на прочность Эффект эксцентричного нагружения болта l Если принять = d 1 , то: 59

Расчет резьбы на прочность Эффект эксцентричного нагружения болта малых значениях угла напряжения изгиба определяют с учетом деформации, допускаемой этим углом (рис. 1. 28, б): l При 60

Расчет резьбы на прочность Эффект эксцентричного нагружения болта l Здесь напряжением и будет меньшее из двух. l Расчетным 61

Расчет резьбы на прочность Эффект эксцентричного нагружения болта напряжением и будет меньшее из двух. Приняв за расчетное первое напряжение, получим: l Расчетным l и/ P 7, 5 l Это отношение позволяет отметить, что эксцентричное нагружение может значительно уменьшать прочность болтов. 62

Расчет резьбы на прочность Эффект эксцентричного нагружения болта l При разработке и изготовлении конструкции соединения необходимо принимать все меры, устраняющие эксцентричное погружение. Например, неровные поверхности деталей под гайками и головками болтов нужно планировать, а в случае, изображенном на рис. 1. 28, подкладывать под гайку косую шайбу и т. п. 63