1.

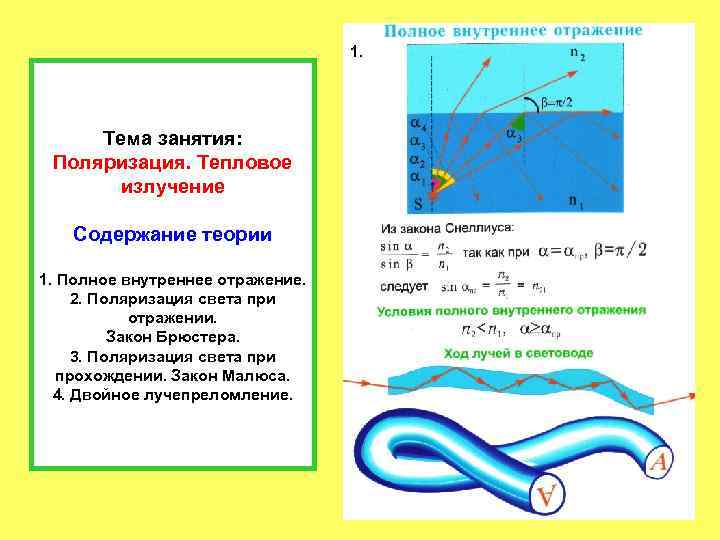
1. Тема занятия: Поляризация. Тепловое излучение Содержание теории 1. Полное внутреннее отражение. 2. Поляризация света при отражении. Закон Брюстера. 3. Поляризация света при прохождении. Закон Малюса. 4. Двойное лучепреломление.

2. Закон Брюстера. При отражении естественного света от диэлектрика с относительным показателем преломления n 21 = n 2/n 1 получается световая волна, полностью поляризованная в плоскости падения, если угол падения удовлетворяет условию : 3. Закон Малюса. Интенсивность света, прошедшего через поляризатор и анализатор определяется выражением: Здесь - угол между главными плоскостями поляризатора и анализатора; I 0 - интенсивность плоскополяризованного света, падающего на поляризатор; I - интенсивность света, прошедшего через поляризатор. 4. Скорости распространения обыкновенного (V 0) и необыкновенного (Ve) лучей в двоякопреломляющем кристалле соответственно равны Здесь n 0 и ne - показатели преломления кристалла для обыкновенного и необыкновенного лучей.

5. Угол поворота плоскости поляризации монохроматического света при прохождении через оптически активное вещество: а) = 0 l - для твердых тел; б) = C 0 l - для растворов, где 0 - удельное вращение; l - толщина оптически активного вещества; C - концентрация оптически активного вещества в растворе. Справочный материал: Показатель преломления стекла: n = 1, 5 Показатель преломления воды: n = 1, 33 Диапазон видимого спектра: 700 нм 420 нм

1 А. (16. 58) Найти угол Б полной поляризации света при отражении от стекла, показатель преломления которого равен n 2 = 1, 57. n 1 = 1 Пусть от диэлектрика с показателем преломления n 2, n 2 = 1, 57 находящегося в воздухе (n 1), отражается свет. Тогда Б - ? относительный показатель преломления n 21 равен: Отраженную волну света, полностью поляризованную в плоскости падения получим, если угол падения луча (1) Б удовлетворяет закону Брюстера: У волны, поляризованной в плоскости падения, световой вектор Е колеблется в направлении, перпендикулярном плоскости падения (т. е. плоскости чертежа). Из выражения (1) для угла Брюстера получаем :

2 А. (16. 62) Луч света проходит жидкость в стеклянном (n 2 = 1, 5) сосуде и отражается от дна. Отражённый луч полностью поляризован при падении на дно сосуда под углом Б = 42 37'. Найти показатель преломления n 1 жидкости. Под каким углом 0 должен падать на дно сосуда луч света, идущий в этой жидкости, чтобы наступило полное внутреннее отражение? n 2 = 1, 5 Б = 42 37 Пусть от границы стекла (показатель преломления n 1 - ? n 2) и жидкости (n 1), отражается свет. Относительный 0 - ? показатель преломления n 21 здесь равен: Волну света, полностью поляризованную в плоскости падения получим, если угол падения Б удовлетворяет закону Брюстера (1), (1) см. рис. 1 -а. Отсюда найдем показатель преломления жидкости (n 1): Угол полного внутреннего отражения 0 находим из закона Снейлиуса (2) при угле преломления 0= /2, рис. 1 -б

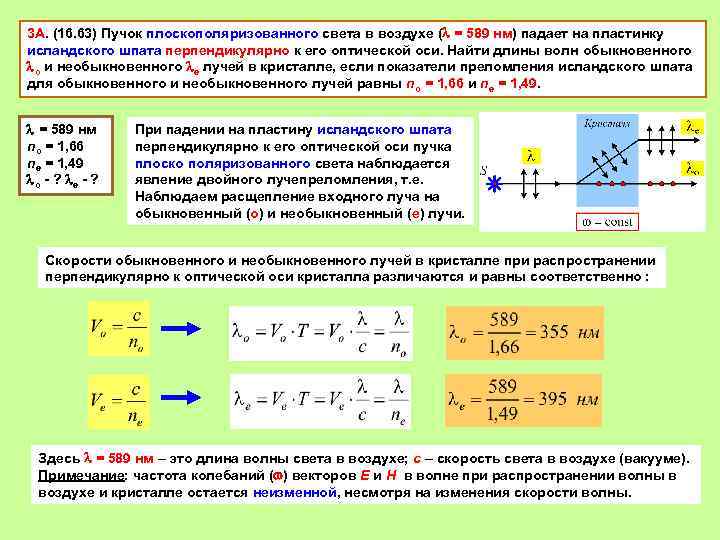
3 А. (16. 63) Пучок плоскополяризованного света в воздухе ( = 589 нм) падает на пластинку исландского шпата перпендикулярно к его оптической оси. Найти длины волн обыкновенного о и необыкновенного е лучей в кристалле, если показатели преломления исландского шпата для обыкновенного и необыкновенного лучей равны no = 1, 66 и ne = 1, 49. = 589 нм При падении на пластину исландского шпата no = 1, 66 перпендикулярно к его оптической оси пучка ne = 1, 49 плоско поляризованного света наблюдается о - ? е - ? явление двойного лучепреломления, т. е. Наблюдаем расщепление входного луча на обыкновенный (о) и необыкновенный (е) лучи. Скорости обыкновенного и необыкновенного лучей в кристалле при распространении перпендикулярно к оптической оси кристалла различаются и равны соответственно : Здесь = 589 нм – это длина волны света в воздухе; с – скорость света в воздухе (вакууме). Примечание: частота колебаний ( ) векторов Е и Н в волне при распространении волны в воздухе и кристалле остается неизменной, несмотря на изменения скорости волны.

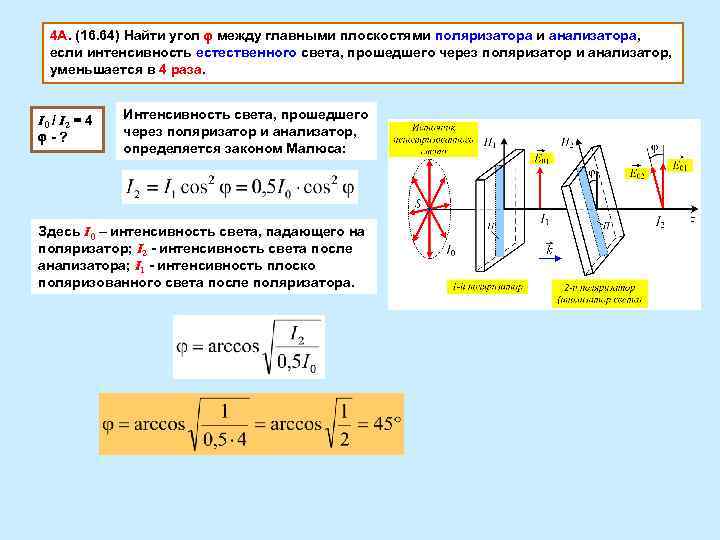
4 А. (16. 64) Найти угол между главными плоскостями поляризатора и анализатора, если интенсивность естественного света, прошедшего через поляризатор и анализатор, уменьшается в 4 раза. I 0 / I 2 = 4 Интенсивность света, прошедшего - ? через поляризатор и анализатор, определяется законом Малюса: Здесь I 0 – интенсивность света, падающего на поляризатор; I 2 - интенсивность света после анализатора; I 1 - интенсивность плоско поляризованного света после поляризатора.

5 А. (16. 65) Естественный свет проходит поляризатор и анализатор, поставленные так, что угол между их главными плоскостями равен . Поляризатор и анализатор поглощают и отражают 8% падающего на них света. Оказалось, что интенсивность луча, вышедшего из анализатора, равна 9% интенсивности естественного света падающего на поляризатор. Найти угол . п = отр = 0, 08 Интенсивность света, прошедшего через I 2 = 0, 09 I 0 поляризатор и анализатор без учета - ? потерь, определяется законом Малюса: С учетом потерь закон Малюса принимает вид: (1) Поскольку интенсивность после поляризатора с учетом потерь равна : Из (1) получаем :

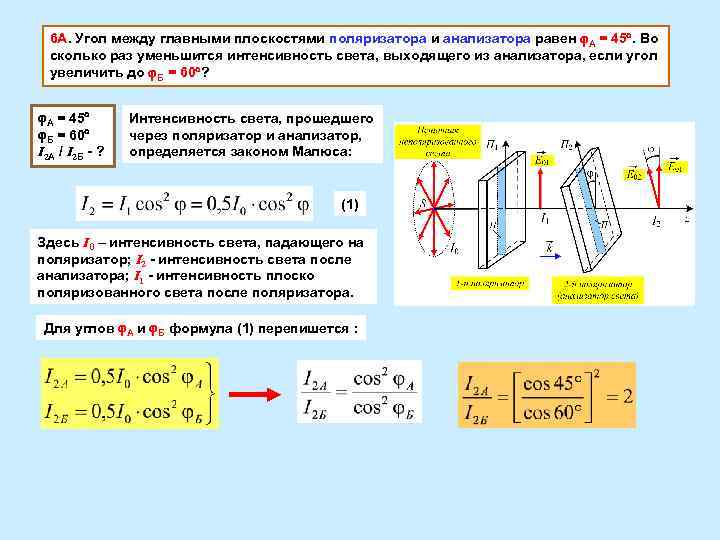
6 А. Угол между главными плоскостями поляризатора и анализатора равен А = 45. Во сколько раз уменьшится интенсивность света, выходящего из анализатора, если угол увеличить до Б = 60 ? А = 45 Интенсивность света, прошедшего Б = 60 через поляризатор и анализатор, I 2 А / I 2 Б - ? определяется законом Малюса: (1) Здесь I 0 – интенсивность света, падающего на поляризатор; I 2 - интенсивность света после анализатора; I 1 - интенсивность плоско поляризованного света после поляризатора. Для углов А и Б формула (1) перепишется :

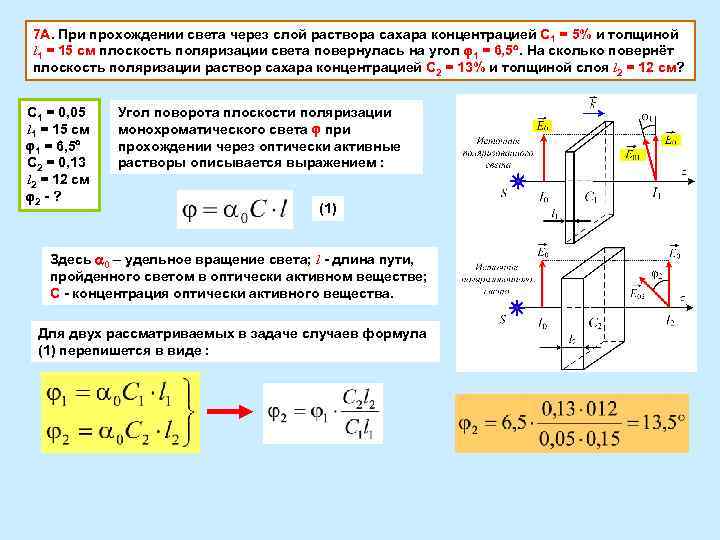
7 А. При прохождении света через слой раствора сахара концентрацией C 1 = 5% и толщиной l 1 = 15 см плоскость поляризации света повернулась на угол 1 = 6, 5. На сколько повернёт плоскость поляризации раствор сахара концентрацией C 2 = 13% и толщиной слоя l 2 = 12 см? C 1 = 0, 05 Угол поворота плоскости поляризации l 1 = 15 см монохроматического света при 1 = 6, 5 прохождении через оптически активные C 2 = 0, 13 растворы описывается выражением : l 2 = 12 см 2 - ? (1) Здесь 0 – удельное вращение света; l - длина пути, пройденного светом в оптически активном веществе; С - концентрация оптически активного вещества. Для двух рассматриваемых в задаче случаев формула (1) перепишется в виде :