◄ § 1. 4. ► П. Прямолинейное движение с_____ − возникает, если а║v 0. Выберем ось X ↑↑ v 0 и спроецируем ур-я (*) и (**) на ось X: Здесь верхний знак (+) соответствует разгону частицы, когда a↑↑v 0; нижний − случаю, когда a↑↓v 0. Исключив время, нетрудно получить полезную формулу: Если частица движется только в одном направлении, то ∆rx = s, и эта ф-ла приобретает вид:
Задача. Чтобы попасть на околоземную орбиту (и там вращаться) ракета должна приобрести 1 -ю космическую скорость v 1=7, 9 км/с. При этом она пройдет атмосферу, толщина которой s ≈ 200 км. С каким ускорением должна двигаться ракета? Из ф-лы (ПФ шк) имеем Замечание. Такое значение ускорения близко к предельному, которое может длительно выдержать тренированный космонавт. Длительность выхода на орбиту составляет < самостоятельно! > t ≈ 50 c. Кратковременно человек может выдержать ускорение до 50 g.
§ 1. 6. КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ЧАСТИЦЫ Вращательное движ. частицы по окружности − частный случай криволинейного движения. Смысл специального рассмотрения этого случая в том, что вращ. движ. − одно из наиболее распространенных в технике. Кроме того, любое движ. твердого тела можно представить как наложение (“сумму”) поступательного и вращат. движений (пример: движение колеса). Для описания вращат. движ. удобно пользоваться не линейными характеристиками ∆r, v, …, которые меняются от точки к точке тела, а угловыми ∆φ, ω, . . . , которые имеют одно и то же значение для всех точек тела. ◄!!! на примере двух точек тела►
Определим угловые характеристики. Угловое перемещение. При движении частицы по окружности её перемещение характеризуют углом поворота ∆φ радиуса-вектора r. Для учета направления вращения его принято изображать направленным отрезком ∆φ, модуль которого равен углу поворота, а направление отвечает правилу правого винта: ∆φ направлен в ту сторону, куда будет двигаться правый винт (ввинчиваться или вывинчиваться), если его вращать в направлении вращения частицы. Если ∆φ очень мал, то соответствующий dφ обладает свойствами вектора. Его называют вектором поворота (угловым перемещением). ◄ Замечание. Вектор dφ является аксиальным (псевдовектором), поскольку его направление связано с правовинтовой договорённостью. ►
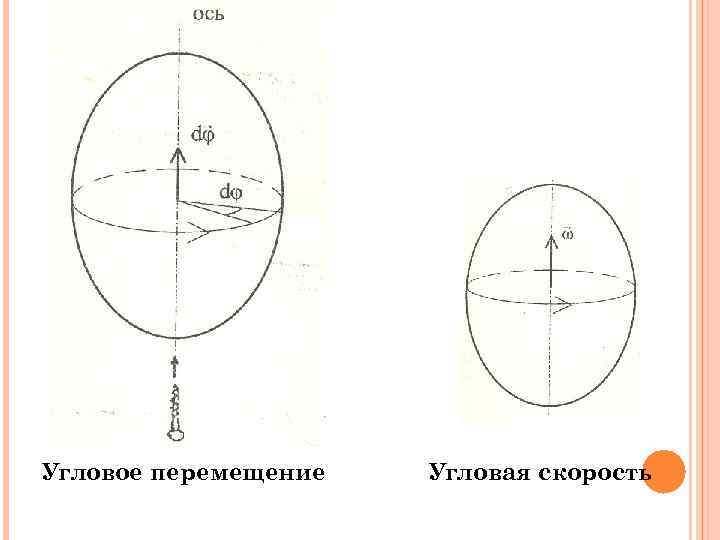Угловое перемещение Угловая скорость
Угловая скорость: Частный случай: равномерное вращение (ω = const) можно охарактеризовать периодом вращения Т − временем, за которое тело совершает один оборот. Число оборотов за единицу времени ν равно Угловое ускорение:
П. Равноускоренное вращение: e =const. Интегрируя, аналогично случаю а=const, получим ф-лы: ◄!применимость► ◄! Спроецируем ур-я (* ) и (** ) на ось Z ↑↑ ω0: Здесь верхний знак (+) соответствует разгону частицы, когда e ↑↑ω0; нижний − случаю, когда e ↑↓ω0. Отсюда легко получить
П. Связь между линейными и угловыми харак-ками. Пусть за время ∆t тело повернулось на угол ∆φ. Тогда точка, находящаяся на расстоянии R от оси, пройдет путь ∆s = R • ∆φ. Линейная скорость этой точки: Продифференцируем полученное соотношение по t: Полное линейное ускорение: Резюме: Нетрудно понять, что связь между векторами v и ω имеет вид: