1 21. Подробно написать, почему у берегов









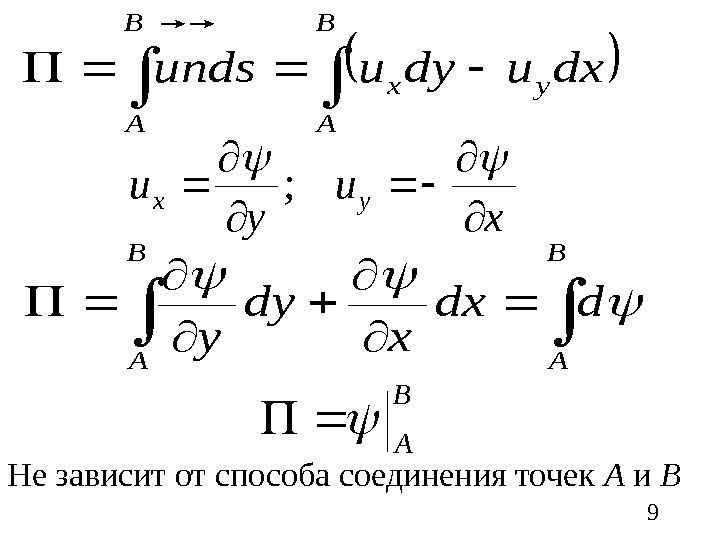






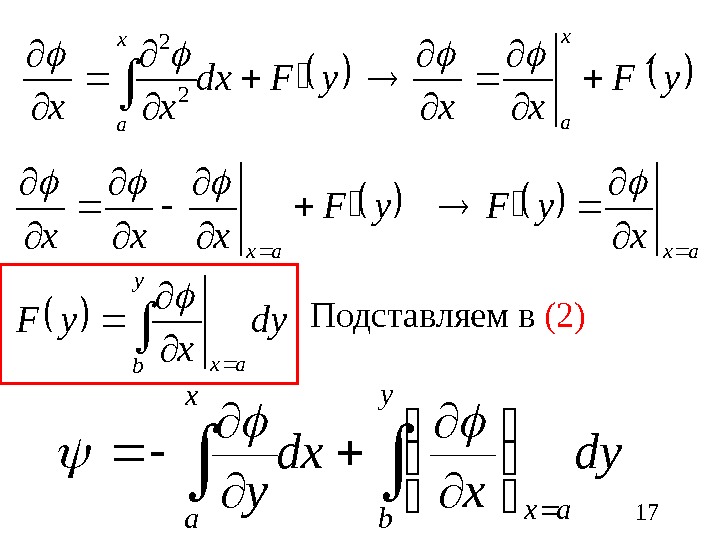








- Размер: 658 Кб
- Количество слайдов: 25
Описание презентации 1 21. Подробно написать, почему у берегов по слайдам

 21. Подробно написать, почему у берегов Перу много рыбы (начать с неравномерного прогрева Солнцем поверхности Земли) 2. Записать уравнение Гельмгольца, раскрыв полную производную по времени. При каких условиях оно существует. 3. Уравнения Эйлера, неразрывности, линии тока, Бернулли-Эйлера, Фридмана
21. Подробно написать, почему у берегов Перу много рыбы (начать с неравномерного прогрева Солнцем поверхности Земли) 2. Записать уравнение Гельмгольца, раскрыв полную производную по времени. При каких условиях оно существует. 3. Уравнения Эйлера, неразрывности, линии тока, Бернулли-Эйлера, Фридмана
 34. Показать, что если на поверхности односвязного объема потенциал скорости имеет постоянное значение, то такое значение будет и в любой точке внутри объема. 5. Записать уравнение движения идеальной жидкости (уравнение Эйлера) 6. Записать выражение для потока скорости через контур АВ и циркуляции скорости через контур L
34. Показать, что если на поверхности односвязного объема потенциал скорости имеет постоянное значение, то такое значение будет и в любой точке внутри объема. 5. Записать уравнение движения идеальной жидкости (уравнение Эйлера) 6. Записать выражение для потока скорости через контур АВ и циркуляции скорости через контур L

 5 Рассмотрим плоское движение u ( u x , u y ) Запишем уравнение линии тока: yx u dy u dx 0 dyudxuxyxy Если ввести такую функцию , что. Вдоль линии тока , v xy u то вдоль линии тока dy y dx x d const 0 d
5 Рассмотрим плоское движение u ( u x , u y ) Запишем уравнение линии тока: yx u dy u dx 0 dyudxuxyxy Если ввести такую функцию , что. Вдоль линии тока , v xy u то вдоль линии тока dy y dx x d const 0 d
 6 На каждой линии тока функция тока сохраняет постоянное значение, которое, вообще говоря, различно для разных линий тока.
6 На каждой линии тока функция тока сохраняет постоянное значение, которое, вообще говоря, различно для разных линий тока.
 7 Поток скорости выразим через функцию тока
7 Поток скорости выразим через функцию тока
 8 B A yx dxudyu dsuu cossin. Поток скорости через контур AB dsnu B A Записать через функцию тока. A B u n dsynuxnu B A yx , cos
8 B A yx dxudyu dsuu cossin. Поток скорости через контур AB dsnu B A Записать через функцию тока. A B u n dsynuxnu B A yx , cos
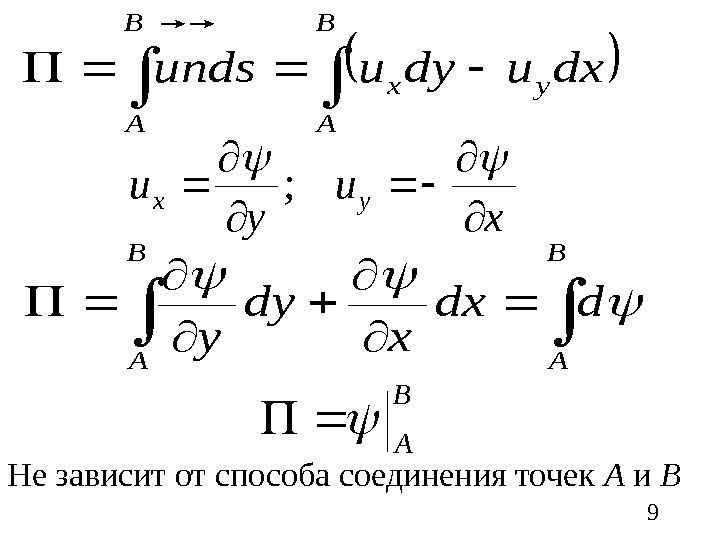 9 B A yx B A dxudyudsnu x u yx ; B A ddx x dy y Не зависит от способа соединения точек А и
9 B A yx B A dxudyudsnu x u yx ; B A ddx x dy y Не зависит от способа соединения точек А и
 10 Найти выражение вихря через функцию тока y u x u z u y u xy z zx y yz x ;
10 Найти выражение вихря через функцию тока y u x u z u y u xy z zx y yz x ;
 11 Для плоского движения u ( u x , u y ) запишем компоненты ротора скорости z xy z zx y yz x yxy u x u z u y u
11 Для плоского движения u ( u x , u y ) запишем компоненты ротора скорости z xy z zx y yz x yxy u x u z u y u
 12 Если движение безвихревое 00 z функция тока удовлетворяет уравнению Лапласа
12 Если движение безвихревое 00 z функция тока удовлетворяет уравнению Лапласа
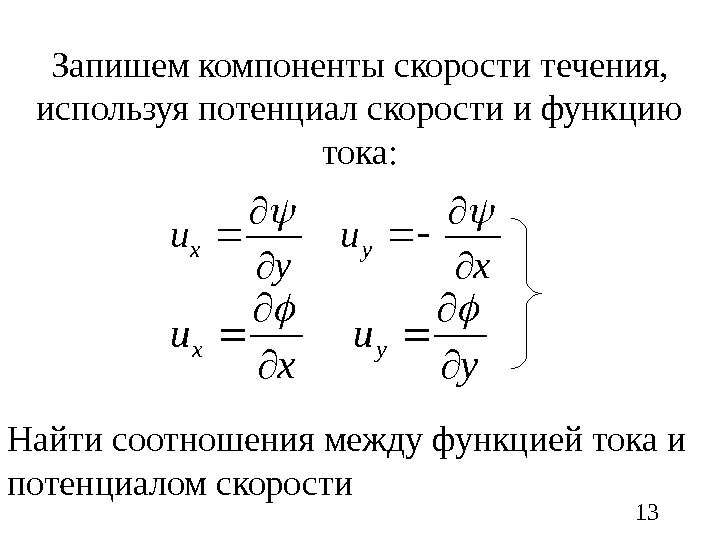
 13 Запишем компоненты скорости течения, используя потенциал скорости и функцию тока: x u y uyx y u x u yx Найти соотношения между функцией тока и потенциалом скорости
13 Запишем компоненты скорости течения, используя потенциал скорости и функцию тока: x u y uyx y u x u yx Найти соотношения между функцией тока и потенциалом скорости
 14 yx yx Последние два равенства перемножаем 0 yyxx Это условие ортогональности линий тока и линий равного потенциала =const = c o n st
14 yx yx Последние два равенства перемножаем 0 yyxx Это условие ортогональности линий тока и линий равного потенциала =const = c o n st
 15 Функция тока через потенциал скорости Пусть известен потенциал скорости ( x , y ) , что возможно для потенциального течения. (1)yx yx
15 Функция тока через потенциал скорости Пусть известен потенциал скорости ( x , y ) , что возможно для потенциального течения. (1)yx yx
 16)( y. Fdx yx a Интегрируем (1) от некоторого значения а до х Для определения F(y) дифференцируем (2)(2) y. Fdx yy x a 22 xy 0 2 2 xy Для потенциального движения
16)( y. Fdx yx a Интегрируем (1) от некоторого значения а до х Для определения F(y) дифференцируем (2)(2) y. Fdx yy x a 22 xy 0 2 2 xy Для потенциального движения
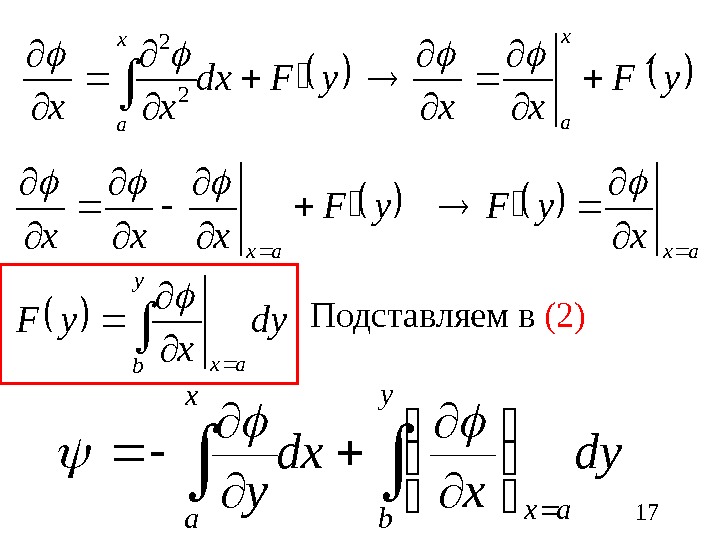 17 y. F xx y. Fdx xx x a 2 2 axaxx y. F xxx y b axdy x y. F dy xdx y y b axx a Подставляем в (2)
17 y. F xx y. Fdx xx x a 2 2 axaxx y. F xxx y b axdy x y. F dy xdx y y b axx a Подставляем в (2)
 18 Потенциал скорости через функцию тока
18 Потенциал скорости через функцию тока
 19 Жидкость несжимаема, заключена в объем с поверхностью S
19 Жидкость несжимаема, заключена в объем с поверхностью S
 20 dxdydz zyxdu. T 22 2 2 21 21 Преобразование Грина для функций φ и φ 1 dxdydz zyxd. S n dxdydz zzyyxx S 2 12 1 111 n –направление внутренней нормали к S
20 dxdydz zyxdu. T 22 2 2 21 21 Преобразование Грина для функций φ и φ 1 dxdydz zyxd. S n dxdydz zzyyxx S 2 12 1 111 n –направление внутренней нормали к S
 21 Если течение безвихревое и φ = φ 1 , то энергия объема определяется выражением:
21 Если течение безвихревое и φ = φ 1 , то энергия объема определяется выражением:
 22 d. S n T zyx S 2 1 0 2 2 2 Энергия объема определяется движением на границе. Когда она равна нулю?
22 d. S n T zyx S 2 1 0 2 2 2 Энергия объема определяется движением на границе. Когда она равна нулю?
 23 Энергия объема равна нулю при условии, что жидкость не протекает через границу, если потенциал на всей границе имеет постоянное значение
23 Энергия объема равна нулю при условии, что жидкость не протекает через границу, если потенциал на всей границе имеет постоянное значение
 24 несжимаемой жидкости, заключенной в замкнутом контуре L (плоская задача)
24 несжимаемой жидкости, заключенной в замкнутом контуре L (плоская задача)
 25=const = c o n s t d. L LL dd. L n T 2 1 Направление обхода выбирается таким образом, чтобы интеграл получился положительным
25=const = c o n s t d. L LL dd. L n T 2 1 Направление обхода выбирается таким образом, чтобы интеграл получился положительным

