1 2 Задача 1. Записать уравнение неразрывности




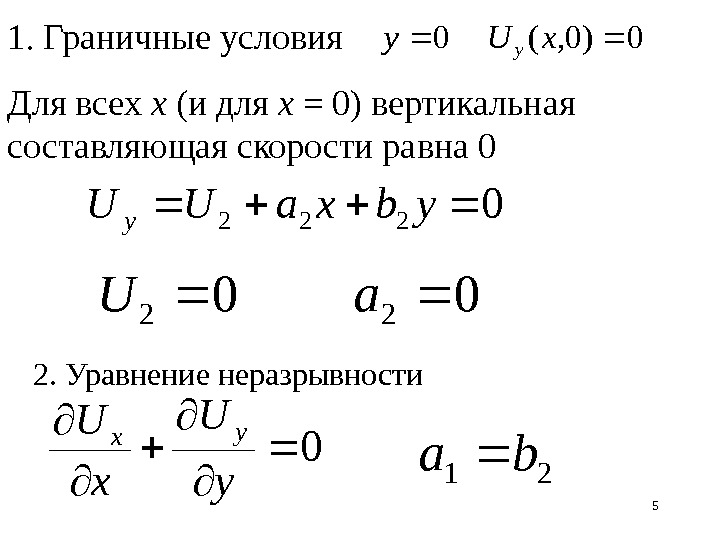

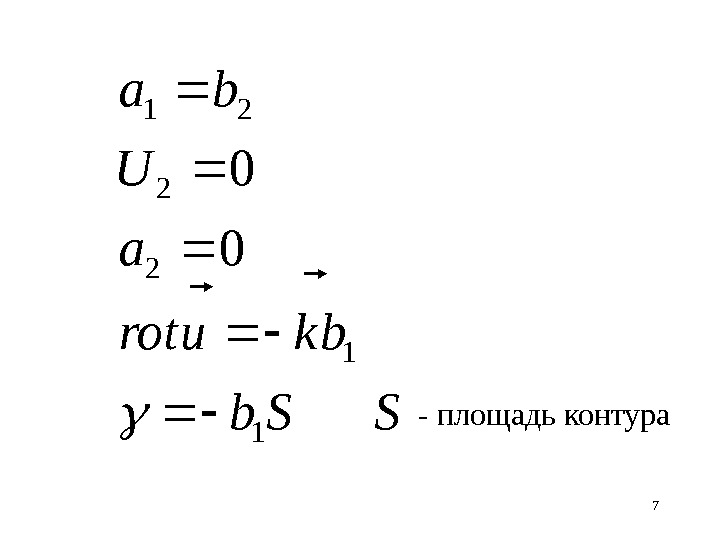






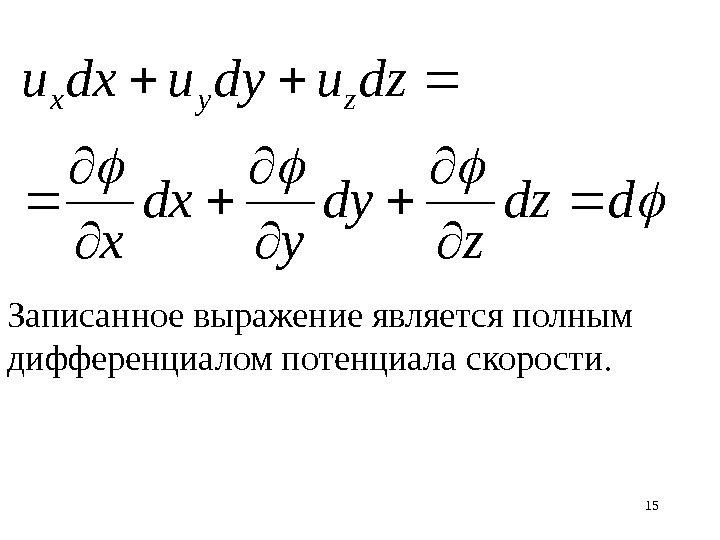
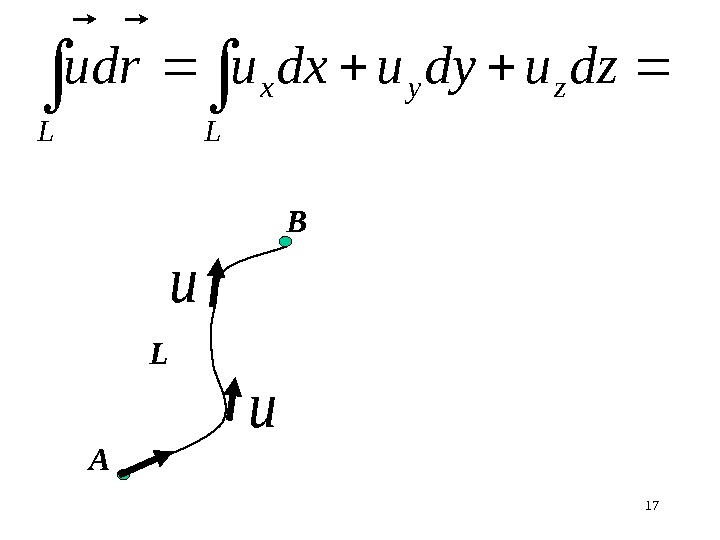
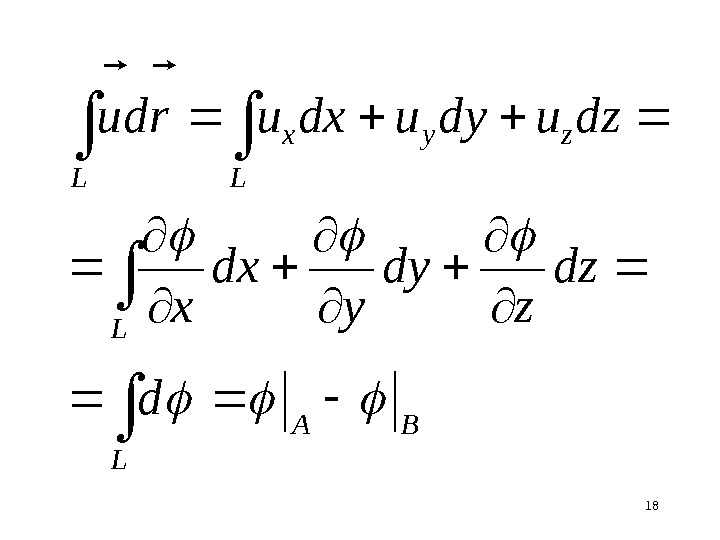










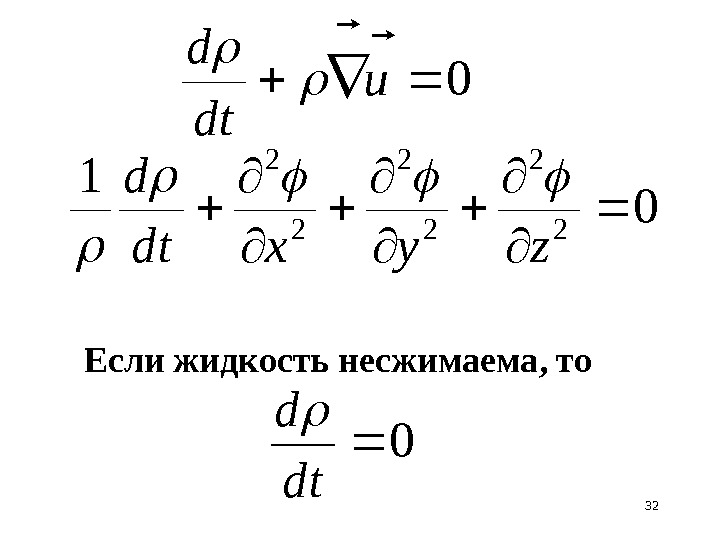





































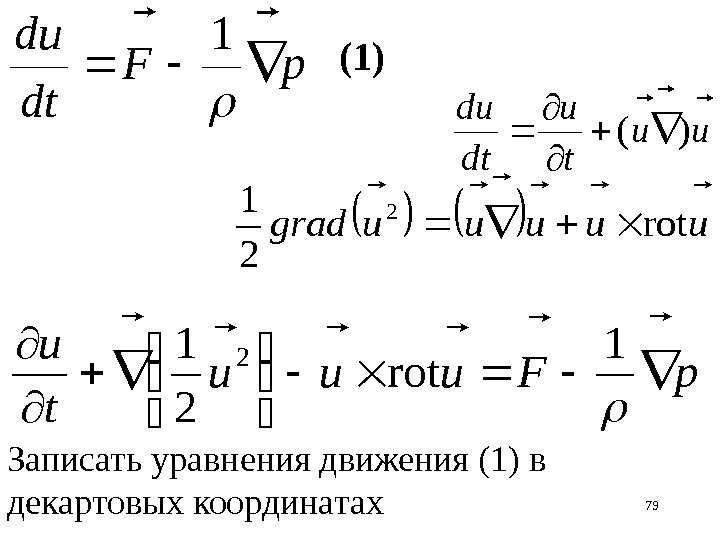
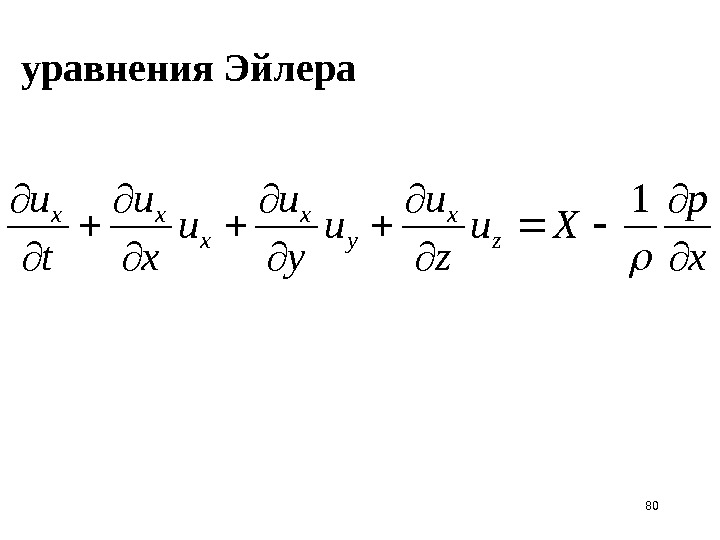








2full_2_potencial_vortex_movement.ppt
- Размер: 2.6 Mегабайта
- Количество слайдов: 88
Описание презентации 1 2 Задача 1. Записать уравнение неразрывности по слайдам

 2 Задача 1. Записать уравнение неразрывности (все известные Вам формы записи)
2 Задача 1. Записать уравнение неразрывности (все известные Вам формы записи)
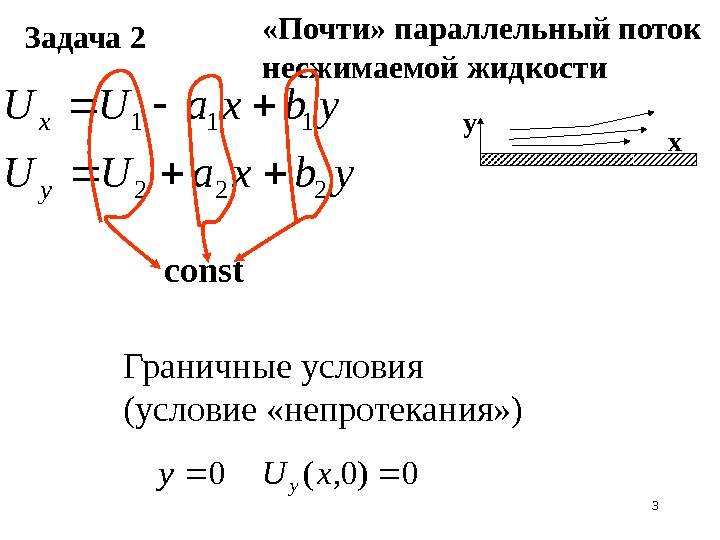
 3 «Почти» параллельный поток несжимаемой жидкостиybxa. UU y x 222 111 Граничные условия (условие «непротекания» ) у х 0)0, (0 x. Uyy Задача 2 const
3 «Почти» параллельный поток несжимаемой жидкостиybxa. UU y x 222 111 Граничные условия (условие «непротекания» ) у х 0)0, (0 x. Uyy Задача 2 const
 4 Используя уравнение неразрывности и граничные условия 1. Найти связь между коэффициентами. 2. Найти ротор и циркуляцию скорости по некоторому контуру, лежащему в плоскости x, y
4 Используя уравнение неразрывности и граничные условия 1. Найти связь между коэффициентами. 2. Найти ротор и циркуляцию скорости по некоторому контуру, лежащему в плоскости x, y
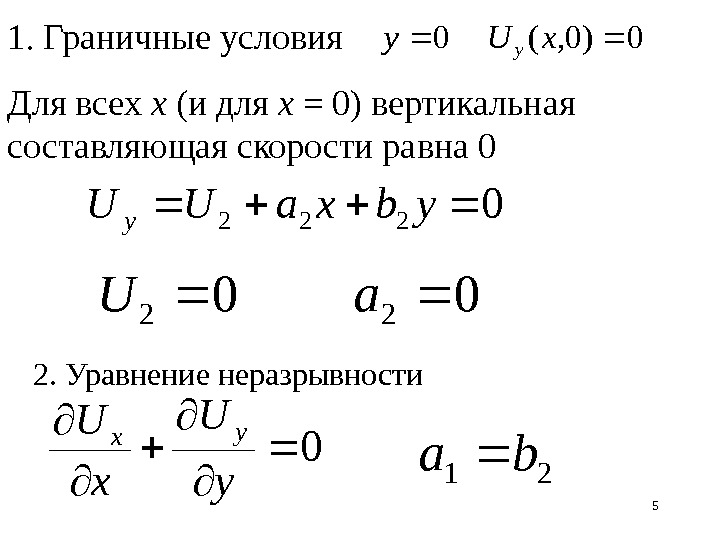 50 022 a. U 1. Граничные условия Для всех х (и для х = 0) вертикальная составляющая скорости равна 0 0)0, (0 x. Uyy 0 222 ybxa. UU y 2. Уравнение неразрывности 0 y U x Uyx 21 ba
50 022 a. U 1. Граничные условия Для всех х (и для х = 0) вертикальная составляющая скорости равна 0 0)0, (0 x. Uyy 0 222 ybxa. UU y 2. Уравнение неразрывности 0 y U x Uyx 21 ba
 6 bk aybyax. U zyx kji u 0 rot аy. U byax. UU y x
6 bk aybyax. U zyx kji u 0 rot аy. U byax. UU y x
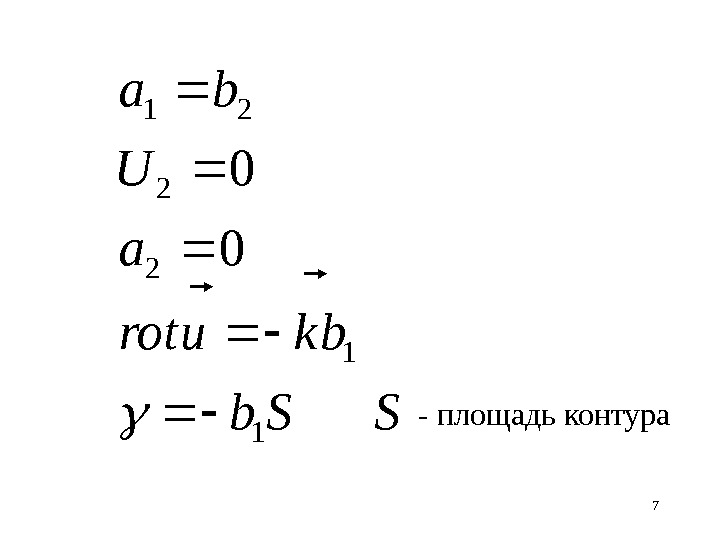 7 SSb bkurota. U ba 0 0 1 12 2 21 — площадь контура
7 SSb bkurota. U ba 0 0 1 12 2 21 — площадь контура
 8 Отсутствует вращательная составляющая движения 0 urot
8 Отсутствует вращательная составляющая движения 0 urot
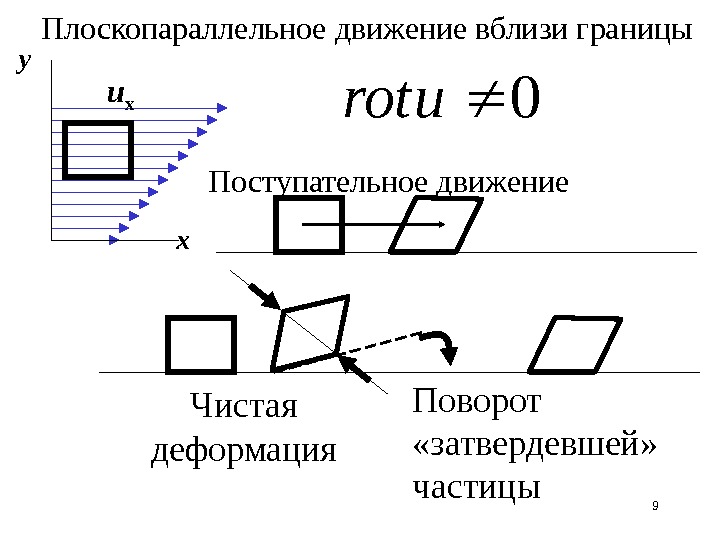
 9 u х ху Чистая деформация Поворот «затвердевшей» частицы. Плоскопараллельное движение вблизи границы Поступательное движение 0 urot
9 u х ху Чистая деформация Поворот «затвердевшей» частицы. Плоскопараллельное движение вблизи границы Поступательное движение 0 urot
 10 Если поле скорости однородно (не меняется) вдоль координат движение жидкости безвихревое u xy 0 00 rot x u zyx kji u constiu
10 Если поле скорости однородно (не меняется) вдоль координат движение жидкости безвихревое u xy 0 00 rot x u zyx kji u constiu

 12 Для безвихревого движения компоненты ротора скорости равны нулю0 0 0 y u x u z u y uxyzxyz Это необходимое и достаточное условие существования потенциала скорости z u y u x u zyx
12 Для безвихревого движения компоненты ротора скорости равны нулю0 0 0 y u x u z u y uxyzxyz Это необходимое и достаточное условие существования потенциала скорости z u y u x u zyx
 13 Скорость является потенциальным вектором для безвихревого движения gradu
13 Скорость является потенциальным вектором для безвихревого движения gradu
 14 dzudyudxu zyx. Запишем выражение (считая t параметром)
14 dzudyudxu zyx. Запишем выражение (считая t параметром)
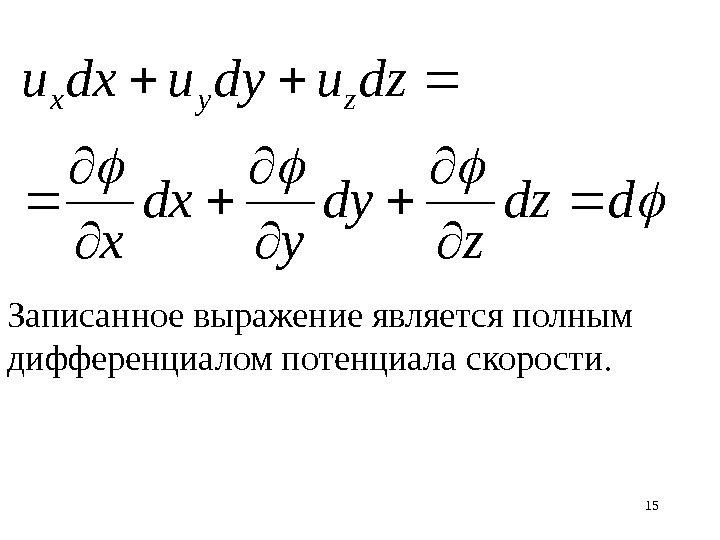 15 ddz z dy y dx x dzudyudxuzyx Записанное выражение является полным дифференциалом потенциала скорости.
15 ddz z dy y dx x dzudyudxuzyx Записанное выражение является полным дифференциалом потенциала скорости.
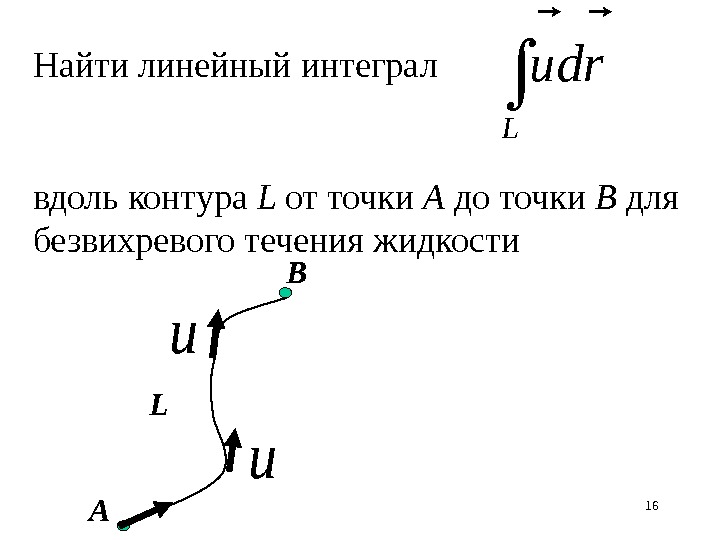
 16 Найти линейный интеграл вдоль контура L от точки А до точки В для безвихревого течения жидкости L rdu L А В u u
16 Найти линейный интеграл вдоль контура L от точки А до точки В для безвихревого течения жидкости L rdu L А В u u
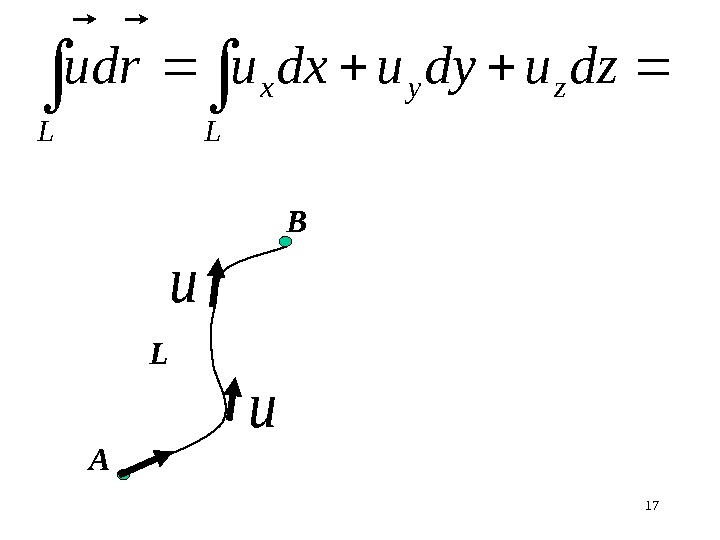 17 L zyx L dzudyudxurdu L А В u u
17 L zyx L dzudyudxurdu L А В u u
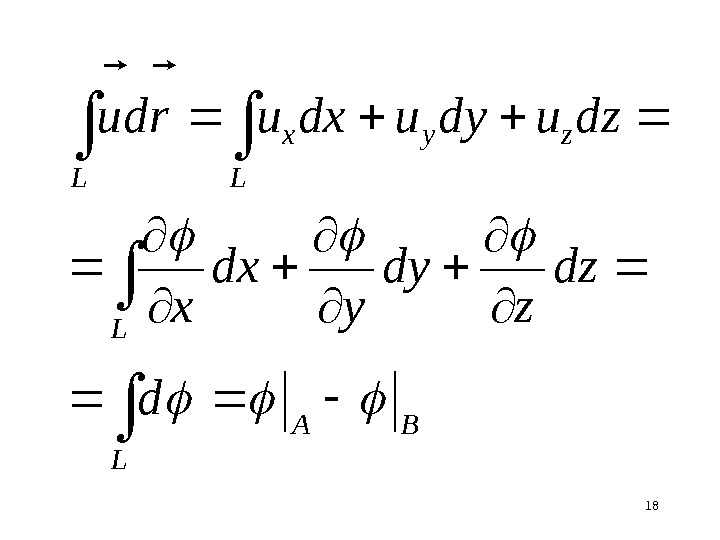 18 BA L L L zyx L d dz z dy y dx x dzudyudxurdu
18 BA L L L zyx L d dz z dy y dx x dzudyudxurdu
 19 Что будет, если точки А и В совпадают?
19 Что будет, если точки А и В совпадают?
 20 Если точки А и В совпадают и циркуляция скорости по любому замкнутому контуру тоже равна нулю0 L d Пусть grad непрерывен и однозначен во всех точках однозвязного объема, тогда однозначен во всем объеме 0 L dru
20 Если точки А и В совпадают и циркуляция скорости по любому замкнутому контуру тоже равна нулю0 L d Пусть grad непрерывен и однозначен во всех точках однозвязного объема, тогда однозначен во всем объеме 0 L dru
 21 Если циркуляция скорости отлична от нуля, то потенциал скорости не существует, так как движение вихревое. Могут ли быть линии тока замкнуты при безвихревом движении жидкости? 0 L dru
21 Если циркуляция скорости отлична от нуля, то потенциал скорости не существует, так как движение вихревое. Могут ли быть линии тока замкнуты при безвихревом движении жидкости? 0 L dru
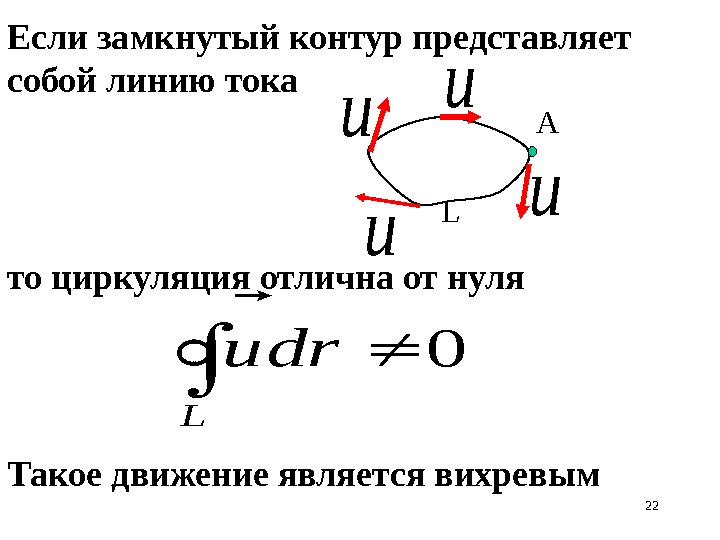
 22 Если замкнутый контур представляет собой линию тока то циркуляция отлична от нуля Такое движение является вихревым А Lu u 0 L dru
22 Если замкнутый контур представляет собой линию тока то циркуляция отлична от нуля Такое движение является вихревым А Lu u 0 L dru
 23 Для безвихревого движения (если есть потенциал скорости) линии тока не могут быть замкнуты.
23 Для безвихревого движения (если есть потенциал скорости) линии тока не могут быть замкнуты.
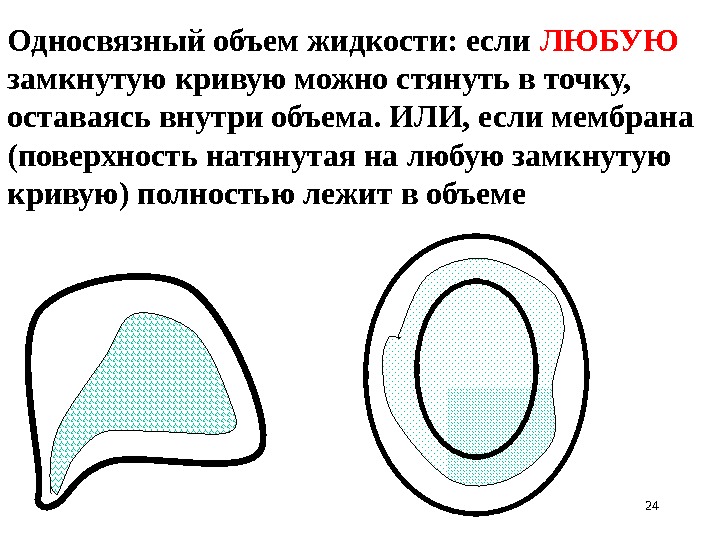
 24 Односвязный объем жидкости: если ЛЮБУЮ замкнутую кривую можно стянуть в точку, оставаясь внутри объема. ИЛИ, если мембрана (поверхность натянутая на любую замкнутую кривую) полностью лежит в объеме
24 Односвязный объем жидкости: если ЛЮБУЮ замкнутую кривую можно стянуть в точку, оставаясь внутри объема. ИЛИ, если мембрана (поверхность натянутая на любую замкнутую кривую) полностью лежит в объеме
 25 Может ли существовать потенциальное ( безвихревое) течение жидкости в односвязном объеме, ограниченном со всех сторон твердыми стенками ? Задача
25 Может ли существовать потенциальное ( безвихревое) течение жидкости в односвязном объеме, ограниченном со всех сторон твердыми стенками ? Задача
 26 В односвязном объеме, ограниченном со всех сторон твердыми стенками, не может существовать незамкнутых линий тока, так как нормальная составляющая скорости на границе равна нулю. В такой области течение всегда вихревое.
26 В односвязном объеме, ограниченном со всех сторон твердыми стенками, не может существовать незамкнутых линий тока, так как нормальная составляющая скорости на границе равна нулю. В такой области течение всегда вихревое.
 27 gradu. Для потенциального движения Показать, что для потенциального течения ускорение также представляет собой потенциальный вектор. Запишем компоненты ускорения, записав крмпоненты скорости z u y u x u zyx
27 gradu. Для потенциального движения Показать, что для потенциального течения ускорение также представляет собой потенциальный вектор. Запишем компоненты ускорения, записав крмпоненты скорости z u y u x u zyx
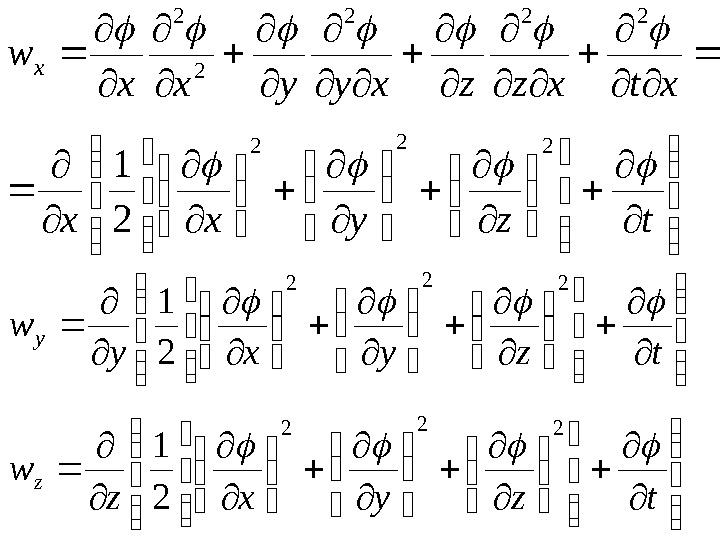
 28 t u u z u u y u u x u w z zz yz xz z y zy yy xy y x zx yx xx x
28 t u u z u u y u u x u w z zz yz xz z y zy yy xy y x zx yx xx x
 29 tzyxx xtxzzxyyxxw x 22 21 tzyxz w tzyxy w z y
29 tzyxx xtxzzxyyxxw x 22 21 tzyxz w tzyxy w z y
 30 tuw 2 21 222 2 xxxx Для потенциального течения ускорение представляет собой потенциальный вектор
30 tuw 2 21 222 2 xxxx Для потенциального течения ускорение представляет собой потенциальный вектор
 31 Запишем уравнение неразрывности для потенциального течения
31 Запишем уравнение неразрывности для потенциального течения
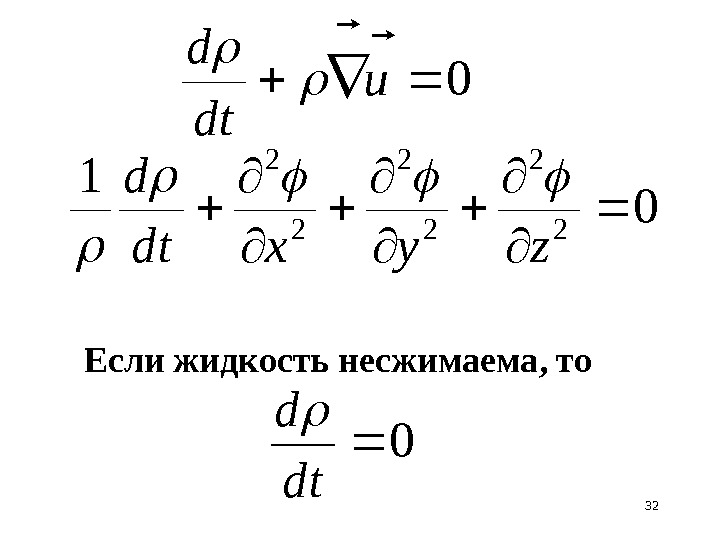 320 1 2 2 2 zyxdt d Если жидкость несжимаема, то 0 u dt d 0 dt d
320 1 2 2 2 zyxdt d Если жидкость несжимаема, то 0 u dt d 0 dt d
 33 Это уравнение Лапласа, решение — гармоническая функция координат 02 2 2 zyx
33 Это уравнение Лапласа, решение — гармоническая функция координат 02 2 2 zyx
 34 Свойства безвихревого движения в односвязном объеме 1. Записать полный поток несжимаемой жидкости через замкнутую поверхность для безвихревого течения (выразить через потенциал скорости)
34 Свойства безвихревого движения в односвязном объеме 1. Записать полный поток несжимаемой жидкости через замкнутую поверхность для безвихревого течения (выразить через потенциал скорости)
 351. Для любой замкнутой поверхности будет иметь место соотношение для несжимаемой жидкости: 0 0 d. Su u n d. S n n n. S n сколько втекает, столько вытекает жидкости Потенциальное течение Вихревое и потенциальное течение Положительное направление нормали
351. Для любой замкнутой поверхности будет иметь место соотношение для несжимаемой жидкости: 0 0 d. Su u n d. S n n n. S n сколько втекает, столько вытекает жидкости Потенциальное течение Вихревое и потенциальное течение Положительное направление нормали
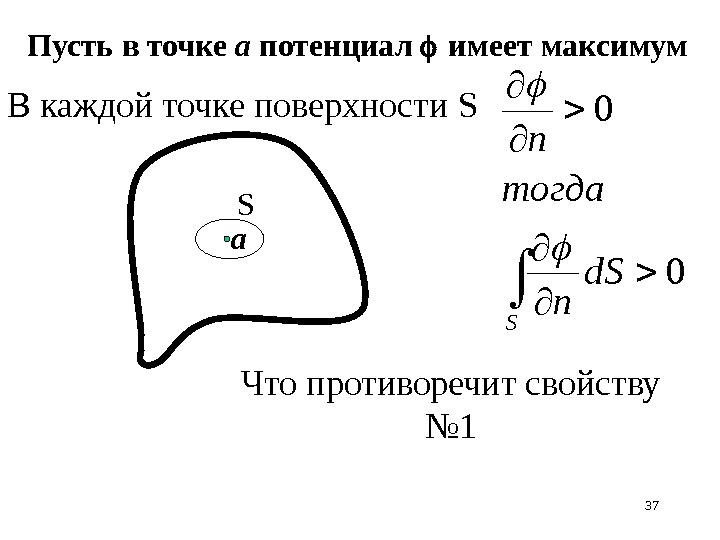
 36 Показать, что 2. ни в одной точке жидкости потенциал скорости не может иметь максимума или минимума. Указание. Пусть есть такая точка. Окружить замкнутой достаточно малой поверхностью и проверить свойство № 1.
36 Показать, что 2. ни в одной точке жидкости потенциал скорости не может иметь максимума или минимума. Указание. Пусть есть такая точка. Окружить замкнутой достаточно малой поверхностью и проверить свойство № 1.
 37 SВ каждой точке поверхности S S d. S n тогда n 0 0 Что противоречит свойству № 1 а. Пусть в точке а потенциал имеет максимум
37 SВ каждой точке поверхности S S d. S n тогда n 0 0 Что противоречит свойству № 1 а. Пусть в точке а потенциал имеет максимум
 38 a au x 3. Ни в одной точке внутри жидкости величина скорости u не может иметь максимум. Минимум может быть, например 0. Пусть скорость в точке а направлена вдоль оси х с имеет максимум u a х (Продифференцировать ур-е Лапласа по х )
38 a au x 3. Ни в одной точке внутри жидкости величина скорости u не может иметь максимум. Минимум может быть, например 0. Пусть скорость в точке а направлена вдоль оси х с имеет максимум u a х (Продифференцировать ур-е Лапласа по х )
 3900 22 22 22 z x y x x x zyxx скорость жидкости удовлетворяет уравнению Лапласа, т. е. обладает свойством № 2 a u x
3900 22 22 22 z x y x x x zyxx скорость жидкости удовлетворяет уравнению Лапласа, т. е. обладает свойством № 2 a u x
 404. В односвязном объеме жидкости, ограниченном твердыми стенками не может существовать безвихревое движение.
404. В односвязном объеме жидкости, ограниченном твердыми стенками не может существовать безвихревое движение.
 41 Если есть свободная поверхность, то безвихревое движение возможно, так как происходит деформация свободной поверхности. Учитывая, что представляет собой гармоническую функцию координат, деформация водной поверхности имеет вид гармонических волн.
41 Если есть свободная поверхность, то безвихревое движение возможно, так как происходит деформация свободной поверхности. Учитывая, что представляет собой гармоническую функцию координат, деформация водной поверхности имеет вид гармонических волн.
 42 Внутри односвязного объема жидкости существует единственное безвихревое движение если заданы на границах объема: а) либо значение потенциала б) либо значения нормальной составляющей скорости в) либо потенциал на части границы и нормальная составляющая скорости на оставшейся части границыn
42 Внутри односвязного объема жидкости существует единственное безвихревое движение если заданы на границах объема: а) либо значение потенциала б) либо значения нормальной составляющей скорости в) либо потенциал на части границы и нормальная составляющая скорости на оставшейся части границыn
 43 n Это справедливо и для внешней области
43 n Это справедливо и для внешней области

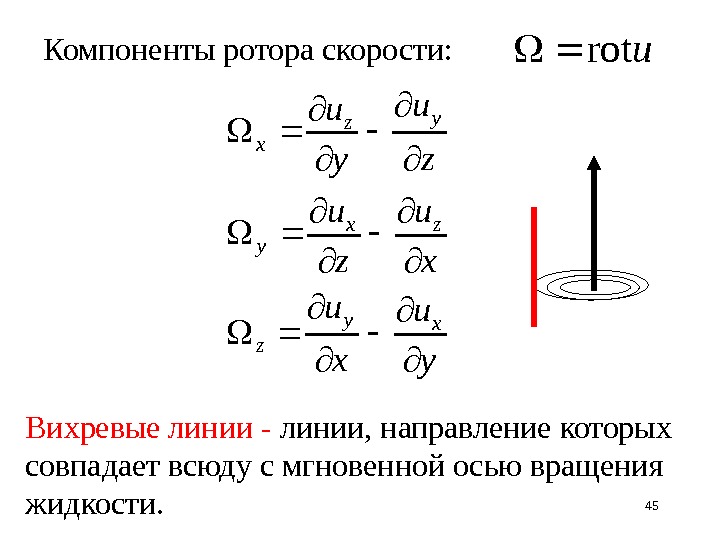
 45 Компоненты ротора скорости: y u x u z u y u xy z zx y yz x Вихревые линии — линии, направление которых совпадает всюду с мгновенной осью вращения жидкости. u rot
45 Компоненты ротора скорости: y u x u z u y u xy z zx y yz x Вихревые линии — линии, направление которых совпадает всюду с мгновенной осью вращения жидкости. u rot
 46 Вычислить
46 Вычислить
 470 0 zyx zy x Тогда по теореме Гаусса получается, что поток вихря сквозь любую замкнутую поверхность равен нулю. 0 S n ds
470 0 zyx zy x Тогда по теореме Гаусса получается, что поток вихря сквозь любую замкнутую поверхность равен нулю. 0 S n ds

 49 Дифференциальное уравнение вихревых линий , параллельных вектору ротора скорости zyx dzdydx
49 Дифференциальное уравнение вихревых линий , параллельных вектору ротора скорости zyx dzdydx
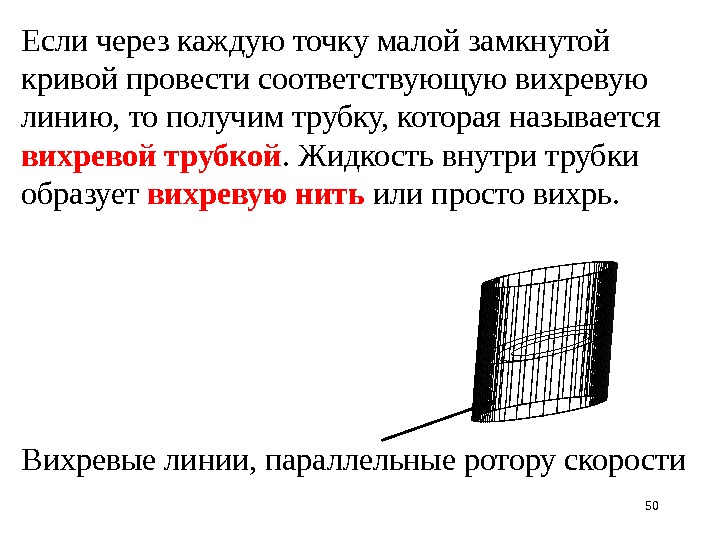
 50 Если через каждую точку малой замкнутой кривой провести соответствующую вихревую линию, то получим трубку, которая называется вихревой трубкой. Жидкость внутри трубки образует вихревую нить или просто вихрь. Вихревые линии, параллельные ротору скорости
50 Если через каждую точку малой замкнутой кривой провести соответствующую вихревую линию, то получим трубку, которая называется вихревой трубкой. Жидкость внутри трубки образует вихревую нить или просто вихрь. Вихревые линии, параллельные ротору скорости
 51 Для каждой точки поверхности вихревой трубки выполняется равенство 0 zyx nml Здесь l, m, n — направляющие.
51 Для каждой точки поверхности вихревой трубки выполняется равенство 0 zyx nml Здесь l, m, n — направляющие.
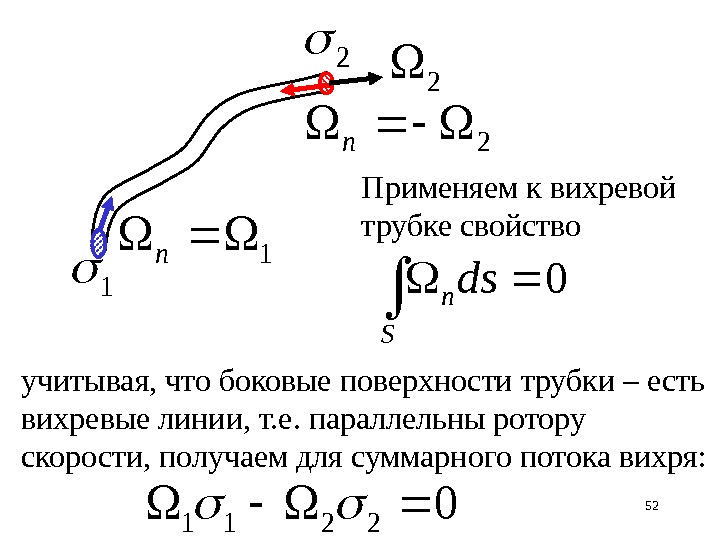
 521 n 2 1 2 n 0 S n ds. Применяем к вихревой трубке свойство учитывая, что боковые поверхности трубки – есть вихревые линии, т. е. параллельны ротору скорости, получаем для суммарного потока вихря:
521 n 2 1 2 n 0 S n ds. Применяем к вихревой трубке свойство учитывая, что боковые поверхности трубки – есть вихревые линии, т. е. параллельны ротору скорости, получаем для суммарного потока вихря:
 532211 Произведение (ротора скорости на площадь нормального сечения трубки) называется интенсивностью вихревой трубки (или вихря). Интенсивность вихря не меняется вдоль вихревой трубки.
532211 Произведение (ротора скорости на площадь нормального сечения трубки) называется интенсивностью вихревой трубки (или вихря). Интенсивность вихря не меняется вдоль вихревой трубки.
 54 Связь интенсивности вихревой трубки и циркуляции скорости SL sdurotrdu теорема Стокса
54 Связь интенсивности вихревой трубки и циркуляции скорости SL sdurotrdu теорема Стокса
 55 Для бесконечно малого плоского сечения трубки (ротор вдоль сечения не меняется) n n S n sdurot , cos n
55 Для бесконечно малого плоского сечения трубки (ротор вдоль сечения не меняется) n n S n sdurot , cos n
 56 Циркуляция по какой-либо замкнутой кривой равна сумме напряжений всех вихрей, охватываемых этой кривой.
56 Циркуляция по какой-либо замкнутой кривой равна сумме напряжений всех вихрей, охватываемых этой кривой.
 57 Разобьем все поле вихрей на вихревые трубки равной интенсивности. В соответствии с число входящих трубок должно быть равно числу выходящих трубок. 0 S n ds
57 Разобьем все поле вихрей на вихревые трубки равной интенсивности. В соответствии с число входящих трубок должно быть равно числу выходящих трубок. 0 S n ds
 58 Вихревая линия во внутренней точке жидкости не может ни начинаться, ни оканчиваться. Все вихревые линии должны образовывать замкнутые вихревые линии, или же, начинаться и кончаться на границах жидкости, пронизывая ее толщу.
58 Вихревая линия во внутренней точке жидкости не может ни начинаться, ни оканчиваться. Все вихревые линии должны образовывать замкнутые вихревые линии, или же, начинаться и кончаться на границах жидкости, пронизывая ее толщу.
 59 Вихри имеют форму цилиндров с горизонтальной осью перпендикулярной направлению потока 1 см bottom 1 3 4 flow
59 Вихри имеют форму цилиндров с горизонтальной осью перпендикулярной направлению потока 1 см bottom 1 3 4 flow
 60 xy z 21 2 1 -центральная часть вихря, 2 -конец основного вихря, 3 -конец вихря-спутника, 4 -дно
60 xy z 21 2 1 -центральная часть вихря, 2 -конец основного вихря, 3 -конец вихря-спутника, 4 -дно
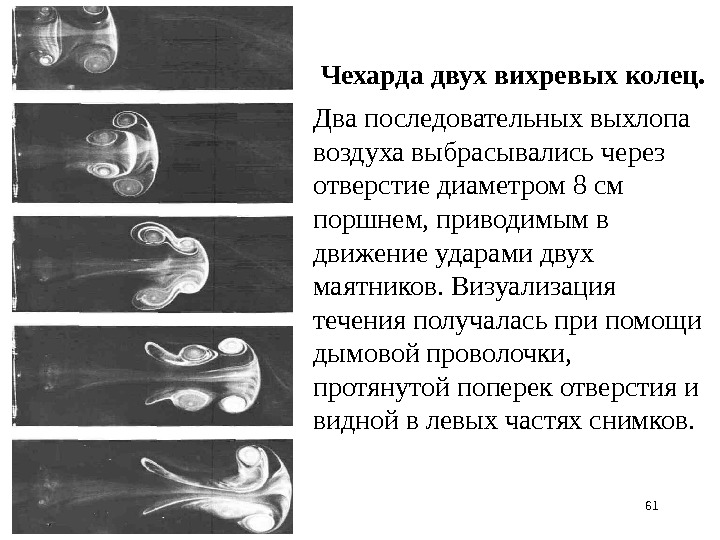
 61 Чехарда двух вихревых колец. Два последовательных выхлопа воздуха выбрасывались через отверстие диаметром 8 см поршнем, приводимым в движение ударами двух маятников. Визуализация течения получалась при помощи дымовой проволочки, протянутой поперек отверстия и видной в левых частях снимков.
61 Чехарда двух вихревых колец. Два последовательных выхлопа воздуха выбрасывались через отверстие диаметром 8 см поршнем, приводимым в движение ударами двух маятников. Визуализация течения получалась при помощи дымовой проволочки, протянутой поперек отверстия и видной в левых частях снимков.
 62 При данном числе Рейнольдса, рассчитанном по диаметру отверстия и примерно равном 1600, второе кольцо движется быстрее, так как находится в индуцированном первым кольцом поле; на третьем фотоснимке второе кольцо уже проскальзывает сквозь первое. Затем процесс повторяется, и на последнем снимке уже первое кольцо проскальзывает сквозь второе. [Yamada, Matsui, 1978]
62 При данном числе Рейнольдса, рассчитанном по диаметру отверстия и примерно равном 1600, второе кольцо движется быстрее, так как находится в индуцированном первым кольцом поле; на третьем фотоснимке второе кольцо уже проскальзывает сквозь первое. Затем процесс повторяется, и на последнем снимке уже первое кольцо проскальзывает сквозь второе. [Yamada, Matsui, 1978]

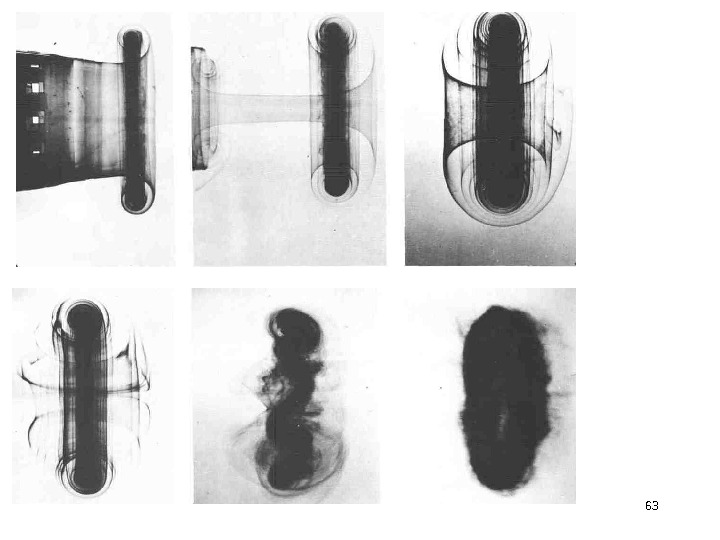
 64 Верхний ряд снимков показывает истечение воды с введенной в нее краской через пятисантиметровое отверстие, в результате чего создается осесимметричное вихревое кольцо. Число Рейнольдса этого кольца равно примерно 15000. Нижний ряд снимков показывает последовательное разрушение кольца из-за неустойчивости. Развиваются синусоидальные возмущения с семью волнами на кольце. Внешние слои кольца в отличие от его ядра искривляются. Амплитуда волн возрастает до тех пор, пока кольцо внезапно не испытает перехода к турбулентности при сохранении видимости его структуры. [Didden, 1977]
64 Верхний ряд снимков показывает истечение воды с введенной в нее краской через пятисантиметровое отверстие, в результате чего создается осесимметричное вихревое кольцо. Число Рейнольдса этого кольца равно примерно 15000. Нижний ряд снимков показывает последовательное разрушение кольца из-за неустойчивости. Развиваются синусоидальные возмущения с семью волнами на кольце. Внешние слои кольца в отличие от его ядра искривляются. Амплитуда волн возрастает до тех пор, пока кольцо внезапно не испытает перехода к турбулентности при сохранении видимости его структуры. [Didden, 1977]
 65 Гексагональное дымовое кольцо. Нарастание волн вокруг вихревого кольца часто называется неустойчивостью Уиднелла по имени первого исследователя. К моменту, показанному на данном снимке, этот процесс привел к замечательной симметричной структуре, созданной дымом в воздухе при числе Рейнольдса, примерно равном 1000. Фото G. J. Jameson, M. Urbicain
65 Гексагональное дымовое кольцо. Нарастание волн вокруг вихревого кольца часто называется неустойчивостью Уиднелла по имени первого исследователя. К моменту, показанному на данном снимке, этот процесс привел к замечательной симметричной структуре, созданной дымом в воздухе при числе Рейнольдса, примерно равном 1000. Фото G. J. Jameson, M. Urbicain
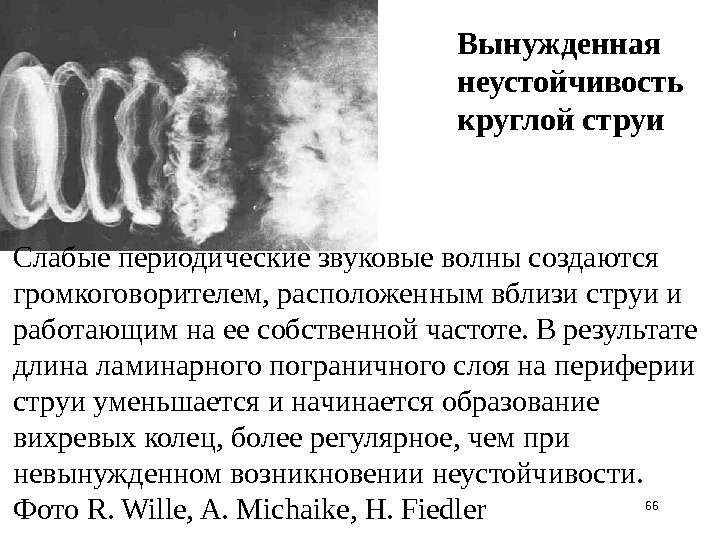
 66 Слабые периодические звуковые волны создаются громкоговорителем, расположенным вблизи струи и работающим на ее собственной частоте. В результате длина ламинарного пограничного слоя на периферии струи уменьшается и начинается образование вихревых колец, более регулярное, чем при невынужденном возникновении неустойчивости. Фото R. Wille, A. Michaike, Н. Fiedler Вынужденная неустойчивость круглой струи
66 Слабые периодические звуковые волны создаются громкоговорителем, расположенным вблизи струи и работающим на ее собственной частоте. В результате длина ламинарного пограничного слоя на периферии струи уменьшается и начинается образование вихревых колец, более регулярное, чем при невынужденном возникновении неустойчивости. Фото R. Wille, A. Michaike, Н. Fiedler Вынужденная неустойчивость круглой струи
 67 Задача 1 Жидкость вращается вокруг оси 0 z как твердое тело с угловой скоростью . Определить ротор скорости внутри вихрей
67 Задача 1 Жидкость вращается вокруг оси 0 z как твердое тело с угловой скоростью . Определить ротор скорости внутри вихрей
 68 cos sin uu uu y x xu yu y x au a x a y cossinu = a xy a
68 cos sin uu uu y x xu yu y x au a x a y cossinu = a xy a
 69 zyxuuu zyx kji u rot 2 2 a 2 rotku j i k u rot 2 rotku 2 2 a ij k u rot Вихрь rot u и циркуляция скорости цилиндрического вихря
69 zyxuuu zyx kji u rot 2 2 a 2 rotku j i k u rot 2 rotku 2 2 a ij k u rot Вихрь rot u и циркуляция скорости цилиндрического вихря
 70 Задача 2. Скорость частиц жидкости пропорциональна расстоянию до оси 0 х и параллельна этой оси: Определить поле вихрей, форму вихревых линий 0 0 22 zyxuuzycu
70 Задача 2. Скорость частиц жидкости пропорциональна расстоянию до оси 0 х и параллельна этой оси: Определить поле вихрей, форму вихревых линий 0 0 22 zyxuuzycu
 71 xy z
71 xy z
 722222 22 00 rot zy y c zy z c zyс zyx kji u zy cz 22 y
722222 22 00 rot zy y c zy z c zyс zyx kji u zy cz 22 y
 732222 zy y c dz zy z c dy Уравнение вихревых линий const 22 x yz z y c z 22 y
732222 zy y c dz zy z c dy Уравнение вихревых линий const 22 x yz z y c z 22 y

 75 Силы массовые – тяжести, инерции – действуют на выделенный объем жидкости независимо от того, существуют ли рядом другие элементы жидкости Силы поверхностные — определяют взаимодействие между соседними элементами на поверхности объема. Внутри объема силы взаимодействия частиц уравновешивают друга.
75 Силы массовые – тяжести, инерции – действуют на выделенный объем жидкости независимо от того, существуют ли рядом другие элементы жидкости Силы поверхностные — определяют взаимодействие между соседними элементами на поверхности объема. Внутри объема силы взаимодействия частиц уравновешивают друга.
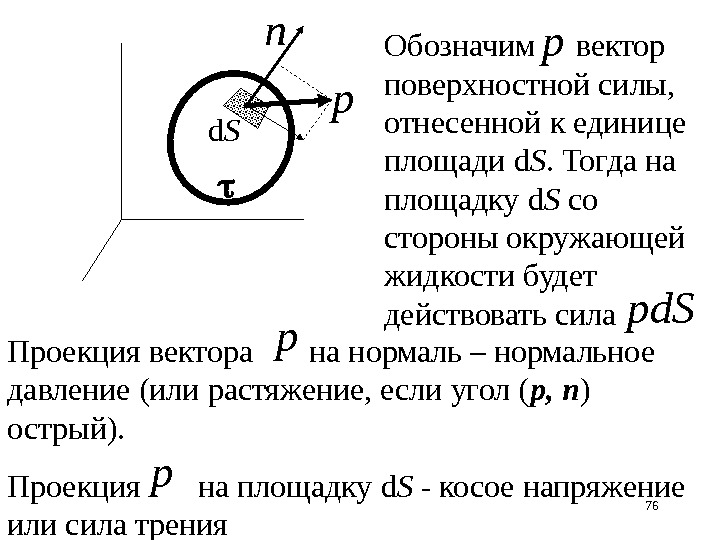
 76 d S Обозначим вектор поверхностной силы, отнесенной к единице площади d S. Тогда на площадку d S со стороны окружающей жидкости будет действовать сила Проекция вектора на нормаль – нормальное давление (или растяжение, если угол ( р, n ) острый). Проекция на площадку d S — косое напряжение или сила трения p p d. Sp p p n
76 d S Обозначим вектор поверхностной силы, отнесенной к единице площади d S. Тогда на площадку d S со стороны окружающей жидкости будет действовать сила Проекция вектора на нормаль – нормальное давление (или растяжение, если угол ( р, n ) острый). Проекция на площадку d S — косое напряжение или сила трения p p d. Sp p p n
 77 Применяем начало Даламбера: В каждый момент времени движения любой материальной системы все силы, приложенные к ней, включая и силы инерции, взаимно уравновешиваются сила массовая — инерции сил вектор главный 0 F dw d. Spdw. F S
77 Применяем начало Даламбера: В каждый момент времени движения любой материальной системы все силы, приложенные к ней, включая и силы инерции, взаимно уравновешиваются сила массовая — инерции сил вектор главный 0 F dw d. Spdw. F S
 78 Уравнение движения идеальной жидкости – существует только нормальная составляющая поверхностной силы npp 0 Sd. Snpdw. F Используем теорему Гаусса 0][ dpw. F Это справедливо для любого объема жидкости – тогда выражение под интегралом равно нулю
78 Уравнение движения идеальной жидкости – существует только нормальная составляющая поверхностной силы npp 0 Sd. Snpdw. F Используем теорему Гаусса 0][ dpw. F Это справедливо для любого объема жидкости – тогда выражение под интегралом равно нулю
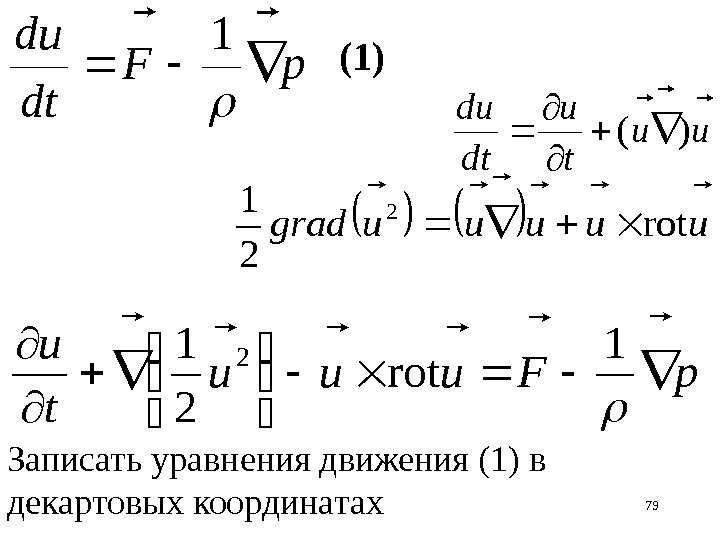 79 p. F dt ud 1 uu tu dt ud )( Записать уравнения движения (1) в декартовых координатах uuuuugrad rot 2 12 p. Fuuu t u 1 rot 2 12 (1)
79 p. F dt ud 1 uu tu dt ud )( Записать уравнения движения (1) в декартовых координатах uuuuugrad rot 2 12 p. Fuuu t u 1 rot 2 12 (1)
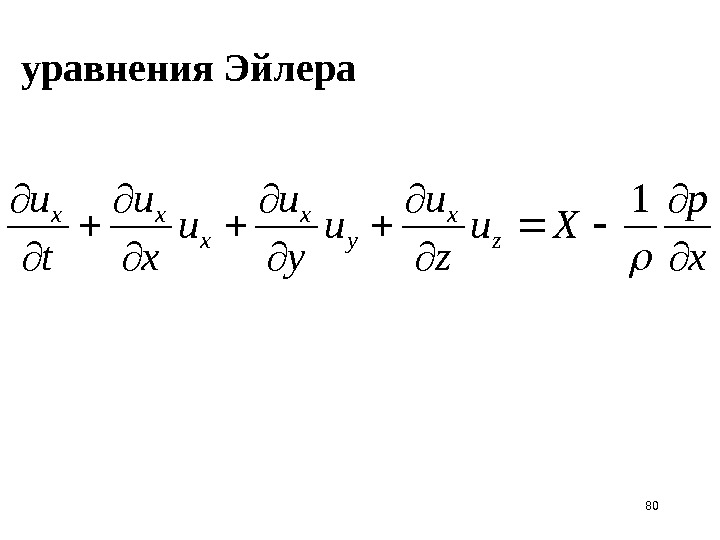 80 xp Xu zu u yu u xu tu zx yx xxx 1 уравнения Эйлера
80 xp Xu zu u yu u xu tu zx yx xxx 1 уравнения Эйлера
 81 Цилиндрические координаты zp F tu u zu uu ru ru p r. F tu u zu uu ru ru r uu rp F ru tu u zu uu ru ru zz zzz rz zrr rr
81 Цилиндрические координаты zp F tu u zu uu ru ru p r. F tu u zu uu ru ru r uu rp F ru tu u zu uu ru ru zz zzz rz zrr rr
 82 Для безвихревого движения pu t F Fp u t uurot 2 1 2 0 22 Массовая сила должна иметь потенциал p. Fuuu t u 1 rot
82 Для безвихревого движения pu t F Fp u t uurot 2 1 2 0 22 Массовая сила должна иметь потенциал p. Fuuu t u 1 rot

 84 Умножим уравнение движения на элементарное перемещение вдоль линии тока. 01 dtupdtu dt ud dtu. F dtu 0 , t. VF pu tp dtdp 0 1 2 12 dt dt dp dtu dt dt d. V Для стационарного движения жидкости в поле потенциальных сил
84 Умножим уравнение движения на элементарное перемещение вдоль линии тока. 01 dtupdtu dt ud dtu. F dtu 0 , t. VF pu tp dtdp 0 1 2 12 dt dt dp dtu dt dt d. V Для стационарного движения жидкости в поле потенциальных сил
 85 Если жидкость баротропна (плотность зависит только от давления) и несжимаема 0 2 1 2 p u. Vd const 2 1 2 p u. V Интеграл движения Бернулли — Эйлера const 21 2 p ugz
85 Если жидкость баротропна (плотность зависит только от давления) и несжимаема 0 2 1 2 p u. Vd const 2 1 2 p u. V Интеграл движения Бернулли — Эйлера const 21 2 p ugz
 86 В поле действия потенциальных сил уравнение Бернулли справедливо: Для вихревого стационарного движения – вдоль линий тока Для безвихревого стационарного двтжения для любых точек жидкости u х ху u xy
86 В поле действия потенциальных сил уравнение Бернулли справедливо: Для вихревого стационарного движения – вдоль линий тока Для безвихревого стационарного двтжения для любых точек жидкости u х ху u xy
 87 Река имеет участок, где оба берега представляют собой сегмент вложенных окружностей с единым центром. Показать, что у берега А скорость течения больше, а уровень ниже, чем у берега В. Считать движение установившимся и безвихревым. z r A B zru u ru z r 1 rot ru zu uzr rot r z u r ru r u 1 rot 011 zuu rrru r zr Уравнение неразрывности
87 Река имеет участок, где оба берега представляют собой сегмент вложенных окружностей с единым центром. Показать, что у берега А скорость течения больше, а уровень ниже, чем у берега В. Считать движение установившимся и безвихревым. z r A B zru u ru z r 1 rot ru zu uzr rot r z u r ru r u 1 rot 011 zuu rrru r zr Уравнение неразрывности
 88 Проекции скорости на оси координат 0 ; ; 0 zr uuu Так как движение безвихревое rot u =0 0 ; 0 r ru z ru Из уравнения неразрывности 0 ru BA uu r uru ; const; Из уравнения Бернулли gu Z B BA A 22 22 BA ZZ
88 Проекции скорости на оси координат 0 ; ; 0 zr uuu Так как движение безвихревое rot u =0 0 ; 0 r ru z ru Из уравнения неразрывности 0 ru BA uu r uru ; const; Из уравнения Бернулли gu Z B BA A 22 22 BA ZZ

