 1
1
 2
2
 Всякая конечная, непрерывная и однозначная функция f(z), первая производная которой конечна для всех точек области между двумя концентрическими окружностями, описанными около начала , может быть разложена в ряд: 3
Всякая конечная, непрерывная и однозначная функция f(z), первая производная которой конечна для всех точек области между двумя концентрическими окружностями, описанными около начала , может быть разложена в ряд: 3
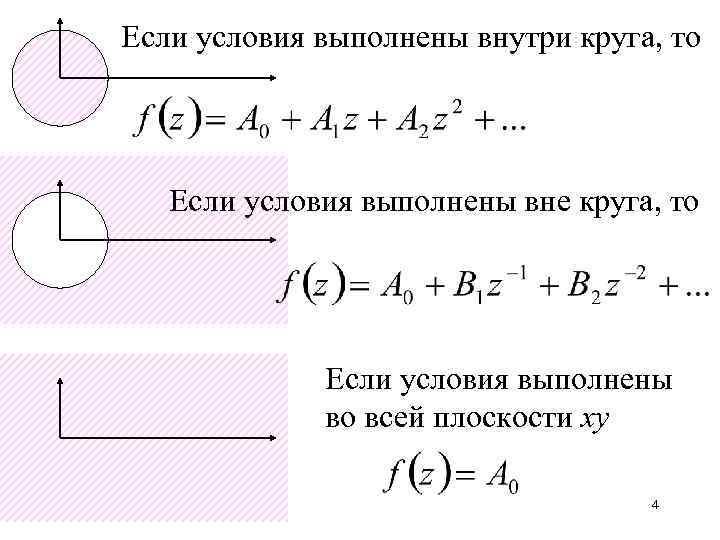 Если условия выполнены внутри круга, то Если условия выполнены вне круга, то Если условия выполнены во всей плоскости ху 4
Если условия выполнены внутри круга, то Если условия выполнены вне круга, то Если условия выполнены во всей плоскости ху 4
 Полагая , вводя полярные координаты , представляя комплексные коэффициенты разложения в виде внутри круга вне круга учитывая Получить потенциал скорости и функцию тока φиψ 5
Полагая , вводя полярные координаты , представляя комплексные коэффициенты разложения в виде внутри круга вне круга учитывая Получить потенциал скорости и функцию тока φиψ 5
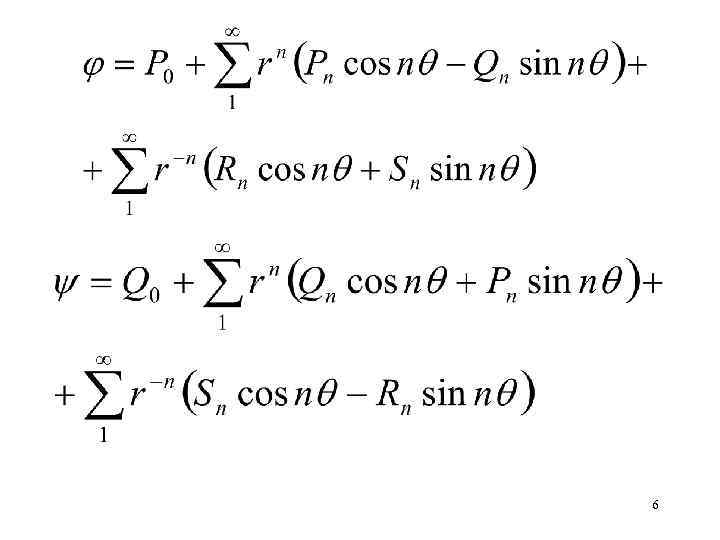 6
6
 Если значение или задано на концентрических окружностях, то это значение может быть разложено в ряд Фурье по косинусам и синусам кратного . Эти ряды должны быть эквивалентны рядам полученным выше. Приравнивая в отдельности коэффициенты при sin(n ) и при cos(n ) , можно получить уравнения для определения Pn, Qn, Rn, Sn. 7
Если значение или задано на концентрических окружностях, то это значение может быть разложено в ряд Фурье по косинусам и синусам кратного . Эти ряды должны быть эквивалентны рядам полученным выше. Приравнивая в отдельности коэффициенты при sin(n ) и при cos(n ) , можно получить уравнения для определения Pn, Qn, Rn, Sn. 7
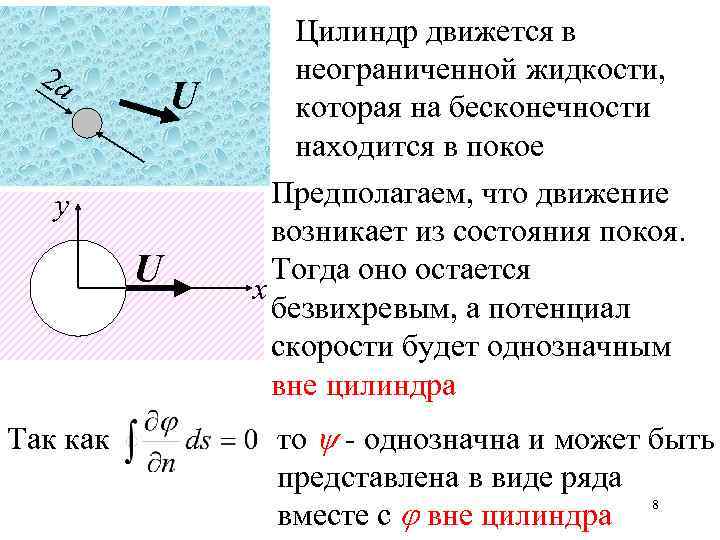 2 a U у U Так как Цилиндр движется в неограниченной жидкости, которая на бесконечности находится в покое Предполагаем, что движение возникает из состояния покоя. Тогда оно остается х безвихревым, а потенциал скорости будет однозначным вне цилиндра то - однозначна и может быть представлена в виде ряда 8 вместе с вне цилиндра
2 a U у U Так как Цилиндр движется в неограниченной жидкости, которая на бесконечности находится в покое Предполагаем, что движение возникает из состояния покоя. Тогда оно остается х безвихревым, а потенциал скорости будет однозначным вне цилиндра то - однозначна и может быть представлена в виде ряда 8 вместе с вне цилиндра
 r U Нормальная составляющая скорости в жидкости на границе с цилиндром равна для r=a Так как Pn=0, Qn =0, то дифференцируя потенциал скорости по r и приравнивая нормальные составляющие скорости на границе цилиндра r=a, получаем: Найти R 9
r U Нормальная составляющая скорости в жидкости на границе с цилиндром равна для r=a Так как Pn=0, Qn =0, то дифференцируя потенциал скорости по r и приравнивая нормальные составляющие скорости на границе цилиндра r=a, получаем: Найти R 9
 Остальные коэффициенты равны нулю Полное решение задачи: Найти линии тока 10
Остальные коэффициенты равны нулю Полное решение задачи: Найти линии тока 10
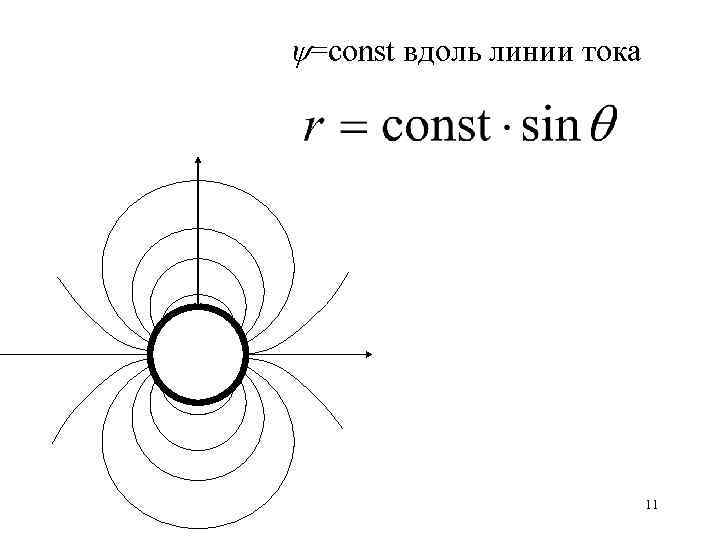 =const вдоль линии тока 11
=const вдоль линии тока 11
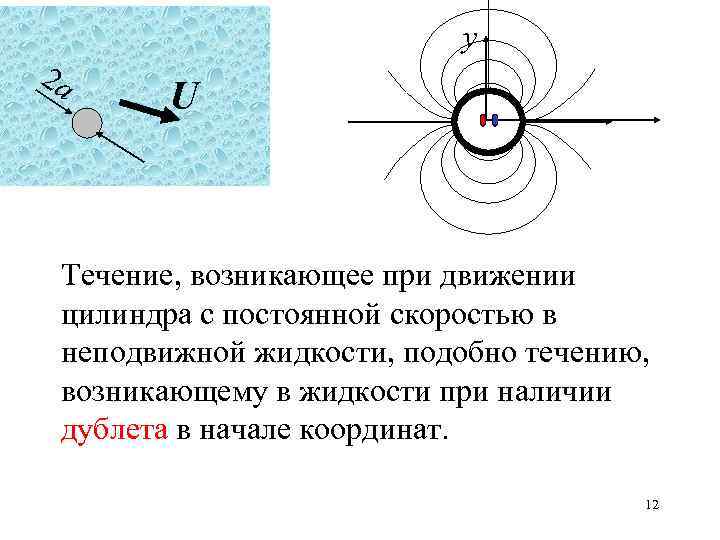 у 2 a U Течение, возникающее при движении цилиндра с постоянной скоростью в неподвижной жидкости, подобно течению, возникающему в жидкости при наличии дублета в начале координат. 12
у 2 a U Течение, возникающее при движении цилиндра с постоянной скоростью в неподвижной жидкости, подобно течению, возникающему в жидкости при наличии дублета в начале координат. 12
 13
13
 Кинетическая энергия жидкости: Кинетическая энергия системы (цилиндр+жидкость), отнесенная к единице длины цилиндра, равна сумме энергии цилиндра ( 1/2 МU 2) и энергии жидкости (1/2 М выт. жидк. U 2) 14
Кинетическая энергия жидкости: Кинетическая энергия системы (цилиндр+жидкость), отнесенная к единице длины цилиндра, равна сумме энергии цилиндра ( 1/2 МU 2) и энергии жидкости (1/2 М выт. жидк. U 2) 14
 15
15
 Если прямолинейном движении цилиндра на него действует внешняя сила Х , отнесенная к единице длины, то уравнение изменения энергии будет: Со стороны жидкости на цилиндр действует сила Она исчезает, если скорость не зависит от времени. 16
Если прямолинейном движении цилиндра на него действует внешняя сила Х , отнесенная к единице длины, то уравнение изменения энергии будет: Со стороны жидкости на цилиндр действует сила Она исчезает, если скорость не зависит от времени. 16
 Определим эту силу используя интеграл движения, записанный через потенциал скорости для нестационарного движения жидкости: q - результирующая скорость: 17
Определим эту силу используя интеграл движения, записанный через потенциал скорости для нестационарного движения жидкости: q - результирующая скорость: 17
 Для того, чтобы найти силу, действующую на цилиндр со стороны окружающей жидкости, надо проинтегрировать давление по границе цилиндра. Проекция на ось х: 18
Для того, чтобы найти силу, действующую на цилиндр со стороны окружающей жидкости, надо проинтегрировать давление по границе цилиндра. Проекция на ось х: 18
 Если цилиндр движется в идеальной жидкости с постоянной во времени скоростью, то со стороны жидкости на него не действует силы. 19
Если цилиндр движется в идеальной жидкости с постоянной во времени скоростью, то со стороны жидкости на него не действует силы. 19
 20
20
 2 a 2 a Пусть цилиндр движется со скоростью U, как показано на рисунке. U -U Сообщим жидкости и цилиндру скорость -U. Тогда жидкость будет обтекать неподвижный цилиндр Запишем комплексный потенциал для плоскопраллельного движения жидкости. 21
2 a 2 a Пусть цилиндр движется со скоростью U, как показано на рисунке. U -U Сообщим жидкости и цилиндру скорость -U. Тогда жидкость будет обтекать неподвижный цилиндр Запишем комплексный потенциал для плоскопраллельного движения жидкости. 21
 Потенциал скорости и функция тока для плоскопараллельного течения n=1 у : r х 22
Потенциал скорости и функция тока для плоскопараллельного течения n=1 у : r х 22
 2 a 2 a U -U Надо прибавить 23
2 a 2 a U -U Надо прибавить 23
 Определим потенциал скорости и функцию тока на границе цилиндра r=a Является ли граница цилиндра линией тока? Каковы линии тока? 24
Определим потенциал скорости и функцию тока на границе цилиндра r=a Является ли граница цилиндра линией тока? Каковы линии тока? 24
 Обтекание круга в лотке Хил-Шоу Подкраска позволяет увидеть линии тока в воде, текущей со скоростью 1 мм/с между двумя стеклянными пластинками, отстоящими на расстояние одного миллиметра. Линии тока абсолютно симметричны, такая картина должна наблюдаться в идеальной жидкости (без вязкости) 25
Обтекание круга в лотке Хил-Шоу Подкраска позволяет увидеть линии тока в воде, текущей со скоростью 1 мм/с между двумя стеклянными пластинками, отстоящими на расстояние одного миллиметра. Линии тока абсолютно симметричны, такая картина должна наблюдаться в идеальной жидкости (без вязкости) 25
 На первый взгляд представляется парадоксальным, что наилучший способ получения безотрывной картины плоского потенциального обтекания цилиндра характерного для идеальной жидкости, состоит в переходе к противоположному крайнему случаю ползущего течения в узком зазоре, для которого влияние сил вязкости является определяющим. Фото D. Н. Регеgrine 26
На первый взгляд представляется парадоксальным, что наилучший способ получения безотрывной картины плоского потенциального обтекания цилиндра характерного для идеальной жидкости, состоит в переходе к противоположному крайнему случаю ползущего течения в узком зазоре, для которого влияние сил вязкости является определяющим. Фото D. Н. Регеgrine 26
 27
27
 Для стационарного движения при отсутствии внешних сил Для стационарного движения -( выполняется вдоль данной линии тока ) Для безвихревого движения -( ) выплняется везде 28
Для стационарного движения при отсутствии внешних сил Для стационарного движения -( выполняется вдоль данной линии тока ) Для безвихревого движения -( ) выплняется везде 28
 Какая сила действует на тело в потоке жидкости, если движение безвихревое? Скорость на границе: y umax=2 U u u=0 x umax 0 29
Какая сила действует на тело в потоке жидкости, если движение безвихревое? Скорость на границе: y umax=2 U u u=0 x umax 0 29
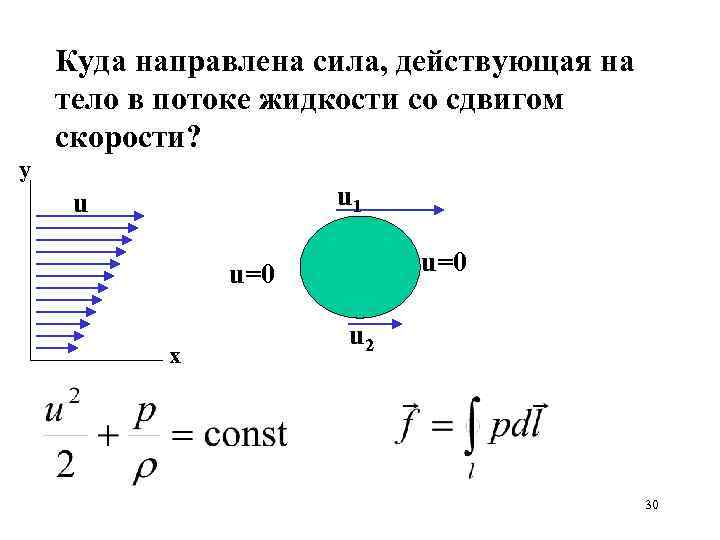 Куда направлена сила, действующая на тело в потоке жидкости со сдвигом скорости? y u 1 u u=0 x u 2 30
Куда направлена сила, действующая на тело в потоке жидкости со сдвигом скорости? y u 1 u u=0 x u 2 30
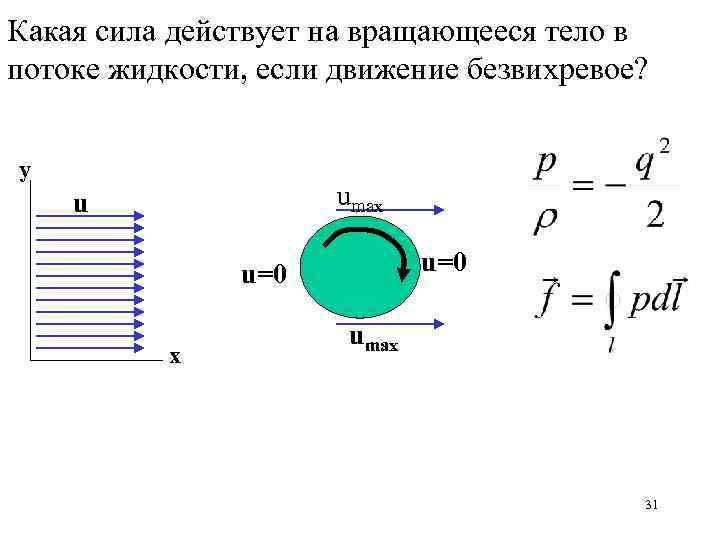 Какая сила действует на вращающееся тело в потоке жидкости, если движение безвихревое? y umax u u=0 x umax 31
Какая сила действует на вращающееся тело в потоке жидкости, если движение безвихревое? y umax u u=0 x umax 31
 32
32
 Обтекание кругового цилиндра при Re=1, 54. При этом числе Рейнольдса картина линий тока, очевидно, уже потеряла ту симметрию передней и задней частей, которая имела место в ползущем 33 течении.
Обтекание кругового цилиндра при Re=1, 54. При этом числе Рейнольдса картина линий тока, очевидно, уже потеряла ту симметрию передней и задней частей, которая имела место в ползущем 33 течении.
 Однако поток сзади все же еще не оторвался. Отрыв начинается примерно при Re = 5, хотя значение числа Рейнольдса начала отрыва точно неизвестно. Линии тока визуализированы с помощью алюминиевого порошка в воде. Фото Sadatoshi Taneda 34
Однако поток сзади все же еще не оторвался. Отрыв начинается примерно при Re = 5, хотя значение числа Рейнольдса начала отрыва точно неизвестно. Линии тока визуализированы с помощью алюминиевого порошка в воде. Фото Sadatoshi Taneda 34
 Обтекание кругового цилиндра при Re=9, 6. Произошел отрыв, и рециркуляционных вихрей. образовалась пара 35
Обтекание кругового цилиндра при Re=9, 6. Произошел отрыв, и рециркуляционных вихрей. образовалась пара 35
 Цилиндр движется в бассейне с водой, содержащей алюминиевый порошок, и подсвечивается световым ножом под свободной поверхностью. Экстраполяция результатов подобных экспериментов на случай неограниченного потока указывает на возможность отрыва при Re=4 -5, тогда как большинство численных расчетов дает Re=5 -7. Фото Sadatoshi Taneda 36
Цилиндр движется в бассейне с водой, содержащей алюминиевый порошок, и подсвечивается световым ножом под свободной поверхностью. Экстраполяция результатов подобных экспериментов на случай неограниченного потока указывает на возможность отрыва при Re=4 -5, тогда как большинство численных расчетов дает Re=5 -7. Фото Sadatoshi Taneda 36
 Обтекание кругового цилиндра при Re=13, 1. По мере увеличения скорости неподвижные вихри начинают вытягиваться в направлении потока. Их длина линейно растет с ростом числа Рейнольдса, пока значение 37 Re не превысит 40
Обтекание кругового цилиндра при Re=13, 1. По мере увеличения скорости неподвижные вихри начинают вытягиваться в направлении потока. Их длина линейно растет с ростом числа Рейнольдса, пока значение 37 Re не превысит 40
 Обтекание кругового цилиндра при Re=26. Расстояние вниз по потоку до центров вихрей также линейно возрастает с ростом числа 38 Рейнольдса.
Обтекание кругового цилиндра при Re=26. Расстояние вниз по потоку до центров вихрей также линейно возрастает с ростом числа 38 Рейнольдса.
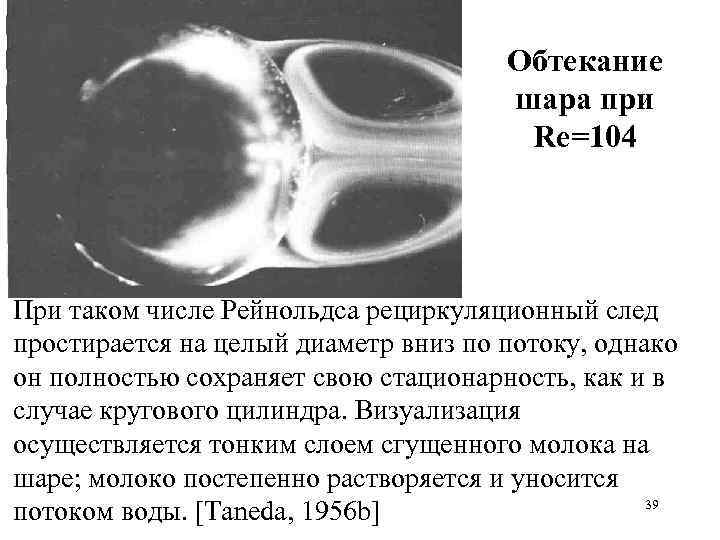 Обтекание шара при Re=104 При таком числе Рейнольдса рециркуляционный след простирается на целый диаметр вниз по потоку, однако он полностью сохраняет свою стационарность, как и в случае кругового цилиндра. Визуализация осуществляется тонким слоем сгущенного молока на шаре; молоко постепенно растворяется и уносится 39 потоком воды. [Taneda, 1956 b]
Обтекание шара при Re=104 При таком числе Рейнольдса рециркуляционный след простирается на целый диаметр вниз по потоку, однако он полностью сохраняет свою стационарность, как и в случае кругового цилиндра. Визуализация осуществляется тонким слоем сгущенного молока на шаре; молоко постепенно растворяется и уносится 39 потоком воды. [Taneda, 1956 b]
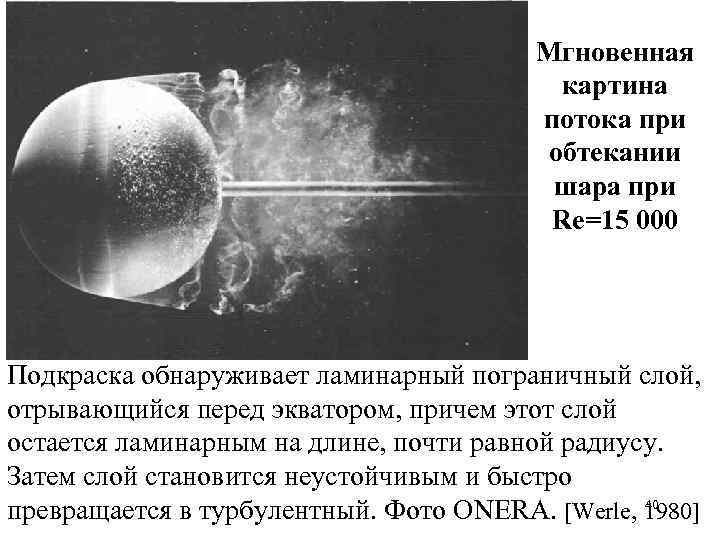 Мгновенная картина потока при обтекании шара при Re=15 000 Подкраска обнаруживает ламинарный пограничный слой, отрывающийся перед экватором, причем этот слой остается ламинарным на длине, почти равной радиусу. Затем слой становится неустойчивым и быстро 40 превращается в турбулентный. Фото ONERA. [Werle, 1980]
Мгновенная картина потока при обтекании шара при Re=15 000 Подкраска обнаруживает ламинарный пограничный слой, отрывающийся перед экватором, причем этот слой остается ламинарным на длине, почти равной радиусу. Затем слой становится неустойчивым и быстро 40 превращается в турбулентный. Фото ONERA. [Werle, 1980]
 41
41
 Силы действующие на элементарный объем воды вблизи дна в замедляющемся потоке Если и p -давление u 1>u 2 y рхн бодная пове Сво u 1 p 1 ость u u 2 p 2 х Придонный слой конечной толщины может быть остановлен этими силами Ffriction 42
Силы действующие на элементарный объем воды вблизи дна в замедляющемся потоке Если и p -давление u 1>u 2 y рхн бодная пове Сво u 1 p 1 ость u u 2 p 2 х Придонный слой конечной толщины может быть остановлен этими силами Ffriction 42
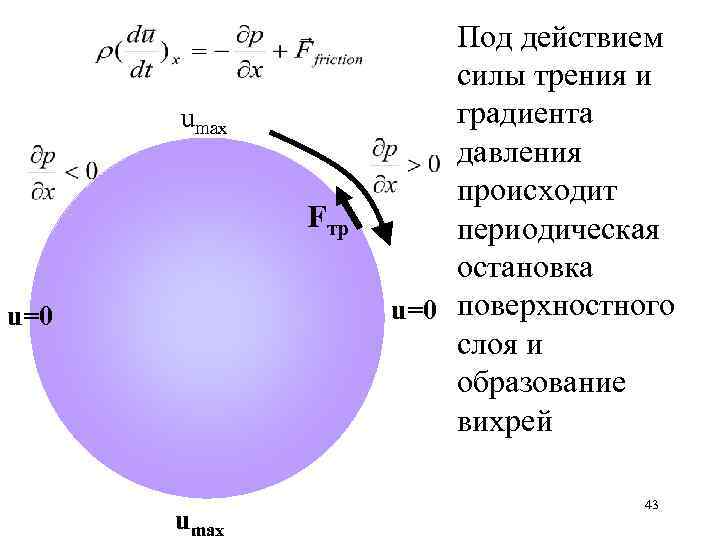 umax Fтр u=0 umax Под действием силы трения и градиента давления происходит периодическая остановка u=0 поверхностного слоя и образование вихрей 43
umax Fтр u=0 umax Под действием силы трения и градиента давления происходит периодическая остановка u=0 поверхностного слоя и образование вихрей 43
 Вихревая дорожка Кармана за круговым цилиндром при Re = 140. Вода обтекает цилиндр диаметром 1 см co скоростью 1, 4 см/с. Визуализация движения осуществляется так: частицы метятся белым коллоидным дымом, создаваемым электролитическим способом и освещаются световым ножом. Видно, что по мере продвижения вниз по потоку на несколько диаметров ширина вихревой пелены возрастает. Фото Sadatoshi 44 Taneda
Вихревая дорожка Кармана за круговым цилиндром при Re = 140. Вода обтекает цилиндр диаметром 1 см co скоростью 1, 4 см/с. Визуализация движения осуществляется так: частицы метятся белым коллоидным дымом, создаваемым электролитическим способом и освещаются световым ножом. Видно, что по мере продвижения вниз по потоку на несколько диаметров ширина вихревой пелены возрастает. Фото Sadatoshi 44 Taneda
 Вихри Кармана в абсолютном движении Камера движется здесь вместе с вихрями, а не с цилиндром. Структура линий тока весьма напоминает картину невязкого течения, рассчитанную Карманом. Визуализация потока осуществляется с помощью частиц, плавающих на воде. Фото R. Wille, снимок взят из статьи [Werle, 1973]. Воспроизведено с соответствующего разрешения из Annual Review of Fluid Mechanics, Vol. 5, © 1973 by Annual Reviews Inc 45
Вихри Кармана в абсолютном движении Камера движется здесь вместе с вихрями, а не с цилиндром. Структура линий тока весьма напоминает картину невязкого течения, рассчитанную Карманом. Визуализация потока осуществляется с помощью частиц, плавающих на воде. Фото R. Wille, снимок взят из статьи [Werle, 1973]. Воспроизведено с соответствующего разрешения из Annual Review of Fluid Mechanics, Vol. 5, © 1973 by Annual Reviews Inc 45
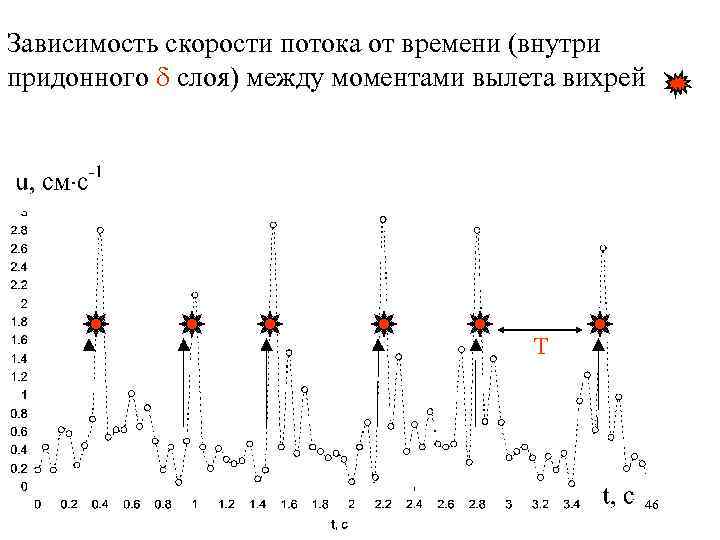 Зависимость скорости потока от времени (внутри придонного d слоя) между моментами вылета вихрей T 46
Зависимость скорости потока от времени (внутри придонного d слоя) между моментами вылета вихрей T 46
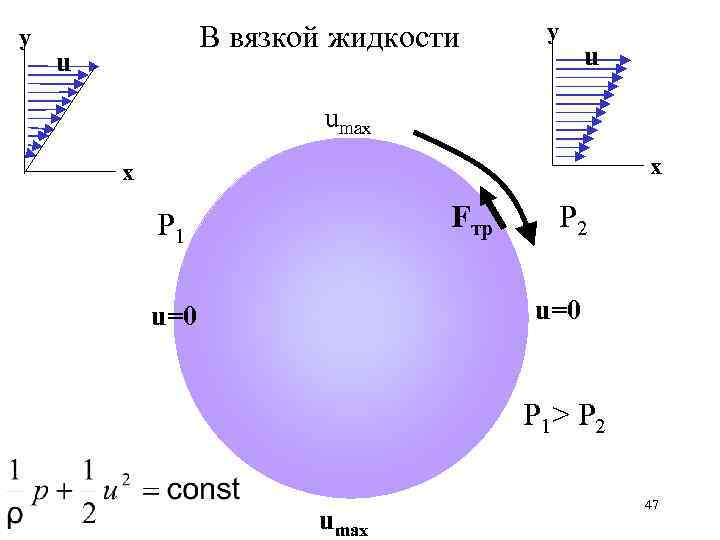 y В вязкой жидкости u y u umax x x Fтр Р 1 Р 2 u=0 Р 1> Р 2 umax 47
y В вязкой жидкости u y u umax x x Fтр Р 1 Р 2 u=0 Р 1> Р 2 umax 47
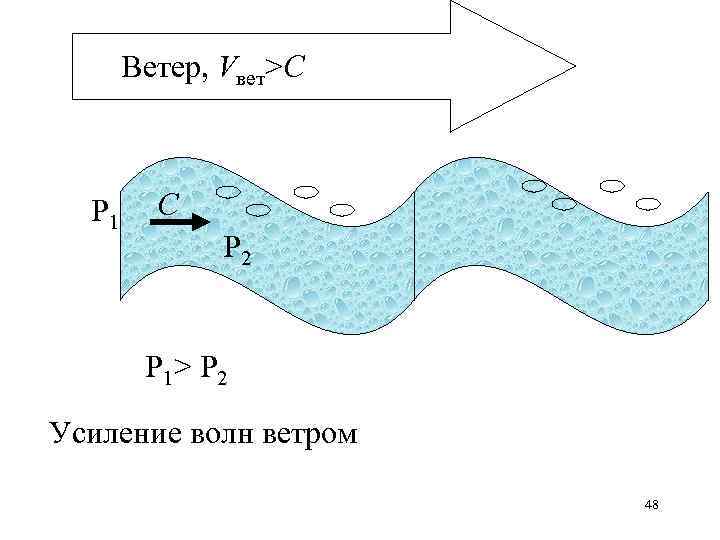 Ветер, Vвет>C Р 1 C Р 2 Р 1> Р 2 Усиление волн ветром 48
Ветер, Vвет>C Р 1 C Р 2 Р 1> Р 2 Усиление волн ветром 48
 49
49
 Для того, чтобы ряд, представляющий комплексный потенциал, соответствовал случаю произвольного безвихревого движения между двумя концентрическими окружностями, к ряду Необходимо прибавить еще член 50
Для того, чтобы ряд, представляющий комплексный потенциал, соответствовал случаю произвольного безвихревого движения между двумя концентрическими окружностями, к ряду Необходимо прибавить еще член 50
 Если A=P+i. Q, то соответствующие выражения для потенциала скорости и функции тока будут: Циклическая константа функции тока 2 Р означает поток через внутреннюю или внешнюю окружности. Циклическая константа потенциала скорости 2 Q означает циркуляцию по некоторой замкнутой кривой, заключающей начало. 51
Если A=P+i. Q, то соответствующие выражения для потенциала скорости и функции тока будут: Циклическая константа функции тока 2 Р означает поток через внутреннюю или внешнюю окружности. Циклическая константа потенциала скорости 2 Q означает циркуляцию по некоторой замкнутой кривой, заключающей начало. 51
 2 a U Цилиндр двигается с постоянной скоростью и вращается с циклической постоянной . Граничные условия будут выполнены, если предположить, что На одной стороне цилиндра скорость больше, а на другой - меньше. Возникает разность давлений. Для поддержания горизонтального движения надо приложить силу в вертикальном 52 направлении.
2 a U Цилиндр двигается с постоянной скоростью и вращается с циклической постоянной . Граничные условия будут выполнены, если предположить, что На одной стороне цилиндра скорость больше, а на другой - меньше. Возникает разность давлений. Для поддержания горизонтального движения надо приложить силу в вертикальном 52 направлении.
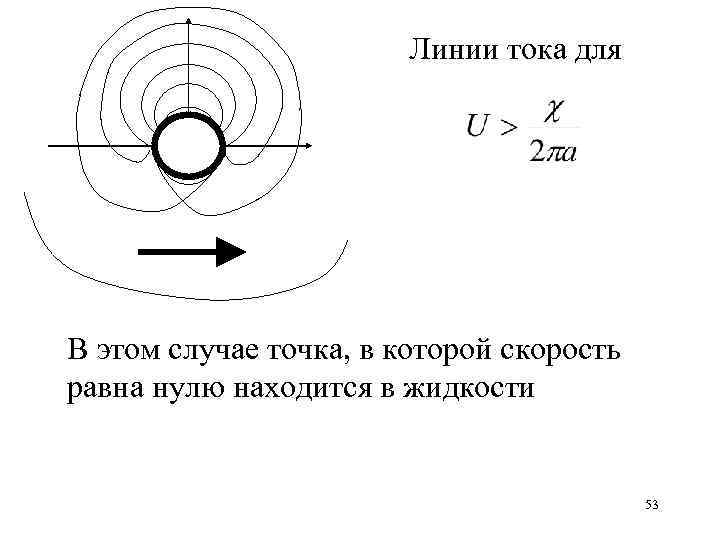 Линии тока для В этом случае точка, в которой скорость равна нулю находится в жидкости 53
Линии тока для В этом случае точка, в которой скорость равна нулю находится в жидкости 53
 54
54
 2 a -U Обтекание вращающегося цилиндра Для r = a Сила действует на цилиндр вдоль вертикальной оси не зависит от радиуса 55
2 a -U Обтекание вращающегося цилиндра Для r = a Сила действует на цилиндр вдоль вертикальной оси не зависит от радиуса 55
 Всякое непрерывное движение жидкости, наполняющей неограниченное пространство и покоящейся в бесконечности, можно рассматривать, как движение, вызванное соответствующим распределением источников и вихрей с конечной плотностью. 56
Всякое непрерывное движение жидкости, наполняющей неограниченное пространство и покоящейся в бесконечности, можно рассматривать, как движение, вызванное соответствующим распределением источников и вихрей с конечной плотностью. 56
 Всякое непрерывное безвихревое циклическое и нециклическое движение несжимаемой жидкости, наполняющей произвольную область, может рассматриваться как движение, вызванное некоторым распределением вихрей по ограничивающей поверхности, которая отделяет область от остального неограниченного пространства. В случае области, простирающейся в бесконечность, это распределение относится к конечной части ограничивающей поверхности при условии, что жидкость покоится в бесконечности. 57
Всякое непрерывное безвихревое циклическое и нециклическое движение несжимаемой жидкости, наполняющей произвольную область, может рассматриваться как движение, вызванное некоторым распределением вихрей по ограничивающей поверхности, которая отделяет область от остального неограниченного пространства. В случае области, простирающейся в бесконечность, это распределение относится к конечной части ограничивающей поверхности при условии, что жидкость покоится в бесконечности. 57


