d6bfdd64a1a9c942e537a41c3336c0ec.ppt
- Количество слайдов: 56
 1
1
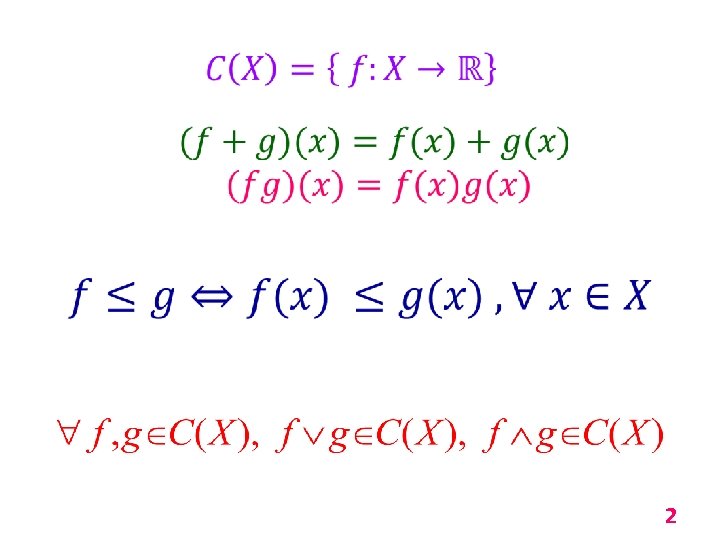 2
2
 Some exceptional properties: 1. Every prime ideal is contained in a unique maximal ideal. 2. Sum of two prime ideals is prime. 3. The prime ideals containing a given prime ideal form a chain. 3
Some exceptional properties: 1. Every prime ideal is contained in a unique maximal ideal. 2. Sum of two prime ideals is prime. 3. The prime ideals containing a given prime ideal form a chain. 3
 4
4
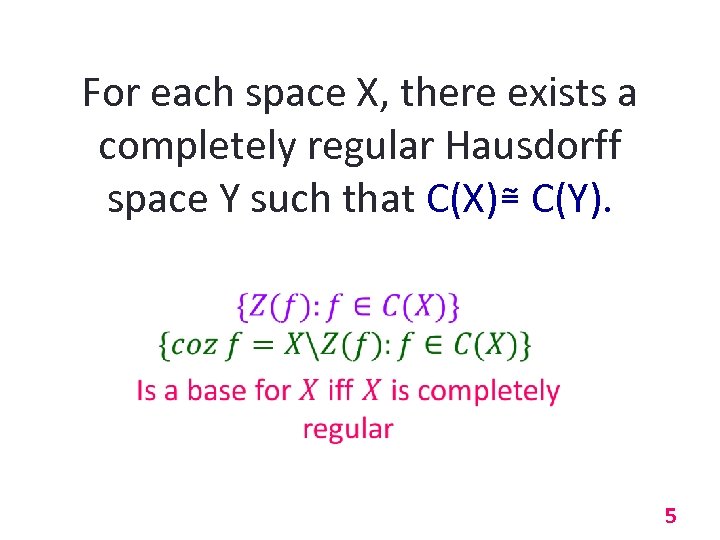 For each space X, there exists a completely regular Hausdorff space Y such that C(X)≅ C(Y). 5
For each space X, there exists a completely regular Hausdorff space Y such that C(X)≅ C(Y). 5
 Major Objective? Elements of C (X ), Ideals of C (X ) • X is connected ⟺ The only idempotents of C(X) are constant functions 0 and 1. 6
Major Objective? Elements of C (X ), Ideals of C (X ) • X is connected ⟺ The only idempotents of C(X) are constant functions 0 and 1. 6
 f∈C(X) is zerodivisor⟺ int Z(f ) ≠ϕ Every element of C(X) is zerodivisor ⟺ X is an almost P-space Problem. Let X be a metric space and A and B be two closed subset of X. If (A⋃B)˚≠ϕ, then either A ˚≠ϕ or B ˚≠ϕ. 7
f∈C(X) is zerodivisor⟺ int Z(f ) ≠ϕ Every element of C(X) is zerodivisor ⟺ X is an almost P-space Problem. Let X be a metric space and A and B be two closed subset of X. If (A⋃B)˚≠ϕ, then either A ˚≠ϕ or B ˚≠ϕ. 7
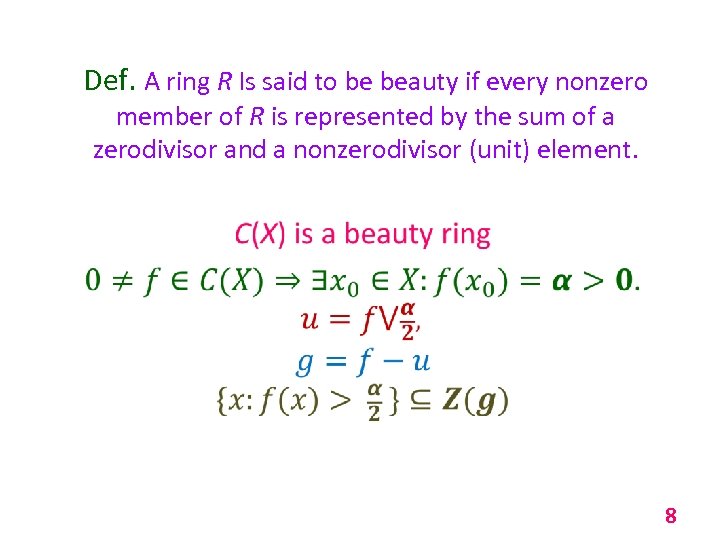 Def. A ring R Is said to be beauty if every nonzero member of R is represented by the sum of a zerodivisor and a nonzerodivisor (unit) element. 8
Def. A ring R Is said to be beauty if every nonzero member of R is represented by the sum of a zerodivisor and a nonzerodivisor (unit) element. 8
 9
9
 ♠. Every member of C(X) can be written as a sum of two zerodivisors 10
♠. Every member of C(X) can be written as a sum of two zerodivisors 10
 i Theorem. C(X) is clean iff X is strongly zero-dimensional. 11
i Theorem. C(X) is clean iff X is strongly zero-dimensional. 11
 Proof: Let X be normal. 12
Proof: Let X be normal. 12
 13
13
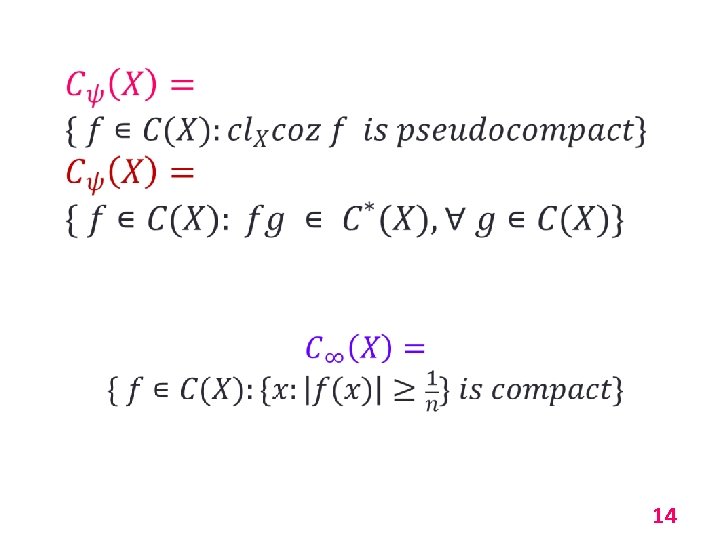 14
14
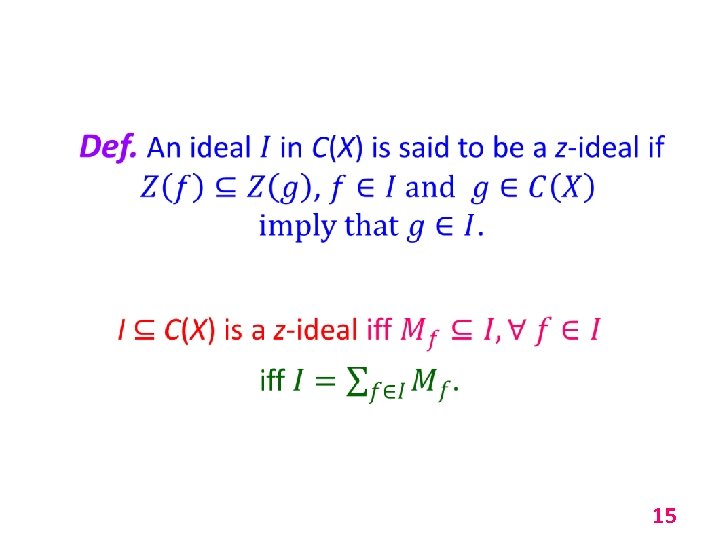 15
15
 1. Every z-ideal is semiprime. 2. Sum of z-ideals is a z-ideal. 3. Sum of a prime ideal and a z-ideal is a prime z-ideal. 4. Prime ideals minimal over a z-ideal are z-ideals. 5. If all prime ideals minimal over an ideal are zideals, then that ideal is also a z-ideal. 6. If a z-ideal contains a prime ideal, then it is a prime ideal. 16
1. Every z-ideal is semiprime. 2. Sum of z-ideals is a z-ideal. 3. Sum of a prime ideal and a z-ideal is a prime z-ideal. 4. Prime ideals minimal over a z-ideal are z-ideals. 5. If all prime ideals minimal over an ideal are zideals, then that ideal is also a z-ideal. 6. If a z-ideal contains a prime ideal, then it is a prime ideal. 16
 Def. An ideal E in a ring R is called essential if it intersects every nonzero ideal nontrivially. • 17
Def. An ideal E in a ring R is called essential if it intersects every nonzero ideal nontrivially. • 17
 18
18
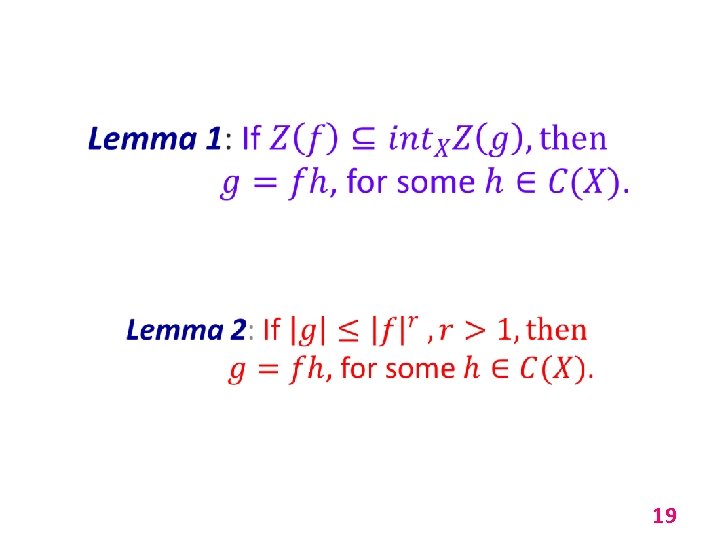 19
19
 20
20
 21
21
 22
22
 23
23
 24
24
 THANKS 25
THANKS 25
 26
26
 z-ideals E. Hewitt, Rings of real-valued continuous unctions, I, Trans. Amer. Math. Soc. 4(1948), 54 -99 27
z-ideals E. Hewitt, Rings of real-valued continuous unctions, I, Trans. Amer. Math. Soc. 4(1948), 54 -99 27
 28
28
 1 - Every ideal in C(X) is a z-ideal 2 - C(X) is a regular ring 3 - X is a P-space (Gillman-Henriksen) Whenever X is compact, then every prime z-ideal is either minimal or maximal if and only if X is the union of a finite number one-point compactification of discrete spaces. (Henriksen, Martinez and Woods) 29
1 - Every ideal in C(X) is a z-ideal 2 - C(X) is a regular ring 3 - X is a P-space (Gillman-Henriksen) Whenever X is compact, then every prime z-ideal is either minimal or maximal if and only if X is the union of a finite number one-point compactification of discrete spaces. (Henriksen, Martinez and Woods) 29
![[1] C. W. Kohls, Ideals in rings of continuous functions, Fund. Math. 45(1957), 28 [1] C. W. Kohls, Ideals in rings of continuous functions, Fund. Math. 45(1957), 28](https://present5.com/presentation/d6bfdd64a1a9c942e537a41c3336c0ec/image-30.jpg) [1] C. W. Kohls, Ideals in rings of continuous functions, Fund. Math. 45(1957), 28 -50 [2] C. W. Kohls, Prime ideals in rings of continuous functions, Illinois J. Math. 2(1958), 505 -536. [3] C. W. Kohls, Prime ideals in rings of continuous functions, II, Duke Math. J. 25(1958), 447 -458. Properties of z-ideals in C(X): Every z-ideal in C(X) is semi prime. Sum of z-ideals is a z-ideal. (Gillman, Jerison)(Rudd) Sum of two prime ideal is a prime (Kohls) z-ideal or all of C(X). (Mason) Sum of a prime ideal and a z-ideal is a prime z-ideal or all of C(X). (Mason) Prime ideals minimal over a z-ideal is a z-ideal. (Mason) If all prime ideals minimal over an ideal in C(X) are z-ideals, that ideal is also a z -ideal. (Mullero+ Azarpanah, Mohamadian) Prime ideals in C(X) containing a given prime ideal form a chain. (Kohls) If a z-i. Ideal in C(X) contains a prime ideal, then it is a prime ideal. (Kohls) 30
[1] C. W. Kohls, Ideals in rings of continuous functions, Fund. Math. 45(1957), 28 -50 [2] C. W. Kohls, Prime ideals in rings of continuous functions, Illinois J. Math. 2(1958), 505 -536. [3] C. W. Kohls, Prime ideals in rings of continuous functions, II, Duke Math. J. 25(1958), 447 -458. Properties of z-ideals in C(X): Every z-ideal in C(X) is semi prime. Sum of z-ideals is a z-ideal. (Gillman, Jerison)(Rudd) Sum of two prime ideal is a prime (Kohls) z-ideal or all of C(X). (Mason) Sum of a prime ideal and a z-ideal is a prime z-ideal or all of C(X). (Mason) Prime ideals minimal over a z-ideal is a z-ideal. (Mason) If all prime ideals minimal over an ideal in C(X) are z-ideals, that ideal is also a z -ideal. (Mullero+ Azarpanah, Mohamadian) Prime ideals in C(X) containing a given prime ideal form a chain. (Kohls) If a z-i. Ideal in C(X) contains a prime ideal, then it is a prime ideal. (Kohls) 30
 31
31
![[1] L. Gillman, M. Henriksen and M. Jerison, On a theorem of Gelfand Kolmogoroff [1] L. Gillman, M. Henriksen and M. Jerison, On a theorem of Gelfand Kolmogoroff](https://present5.com/presentation/d6bfdd64a1a9c942e537a41c3336c0ec/image-32.jpg) [1] L. Gillman, M. Henriksen and M. Jerison, On a theorem of Gelfand Kolmogoroff concerning maximal ideals in rings of continuous functions, Proc. Amer. Math. Soc. 5(1954), 447 -455. [2] T. Shirota, A class of topological spaces, Osaka Math. J. 4(1952), 23 -40. Question: Is the sum of every two closed ideals in C(X) a closed ideal? 32
[1] L. Gillman, M. Henriksen and M. Jerison, On a theorem of Gelfand Kolmogoroff concerning maximal ideals in rings of continuous functions, Proc. Amer. Math. Soc. 5(1954), 447 -455. [2] T. Shirota, A class of topological spaces, Osaka Math. J. 4(1952), 23 -40. Question: Is the sum of every two closed ideals in C(X) a closed ideal? 32
 33
33
 Relative z-ideals rez-ideals F. Azarpanah and A. Taherifar, Relative z-ideals in C(X), Topology Appl. 156(2009), 1711 -1717. So relative z-ideals are also bridges 34
Relative z-ideals rez-ideals F. Azarpanah and A. Taherifar, Relative z-ideals in C(X), Topology Appl. 156(2009), 1711 -1717. So relative z-ideals are also bridges 34
![[1] C. B. Huijsmans and Depagter, on z-ideals and d-ideals in Riesz spaces I, [1] C. B. Huijsmans and Depagter, on z-ideals and d-ideals in Riesz spaces I,](https://present5.com/presentation/d6bfdd64a1a9c942e537a41c3336c0ec/image-35.jpg) [1] C. B. Huijsmans and Depagter, on z-ideals and d-ideals in Riesz spaces I, Indag. Math. 42(A 83)(1980), 183 -195. [2] G. Mason, z-ideals and quotient rings of reduced rings, Math. Japon. 34(6)(1989), 941 -956. [3] S. Larson, Sum of semiprime, z and d l-ideals in class of f-rings, Proc. Amer. Math. Sco. 109(4)(1990), 895 -901. 35
[1] C. B. Huijsmans and Depagter, on z-ideals and d-ideals in Riesz spaces I, Indag. Math. 42(A 83)(1980), 183 -195. [2] G. Mason, z-ideals and quotient rings of reduced rings, Math. Japon. 34(6)(1989), 941 -956. [3] S. Larson, Sum of semiprime, z and d l-ideals in class of f-rings, Proc. Amer. Math. Sco. 109(4)(1990), 895 -901. 35
 36
36
 37
37
![[1] F. Azarpanah, O. A. S. Karamzadeh and A. Rezaei Aliabad, On ideal consisting [1] F. Azarpanah, O. A. S. Karamzadeh and A. Rezaei Aliabad, On ideal consisting](https://present5.com/presentation/d6bfdd64a1a9c942e537a41c3336c0ec/image-38.jpg) [1] F. Azarpanah, O. A. S. Karamzadeh and A. Rezaei Aliabad, On ideal consisting entirely zero divisors, Comm. Algebra, 28(2)(2000), 1061 -1073. [2] G. Mason, Prime ideals and quotient of reduced rings, Math. Japon. 34(6)(1989), 941 -956. [3] F. Azarpanah and M. Karavan, On nonregular ideals and z 0–ideals in C(X), Cech. Math. J. 55(130)(2005), 397 -407. 38
[1] F. Azarpanah, O. A. S. Karamzadeh and A. Rezaei Aliabad, On ideal consisting entirely zero divisors, Comm. Algebra, 28(2)(2000), 1061 -1073. [2] G. Mason, Prime ideals and quotient of reduced rings, Math. Japon. 34(6)(1989), 941 -956. [3] F. Azarpanah and M. Karavan, On nonregular ideals and z 0–ideals in C(X), Cech. Math. J. 55(130)(2005), 397 -407. 38
 39
39
![[F. Azarpanah and R. Mohamadian] 40 [F. Azarpanah and R. Mohamadian] 40](https://present5.com/presentation/d6bfdd64a1a9c942e537a41c3336c0ec/image-40.jpg) [F. Azarpanah and R. Mohamadian] 40
[F. Azarpanah and R. Mohamadian] 40
![Let X be a quasi space: Questions: [3] F. Azarpanah and M. Karavan, On Let X be a quasi space: Questions: [3] F. Azarpanah and M. Karavan, On](https://present5.com/presentation/d6bfdd64a1a9c942e537a41c3336c0ec/image-41.jpg) Let X be a quasi space: Questions: [3] F. Azarpanah and M. Karavan, On nonregular ideals and z 0– ideals in C(X), Cech. Math. J. 55(130)(2005), 397 -407. 41
Let X be a quasi space: Questions: [3] F. Azarpanah and M. Karavan, On nonregular ideals and z 0– ideals in C(X), Cech. Math. J. 55(130)(2005), 397 -407. 41
 Essential (large) ideals Uniform (Minimal) ideals The Socle of C(X) Socle of R = S(R) = Intersection of essential ideals = Sum of uniform ideals of R 42
Essential (large) ideals Uniform (Minimal) ideals The Socle of C(X) Socle of R = S(R) = Intersection of essential ideals = Sum of uniform ideals of R 42
 43
43
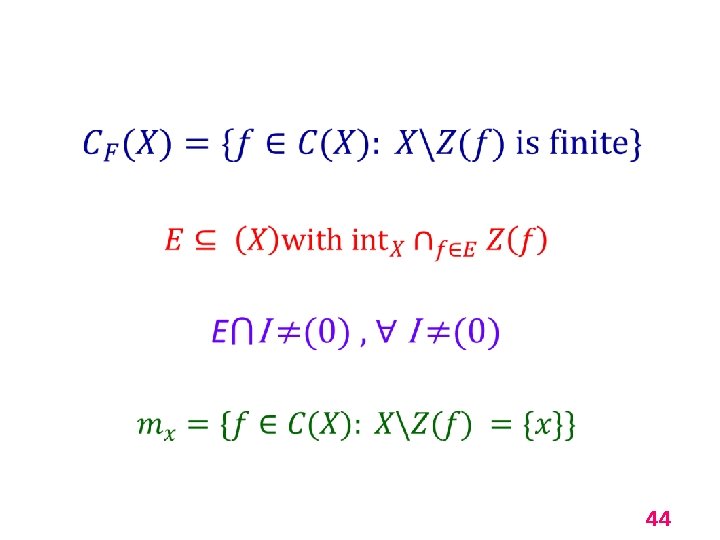 44
44
 * When is the socle of C(X) an essential ideal? Fact: (a) The socle of C(X) is essential iff the set of isolated points of X is dense in X. (b) Every intersection of essential ideals of C(X) is essential iff the set of isolated points of X is dense in X. 45
* When is the socle of C(X) an essential ideal? Fact: (a) The socle of C(X) is essential iff the set of isolated points of X is dense in X. (b) Every intersection of essential ideals of C(X) is essential iff the set of isolated points of X is dense in X. 45
 46
46
![[1] F. Azarpanah, Essential ideals in C(X), Period. Math. Hungar. , 31(2)(1995), 105 -112. [1] F. Azarpanah, Essential ideals in C(X), Period. Math. Hungar. , 31(2)(1995), 105 -112.](https://present5.com/presentation/d6bfdd64a1a9c942e537a41c3336c0ec/image-47.jpg) [1] F. Azarpanah, Essential ideals in C(X), Period. Math. Hungar. , 31(2)(1995), 105 -112. [2] F. Azarpanah, Intersection of essential ideals in C(X), Proc. Amer. Math. Soc. 125(1997), 2149 -2154. [3] O. A. S. Karamzadeh and M. Rostami, On intrinsic topology and some related ideals of C(X), Proc. Amer. Math. Soc. 93(1985), 73 -84. 47
[1] F. Azarpanah, Essential ideals in C(X), Period. Math. Hungar. , 31(2)(1995), 105 -112. [2] F. Azarpanah, Intersection of essential ideals in C(X), Proc. Amer. Math. Soc. 125(1997), 2149 -2154. [3] O. A. S. Karamzadeh and M. Rostami, On intrinsic topology and some related ideals of C(X), Proc. Amer. Math. Soc. 93(1985), 73 -84. 47
 # Every factor ring of C(X) modulo a principal ideal contains a nonessential prime ideal iff X is an almost P-space with a dense set of isolated points. 48
# Every factor ring of C(X) modulo a principal ideal contains a nonessential prime ideal iff X is an almost P-space with a dense set of isolated points. 48
 F. Azarpanah, O. A. S. Karamzadeh and S. Rahmati, C(X) vs. C(X) modulo its socle, Colloquium Math. 111(2)(2008), 315 -365. F. Azarpanah, S. Afrooz and O. A. S. Karamzadeh, Goldie dimension of rings of fractions of C(X), submitted. Clean elements Clean ideals An element of a ring R is called clean if it is the sum of a unit and an idempotent. A subset S of R is called clean if each element of S is clean. 49
F. Azarpanah, O. A. S. Karamzadeh and S. Rahmati, C(X) vs. C(X) modulo its socle, Colloquium Math. 111(2)(2008), 315 -365. F. Azarpanah, S. Afrooz and O. A. S. Karamzadeh, Goldie dimension of rings of fractions of C(X), submitted. Clean elements Clean ideals An element of a ring R is called clean if it is the sum of a unit and an idempotent. A subset S of R is called clean if each element of S is clean. 49
 W. K. Nicholson, Lifting idempotents and exchange rings, Trans. Amer. Math. Soc. 229(1977), 269 -278. R. B. Warfield, A krull-Scmidt theorem for infinite sum of modules, Proc. Amer. Math. Soc. 22(1969), 460 -465. C(X) is clean iff C(X) is an exchange ring. 50
W. K. Nicholson, Lifting idempotents and exchange rings, Trans. Amer. Math. Soc. 229(1977), 269 -278. R. B. Warfield, A krull-Scmidt theorem for infinite sum of modules, Proc. Amer. Math. Soc. 22(1969), 460 -465. C(X) is clean iff C(X) is an exchange ring. 50
 X is strongly zero dimensional if every functionally open cover of X has an open refinement with disjoint members. 51
X is strongly zero dimensional if every functionally open cover of X has an open refinement with disjoint members. 51
 Th. The following statements are equivalent: 1. C(X) is a clean ring. 2. C*(X) is a clean ring. 3. The set of clean elements of C(X) is a subring. 4. X is strongly zero-dimensional. 5. Every zerodivisor element is clean. 6. C(X) has a clean prime ideal. 52
Th. The following statements are equivalent: 1. C(X) is a clean ring. 2. C*(X) is a clean ring. 3. The set of clean elements of C(X) is a subring. 4. X is strongly zero-dimensional. 5. Every zerodivisor element is clean. 6. C(X) has a clean prime ideal. 52
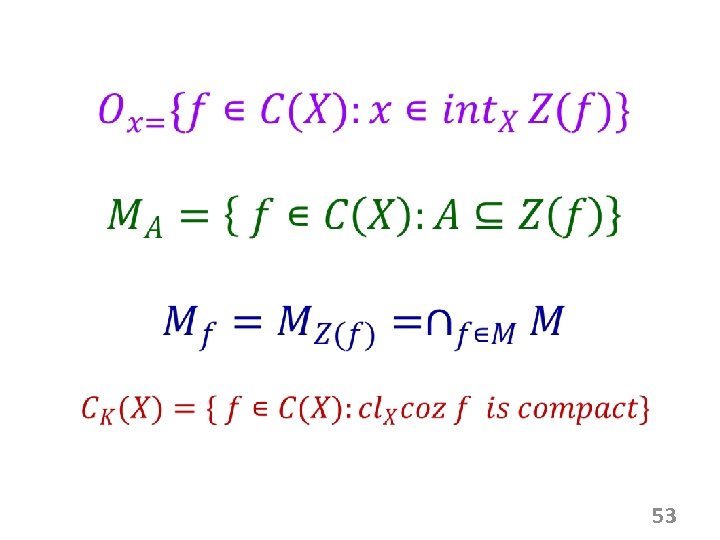 53
53
 F. Azarpanah, When is C(X) a clean ring? Acta Math. Hungar. 94(1 -2)(2002), 53 -58 54
F. Azarpanah, When is C(X) a clean ring? Acta Math. Hungar. 94(1 -2)(2002), 53 -58 54
 J. Martinez and E. R. Zenk, Yosida frames, J. pure Appl. Algebra, 204(2006), 473 -492. 55
J. Martinez and E. R. Zenk, Yosida frames, J. pure Appl. Algebra, 204(2006), 473 -492. 55
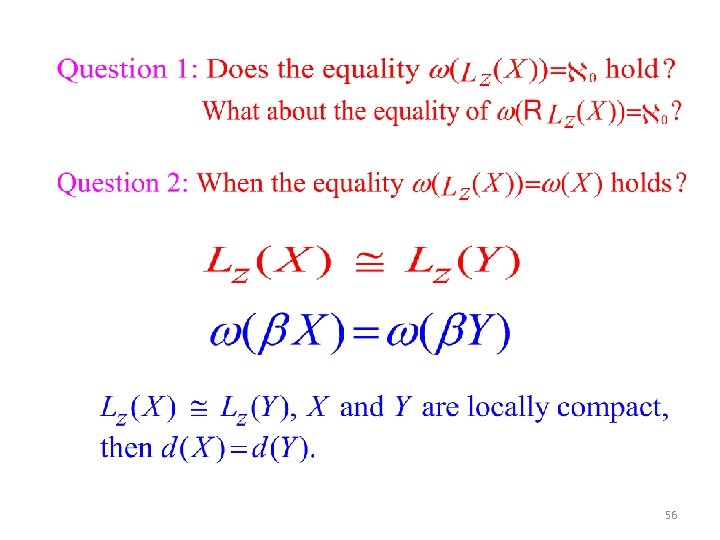 56
56


