1
2
Пусть движение происходит в плоскости х, у. Вихревые линии являются прямыми, параллельными оси z. Решение этого уравнения дает значение ψ в точке (х, у): - значение в точке , а 3
Добавочная функция 0 есть какое-либо решение однородного уравнения и позволяет удовлетворить граничным условиям. В случае безграничной жидкости, которая покоится на бесконечности 0 сводится к постоянной. 4
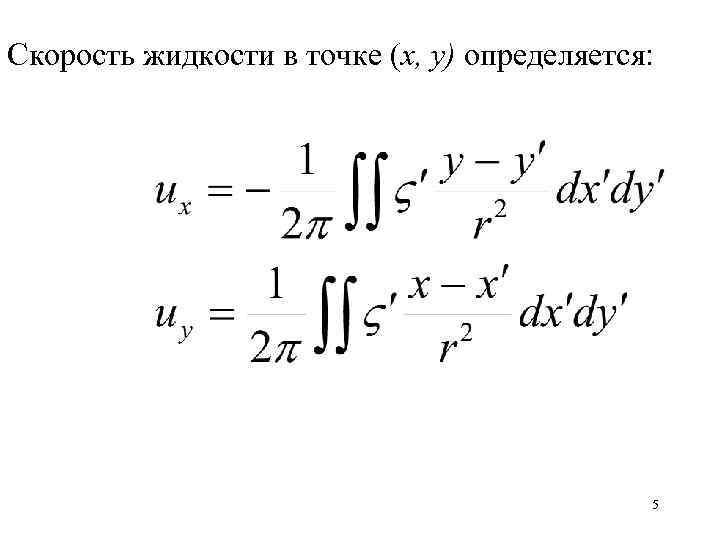Скорость жидкости в точке (х, у) определяется: 5
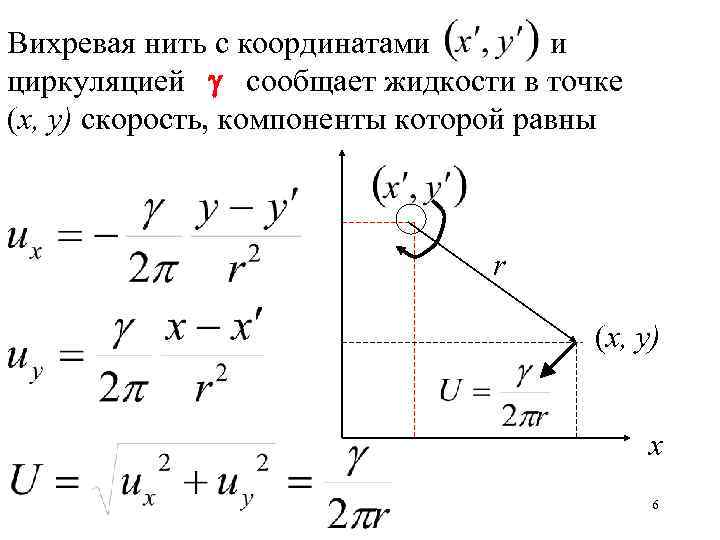Вихревая нить с координатами и циркуляцией сообщает жидкости в точке (х, у) скорость, компоненты которой равны r (х, у) х 6
Вычислим интегралы: - интегрирование распространяется на всю область, где Интегрирование по поверхности каждый раз распространяется по сечению всех вихрей 7
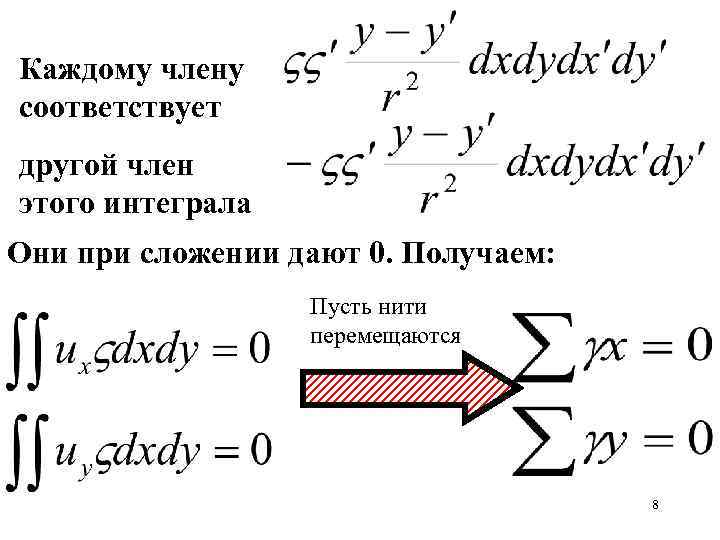Каждому члену соответствует другой член этого интеграла Они при сложении дают 0. Получаем: Пусть нити перемещаются 8
Так как напряжение каждого вихря от времени не зависит, то точка с координатами в течение всего времени остается неподвижной. Эту точку можно назвать центром системы вихрей, а прямую, параллельную оси z, проходящую через эту точку, - осью системы. Если , то центр лежит в бесконечности. 9
Одна вихревая нить в точке (х, у), вектор вихря внутри бесконечно малого сечения имеет постоянное значение Где центр системы ? у r х Центр одиночного вихря не смещается во времени. 10
Внутри круга радиуса а жидкость вращается как твердое тело с угловой скоростью . Определить скорость вне круга. у а r х На границе вихря скорость равна a. 11
r Две параллельные прямые вихревые нити в точках z 1 и z 2. Показать, что нити всегда сохраняют одинаковое расстояние друг от друга и вращаются с постоянной угловой скоростью вокруг общего центра С. Пусть циркуляция одной нити равна 1 , а второй 2. 12 Запишите комплексный потенциал для 2 нитей.
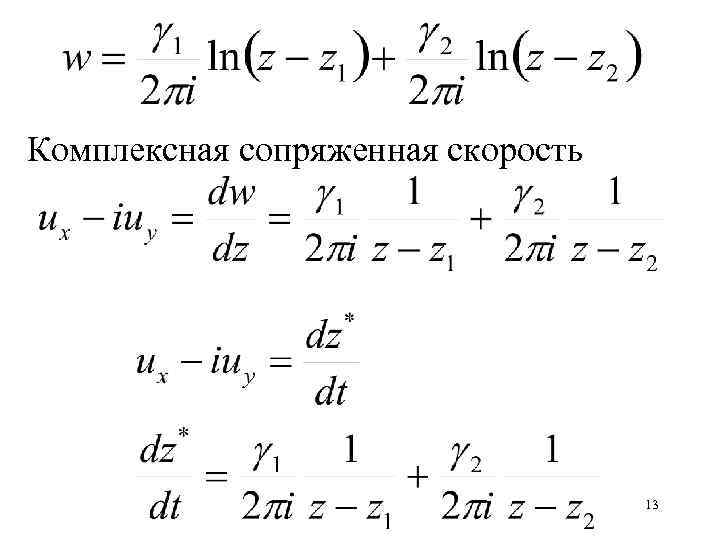Комплексная сопряженная скорость 13
Скорость первого вихря в точке z 1 (сам на себя не действует) Скорость второго вихря в точке z 2 Отделяем мнимые и действительные части. Обозначим расстояние между вихрями 14
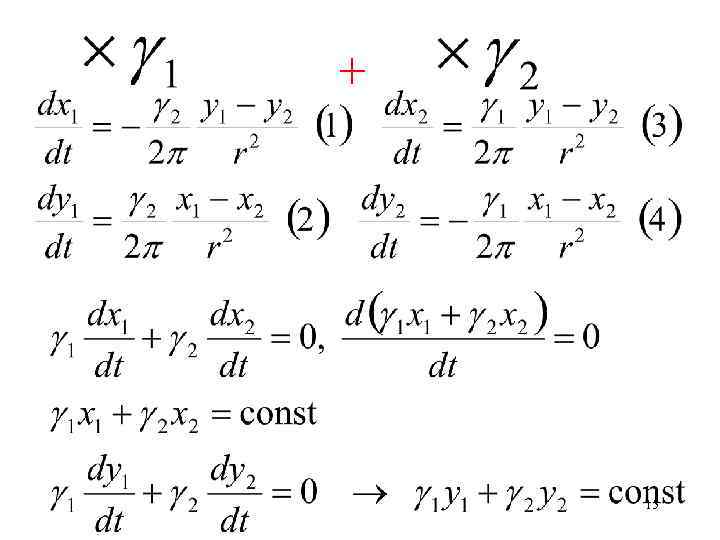+ 15
Получаем интеграл движения центра инерции системы двух вихрей Точка С с координатами Остается неподвижной во все время движения 16
• Получим расстояние между вихрями 17
Вычитаем из первого третье уравнение, из второго – четвертое. 18
Интегрируем и получаем: Расстояние между вихрями не меняется в процессе перемещения 19
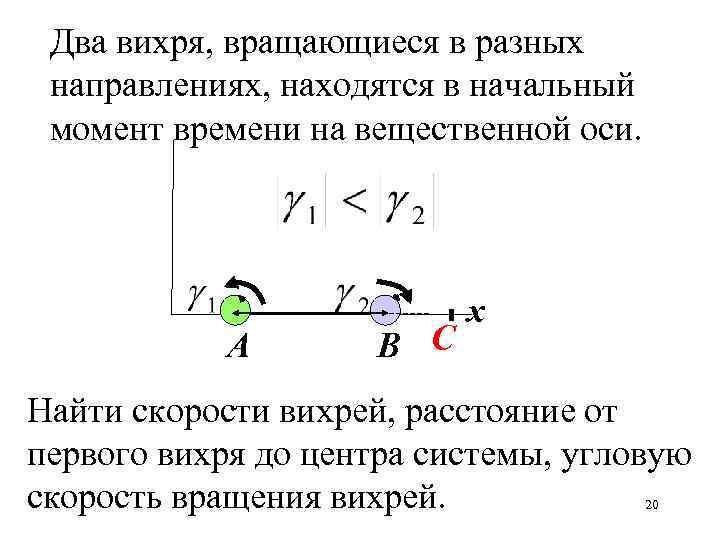Два вихря, вращающиеся в разных направлениях, находятся в начальный момент времени на вещественной оси. A B С x Найти скорости вихрей, расстояние от первого вихря до центра системы, угловую скорость вращения вихрей. 20
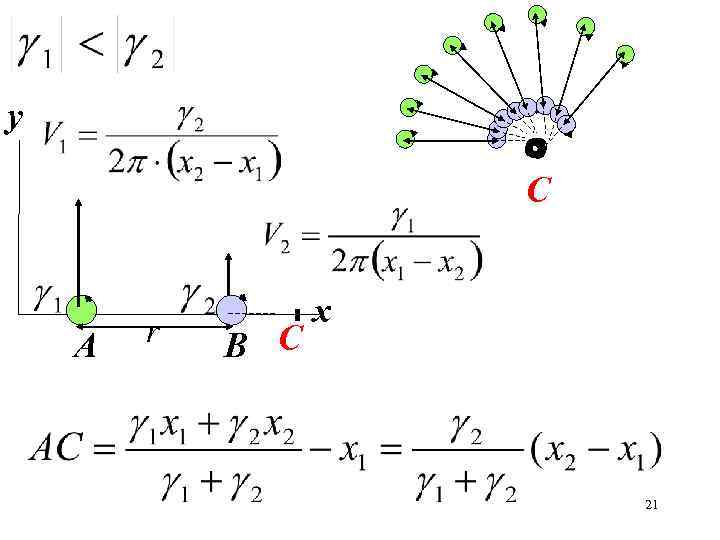y O O O O С A r B С x 21
Угловая скорость вращения вихрей вокруг центра С Показать, что угловые скорости вихрей равны Где будет точка С, если вихри вращаются в одном направлении? 22
Как будут двигаться 2 вихря радиуса а, если они имеют циркуляцию разного знака, но одинаковую по модулю? Вихри вращаются как твердое тело. 23
Движение двух вихрей с противоположным направлением вращения и А а В С АС= V 1=V 2= Вихри двигаются по прямой с одинаковой скоростью 24
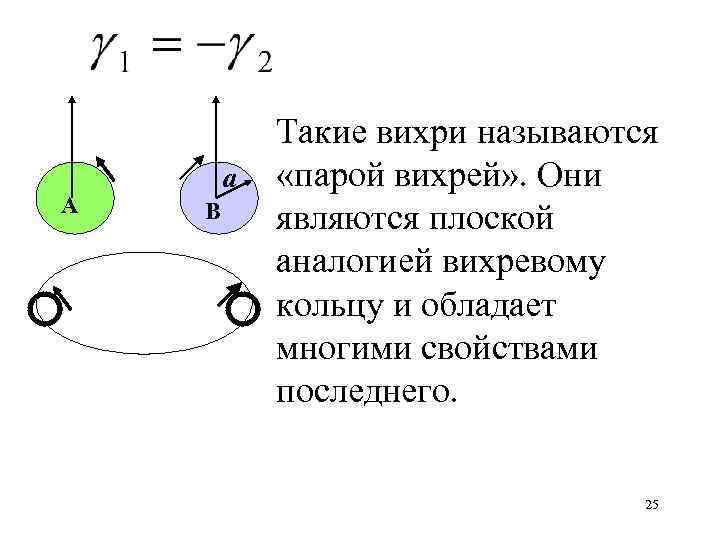А а В Такие вихри называются «парой вихрей» . Они являются плоской аналогией вихревому кольцу и обладает многими свойствами последнего. 25
Куда двигается кольцевой вихрь? 26
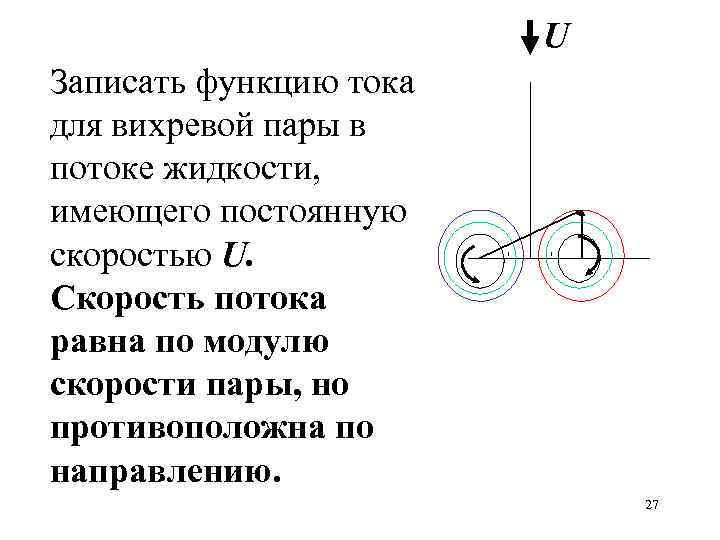U Записать функцию тока для вихревой пары в потоке жидкости, имеющего постоянную скоростью U. Скорость потока равна по модулю скорости пары, но противоположна по направлению. 27
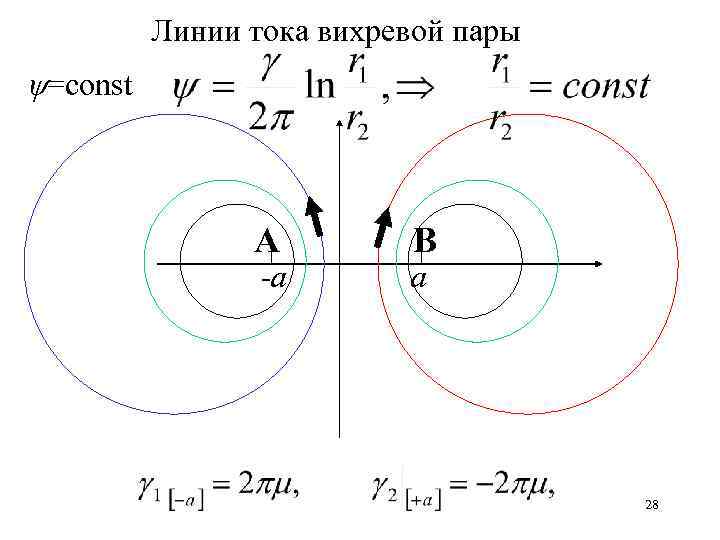Линии тока вихревой пары =const А -а В а 28
Функция тока для течения, имеющего постоянную скорость вдоль оси ординат 29
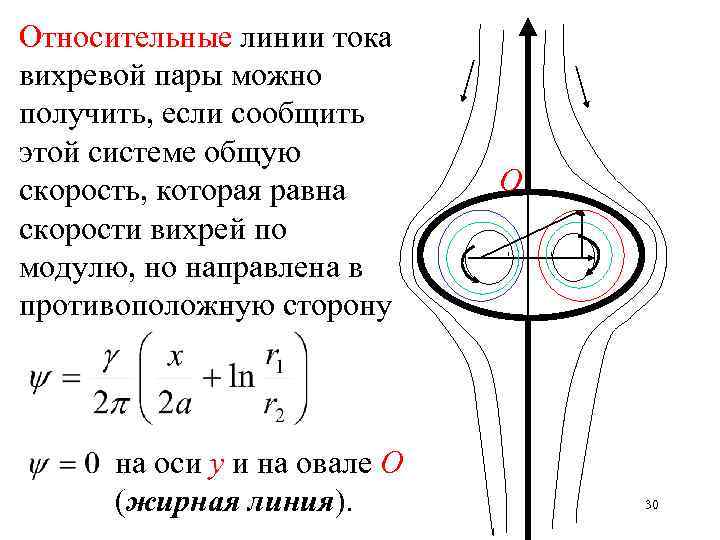Относительные линии тока вихревой пары можно получить, если сообщить этой системе общую скорость, которая равна скорости вихрей по модулю, но направлена в противоположную сторону на оси у и на овале О (жирная линия). О 30
Жидкость внутри овала С движется вместе с вихрями. Жидкость вне овала С обтекает этот овал как твердый цилиндр. Полуоси овала С приблизительно имеют длину 2. 09 а и 1. 73 а. 31
Найти в ортогональной системе координат уравнения линий тока для 1) случая двух вихрей одинаковой интенсивности 2) пары вихрей 32
z 2 z 1 На линии тока 33
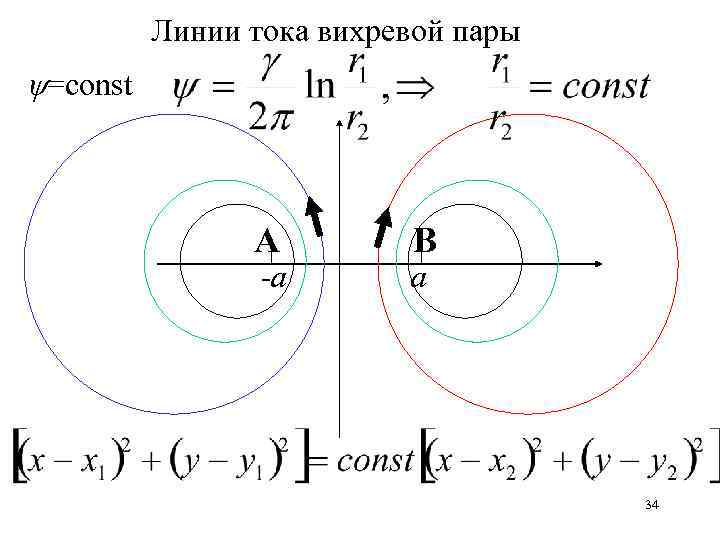Линии тока вихревой пары =const А -а В а 34
а 35
Найти скорость перемещения вихря у твердой стенки 36
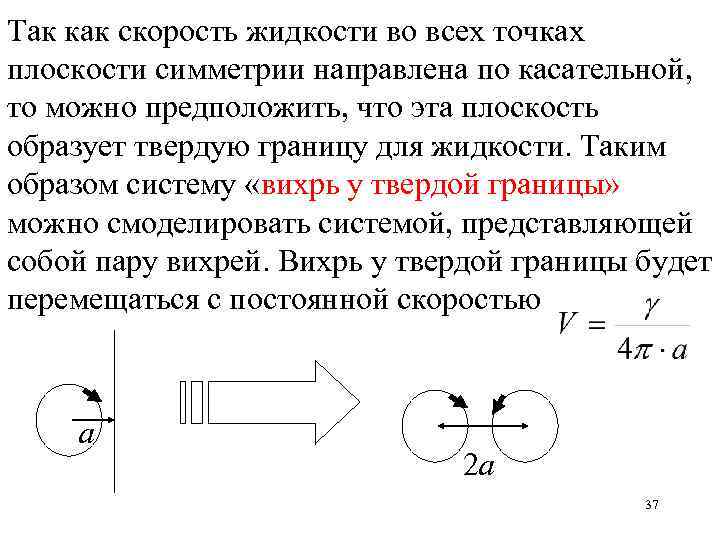Так как скорость жидкости во всех точках плоскости симметрии направлена по касательной, то можно предположить, что эта плоскость образует твердую границу для жидкости. Таким образом систему «вихрь у твердой границы» можно смоделировать системой, представляющей собой пару вихрей. Вихрь у твердой границы будет перемещаться с постоянной скоростью а 2 а 37
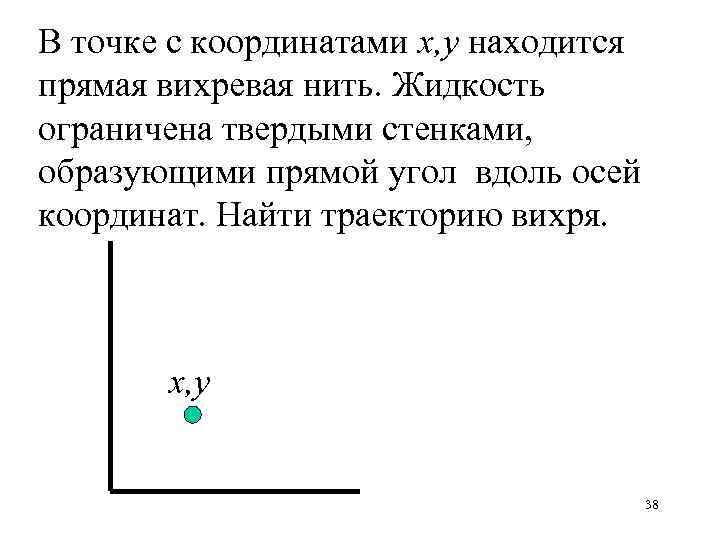В точке с координатами х, у находится прямая вихревая нить. Жидкость ограничена твердыми стенками, образующими прямой угол вдоль осей координат. Найти траекторию вихря. x, y 38
Так как циркуляция скорости вихря постоянна, то течение стационарно. В этом случае траектория вихря совпадает с линией тока, проходящей через точку (x, y) Для того, чтобы описать влияние стенки, расположенной вдоль мнимой оси, поместим вихрь той же интенсивности, но с противоположным знаком циркуляции в точку (-x, y ) (отразим вихрь) 39
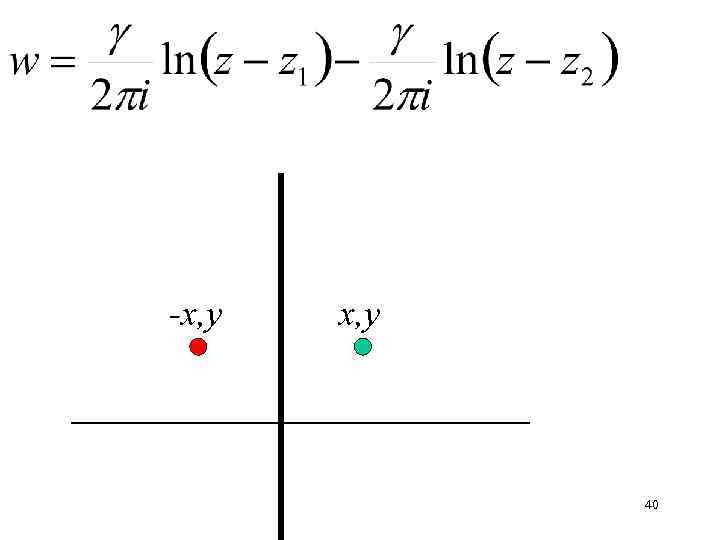-x, y 40
Для того, чтобы описать влияние стенки, расположенной вдоль действительной оси, поместим вихри той же интенсивности, но с противоположными знаками циркуляции в точки (-x, -y ) и (x, -y ) 41
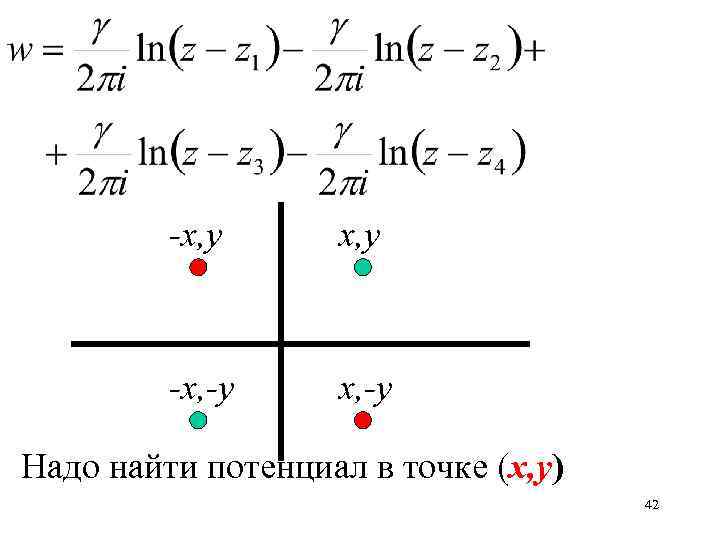-x, y -x, -y Надо найти потенциал в точке (x, y) 42
На линии тока =const, т. е. 43
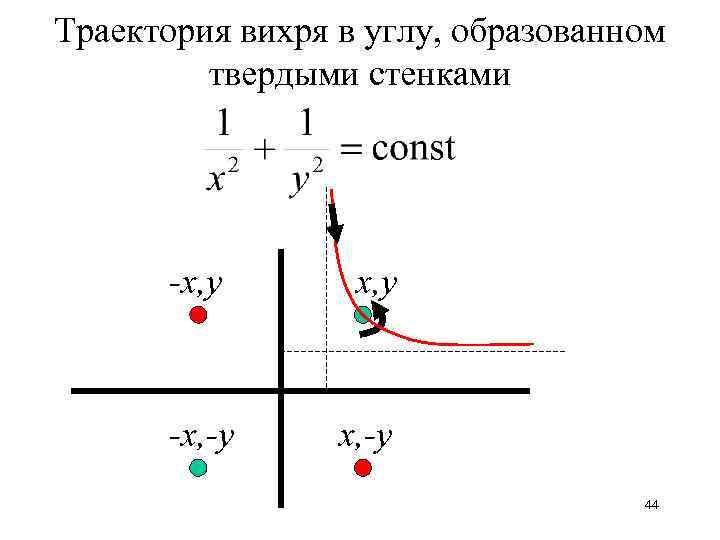Траектория вихря в углу, образованном твердыми стенками -x, y -x, -y 44
n точечных вихрей, расположенных в точках z 1, …, zn и имеющих интенсивности 1, …, n Комплексный потенциал Комплексная скорость Записать уравнение движения вихря в точке zp (k=p) 45
Уравнение движения вихря в точке zp (k=p) Умножая на p zp и суммируя по переменной p от 1 до n, получаем Отделить мнимую и действительную части 46
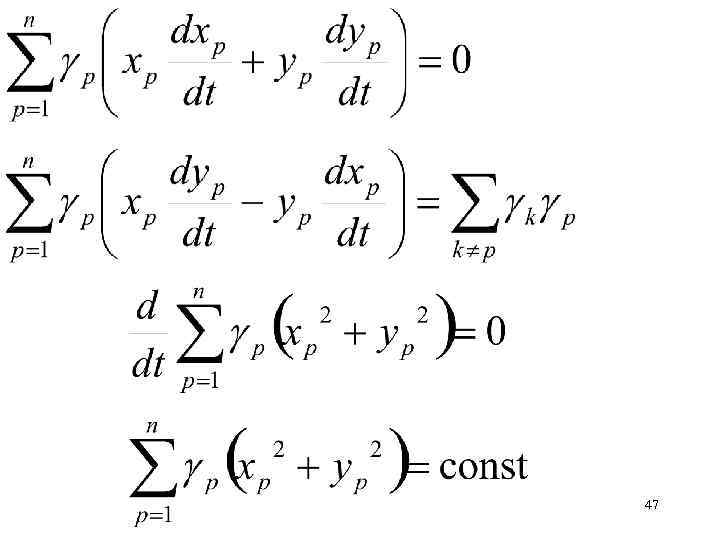47
Сумма моментов инерции масс p относительно начала координат не меняется со временем 48
49
50
51
52
53
54
55
56
57
58
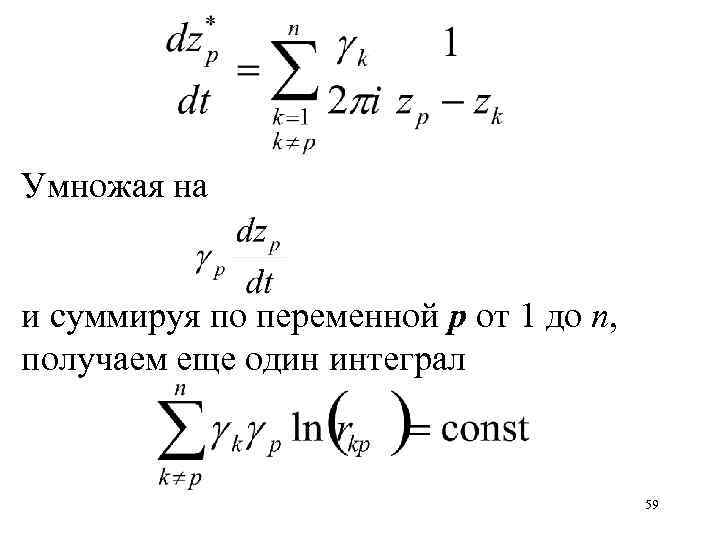Умножая на и суммируя по переменной p от 1 до n, получаем еще один интеграл 59
60
Экспериментальные данные показывают, что диаметр вихрей спутников примерно в три-четыре раза меньше диаметра основного вихря в момент формирования 61
62
Конец третьего перелета вихря Т=0. 82 с s=1. 7 см 2 a=0. 16 см 63
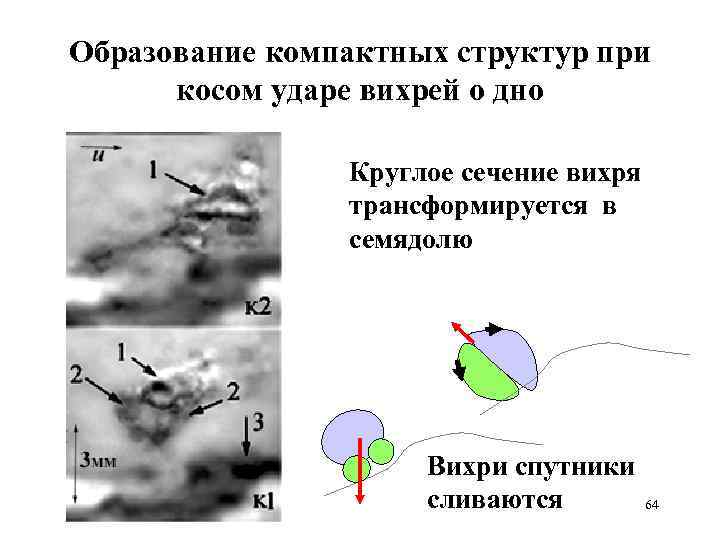Образование компактных структур при косом ударе вихрей о дно Круглое сечение вихря трансформируется в семядолю Вихри спутники сливаются 64
4 3 ? ? Возможно вихри спутники слились в один вихрь и возникла компактная пара 2 1 65
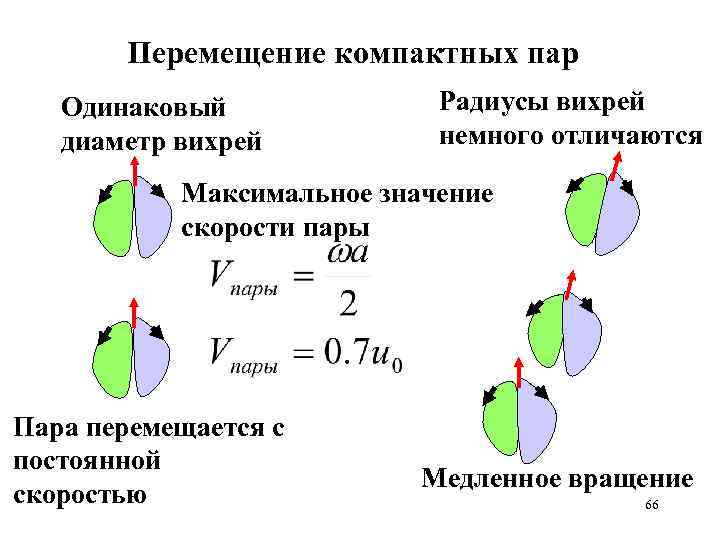Перемещение компактных пар Одинаковый диаметр вихрей Радиусы вихрей немного отличаются Максимальное значение скорости пары Пара перемещается с постоянной скоростью Медленное вращение 66
Компактные вихревые структуры поднимаются вверх с постоянной скоростью 67
Формирование диполя - некомпактной структуры из двух вихрей 68
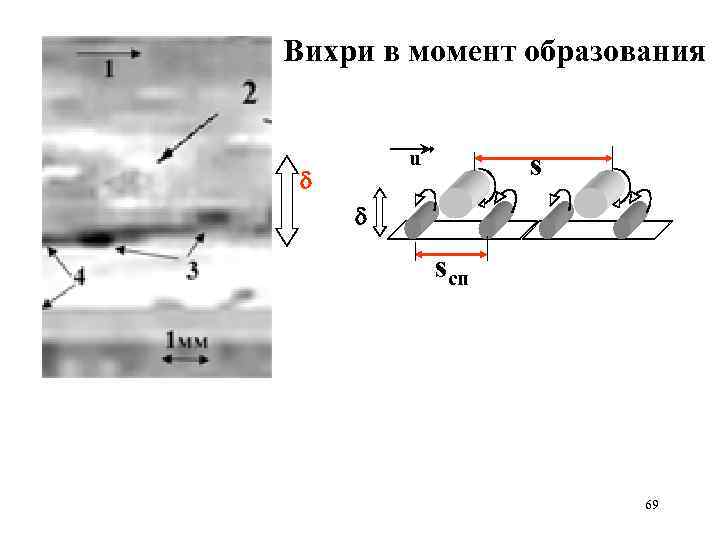Вихри в момент образования u s sсп 69
Взаимодействие вихрей одного знака в однородной жидкости вблизи подстилающей поверхности s a Если s/a<5. 7, то вихри сближаются и сливаются в один вихрь Егоров О. В. , Мартынов С. Л. , Мельникова О. Н. Влияние волнового характера скорости потока в придонном слое на формирование вихрей. // Известия РАН, серия физическая. 2002. Т. 66. № 12. 70
Формирование диполя асп=0. 35 мм sсп=2 мм 3 - основной вихрь, 4 - спутники направление потока диполь кадр 2 а = 0. 5 мм 1. 4 мм дно кадр 1 Т=0. 15 с s=0. 4 см 71
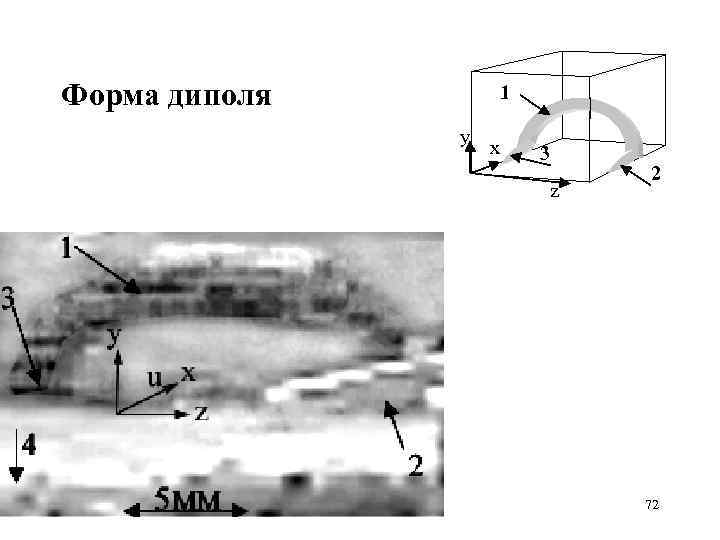Форма диполя 1 y x 3 z 2 72
Вихри в диполе сохраняют круглое сечение 73
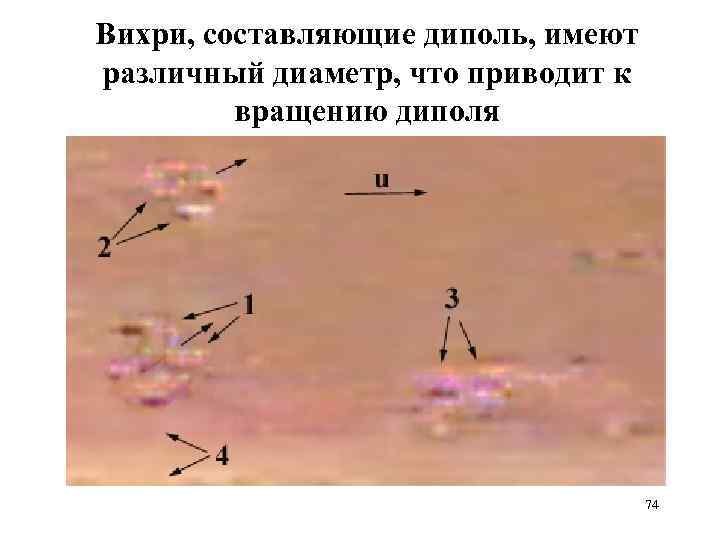Вихри, составляющие диполь, имеют различный диаметр, что приводит к вращению диполя 74
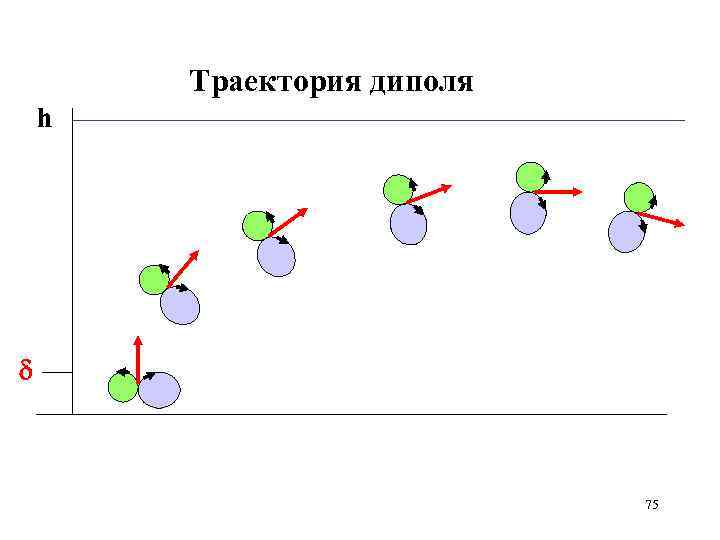Траектория диполя h 75
Максимальная скорость подъема диполя Максимальная горизонтальная скорость диполя Еречнев Д. А. , Еречнева К. В. , Жмур В. В. , Мельникова О. Н. Влияние когерентных структур на коэффициент турбулентного трения в тормозящихся потоках воды и воздуха. // Известия РАН. Физика океана и атмосферы. 76 2003. Т. 39. № 1.
Рассмотрим поток, в котором параметры вихрей сильно меняются за время перелета Расстояние между вихрями спутниками sсп >5. 7 асп 77
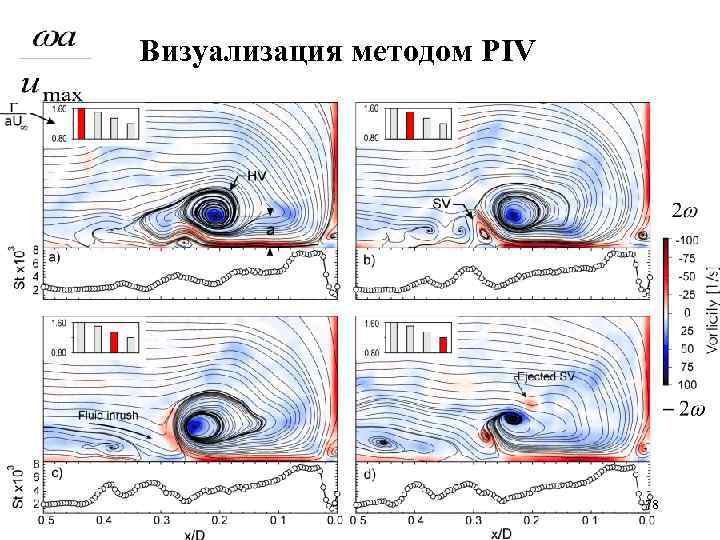Визуализация методом PIV 78
Отрыв вихря спутника в верхней части траектории основного вихря s = 1. 4 cм а = 1. 5 мм 79
Отрыв вихря спутника в верхней части траектории основного вихря Расстояние между вихрями спутниками sсп >5. 7 асп 1 перелет max x max Горизонтальная скорость вихря спутника uфон 80
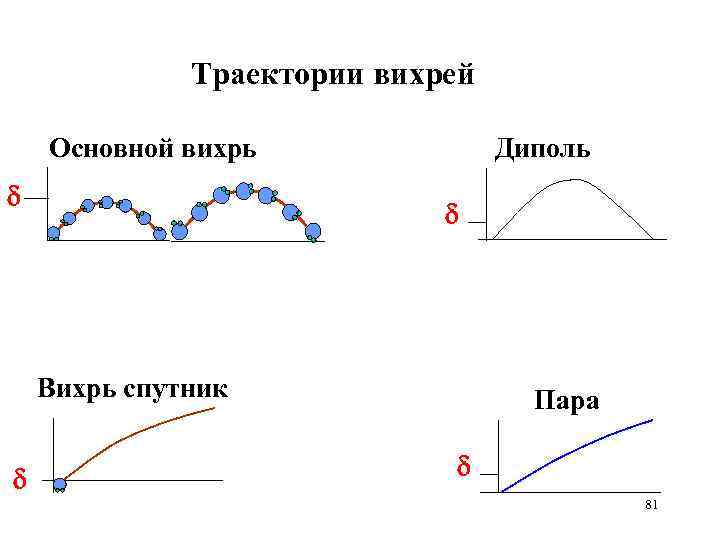Траектории вихрей Основной вихрь Диполь Вихрь спутник Пара 81