1 2 3 Пусть движение происходит













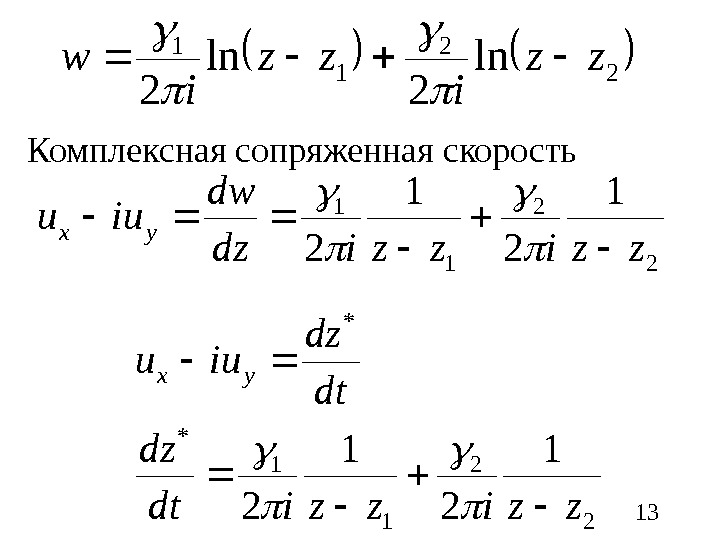




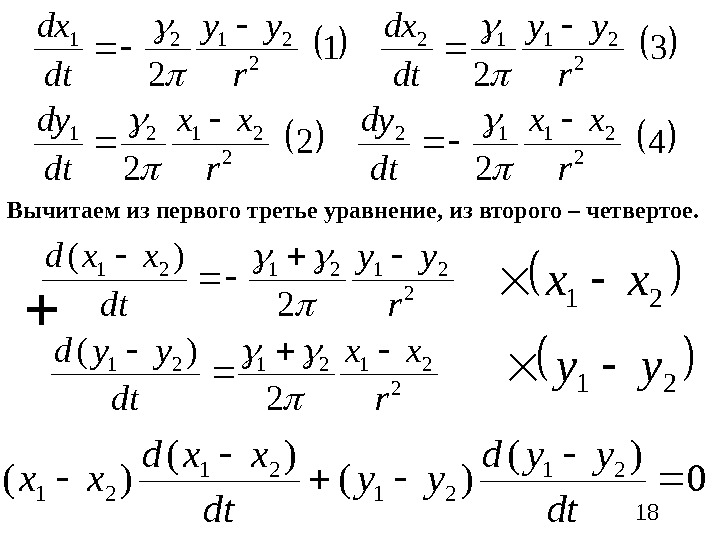















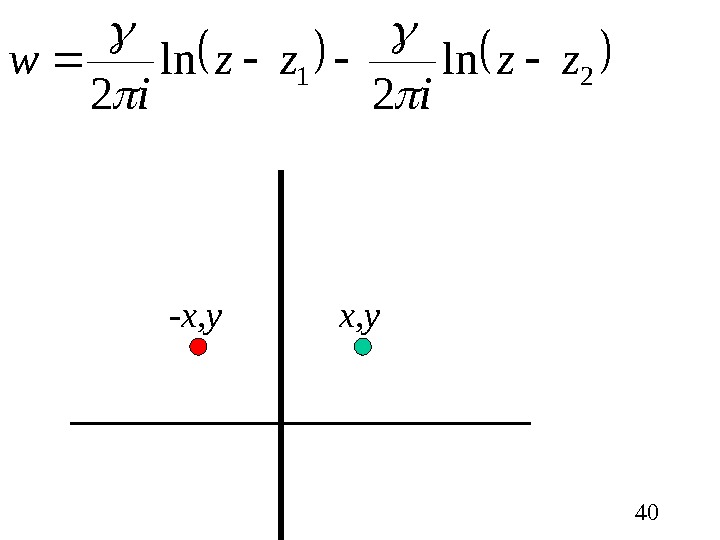

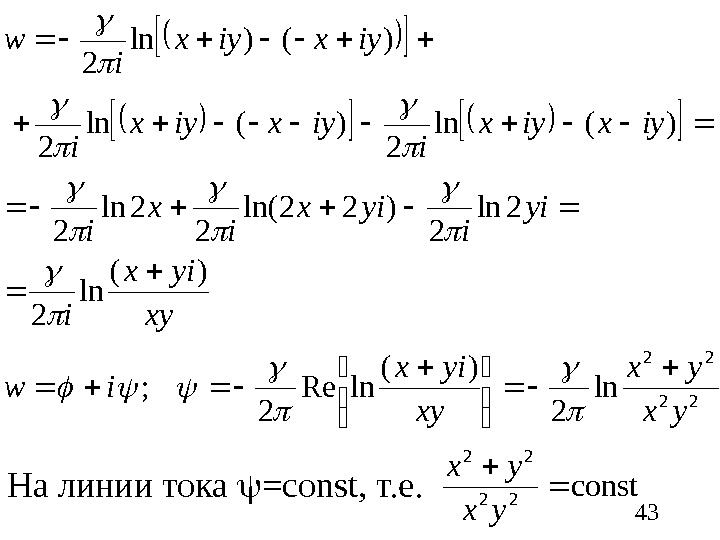


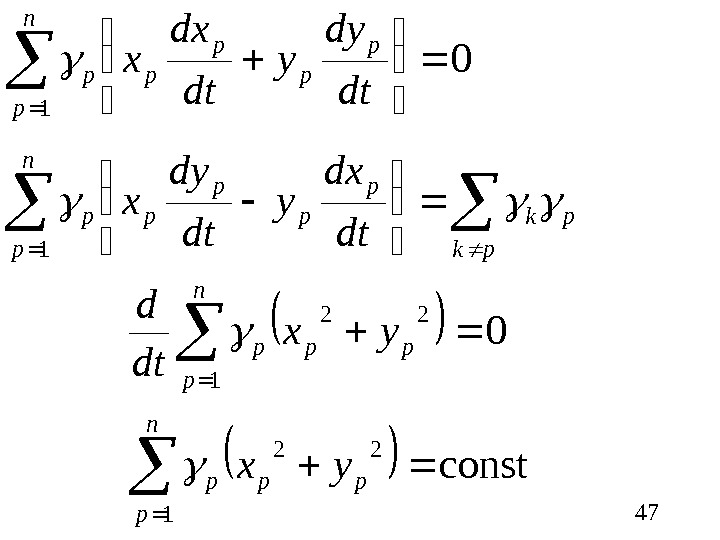



















- Размер: 3.1 Mегабайта
- Количество слайдов: 81
Описание презентации 1 2 3 Пусть движение происходит по слайдам


 3 Пусть движение происходит в плоскости х, у. Вихревые линии являются прямыми, параллельными оси z. 0 , 0 , rotu 0 ln 2 1 ydxrd xu yu yx — значение в точке , а yx, 21 22 yyxxr. Решение этого уравнения дает значение ψ в точке (х, у):
3 Пусть движение происходит в плоскости х, у. Вихревые линии являются прямыми, параллельными оси z. 0 , 0 , rotu 0 ln 2 1 ydxrd xu yu yx — значение в точке , а yx, 21 22 yyxxr. Решение этого уравнения дает значение ψ в точке (х, у):
 4 Добавочная функция 0 есть какое-либо решение однородного уравнения 0 0 и позволяет удовлетворить граничным условиям. В случае безграничной жидкости, которая покоится на бесконечности 0 сводится к постоянной.
4 Добавочная функция 0 есть какое-либо решение однородного уравнения 0 0 и позволяет удовлетворить граничным условиям. В случае безграничной жидкости, которая покоится на бесконечности 0 сводится к постоянной.
 5 Скорость жидкости в точке ( х, у) определяется: ydxd r xx u ydxd r yy u y x
5 Скорость жидкости в точке ( х, у) определяется: ydxd r xx u ydxd r yy u y x
 6 Вихревая нить с координатами и циркуляцией сообщает жидкости в точке ( х, у) скорость, компоненты которой равныyx, 2 2 r xx u r yy u y x х yx, ( х, у)r r U 2 r uu. U yx
6 Вихревая нить с координатами и циркуляцией сообщает жидкости в точке ( х, у) скорость, компоненты которой равныyx, 2 2 r xx u r yy u y x х yx, ( х, у)r r U 2 r uu. U yx
 7 Вычислим интегралы: dxdyu yx и — интегрирование распространяется на всю область, где 0 ydxdxdyd r yy dxdyu x 2 2 1 — Интегрирование по поверхности каждый раз распространяется по сечению всех вихрей
7 Вычислим интегралы: dxdyu yx и — интегрирование распространяется на всю область, где 0 ydxdxdyd r yy dxdyu x 2 2 1 — Интегрирование по поверхности каждый раз распространяется по сечению всех вихрей
 8 Каждому члену соответствует другой член этого интегралаydxdxdyd r yy 2 Они при сложении дают 0. Получаем: 0 0 dxdyu y x 0 0 y x Пусть нити перемещаются
8 Каждому члену соответствует другой член этого интегралаydxdxdyd r yy 2 Они при сложении дают 0. Получаем: 0 0 dxdyu y x 0 0 y x Пусть нити перемещаются
 9 Так как напряжение каждого вихря от времени не зависит, то точка с координатами y y x x в течение всего времени остается неподвижной. Эту точку можно назвать центром системы вихрей, а прямую, параллельную оси z , проходящую через эту точку, — осью системы. Если , то центр лежит в бесконечности.
9 Так как напряжение каждого вихря от времени не зависит, то точка с координатами y y x x в течение всего времени остается неподвижной. Эту точку можно назвать центром системы вихрей, а прямую, параллельную оси z , проходящую через эту точку, — осью системы. Если , то центр лежит в бесконечности.
 10 Одна вихревая нить в точке ( х, у ), вектор вихря внутри бесконечно малого сечения имеет постоянное значение Где центр системы ? уy yхx x сс ху r r U 2 Центр одиночного вихря не смещается во времени.
10 Одна вихревая нить в точке ( х, у ), вектор вихря внутри бесконечно малого сечения имеет постоянное значение Где центр системы ? уy yхx x сс ху r r U 2 Центр одиночного вихря не смещается во времени.
 11 Внутри круга радиуса а жидкость вращается как твердое тело с угловой скоростью . Определить скорость вне круга. ху r r U 2 r a U а 2 2 2 На границе вихря скорость равна a. а
11 Внутри круга радиуса а жидкость вращается как твердое тело с угловой скоростью . Определить скорость вне круга. ху r r U 2 r a U а 2 2 2 На границе вихря скорость равна a. а
 12 Две параллельные прямые вихревые нити в точках z 1 и z 2. Показать, что нити всегда сохраняют одинаковое расстояние друг от друга и вращаются с постоянной угловой скоростью вокруг общего центра С. Пусть циркуляция одной нити равна 1 , а второй 2 . r Запишите комплексный потенциал для 2 нитей.
12 Две параллельные прямые вихревые нити в точках z 1 и z 2. Показать, что нити всегда сохраняют одинаковое расстояние друг от друга и вращаются с постоянной угловой скоростью вокруг общего центра С. Пусть циркуляция одной нити равна 1 , а второй 2 . r Запишите комплексный потенциал для 2 нитей.
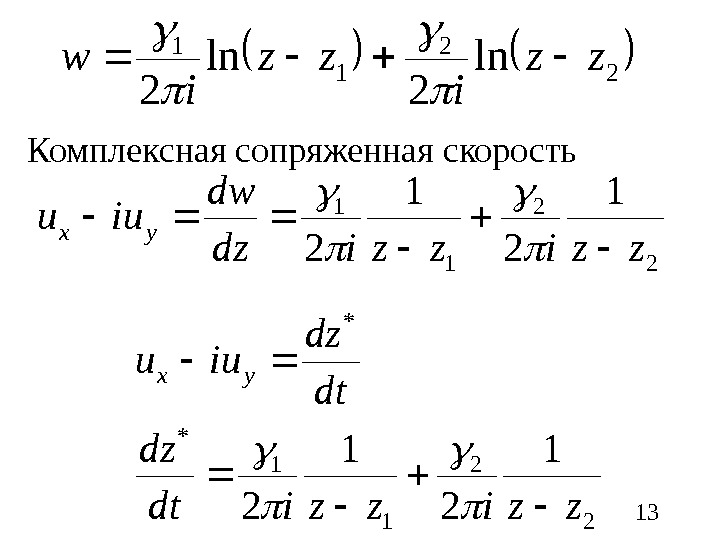 1322 11 ln 2 zz iw Комплексная сопряженная скорость 2 2 1 1 1 2 zzizzidz dw iuu yx 2 2 1 1 * * 1 2 zzizzidt dz iuu yx
1322 11 ln 2 zz iw Комплексная сопряженная скорость 2 2 1 1 1 2 zzizzidz dw iuu yx 2 2 1 1 * * 1 2 zzizzidt dz iuu yx
 14 Скорость первого вихря в точке z 1 (сам на себя не действует)21 2 * 1 1 2 zzidt dz 12 1 * 2 1 2 zzidt dz Скорость второго вихря в точке z 2 Отделяем мнимые и действительные части. Обозначим расстояние между вихрями 2 212 yyxxr
14 Скорость первого вихря в точке z 1 (сам на себя не действует)21 2 * 1 1 2 zzidt dz 12 1 * 2 1 2 zzidt dz Скорость второго вихря в точке z 2 Отделяем мнимые и действительные части. Обозначим расстояние между вихрями 2 212 yyxxr
 15 4 2 2 2 3 2 1 2 2 2112 2 2121 r xx dtdy r yy dtdx 1 2 + const 0 const 0 , 0 22112 21 1 yy dtdy xx dt xxd dtdx
15 4 2 2 2 3 2 1 2 2 2112 2 2121 r xx dtdy r yy dtdx 1 2 + const 0 const 0 , 0 22112 21 1 yy dtdy xx dt xxd dtdx
 16 const 21 2211 yy xx. Получаем интеграл движения центра инерции системы двух вихрей Точка С с координатами 21 2211 ; yy yxx x cc Остается неподвижной во все время движения
16 const 21 2211 yy xx. Получаем интеграл движения центра инерции системы двух вихрей Точка С с координатами 21 2211 ; yy yxx x cc Остается неподвижной во все время движения
 17 • Получим расстояние между вихрями
17 • Получим расстояние между вихрями
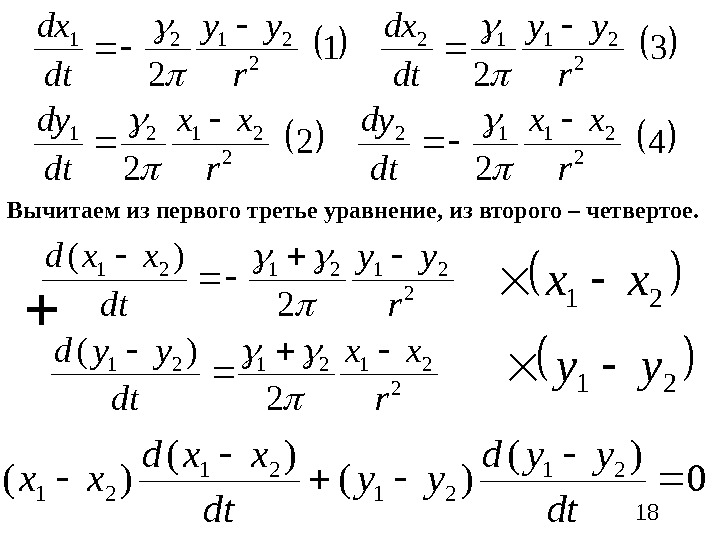 18 4 2 2 2 3 2 1 2 2 2112 2 2121 r xx dtdy r yy dtdx Вычитаем из первого третье уравнение, из второго – четвертое. 2)( 2 212121 r xx dt yyd r yy dt xxd 21 xx 21 yy 0 )( )( 21 21 dt yyd yy dt xxd xx
18 4 2 2 2 3 2 1 2 2 2112 2 2121 r xx dtdy r yy dtdx Вычитаем из первого третье уравнение, из второго – четвертое. 2)( 2 212121 r xx dt yyd r yy dt xxd 21 xx 21 yy 0 )( )( 21 21 dt yyd yy dt xxd xx
 19 const )( )( 2 21 r yyxx. Интегрируем и получаем: Расстояние между вихрями не меняется в процессе перемещения
19 const )( )( 2 21 r yyxx. Интегрируем и получаем: Расстояние между вихрями не меняется в процессе перемещения
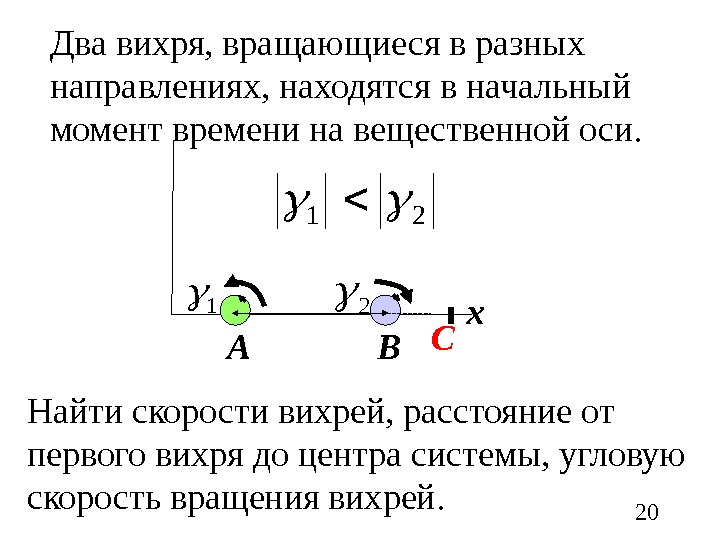
 2021 A B x СДва вихря, вращающиеся в разных направлениях, находятся в начальный момент времени на вещественной оси. 21 Найти скорости вихрей, расстояние от первого вихря до центра системы, угловую скорость вращения вихрей.
2021 A B x СДва вихря, вращающиеся в разных направлениях, находятся в начальный момент времени на вещественной оси. 21 Найти скорости вихрей, расстояние от первого вихря до центра системы, угловую скорость вращения вихрей.
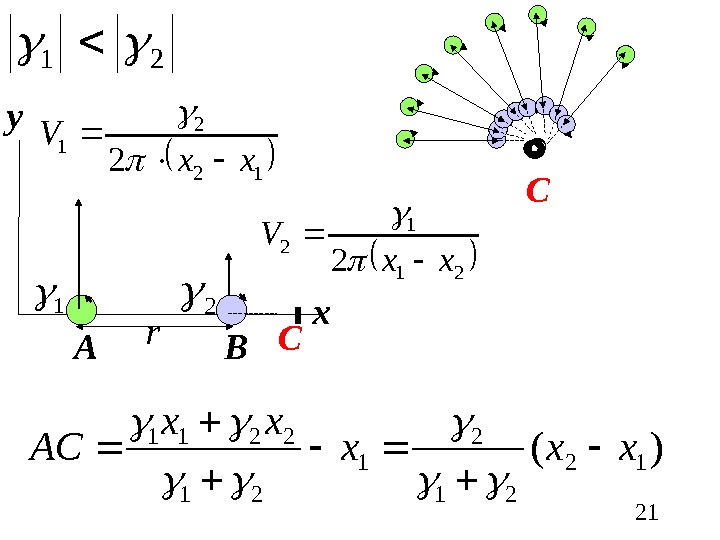
 2121 A B xy 21 12 2 1 2 хх V 21 1 2 2 хх V )( 12 21 2 1 21 2211 ххххх A С С O OOOOOOO С r
2121 A B xy 21 12 2 1 2 хх V 21 1 2 2 хх V )( 12 21 2 1 21 2211 ххххх A С С O OOOOOOO С r
 22 2 211 1 2 r. AС V Угловая скорость вращения вихрей вокруг центра С Показать, что угловые скорости вихрей равны Где будет точка С, если вихри вращаются в одном направлении?
22 2 211 1 2 r. AС V Угловая скорость вращения вихрей вокруг центра С Показать, что угловые скорости вихрей равны Где будет точка С, если вихри вращаются в одном направлении?
 23 Как будут двигаться 2 вихря радиуса а , если они имеют циркуляцию разного знака, но одинаковую по модулю? Вихри вращаются как твердое тело.
23 Как будут двигаться 2 вихря радиуса а , если они имеют циркуляцию разного знака, но одинаковую по модулю? Вихри вращаются как твердое тело.
 24 Движение двух вихрей с противоположным направлением вращения и С А 21 А С = V 1 =V 2 = Вихри двигаются по прямой с одинаковой скоростью АВ а 2 а В ABAС 21 2 ВA V 2 2 1 AB V 2 1 2 2 2 а
24 Движение двух вихрей с противоположным направлением вращения и С А 21 А С = V 1 =V 2 = Вихри двигаются по прямой с одинаковой скоростью АВ а 2 а В ABAС 21 2 ВA V 2 2 1 AB V 2 1 2 2 2 а
 2521 А а В Такие вихри называются «парой вихрей» . Они являются плоской аналогией вихревому кольцу и обладает многими свойствами последнего.
2521 А а В Такие вихри называются «парой вихрей» . Они являются плоской аналогией вихревому кольцу и обладает многими свойствами последнего.
 26 Куда двигается кольцевой вихрь?
26 Куда двигается кольцевой вихрь?
 27 U Записать функцию тока для вихревой пары в потоке жидкости, имеющего постоянную скоростью U. Скорость потока равна по модулю скорости пары, но противоположна по направлению.
27 U Записать функцию тока для вихревой пары в потоке жидкости, имеющего постоянную скоростью U. Скорость потока равна по модулю скорости пары, но противоположна по направлению.
 28= const а- аconst r r 2 1 , ln 2 , 2 21 aa. Линии тока вихревой пары А В
28= const а- аconst r r 2 1 , ln 2 , 2 21 aa. Линии тока вихревой пары А В
 29 парыпотока VU Ux. Udxx. U Функция тока для течения, имеющего постоянную скорость вдоль оси ординат a. BAAB V пары 422 21 ax потока
29 парыпотока VU Ux. Udxx. U Функция тока для течения, имеющего постоянную скорость вдоль оси ординат a. BAAB V пары 422 21 ax потока
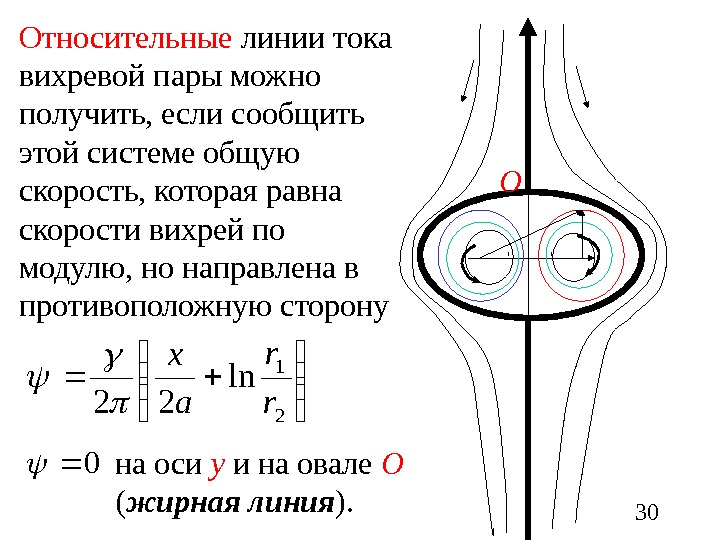
 30 Относительные линии тока вихревой пары можно получить, если сообщить этой системе общую скорость, которая равна скорости вихрей по модулю, но направлена в противоположную сторону 2 1 ln 22 r r a x 0 О на оси у и на овале О ( жирная линия ).
30 Относительные линии тока вихревой пары можно получить, если сообщить этой системе общую скорость, которая равна скорости вихрей по модулю, но направлена в противоположную сторону 2 1 ln 22 r r a x 0 О на оси у и на овале О ( жирная линия ).
 31 Жидкость внутри овала С движется вместе с вихрями. Жидкость вне овала С обтекает этот овал как твердый цилиндр. Полуоси овала С приблизительно имеют длину 2. 09 а и 1. 73 а.
31 Жидкость внутри овала С движется вместе с вихрями. Жидкость вне овала С обтекает этот овал как твердый цилиндр. Полуоси овала С приблизительно имеют длину 2. 09 а и 1. 73 а.
 32 Найти в ортогональной системе координат уравнения линий тока для 1) случая двух вихрей одинаковой интенсивности 2) пары вихрей
32 Найти в ортогональной системе координат уравнения линий тока для 1) случая двух вихрей одинаковой интенсивности 2) пары вихрей
 3321 ln 2 zz i w 21 ln 2 zzzz iw 21 ln 2 rr На линии тока constyyxx constrr const 2 22 22 12 1 21 z 2 z
3321 ln 2 zz i w 21 ln 2 zzzz iw 21 ln 2 rr На линии тока constyyxx constrr const 2 22 22 12 1 21 z 2 z
 34= const а- аconst r r 2 1 , ln 2 Линии тока вихревой пары А В 2 22 22 12 1 yyxxconstyyxx
34= const а- аconst r r 2 1 , ln 2 Линии тока вихревой пары А В 2 22 22 12 1 yyxxconstyyxx
 35 а
35 а
 36 Найти скорость перемещения вихря у твердой стенки
36 Найти скорость перемещения вихря у твердой стенки
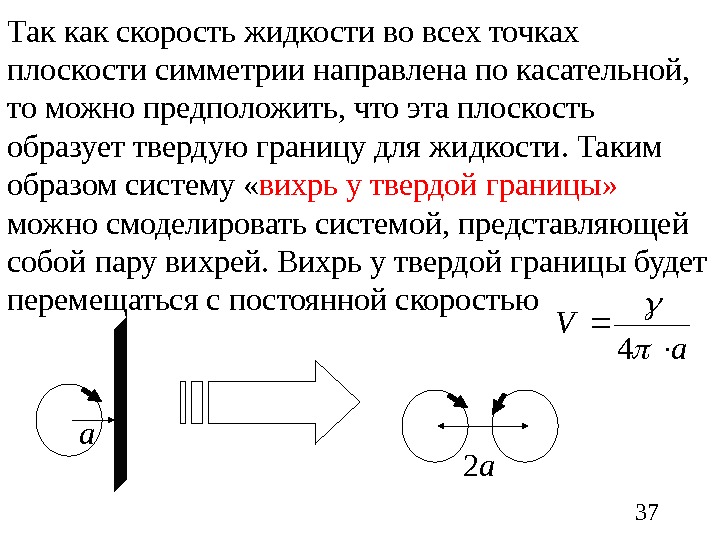
 37 Так как скорость жидкости во всех точках плоскости симметрии направлена по касательной, то можно предположить, что эта плоскость образует твердую границу для жидкости. Таким образом систему « вихрь у твердой границы» можно смоделировать системой, представляющей собой пару вихрей. Вихрь у твердой границы будет перемещаться с постоянной скоростью а 2 аа V
37 Так как скорость жидкости во всех точках плоскости симметрии направлена по касательной, то можно предположить, что эта плоскость образует твердую границу для жидкости. Таким образом систему « вихрь у твердой границы» можно смоделировать системой, представляющей собой пару вихрей. Вихрь у твердой границы будет перемещаться с постоянной скоростью а 2 аа V
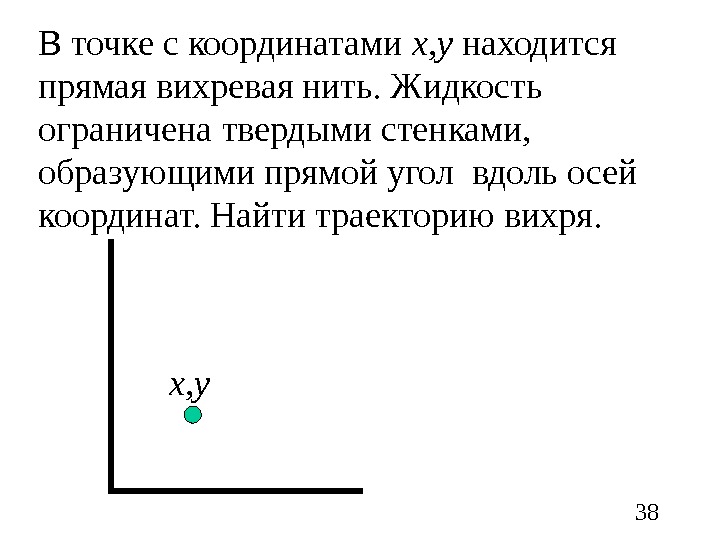
 38 x, y. В точке с координатами х, у находится прямая вихревая нить. Жидкость ограничена твердыми стенками, образующими прямой угол вдоль осей координат. Найти траекторию вихря.
38 x, y. В точке с координатами х, у находится прямая вихревая нить. Жидкость ограничена твердыми стенками, образующими прямой угол вдоль осей координат. Найти траекторию вихря.
 39 Так как циркуляция скорости вихря постоянна, то течение стационарно. В этом случае траектория вихря совпадает с линией тока, проходящей через точку ( x, y ) Для того, чтобы описать влияние стенки, расположенной вдоль мнимой оси, поместим вихрь той же интенсивности, но с противоположным знаком циркуляции в точку ( — x, y ) (отразим вихрь)
39 Так как циркуляция скорости вихря постоянна, то течение стационарно. В этом случае траектория вихря совпадает с линией тока, проходящей через точку ( x, y ) Для того, чтобы описать влияние стенки, расположенной вдоль мнимой оси, поместим вихрь той же интенсивности, но с противоположным знаком циркуляции в точку ( — x, y ) (отразим вихрь)
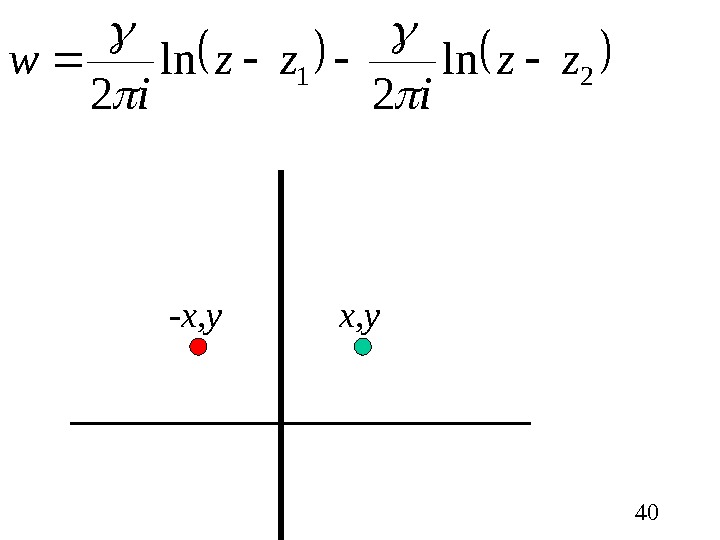 4021 ln 2 zz i w x, y- x, y
4021 ln 2 zz i w x, y- x, y
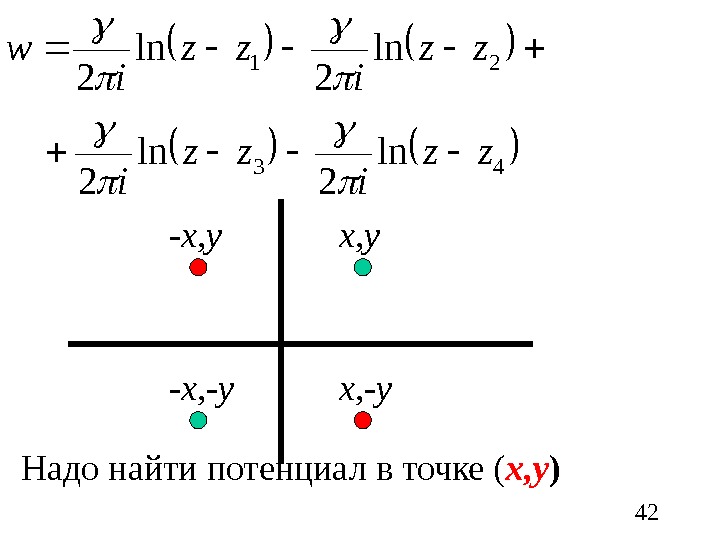
 41 Для того, чтобы описать влияние стенки, расположенной вдоль действительной оси, поместим вихри той же интенсивности, но с противоположными знаками циркуляции в точки ( — x, — y ) и ( x, — y )
41 Для того, чтобы описать влияние стенки, расположенной вдоль действительной оси, поместим вихри той же интенсивности, но с противоположными знаками циркуляции в точки ( — x, — y ) и ( x, — y )
 42 x, y- x, y x, — y- x, — y 43 21 ln 2 ln 2 zz izz iw Надо найти потенциал в точке ( x, y )
42 x, y- x, y x, — y- x, — y 43 21 ln 2 ln 2 zz izz iw Надо найти потенциал в точке ( x, y )
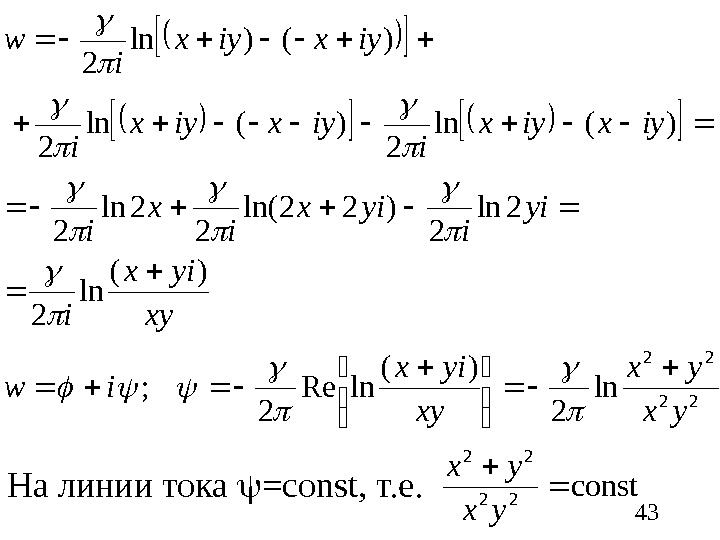 43 22 22 ln 2)( ln. Re 2 ; )( ln 2 2 ln 2)22 ln( 22 ln 2 )(ln 2 )()ln 2 yx yx xy yix iw xy yix i yi iyix ix i iyxiyx iw На линии тока = const , т. е. const 22 22 yx yx
43 22 22 ln 2)( ln. Re 2 ; )( ln 2 2 ln 2)22 ln( 22 ln 2 )(ln 2 )()ln 2 yx yx xy yix iw xy yix i yi iyix ix i iyxiyx iw На линии тока = const , т. е. const 22 22 yx yx
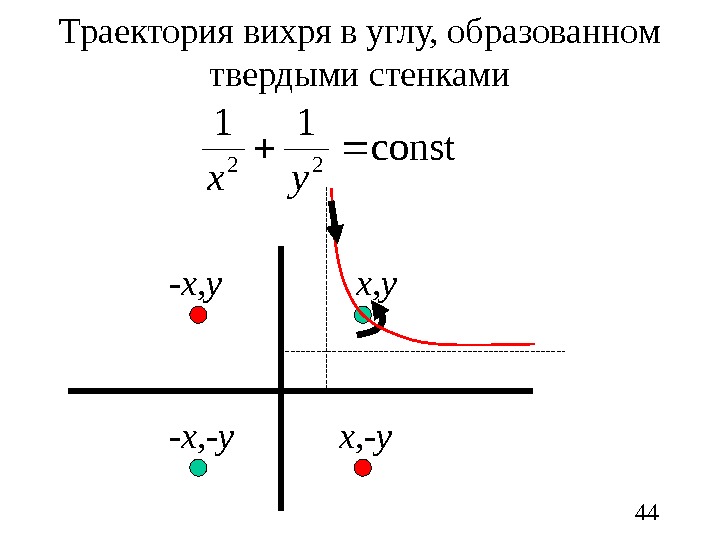
 44 const 11 22 yxx, y- x, y x, — y- x, — y. Траектория вихря в углу, образованном твердыми стенками
44 const 11 22 yxx, y- x, y x, — y- x, — y. Траектория вихря в углу, образованном твердыми стенками
 45 n точечных вихрей, расположенных в точках z 1 , …, z n и имеющих интенсивности 1 , …, n k k yx k n k k zzidzdw iuu zz izw 1 2 ln 2)( 1 1 Комплексный потенциал Комплексная скорость Записать уравнение движения вихря в точке z p (k=p)
45 n точечных вихрей, расположенных в точках z 1 , …, z n и имеющих интенсивности 1 , …, n k k yx k n k k zzidzdw iuu zz izw 1 2 ln 2)( 1 1 Комплексный потенциал Комплексная скорость Записать уравнение движения вихря в точке z p (k=p)
 46 kpn pkk kp zzidtdz 1 2 1* Уравнение движения вихря в точке z p (k=p) Умножая на p z p и суммируя по переменной p от 1 до n , получаем pk pkpn p pp idt dz z 2 1 * 1 Отделить мнимую и действительную части
46 kpn pkk kp zzidtdz 1 2 1* Уравнение движения вихря в точке z p (k=p) Умножая на p z p и суммируя по переменной p от 1 до n , получаем pk pkpn p pp idt dz z 2 1 * 1 Отделить мнимую и действительную части
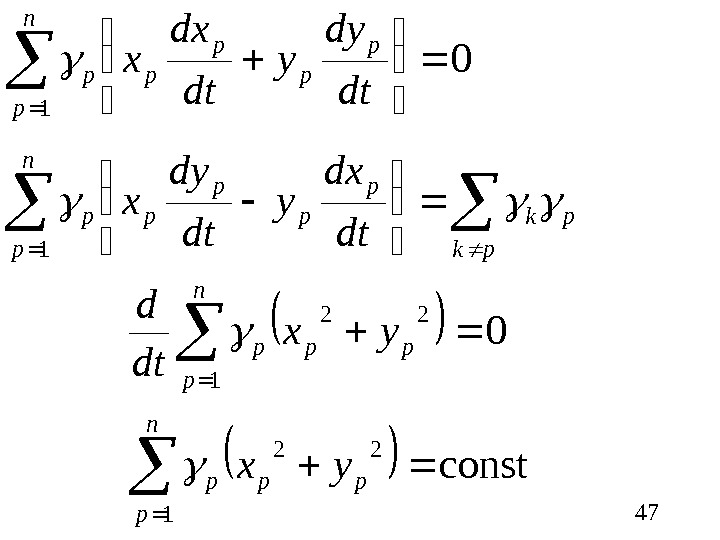 4701 n p p pp dtdy y dtdx x pk pkn p p pp pp dtdx y dtdy x 1 const 0 1 22 n p ppp yx yx dt d
4701 n p p pp dtdy y dtdx x pk pkn p p pp pp dtdx y dtdy x 1 const 0 1 22 n p ppp yx yx dt d
 48 const 1 2 n p pp r. Сумма моментов инерции масс p относительно начала координат не меняется со временем
48 const 1 2 n p pp r. Сумма моментов инерции масс p относительно начала координат не меняется со временем










 59 kpn pkk kp zzidtdz 1 2 1* Умножая на и суммируя по переменной p от 1 до n , получаем еще один интеграл dtdz p p constln n pk kppk r
59 kpn pkk kp zzidtdz 1 2 1* Умножая на и суммируя по переменной p от 1 до n , получаем еще один интеграл dtdz p p constln n pk kppk r

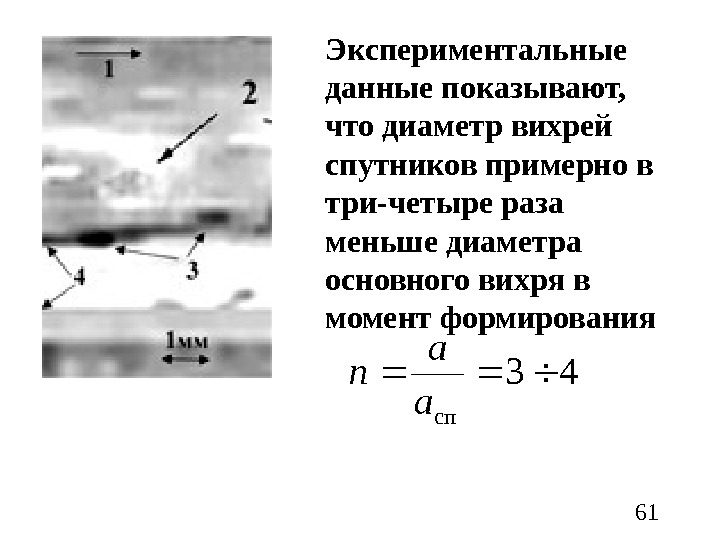
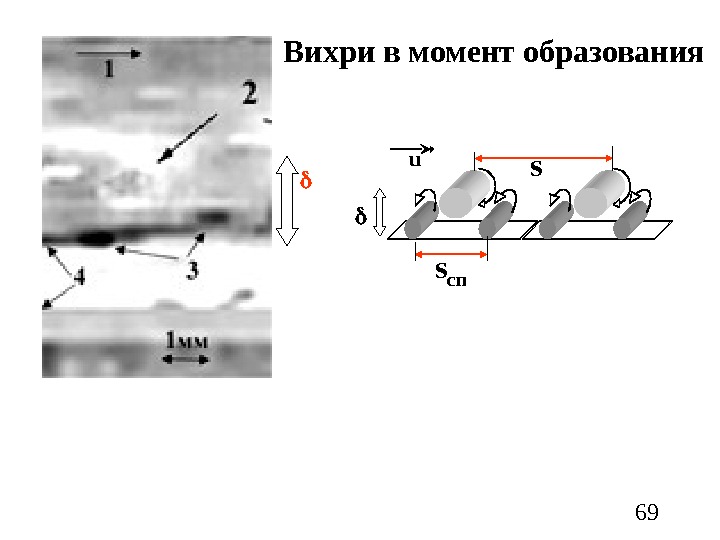
 61 Экспериментальные данные показывают, что диаметр вихрей спутников примерно в три-четыре раза меньше диаметра основного вихря в момент формирования 43 сп а а n
61 Экспериментальные данные показывают, что диаметр вихрей спутников примерно в три-четыре раза меньше диаметра основного вихря в момент формирования 43 сп а а n

 63 Конец третьего перелета вихряс см u 2. 18 max с см u 7. 20 см 23. 0 1 053. 0 cux 1 5. 23 с Т=0. 82 с s =1. 7 см см 25. 1 max ct 15. 0 max 2 a= 0. 16 см
63 Конец третьего перелета вихряс см u 2. 18 max с см u 7. 20 см 23. 0 1 053. 0 cux 1 5. 23 с Т=0. 82 с s =1. 7 см см 25. 1 max ct 15. 0 max 2 a= 0. 16 см
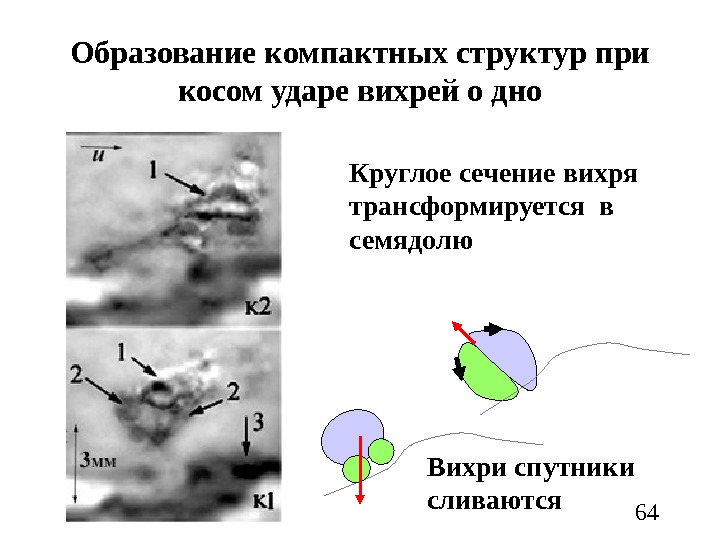
 64 Образование компактных структур при косом ударе вихрей о дно Круглое сечение вихря трансформируется в семядолю Вихри спутники сливаются
64 Образование компактных структур при косом ударе вихрей о дно Круглое сечение вихря трансформируется в семядолю Вихри спутники сливаются
 65124 3 ? ? Возможно вихри спутники слились в один вихрь и возникла компактная пара
65124 3 ? ? Возможно вихри спутники слились в один вихрь и возникла компактная пара
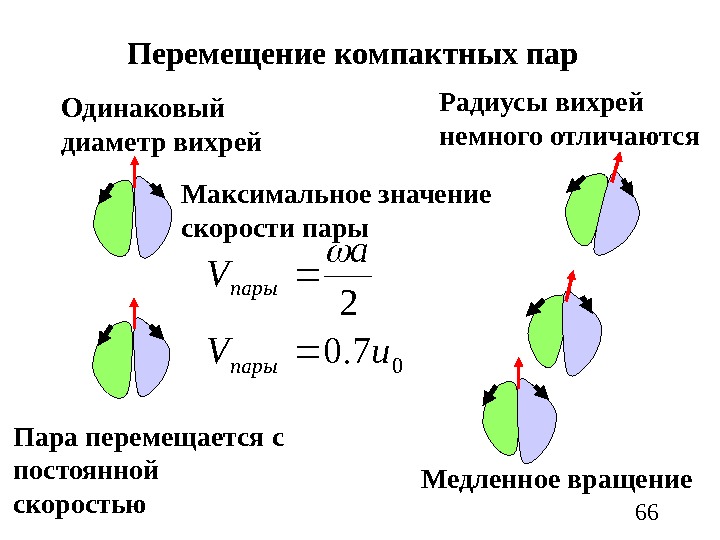
 66 Перемещение компактных пар Одинаковый диаметр вихрей Пара перемещается с постоянной скоростью 07. 0 2 u. V a V пары Радиусы вихрей немного отличаются Медленное вращение. Максимальное значение скорости пары
66 Перемещение компактных пар Одинаковый диаметр вихрей Пара перемещается с постоянной скоростью 07. 0 2 u. V a V пары Радиусы вихрей немного отличаются Медленное вращение. Максимальное значение скорости пары
 67 Компактные вихревые структуры поднимаются вверх с постоянной скоростью07. 0 u. Vпар 0 u. Uпар
67 Компактные вихревые структуры поднимаются вверх с постоянной скоростью07. 0 u. Vпар 0 u. Uпар
 68 Формирование диполя — некомпактной структуры из двух вихрей
68 Формирование диполя — некомпактной структуры из двух вихрей
 69 u s сп s. Вихри в момент образования
69 u s сп s. Вихри в момент образования
 70 Взаимодействие вихрей одного знака в однородной жидкости вблизи подстилающей поверхности s a Если s/a<5. 7 , то вихри сближаются и сливаются в один вихрь Егоров О. В. , Мартынов С. Л. , Мельникова О. Н. Влияние волнового характера скорости потока в придонном слое на формирование вихрей. // Известия РАН, серия физическая. 2002. Т. 66. № 12. С. 1709 —
70 Взаимодействие вихрей одного знака в однородной жидкости вблизи подстилающей поверхности s a Если s/a<5. 7 , то вихри сближаются и сливаются в один вихрь Егоров О. В. , Мартынов С. Л. , Мельникова О. Н. Влияние волнового характера скорости потока в придонном слое на формирование вихрей. // Известия РАН, серия физическая. 2002. Т. 66. № 12. С. 1709 —
 71 направление потока 3 — основной вихрь, 4 — спутникис см u 40 max с см u 5. 40 см 14. 0 1 1 cux 1 3. 64 с Т=0. 15 с s =0. 4 смдно 1. 4 мм диполь. Формирование диполя а сп =0. 35 мм s сп =2 мм кадр 1 кадр 2 а = 0. 5 мм
71 направление потока 3 — основной вихрь, 4 — спутникис см u 40 max с см u 5. 40 см 14. 0 1 1 cux 1 3. 64 с Т=0. 15 с s =0. 4 смдно 1. 4 мм диполь. Формирование диполя а сп =0. 35 мм s сп =2 мм кадр 1 кадр 2 а = 0. 5 мм
 72 Форма диполя xy z
72 Форма диполя xy z
 73 Вихри в диполе сохраняют круглое сечение
73 Вихри в диполе сохраняют круглое сечение
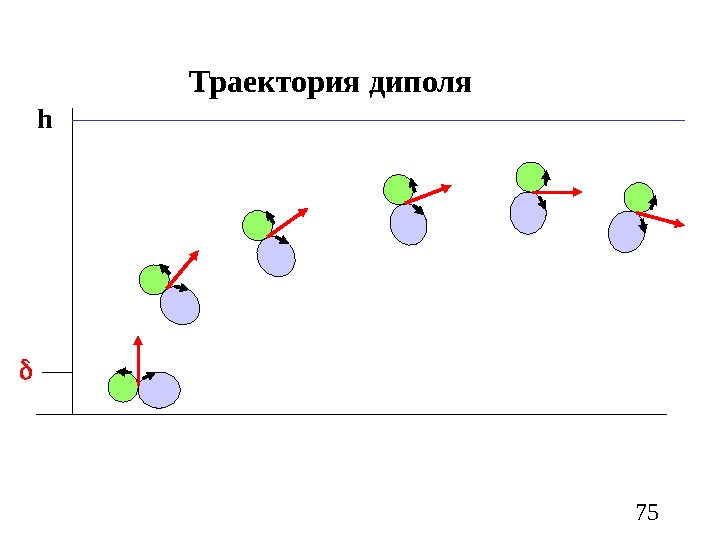
 74 Вихри, составляющие диполь, имеют различный диаметр, что приводит к вращению диполя
74 Вихри, составляющие диполь, имеют различный диаметр, что приводит к вращению диполя
 75 Траектория диполя h
75 Траектория диполя h
 7607. 0 2 u. V a V дип Максимальная скорость подъема диполя Максимальная горизонтальная скорость диполя 0 7 u. Uдип Еречнев Д. А. , Еречнева К. В. , Жмур В. В. , Мельникова О. Н. Влияние когерентных структур на коэффициент турбулентного трения в тормозящихся потоках воды и воздуха. // Известия РАН. Физика океана и атмосферы. 2003. Т. 39. № 1.
7607. 0 2 u. V a V дип Максимальная скорость подъема диполя Максимальная горизонтальная скорость диполя 0 7 u. Uдип Еречнев Д. А. , Еречнева К. В. , Жмур В. В. , Мельникова О. Н. Влияние когерентных структур на коэффициент турбулентного трения в тормозящихся потоках воды и воздуха. // Известия РАН. Физика океана и атмосферы. 2003. Т. 39. № 1.
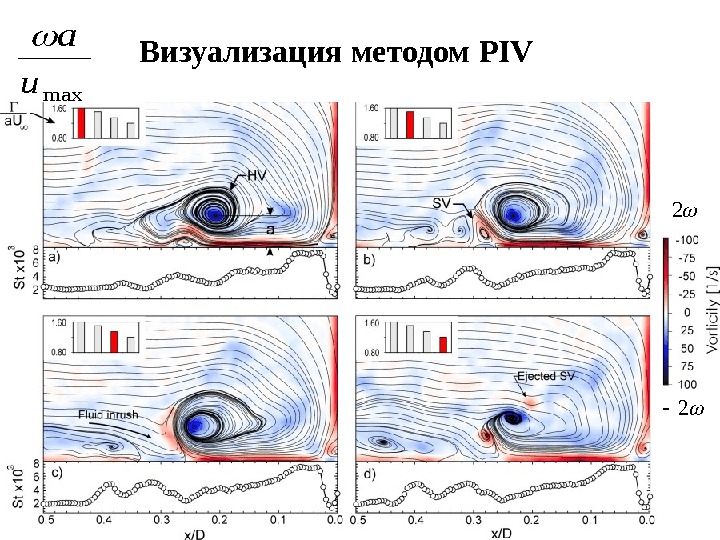
 77 Рассмотрим поток, в котором параметры вихрей сильно меняются за время перелета Расстояние между вихрями спутниками s сп > 5. 7 а сп
77 Рассмотрим поток, в котором параметры вихрей сильно меняются за время перелета Расстояние между вихрями спутниками s сп > 5. 7 а сп
 78 Визуализация методом PIVmaxu а
78 Визуализация методом PIVmaxu а
 79 Отрыв вихря спутника в верхней части траектории основного вихряс см u 2. 8 max 1 3. 2 с 1 035. 0 cux см/с5. 00 u мм 4. 4 а = 1. 5 ммs = 1. 4 cм
79 Отрыв вихря спутника в верхней части траектории основного вихряс см u 2. 8 max 1 3. 2 с 1 035. 0 cux см/с5. 00 u мм 4. 4 а = 1. 5 ммs = 1. 4 cм
 80 max x 1 перелет. Расстояние между вихрями спутниками s сп > 5. 7 а сп. Отрыв вихря спутника в верхней части траектории основного вихря xсп vutu 000 0 u фон сп. Горизонтальная скорость вихря спутникаtuuфон
80 max x 1 перелет. Расстояние между вихрями спутниками s сп > 5. 7 а сп. Отрыв вихря спутника в верхней части траектории основного вихря xсп vutu 000 0 u фон сп. Горизонтальная скорость вихря спутникаtuuфон
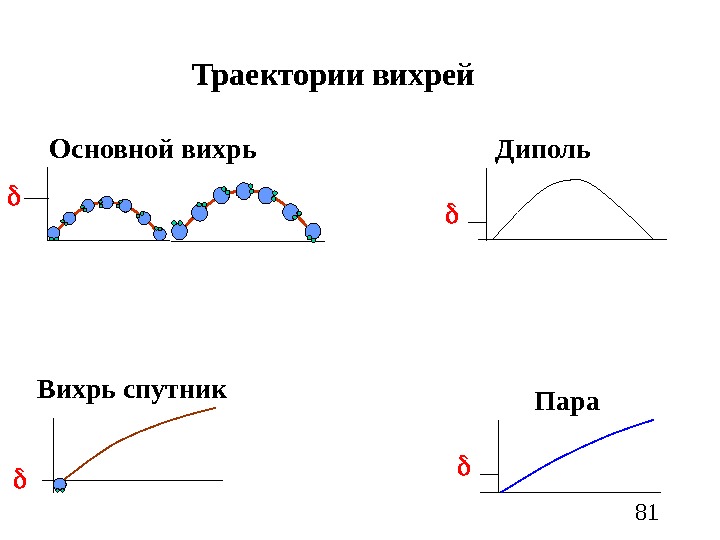
 81 Траектории вихрей Основной вихрь Диполь Пара Вихрь спутник
81 Траектории вихрей Основной вихрь Диполь Пара Вихрь спутник

