1 2 3 Литература
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
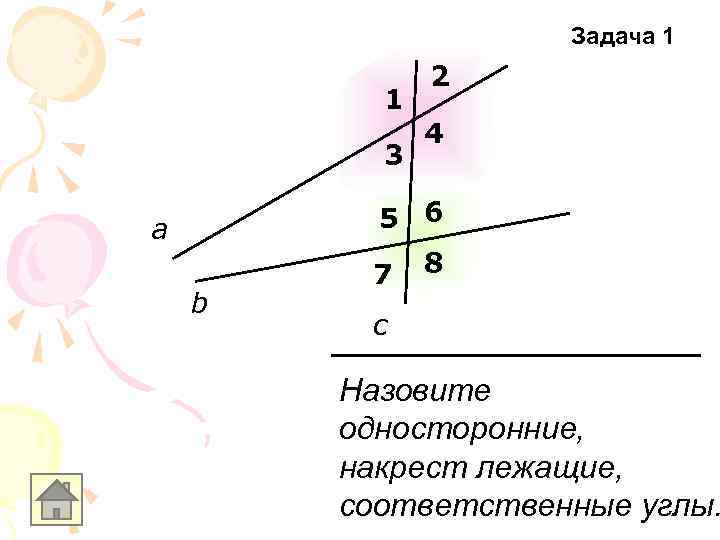Задача 1 1 3 2 4 5 6 а b 7 8 c Назовите односторонние, накрест лежащие, соответственные углы.
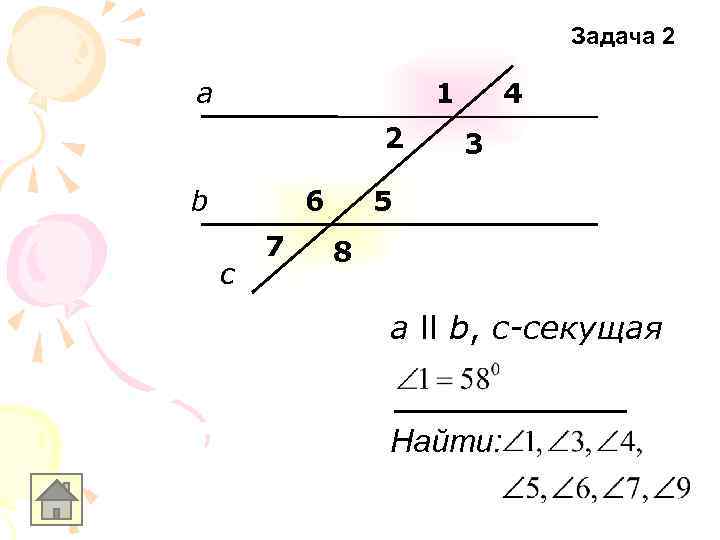Задача 2 а 1 2 b 6 c 7 4 3 5 8 а ll b, с-секущая Найти:
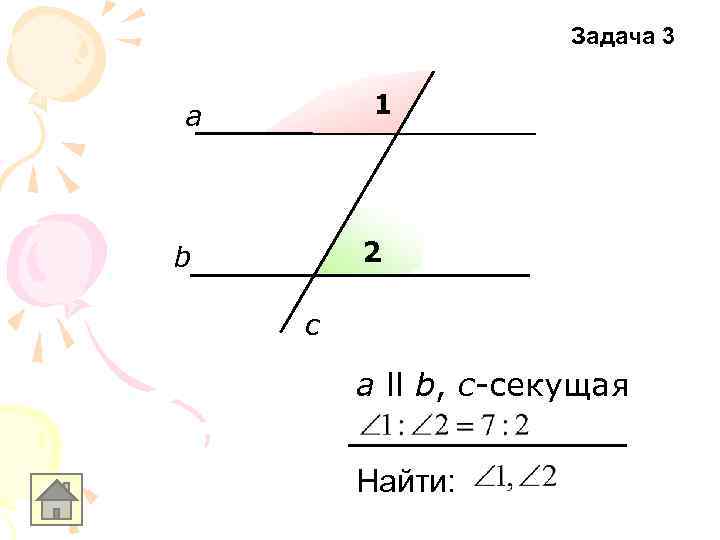Задача 3 1 а 2 b c а ll b, с-секущая Найти:
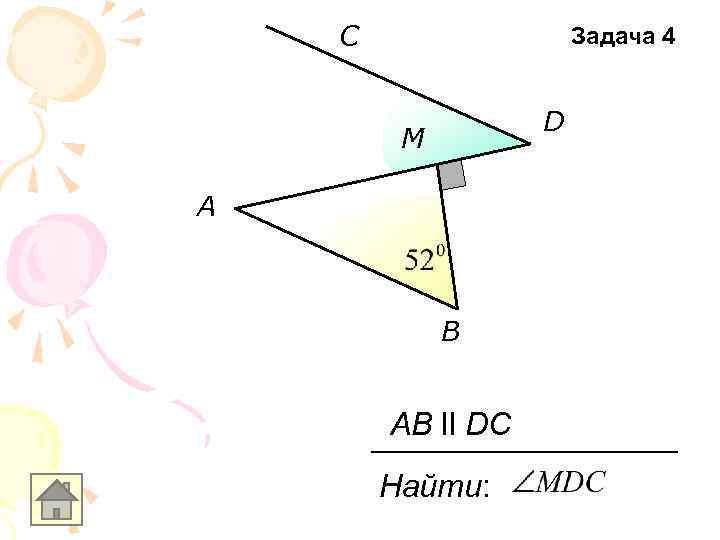C Задача 4 D M A B AB ll DC Найти:
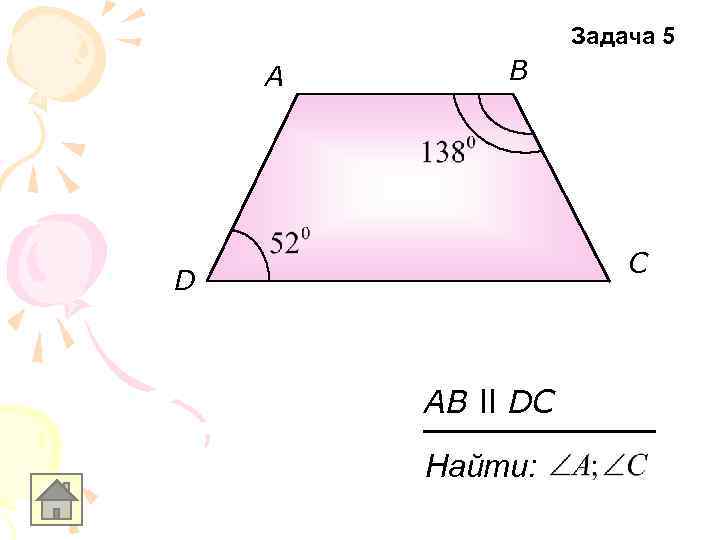Задача 5 A B С D AB ll DC Найти:
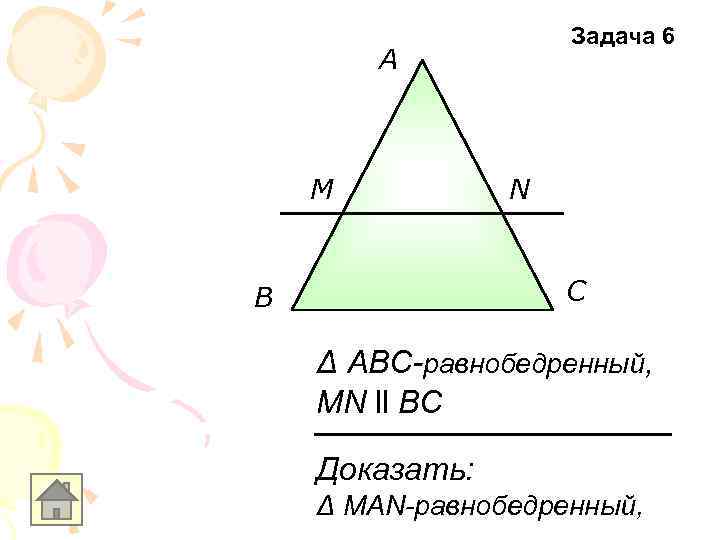Задача 6 A M N С В Δ ABC-равнобедренный, MN ll BC Доказать: Δ MAN-равнобедренный,
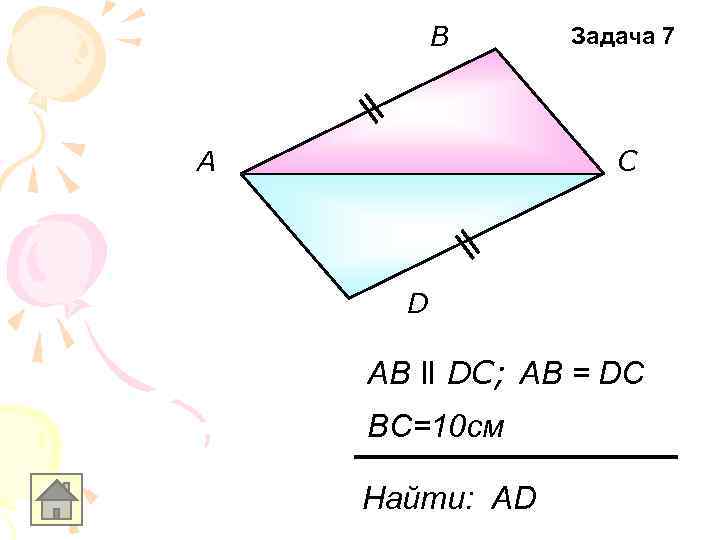В А Задача 7 С D AB ll DC; AB = DC BC=10 см Найти: АD
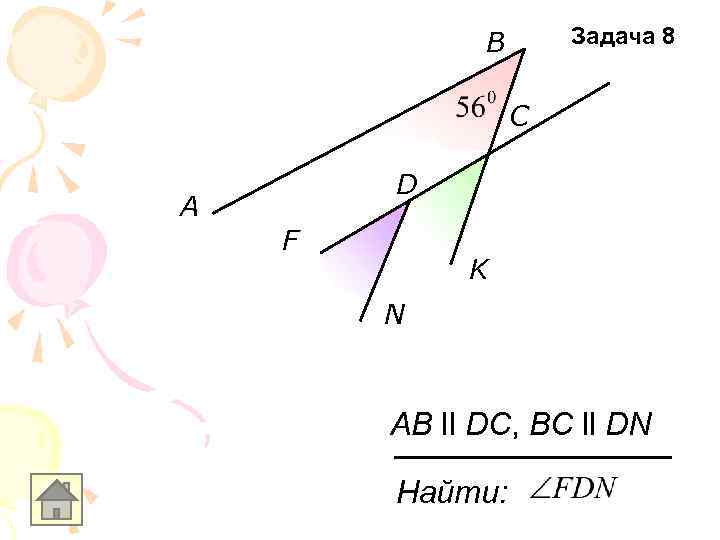Задача 8 B C D A F K N AB ll DC, BC ll DN Найти:
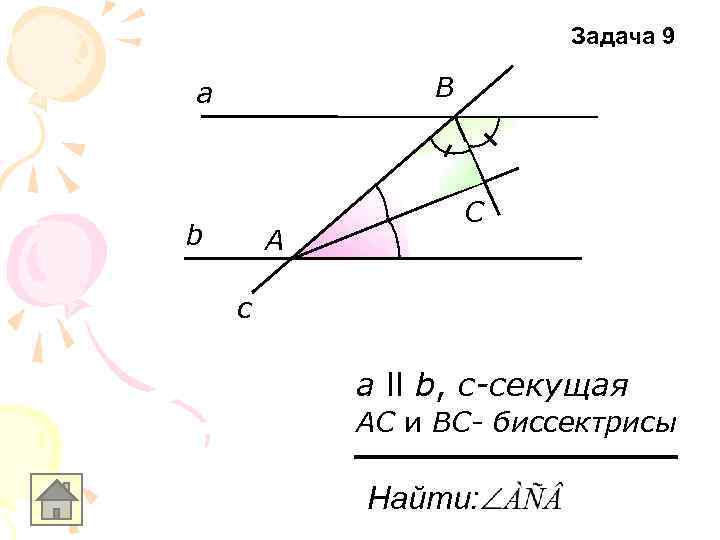Задача 9 В а b А С c а ll b, с-секущая АС и ВС- биссектрисы Найти:
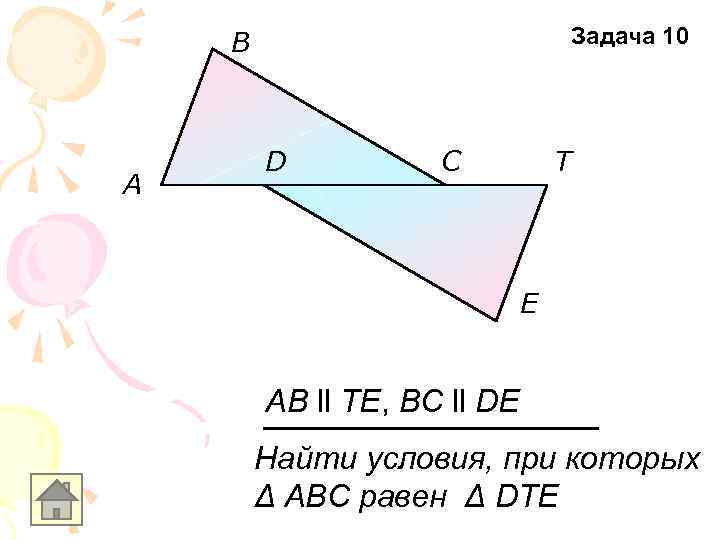Задача 10 B A D C T E AB ll TE, BC ll DE Найти условия, при которых Δ АВС равен Δ DTE
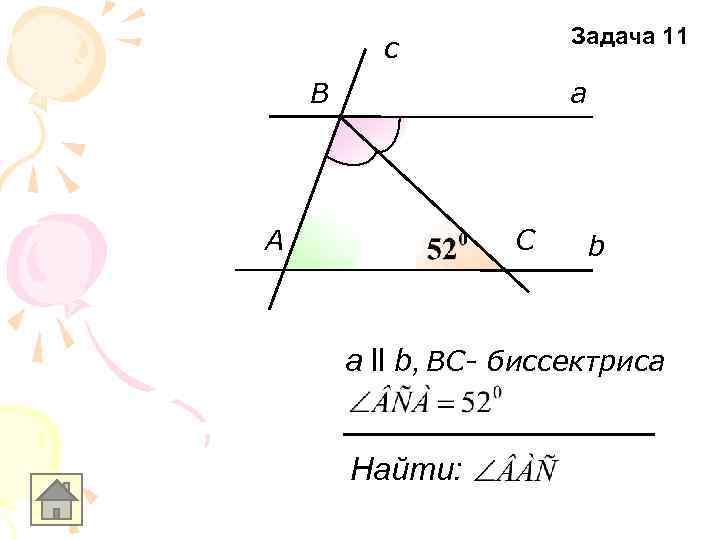Задача 11 c B a А C b а ll b, ВC- биссектриса Найти:
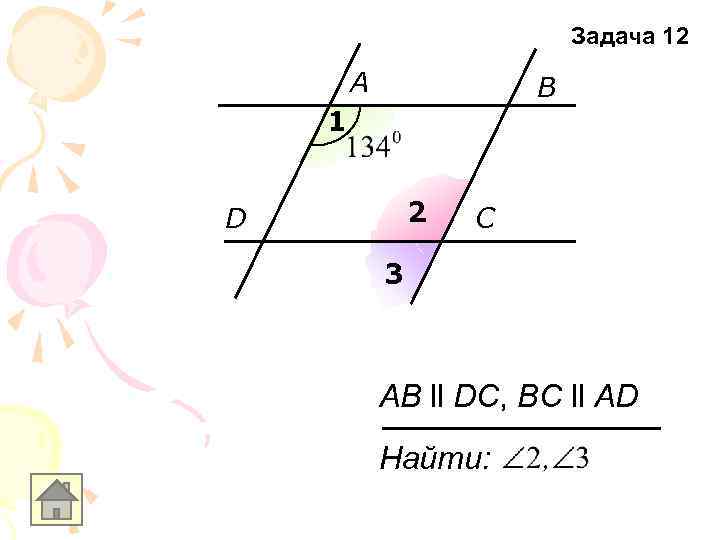Задача 12 A B 1 2 D C 3 AB ll DC, BC ll AD Найти:
Задача 13 В M O N С А MN ll AC АO и СO- биссектрисы Доказать: MN=AM+CN
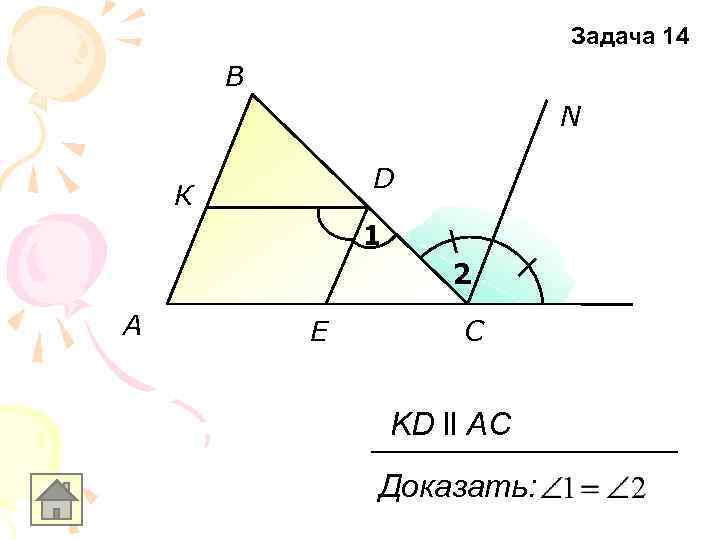Задача 14 B N D К 1 2 A E C KD ll AC Доказать:
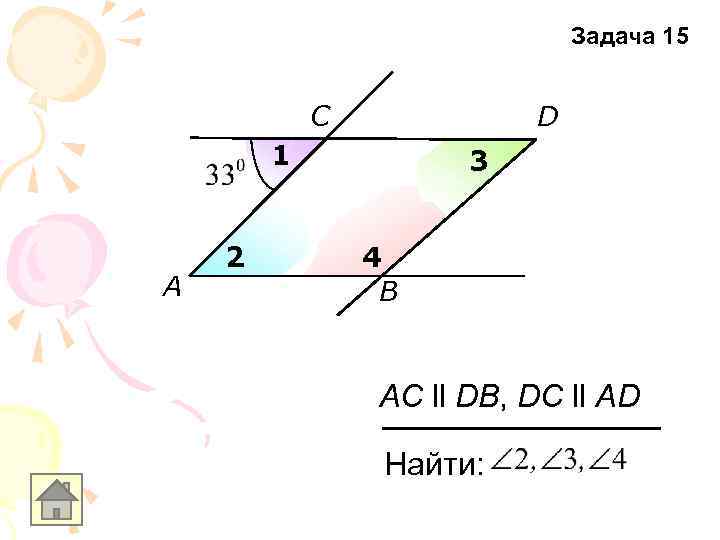Задача 15 C D 1 A 2 3 4 B AC ll DB, DC ll AD Найти:
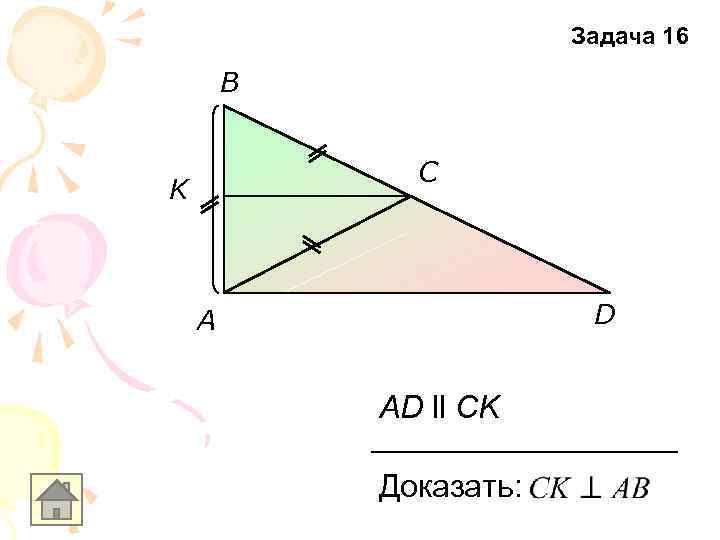Задача 16 B C K D A AD ll CK Доказать:
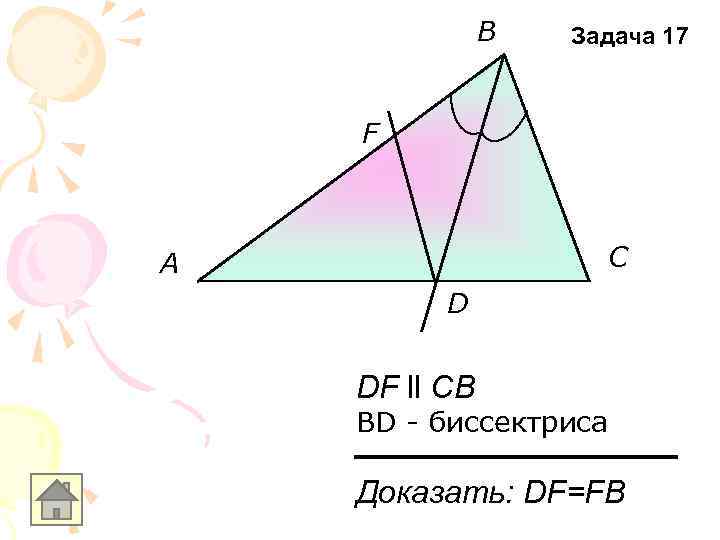B Задача 17 F C A D DF ll CB BD - биссектриса Доказать: DF=FB
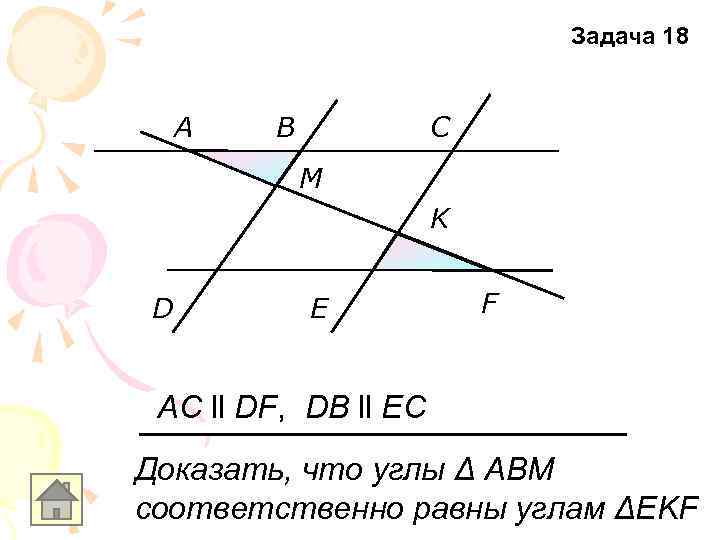Задача 18 A B C M K D E F AC ll DF, DB ll EC Доказать, что углы Δ АВМ соответственно равны углам ΔEKF
Задача 19 D С 1 F 2 B A АB ll DF, Доказать: АB=СВ
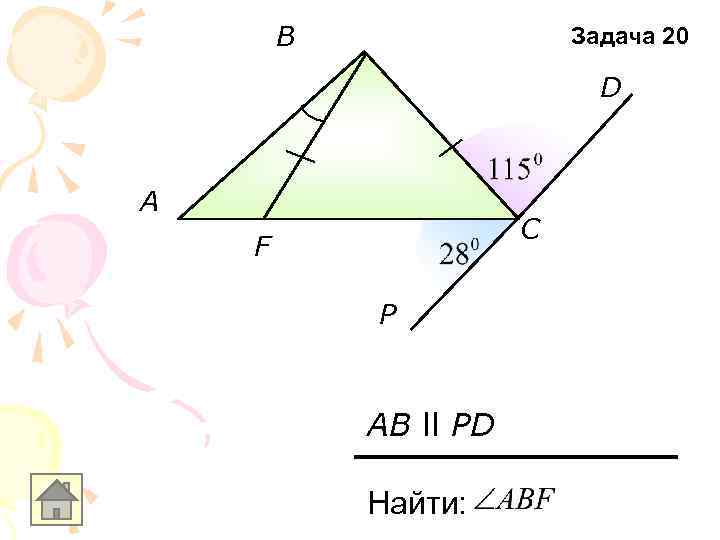B Задача 20 D A C F P AB ll PD Найти:
Задача 21 В К Р С A АС ll КР, СК-биссектриса Доказать: Δ KPC-равнобедренный
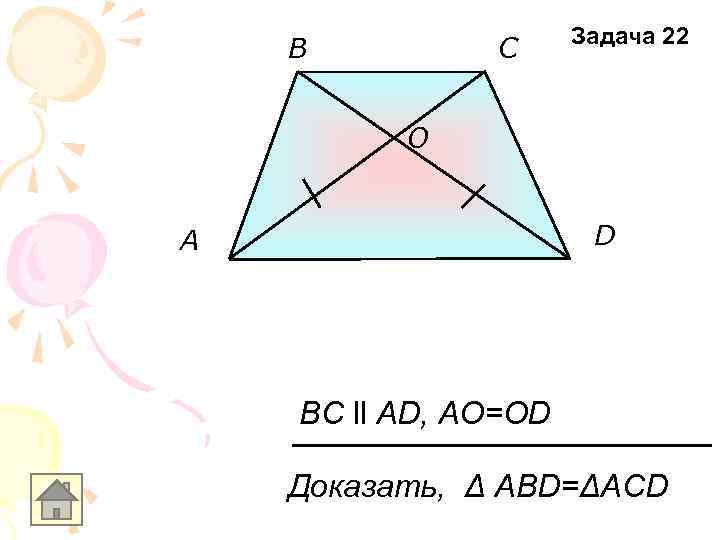B C Задача 22 O D A BC ll AD, AO=OD Доказать, Δ АВD=ΔACD
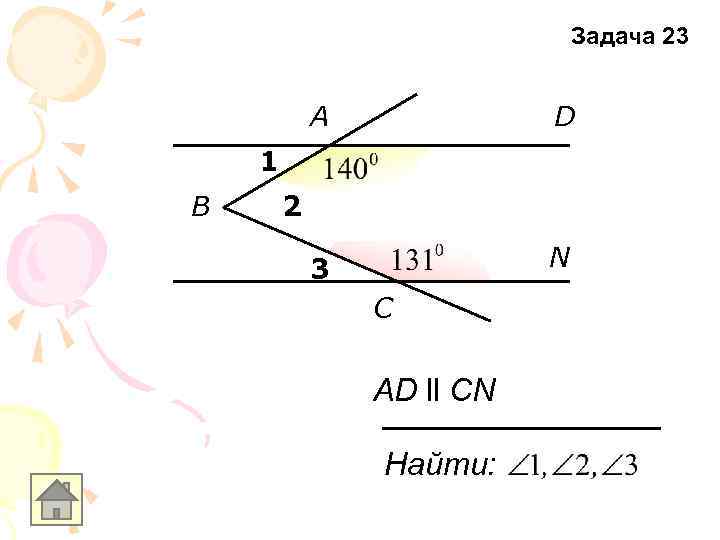Задача 23 A D 3 N 1 B 2 C AD ll CN Найти:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
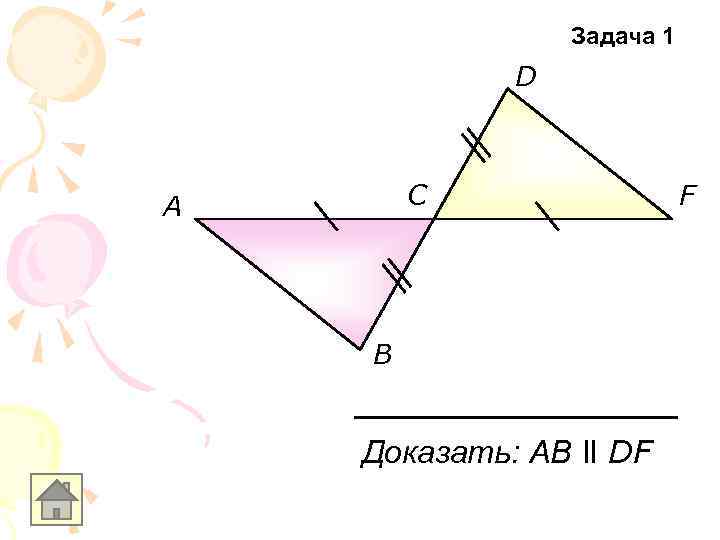Задача 1 D C A B Доказать: АB ll DF F
Задача 2 Найти параллельные прямые
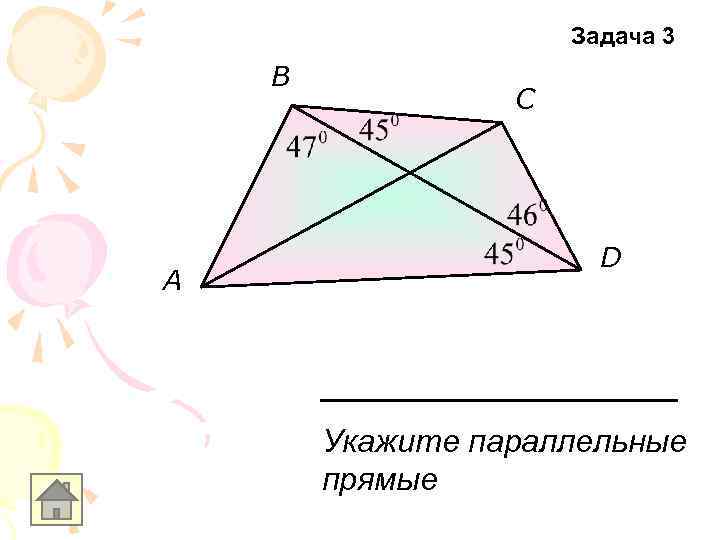Задача 3 B A C D Укажите параллельные прямые
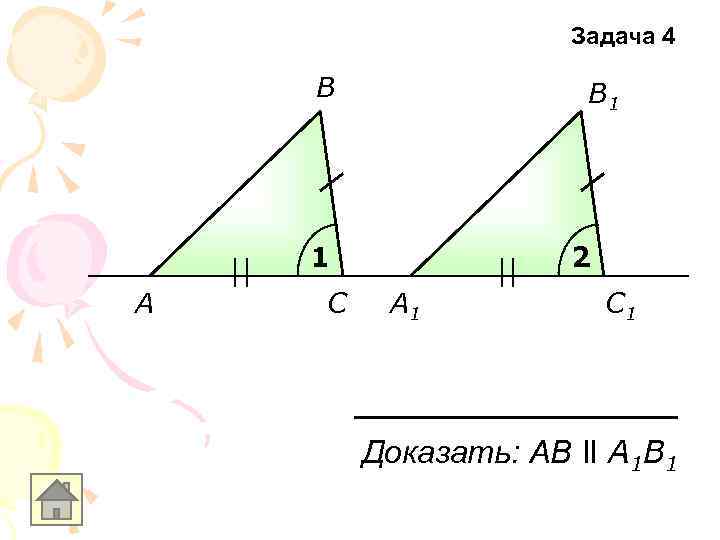Задача 4 В В 1 1 A С 2 A 1 С 1 Доказать: АB ll A 1 B 1
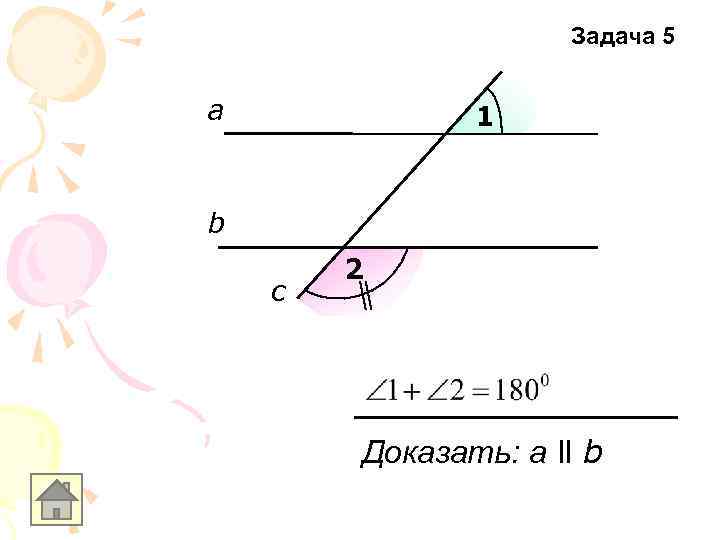Задача 5 а 1 b c 2 Доказать: a ll b
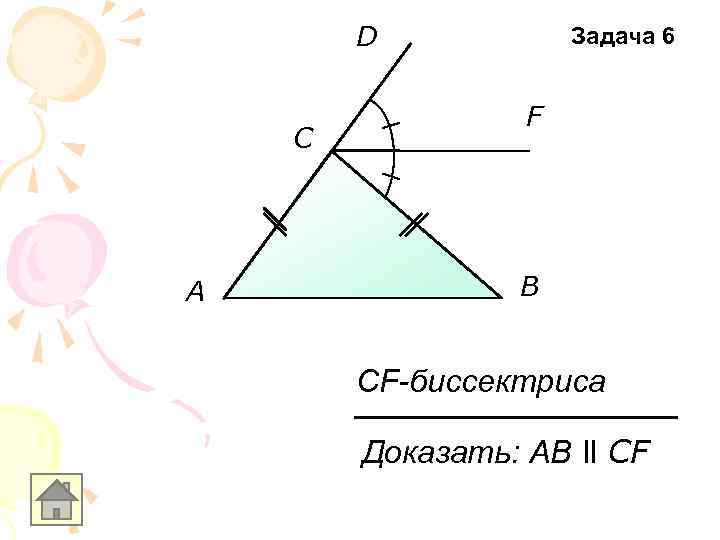D C A Задача 6 F B CF-биссектриса Доказать: АB ll CF
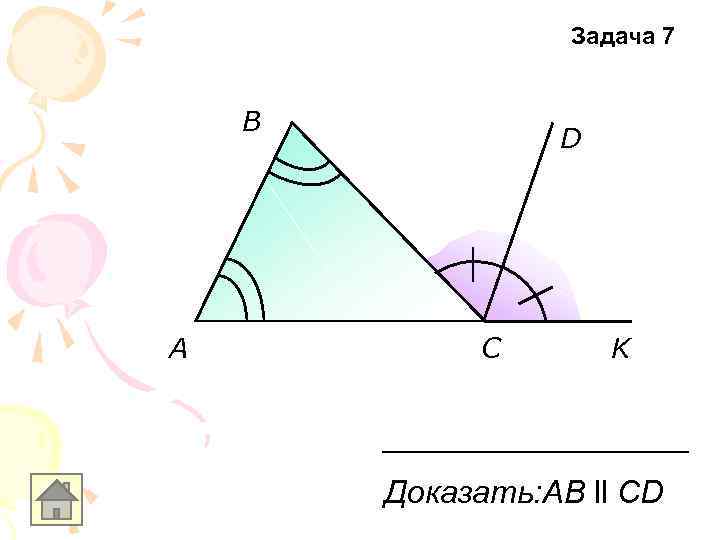Задача 7 B A D C K Доказать: AB ll CD
Задача 8 В К A D С Доказать: АС ll КР
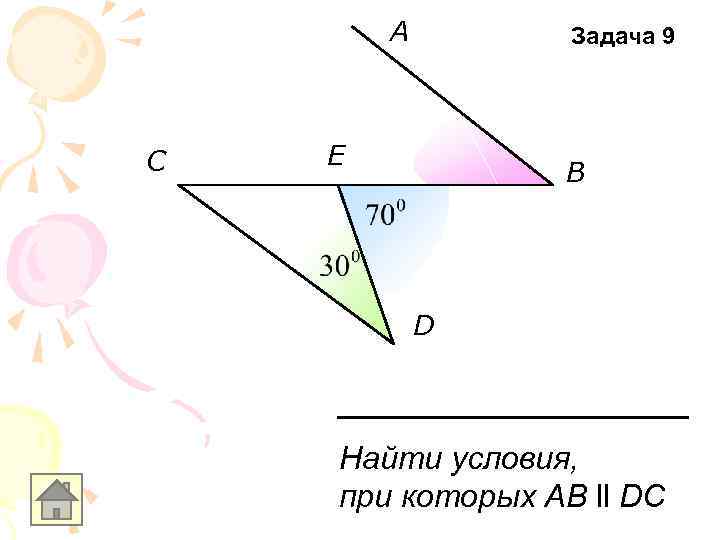A C Задача 9 E B D Найти условия, при которых AB ll DC
Задача 10 M A B C D F Найти условия, при которых FB ll CM
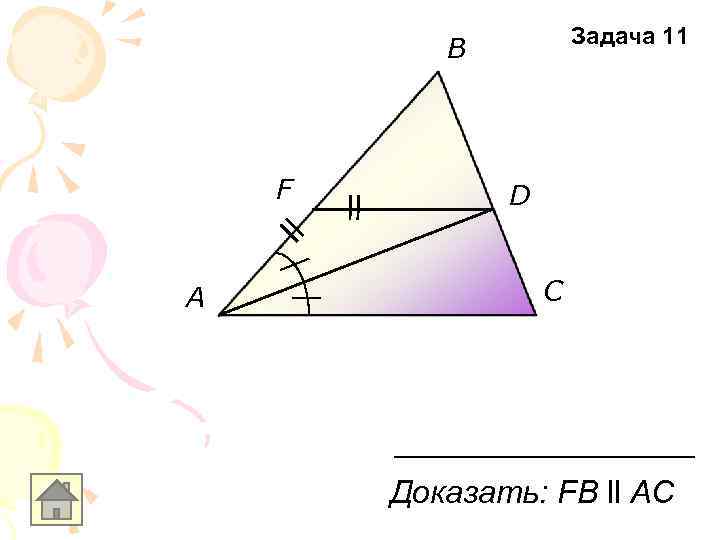Задача 11 B F A D C Доказать: FВ ll АС
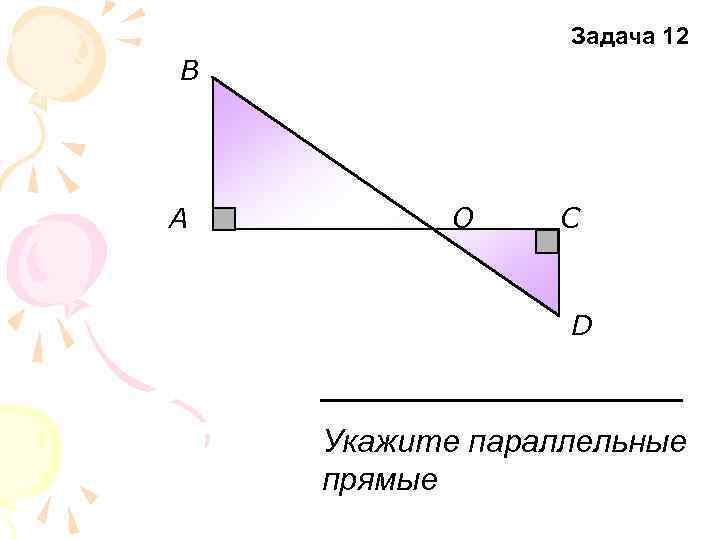Задача 12 В A О С D Укажите параллельные прямые
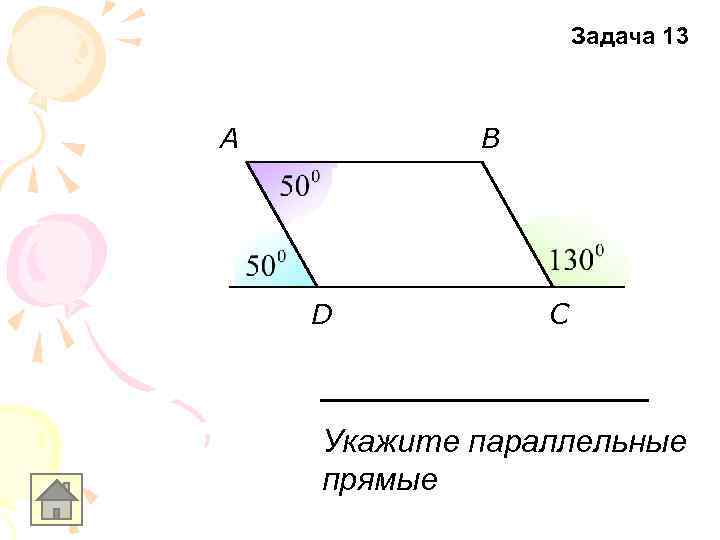Задача 13 A B D C Укажите параллельные прямые
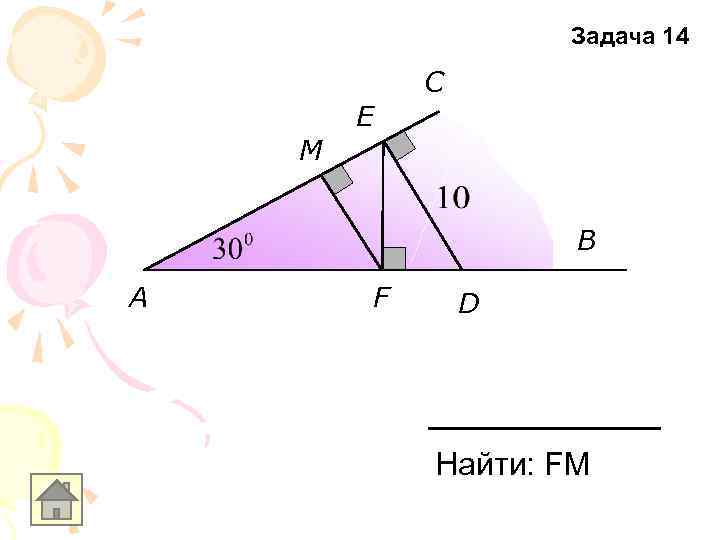Задача 14 C E M B A F D Найти: FM
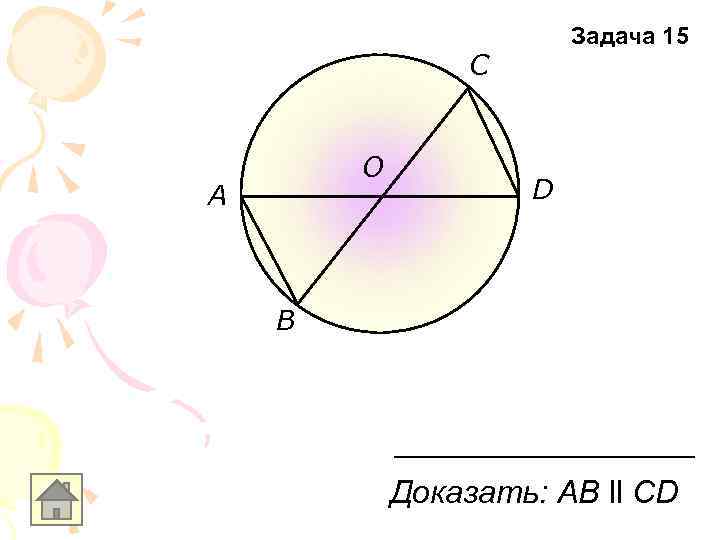Задача 15 С О A D B Доказать: AВ ll CD
Задача 16 C A O D B Доказать: FВ ll АС
1 2 3 4 5 6 7 8 9 10
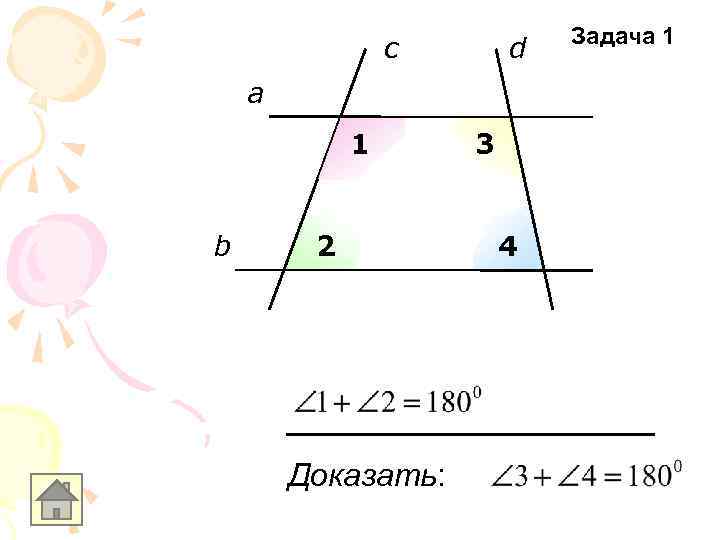c d a 1 b 2 Доказать: 3 4 Задача 1
Задача 2 c 1 а b 4 3 2 d Найти:
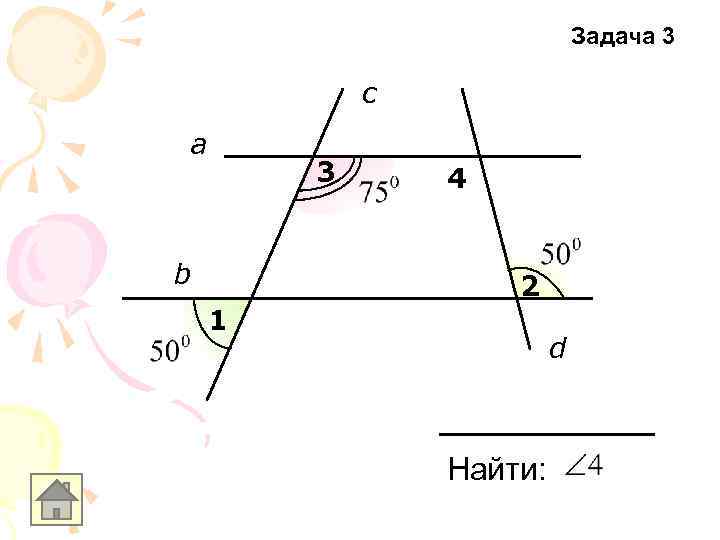Задача 3 c а 3 b 4 2 1 d Найти:
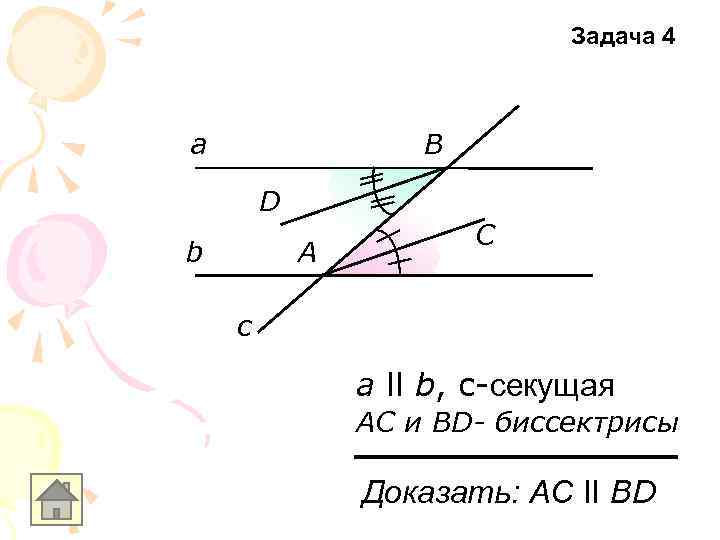Задача 4 а В D b А С c а ll b, с-секущая АС и ВD- биссектрисы Доказать: АС ll ВD
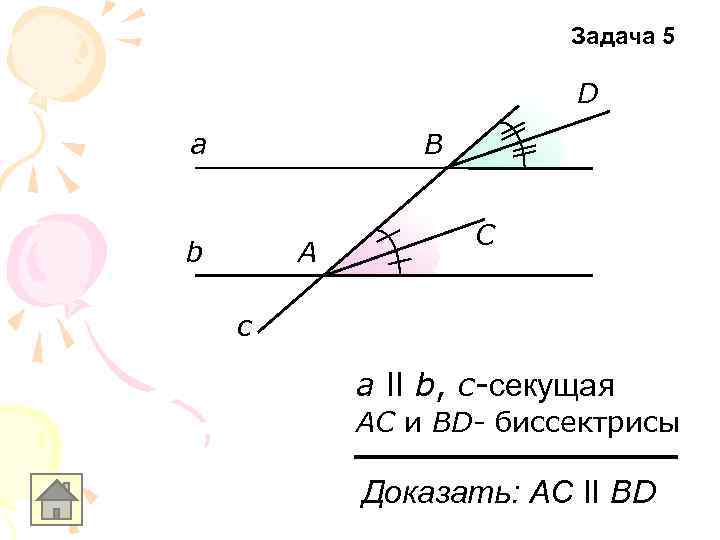Задача 5 D а В b А С c а ll b, с-секущая АС и ВD- биссектрисы Доказать: АС ll ВD
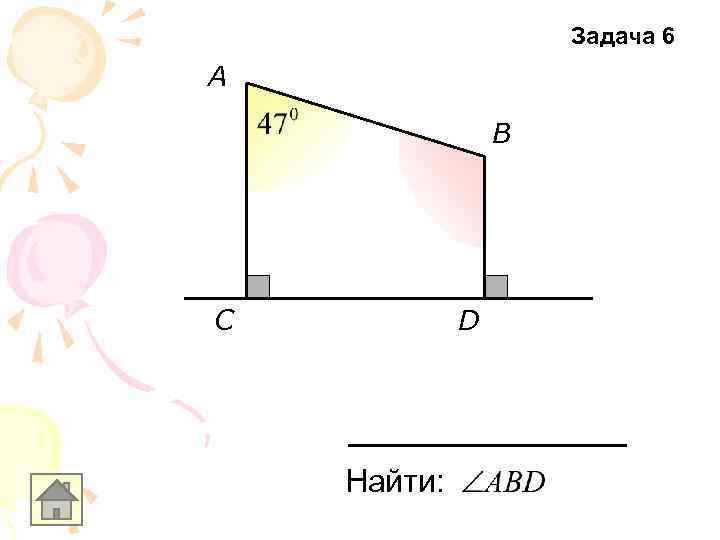Задача 6 A B С D Найти:
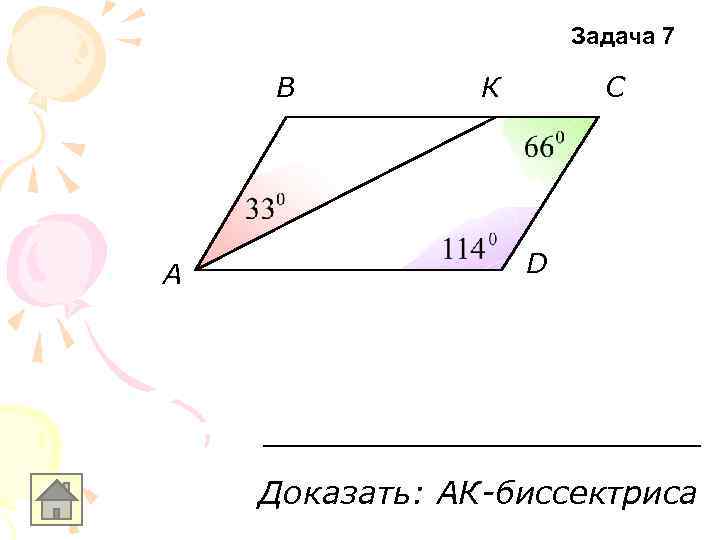Задача 7 В A К С D Доказать: АК-биссектриса
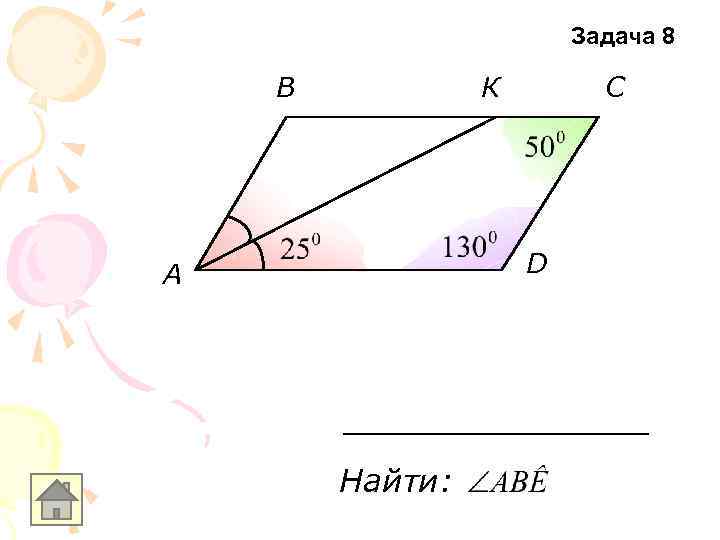Задача 8 В К С D A Найти:
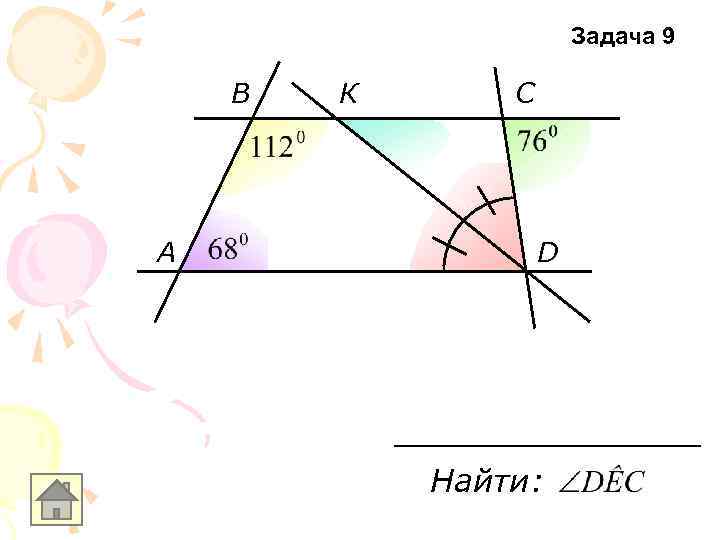Задача 9 В A К С D Найти:
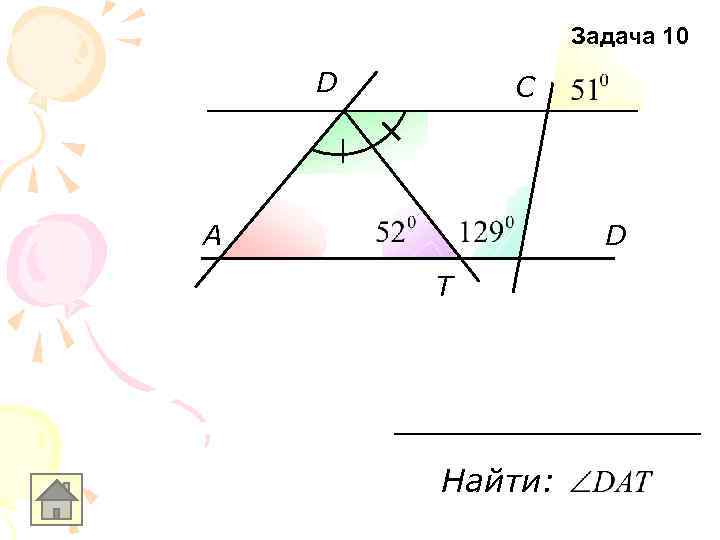Задача 10 D C A D T Найти:
1. Ершова А. П. , Голобородько В. В, Ершова А. С Самостоятельные и контрольные работы по алгебре и геометриидля 7 класса. -М: Илекса, 2004. -176 с. 2. Саврасова С. М. , Ястребинецкий Г. А. Упражнения по планиметрии на готовых чертежах. М. : просвещение, 1987. -112 с. : ил. 3. Зив Б. Г. и др. Задачи по геометрии: Пособие для учащихся 7 -11 кл. общеобразоват. учреждений. -М. : Просвещение, 2000. -271 с. : ил. 4. Рабинович Е. М. Сборник задач на готовых чертежах. -К. : 1996. -56 с. 5. Гаврилова Н. Ф. Поурочные разработки по геометрии: 7 класс. -2 -е изд. , перераб. и доп. -М. : ВАКО, 2009. -304 с.