1 2









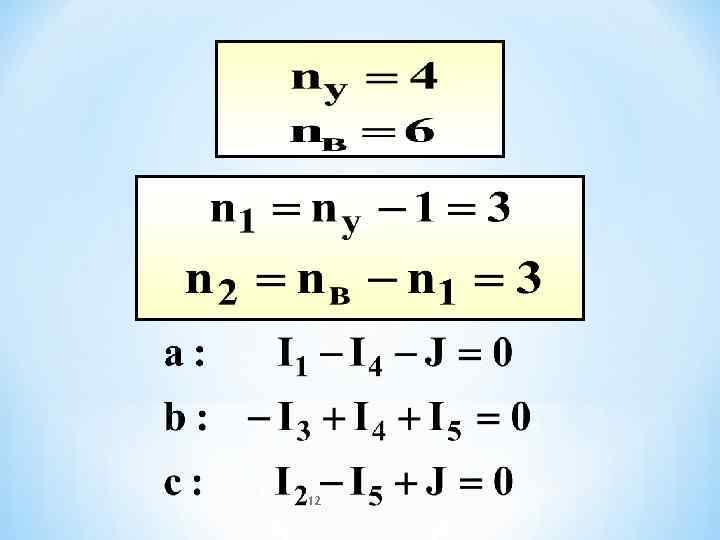
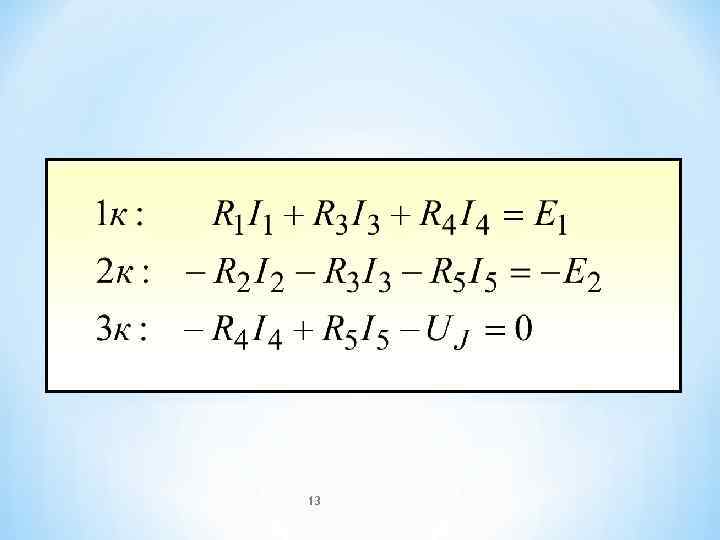




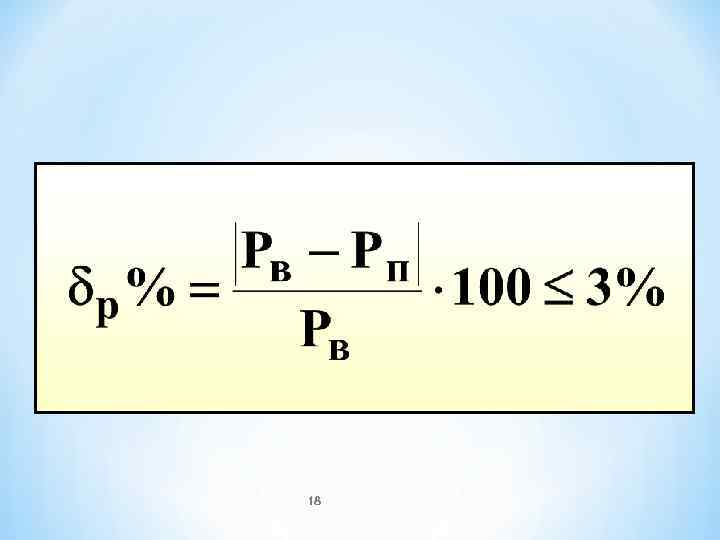













 1
1
 2
2
 * Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах 3
* Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах 3
 4
4
 * Для любого узла цепи алгебраическая сумма токов равна нулю, причем со знаком “ + ” принимаются токи, входящие в узел 5
* Для любого узла цепи алгебраическая сумма токов равна нулю, причем со знаком “ + ” принимаются токи, входящие в узел 5
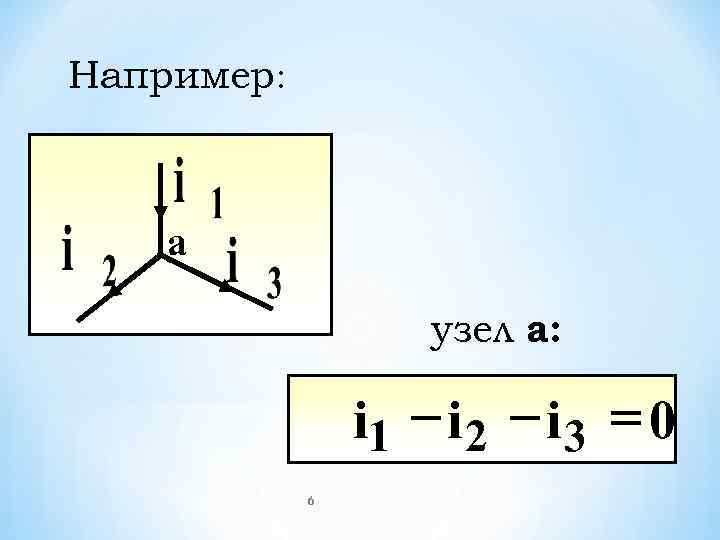
 Например: а узел а: i 1 - i 2 - i 3 = 0 6
Например: а узел а: i 1 - i 2 - i 3 = 0 6
 * Физически первый закон Кирхгофа – это закон непрерывности электрического тока Для любого контура цепи алгебраическая сумма напряжений на пассивных элементах и источниках тока равна алгебраической сумме ЭДС 7
* Физически первый закон Кирхгофа – это закон непрерывности электрического тока Для любого контура цепи алгебраическая сумма напряжений на пассивных элементах и источниках тока равна алгебраической сумме ЭДС 7
 * Со знаком “+” принимаются те слагаемые, положительные направления которых совпадают с направлением обхода контура 8
* Со знаком “+” принимаются те слагаемые, положительные направления которых совпадают с направлением обхода контура 8
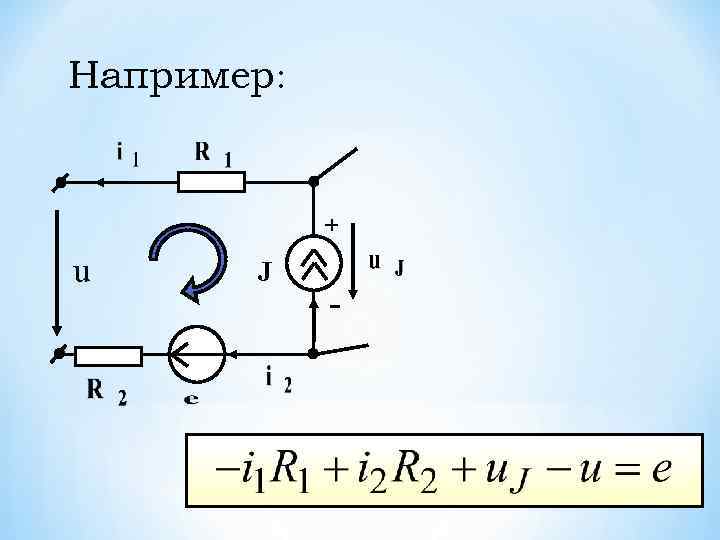
 Например: + u J - 9
Например: + u J - 9
 * Физически второй закон Кирхгофа характеризует равновесие напряжений в любом контуре цепи Решение системы уравнений, составленных по законам Кирхгофа, позволяет определить все токи и напряжения в рассматриваемой цепи 10
* Физически второй закон Кирхгофа характеризует равновесие напряжений в любом контуре цепи Решение системы уравнений, составленных по законам Кирхгофа, позволяет определить все токи и напряжения в рассматриваемой цепи 10
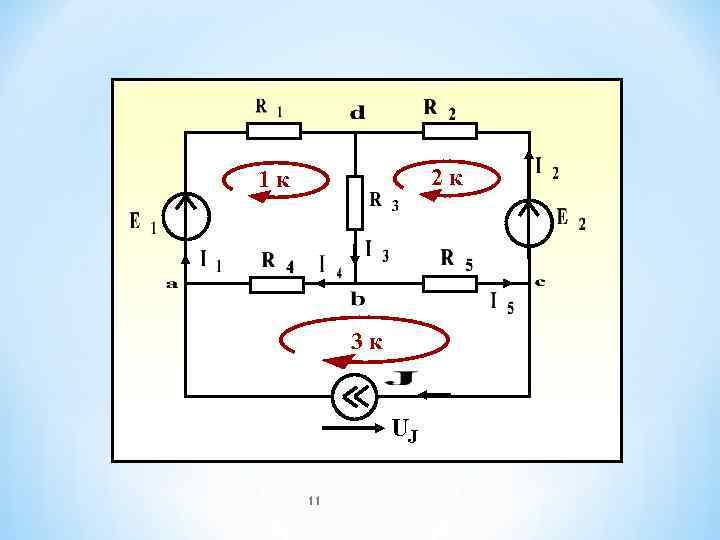
 1 к 2 к 3 к UJ 11
1 к 2 к 3 к UJ 11
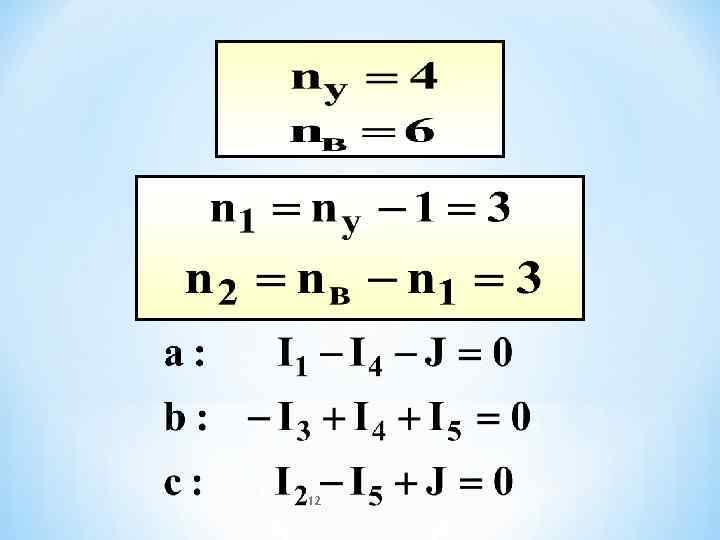 12
12
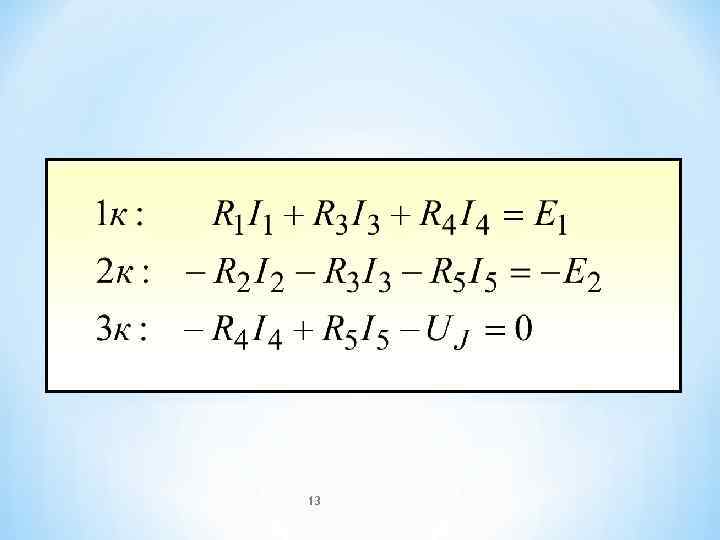 13
13
 14
14
 Для любого момента времени сумма вырабатываемых мощностей источников равна сумме потребляемых мощностей во всех пассивных элементах рассматриваемой цепи или 15
Для любого момента времени сумма вырабатываемых мощностей источников равна сумме потребляемых мощностей во всех пассивных элементах рассматриваемой цепи или 15
 * Эта теорема является законом сохранения энергии в электрической цепи и применяется как баланс мощностей для проверки правильности расчетов 16
* Эта теорема является законом сохранения энергии в электрической цепи и применяется как баланс мощностей для проверки правильности расчетов 16
 Составим баланс мощностей для резистивной цепи с постоянными напряжениями и токами предыдущего примера 17
Составим баланс мощностей для резистивной цепи с постоянными напряжениями и токами предыдущего примера 17
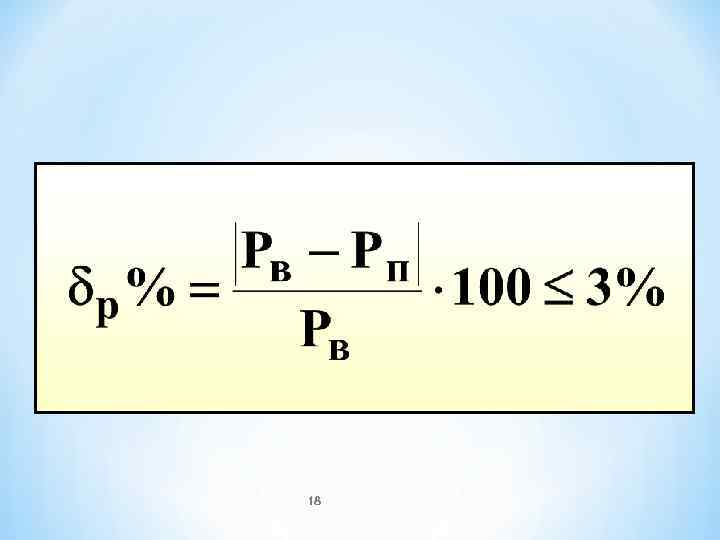 18
18
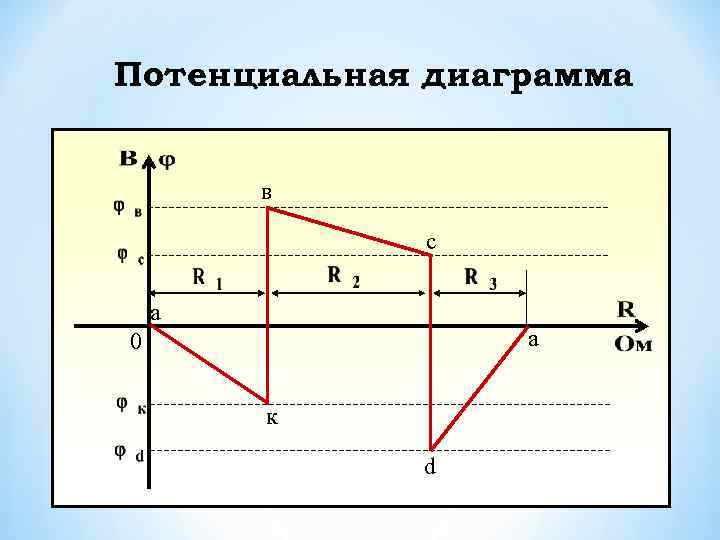
 Потенциальная диаграмма - это графическое изображение второго закона Кирхгофа, которая применяется для проверки правильности расчетов в линейных резистивных цепях Потенциальная диаграмма строится для контура без источников тока, причем потенциалы точек начала и конца диаграммы должны получиться одинаковыми 19
Потенциальная диаграмма - это графическое изображение второго закона Кирхгофа, которая применяется для проверки правильности расчетов в линейных резистивных цепях Потенциальная диаграмма строится для контура без источников тока, причем потенциалы точек начала и конца диаграммы должны получиться одинаковыми 19
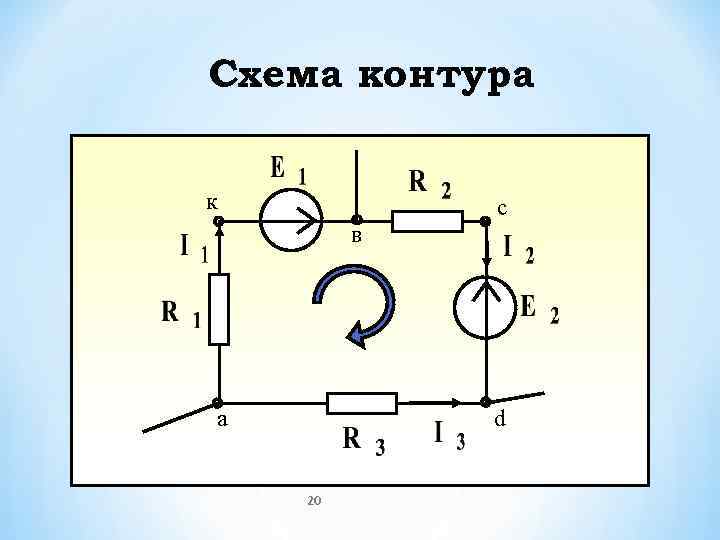
 Схема контура к c в а d 20
Схема контура к c в а d 20
 Потенциалы точек контура : 21
Потенциалы точек контура : 21
 Потенциальная диаграмма в с a 0 a к d 22
Потенциальная диаграмма в с a 0 a к d 22
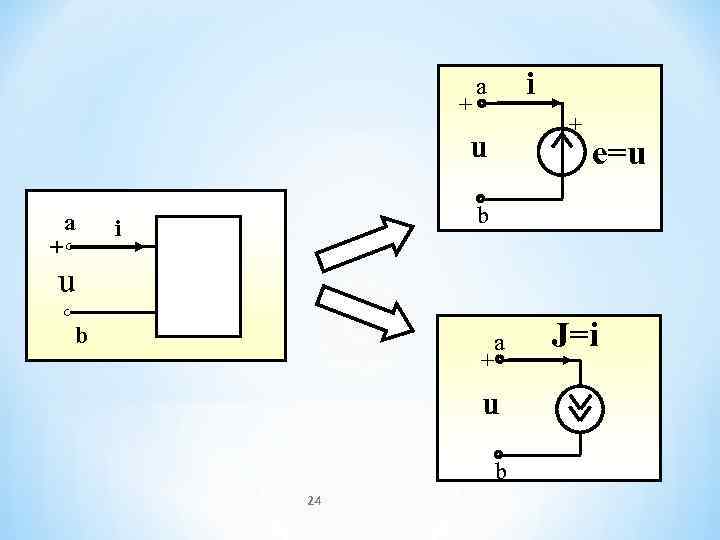
 Теорема компенсации справедлива для линейных и нелинейных цепей и может быть доказана при помощи законов Кирхгофа Любой элемент цепи можно заменить источником ЭДС или источником тока, причем ЭДС равна напряжению элемента, а ток источника равен току этого элемента 23
Теорема компенсации справедлива для линейных и нелинейных цепей и может быть доказана при помощи законов Кирхгофа Любой элемент цепи можно заменить источником ЭДС или источником тока, причем ЭДС равна напряжению элемента, а ток источника равен току этого элемента 23
 a i + u e=u а b i + u b a J=i + u b 24
a i + u e=u а b i + u b a J=i + u b 24
 * Теорему компенсации удобно использовать если задано напряжение u или ток i на участке цепи 25
* Теорему компенсации удобно использовать если задано напряжение u или ток i на участке цепи 25
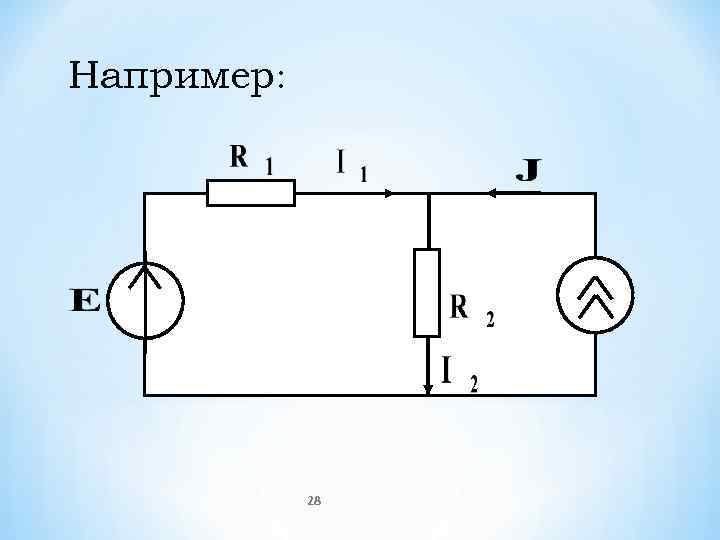
 Свойства линейных цепей рассмотрим на примере резистивных цепей с постоянными напряжениями и токами, причем эти свойства могут быть доказаны при помощи законов Ома и Кирхгофа 1. Принцип наложения 26
Свойства линейных цепей рассмотрим на примере резистивных цепей с постоянными напряжениями и токами, причем эти свойства могут быть доказаны при помощи законов Ома и Кирхгофа 1. Принцип наложения 26
 * Ток (напряжение) в любой ветви можно рассматривать как алгебраическую сумму составляющих от действия каждого источника в отдельности При этом со знаком “+” пишутся те составляющие, направления которых совпадает с направлением результирующих величин 27
* Ток (напряжение) в любой ветви можно рассматривать как алгебраическую сумму составляющих от действия каждого источника в отдельности При этом со знаком “+” пишутся те составляющие, направления которых совпадает с направлением результирующих величин 27
 Например: 28
Например: 28
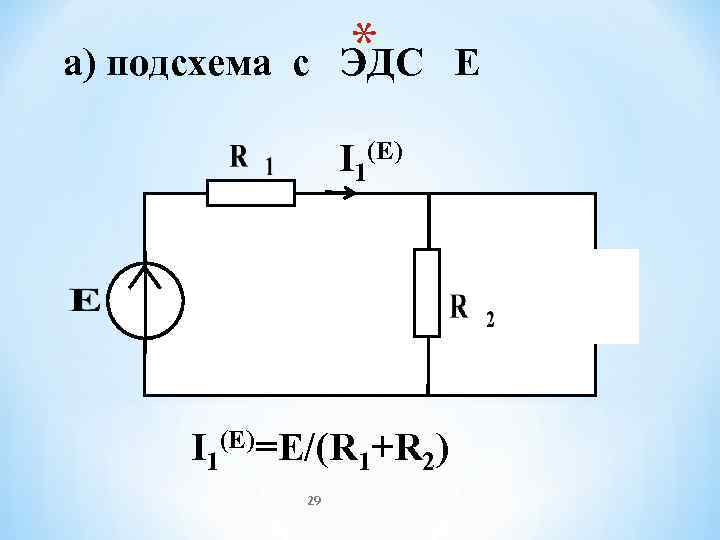
 * а) подсхема с ЭДС Е I 1(E)=E/(R 1+R 2) 29
* а) подсхема с ЭДС Е I 1(E)=E/(R 1+R 2) 29
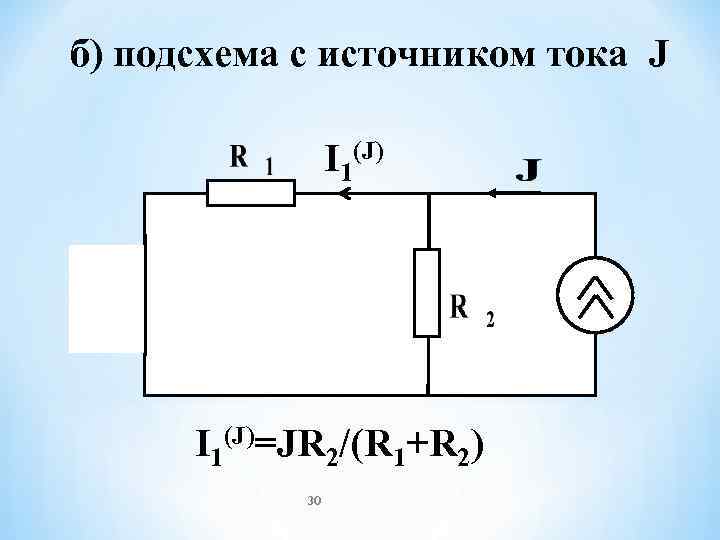
 б) подсхема с источником тока J I 1(J)=JR 2/(R 1+R 2) 30
б) подсхема с источником тока J I 1(J)=JR 2/(R 1+R 2) 30
 31
31
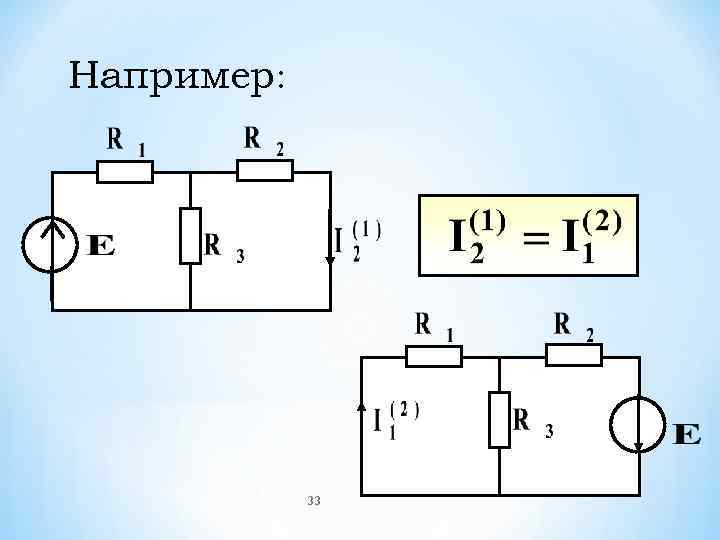
 * Перестановка единственного источника ЭДС из ветви m в ветвь n создает в ветви m ток, равный току в ветви n до перестановки источника 32
* Перестановка единственного источника ЭДС из ветви m в ветвь n создает в ветви m ток, равный току в ветви n до перестановки источника 32
 Например: 33
Например: 33
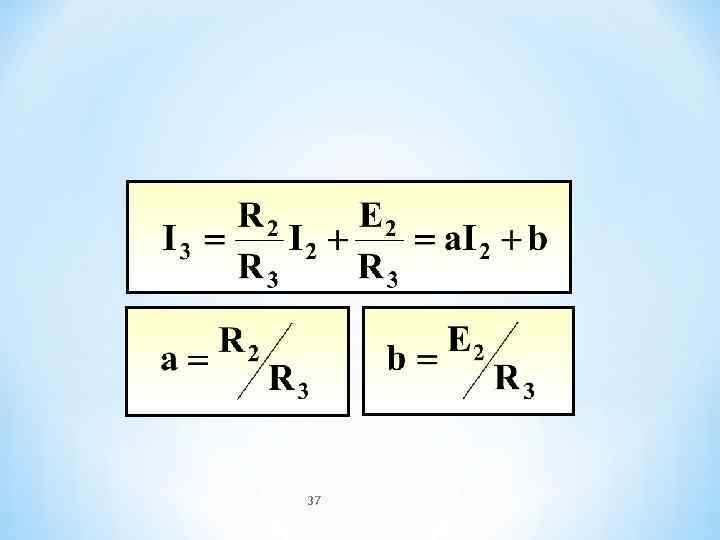
 * y=ax+b где y и x-напряжения или токи, а, b - постоянные коэффициенты 34
* y=ax+b где y и x-напряжения или токи, а, b - постоянные коэффициенты 34
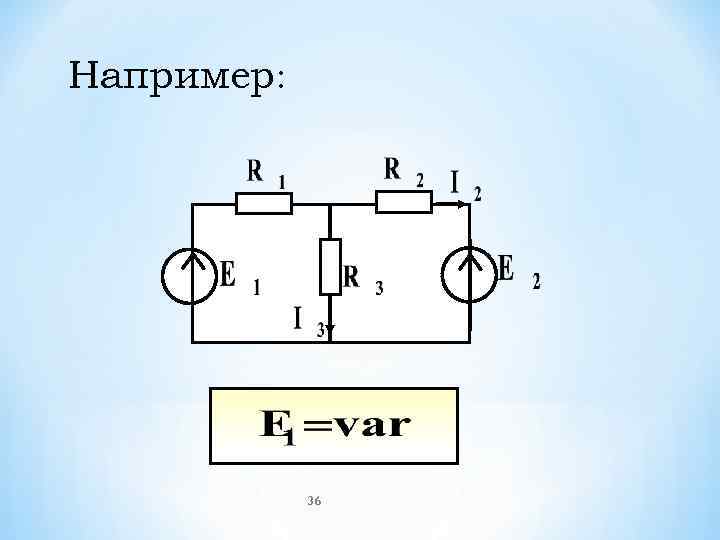
 * При изменении в цепи одного параметра (ЭДС, ток источника тока, сопротивление резистивного элемента) между двумя токами (напряжениями) существует линейная зависимость 35
* При изменении в цепи одного параметра (ЭДС, ток источника тока, сопротивление резистивного элемента) между двумя токами (напряжениями) существует линейная зависимость 35
 Например: 36
Например: 36
 37
37
 * IК = EГ /(RК +RГ )= = JГ /( 1+ RК / RГ ) где EГ = UК(ХХ) , JГ = IК(КЗ) =ЕГ / RГ, RГ = RЭКВ 38
* IК = EГ /(RК +RГ )= = JГ /( 1+ RК / RГ ) где EГ = UК(ХХ) , JГ = IК(КЗ) =ЕГ / RГ, RГ = RЭКВ 38
 * Ток IK в любой к-ветви можно определить от действия ЭДС ЕГ или источника тока JГ эквивалентного генератора У этого генератора ЭДС EГ равна напряжению холостого хода UK(XX) , когда IK=0, а ток источника тока JГ равен току короткого замыкания IK(KЗ), когда UK = 0 При этом сопротивление RГ генератора равно эквивалентному сопротивлению RЭКВ цепи относительно зажимов сопротивления RК 39
* Ток IK в любой к-ветви можно определить от действия ЭДС ЕГ или источника тока JГ эквивалентного генератора У этого генератора ЭДС EГ равна напряжению холостого хода UK(XX) , когда IK=0, а ток источника тока JГ равен току короткого замыкания IK(KЗ), когда UK = 0 При этом сопротивление RГ генератора равно эквивалентному сопротивлению RЭКВ цепи относительно зажимов сопротивления RК 39
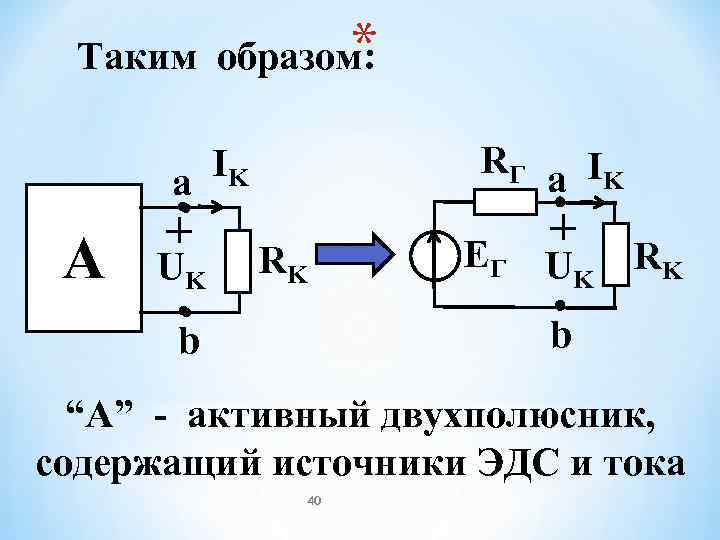
 * Таким образом: IK RГ a IK a А UK RK Е Г U RK K b “А” - активный двухполюсник, содержащий источники ЭДС и тока 40
* Таким образом: IK RГ a IK a А UK RK Е Г U RK K b “А” - активный двухполюсник, содержащий источники ЭДС и тока 40
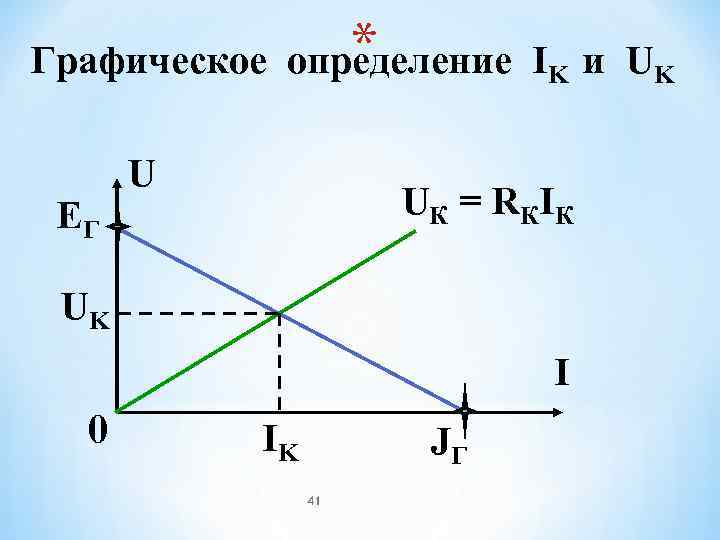
 * Графическое определение IK и UK U EГ U К = R КI К UK I 0 IK JГ 41
* Графическое определение IK и UK U EГ U К = R КI К UK I 0 IK JГ 41
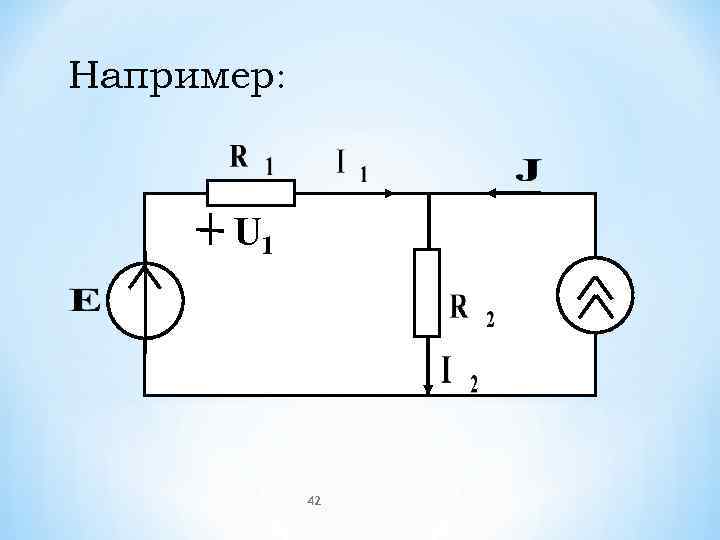
 Например: U 1 42
Например: U 1 42
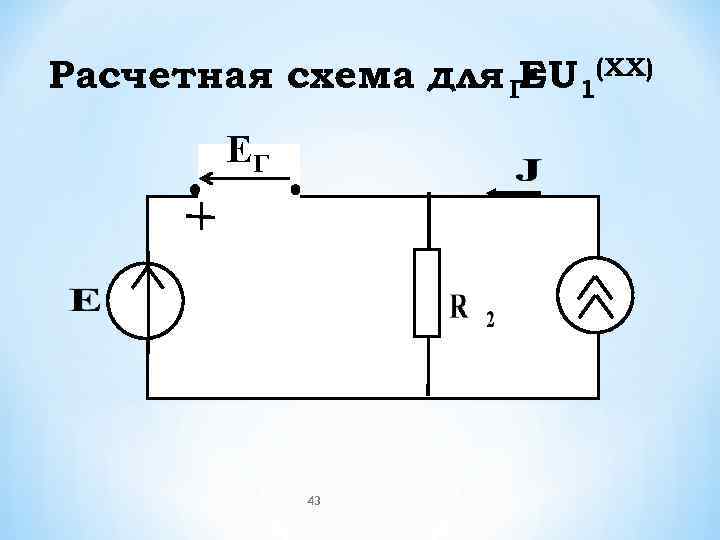
 Расчетная схема для Г=U 1(XX) ЕГ 43
Расчетная схема для Г=U 1(XX) ЕГ 43
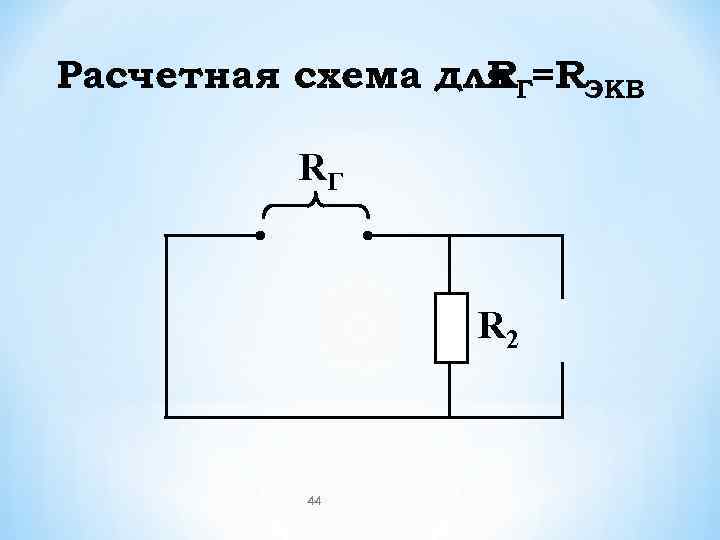
 Расчетная схема для Г=RЭКВ R RГ R 2 44
Расчетная схема для Г=RЭКВ R RГ R 2 44
 * Для тока I 1 имеем: E Г = E – R 2 J JГ = E / R 2 - J RГ = R 2 I 1= EГ /(RГ + R 1) = = E /(R 1 + R 2) – R 2 J /(R 1+ R 2) 45
* Для тока I 1 имеем: E Г = E – R 2 J JГ = E / R 2 - J RГ = R 2 I 1= EГ /(RГ + R 1) = = E /(R 1 + R 2) – R 2 J /(R 1+ R 2) 45

