
1

2

1. Подробно написать, почему у берегов Перу много рыбы (начать с неравномерного прогрева Солнцем поверхности Земли) 2. Записать уравнение Гельмгольца, раскрыв полную производную по времени. При каких условиях оно существует. 3. Уравнения Эйлера, неразрывности, линии тока, Бернулли-Эйлера, Фридмана 3

1. Показать, что если на поверхности односвязного объема потенциал скорости имеет постоянное значение, то такое значение будет и в любой точке внутри объема. 2. Записать уравнение движения идеальной жидкости (уравнение Эйлера) 3. Записать выражение для потока скорости через контур АВ и циркуляции скорости через контур L 4

1. Выражение скорости течения через функцию тока 2. Чему равна функция тока на линии тока? 3. Условие аналитичности функции w= +i комплексного аргумента z=x+iy 4. Написать выражение комплексной скорости 5

Рассмотрим плоское движение u(ux, uy) Запишем уравнение линии тока: Вдоль линии тока Если ввести такую функцию , что то вдоль линии тока 6

На каждой линии тока функция тока сохраняет постоянное значение, которое, вообще говоря, различно для разных линий тока. 7

Поток скорости выразим через функцию тока 8

Поток скорости через контур AB B A Записать через функцию тока 9
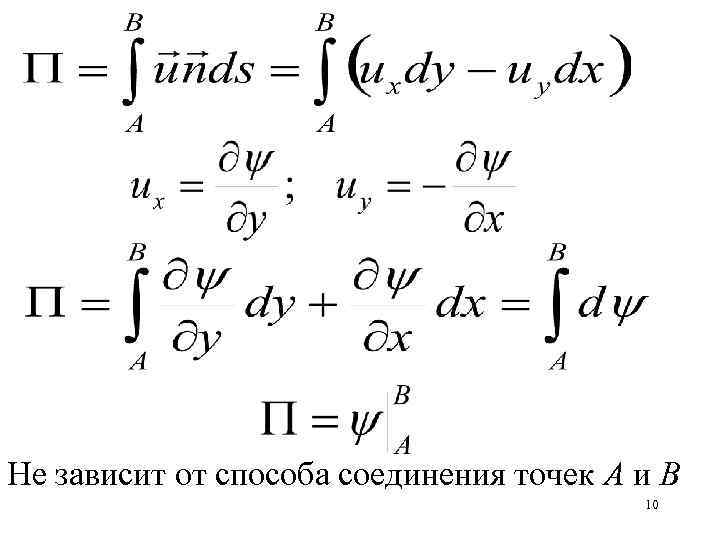
Не зависит от способа соединения точек А и B 10

Найти выражение вихря через функцию тока 11

Для плоского движения u(ux, uy) запишем компоненты ротора скорости Если движение безвихревое 12 функция тока удовлетворяет уравнению Лапласа

Запишем компоненты скорости течения, используя потенциал скорости и функцию тока: 13
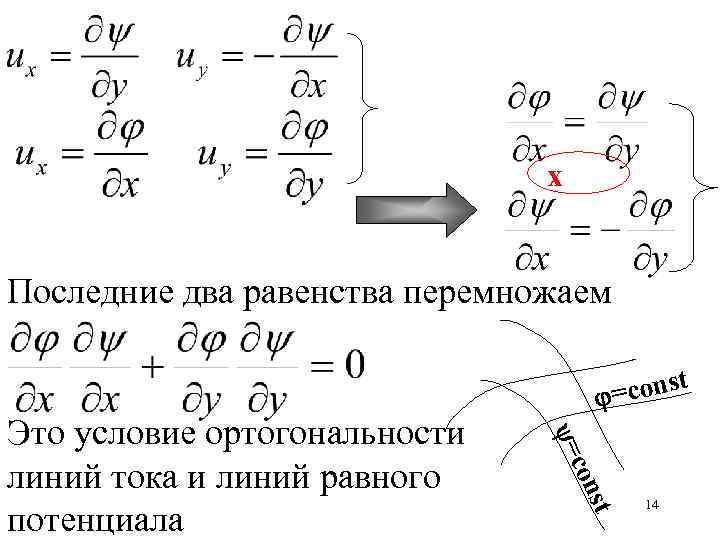
х Последние два равенства перемножаем = st con Это условие ортогональности линий тока и линий равного потенциала t =cons 14

Потенциал скорости через функцию тока Пусть известен потенциал скорости (x, y). (1) 15

Интегрируем (1) от некоторого значения а до х (2) Для определения F(y) дифференцируем (2) 16
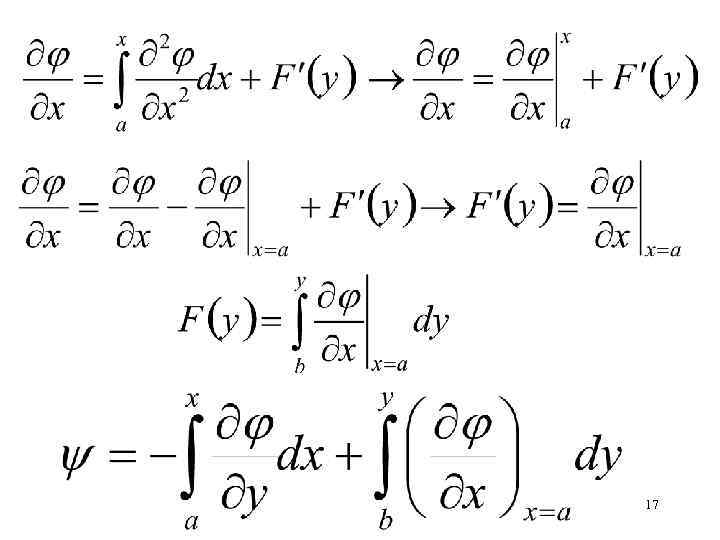
17

Жидкость несжимаема, заключена в объем с поверхностью S 18

Преобразование Грина n –направление внутренней нормали к S 19

Если Энергия объема определяется движением на границе. Когда она равна нулю? 20

Энергия объема равна нулю при условии, что жидкость не протекает через границу, если потенциал на всей границе имеет постоянное значение 21

объема несжимаемой жидкости, ограниченного замкнутым контуром L (плоская задача) 22
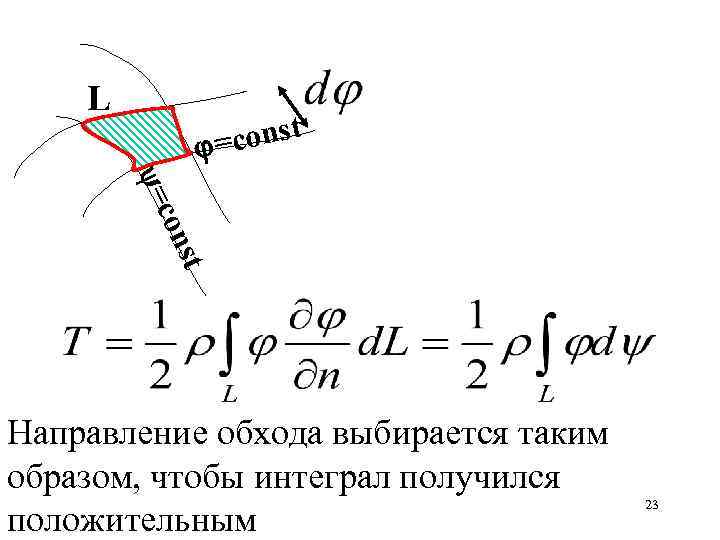
L const = = st con Направление обхода выбирается таким образом, чтобы интеграл получился положительным 23

w= +i 24

Условия Коши-Римана для и 25

iy i 1 х Условия Коши-Римана для и это условия аналитичности функции w= +i комплексного аргумента z=x+iy. Это значит, что эта функция w=f(z) имеет определенную производную ux -uy 26

Производная комплексной функции 27

D = x(x 0, y 0)D x + y(x 0, y 0)D y +x (x, y); D = x(x 0, y 0)D x+ y(x 0, y 0)D y + h (x, y); V(x, y)=x (x, y)+ih (x, y) 28
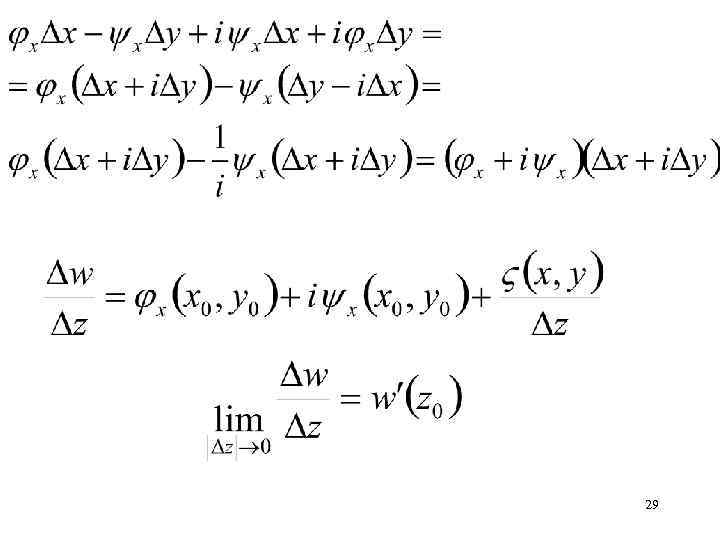
29
![iy i 1 х Построить отрезок [(1, i), (2, -2 i)] 30 iy i 1 х Построить отрезок [(1, i), (2, -2 i)] 30](https://present5.com/presentation/16510224_281517172/image-30.jpg)
iy i 1 х Построить отрезок [(1, i), (2, -2 i)] 30

iy х - комплексная скорость Функция w= +i называется комплексным потенциалом, однозначно определяет плоское течение 31

Задан комплексный потенциал a – действительная величина, константа Определить линии тока, линии равного потенциала, поле скорости 32
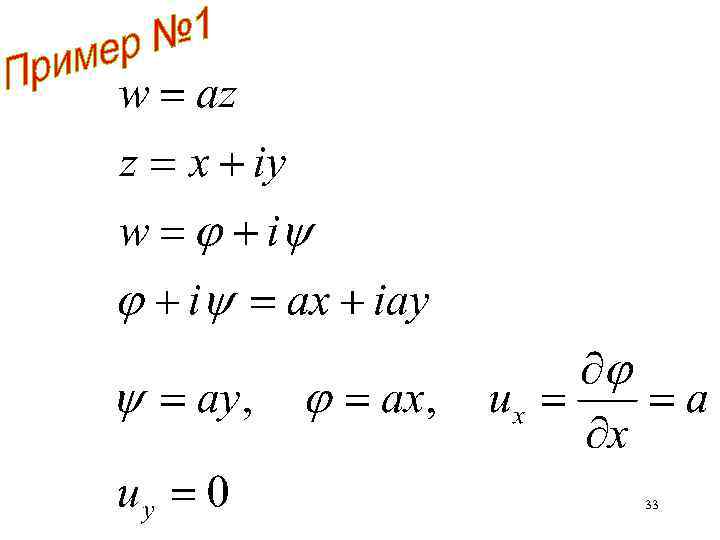
33

На линии тока функция тока сохраняет постоянное значение y Линия тока х 34
![Найти поток скорости через отрезок [i, 1]. Найти энергию объема, заключенного внутри контура [(1), Найти поток скорости через отрезок [i, 1]. Найти энергию объема, заключенного внутри контура [(1),](https://present5.com/presentation/16510224_281517172/image-35.jpg)
Найти поток скорости через отрезок [i, 1]. Найти энергию объема, заключенного внутри контура [(1), (1, i), (0)] 35

iy В i А 1 х 36
![iy Энергия объема, заключенного внутри контура [(1), (1, i), (0)] i (1, i) 1 iy Энергия объема, заключенного внутри контура [(1), (1, i), (0)] i (1, i) 1](https://present5.com/presentation/16510224_281517172/image-37.jpg)
iy Энергия объема, заключенного внутри контура [(1), (1, i), (0)] i (1, i) 1 х 37
![iy Энергия объема, заключенного внутри контура [(1), (1, i), (0)] i (1, i) 1 iy Энергия объема, заключенного внутри контура [(1), (1, i), (0)] i (1, i) 1](https://present5.com/presentation/16510224_281517172/image-38.jpg)
iy Энергия объема, заключенного внутри контура [(1), (1, i), (0)] i (1, i) 1 х 38

a, b – вещественные Найти: потенциал скорости, функцию тока, скорость, комплексную скорость, линии тока 39

uy a ux b 40

iy a х b 41

вдоль линии тока Линии тока определены как: iy = a co ns t х b 42
![Найти поток через отрезок [(0), (a, -bi)] Найти энергию объема, ограниченного контуром [(1. i), Найти поток через отрезок [(0), (a, -bi)] Найти энергию объема, ограниченного контуром [(1. i),](https://present5.com/presentation/16510224_281517172/image-43.jpg)
Найти поток через отрезок [(0), (a, -bi)] Найти энергию объема, ограниченного контуром [(1. i), (-1. i). (-1. -i), (1. -i)] Найти циркуляцию скорости по этому контуру 43
![Найти поток через отрезок [(0), (a, -bi)] iy iy a b = a х Найти поток через отрезок [(0), (a, -bi)] iy iy a b = a х](https://present5.com/presentation/16510224_281517172/image-44.jpg)
Найти поток через отрезок [(0), (a, -bi)] iy iy a b = a х co n st х b 44
![Найти энергию объема, ограниченного контуром [(1, i), (-1, i). (-1, -i), (1, -i)] (-1, Найти энергию объема, ограниченного контуром [(1, i), (-1, i). (-1, -i), (1, -i)] (-1,](https://present5.com/presentation/16510224_281517172/image-45.jpg)
Найти энергию объема, ограниченного контуром [(1, i), (-1, i). (-1, -i), (1, -i)] (-1, i) (-1, -i) (1, -i) х 45

Найти потенциал скорости, функцию тока, компоненты скорости 46

47

Найти линии тока Вектор скорости нарисовать Нарисовать вектор комплексной скорости Можно ли заменить оси координат твердыми стенками? 48

y z х Линии х=0 и у=0 являются частями одной и той же линии тока =0. 49

Нарисовать линии равного потенциала 50
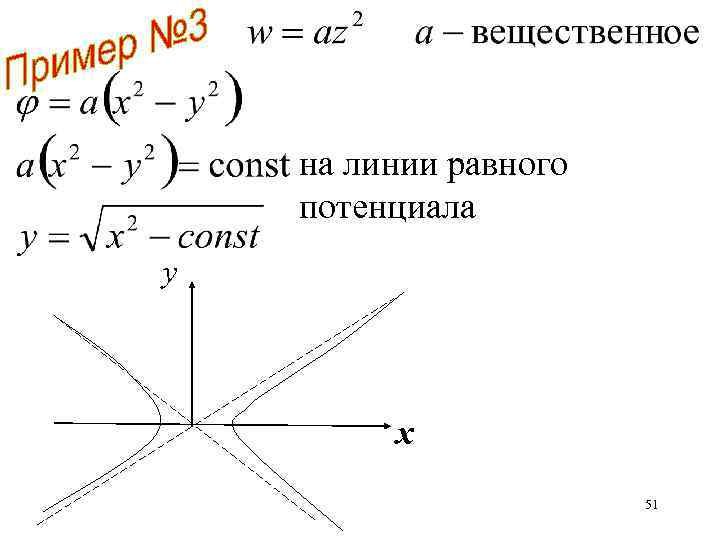
на линии равного потенциала y х 51
![Найти поток скорости через отрезок [i, 1] 52 Найти поток скорости через отрезок [i, 1] 52](https://present5.com/presentation/16510224_281517172/image-52.jpg)
Найти поток скорости через отрезок [i, 1] 52

1. Уравнение Фридмана и Гельмгольца 2. Можно ли вызвать движение неподвижной идеальной жидкости, если приложить постоянное давление по всему объему? 53
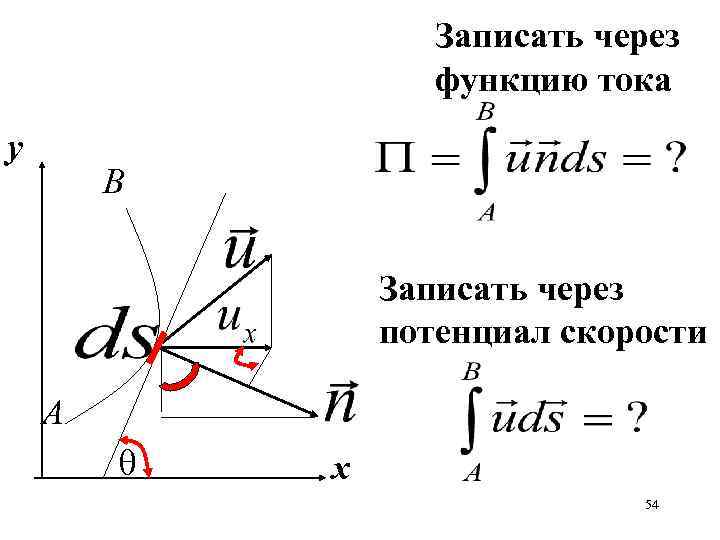
Записать через функцию тока у B Записать через потенциал скорости A х 54
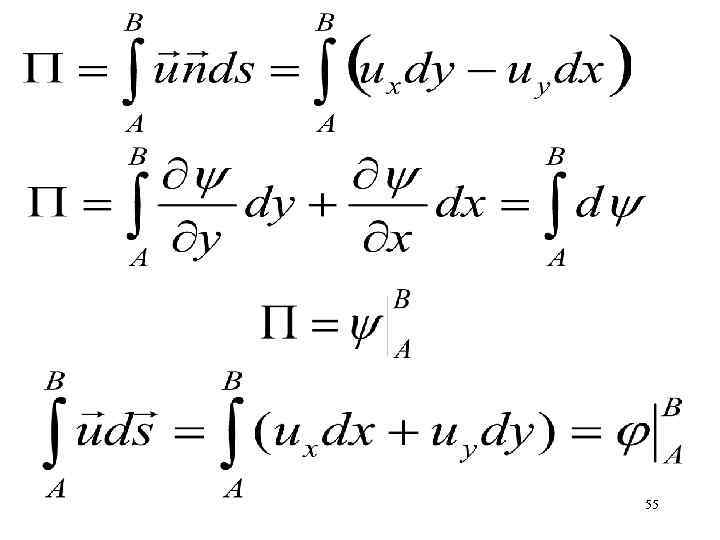
55

Найти потенциал скорости и функцию тока 56
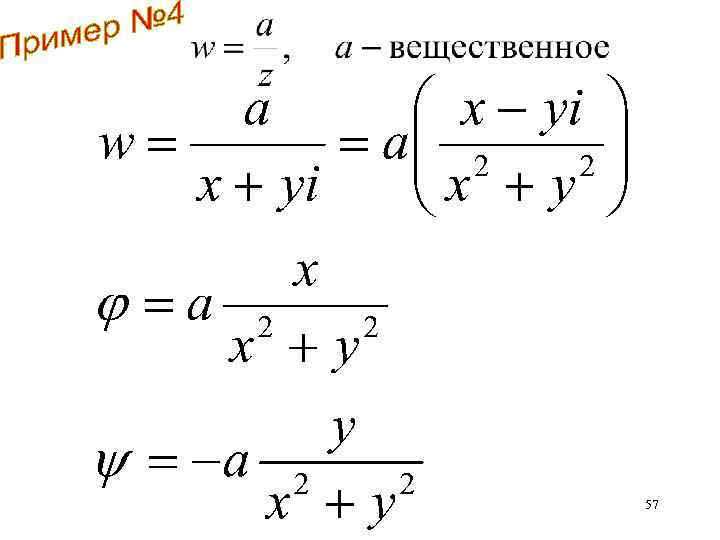
57

Определить комплексную скорость 58

Значение скорости становится бесконечно большим в начале координат. Исключаем эту точку, окружив произвольной замкнутой линией. 59

Начало координат - особая точка для комплексного потенциала (простой полюс) и для комплексной скорости (двукратный полюс). Движение потенциально везде, кроме особой точки. Линии тока незамкнутые. 60
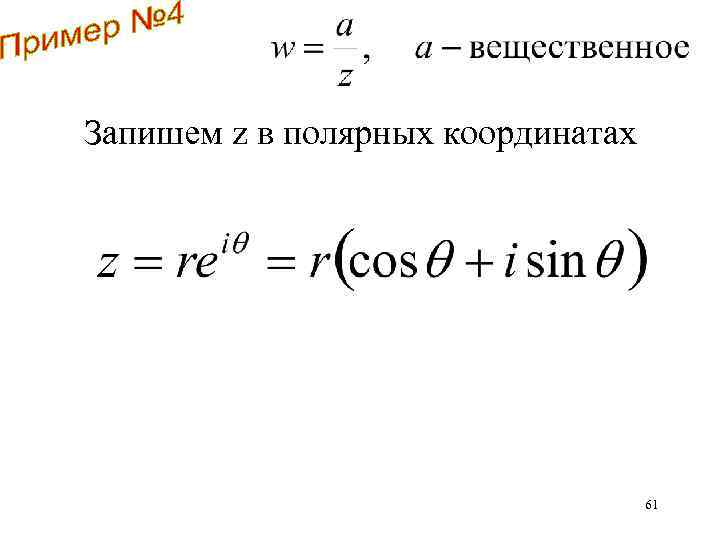
Запишем z в полярных координатах 61
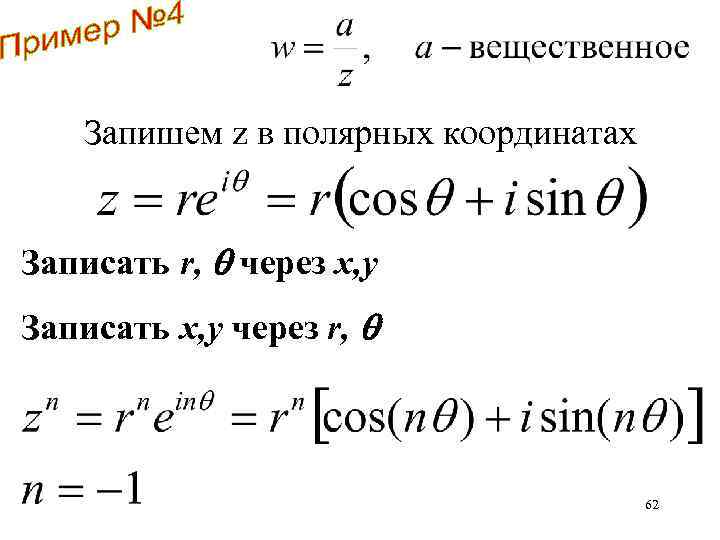
Запишем z в полярных координатах Записать r, через х, у Записать х, у через r, 62
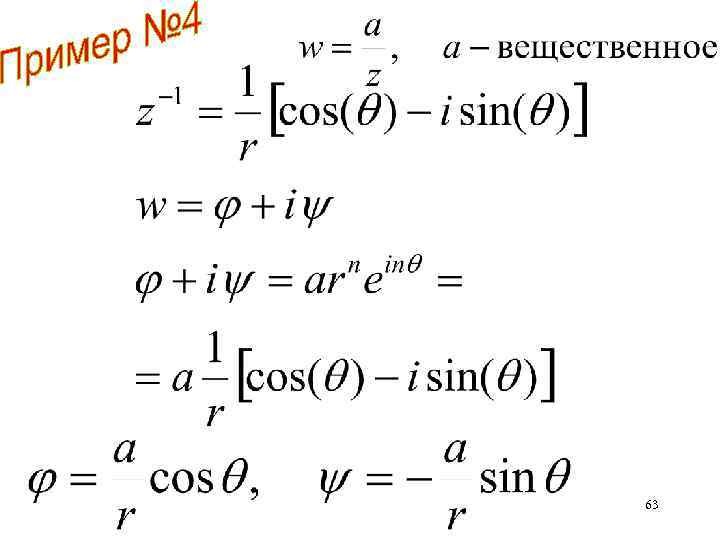
63

Нарисовать линии тока линии равного потенциала 64
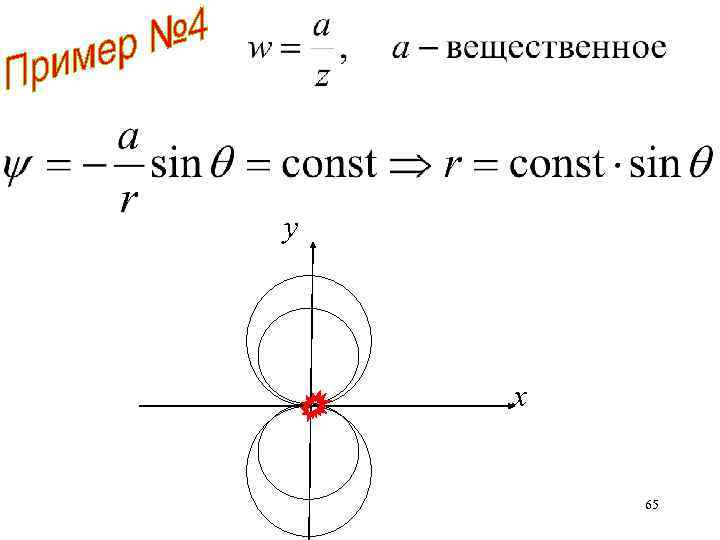
y х 65

y х 66

Определить и построить компоненты скорости ur, u , для = /4 67
![Определить поток через отрезок [(0, i), (0, -i)] 68 Определить поток через отрезок [(0, i), (0, -i)] 68](https://present5.com/presentation/16510224_281517172/image-68.jpg)
Определить поток через отрезок [(0, i), (0, -i)] 68

Линии тока Эквипотенциальные линии 69
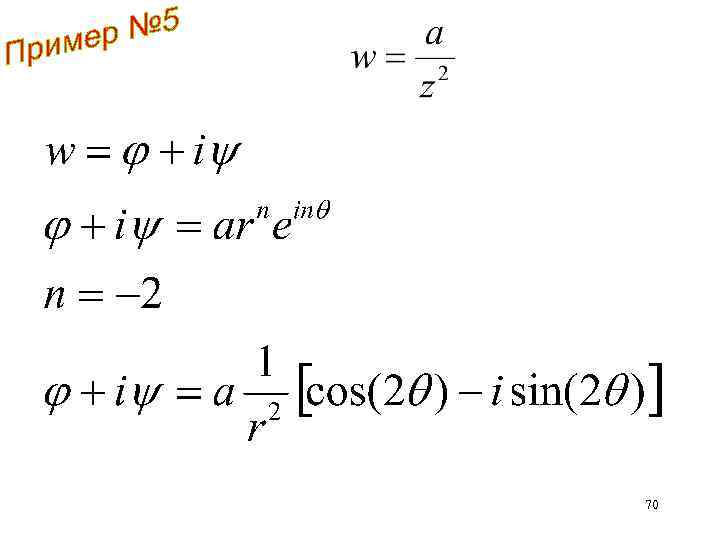
70

Лемниската Бернулли 71
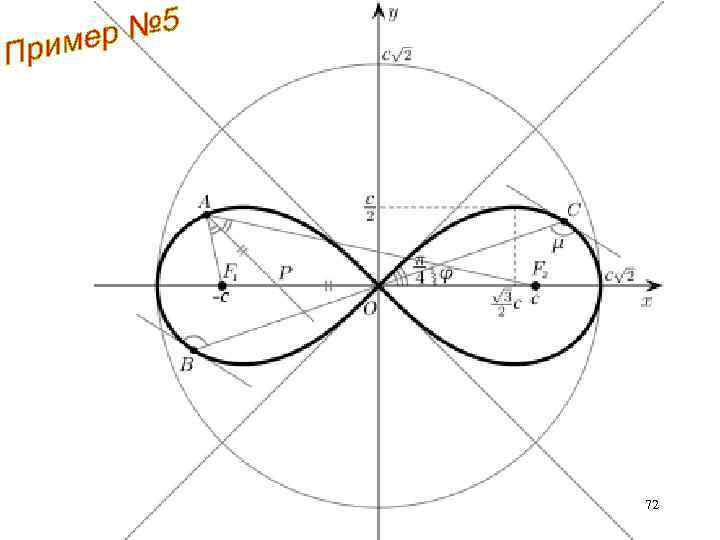
72
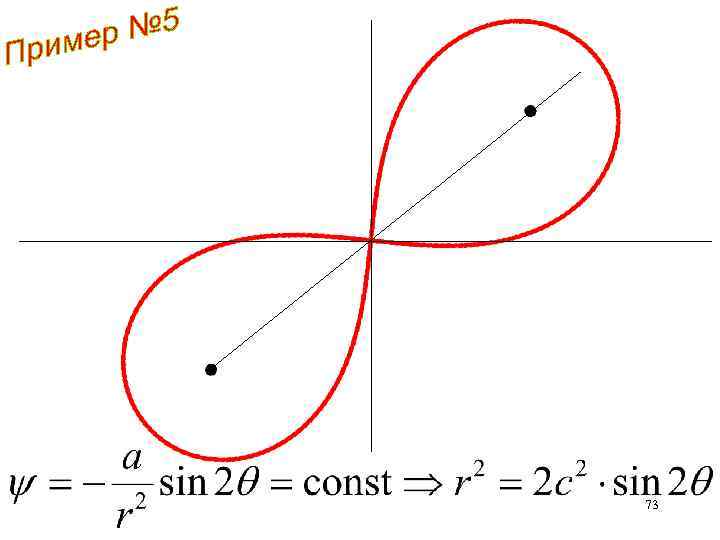
73
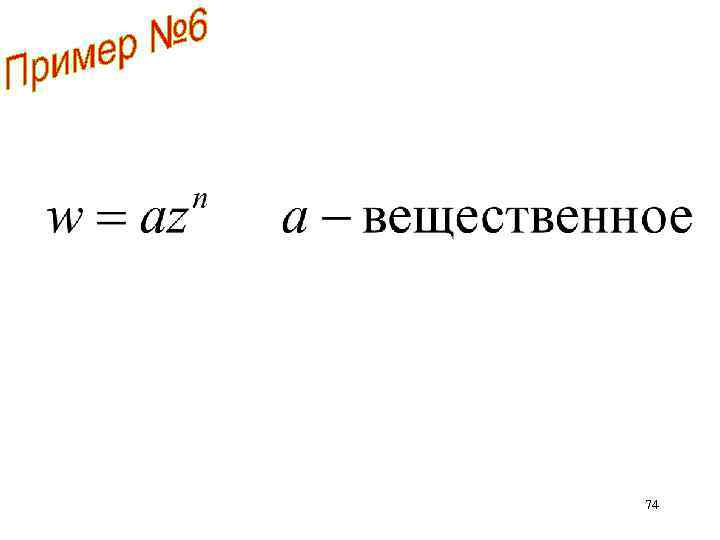
74
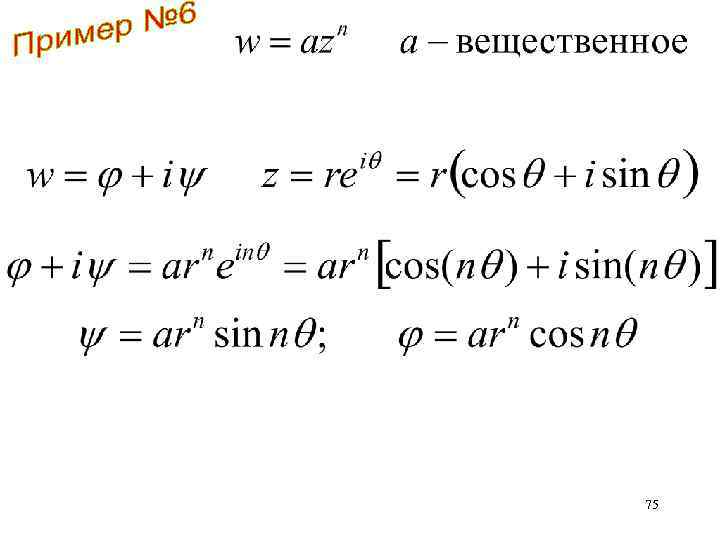
75

Линии = 0 и представляют собой части одной и той же линии тока = 0. = 0 Если положить , то получим безвихревое движение в углу, между двух твердых наклонных стенок = 0 76

Решение: На линии тока st on c = = const Построить для тупого угла 77

На линии тока = const /2 78

79

Найти скорость ur и скорость u Определить значения скорости в начале координат при 80

Компоненты скорости в направлении r и в перпендикулярном направлении : 81

< В начале координат скорость равна нулю = В начале координат скорость конечна > В начале координат скорость бесконечна 82

На участке трубы постоянного диаметра длиной 2 м приложен градиент давления (линейная зависимость от продольной координаты). Определить градиент давления на этом участке, если скорость воды возрастает от 0 до 1 м/с, а движение идеальной жидкости. Куда направлен градиент давления? 83
Осборн Рейнольдс P 0 P 84

85

Найти потенциал скорости и функцию тока 86

Найти линии тока и линии равного потенциала 87
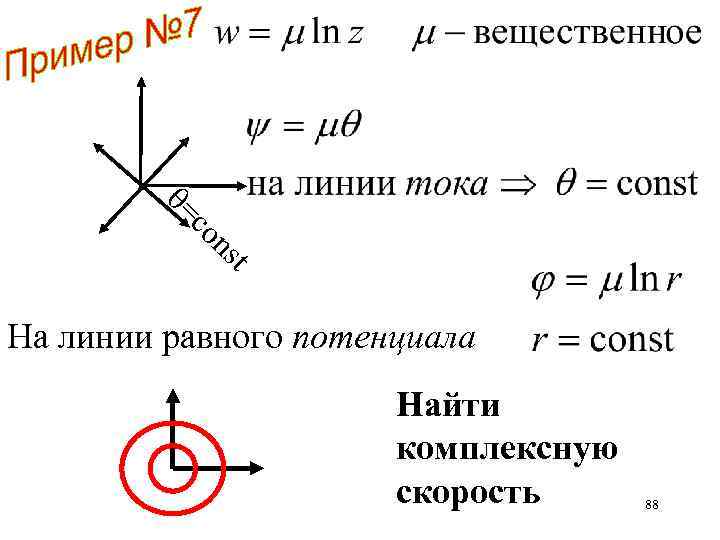
= co t ns На линии равного потенциала Найти комплексную скорость 88

В начале координат особая точка для скорости и комплексного потенциала. Исключаем эту точку, окружив произвольной замкнутой линией. Записать компоненты скорости. Построить линии равной скорости 89

Линии равной скорости концентрические окружности. В начале координат - особая точка. Поле скорости непрерывно и конечно во всех точках кроме одной. Начало должно быть исключено с помощью описанной вокруг него 90 замкнутой кривой.

Гидродинамическое истолкование потенциала = co t ns Источник из начала координат. Определить поток массы в единицу времени. 91

Поток массы (мощность источника), проходящий через окружность радиуса r в единицу времени, определяется произведением радиальной скорости на длину окружности Мощность источника 2 не зависит от радиуса (сохранение массы). Если <0, то определяет сток. 92

Если в точках плоскости z = a 1, a 2, …an находятся источники или стоки мощностью 2 1, 2 2, …, 2 n k – модуль, k – аргумент числа (z – ak) 93

Два источника мощностью 2 находятся в точках (а 1=а) и (а 2=-а). Определить функцию тока в точках (а i), (- а i), (0). a 94
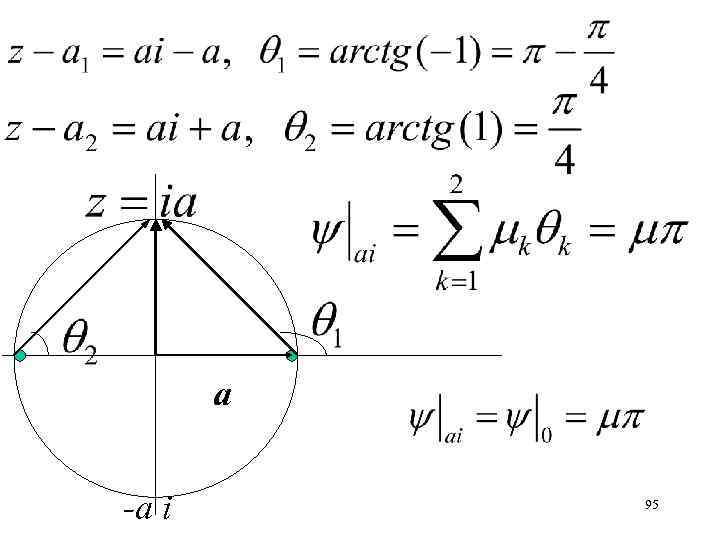
a -а i 95
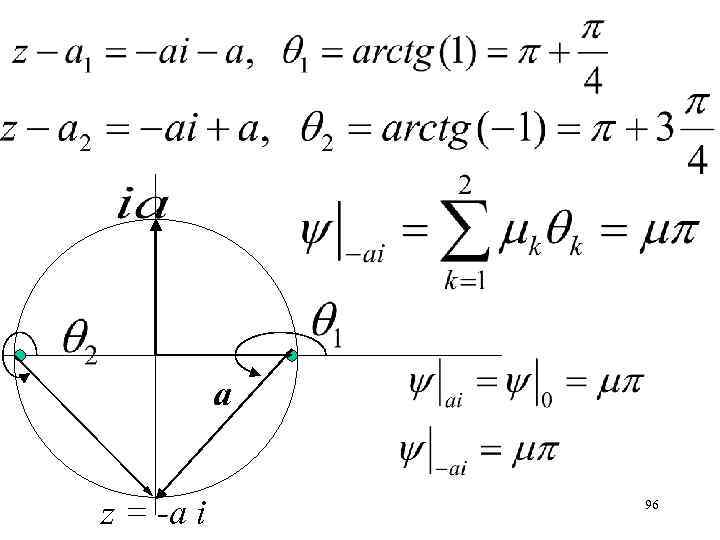
a z = -а i 96
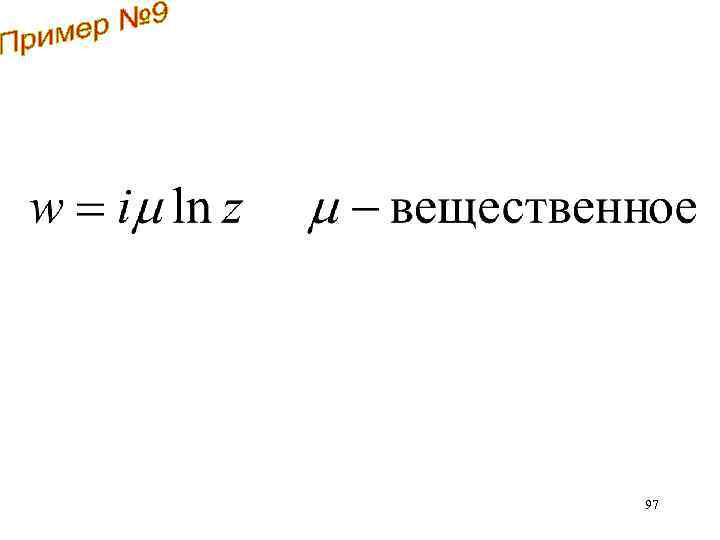
97

Описывает течение от источника Линии тока r = const концентрические окружности. Определить компоненты скорости 98

Определить ротор скорости 99
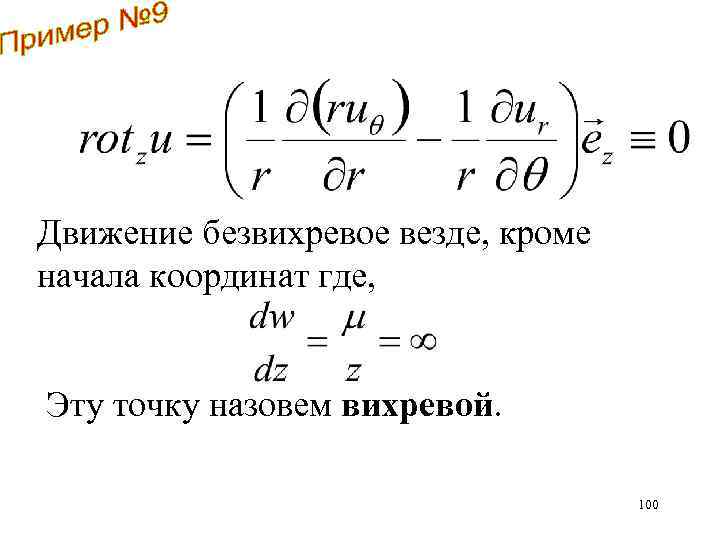
Движение безвихревое везде, кроме начала координат где, Эту точку назовем вихревой. 100

Вычислить потенциал скорости для = 0 = 2 101

Потенциал скорости - неоднозначная функция координат на плоскости ОХУ. При обходе вокруг начала координат величина потенциала меняется на. st on =c =0 = - 2 102

Определить циркуляцию скорости 103

Скорость: Циркуляция скорости по замкнутому контуру L: r L d. L Циркуляцию скорости назовем интенсивностью вихревой точки 104

Вихревая точка, расположенная в начале координат z = 0 создает плоское движение, определяемое комплексным потенциалом 105

Если вихревая точка не в начале координат, а в точке z = a, то Для n точек с интенсивностями 1, …, n 106

Точка на комплексной плоскости полностью определяется радиус-вектором с началом в начале координат, угол отсчитывается от положительного направления оси 0 х у2 у1 х2 х1 х 107
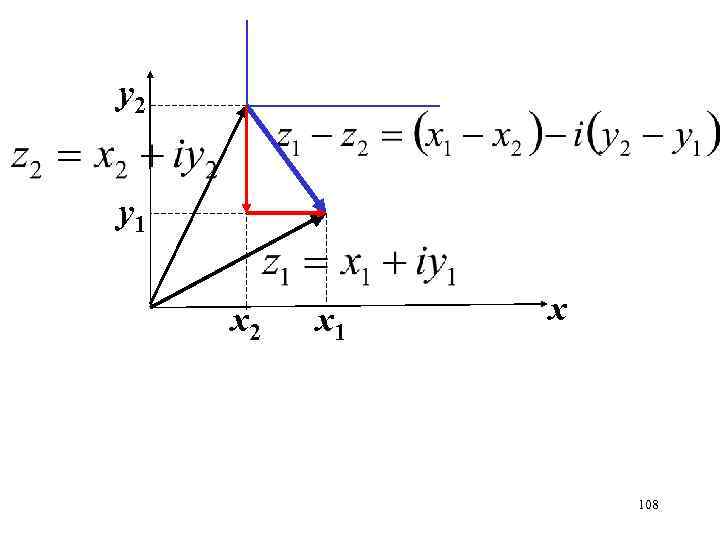
у2 у1 х2 х1 х 108
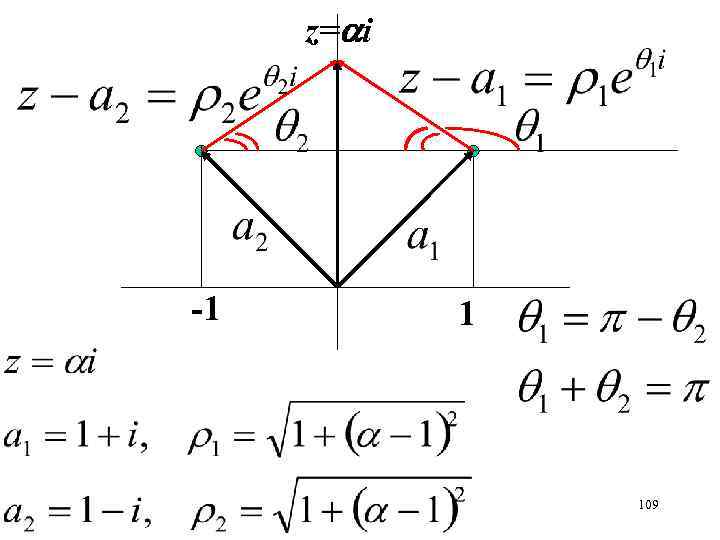
z= i -1 1 109
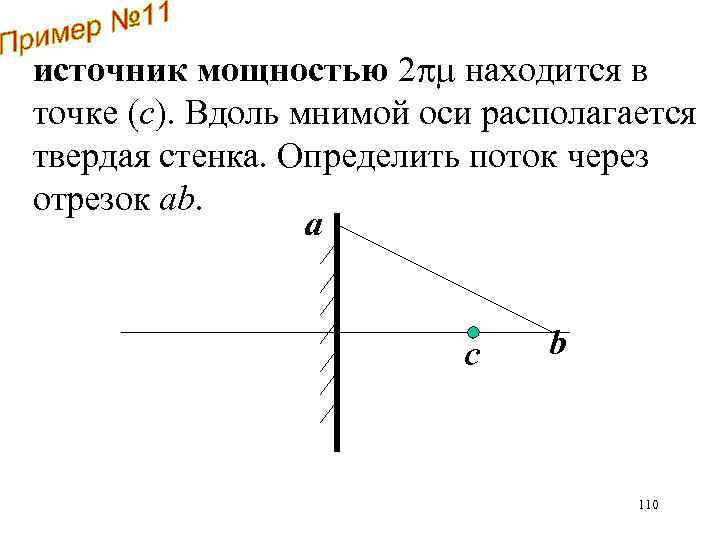
источник мощностью 2 находится в точке (с). Вдоль мнимой оси располагается твердая стенка. Определить поток через отрезок ab. a с b 110
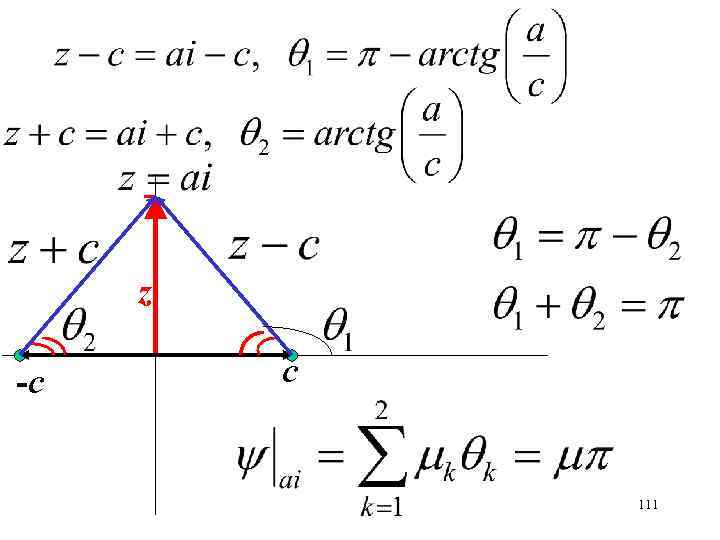
z -с с 111

аi -c c z=b Половина всего потока массы 112

источник мощностью 2 находится в точке (с), вдоль мнимой оси располагается твердая стенка. Определить поток через отрезок ab. a с b 113
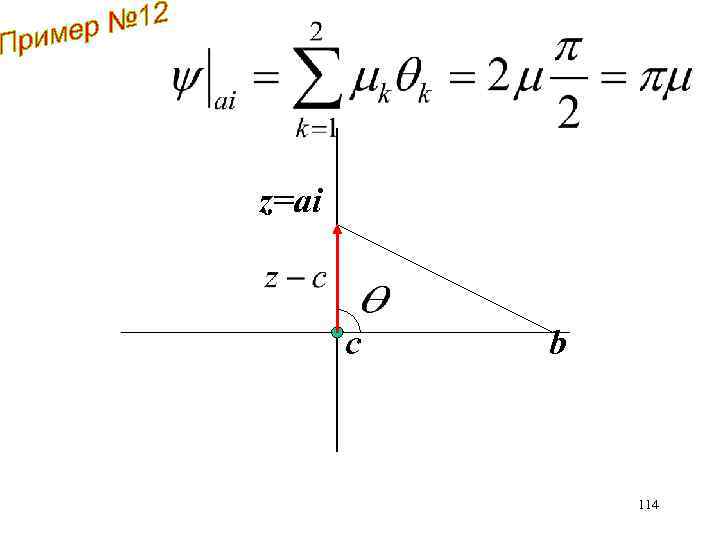
z=ai с b 114

ai с z=b Половина всего потока массы 115

ЗАДАЧА 4 В начале координат помещен сток интенсивности 2 , вдоль оси х и оси у установлены стенки, образующие прямой угол. Определить комплексный потенциал и поток через отрезок [z=1, z=i]. Определить скорость в точке z=1. 116

z=i с 1 117

i с Полный поток массы z=1 118

ЗАДАЧА 5 В точке z=1+i имеeтся источник интенсивности 2 , а в начале координат сток интенсивности -2 . Вдоль оси х и вдоль оси у установлены стенки, образующие прямой угол. Определить комплексный потенциал, линии тока и скорость в точке z=1. 119
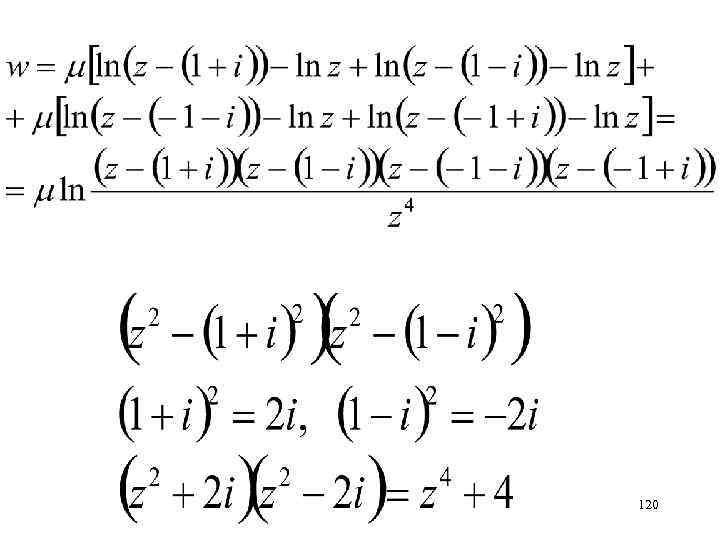
120

z=1 121
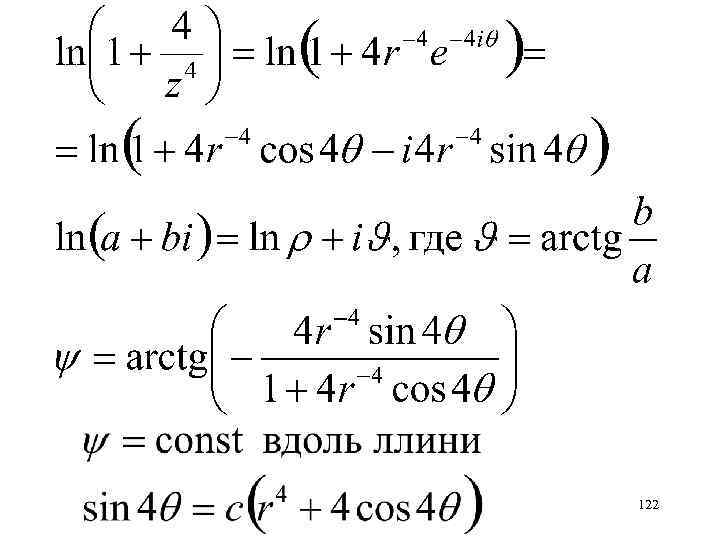
122

Две вихревые точки i -1 1 Какой интенсивностью должны обладать точки, чтобы вертикальная ось совпадала с линией тока? 123

Две вихревые точки i -1 1 Для произвольной точки на вертикальной оси z = αi 124
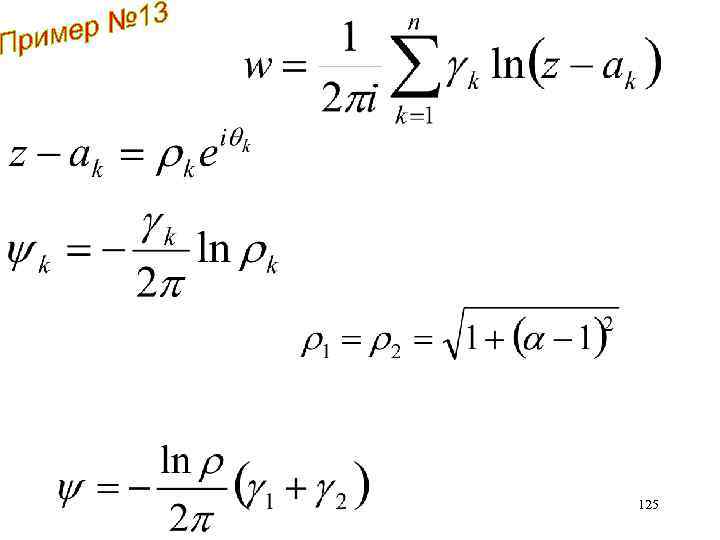
125
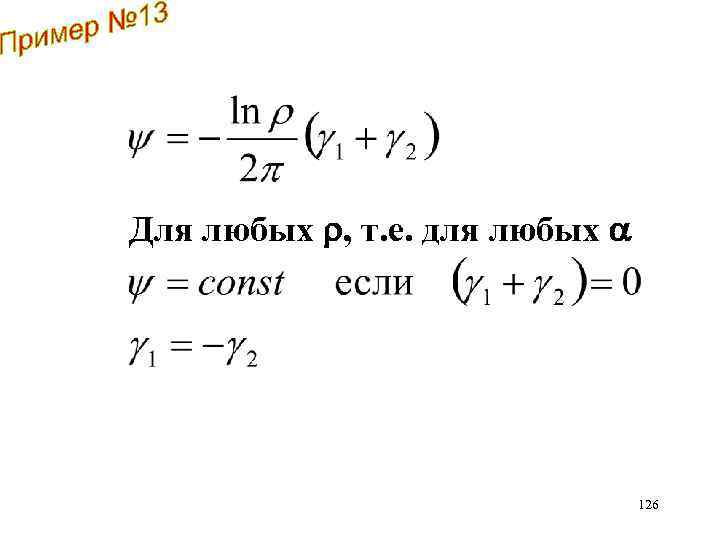
Для любых , т. е. для любых 126

1. Исследовать течение жидкости, которое описывается комплексным потенциалом 2. a, b - вещественные 127

Начало координат представляет собой особенность - совокупность вихревой точки интенсивности и источника мощностью m =(2 ) 128
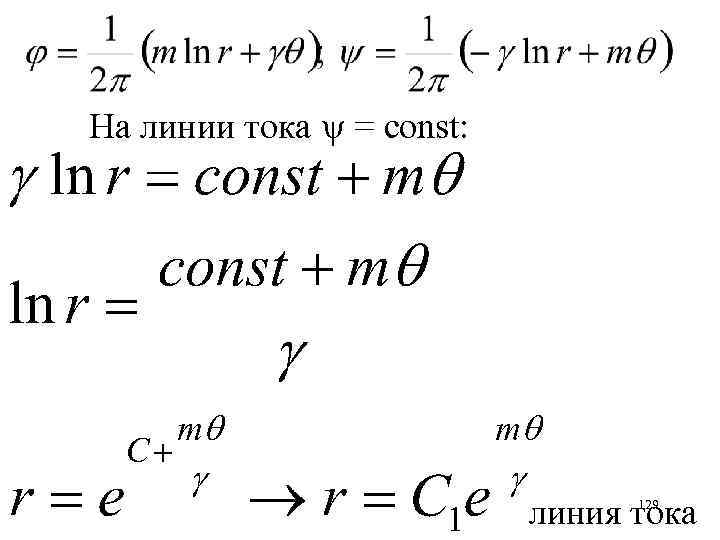
На линии тока = const: линия тока 129

линии тока линии равного потенциала = co t ns 130

131

Структура аналитической функции w(z) вполне определяется распределением на плоскости z особых точек функции и их характером. Теория вычетов позволяет выразить циркуляцию и поток скорости по любому контуру, если для комплексной скорости известны распределения простых полюсов и им соответствующие вычеты 132

Если простые полюсы функции U* лежат в точках z=a 1, z=a 2, …z=an и вычеты им соответствующие есть А 1, А 2, …Аn, то линейный интеграл от функции U* по замкнутому контуру L , заключающему полюсы в точках z=a 1, z=a 2, …z=an , дает 133

Циркуляция скорости Поток скорости через по контуру L контур L 134

Выделим действительную и мнимую часть каждого вычета Тогда получаем 135

136
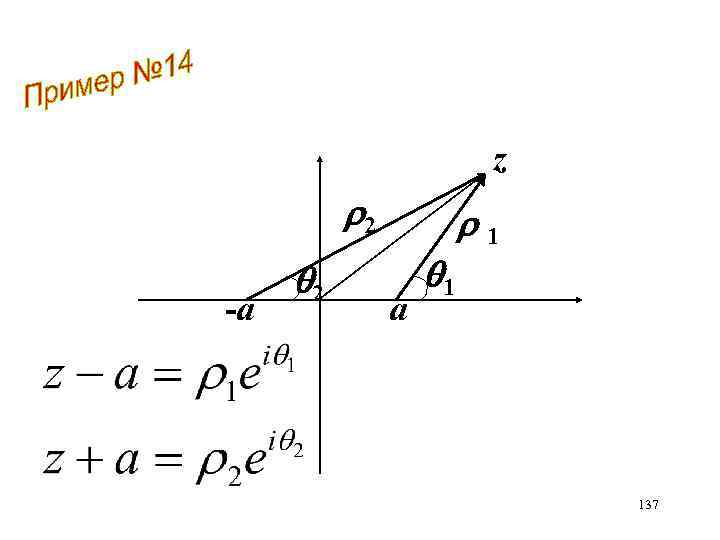
z 2 -а 2 а 1 1 137
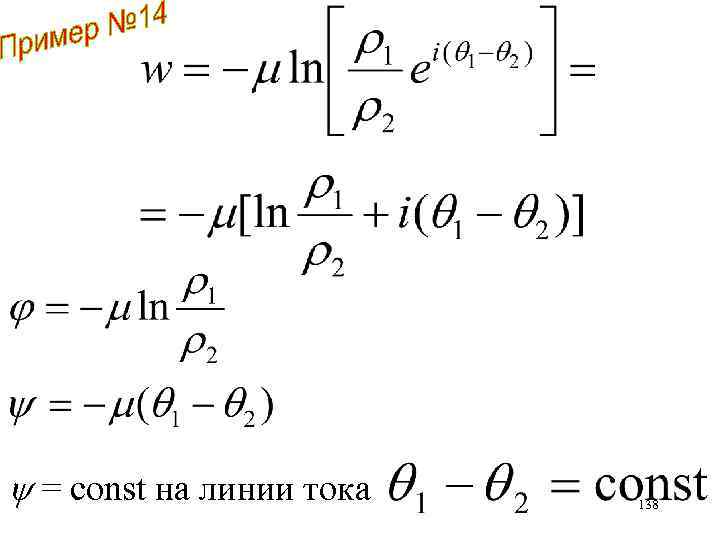
= const на линии тока 138

Линии тока z 1 -а 2 1 139
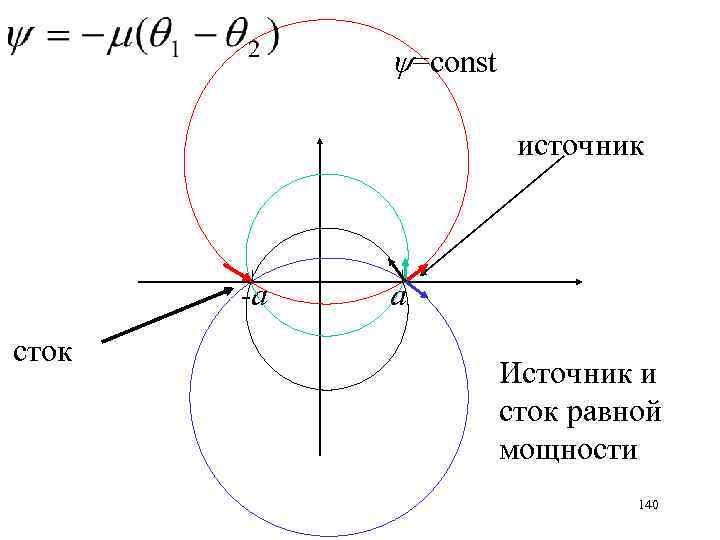
=const источник -а сток а Источник и сток равной мощности 140

141
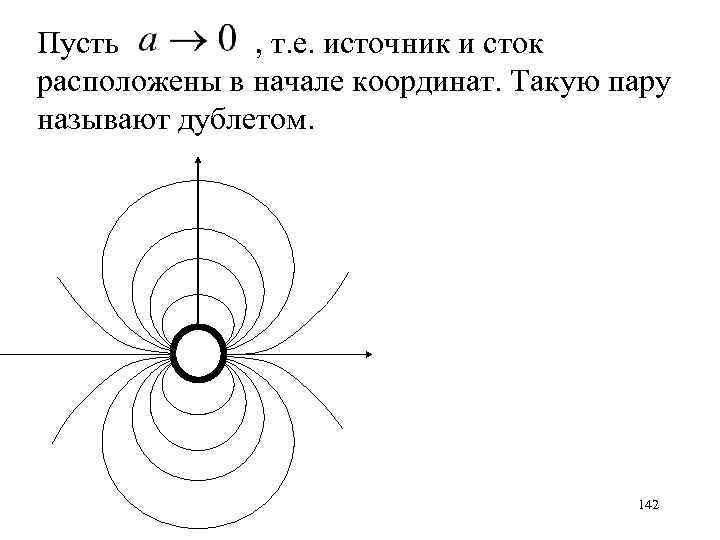
Пусть , т. е. источник и сток расположены в начале координат. Такую пару называют дублетом. 142

Пусть малое расстояние между источником и стоком будет обозначено s z r 1 1 2 r 2 s С точностью до малых величин второго порядка малости 143

Разлагаем в ряд При s 0 получаем для потенциала скорости Для сопряженной функции тока по формуле Получаем 144

Для комплексного потенциала получаем Если ось дублета s составляет угол с 0 х 145

Если на плоскости 0 ху в точках z = an помещены дублеты моменты которых равны Mn , а оси дублетов составляет угол n с вещественной осью 0 х, то комплексный потенциал определяется: 146

Дублет находится в точке z = a, где а > 0, вещественное. Определить поток жидкости через отрезок [z = 0, z = i] Определить горизонтальную составляющу скорости в точке z = i 147
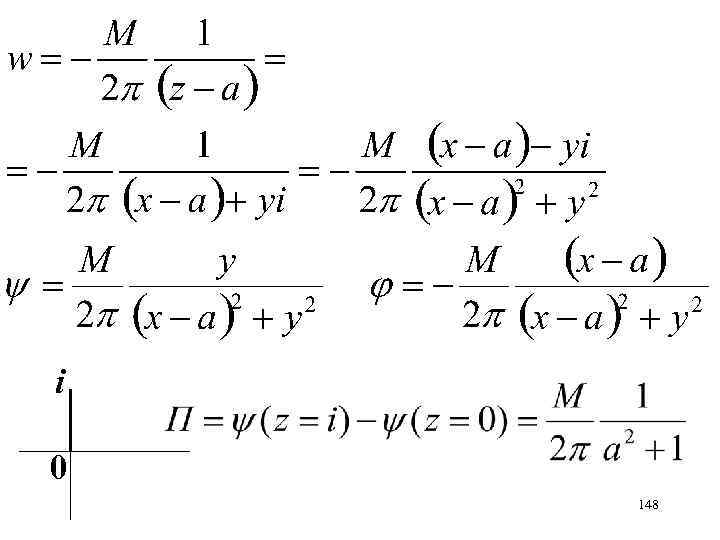
i 0 148
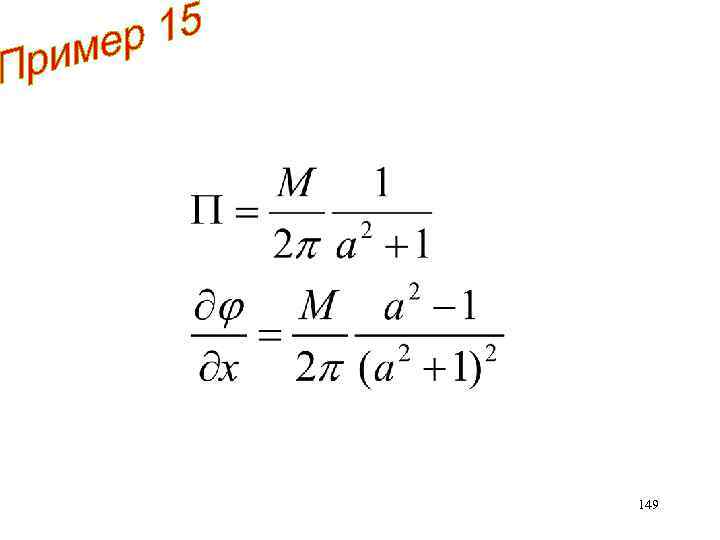
149
![Определить поток жидкости через отрезок [-a+i, a+i] 150 Определить поток жидкости через отрезок [-a+i, a+i] 150](https://present5.com/presentation/16510224_281517172/image-150.jpg)
Определить поток жидкости через отрезок [-a+i, a+i] 150

линии тока r 1 а с = 1 -а r 2 151
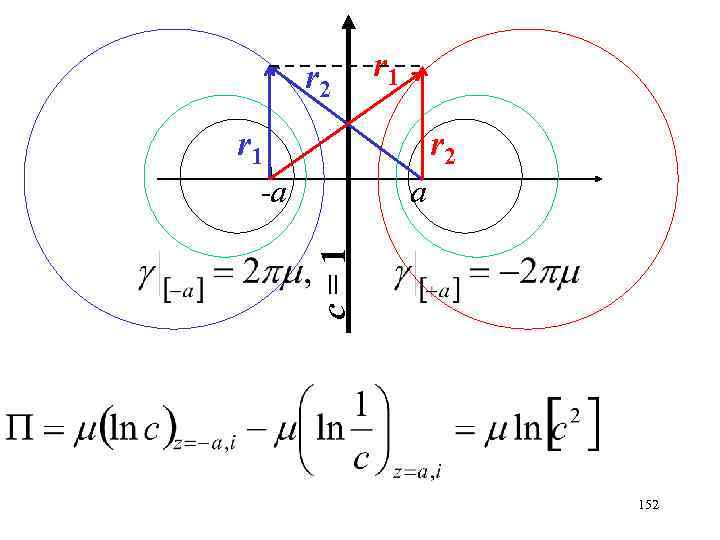
r 2 r 1 r 2 а с = 1 -а 152
153

Исследовать течение жидкости (плоское, безвихревое), которое описывается потенциалом скорости , с > 0 - вещественное Указать 2 линии тока Какой объем жидкости протекает в единицу времени через отрезок z 2 z 1 [z 1=0, z 2=1+i]? 154
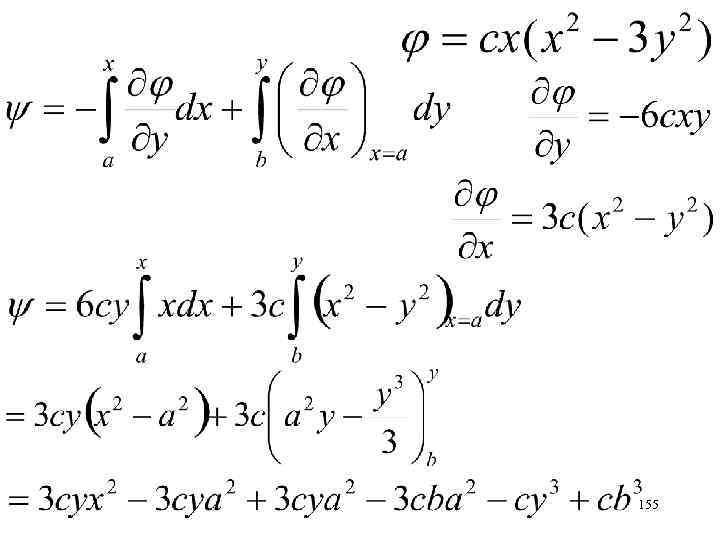
155
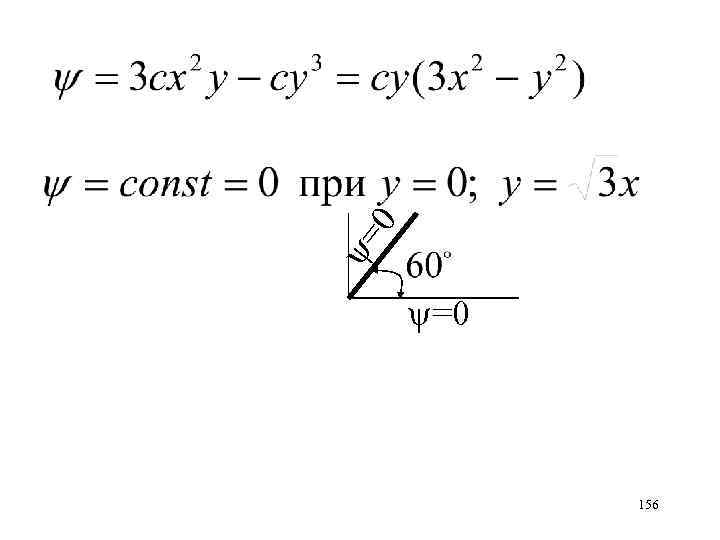
0 = =0 156
![[z 1=0, z 2=1+i] у 1 z 2 z 1 1 х 157 [z 1=0, z 2=1+i] у 1 z 2 z 1 1 х 157](https://present5.com/presentation/16510224_281517172/image-157.jpg)
[z 1=0, z 2=1+i] у 1 z 2 z 1 1 х 157

ЗАДАЧА 1 Найти линии тока, получить проекции скорости, посчитать поток через отрезок [z = 0, z = 1+31/2 i] 158
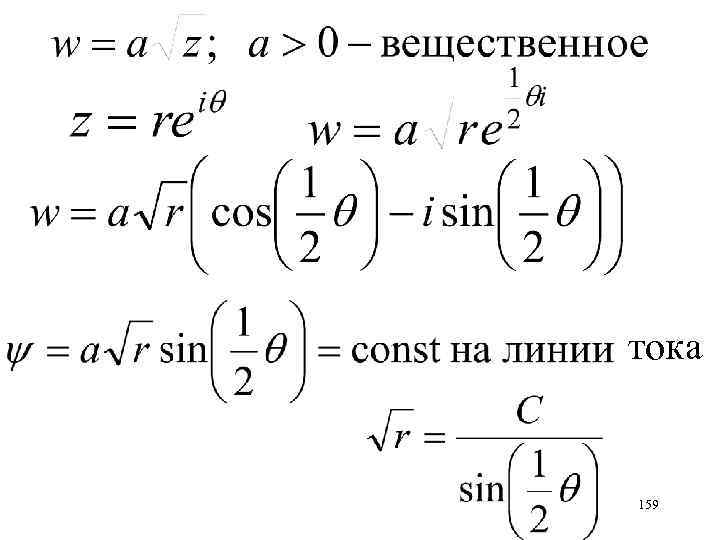
тока 159

160

ЗАДАЧА 2 Найти функцию тока. В каких точках находятся источники и стоки? Найти уравнение линий тока. Показать, что линиями тока являются оси координат и окружность r = 1. Какой объем жидкости протекает в единицу времени через отрезок [z 1=i, z 2=1/2]? 161

Источники в точках z 1=+1, z 2= -1; сток z = 0 162

Уравнение линий тока Линиями тока, в частности, являются оси координат и окружность 163

ЗАДАЧА 3 В верхней полуплоскости имеются 2 источника интенсивности m 1, m 2 и 2 вихря интенсивности 1, 2. Показать, что если поместить в сопряженных точках источники той же интенсивности, а вихри интенсивности ( - 1), (- 2), то вещественная ось будет линией тока. 164

Эти же формулы имеют место для источника, помещенного на одинаковом расстоянии от двух параллельных твердых стенок, имеющих координаты y х 165

-3 а -2 а а О а 2 а 3 а Источники одинаковой мощности на равном расстоянии 166

Задача Течение определяется потенциалом Найти поток жидкости через окружность И циркуляцию скорости по этой окружности 167
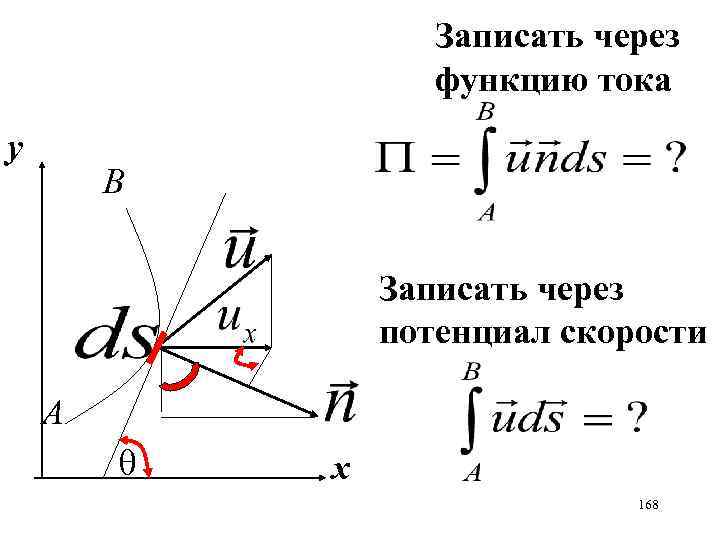
Записать через функцию тока у B Записать через потенциал скорости A х 168

169
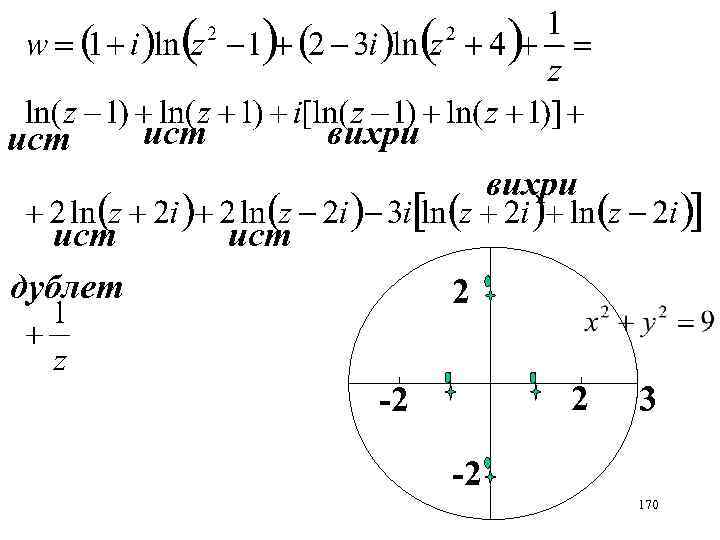
ист вихри ист дублет ист 2 2 -2 3 -2 170

вихри 171

ист 172

дублет 173

174
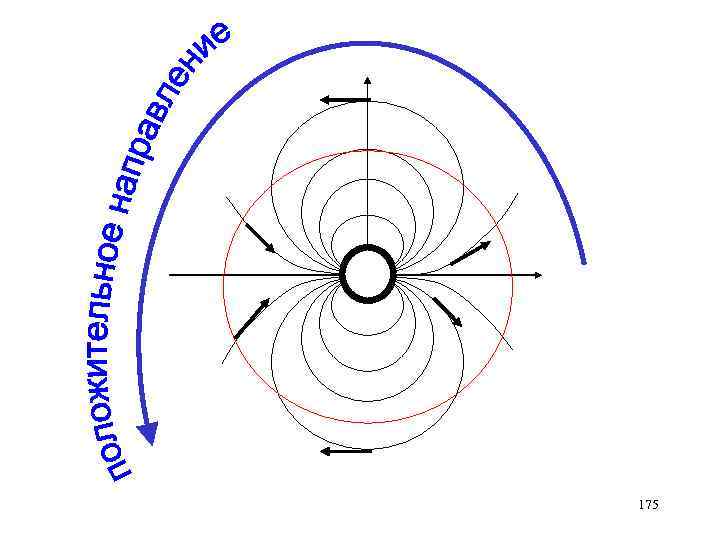
175

Поток массы (мощность источника), проходящий через окружность радиуса r в единицу времени, определяется произведением радиальной скорости на длину окружности Мощность источника 2 не зависит от радиуса (сохранение массы). Если <0, то определяет сток. 176
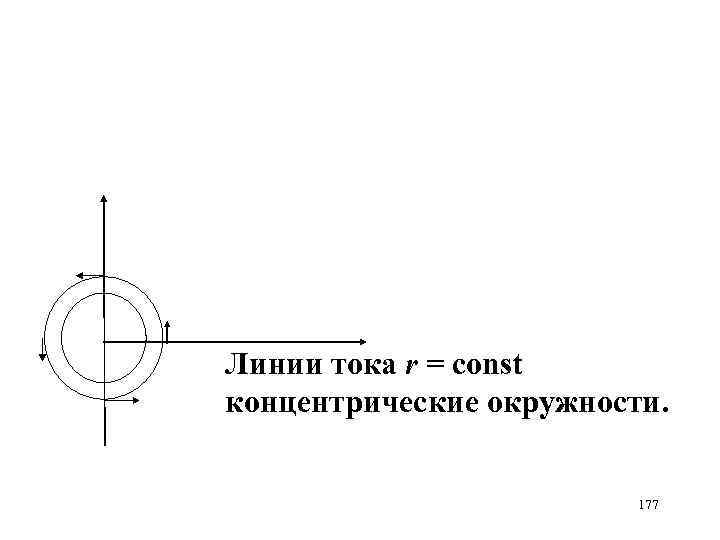
Линии тока r = const концентрические окружности. 177

Скорость: Циркуляция скорости по замкнутому контуру L: r L d. L Циркуляцию скорости назовем интенсивностью вихревой точки 178